The Marshall-Olkin length-biased exponential distribution and its applications

1 Introduction

Most of the statistical analyses deal with real life data sets under appropriate selection of models. The model selection is also an important issue for reliable estimation of the model parameters. Recently, some generalizations of the exponential distribution are proposed for modeling lifetime data due to some interesting properties such as “lack of memory” (Ristić and Kundu, 2015).

Many generalizations of the exponential distribution are developed in recent years such as the exponentiated exponential (Gupta and Kundu, 1999, 2001), generalized exponentiated moment exponential (Iqbal et al., 2014), extended exponentiated exponential (Abu-Youssef et al., 2015), Marshall-Olkin exponential Weibull (Pogány et al., 2015), Marshall-Olkin generalized exponential (Ristic and Kundu, 2015), and exponentiated moment exponential (Hasnain et al., 2015) distributions.

In the rest of the paper, we define the new model in Section 2, the statistical properties of the proposed distribution are discussed in Section 3, and estimation of parameters by using maximum likelihood estimation method is presented in Section 4. A simulation study and an application of proposed model on real life data set are provided in Section 5. In Section 6, concluding remarks are presented.

2 The new model

The weighted or moment distributions arise in the context of unequal probability sampling; have a great importance in reliability, biomedicine, and ecology, among others.

Dara and Ahmad (2012) proposed the moment exponential distribution (here we will call it Length-Biased Exponential (LBE) distribution) through assigning weight to the exponential distribution by following the idea of Fisher (1934). Dara and Ahmad (2012) proved that the LBE is more flexible than the exponential distribution.

The Probability Density Function (PDF) and Cumulative Distribution Function (CDF) of LBE distribution are;

The procedure of adding one or two shape parameters to a family of distributions for getting more flexibility is a well-known technique in the literature. Marshall and Olkin (1997) proposed a simple method of adding a shape parameter into a family of distributions. Considering a baseline CDF, $G(x)$ , of a random variable $X$ , then the CDF of the Marshall and Olkin-G (MO-G) family of distributions is

The corresponding PDF (3) is given by

The major motivation of the MO family is given as follows: Let $Z_N=\mathit{min}\{T_1\text{,}\dots \text{,}{T}_N\}\text{,}$ where $T_1\text{,}\dots \text{,}{T}_N$ are a sequence of IID random variables from $G(x)$ and $N$ is a random variable with probability mass function $\gamma (1-{\gamma }^{n-1})\text{,}n=1\text{,}2\text{,}\dots$ . Then, the CDF of $Z_N$ is defined by; $$P(Z_N⩽x)=1-{\displaystyle \sum _{n=1}^{\infty }}P(Z_N⩽x|N=n)P(N=n)=\frac{G(x)}{G(x)+\gamma \overline{G}(x)}\text{,}$$ which is equivalent to (3).

Several authors used the MO-G family to extend well-known distributions in the last few years for getting more flexible models. For example, the extended Weibull distribution (Marshall and Olkin, 1997), MO Weibull (Ghitany et al., 2005), MO Pareto (Ghitany, 2005), MO gamma (Ristic et al., 2007), MO Lomax (Ghitany et al., 2007), MO linear failure-rate (Ghitany and Kotz, 2007), MO log-logistic (Gui, 2013), MO Frechet (Krishna et al., 2013) and MO exponential Weibull (Pogány et al., 2015) distributions.

In this article, we proposed a new extension of the LBE distribution called the Marshall Olkin Length-Biased Exponential (MOLBE) distribution. In fact, the new model is constructed using the MO family of distributions. A comprehensive description of some of its mathematical properties with the hope that it will attract wider applications in reliability, engineering and other areas of research is provided. It is justified that the MOLBE distribution can provide good fits for a real life data set.

The new distribution can be defined by inserting Eq. (2) in Eq. (3). Then, the CDF of the MOLBE model, say $F(x)=F(x\text{;}\gamma \text{,}\beta )$ is;

By putting Eqs. (1) and (2) in Eq. (4), we obtain the PDF of the MOLBE distribution

For $\gamma =1$ , the MOLBE reduces to the LBE distribution.

The Survival Function (SF) and the Hazard Rate Function (HRF) of X are; $$S(x)=\frac{\gamma \left(1+\frac{x}{\beta }\right)\text{exp}(-x/\beta )}{1-(1-\gamma )\left(1+\frac{x}{\beta }\right)\text{exp}(-x/\beta )}$$ and $$h(x)=\frac{\frac{x}{{\beta }^2}}{\left(1+\frac{x}{\beta }\right)\left[1-(1-\gamma )\left(1+\frac{x}{\beta }\right)\text{exp}(-x/\beta )\right]}\text{.}$$

By using the following generalized binomial expansion and the power series (for), $${(1-a)}^{-n}={\displaystyle \sum _{k=0}^{\infty }}\frac{\mathrm{\Gamma }(n+k)}{\mathrm{\Gamma }(n)\mathrm{\Gamma }(k+1)}{a}^k\text{and}{(1+z)}^b={\displaystyle \sum _{j=0}^{\infty }}\left(\begin{array}{c}\hfill b\hfill \\ \hfill j\hfill \end{array}\right)z^j\text{,}|Z|>0\text{,}$$

Ay useful linear representation for the PDF of Eq. (6) is;

A simple motivation of the MOLBE distribution follows by considering a parallel system with $Z$ independent components and suppose that a random variable $Z$ has the geometric distribution with the probability mass function $P(Z=z)={\gamma }^{-1}{(1-{\gamma }^{-1})}^{z-1}\text{,}z=1\text{,}2\text{,}\dots$ and. $\gamma >1$ Let $X_1\text{,}{X}_2\text{,}\dots$ represent the lifetimes of each component and suppose that they have the LBE distribution given in (1). Then a random variable $T=\mathit{max}(X_1\text{,}\dots \text{,}{X}_z)$ represents the lifetime of the system. Therefore, the random variable $T$ follows the MOLBE in (5).

Figs. 1 and 2 show some possible shapes of the PDF, and HRF of the MOLBE distribution for selected values of parameters.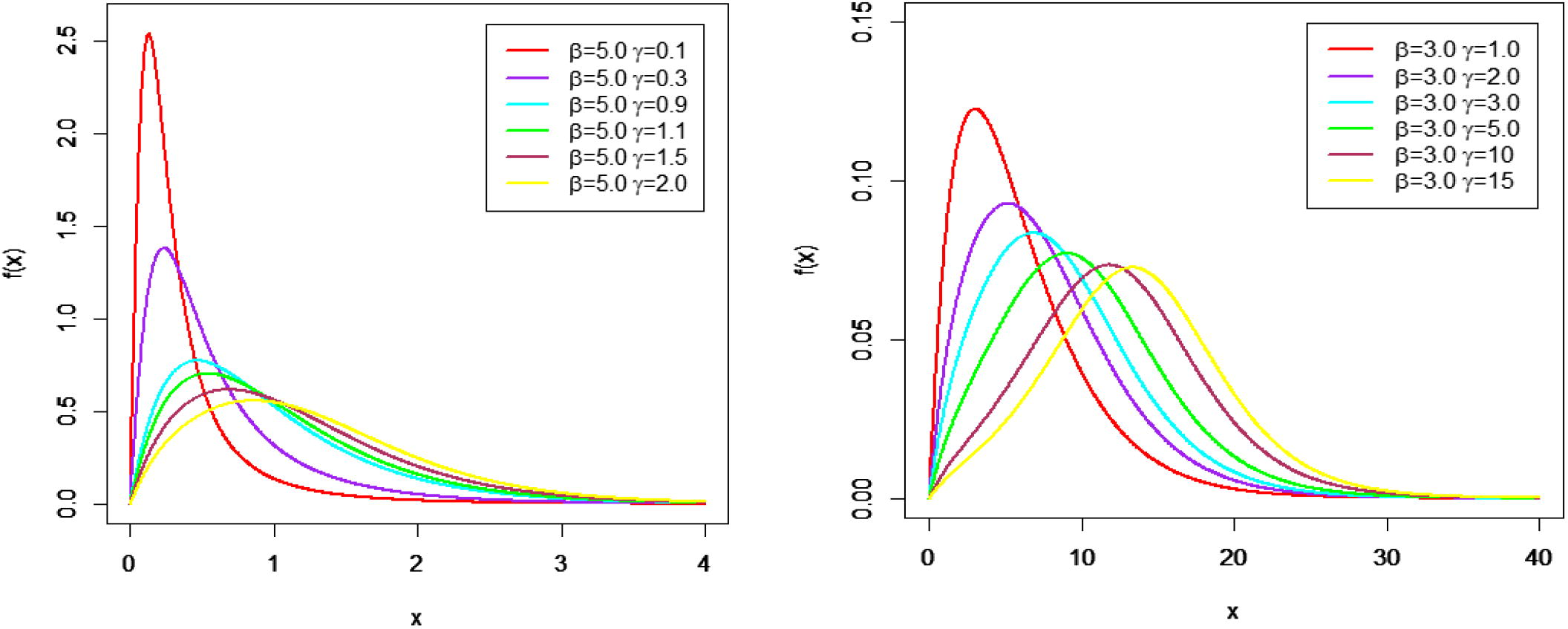

Close

Fig. 1

Graph for MO-ME density function at different parameter values.

Export to PPT

Close

Fig. 2

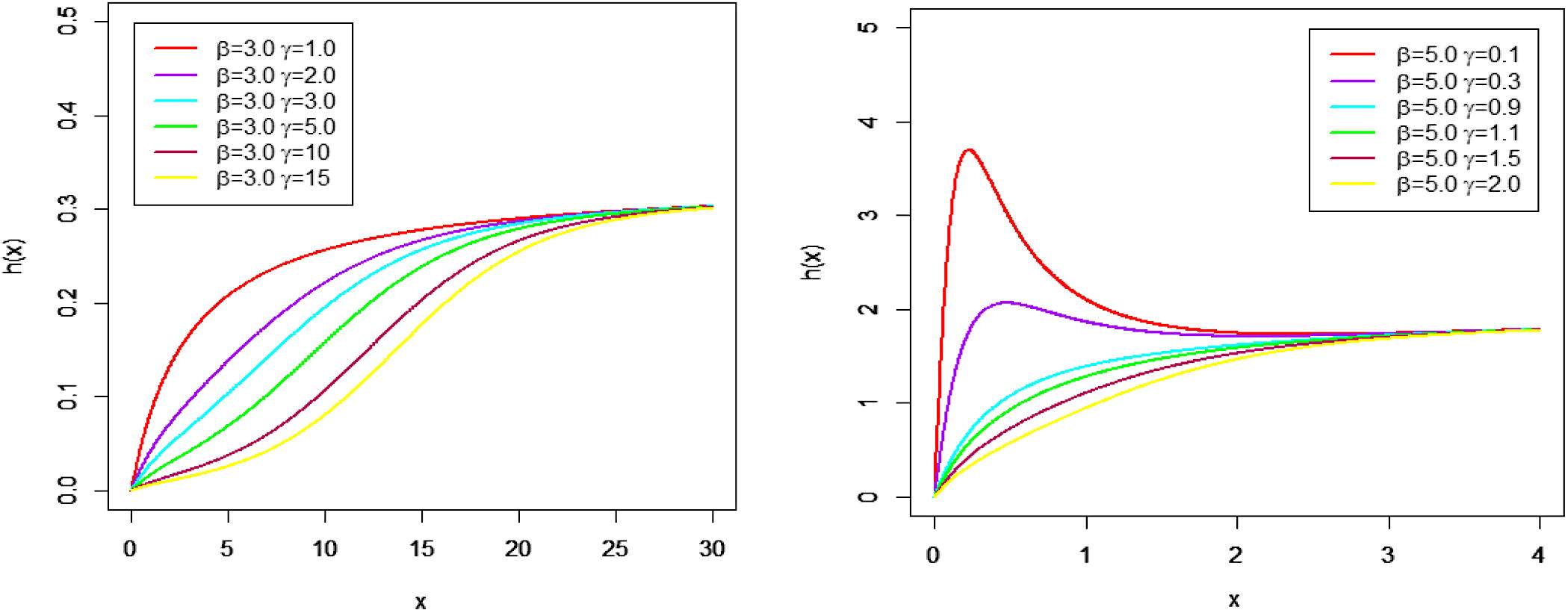
Graph for hazard rate function at different parameter values.

Export to PPT

Fig. 1 shows the unimodal behavior for the density of the MOLBE distribution with various choices of parameters. Fig. 2 shows that the HRF of the MOLBE model can be increasing or unimodal.

3 Mathematical properties

In this section, some fundamental properties of MOLBE distribution including moments, generating function, incomplete moments, entropies, mean residual life and mean inactivity time are presented.

3.1

3.1 Moments

The th moment of is defined by; $${\mu }_r^{\prime }={\int }_0^{\infty }{x}^{r}f(x\text{;}\gamma \text{,}\beta )\mathit{dx}\text{.}$$

Using (7), we can write $$\begin{array}{cc}{\mu }_r^{\prime }\hfill & =\gamma {\displaystyle \sum _{k\text{,}j=0}^{\infty }}\frac{(k+1){(1-\gamma )}^k}{{\beta }^{j+2}}\left(\begin{array}{c}\hfill k\hfill \\ \hfill j\hfill \end{array}\right){\int }_0^{\infty }{x}^{j+r+1}{e}^{-(k+1)\frac{x}{\beta }}\mathit{dx}\hfill \\ \hfill & =\gamma {\displaystyle \sum _{k\text{,}j=0}^{\infty }}\frac{(k+1){(1-\gamma )}^k}{{\beta }^{j+2}}\left(\begin{array}{c}\hfill k\hfill \\ \hfill j\hfill \end{array}\right){\int }_0^{\infty }\frac{z^{j+r+1}{\beta }^{j+r+1}}{{(k+1)}^{j+r+1}}{e}^{-z}\frac{\beta }{(k+1)}\mathit{dz}\text{.}\hfill \end{array}$$

After some algebra, we have $${\mu }_r^{\prime }=\gamma {\displaystyle \sum _{k\text{,}j=0}^{\infty }}\frac{{(1-\gamma )}^k{\beta }^r}{{(k+1)}^{j+r+1}}\left(\begin{array}{c}\hfill k\hfill \\ \hfill j\hfill \end{array}\right)\mathrm{\Gamma }(j+r+2)\text{.}$$

The moment generating function of $X$ is defined by $$M_x(t)={\int }_0^{\infty }{e}^{\mathit{tx}}f(x\text{;}\gamma \text{,}\beta )\mathit{dx}=\gamma {\displaystyle \sum _{k\text{,}j=0}^{\infty }}\frac{(k+1){(1-\gamma )}^k}{{\beta }^{j+2}}\left(\begin{array}{c}\hfill k\hfill \\ \hfill j\hfill \end{array}\right){\int }_0^{\infty }{x}^{j+1}{e}^{-(k+1-\beta t)\frac{x}{\beta }}{e}^{\mathit{tx}}\mathit{dx}\text{.}$$

Thus, we have $$M_x(t)=\gamma {\displaystyle \sum _{k\text{,}j=0}^{\infty }}\frac{(k+1){(1-\gamma )}^k}{{(k+1-\beta t)}^{j+2}}\left(\begin{array}{c}\hfill k\hfill \\ \hfill j\hfill \end{array}\right)\mathrm{\Gamma }(j+2)\text{.}$$ The effects of the parameters on the mean, variance, skewness and kurtosis are displayed in Figs. 3 and 4, respectively.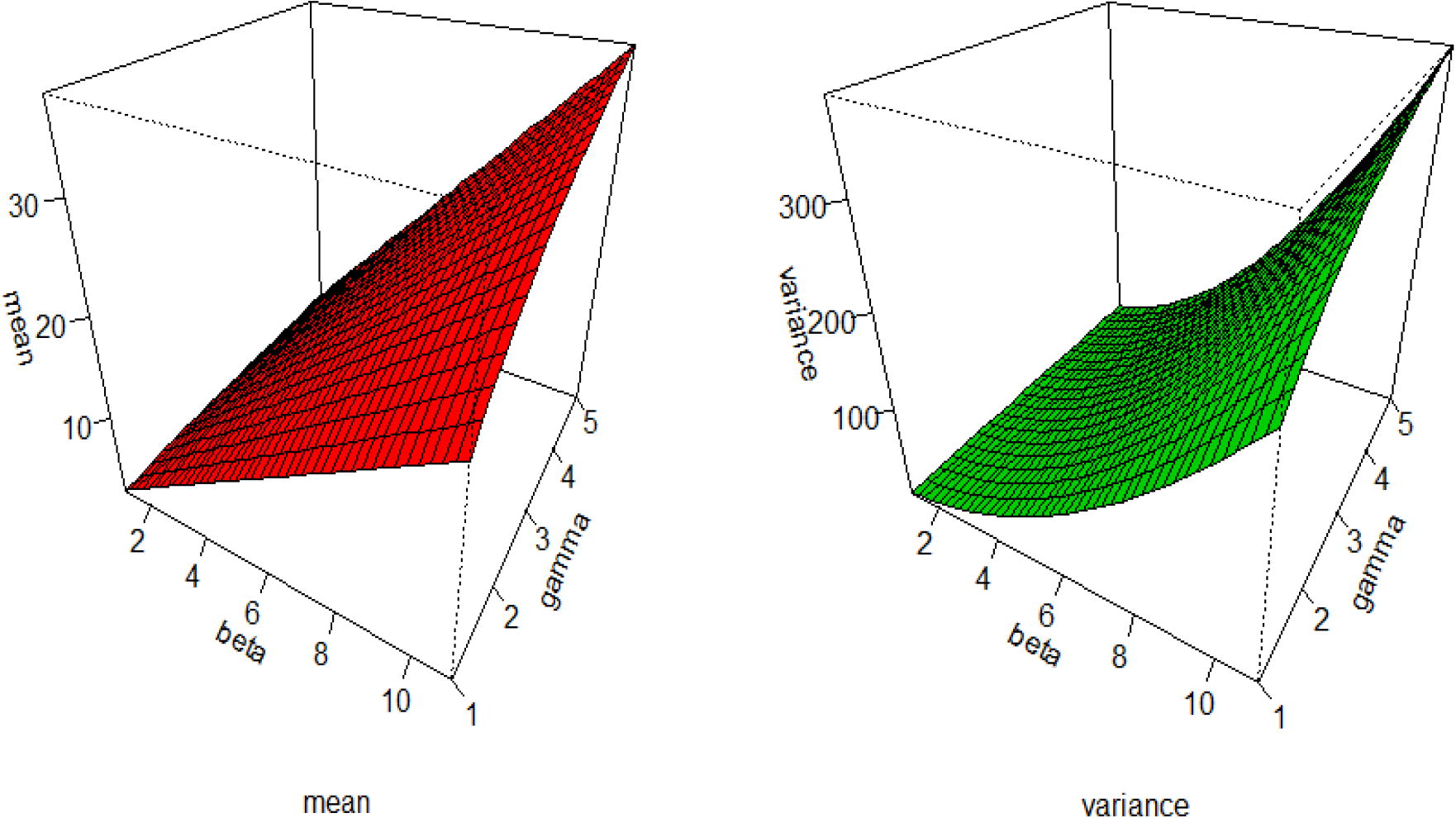

Close

Fig. 3

Plots of the mean and variance for the MOLBE distribution.

Export to PPT

Close

Fig. 4

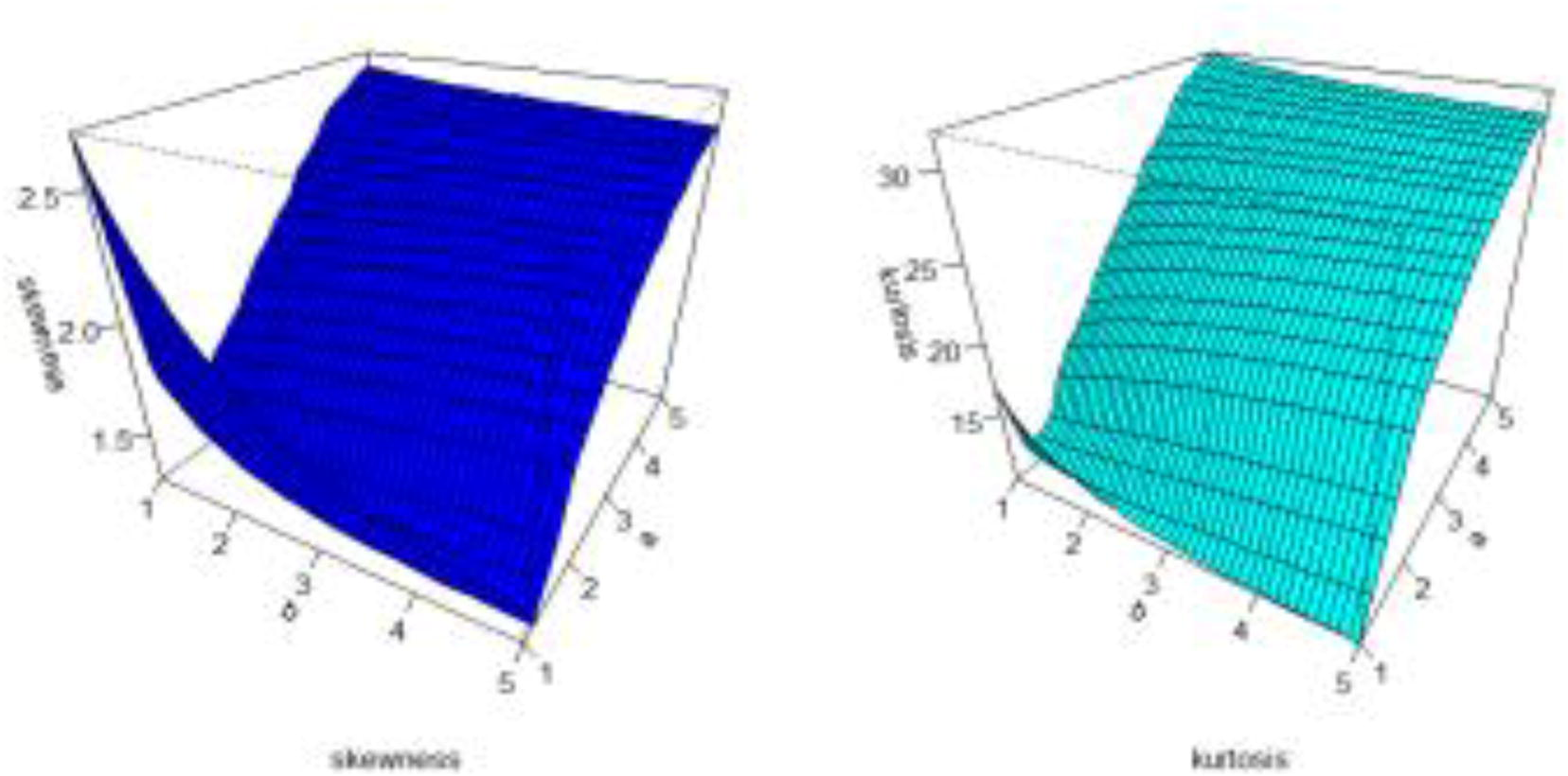
Plots of the skewness and kurtosis for the MOLBE distribution.

Export to PPT

The rth incomplete moment of $X$ is defined by $${\phi }_r(t)={\int }_0^t{x}^{r}f(x\text{;}\gamma \text{,}\beta )\text{d}x\text{.}$$

Based on Eq. (7), we obtain $$\begin{array}{cc}{\phi }_r(t)\hfill & =\gamma {\displaystyle \sum _{k\text{,}j=0}^{\infty }}\frac{(k+1){(1-\gamma )}^k}{{\beta }^{j+2}}\left(\begin{array}{c}\hfill k\hfill \\ \hfill j\hfill \end{array}\right){\int }_0^t{x}^{j+r+1}{e}^{-(k+1)\frac{x}{\beta }}\mathit{dx}\hfill \\ \hfill & =\gamma {\displaystyle \sum _{k\text{,}j=0}^{\infty }}\frac{{(1-\gamma )}^k{\beta }^r}{{(k+1)}^{j+r+1}}\left(\begin{array}{c}\hfill k\hfill \\ \hfill j\hfill \end{array}\right){\int }_0^t{z}^{j+r+1}{e}^{-z}\mathit{dz}\text{.}\hfill \end{array}$$

Then, the rth incomplete moment of $X$ reduces to

(8)

$${\phi }_r(t)=\gamma {\displaystyle \sum _{k\text{,}j=0}^{\infty }}\frac{{(1-\gamma )}^k{\beta }^r}{{(k+1)}^{j+r+1}}\left(\begin{array}{c}\hfill k\hfill \\ \hfill j\hfill \end{array}\right)\gamma (j+r+2\text{,}t)\text{,}$$ where $\gamma (j+r+2\text{,}x)$ is the lower incomplete gamma function.

4 Estimation

In this section, the unknown parameters of the MOLBE distribution are estimated by using the maximum likelihood method. Let $x_1\text{,}{x}_2\text{,}\dots \dots x_n$ be a random sample of size $n$ from the MOLBE distribution and let $\mathit{\rho }={(\gamma \text{,}\beta )}^T$ be the vector of parameters. The likelihood function for the MOLBE distribution is; $$L(x_1\text{,}{x}_2\text{,}\dots x_n\text{;}\mathit{\rho })=\frac{{\gamma }^n}{{\beta }^{2n}}{\displaystyle \prod _{i=1}^n}{x}_i\text{exp}(-x_i/\beta ){[1-(1-\gamma )(1+\frac{x_i}{\beta })\text{exp}(-x_i/\beta )]}^{-2}\text{.}$$

The log-likelihood function, $\ell (\mathit{\rho })\text{,}$ reduces to $$\ell (\mathit{\rho })=n\log \gamma -2n\log \beta +{\displaystyle \sum _{i=0}^n}{x}_i-{\displaystyle \sum _{i=0}^n}\frac{x_i}{\beta }-2{\displaystyle \sum _{i=0}^n}\log \left[1-(1-\gamma )\left(1+\frac{x_i}{\beta }\right)\text{exp}(-x_i/\beta )\right]\text{.}$$

The score vector components, $U(\mathit{\rho })=(\partial \ell (\mathit{\rho })/\partial \gamma \text{,}\partial \ell (\mathit{\rho })/\partial \beta )$ , are given by $$\frac{\partial \ell (\mathit{\rho })}{\partial \gamma }=\frac{n}{\gamma }-2{\displaystyle \sum _{i=0}^n}\frac{\left(1+\frac{x_i}{\beta }\right)\text{exp}(-x_i/\beta )}{1-(1-\gamma )\left(1+\frac{x_i}{\beta }\right)\text{exp}(-x_i/\beta )}$$

and $$\frac{\partial \ell (\mathit{\rho })}{\partial \beta }=\frac{-2n}{\beta }+{\displaystyle \sum _{i=0}^n}\frac{x_i}{{\beta }^2}-2{\displaystyle \sum _{i=0}^n}\frac{(1-\gamma )\frac{x_i}{{\beta }^2}\left(2+\frac{x_i}{\beta }\right)\text{exp}(-x_i/\beta )}{1-(1-\gamma )\left(1+\frac{x_i}{\beta }\right)\text{exp}(-x_i/\beta )}\text{.}$$

The complicated system of nonlinear equations obtained from $U(\mathit{\rho })=0$ can be solved using numerical Newton–Raphson type methods. However, it is much simpler to maximize the log-likelihood function directly by means of the R (optim function), SAS (PROC NLMIXED), Mathcad or Ox program (sub-routine MaxBFGS).

5 Data analysis

In this section, some simulation results are provided to observe the behavior of the MLEs in terms of the sample size $n$ . The importance of the MOLBE distribution using real data is also illustrated.

5.2

5.2 Application

In this section, the importance and flexibility of the new distribution is illustrated by using a real life data set. The data represent the tensile strength of 100 carbon fibers (Flaih et al., 2012). The data are: 3.7, 3.11, 4.42, 3.28, 3.75, 2.96, 3.39, 3.31, 3.15, 2.81, 1.41, 2.76, 3.19, 1.59, 2.17, 3.51, 0.84, 1.61, 1.57, 1.89, 2.74, 3.27, 2.41, 3.09, 2.43, 2.53, 2.81, 3.31, 2.35, 2.77, 2.68, 4.91, 1.57, 2.00, 1.17, 2.17, 0.39, 2.79, 1.08, 2.88, 2.73, 2.87, 3.19, 1.87, 2.95, 2.67, 4.20, 2.85, 2.55, 2.17, 2.97, 3.68, 0.81, 1.22, 5.08, 1.69, 3.68, 4.70, 2.03, 2.82, 2.50, 1.47, 3.22, 3.15, 2.97, 2.93, 3.33, 2.56, 2.59, 2.83, 1.36, 1.84, 5.56, 1.12, 2.48, 1.25, 2.48, 2.03, 1.61, 2.05, 3.60, 3.11, 1.69, 4.90, 3.39, 3.22, 2.55, 3.56, 2.38, 1.92, 0.98, 1.59, 1.73, 1.71, 1.18, 4.38, 0.85, 1.80, 2.12, 3.65.

We shall compare the fits of the MOLBE model with other seven models namely:

1. The Exponential (E) distribution (Nadarajah and Kotz, 2006) with CDF given by $$F(x)=1-e^{-\frac{x}{\beta }}\text{,}x>0\text{,}\beta >0\text{.}$$

2. The Marshall-Olkin extended exponential (MOEE) distribution (Srivastava et al., 2011) with CDF given by $$F(x)=\frac{1-e^{-\beta x}}{1-(1-\gamma )e^{-\beta x}}\text{,}x>0\text{,}\beta \text{,}\gamma >0\text{.}$$

3. The Exponentiated Exponential (EE) distribution (Gupta and Kundu, 2001) with CDF given by $$F(x)={(1-e^{-\beta x})}^{\alpha }\text{,}x>0\text{,}\beta \text{,}\alpha >0\text{.}$$

4. Moment Exponential (ME) distribution (Dara and Ahmad, 2012) with CDF given by $$F(x)=1-\left(1+\frac{x}{\beta }\right)e^{-\frac{x}{\beta }}\text{,}x>0\text{,}\beta >0\text{.}$$

5. Exponentiated Moment exponential (EME) (Hasnain et al., 2015) with CDF given by $$F(x)={\left[1-\left(1+\frac{x}{\beta }\right)e^{-\frac{x}{\beta }}\right]}^{\alpha }\text{,}x>0\text{,}\beta \text{,}\alpha >0\text{.}$$

The fitted models are assessed based on some goodness-of-fit statistics named: the Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), Cramér-von Mises (W), Anderson–Darling (AD) and the maximized log-likelihood ( $\ell$ ).

Tables 2 and 3 provide the MLEs of the model parameters and goodness-of-fit measures, respectively. Fig. 5 shows the fitted densities and estimated CDF of the MOLBE distribution.

Table 2 MLEs for the real data set.

Distribution	Estimated Parameters
	$\alpha$	$\gamma$	$\beta$
MOLBE	–	23.77	0.515922
E	–	–	0.382936
BE	5.99635	191.696	0.0118252
MOEE	–	77.7225	1.69322
EE	7.878	–	1.021
ME	–	–	1.3057
EME	3.51349	–	0.775339

Table 3 Some goodness-of-fit measures.

Distribution	AIC	BIC	$\ell$	A	W
MOLBE	285.956	291.166	−140.978	1.09176	0.21034
E	393.977	396.582	−195.989	17.5557	3.48081
BE	291.056	298.871	−142.528	0.77823	0.15443
MOEE	286.720	291.930	−141.360	0.39549	0.06058
EE	294.910	300.120	−145.455	1.25447	0.23611
ME	333.857	336.462	−165.928	8.14797	1.45650
EME	292.749	297.959	−144.374	1.09176	0.21035

Close

Fig. 5

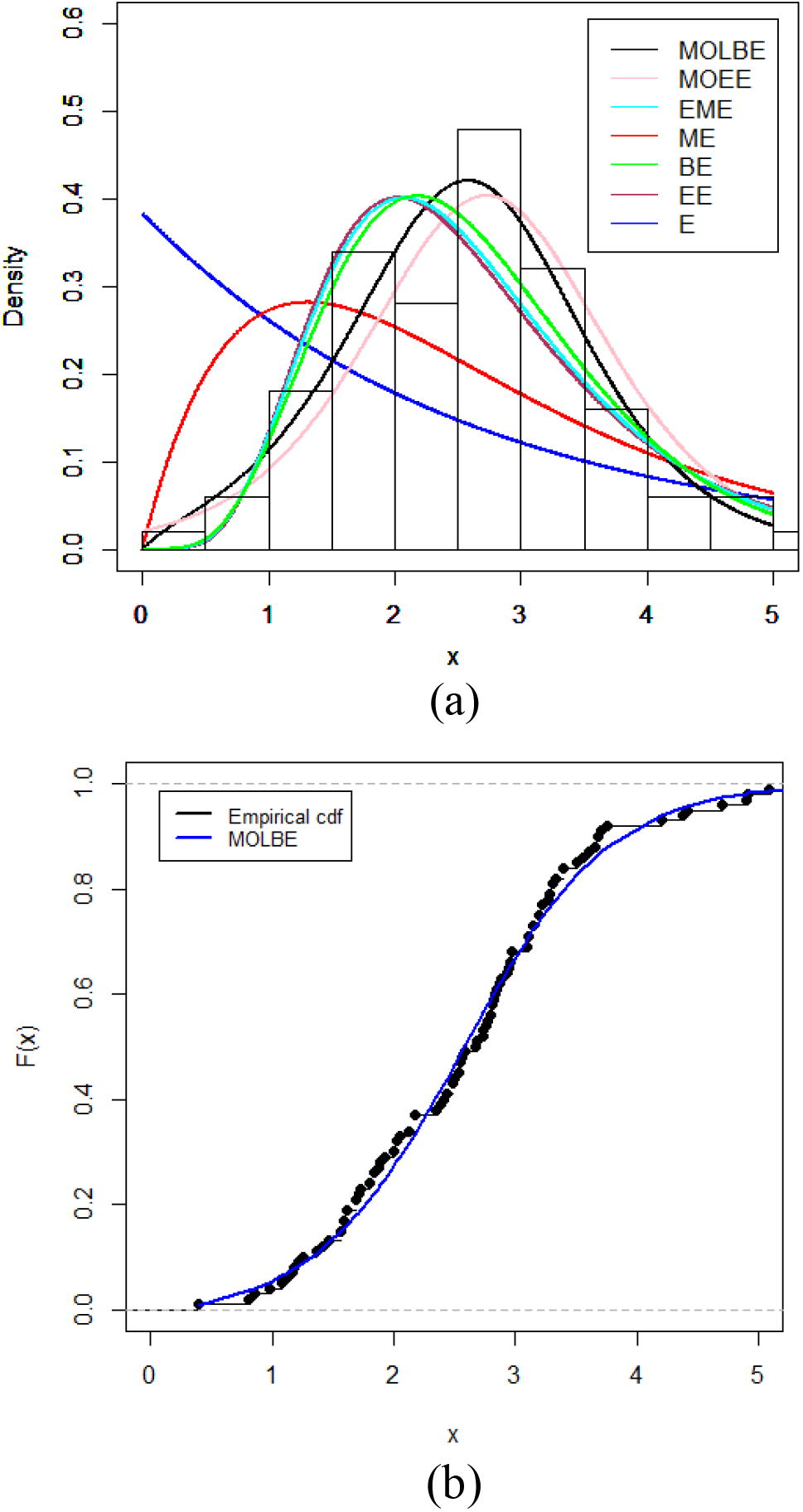
(a) Fitted densities of the MOLBE distribution and other competitive models. (b) Estimated cdf of the MOLBE model and the empirical cdf for the data.

Export to PPT

It is clear, from the figures in Table 3 and the plots in Fig. 5, that the MOLBE and MOEE distributions provide good fits to these data. Thus, the MOLBE and MOEE distributions are potential competitors.

6 Conclusions

In this paper, the two-parameter Marshall-Olkin length-biased exponential (MOLBE) distribution is proposed which extends the length-biased exponential (LBE) distribution pioneered by Dara and Ahmad (2012). The mathematical properties of the MOLBE distribution are derived including ordinary and incomplete moments, generating function, entropies, mean residual life and mean inactivity time. The estimation of the model parameters based on MLE are also discussed. The proposed distribution is applied to a real life data set. It provides a better fit than several other competitive models. It is inferred that MOLBE distribution will provide a superior fit to the wider range of applications in statistics.