Solitary waves solutions of the MRLW equation using quintic B-splines

K.R. Raslan; Talaat S. EL-Danaf

doi:10.1016/j.jksus.2010.04.004

View/Download PDF

Buy Reprints

PDF

Translate this page into:

ORIGINAL ARTICLE

22 (

); 161-166

doi:

10.1016/j.jksus.2010.04.004

Solitary waves solutions of the MRLW equation using quintic B-splines

K.R. Raslan^a,c,*, Talaat S. EL-Danaf^b

a Community College in Riyadh, King Saud University, Saudi Arabia

b Mathematics Department, Faculty of Science, Menoufia University, Shebein El-Koom, Egypt

c Mathematics Department, Faculty of Science, Al-Azhar University, Nasr-City, Cairo, Egypt

*Corresponding author at: Community College in Riyadh, King Saud University, Saudi Arabia kamal_raslan@yahoo.com (K.R. Raslan)

Received: 2010-3-23, Accepted: 2010-4-13, Published: 2010-07-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Abstract

In this paper, B-spline finite element method is used to solve the Modified Regularized Long Wave (MRLW) equation. The proposed approach involves a collocation method using quintic B-splines at the knot points as element shape. Time integration of the resulting system of ordinary differential equation is effected using the fourth order Runge–Kutta method, instead of the difference method. The resulting system of ordinary differential equations is integrated with respect to time. Three invariants of motion are evaluated to determine the conservation properties of the suggested scheme. The suggested numerical scheme leads to accurate and efficient results. Moreover, interaction two and three solitary waves are studied through computer simulation and the development of the Maxwellian initial condition into solitary waves is also shown.

Keywords

MRLW

B-splines

Solitons

Collocation method

Show Related Articles from PubMed

1 Introduction

Solitary waves are wave packets or pulses, which propagate in nonlinear dispersive media. Due to dynamical balance between the nonlinear and dispersive effects these waves retain a stable waveform. The Regularized Long Wave (RLW) equation of the form:

(1)

u_{t} + u_{x} + {uu}_{x} - δ u_{xxt} = 0,

where

δ

is a positive constant, was originally introduced to describe the behavior of the undular bore by Peregrine (1966). This equation is very important in physics media since it describes phenomena with weak nonlinearity and dispersion waves, including nonlinear transverse waves in shallow water, ion-acoustic and magneto hydrodynamic waves in plasma and phonon packets in nonlinear crystals. The solutions of this equation are kinds of solitary waves named solitons whose shape is not affected by a collision. RLW equation was solved numerically by various forms of finite element methods (Alexander and Morris, 1979; Gardner and Gardner, 1990; Gardner et al., 1995, 1996; Dag, 2000; Khalifa et al., 1979; Soliman and Raslan, 2001; Dag et al., 2004; Raslan, 2005; Soliman and Hussien, 2005 ) such as Galerkin method, least square method and collocation method with quadratic B-splines, cubic B-splines and recently septic splines. Indeed, the RLW equation is special case of the Generalized Long Wave (GRLW) equation, which has the form:

(2)

u_{t} + u_{x} + μ u^{p} u_{x} - δ u_{xxt} = 0,

where

μ

and δ are positive constants and p is a positive integer. The GRLW equation is studied by authors Zhang (2005) with finite difference method for a Cauchy problem and Kaya and El-Sayed (2003) with adomian decomposition method (ADM). Also, there are other studies on RLW, EWE, and GRLW equations (Ramos, 2007; Lu, 2008; Ramos, 2007; Soliman and Abdou, 2007; Shivamoggi, 2002 ). In this paper, we consider another special case of the GRLW which is called the Modified Regularized Long Wave (MRLW) equation. This equation was considered by Gardner et al. (1997) using Petrov–Galerkin method with quintic B-splines finite element. Here, a collocation method with quintic B-spline finite elements and uses the fourth order Runge–Kutta method to solve the system of first order ordinary differential equations instead of the finite difference method (Dag, 2000; Khalifa et al., 1979; Soliman and Raslan, 2001; Dag et al., 2004; Raslan, 2005; Soliman and Hussien, 2005; Zhang, 2005; Ramadan et al., 2005; El-Danaf et al., 2005; Hereman et al., 1986 ) which are accurate and efficient. The interaction of solitary waves and other properties of the MRLW equation are also studied.

2 The Governing equation and direct algebraic method (Gardner et al., 1997; Khalifa et al., 2007a,b; Hereman et al., 1986; Raslan, 2008 )

Consider the MRLW equation of the form

(3)

u_{t} + u_{x} + 6 u^{2} u_{x} - u_{xxt} = 0, a ⩽ x ⩽ b, t ⩾ 0,

where the subscripts

x and t

denote differentiation, is considered with the boundary conditions

u \to 0 as x \to \pm \infty

. In this work, periodic boundary conditions on the region

a ⩽ x ⩽ b

are assumed in the form:

(4)

\begin{matrix} u (a, t) = u (b, t) = 0, \\ u_{x} (a, t) = u_{x} (b, t) = 0, \\ u_{xx} (a, t) = u_{xx} (b, t) = 0, \end{matrix}\}

and the initial conditions to be used will be prescribed later. To find the traveling wave solution of Eq. (3), we introduce the wave variable

ξ = x - ct

, where c represents the arbitrary constant velocity of the wave traveling in the positive direction on the x axis and

u (x, t) = f (ξ)

. So Eq. (3) takes the form:

(5)

- {cf}_{ξ} (ξ) + f_{ξ} (ξ) + 6 f^{2} (ξ) f_{ξ} (ξ) + {cf}_{ξ ξ ξ} (ξ) = 0 .

Integrating Eq. (5) gives

(6)

(1 - c) f (ξ) + 2 (f (ξ))^{3} + {cf}_{ξ ξ} (ξ) = 0,

where the constant of integration equal zero since the solitary wave solution and its derivatives equal zero as

ξ \to \pm \infty

. The linear equation from (6) has the solution in the form

f (ξ) = e^{k ξ}, k = \pm \sqrt{\frac{c - 1}{c}}

. We define

g (ξ) = e^{k ξ}

and let

f (ξ) = \sum_{n = 1}^{\infty} a_{n} (g (ξ))^{n}

. From Eq. (5), we get the recursion relation (RR)

(7)

({ck}^{2} n^{2} - c + 1) a_{n} + 2 \sum_{m = 2}^{n - 1} \sum_{l = 1}^{m - 1} a_{n - m} a_{m - l} a_{l} = 0, n ⩾ 3,

where the coefficients, in general, are of the form

(8)

\begin{matrix} a_{2 n} = 0, & n ⩾ 1, \\ a_{2 n + 1} = \frac{a_{1}^{2 n + 1}}{2^{2 n} (1 - c)^{n}}, & n ⩾ 0, \end{matrix}\}

and then the exact solutions of Eq. (3) take the forms

(9)

\begin{matrix} u (x, t) = \frac{(4 - 4 c) e^{\sqrt{\frac{c - 1}{c}} (x - ct)} a_{1}}{4 - 4 c + e^{2 \sqrt{\frac{c - 1}{c}} (x - ct)} a_{1}^{2}}, \\ u (x, t) = \frac{(4 - 4 c) e^{\sqrt{\frac{c - 1}{c}} (x - ct)} a_{1}}{(4 c - 4) e^{2 \sqrt{\frac{c - 1}{c}} (x - ct)} - a_{1}^{2}}, \end{matrix}\}

In Eq. (9) if we choose

a_{1} = \sqrt{4 c - 4}

then the solitary wave solution of MRLW equation reduces to:

(10)

u (x, t) = \sqrt{c - 1} \sec h (\sqrt{\frac{c - 1}{c}} (x - ct)),

if we replace c by

c + 1

we get the solution, which is the same solitary wave solution of the MRLW equation appears in other papers (Gardner et al., 1997; Khalifa et al., 2007b) .

(11)

u (x, t) = \sqrt{c} \sec h (\sqrt{\frac{c}{c + 1}} (x - (c + 1) t - x_{0})) .

Hence, this method may not yield the analytical solutions for many PDEs like in interaction solitary and the Maxwellian initial condition. Therefore, the numerical analysis plays a very important role for obtaining the accurate approximate solutions in these cases and that is our objective in this study. Also, Eq. (3) has three invariants as in the form (Gardner et al., 1997; Khalifa et al., 2007b):

(12)

\begin{matrix} I_{1} = \int_{a}^{b} udx, \\ I_{2} = \int_{a}^{b} (u^{2} + u_{x}^{2}) dx, \\ I_{3} = \int_{a}^{b} (u^{4} - u_{x}^{2}) dx, \end{matrix}\}

we point out that these invariants help us to test the numerical schemes especially for equations with no analytical solution and during the interaction of solitons.

3 Collocation method for solving MRLW equation

In this section, we apply the method with the function $B_{j}$ as quintic B-splines. We consider the approximate solution to the solution $u (x, t)$ is given by

(13)

u_{N} (x, t) = \sum C_{j} (t) B_{j} (x),

where

C_{j} (t)

are time dependent parameters to be determined at each time level and

B_{j} (x)

are the quintic B-splines given by:

(14)

B_{i} (x) = \frac{1}{h^{5}} \{\begin{matrix} (x - x_{i - 3})^{5}, & x_{i - 3} ⩽ x ⩽ x_{i - 2}, \\ (x - x_{i - 3})^{5} - 6 (x - x_{i - 2})^{5}, & x_{i - 2} ⩽ x ⩽ x_{i - 1}, \\ (x - x_{i - 3})^{5} - 6 (x - x_{i - 2})^{5} + 15 (x - x_{i - 1})^{5}, & x_{i - 1} ⩽ x ⩽ x_{i}, \\ (- x + x_{i + 3})^{5} + 6 (x - x_{i + 2})^{5} - 15 (x - x_{i + 1})^{5}, & x_{i} ⩽ x ⩽ x_{i + 1}, \\ (- x + x_{i + 3})^{5} + 6 (x - x_{i + 2})^{5}, & x_{i + 1} ⩽ x ⩽ x_{i + 2}, \\ (- x + x_{i + 3})^{5}, & x_{i + 2} ⩽ x ⩽ x_{i + 3}, \\ 0, & otherwise . \end{matrix}

Then, the discredited equations for the space derivative are derived as

(15)

\sum (B_{j} (x) - B_{j}^{″} (x)) {\dot{C}}_{j} (t) = - (1 + 6 {(\sum C_{j} (t) B_{j} (x))}^{2}) \sum C_{j} (t) B_{j}^{'} (x),

where x takes the values at the selected collocation knot points for quintic B-spline. The values of

B_{j} (x)

and its first and second derivatives at knots points are given in Table 1.

Table 1 The values of quintic B-spline and its first and second derivatives at the knots points.

$x$	$x_{j - 2}$	$x_{j - 1}$	$x_{j}$	$x_{j + 1}$	$x_{j + 2}$
$B_{i}$	1	26	66	26	1
$B_{i}^{'}$	$5 / h$	$50 / h$	0	$- 50 / h$	$- 5 / h$
$B_{i}^{″}$	$20 / h^{2}$	$40 / h^{2}$	$- 120 / h^{2}$	$40 / h^{2}$	$20 / h^{2}$

From these equations a system of first order ordinary differential equations can be obtained of the form:

(16)

A \dot{C} (t) = F (C (t)) .

Several others studies solved the first order ordinary differential system (16) by using the central difference approximation for

C

, but in the present studies we solve the system (16) using fourth order Runge–Kutta method.

(17)

\begin{matrix} {AK}_{1} = F (C^{n}), \\ {AK}_{2} = F (C^{n} + \frac{1}{2} K_{1}), \\ {AK}_{3} = F (C^{n} + \frac{1}{2} K_{2}), \\ {AK}_{4} = F (C^{n} + K_{3}), \end{matrix}\}

and we solved the last equations and using

(18)

C^{n + 1} = C^{n} + \frac{k (K_{1} + 2 K_{2} + 2 K_{3} + K_{4})}{6} .

where

K_{1}, K_{2}, K_{3} and K_{4}

can be found by solving four systems (17). Once the parameter

C

has been determined at a specified time we can compute the solution at the required knots the time evolution of the approximate solution

u_{N} (x, t)

is determined from that of the vector

C^{n}

which is found by repeatedly applying the above procedure once the starting vector

C^{0}

has been computed from the initial condition.

4 Numerical tests and results

In this section we present some numerical tests of our scheme for the solution of MRLW equation for single solitary waves in addition to determining the solution of two and three solitary waves interaction at different time levels. Also to show the development of Maxwellian initial condition into solitary waves. The numerical solution must preserve the conservation laws during propagation.

4.1

4.1 Propagation of single solitary waves

To examine the validated and the efficiency of our scheme, we consider two cases in our numerical work, since $L_{\infty} -error norm$ and $L_{2}$ -error norm are used to compare our numerical solutions with the exact solution of Eq. (3). Also the quantities $I_{1}, I_{2} and I_{3}$ are evaluated to measure the conservation properties of the collocation scheme, the analytical values of these invariants can be found as (Gardner et al., 1997): $I_{1} = \frac{π \sqrt{c}}{2}, I_{2} = c + \frac{4 c}{3} and I_{3} = \frac{2 c^{2}}{3} - \frac{4 c}{3}$ . In the first case, we choose the parameters $c = 1, Δ x = 0.2, Δ t = 0.1 and x_{0} = 40$ . The conservation properties and the $L_{2}$ -error norm and $L_{\infty}$ -error norms. The analytical values for the invariants are $I_{1} = 4.44288, I_{2} = 3.29983 and I_{3} = 1.41421$ are illustrated in Table 2 below. Moreover, Table 3 represents the values of the invariants and error norms of the present method at time 10 against the results of Gardner et al. (1997) and Khalifa et al. (2007b).

Table 2 Invariants and errors for single solitary wave for

c = 1, Δ x = 0.2, Δ t = 0.1 and x_{0} = 40, 0 ⩽ x ⩽ 100

T	I₁	I₂	I₃	L₂-error norm	L_∞-error norm
0	4.442883	3.298731	1.415311	2.855687E−6	2.145767E−6
1	4.442883	3.298723	1.415301	2.257935E−5	1.645088E−5
2	4.442883	3.298712	1.415290	4.273932E−5	2.598763E−5
3	4.442885	3.298702	1.415280	6.246631E−5	3.492832E−5
4	4.442884	3.298692	1.415270	8.416529E−5	4.494190E−5
5	4.442884	3.298681	1.415260	1.078404E−4	5.537271E−5
6	4.442883	3.298672	1.415250	1.334255E−4	6.842613E−5
7	4.442883	3.298661	1.415240	1.620302E−4	8.213520E−5
8	4.442884	3.298652	1.415230	1.931854E−4	9.953976E−5
9	4.442882	3.298642	1.415219	2.265411E−4	1.171231E−4
10	4.442882	3.298630	1.415209	2.632212E−4	1.369715E−4

Table 3 Invariants and errors for single solitary wave for

c = 1, Δ x = 0.2, Δ t = 0.1 and x_{0} = 40, 0 ⩽ x ⩽ 100

, time = 10.

Method	I₁	I₂	I₃	L₂ × 10³	L_∞ × 10³
Analytical	4.44288	3.29983	1.41421	0	0
Present	4.44288	3.29863	1.415209	0.26322	0.13697
Gardner et al. (1997)	4.442	3.299	1.413	19.39	9.24
Gardner et al. (1997)	4.440	3.296	1.411	20.3	11.2
Khalifa et al. (2007b)	4.44288	3.29983	1.41420	9.30196	5.43718

Also, Table 3 represents the values of the invariants and errors norms of the present method at time 10 against the recorded results of Gardner et al. (1997) and Khalifa et al. (2007b).

We find that our scheme provides good results than others. The motion of solitary wave using our scheme is plotted at time 10 in Fig. 1.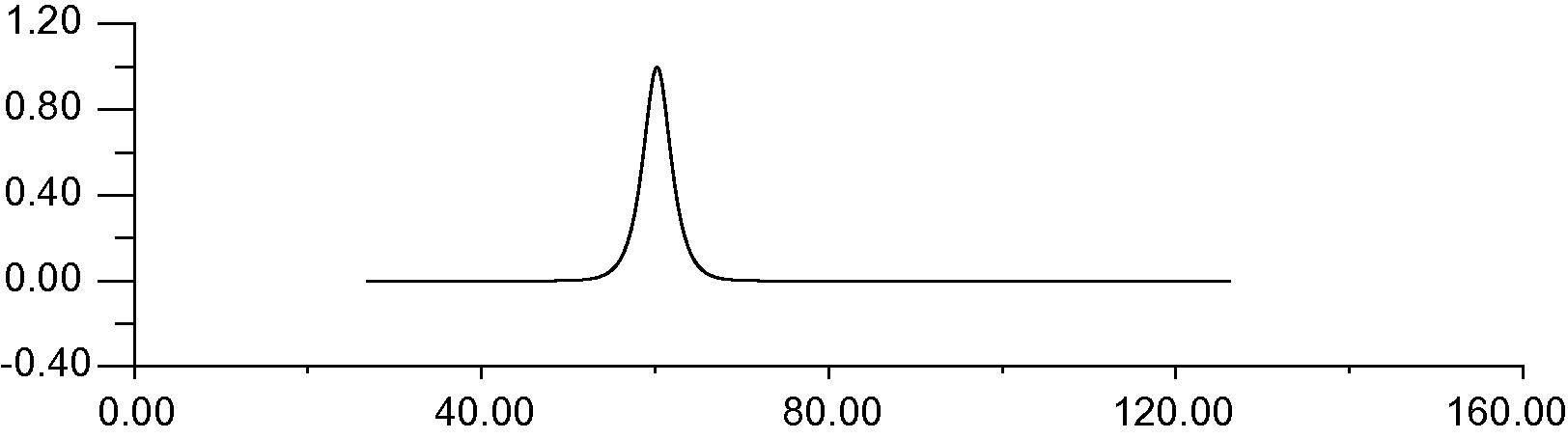

Single solitary wave with c = 1 , Δ x = 0.2 , Δ t = 0.1 and x 0 = 40 , 0 ⩽ x ⩽ 100 , T = 10.

In the second case, we choose the parameters $c = 0.3, Δ x = 0.2, Δ t = 0.1 and x_{0} = 40$ then the amplitude is 0.54772. The analytical values of the invariants are $I_{1} = 3.58197, I_{2} = 1.34508 and I_{3} = 0.153723$ . The changes of the invariants from the initial variants approach to zero throughout and agree with the analytical values for the three invariants, which indicated that our scheme is satisfactorily conservative. Errors are satisfactorily small, since $L_{2} -error norm = 1.9193 \times 10^{- 5} and L_{\infty} -error norm = 8.970499 \times 10^{- 6}$ at time 10. The results for the second case are shown in Table 4.

Table 4 Invariants and errors for single solitary wave for

c = 0.3, Δ x = 0.2, Δ t = 0.1 and x_{0} = 40, 0 ⩽ x ⩽ 100

T	I₁	I₂	I₃	L₂-error norm	L_∞-error norm
1	3.581964	1.344973	0.1538265	2.142769E−06	1.221895E−06
2	3.581966	1.344973	0.1538264	4.352044E−06	2.086163E−06
3	3.581964	1.344973	0.1538264	6.752275E−06	3.129244E−06
4	3.581965	1.344973	0.1538264	8.884196E−06	4.291534E−06
5	3.581964	1.344973	0.1538264	1.087434E−05	5.215406E−06
6	3.581965	1.344973	0.1538264	1.292003E−05	6.198883E−06
7	3.581964	1.344972	0.1538264	1.472382E−05	7.271767E−06
8	3.581964	1.344973	0.1538264	1.632736E−05	7.659197E−06
9	3.581960	1.344972	0.1538264	1.784318E−05	8.493662E−06
10	3.581958	1.344973	0.1538264	1.919314E−05	8.970499E−06

4.2

4.2 Interaction of two solitary waves

Interaction of two positive solitary waves is studied using the initial conditions given by the linear sum of two well-separated solitary waves of various amplitudes:

(19)

u (x, 0) = A_{1} \sec h (p_{1} (x - x_{1})) + A_{2} \sec h (p_{2} (x - x_{2})),

where

A_{i} = \sqrt{c_{i}}, p_{i} = \sqrt{\frac{c_{i}}{c_{i} + 1}}, i = 1, 2, x_{i} and c_{i}

are arbitrary constants. The analytical values of the conservation laws of this case can be found as

I_{1} = \frac{π {\sqrt{c}}_{1}}{p_{1}} + \frac{π {\sqrt{c}}_{2}}{p_{2}}, I_{2} = \frac{2 c_{1}}{p_{1}} + \frac{2 c_{2}}{p_{2}} + \frac{2 p_{1} c_{1}}{3} + \frac{2 p_{2} c_{2}}{3} and I_{3} = \frac{4 c_{1}^{2}}{3 p_{1}} + \frac{4 c_{2}^{2}}{3 p_{2}} - \frac{2 p_{1} c_{1}}{3} - \frac{2 p_{2} c_{2}}{3}

. In our computational work, we choose

c_{1} = 4, c_{2} = 1, x_{1} = 25, x_{2} = 55, δ = 1, Δ x = 0.2, Δ t = 0.05

with interval [0, 250], then the amplitudes are in ratio 2:1, where

A_{1} = 2 A_{2}

. The analytical values for the invariants of this case are

I_{1} = 11.467698, I_{2} = 14.629243 and I_{3} = 22.880466

and the changes in I₁, I₂ and I₃ as seen in Table 5 are small. Also, Fig. 2 shows the computer plot of the interaction of these solitary waves at different time levels, where the simulation is done to t = 14.

Table 5 Invariants of interaction two solitary waves of MRLW equation

c_{1} = 4, c_{2} = 1, x_{1} = 25, x_{2} = 55, [0, 250]

Time	I₁	I₂	I₃
1	11.467700	14.617920	22.885030
2	11.467700	14.616560	22.879620
3	11.467700	14.615220	22.874220
4	11.467700	14.613870	22.868820
5	11.467770	14.612520	22.863410
6	11.467620	14.611190	22.858020
7	11.467270	14.609970	22.852570
8	11.466890	14.609760	22.846460
9	11.466490	14.613410	22.839010
10	11.466050	14.608160	22.842790

(a) Interaction two solitary waves with c1 = 4, c2 = 1, x1 = 25, x2 = 55, [0, 250] at times T = 0. (b) Interaction two solitary waves with c1 = 4, c2 = 1, x1 = 25, x2=55, [0, 250] at times T = 14.

4.3

4.3 Interaction of three solitary waves

The interaction of three MRLW solitary waves having different amplitudes and traveling in the same direction is illustrated. We consider the MRLW equation with initial conditions given by the linear sum of three well-separated solitary waves of various amplitudes:

(20)

u (x, 0) = A_{1} \sec h (p_{1} (x - x_{1})) + A_{2} \sec h (p_{2} (x - x_{2})) + A_{3} \sec h (p_{3} (x - x_{3})),

where

A_{i} = \sqrt{c_{i}}, p_{i} = \sqrt{\frac{c_{i}}{c_{i} + 1}}, i = 1, 2, 3, x_{i} and c_{i}

are arbitrary constants. The analytical values of the conservation laws of this case can be found as:

\begin{matrix} I_{1} = \frac{π {\sqrt{c}}_{1}}{p_{1}} + \frac{π {\sqrt{c}}_{2}}{p_{2}} + \frac{π {\sqrt{c}}_{3}}{p_{3}}, \\ I_{2} = \frac{2 c_{1}}{p_{1}} + \frac{2 c_{2}}{p_{2}} + \frac{2 c_{3}}{p_{3}} + \frac{2 p_{1} c_{1}}{3} + \frac{2 p_{2} c_{2}}{3} + \frac{2 p_{3} c_{3}}{3}, \\ I_{3} = \frac{4 c_{1}^{2}}{3 p_{1}} + \frac{4 c_{2}^{2}}{3 p_{2}} + \frac{4 c_{3}^{2}}{3 p_{3}} - \frac{2 p_{1} c_{1}}{3} - \frac{2 p_{2} c_{2}}{3} - \frac{2 p_{3} c_{3}}{3} . \end{matrix}

In our computational work, we choose

c_{1} = 4, c_{2} = 1, c_{3} = 0.25, x_{1} = 15, x_{2} = 45, x_{3} = 60

with interval [0, 250], then the amplitudes are in ratio 4:2:1, where A₁ = 2A₂ = 4A₃. The analytical values for the invariants of this case are I₁ = 14.9801, I₂ = 15.8218 and I₃ = 22.9923 and we find from our numerical scheme, that the invariants I₁, I₂ and I₃ for interaction of these solitary waves are sensible constants, comparing with their big amplitudes, the changes are

5 \times 10^{- 2}, 5 \times 10^{- 3} and 1 \times 10^{- 2}

percent, respectively, for the computer run and the results are recorded in Table 3. Fig. 3 shows details of interaction of these solitary waves at different time levels, and the simulation is done to t = 10 (see Table 6).

c 1 = 4 , c 2 = 1 , c 3 = 0.25 , x 1 = 15 , x 2 = 45 , x 3 = 60 , [ 0 , 250 ] , T = 1. (b) c 1 = 4 , c 2 = 1 , c 3 = 0.25 , x 1 = 15 , x 2 = 45 , x 3 = 60 , [ 0 , 250 ] , T = 5. (c) c 1 = 4 , c 2 = 1 , c 3 = 0.25 , x 1 = 15 , x 2 = 45 , x 3 = 60 , [ 0 , 250 ] , T = 10.

Table 6 Invariants of interaction three solitary waves of MRLW equation

c_{1} = 4, c_{2} = 1, c_{3} = 0.25, x_{1} = 15, x_{2} = 45, x_{3} = 60, [0, 250]

Time	I₁	I₂	I₃
1	14.980110	15.826100	23.012800
2	14.980090	15.824760	23.007380
3	14.980180	15.823430	23.001970
4	14.979930	15.822100	22.996530
5	14.979550	15.820770	22.991110
6	14.979140	15.819470	22.985690
7	14.978740	15.818400	22.980090
8	14.978040	15.818480	22.973750
9	14.974250	15.822740	22.965790
10	14.930390	15.822500	22.964190

4.4

4.4 The Maxwellian initial condition

The fourth numerical test of our scheme is concerned with the generation of a train of solitary waves from Maxwellian initial condition:

(21)

u (x, 0) = e^{- (x - 40)^{2}},

into a train of solitary waves is examined. In this section, we consider the MRLW equation of the form

(22)

u_{t} + u_{x} + 6 u^{2} u_{x} - δ u_{xxt} = 0,

as it is known, with the Maxwellian Eq. (21), the behavior of the solution depends on the values of

δ

. For

δ ≫ δ_{c}

, where

δ_{c}

is some critical value. The Maxwellian does not break up into solutions but exhibits rapidly oscillating wave packets. When

δ \approx δ_{c}

the mixed type of solutions is found which consists of a leading soliton and an oscillating tail. For

δ ≪ δ_{c}

the Maxwellian breaks up into a number of solitons according to the value of

δ

. The recorded values of the invariants I₁, I_2, I₃ are given in Table 7. The conservation properties are all good.

Table 7 Computed values I₁, I₂, I₃ for Maxwellian initial condition when h = 0.1, k = 0.1, [0, 100].

δ	Time	I₁	I₂	I₃
1	2	1.772449	2.506352	−0.3668149
	4	1.772446	2.506235	−0.3666974
	6	1.772447	2.506171	−0.3666326
	8	1.772446	2.506123	−0.3665860
	10	1.772444	2.506092	−0.3665553

0.5	2	1.772451	1.879888	0. 2596494
	4	1.772446	1.879855	0.2596828
	6	1.772449	1.879841	0.2596973
	8	1.772450	1.879834	0.2597050
	10	1.772449	1.879828	0.2597092

0.1	2	1.772452	1.378607	0.7608777
	4	1.772451	1.378577	0.7608364
	6	1.772451	1.378546	0.7607937
	8	1.772451	1.378515	0.7607529
	10	1.772453	1.378483	0.7607117

0.04	2	1.772453	1.302368	0.8343938
	4	1.772453	1.300995	0.8320332
	6	1.772453	1.299635	0.8296967
	8	1.772451	1.298285	0.8273833
	10	1.772440	1.296948	0.8250930

By decreasing the value of $δ$ , more solitary waves are obtained. When $δ = 0.1$ , a single solitary wave is generated for our scheme, when $δ = 0.04$ a train of two stable solitary waves is generated, and so on. The total number of solitary waves generated for various values of $δ$ are in agreement with the results found in Gardner et al. (1997) and Khalifa et al. (2007b) (Fig. 4).

Maxwellian initial condition, Δ x = 0.1 , Δ t = 0.1 , [ 0 , 100 ] , δ = 1 . (b) Maxwellian initial condition, Δ x = 0.1 , Δ t = 0.1 , [ 0 , 100 ] , δ = 0.1 . (c) Maxwellian initial condition, Δ x = 0.1 , Δ t = 0.1 , [ 0 , 100 ] , δ = 0.04 .

5 Conclusion

A numerical method based on collocation method using quintic B-spline finite elements within the collocation method leads to a system of first order differential equations is solved by fourth order Runge–Kutta method, which shows good conservation. The efficiency of the method is tested on the problems of propagation of single solitary wave, interaction of two and three solitary waves and development of train of solitary waves from Maxwellian initial condition. The three invariants of motion are constant in all the computer simulations described here. The problems presented in this paper suggest that the methods should be considered as one of possible ways of solving these kinds of nonlinear partial differential equations.

References

Alexander M.E., Morris J.L., . Galerkin methods applied to some model equations for nonlinear dispersive waves. J. Comput. Phys.. 1979;30:428-451.
[Google Scholar]
Dag I., . Least squares quadratic B-splines finite element method for the regularized long wave equation. Comput. Methods Appl. Mech. Eng.. 2000;182:205-215.
[Google Scholar]
Dag I., Saka B., Irk D., . Application of cubic B-splines for numerical solution of the RLW equation. Appl. Math. Comput.. 2004;195:373-389.
[Google Scholar]
El-Danaf Talaat S., Ramadan Mohamed A., Abd Alaal Faysal E.I., . The use of adomian decomposition method for solving the regularized long-wave equation. Chaos Soliton Fract.. 2005;26(3):747-757.
[Google Scholar]
Gardner L.R.T., Gardner G.A., . Solitary wave of the regularized long wave equation. J. Comput. Phys.. 1990;91:441-459.
[Google Scholar]
Gardner L.R.T., Gardner G.A., Dag I., . A B-spline finite element method for the regularized long wave equation. Commun. Numer. Methods Eng.. 1995;11:59-68.
[Google Scholar]
Gardner L.R.T., Gardner G.A., Dogan A., . A least squares finite element scheme for the RLW equation. Commun. Numer. Methods Eng.. 1996;12:795-804.
[Google Scholar]
Gardner L.R.T., Gardner G.A., Ayoub F.A., Amein N.K., . Approximations of solitary waves of the MRLW equation by B-spline finite element. Arab. J. Sci. Eng.. 1997;22:183-193.
[Google Scholar]
Hereman W., Banerjee P.P., Korpel A., Assanto G., Van Immerzeele A., Meerpoel A., . Exact solitary wave solutions of non-linear evolution and wave equations using a direct algebraic method. J. Phys. A. 1986;19:607-628.
[Google Scholar]
Kaya D., El-Sayed S.M., . An application of the decomposition method for the generalized KdV and RLW equations. Chaos Soliton Fract.. 2003;17:869-877.
[Google Scholar]
Khalifa, A.K., 1979. Theory and Applications of the Collocation Method with Splines for Ordinary and Partial Differential Equations, Ph.D. Thesis, Heriot-Watt University, 1979.
Khalifa A.K., Raslan K.R., Alzubaidi H.M., . A finite difference scheme for the MRLW and solitary wave interactions. Appl. Math. Comput.. 2007;189:346-354.
[Google Scholar]
Khalifa A.K., Raslan K.R., Alzubaidi H.M., . A collocation method with cubic B-splines for solving the MRLW equation. Comput. Appl. Math.. 2007;212:406-418.
[Google Scholar]
Lu Junfeng, . He’s variational iteration method for the modified equal width equation. Chaos Soliton Fract.. 2008;39(5):2102-2109.
[Google Scholar]
Peregrine D.H., . Calculations of the development of an undular bore. J. Fluid Mech.. 1966;25(2):321.
[Google Scholar]
Ramadan Mohamed A., El-Danaf Talaat S., Abd Alaal Faisal E.I., . A numerical solution of the Burgers’ equation using septic B-splines. Chaos Soliton Fract.. 2005;26(3):795-804.
[Google Scholar]
Ramos J.I., . Solitary waves of the EW and RLW equations. Chaos Soliton Fract.. 2007;34(5):1498-1518.
[Google Scholar]
Ramos J.I., . Solitary wave interactions of the GRLW equation. Chaos Soliton Fract.. 2007;33(2):479-491.
[Google Scholar]
Raslan K.R., . A computational method for the regularized long wave (RLW) equation. Appl. Math. Comput.. 2005;167:1101-1118.
[Google Scholar]
Raslan K.R., . Exact solitary wave solutions of equal width wave and related equations using a direct algebraic method. Int. J. Nonlinear Sci., UK. 2008;6:246-254.
[Google Scholar]
Shivamoggi, Bhimsen K., Rollins, David K., 2002. Evolution of solitary-wave solution of the perturbed regularized long-wave equation. Chaos Soliton Fract. 13 (5), 1129–1136.
Soliman A.A., Abdou M.A., . Exact travelling wave solutions of nonlinear partial differential equations. Chaos Soliton Fract.. 2007;32(2):808-815.
[Google Scholar]
Soliman A.A., Hussien M.H., . Collocation solution for RLW equation with septic splines. Appl. Math. Comput.. 2005;161:623-636.
[Google Scholar]
Soliman A.A., Raslan K.R., . Collocation method using quadratic B-spline for the RLW equation. Int. J. Comput. Math.. 2001;78:399-412.
[Google Scholar]
Zhang L., . A finite difference scheme for generalized long wave equation. Appl. Math.. 2005;168(2):962-972.
[Google Scholar]

Introduction

The Governing equation and direct algebraic method (Gardner et al., 1997; Khalifa et al., 2007a,b; Hereman et al., 1986; Raslan, 2008)

Collocation method for solving MRLW equation

Numerical tests and results

Propagation of single solitary waves
Interaction of two solitary waves
Interaction of three solitary waves
The Maxwellian initial condition

Conclusion

Fulltext Views
26

PDF downloads
4

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Alexander M.E., Morris J.L., . Galerkin methods applied to some model equations for nonlinear dispersive waves. J. Comput. Phys.. 1979;30:428-451.
[Google Scholar]

[2] Dag I., . Least squares quadratic B-splines finite element method for the regularized long wave equation. Comput. Methods Appl. Mech. Eng.. 2000;182:205-215.
[Google Scholar]

[3] Dag I., Saka B., Irk D., . Application of cubic B-splines for numerical solution of the RLW equation. Appl. Math. Comput.. 2004;195:373-389.
[Google Scholar]

[4] El-Danaf Talaat S., Ramadan Mohamed A., Abd Alaal Faysal E.I., . The use of adomian decomposition method for solving the regularized long-wave equation. Chaos Soliton Fract.. 2005;26(3):747-757.
[Google Scholar]

[5] Gardner L.R.T., Gardner G.A., . Solitary wave of the regularized long wave equation. J. Comput. Phys.. 1990;91:441-459.
[Google Scholar]

[6] Gardner L.R.T., Gardner G.A., Dag I., . A B-spline finite element method for the regularized long wave equation. Commun. Numer. Methods Eng.. 1995;11:59-68.
[Google Scholar]

[7] Gardner L.R.T., Gardner G.A., Dogan A., . A least squares finite element scheme for the RLW equation. Commun. Numer. Methods Eng.. 1996;12:795-804.
[Google Scholar]

[8] Gardner L.R.T., Gardner G.A., Ayoub F.A., Amein N.K., . Approximations of solitary waves of the MRLW equation by B-spline finite element. Arab. J. Sci. Eng.. 1997;22:183-193.
[Google Scholar]

[9] Hereman W., Banerjee P.P., Korpel A., Assanto G., Van Immerzeele A., Meerpoel A., . Exact solitary wave solutions of non-linear evolution and wave equations using a direct algebraic method. J. Phys. A. 1986;19:607-628.
[Google Scholar]

[10] Kaya D., El-Sayed S.M., . An application of the decomposition method for the generalized KdV and RLW equations. Chaos Soliton Fract.. 2003;17:869-877.
[Google Scholar]

[11] Khalifa, A.K., 1979. Theory and Applications of the Collocation Method with Splines for Ordinary and Partial Differential Equations, Ph.D. Thesis, Heriot-Watt University, 1979.

[12] Khalifa A.K., Raslan K.R., Alzubaidi H.M., . A finite difference scheme for the MRLW and solitary wave interactions. Appl. Math. Comput.. 2007;189:346-354.
[Google Scholar]

[13] Khalifa A.K., Raslan K.R., Alzubaidi H.M., . A collocation method with cubic B-splines for solving the MRLW equation. Comput. Appl. Math.. 2007;212:406-418.
[Google Scholar]

[14] Lu Junfeng, . He’s variational iteration method for the modified equal width equation. Chaos Soliton Fract.. 2008;39(5):2102-2109.
[Google Scholar]

[15] Peregrine D.H., . Calculations of the development of an undular bore. J. Fluid Mech.. 1966;25(2):321.
[Google Scholar]

[16] Ramadan Mohamed A., El-Danaf Talaat S., Abd Alaal Faisal E.I., . A numerical solution of the Burgers’ equation using septic B-splines. Chaos Soliton Fract.. 2005;26(3):795-804.
[Google Scholar]

[17] Ramos J.I., . Solitary waves of the EW and RLW equations. Chaos Soliton Fract.. 2007;34(5):1498-1518.
[Google Scholar]

[18] Ramos J.I., . Solitary wave interactions of the GRLW equation. Chaos Soliton Fract.. 2007;33(2):479-491.
[Google Scholar]

[19] Raslan K.R., . A computational method for the regularized long wave (RLW) equation. Appl. Math. Comput.. 2005;167:1101-1118.
[Google Scholar]

[20] Raslan K.R., . Exact solitary wave solutions of equal width wave and related equations using a direct algebraic method. Int. J. Nonlinear Sci., UK. 2008;6:246-254.
[Google Scholar]

[21] Shivamoggi, Bhimsen K., Rollins, David K., 2002. Evolution of solitary-wave solution of the perturbed regularized long-wave equation. Chaos Soliton Fract. 13 (5), 1129–1136.

[22] Soliman A.A., Abdou M.A., . Exact travelling wave solutions of nonlinear partial differential equations. Chaos Soliton Fract.. 2007;32(2):808-815.
[Google Scholar]

[23] Soliman A.A., Hussien M.H., . Collocation solution for RLW equation with septic splines. Appl. Math. Comput.. 2005;161:623-636.
[Google Scholar]

[24] Soliman A.A., Raslan K.R., . Collocation method using quadratic B-spline for the RLW equation. Int. J. Comput. Math.. 2001;78:399-412.
[Google Scholar]

[25] Zhang L., . A finite difference scheme for generalized long wave equation. Appl. Math.. 2005;168(2):962-972.
[Google Scholar]

Solitary waves solutions of the MRLW equation using quintic B-splines

Abstract

Keywords

MRLW

B-splines

Solitons

Collocation method

1 Introduction

2 The Governing equation and direct algebraic method (Gardner et al., 1997; Khalifa et al., 2007a,b; Hereman et al., 1986; Raslan, 2008)

3 Collocation method for solving MRLW equation

4 Numerical tests and results

4.1 Propagation of single solitary waves

4.2 Interaction of two solitary waves

4.3 Interaction of three solitary waves

4.4 The Maxwellian initial condition

5 Conclusion

References

2 The Governing equation and direct algebraic method (Gardner et al., 1997; Khalifa et al., 2007a,b; Hereman et al., 1986; Raslan, 2008 )