Solitary kinetic Alfvén waves in nonextensive electron-positron-ion plasma

1 Introduction

It is widely believed that electron-positron plasmas form the major constituents of several astrophysical situations such as the early universe (Rees,1983; Sadiq et al., 2014), active galactic nuclei (Miller and Witta, 1987), pulsar magnetosphere (Michel, 1991), solar atmosphere (Tandberg-Hansen and Emslie, 1988; Kozlovsky et al.,2004) etc. However, most of the astrophysical plasmas usually contain ions, in addition to the electrons and positrons forming electron-positron-ion (e-p-i) plasmas. For instance, outflows of electron-positron plasma from pulsars, when enters into interstellar cold low density electron-ion plasmas, forms two temperature e-p-i plasmas. Similarly, in many astrophysical contexts such as interstellar medium, positrons are created due to the interactions of cosmic ray nuclei with interstellar atoms thereby forming the e-p-i plasmas. In laboratories, e-p-i plasmas can be created (Surko and Murphy, 1990; Greaves and Surko, 1995) by injecting positrons into tokamak plasmas. During the last few decades, a great deal of work has been done on linear and nonlinear behavior of unmagnetized as well as magnetized e-p-i plasmas to understand the basic properties of waves excited there and to explain different aspects of astrophysical environments. Among these, investigations of nonlinear structures of kinetic Alfvén waves (KAWs) in e-p-i plasmas have also drawn much attention of several authors (Kakati and Goswami, 1998, 2000; Mahmood et al., 2005; Sah, 2010; Akbari-Moghanjoughi, 2011; Dubinov et al., 2012; Adnan et al., 2016). KAWs are basically dispersive Alfvén waves and can be excited in plasmas for Q ≪ β ≪ 1 ( $\beta$ is the thermal to magnetic pressure ratio; Q is the electron-to-ion mass ratio) when shear Alfvén waves, modified by perpendicular wave length effects, propagate obliquely to the direction of ambient magnetic field. The dispersive character of KAWs when balanced with nonlinear steepening may lead to the formation of nonlinear structures like solitons and double layers. Investigations of nonlinear structures of dispersive Alfvén waves in plasmas are important because they can play a significant role in explaining electromagnetic fluctuations, particle energization process and solitary structures observed in space, astrophysical and laboratory plasmas (Jafelice and Opher, 1987; Stasiewicz et al., 2000). This type of study has got rich support from space based satellite observations (Wahlund et al., 1994; Louran et al., 1994) which have revealed strong electromagnetic solitary like structures having possible interpretations of being dip or hump-type solitary KAWs.

In their study of solitary KAWs in Maxwellian e-p-i plasma, Kakati and Goswami (1998) reported the existence of two types of compressive solitary waves whose existence regions were determined by the positron densities and other plasma parameters. In the same plasma model, they also predicted the existence of small amplitude kinetic Alfvén compressive double layers (DLs) at sub-Alfvénic speeds and rarefactive double layers in sub and super-Alfvénic regions (Kakati and Goswami, 2000). Later, Sah (2010) extended this study by including finite ion temperature effect and reported the existence of compressive solitons and double layers both at sub and super-Alfvénic speeds. In all these investigations, electrons and positrons were assumed to follow Maxwellian distributions. Recently, Adnan et al. (2016) has reported the existence of small amplitude sub-Alfvénic compressive solitary KAWs in superthermal e-p-i plasma. However, in most of the astrophysical plasmas, the velocity distributions of energetic particles are not purely Maxwellian. The deviation from the Maxwellian distribution can be attributed to the fact that the high energy plasma particles interact via long-range Coulomb forces together with the gravitational effect. It has been suggested that such high energetic particles can be modeled more effectively by nonextensive q-distribution (Silva et al., 1998; Lima et al., 2000; Ferdousi et al., 2015) which is based on non-additive q entropic measure (Tsallis, 1988). A number of articles have been published recently dealing with different nonlinear wave modes in nonextensive electron-ion plasmas (Tribeche et al., 2010; Liu et al., 2011; Ahmed and Sah, 2014; Saha and Chatterjee, 2015; Saha et al., 2015) as well as e-p-i plasmas (El-Awady and Moslem, 2011; El-Tantawy et al., 2012; Ferdousi et al., 2015). To the best of our knowledge, no study has yet been reported on nonlinear structures of KAWs in nonextensive e-p-i plasmas.

In this paper we, therefore, wish to extend the kinetic Alfvén wave problem in three component e-p-i plasma whose constituents are extensive ion fluid, and nonextensive electrons and positrons. It is to be noted that if the ion temperature becomes comparable to electron/positron temperature, Landau damping becomes appreciable and fluid dynamics will be broken down. Moreover, for large electron-to-ion temperature ratio the ion nonextensive parameter has the little effect (Liu et al., 2009). Hence, in the present work, the ions are treated as the fluid to get rid of Landau damping effect; and electrons, positrons are treated as nonextensive, obeying q-distribution to include long range interactions. The result of this investigation, therefore, may be relevant to long-range interaction systems such as interstellar and astrophysical plasmas. Our investigation shows that the plasma system considered here can support only sub-Alfvénic compressive kinetic Alfvén solitons whose amplitude and width decrease with increasing nonextensive parameter (q). This is quite different from the behavior of kinetic Alfvén solitons in superthermal e-p-i plasma (Adnan et al., 2016) where both amplitude and width of solitary KAWs increase with the rise of superthermal parameter kappa ( $\kappa$ ).

2 Linear dispersion relation of KAWs

We consider three-component magnetized collisionless plasma comprising of inertial ions, warm electrons and positrons obeying q-nonextensive distributions. The direction of ambient magnetic field is supposed to be along Z-axis i.e. ${\mathit{B}}_{\mathit{o}}=B_o{\mathit{e}}_{\mathit{z}}$ .The highly magnetized electrons and positrons of negligible inertia are assumed to flow along the direction of ambient magnetic field (Kalita and Bhatta, 1997). For time scales of the order of inverse of ion cyclotron frequency, electrons and positrons have time to relax into distributions (Sheerin and Ong, 1979) which we consider to be q-nonextensive along Z-axis. In order to model the effects of electrons’ nonextensivity, we refer to the following one dimensional q-distribution function (Silva et al., 1998; Liu et al., 2011)

The constant of normalization is

Hence, the limits of integration of $f(v_z\text{,}\psi )$ over the velocity space should be from $-\infty$ to $+\infty$ for $-1<q<1$ and $-v_{\mathit{max}}$ to $+v_{\mathit{max}}$ for $q>1$ . However, the integration yields the same result in either of these cases (Liu et al., 2011).

In the same way, we can model nonextensive positrons by the following distribution function

The equation of state of an ideal gas of electrons at thermal pressure P and temperature $T_e$ in the nonextensive kinetic theory (Liu et al., 2011) is obtained as

In the limit q → 1, the effective temperature reduces to the thermal temperature for the Maxwellian distribution.The effective temperature will change with the values of $T_e$ on keeping q constant. From Eq. (6), we find that $q>1/3$ . Hence, the range of q values greater than $1/3$ will be used in our subsequent analysis.

The ratio between the effective plasma thermal pressure and magnetic pressure is ${\beta }_{\mathit{eff}}=\beta T_{\mathit{eff}}/T_e$ ( $\beta =\frac{2{\mu }_o{n}_{\mathit{io}}{T}_e}{B_o^2}$ ; $n_{\mathit{io}}$ being equilibrium ion density). We assume that ${\beta }_{\mathit{eff}}$ and hence $\beta$ is small but much larger than the electron-to-ion mass ratio i.e. $m_e/m_i$  ≪  ${\beta }_{\mathit{eff}}$  ≪ 1. Under low β plasma assumption, the compressive component of the magnetic field perturbations, $B_{1z}$ can be ignored. This fact leads us to use two potential fields (Kadomtsev, 1965) to represent the electric field as

This allows that only shear perturbations in the magnetic field are present which are expressed as $B_z=B_o$ (constant), $B_x=0$ .

The set of equations governing the dynamics of KAWs (Yu and Shukla, 1978) for small but finite β ( $m_e/m_i$  ≪  ${\beta }_{\mathit{eff}}$  ≪ 1) e-p-i plasma are as follows

For current density in the Z-direction, Faraday’s law and Ampere’s law together give

Contributions to parallel current density $j_z$ come from electrons, positrons and ions. Thus, by making use of continuity equations for electrons and positrons, we get

Quasi-neutrality condition reads

Number densities of electrons and positrons are given by Eqs. (4) and (5).

Linearizing Eqs .(4), (5) and (8)–(13) and assuming that all the perturbed physical quantities vary as ${\text{e}}^{i(k_{x}x+k_{z}z-\omega t)}$ , one can form a matrix equation about amplitude vectors of perturbed electric fields, in which coefficient matrix involves wave frequency $\omega$ and wave vector ( $k_x\text{,}0\text{,}{k}_z$ ). The dispersion relation is then obtained by letting the determinant of the coefficient matrix equal to zero. Thus,we get the following dispersion relation for our nonextensive e-p-i plasma model

In the absence of positrons ( $r=0$ ), the dispersion relation (Eq. (14)) reduces to that obtained by Liu et al. (2011). On the other hand, in the limit q → 1 and $r=0$ , this dispersion relation can be reduced to that well-known form obtained by Hasegawa (1977). Eq. (14) shows the coupling of Alfvén wave with ion acoustic wave. However, these modes decouple for low β plasma and the dispersion relation of KAWs becomes

The dispersion relation of KAWs in Maxwellian e-p-i plasma (Shukla et al., 2004) can be recovered from Eq. (15) in the limit q → 1. Eq. (15) indicates that for its oblique propagation to the direction of ambient magnetic field, Alfvén wave becomes dispersive due to finite ion gyroradius effect ( ${\rho }_i$ ).

In order to see how the frequency of KAWs varies with positron density and nonextensive parameter, we have plotted parallel phase velocity of KAWs against r and q while keeping $k_x{v}_A/\mathrm{\Omega }$ as constant (Fig. 1). The values of other parameters are indicated in each of the panels of Fig. 1. It is evident from the panels of Fig. 1 that the frequency of KAWs decreases with increase in positron density (r), nonextensive parameter (q) and electron temperture ( $\alpha$ ). The reduction of frequency of KAWs due the presence of positron compoent (Fig. 1(a)) in e-i magnetoplasma agrees to the prediction of Shukla et al.(2004).We also find from Fig. 1 that frequency of KAWs is greater (for q < 1) or less (for q > 1) than that in usual Maxwellian (q → 1) plasma.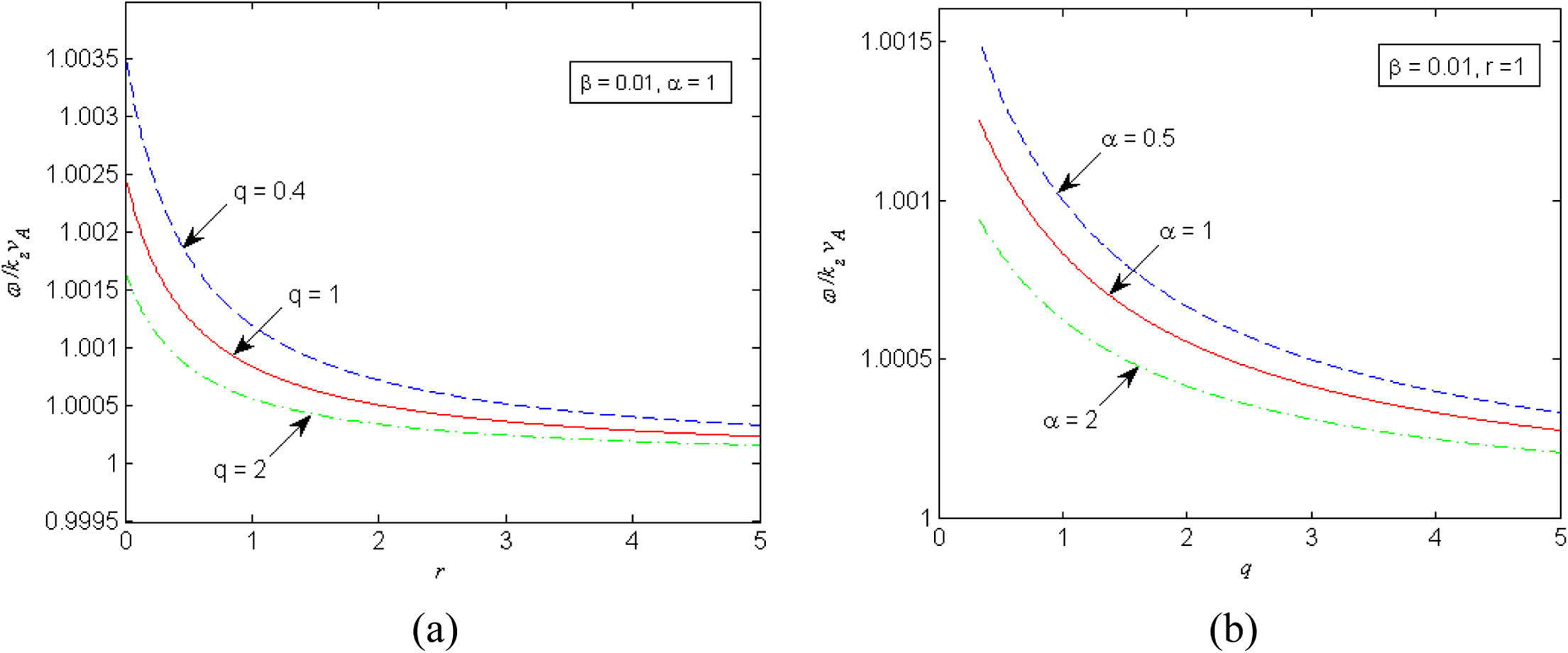

Close

Fig. 1

Plots of $\omega /k_z{v}_A$ against r (panel ‘a’) and q (panel ‘b’) depicting the effects of q and $\alpha$ respectively for constant $k_x{v}_A/\mathrm{\Omega }$ . The values of other parameters are indicated in each figure.

Export to PPT

3 Derivation of Sagdeev potential in small amplitude limit

In order to obtain one dimensional time-stationary planar solutions, we define moving co-ordinate by $\eta =K_{x}x+K_{z}z-\mathit{Mt}$ , where $M=V/C_s$ is the Mach number, V is the speed of nonlinear structures and K_x, K_z are direction cosines related by $K_x^2+K_z^2=1$ . Further, on normalizing time to inverse of ion cyclotron frequency ${\mathrm{\Omega }}^{-1}$ ,components of velocities to ion-acoustic speed $C_s$ , space coordinates to equivalent ion gyroradius ( $C_s/\mathrm{\Omega }$ ), electric potentials to $T_e/e$ and particle densities to their respective equilibrium values, we get from Eqs. (4), (5) and (8)–(13)

Integrating Eqs. (18) and (19), we get

Eq. (20) along with Eqs. (23) and (24) gives

Integrating Eq. (21) twice, we get after substitution of Eq. (24)

In deriving Eqs. (23)–(27), we have replaced n_i by n and use the boundary condtions $v_x=v_z={\partial }_{\eta }n=0$ and $n=1$ at $|\eta |$  = ∞ for localized solutions to determine the constants of integrations.

Subtracting Eq. (27) from Eq. (26), we get

The integral (Eq. (30)) can not simply have an analytical solution. So, we go for small amplitude limit to obtain the expression for pseudopotential. Expanding Sagdeev potential near $\psi \approx 0$ and retaining terms up to order ${\psi }^3$ , we get

The Eq. (29) can now be simplified to the form

4 Results and discussion

In order to obtain solitary wave solution in the small amplitude limit, we impose the boundary condition $V(\psi )=0$ at $\psi ={\psi }_{\mathit{max}}$ ( ${\psi }_{\mathit{max}}$ is the soliton amplitude) in the Eq. (31) to obtain

Using this result in Eq. (34) and then integrating it, we obtain soliton solution of the form

Or

The inequalities (37) and (38) lead to the following condition if we consider the fact that $q>1/3$ and $\beta \ll 1$

In order to identify the nature of solitary KAWs, we have surface plotted B against soliton parallel velocity ( $a$ ) and nonextensive paramter ( $q$ ) for different values of other plasma parameters based on the inequality given by (39) (Fig. 2). It is evident from each of the panels of Fig. 2 that only compressive ( $B<0$ ) type of solitary KAWs can exist in the nonextensive e-p-i plasma model considered here. The result that the existence of sub-Alfvénic compressive solitons in our nonextensive e-p-i plasma model agrees to that reported in (Adnan et al., 2016; Kakati and Goswami, 1998) but differs from (Sah, 2010) which showed the existence of both sub and super-Alfvénic compressive solitons in Maxwellian e-p-i plasma.

Close

Fig. 2

Surface plots of B against $a$ and $q$ indicating the nature of solitary KAWs for different values of $r=0.5$ (red surface), $r=1$ (green surface), $r=1.5$ (blue surface) [panel (a)]; and $\alpha =0.5$ (red surface), $\alpha =1.5$ (green surface), $\alpha =2$ (blue surface) [panel (b)].The values of other parameters are as indicated in each panel.

Export to PPT

The shapes of sub-Alfvénic compressive solitary KAWs incorporating effects of various plasma parameters are shown in Fig. 3. It is observed from the panel (a) of Fig. 3 that both amplitude and width of solitary KAWs decrease with increase in nonextensive parameter (q).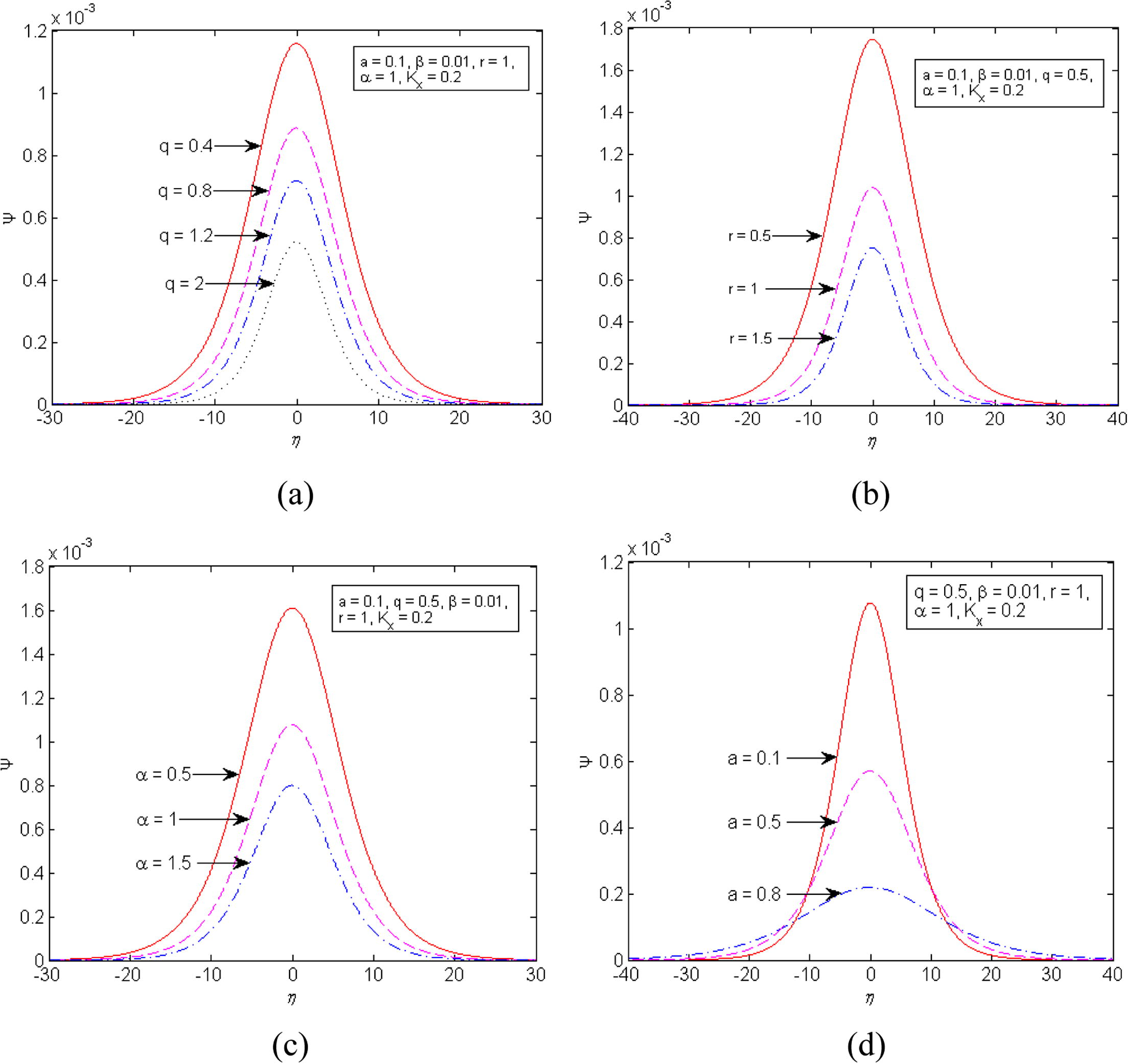

Close

Fig. 3

Potential profiles of solitary KAWs for different values of (a) $q$ , (b) $r$ , (c) $\alpha$ and (d) $a$ . The values of other parameters are as indicated in each panel.

Export to PPT

However, it has been reported in (Adnan et al., 2016) that both amplitude and width of solitary KAWs increase with the rise of superthermality parameter ( $\kappa$ ). It is seen from panels (b) and (c) of Fig. 3 that amplitude as well as width of solitary KAWs decreases with the rise of positron concentration ( $r$ ) and electron temperature ( $\alpha )$ . We find from the panel (d) of Fig. 3 that solitary KAWs broaden with corresponding decrease of amplitudes as they propagate with increasing sub-Alfvénic speeds.

5 Conclusions

Following q-nonextensive distributions for electrons and positrons in low but finite $\beta$ collisionless e-p-i plasma, we have derived linear dispersion relation of KAWs and have also investigated small amplitude solitary KAWs through Sagdeev pseudopotential approach. Linear analysis of KAWs shows that the frequency of the wave decreases with increase in each of the parameters r, q and $\alpha$ . Moreover, frequency of KAWs is found to be greater (for q < 1) or less (for q > 1) than that in usual Maxwellian (q→1) plasma. Nonlinear analysis of KAWs shows the existence of sub-Alfvénic compressive solitary waves in the nonextensive e-p-i plasma system under consideration. Amplitudes of solitary KAWs are found to be decreased on increasing r, $\alpha$ and q. Moreover, solitary KAWs broaden with corresponding decrease of amplitudes as they propagate with increasing sub-Alfvénic speeds. Considering the wide relevance of KAWs in space, astrophysical and other plasma environments (Sah, 2010), the results of the present theoretical investigations might be useful in understanding the formation of low frequency electromagnetic noises/small amplitude localized fluctuations in such regions dominated by magnetized e-p-i plasmas having nonextensive electrons and positrons.