Sine-Gordon expansion method for exact solutions to conformable time fractional equations in RLW-class
⁎Corresponding author. alperkorkmaz7@gmail.com (Alper Korkmaz)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The Sine-Gordon expansion method is implemented to construct exact solutions some conformable time fractional equations in Regularized Long Wave (RLW)-class. Compatible wave transform reduces the governing equation to classical ordinary differential equation. The homogeneous balance procedure gives the order of the predicted polynomial-type solution that is inspired from well-known Sine-Gordon equation. The substitution of this solution follows the previous step. Equating the coefficients of the powers of predicted solution leads a system of algebraic equations. The solution of resultant system for coefficients gives the necessary relations among the parameters and the coefficients to be able construct the solutions. Some solutions are simulated for some particular choices of parameters.
Keywords
35C07
35R11
35Q53
Sine-Gordon expansion method
Conformable time fractional RLW equation
Conformable time fractional modified RLW equation
Conformable time fractional symmetric-RLW equation

1 Introduction
Even though some nonlinear partial differential equations are integrable, it may be not easy to integrate them. Instead, a predicted solution with parameters are assumed to be a solution of governing equations and the relations among the parameters are investigated. The logic is simply based on the similarity with exponential-type solutions to the ordinary differential equations with constant coefficients. These predicted solutions are of various forms covering exponential, hyperbolic, trigonometric or rational functions, and more. Moreover the interaction of various types of waves were also determined by using analytical techniques (Ma and Zhou, 2018; Zhang and Ma, 2017; Zhao and Ma, 2017; Yang et al., 2017; Ma et al., 2018). Parallel to the recent developments in computer algebra in the last four decades, a tendency has been observed to determine exact solutions to nonlinear PDEs by following the procedure that starts with a predicted solution. Recently, this tendency has focused on exact solutions to fractional nonlinear partial differential equations. Many of techniques implemented to nonlinear PDEs to find exact solutions have been adapted for fractional nonlinear PDES (Korkmaz and Hosseini, 2017; Hosseini and Ansari, 2017; Kumar et al., 2017; Korkmaz, 2017a,b; Hosseini et al., 2017a,b; Kumar et al., 2018a,b; Rezazadeh et al., 2018; Singh et al., 2017a,b; Guner et al., 2017a,b). We also derive exact solutions to some conformable fractional equations in RLW-class modeling various wave phenomena both in nature or technology implementations. Different from previous studies, we adapt Sine-Gordon expansion approach to determine exact solutions to governing equations in fractional RLW-class.
The first equation considered in this study is the RLW equation
The second equation to discuss exact solutions here is the modified RLW (mRLW) equation of the form
The last equation to derive the exact solutions is the symmetric RLW (sRLW) equation
Before starting the solution procedure, we should give some significant properties of conformable fractional derivative. Thus, the next section focuses on conformable fractional derivative definition and some important properties. We explain the solution procedure in the third section. The following sections cover implementations of the proposed procedure to some conformable fractional PDEs in RLW-class.
2 Conformable fractional derivative
The conformable derivative of order
Assume that the order of the derivative
-
-
-
-
-
-
Conformable fractional differential operator satisfies some critical fundamental properties like the chain rule, Taylor series expansion and Laplace transform (Abdeljawad, 2015).
Let
3 Sine-Gordon expansion method
The compatible fractional form
4 Solutions to the conformable time fractional RLW equation
The traveling wave transform
Set 1:
Set 2:
Set 3:
Set 4:
Set 5:
Set 6:
Using these solution sets of algebraic equations, we construct the solutions to (1) as
A particular form of

- The solution
5 Solutions to the conformable time fractional mRLW equation
The traveling wave transform
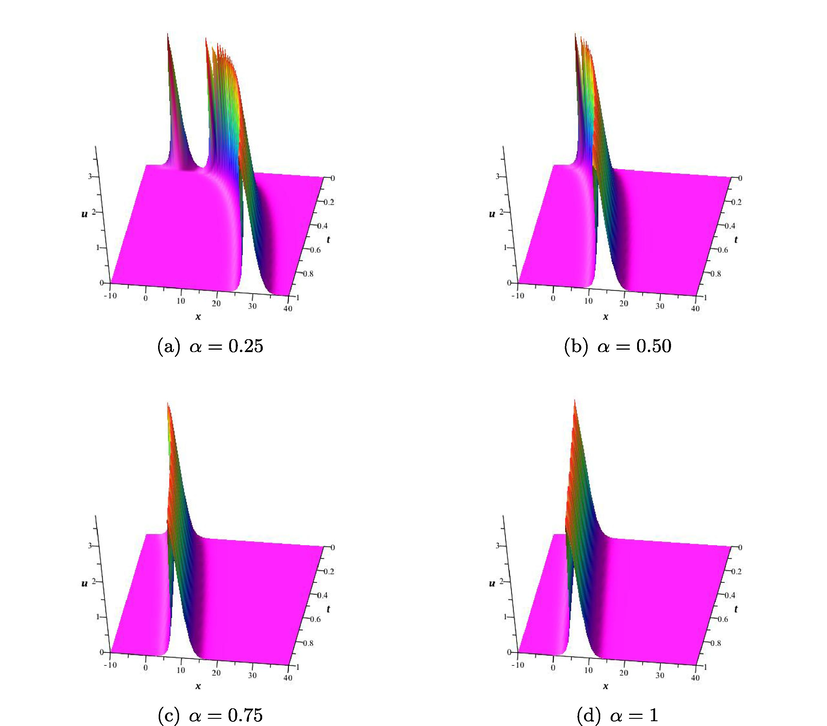
- The solution
6 Solutions to the conformable time fractional sRLW equation
The traveling wave transform
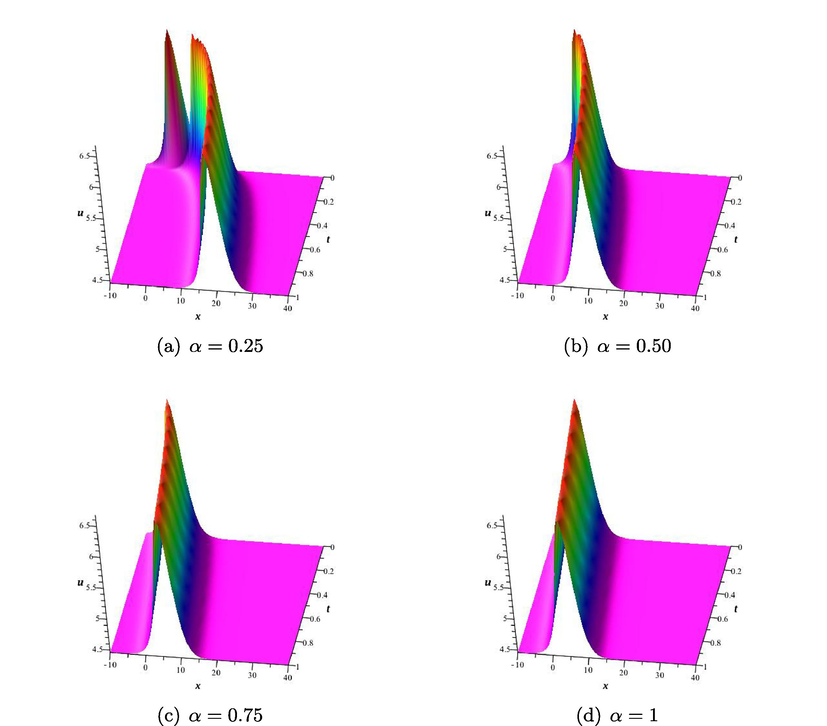
- The solution
7 Conclusion
In the paper, exact solutions of some conformable fractional equations in the RLW-class are investigated by using Sine-Gordon expansion approach. Using compatible wave transform, the equations are reduced to some ODEs. Then, the predicted solutions are substituted into the resultant ODE. Equating the coefficients of cosine and sine functions and their multiplications to zero leads to some algebraic system of equation. Solving this system gives the relations among the parameters. The method differs from many classical method since the terms in the series are multiplication of powers of different hyperbolic functions. In conclusion, some real and complex solutions that are combinations of powers of hyperbolic tangent and hyperbolic secant functions are determined explicitly. Graphical representations of some real valued solutions are depicted in some finite domains to comprehend the effects of
References
- Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. London A: Math., Phys. Eng. Sci.. 1972;272(1220):47-78.
- [Google Scholar]
- Approximations of solitary waves of the MRLW equation by B-spline finite element. Arab. J. Sci. Eng.. 1997;22:183-193.
- [Google Scholar]
- Tanh-type and sech-type solitons for some space-time fractional PDE models. Eur. Phys. J. Plus. 2017;132(92):1-12.
- [Google Scholar]
- Dark solutions of space-time fractional Sharma-Tasso-Olver and potential Kadomtsev-Petviashvili Equations. Commun. Theor. Phys.. 2017;67(2):182-188.
- [Google Scholar]
- New exact solutions of nonlinear conformable time-fractional Boussinesq equations using the modified Kudryashov method. Waves Random Complex Media 2017:1-9.
- [Google Scholar]
- Bright and singular soliton solutions of the conformable time-fractional Klein-Gordon equations with different nonlinearities. Waves Random Complex Media 2017:1-9.
- [Google Scholar]
- Modified Kudryashov method for solving the conformable time-fractional Klein-Gordon equations with quadratic and cubic nonlinearities. Optik-Int. J. Light Electron Opt.. 2017;130:737-742.
- [Google Scholar]
- Petrov-Galerkin finite element method for solving the MRLW equation. Math. Sci.. 2013;7(1):25.
- [Google Scholar]
- Numerical approximation to a solution of the modified regularized long wave equation using quintic B-splines. Boundary Value Prob.. 2013;2013(1):27.
- [Google Scholar]
- A collocation method with cubic B-splines for solving the MRLW equation. J. Comput. Appl. Math.. 2008;212(2):406-418.
- [Google Scholar]
- Exact solutions of space-time fractional EW and modified EW equations. Chaos, Solitons Fractals. 2017;96:132-138.
- [Google Scholar]
- Exact solutions to (3 + 1) conformable time fractional Jimbo-Miwa, Zakharov-Kuznetsov and modified Zakharov-Kuznetsov equations. Commun. Theor. Phys.. 2017;67(5):479-482.
- [Google Scholar]
- Complex wave solutions to mathematical biology models I: Newell-Whitehead-Segel and Zeldovich equations. . 2018;13(8):081004-1. 1
- [Google Scholar]
- Exact solutions of a nonlinear conformable time-fractional parabolic equation with exponential nonlinearity using reliable methods. Opt. Quant. Electron.. 2017;49(8):278.
- [Google Scholar]
- A new analysis for fractional model of regularized long wave equation arising in ion acoustic plasma waves. Math. Methods Appl. Sci.. 2017;40(15):5642-5653.
- [Google Scholar]
- Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Physica A. 2018;492:155-167.
- [Google Scholar]
- A new numerical algorithm for fractional Fitzhugh-Nagumo equation arising in transmission of nerve impulses. Nonlinear Dyn.. 2018;91(1):307-317.
- [Google Scholar]
- Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation. Int. J. Non-Linear Mech.. 1996;31(3):329-338.
- [Google Scholar]
- A transformed rational function method and exact solutions to the 3 + 1 dimensional Jimbo-Miwa equation. Chaos, Solitons Fractals. 2009;42(3):1356-1363.
- [Google Scholar]
- Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J. Diff. Equ.. 2018;264(4):2633-2659.
- [Google Scholar]
- A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr.. 2010;82(6) 065003
- [Google Scholar]
- Diversity of interaction solutions to the (2 + 1)-dimensional Ito equation. Comput. Math. Appl.. 2018;75:289-295.
- [Google Scholar]
- Numerical solutions of RLW equation using Galerkin method with extrapolation techniques. Comput. Phys. Commun.. 2012;183(8):1609-1616.
- [Google Scholar]
- Calculations of the development of an undular bore. J. Fluid Mech.. 1966;25(02):321-330.
- [Google Scholar]
- Traveling wave solution of conformable fractional generalized reaction Duffing model by generalized projective Riccati equation method. Opt. Quant. Electron.. 2018;50(3):150.
- [Google Scholar]
- Numerical analysis of the regularized long-wave equation: anelastic collision of solitary waves. Il Nuovo Cimento B (1971–1996). 1978;46(1):179-188.
- [Google Scholar]
- A symmetric regularized-long-wave equation. Phys. Fluids (1958-1988). 1984;27(1):4-7.
- [Google Scholar]
- A novel numerical approach for a nonlinear fractional dynamical model of interpersonal and romantic relationships. Entropy. 2017;19(7):375.
- [Google Scholar]
- A hybrid computational approach for Jeffery-Hamel flow in non-parallel walls. Neural Comput. Appl. 2017:1-7.
- [Google Scholar]
- Collocation method using quartic B-splines for solving the modified RLW equation. Indian J. Sci. Technol.. 2017;10(31)
- [Google Scholar]
- J. Comput. Nonlinear Dyn.. 1996;224:77-84.
- Lump and lump-soliton solutions to the (2 + 1)-dimensional Ito equation. Anal. Math. Phys. 2017:1-10.
- [Google Scholar]
- Mixed lump-kink solutions to the BKP equation. Comput. Math. Appl.. 2017;74(3):591-596.
- [Google Scholar]
- Mixed lump-kink solutions to the KP equation. Comput. Math. Appl.. 2017;74(6):1399-1405.
- [Google Scholar]






