Sinc and B-Spline scaling functions for time-fractional convection-diffusion equations

1 Introduction.

The fractional differential equations, which have arised in numerous fields of engineering and science, is developed to the varied mathematical models by several studies (Kilbas et al., 2006; Hilfer, 2000; Carpinteri and Mainardi, 1997; Metzler and Klafter, 2000). The fractional partial differential equations can be classified into space-fractional differential equation and time-fractional differential equation. Here we consider the time-fractional convection-diffusion equation with variable coefficients

In Eq. (1) the Liouville-Caputo type of the fractional derivative of order $0<\gamma ⩽1$ is defined by

Time-fractional diffusion equations are derived by considering continuous time random walk problems, which are in general non-Markovian processes. The physical interpretation of the fractional derivative is that it represents a degree of memory in the diffusing material (Metzler and Klafter, 2000). In time-fractional convection-diffusion equation, the fractional derivative is considered in the Caputo sense. The general response expression contains a parameter describing the order of the fractional derivative that can be varied to obtain various responses. In the case of $\gamma =1$ , the fractional equation reduces to a classical convection-diffusion equation with nonlinear source term. The convection-diffusion equations are widely used in science and engineering as mathematical models for computational simulations, such as in oil reservoir simulations, transport of mass and energy, and global weather production, in which an initially discontinuous profile is propagated by diffusion and convection, the latter with a speed of c (Momani, 2007; Sincovec and Madsen, 1975).

There are several methods for approximating the solution of the problem (1)–(3). Chen et al. (2010) used Haar wavelet method to determine the solution of the problem (1)–(3). Yang et al. (2015) used the local fractional similarity solution for the non-differentiable diffusion equation defined on Cantor sets. Yang and Srivastava et al. investigated general fractional derivatives with a non-singular power-law kernel, also the anomalous diffusion models with non-singular power-law kernel have been discussed in detail in Yang et al. (2017). Mahto et al. established the approximate controllability of the sub-diffusion equation by applying a unique continuation property via internal control which acts on a sub-domain in Mahto et al. (2019). Yang et al. (2016) proposed a new numerical technique based upon a certain two dimensional extended differential transform via local fractional derivatives and derive its associated basic theorems and properties for solving the local fractional diffusion equation. Zhukovsky and Srivastava (2017) obtained solutions for differential equations, describing a broad range of physical problems by the operational method with recourse to inverse differential operators, integral transforms and operational exponent. Generalized families of orthogonal polynomials and special functions have been employed with recourse to their operational definitions in Gaoa et al. (2016) a coupling of the variational iteration method with the Sumudu transform via the local fractional calculus operator have been proposed for a class of local fractional diffusion equations. Murio (2008) applied an implicit finite difference scheme to solve the time-fractional diffusion equations. Finite difference approximation is developed for fractional equations in Meerschaert and Tadjeran (2004), Ren et al. (2013), Su et al. (2010). In Jiang and Ma (2011) and Roop (2006) used high-order finite element schemes to approximate the time fractional partial differential equations. RBF meshless method for fractional diffusion equations are studied in Uddin and Haq (2011) and Piret and Hanert (2013). The numerical contour integral approach is developed for solving the time-fractional diffusion equations in Vong and Lyu (2017). To solve the fractional diffusion equations in Lin et al. (2014), the preconditioned iterative schemes is applied. The combination of single exponential transformation of Sinc and Legendre collocation method applied for a class of fractional convection-diffusion equations with variable coefficients in Saadatmandi et al. (2012). Eftekhari (2019) used a combination of the Sinc method and the Euler polynomials to solve the convection diffusion equations including time-fractional derivative of Liouville-Caputo type. Mirzaee et al. considered the fractional stochastic diffusion equations, nonlinear integral equations and integro-differential equations in Mirzaee and Alipour (2020), Mirzaee and Samadyar (2020), Alipour and Mirzaee (2020), Mirzaee and Alipour (2020), Mirzaee and Alipour (2019), Mirzaee and Samadyar (2019), Mirzaee and Samadyar (2018), Mirzaee and Samadyar (2019), Mirzaee and Samadyar (2018) and applied several approaches to solve those problems such as: Quintic B-spline collocation method, finite difference method, meshless method, iterative algorithm, bilinear spline interpolation, orthonormal Bernstein collocation method.

Dehghan et al. (2013) used Ritz-Galerkin method combine with Bernstein multi-scaling functions and cubic B-spline functions to solve an inverse heat conduction problem. He, also used the cubic B-spline scaling functions and Chebyshev cardinal functions to approximate the solution of Riccati equation in Lakestani and Dehghan (2010). Dehghan and his colleagues solved nonlinear fractional partial differential equations by using homotopy analysis method in Dehghan et al. (2010). The two-dimensional Schrodinger equation with nonhomogeneous boundary conditions has been considered in Dehghan and Emami-Naeini (2013) and Sinc-collocation and Sinc- Galerkin methods has been used to approximate this problem. In Dehghan (2004), the two-level fully explicit and fully implicit finite difference approximations are developed and compared for solving the three-dimensional advection-diffusion equation with constant coefficient by Dehghan et al. In Irandoust-pakchin et al. (2014), Irandoust-pakchin et al. has been concerned the construction of biorthogonal multiwavelet basis in the unit interval to form a biorthogonal flatlet multiwavelet system, then the system has been used to solve a fractional convection-diffusion equation.

To discretize the time-fractional convection diffusion problem (1)–(3) in our approach, the spatial discretization is proposed by Sinc interpolation method combine with the double exponential transformation, and the temporal discretization is proposed by the B-Spline scaling functions. Recently, the double exponential transformation (Mori and Sugihara, 2001) has been developed for the Sinc numerical methods and appllied in quadrature and differential equations (Sugihara and Matsuo, 2004; Stenger, 1993; Lund and Bowers, 1992; Tanaka et al., 2009). DE-Sinc-collocation method has been used to solve the nonlinear second order two-point boundary value problems in Rashidinia et al. (2014). Sinc numerical approximation method for Liouville-Caputo’s fractional derivatives developed in Okayama et al. (2010), Okayama et al. (2010), and Baumann and Stenger (2011).

The B-spline scaling functions which are compactly supported and specially constructed for the bounded interval are introduced in Daubechies (1988) and Chui (1992). The authors of Lakestani and Dehghan (2012), Cohen (2003), Micula and Micula (1998) by using the linear B-spline scaling functions constructed the operational matrix of fractional derivative in the Liouville-Caputo sense. In this manuscript, we consider the B-spline scaling functions which are satisfied all the properties on a bounded interval. The authors in Goswami et al. (1995) by using wavelets on a bounded interval approximate the solution of first-kind integral equations.

Our method consists of reducing the problem to the solution of algebraic equations by expanding the required approximate solution as the elements of the B-Spline scaling functions in time and the Sinc functions combine with the double exponential transformation in space with unknown coefficients. The properties of Sinc functions and B-Spline scaling functions are then utilized to evaluate the unknown coefficients. The sinc method is efficient for boundary value problems with homogeneous conditions, and due to the exponential convergence nature of the Sinc-collocation method combine with the double exponential transformation, one can get the considerable accurate results (see the Theorem 1). To the best of the authors’ knowledge, such approach has not been employed for solving fractional partial differential equations.

The article is composed as follows. In Section (2), we present some properties of Sinc interpolation scheme. In Section (3), the B-spline scaling functions on the bounded interval has been introduced. In Section (4), we developed the B-Spline-Sinc approximation method to apply time-fractional convectiondiffusion equations. The complexity analysis is given in Section (5). Finally, in Section (6), we applied the presented method on some examples. We compared our results with the outcomes in the existing schemes.

2 The Sinc properties

Definition of the Sinc function is as follows Stenger (1993) and Lund and Bowers (1992) $$\mathit{Sinc}(x)=\left\{\begin{array}{c}\frac{\mathit{sin}(\pi x)}{\pi x},x\ne 0\hfill \\ 1,x=0,\hfill \end{array}\right.$$ and the k-th shifed Sinc function is defined by $$S(k,h)(x)=\mathit{Sinc}\left(\frac{x}{h}-k\right),$$ where $h>0$ and $k\in \mathbb{Z}$ .

The following double exponential transformation maps the real line to a finite interval $(a,b)$ , then we can apply the Sinc function on a finite interval $(a,b)$ (Mori and Sugihara, 2001; Sugihara and Matsuo, 2004; Tanaka et al., 2009) $$x=\psi (s)=\frac{b(\mathit{tanh}(\frac{\pi }{2}\mathit{sinh}(s))+1)-a(\mathit{tanh}(\frac{\pi }{2}\mathit{sinh}(s))-1)}{2},$$ and the inverse mapping is defined by $$s={(\psi )}^{-1}(x)=\mathit{log}\left[\frac{1}{\pi }\mathit{log}(\frac{x-a}{b-x})+\sqrt{1+{\left(\frac{1}{\pi }\mathit{log}(\frac{x-a}{b-x})\right)}^2}\right],$$ then the collocation points of Sinc are $x_k=\psi (\mathit{kh})$ .

The cardinal Sinc expansion of given function $g(x)$ , which is defined in real line and also vanishes on end points, is defined by Lund and Bowers (1992)

3 B-spline scaling functions

By integral convolution, we can define the m-th order cardinal B-spline $N_m(t)$ for $m⩾2$ as follow

In this article, to approximate the unknown function in time, we consider the quadratic B-spline scaling functions with $m=3$ , in the bounded interval $[0,1]$ as basis functions.

Let the multiresolution spaces $V_J$ is generated by tensor product type, and $$V_J=\mathit{span}\{{\phi }_{J,l}=2^{J/2}\phi (2^{J}t-l)\text{;}l\in Z\}$$

In order to have at least one complete inner scaling function in the bounded interval $[0,1]$ , the condition

By using (9) and (10) the inner B-Spline scaling functions of order $m=3$ are given by

The Liouville-Caputo fractional derivative of order $0<\gamma <1$ for the inner scaling functions can be obtained by

4 The B-Spline-Sinc method for the fractional diffusion equations

We apply B-Spline scaling functions of order $m=3$ and Sinc interpolation that defined in Sections 2 and 3, and by changing of variable $x=\psi (s)=\frac{b-a}{2}\mathit{tanh}(\frac{\pi }{2}\mathit{sinh}(s))+\frac{b+a}{2}$ to applied Sinc-collocation method and setting $u(\psi (s),t)=v(s,t)$ in Eqs. (1) we transforme the problem (1)–(2) into following problem (see Rashidinia et al., 2014)

Note: If the boundary conditions (2) are nonhomogeneous as follows $$u(a,t)=\alpha (t),u(b,t)=\beta (t),t\in (0,T],$$ then by using the following change of variable we can reformulate the boundary conditions (2) to homogeneous one $$u(x,t)=U(x,t)+\frac{b-x}{b-a}\alpha (t)+\frac{x-a}{b-a}\beta (t)\text{.}$$

Here we explain B-Spline-Sinc algorithm to approximat the solution of Eq. (22).

5 Complexity analysis

We begin with Eqs. (24)–(26). The total number of instructions in each Eqs. (24)–(26) is ${(2M+1)}^2{(2^J+2)}^2$ , therefore the total instructions in system (27)-(28) is

We applied LU factorization to solve the $(2M+1)(2^J+2)\times (2M+1)(2^J+2)$ system (27)-(28), thus, the computational complexity of LU factorization is on the order of $O(8^J{M}^3)$ .

6 Numerical illustration

To compared our approach with the method in Chen et al. (2010) and Saadatmandi et al. (2012), we apply the B-spline-Sinc method on the following example to show that the approximation of solution of time-fractional convection-diffusion equation by our method is more accurate. In this section we assume $J=3,d=\frac{\pi }{2},\rho =\pi ,h=\frac{\mathit{log}(\frac{\pi \mathit{dM}}{\rho })}{M}$ , and also by choosing various values of M. The computation developed on personal computer with 8 GB memory by Mathematica 12.1 software.

6.1

6.1 Example 1

Consider the following time fractional diffusion equation (Chen et al., 2010; Saadatmandi et al., 2012)

(30)

$${}_0{D}_t^{\gamma }u(x,t)+x\frac{\partial u(x,t)}{\partial x}+\frac{{\partial }^{2}u(x,t)}{\partial x^2}=2t^{\gamma }+2x^2+2,x\in (0,1),0<t⩽1,$$ with boundary conditions

(31)

$$u(0,t)=2t^{2\gamma }\frac{\mathrm{\Gamma }(\gamma +1)}{\mathrm{\Gamma }(2\gamma +1)},u(1,t)=2t^{2\gamma }\frac{\mathrm{\Gamma }(\gamma +1)}{\mathrm{\Gamma }(2\gamma +1)}+1,t\in (0,1],$$ and initial condition

(32)

$$u(x,0)=x^2,x\in [a,b],$$ the exact solution is $u(x,t)=x^2+2t^{2\gamma }\frac{\mathrm{\Gamma }(\gamma +1)}{\mathrm{\Gamma }(2\gamma +1)}$ .

Fig. 1 shows a comparison of exact solution and approximate solution with $M=20$ and maximum absolute error in the solution on $(x,t)\in [0,1]\times (0,1]$ for Example 1 according to the number of Sinc point $M=15$ and $M=20$ by applying the B-Spline-Sinc method with $\gamma =0.8$ .

Close

Fig. 1

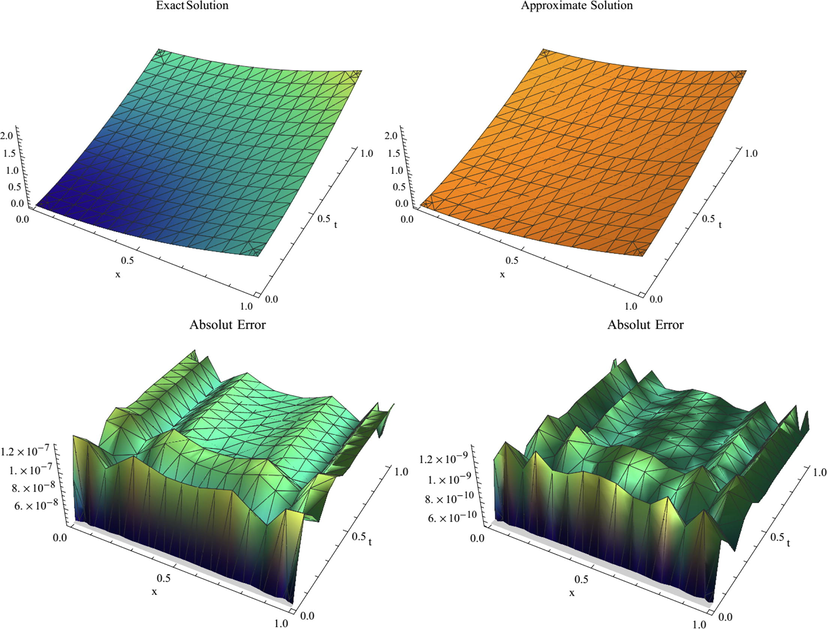
Top: Comparison of exact solution and approximate solution with $M=20$ and $J=3$ by applying presented method with $\gamma =0.8$ for Example 1. Bottom: Maximum absolute error according to the number of central Sinc point $M=15$ (left) and $M=20$ (right) with $\gamma =0.8$ for Example 1.

Export to PPT

Absolute error with $M=20$ at the time point $t=1$ and maximum absolute errors in the solution on $(x,t)\in [0,1]\times (0,1]$ according to the number of Sinc point $3⩽M⩽25$ plotted in Fig. 2.

Close

Fig. 2

Graph of absolute error with $M=20$ at the time point $t=1$ (left) and maximum absolute error on $(x,t)\in [0,1]\times (0,1]$ according to the number of central Sinc point M (right) with $\gamma =0.8$ for Example 1.

Export to PPT

The comparison of the results of BSpline method combine with Sinc function and the results given in Chen et al. (2010) and Saadatmandi et al. (2012) at the time $t=0.5$ with $\gamma =\frac{1}{2}$ is shown in Table 1. In Table 1 we show a comparison between our method, according to the number of central Sinc point $M=5,20$ and $J=3$ for B-Spline basis function, and Sinc-Legendre method (Saadatmandi et al., 2012) according to the number of central Sinc and Legendre point $M=15,25$ and $n=7$ respectively, and Wavelet method (Chen et al., 2010) with $M=32,64$ . In Table 1, one can see that the results given by B-Spline-Sinc method according to the number of central Sinc point $M=5$ are better than Wavelet method with the number of basis function $M=32$ and 64, also the given results by B-Spline-Sinc method with $M=5$ are very close to the results obtained by Sinc-Legendre method with the central point M = 15 and 25. The results obtained by presented method with M = 20 are too better than both Wavelet and Sinc-Legendre scheme.

Table 1 Comparison of absolute error for Example 1 with $\gamma =\frac{1}{2}$ and $t=\frac{1}{2}$ .

	B-Spline-Sinc method		Wavelet method (Chen et al., 2010)		Sinc-Legendre method (Saadatmandi et al., 2012)
x	$M=5$	$M=20$	$M=32$	$M=64$	$M=15$	$M=25$
$0.1$	$6.481e-04$	$1.369e-09$	$6.093e-03$	$1.210e-03$	$6.994e-05$	$6.462e-06$
$0.2$	$4.109e-04$	$7.591e-10$	$4.843e-03$	$1.259e-03$	$1.721e-04$	$1.578e-05$
$0.3$	$5.493e-04$	$1.184e-09$	$2.750e-02$	$1.865e-03$	$2.472e-04$	$2.272e-05$
$0.4$	$5.198e-04$	$1.068e-09$	$1.937e-02$	$7.412e-03$	$2.912e-04$	$2.674e-05$
$0.5$	$4.912e-04$	$9.819e-10$	$1.000e-06$	$1.000e-06$	$3.004e-04$	$2.759e-05$
$0.6$	$5.063e-04$	$1.039e-09$	$4.359e-02$	$7.460e-03$	$2.760e-04$	$2.534e-05$
$0.7$	$5.045e-04$	$1.031e-09$	$1.734e-02$	$1.724e-03$	$2.213e-04$	$2.035e-05$
$0.8$	$5.040e-04$	$1.030e-09$	$7.750e-02$	$4.990e-03$	$1.440e-04$	$1.320e-05$
$0.9$	$5.037e-04$	$1.031e-09$	$4.443e-02$	$1.678e-02$	$5.026e-05$	$4.653e-06$

The Table 1 and figurs 1 and 2 show that we can obtain more notable results than the methods in Chen et al. (2010) and Saadatmandi et al. (2012).