Translate this page into:
Simultaneous heat and mass transfer in natural convection about an isothermal vertical plate
*Corresponding author. Tel./fax: +98 841 2238527 farzad_khani59@yahoo.com (F. Khani)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 24 November 2010
Abstract
The homotopy analysis method has been used to derive a highly accurate analytic solution for simultaneous natural convection and mass transfer from an isothermal vertical plate. Velocity, temperature, and concentration profiles are presented for a fixed Prandtl number of 0.71 and for Schmidt numbers of 0.5, 5, and 10 and for the buoyancy ratio of 0 (pure mass transfer), 0.5 (simultaneous heat and mass transfer), and 1 (pure heat transfer). The present results corroborate well with the numerical results reported in other research literature on the problem. The auxiliary parameter in the homotopy analysis method is derived by using the averaged residual error concept which significantly reduces the computational time. The use of optimal auxiliary parameter provides a superior control on the convergence and accuracy of the analytic solution.
Keywords
Vertical plate
Natural convection
Simultaneous heat and mass transfer
Homotopy analysis method
Optimal convergence-control parameter
1 Introduction
The problem of simultaneous heat and mass transfer from an isothermal vertical flat plate is of fundamental importance to the thermal science community. The pioneering contributions to the problem were made by Gebhart and Pera (1971), Mollendorf and Gebhart (1974), Taunton et al. (1970), and Bottemanne (1972a,b). Because of simultaneous heat and mass transfer, the transport process is driven by the interaction of velocity, concentration and thermal boundary layers. The velocity, concentration, and temperature profiles depend on whether the buoyancy forces due to temperature difference and concentration difference aid (aiding flow) or oppose each other (opposing flow). Bottemanne (1972a,b) considered mass transfer due to the injection of water vapor from the plate into the surrounding fluid. He found that for the aiding flow, the heat and mass transfer processes can be treated independent of each other and the results combined to predict the case when the two processes occur simultaneously. This work was examined by Schenk et al. (1976) who noted that Bottemanne’s conclusion was valid because the Prandtl number Pr = 0.71 and Schmidt number Sc = 0.94 used by him were nearly the same. The numerical computations of Schenk et al. (1976) led to the conclusion that for Pr = 0.7 and 0.6 < Sc < 0.9, the mutual interaction of heat and mass transfer processes was indeed minimal and the two processes can be treated separately and the two results added. This approach gives results that are in error by about 2%, when compared with the result from the simultaneous analysis. The numerical method used by Schenk et al. (1976) involved an iterative procedure to solve the coupled similarity equations for the stream function, temperature, and concentration.
In the present work, we revisit the problem considered by Bottemanne (1972b) and provide a highly accurate analytical solution of the problem using the homotopy analysis method (HAM). In recent years, the homotopy analysis method (HAM) (Liao, 1999, 2003, 2009; Liao and Tan, 2007), has been successfully applied to many nonlinear problems in science and engineering (Molabahrami and Khani, 2009; Khani et al., 2009a,b,c; Khani and Aziz, 2010; Darvishi and Khani, 2009; Aziz and Khani, 2009). Unlike the perturbation techniques, HAM is independent of any small physical parameters. More importantly, unlike the perturbation and non-perturbation methods, HAM provides a simple way to ensure the convergence of series solution so that one can always get accurate enough approximations even for the strongly nonlinear problems. Furthermore, HAM provides the freedom to choose the so- called auxiliary linear operator so that one can approximate a nonlinear problem more effectively by means of better base functions, as demonstrated by Liao and Tan (2007). The degree of freedom is so large that even the second-order nonlinear two-dimensional Gelfand equation can be solved by means of a 4th-order auxiliary linear operator within the framework of the HAM as shown in Liao and Tan (2007). Especially, by means of the HAM, a few new solutions of some nonlinear problems (Liao, 2005, 2006) have been achieved which otherwise were not solvable by other analytic methods.
2 Formulation of the problem
The physical model and the coordinate system are shown in Fig. 1 where heat and water vapour are transferred simultaneously from the vertical flat plate to the environment. The directions of the velocity components u and v are also indicated. The boundary layer equations for this model can be written as (Bottemanne, 1972a; Schenk et al., 1976)
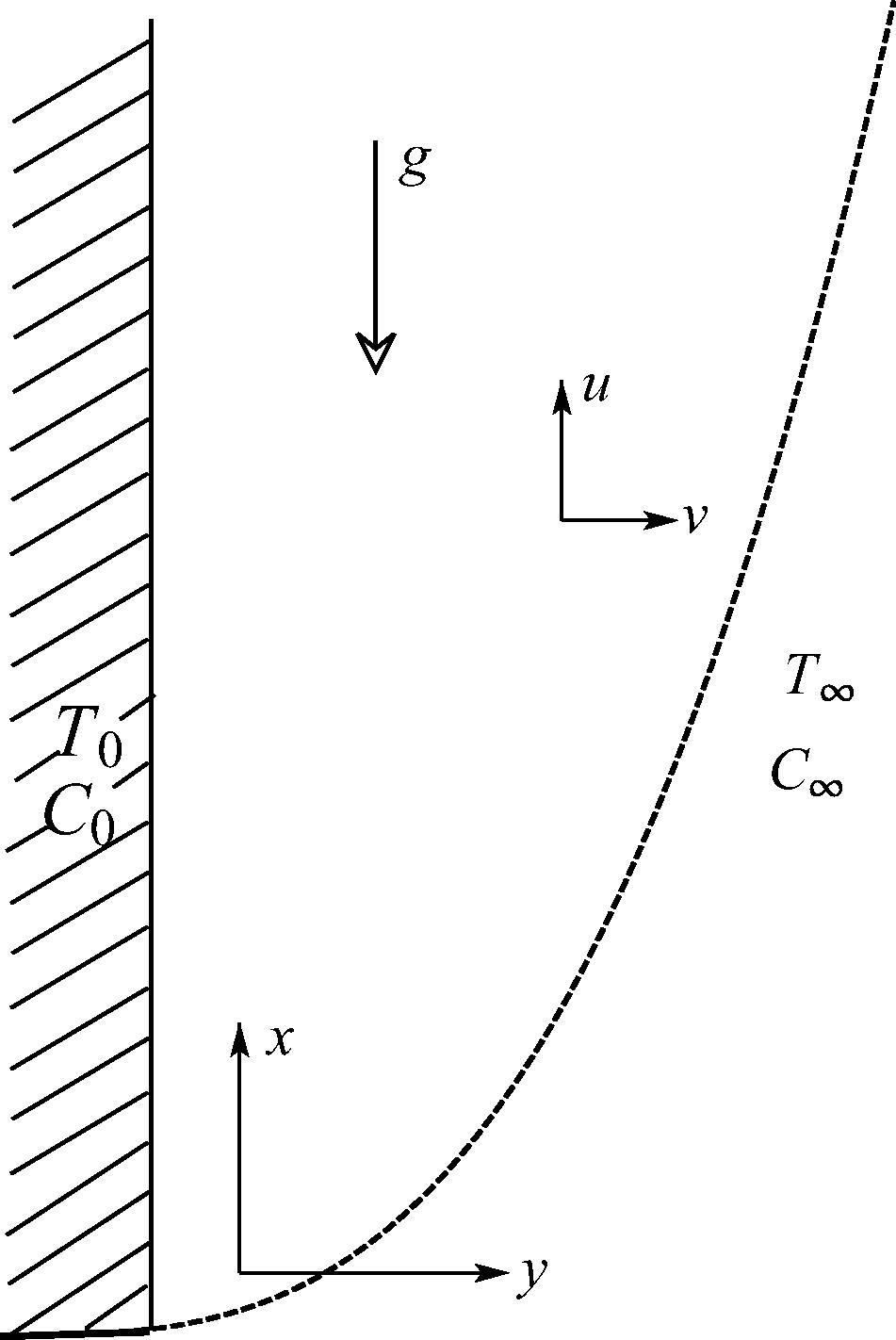
Physical model and coordinate system.
3 HAM solution
In view of the boundary conditions (9) and (10), f(η), υ(η), and ω(η) can be expressed by the set of base functions of the form
Let q ∈ [0, 1] denotes an embedding parameter and ℏ1, ℏ2, and ℏ3 are non-zero auxiliary parameters. Then we construct the following zeroth-order deformation equations
4 Results and discussion
At the mth-order approximation, we have the analytic solutions of (6)–(8), namely
As pointed out by Liao (2009), the convergence and the rate of approximation for the HAM solution strongly depends upon ℏ. In order to obtain the admissible value of ℏ for the present problem, we set ℏ1 = ℏ2 = ℏ3 = ℏ and the ℏ-curves are plotted for 13th-order of approximations. This helps us to determine the valid region of ℏ, which corresponds to the line segment almost parallel to the horizontal axis. Figs. 2–4 show the valid region of ℏ for
, and
, respectively. The parameters chosen for establishing the region of convergence were Pr = 0.71, Sc = 0.1, and δ = 0.5. In fact, the interval for the admissible values of ℏ shrinks as the parameters increase. In theory, at the mth-order of approximation, one can define the exact square residual errors
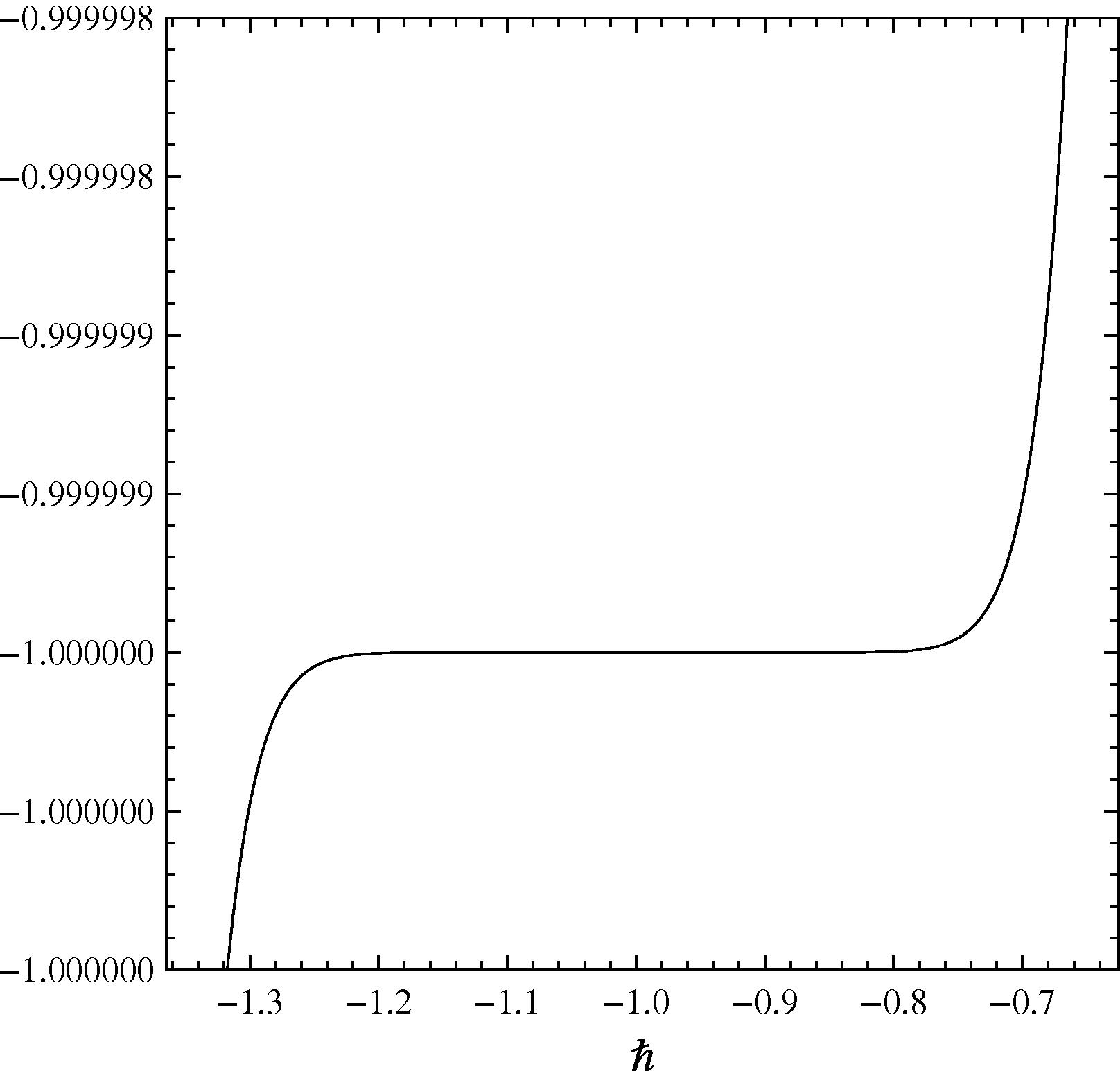
The curve of the
versus ℏ at Pr = 0.71, Sc = 0.1, and δ = 0.5 for the 13th-order approximation when ℏ1 = ℏ2 = ℏ3 = ℏ.
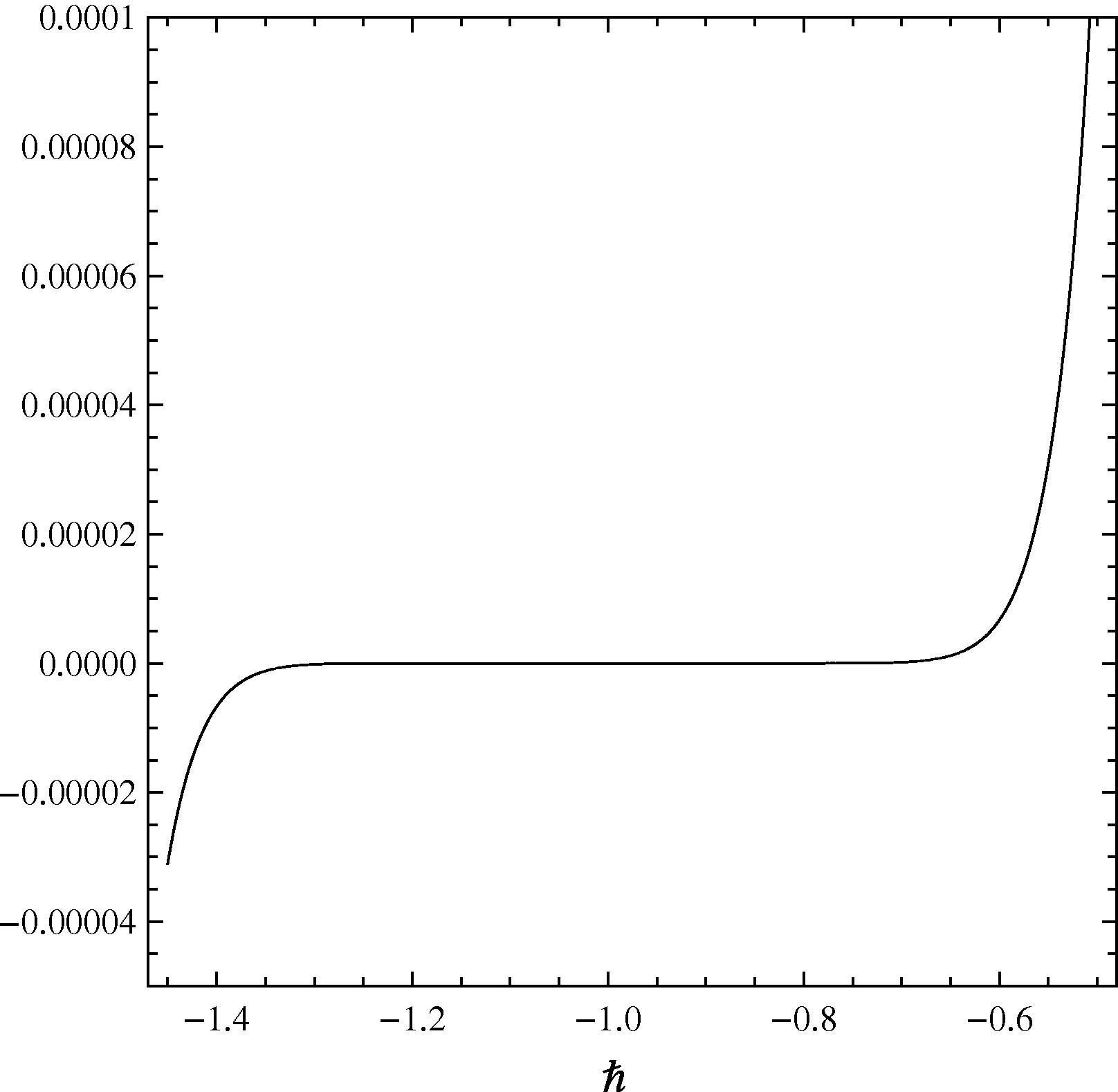
The curve of the
versus ℏ at Pr = 0.71, Sc = 0.1, and δ = 0.5 for the 13th-order approximation when ℏ1 = ℏ2 = ℏ3 = ℏ.
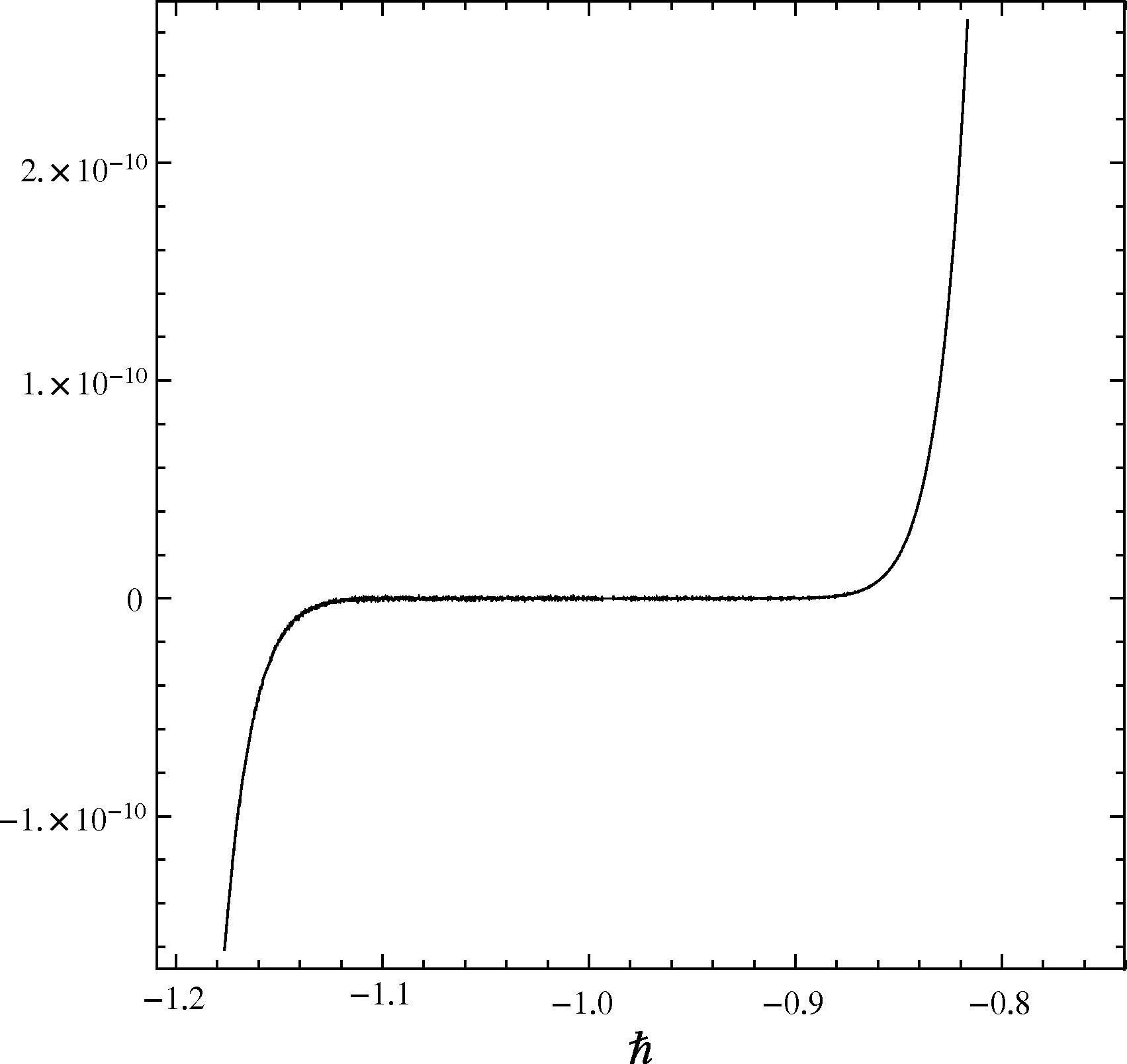
The curve of the
versus ℏ at Pr = 0.71, Sc = 0.1, and δ = 0.5 for the 13th-order approximation when ℏ1 = ℏ2 = ℏ3 = ℏ.
Pr = 0.71 δ = 0.5
Sc
ℏ1
ℏ2
ℏ3
0.5
−1.23
−1.21
−1.22
5
−0.95
−1.10
−1.13
10
−0.72
−0.92
−0.93
Pr = 0.71 Sc = 0.1
δ
ℏ1
ℏ2
ℏ3
0
−1.12
−1.02
−1.05
0.5
−0.84
−1.10
−0.87
1
−0.83
−0.81
−0.84
Fig. 5 shows the distribution of the vertical component of the velocity as a function of the similarity variable for Schmidt number Sc = 0.5, 5, and 10 with Pr = 0.71 and δ = 0.5. In each case, the peak velocity occurs at η = 1. However, the magnitude of the peak velocity decreases as the Schmidt number Sc increases. This behavior is consistent with the velocity profiles presented in Fig. 1 of Schenk et al. (1976). The temperature profiles corresponding to the velocity profiles in Fig. 5 are illustrated in Fig. 6. These profiles show that as the Schmidt number Sc increases, the local temperature in the thermal boundary layer increases. The same pattern can be gleaned from the temperature distributions in Fig. 1 of Schenk et al. (1976). The concentration profiles corresponding to the velocity profiles of Fig. 5 and temperature profiles of Fig. 6 are provided in Fig. 7. Both the thickness of the concentration boundary layer and the local concentration decrease sharply as the Schmidt number increases. The thinning of the concentration boundary layer with the increase in Sc can also be observed distinctly in the results presented in Schenk et al. (1976).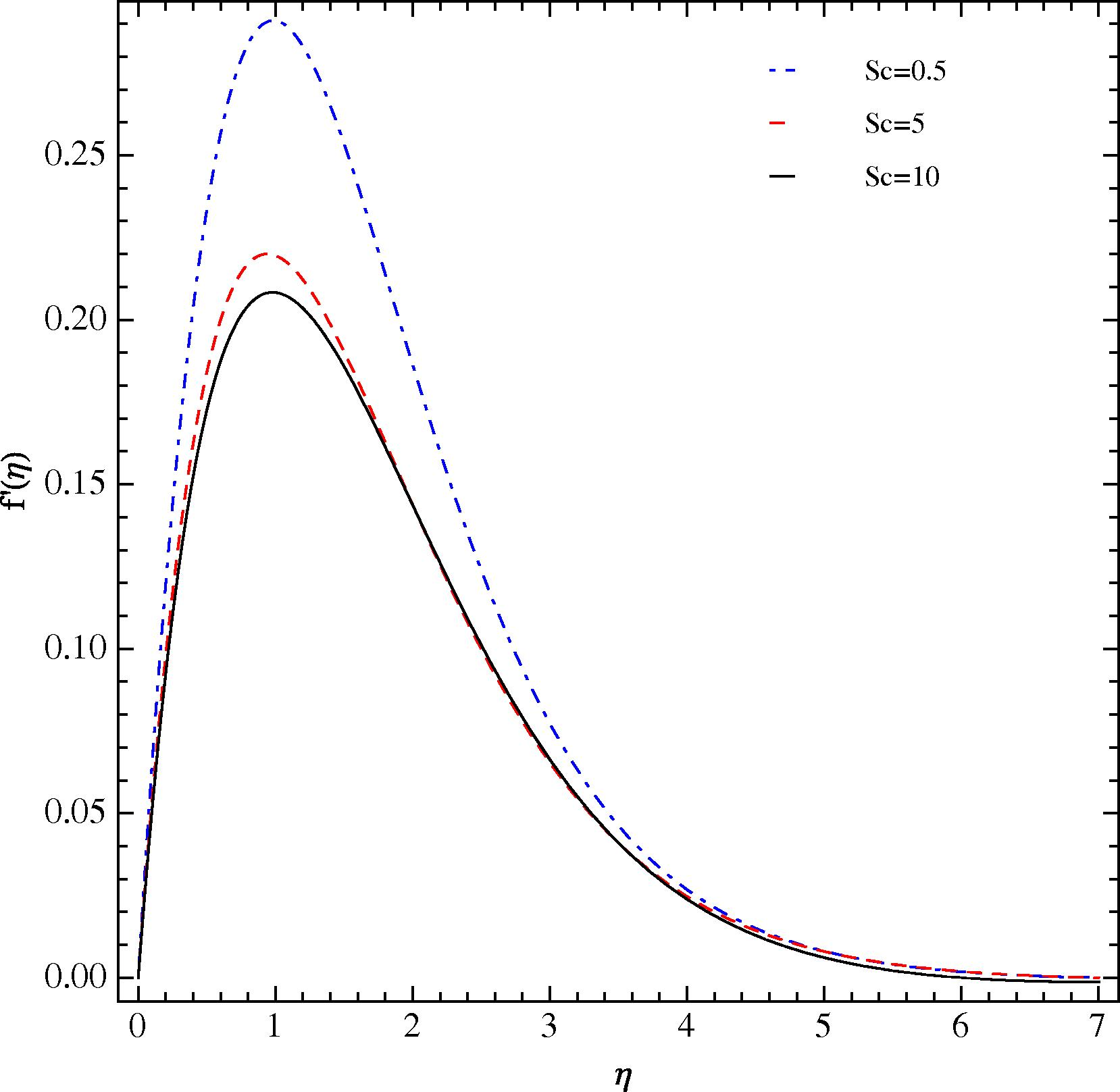
Influence of Sc on
at Pr = 0.71 and δ = 0.5 at the optimal values of ℏ1, ℏ2, and ℏ3.
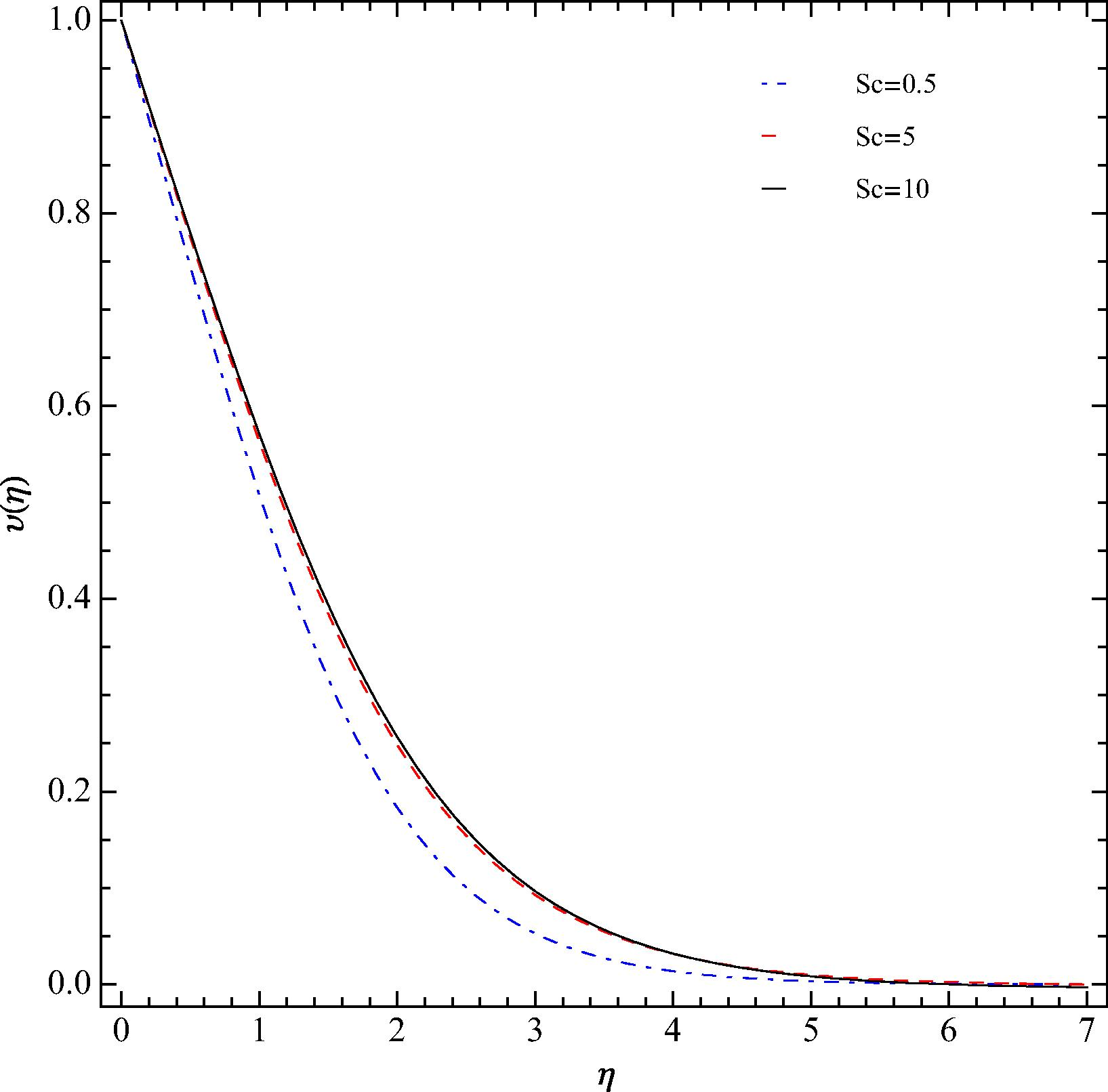
Influence of Sc on υ(η) at Pr = 0.71 and δ = 0.5 at the optimal values of ℏ1, ℏ2, and ℏ3.
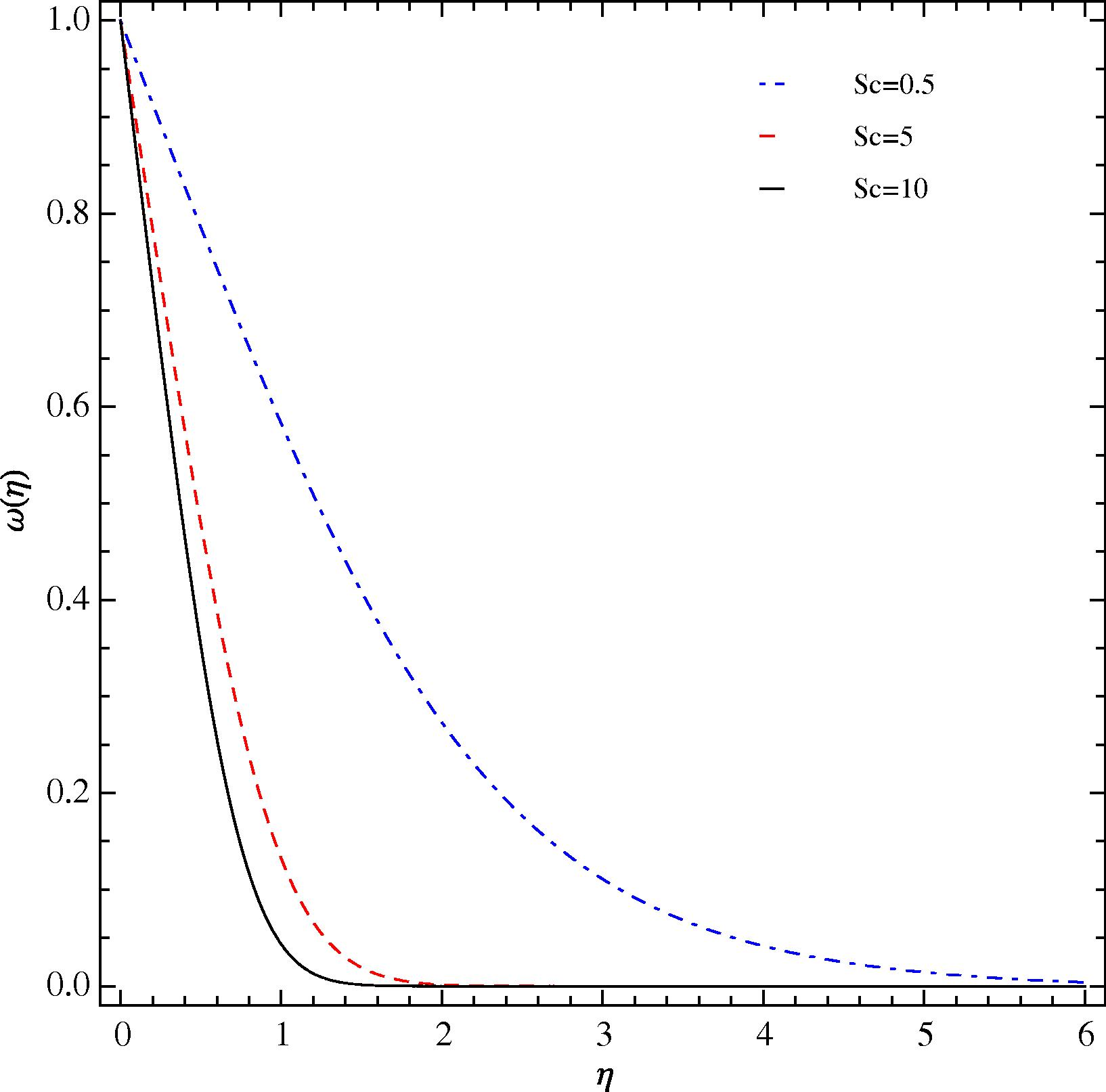
Influence of Sc on ω(η) at Pr = 0.71 and δ = 0.5 at the optimal values of ℏ1, ℏ2, and ℏ3.
We now turn to the results which demonstrate the effect of varying the parameter δ. The parameter δ represents the ratio of thermal buoyancy force and the total body force (algebraic sum of gravity, thermal and concentration buoyancy forces). Thus δ = 0 corresponds to zero thermal buoyancy force which means the process is pure mass transfer driven. Similarly, δ = 1 implies a pure heat transfer process. The effect of δ on the velocity distribution in the hydrodynamic boundary is shown in Fig. 8 for Pr = 0.71 and Sc = 0.1. The highest peak velocity occurs for δ = 0, i.e., for the pure mass transfer process. The lowest peak velocity occurs for δ = 1, i.e., for the pure heat transfer process. The hydrodynamic boundary is thickest for pure mass transfer and thinnest for pure heat transfer with the thickness for simultaneous heat and mass transfer falling in the middle. The pattern exhibited by the present results matches with the results reported in Schenk et al. (1976). The temperature profiles corresponding to the velocity profiles of Fig. 8 are given in Fig. 9. The highest temperatures occur in the pure heat transfer case (δ = 1). The lowest temperature are predicted for the pure mass transfer situation. The concentration profiles shown in Fig. 10 for the three values of delta show that the species concentration is highest for the pure heat transfer case and lowest for the pure mass transfer case. The concentration curve for the case of simultaneous heat and mass transfer falls in the middle. The temperature and concentration results presented here corroborate with the results cited in Schenk et al. (1976).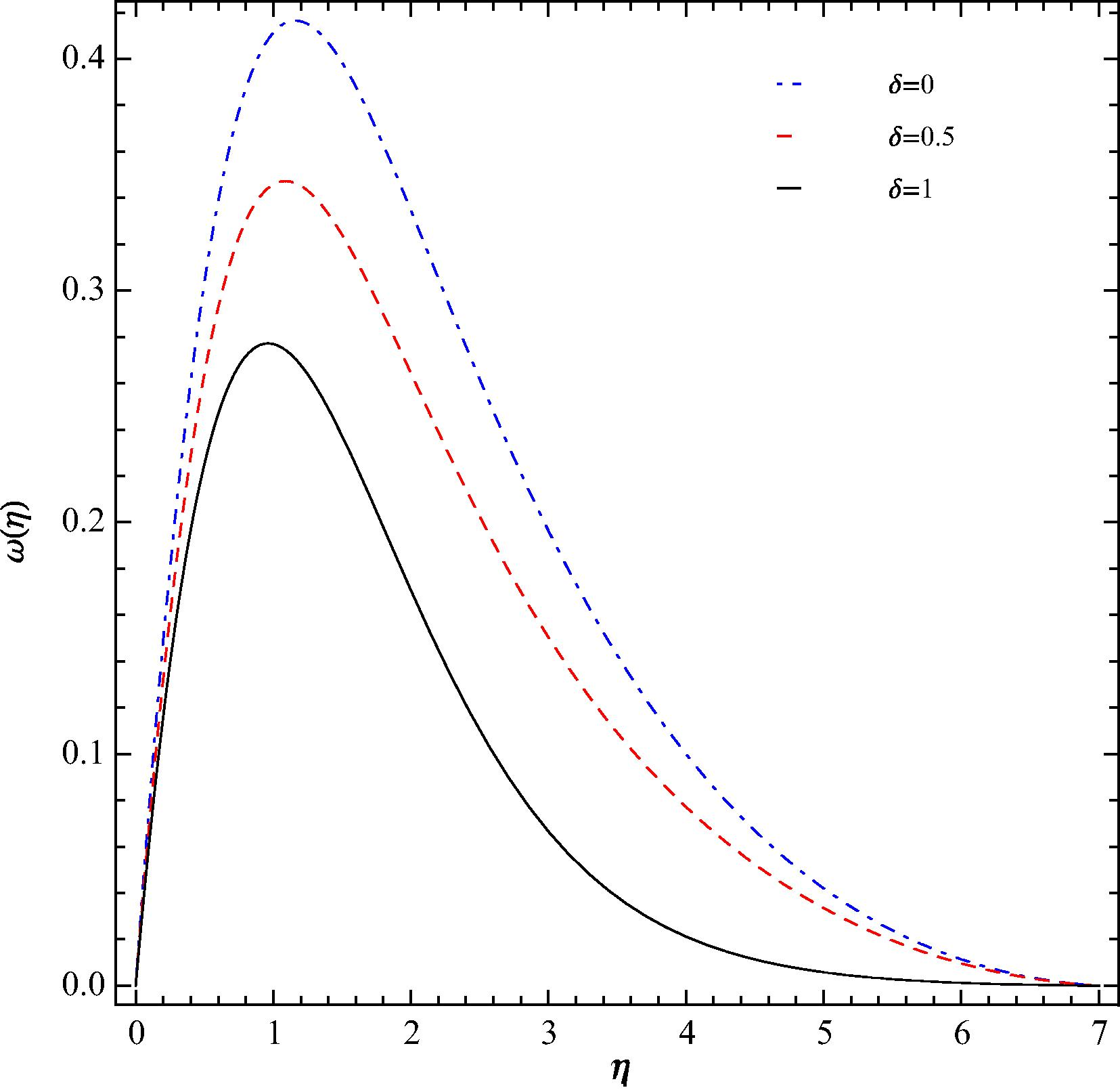
Influence of δ on
at Pr = 0.71 and Sc = 0.1 at the optimal values of ℏ1, ℏ2, and ℏ3.
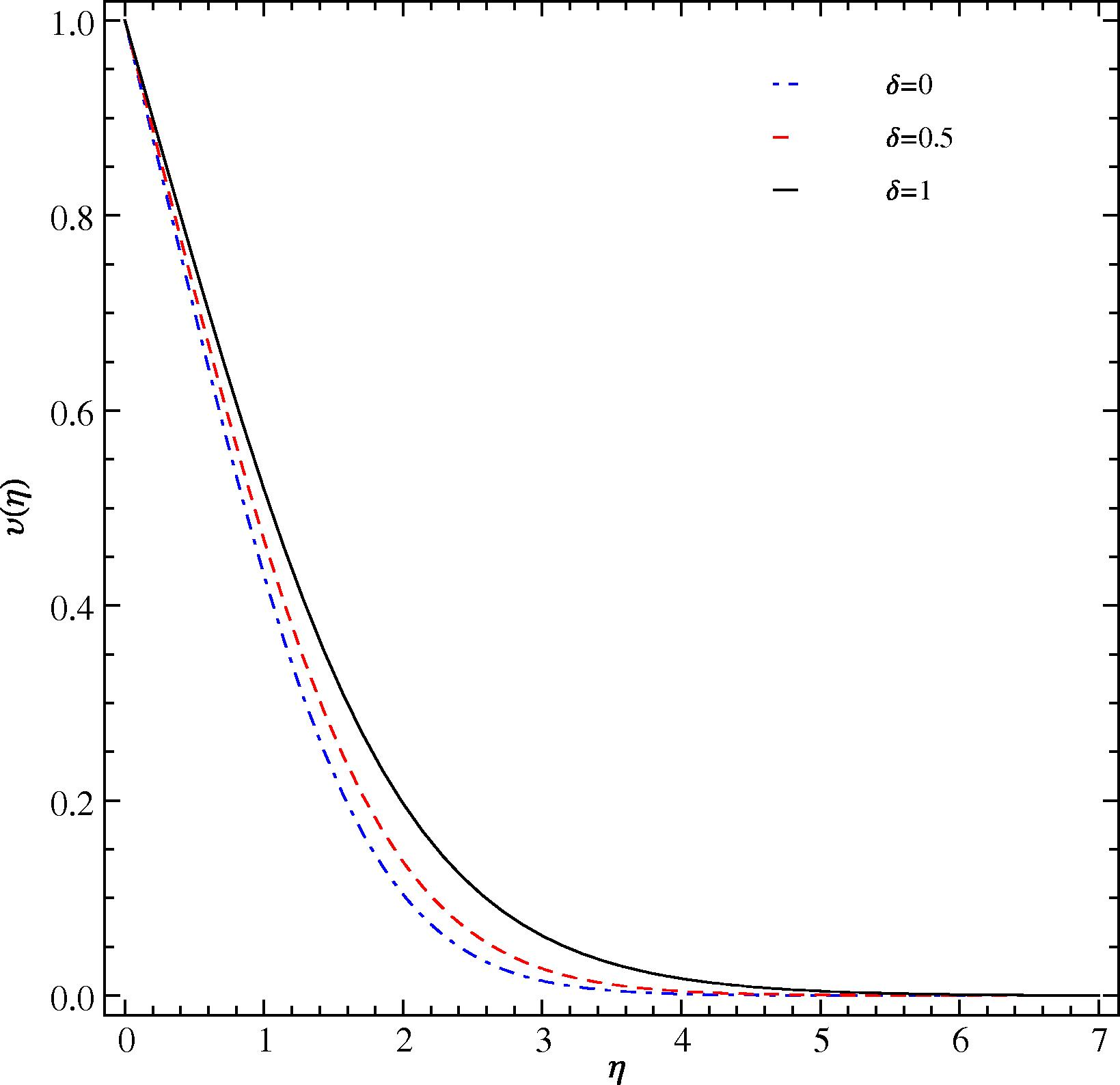
Influence of δ on υ(η) at Pr = 0.71 and Sc = 0.1 at the optimal values of ℏ1, ℏ2, and ℏ3.
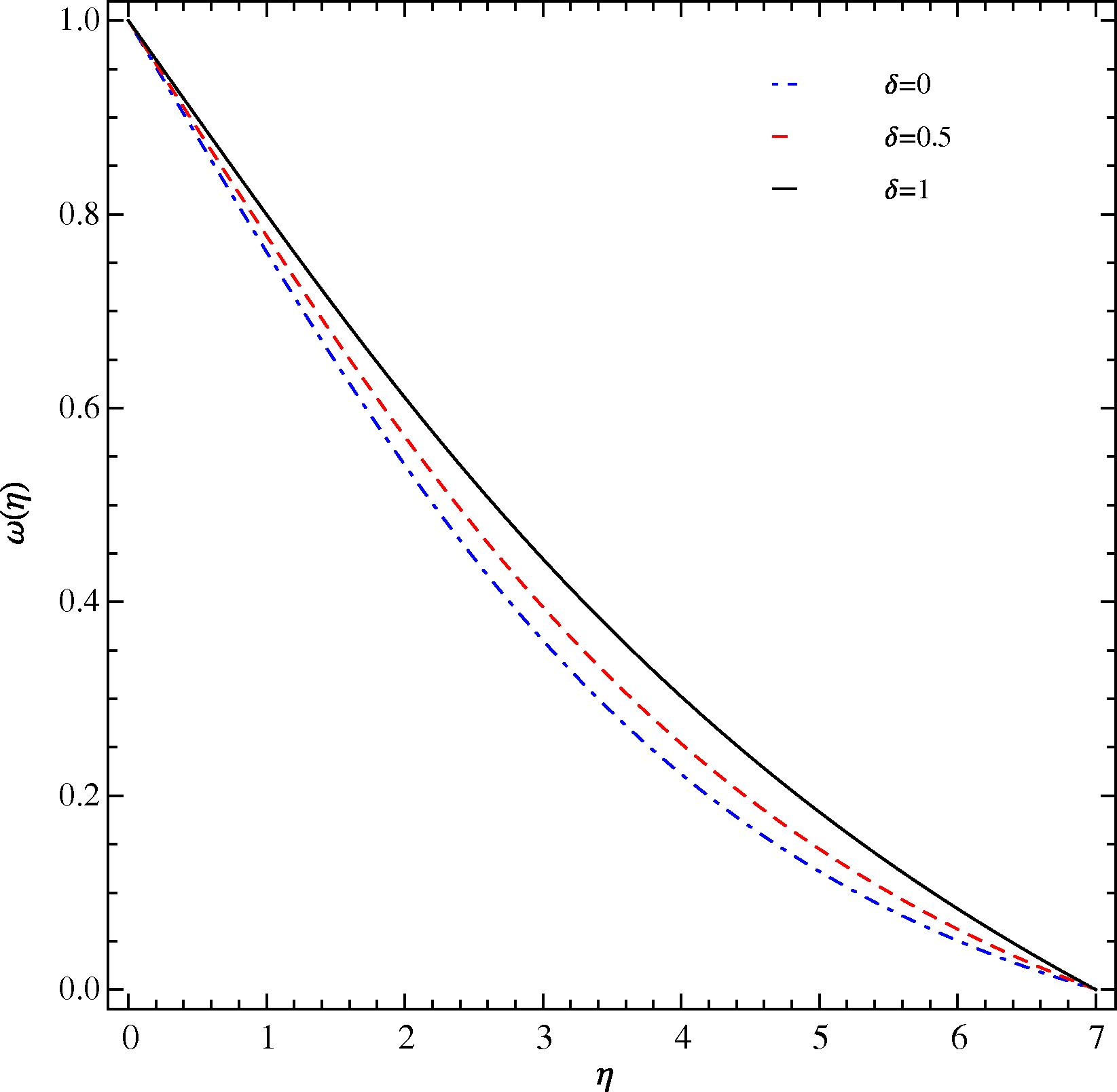
Influence of δ on ω(η) at Pr = 0.71 and Sc = 0.1 at the optimal values of ℏ1, ℏ2, and ℏ3.
Since the focus of this paper is to demonstrate the usefulness and accuracy of the homotopy analysis method, no attempt has been made to discuss the physical interpretations of the results. In any case, the physical interpretations are well documented in the previous research papers on the problem (Bottemanne, 1972a,b, 1976) and well known to the thermal science research community.
5 Conclusions
The homotopy analysis method has been successfully implemented to develop an analytic solution for simultaneous natural convection and mass transfer from an isothermal vertical plate. The effects of Schmidt number and the buoyancy ratio on the velocity, concentration, and temperature profiles in the respective boundary layers are illustrated with graphs. When compared with the other results reported in the literature, the present results are found to be highly accurate and consistent with the other results pertaining to the same problem. The use of concept of averaged residual recently introduced by Liao (2010) greatly improves the rate of the convergence of the analytic solution by allowing the determination of the optimal auxiliary parameter.
Acknowledgement
This work is partly supported by Bakhtar Institute of Higher Education of Iran.
References
- Analytic solutions for a rotating radial fin of rectangular and various convex parabolic profiles. Commun. Nonlinear Sci. Numer. Simulat. 2009
- [CrossRef] [Google Scholar]
- Experimental results of pure and simultaneous heat and mass transfer by free convection about a vertical cylinder for Pr = 0.71 and Sc = 0.63. Appl. Sci. Res.. 1972;25(1):372-382.
- [Google Scholar]
- Theoretical solution of simultaneous heat and mass transfer by free convection about a vertical flat plate. Appl. Sci. Res.. 1972;25(1):37-149.
- [Google Scholar]
- A series solution of the foam drainage equation. Comput. Math. Appl.. 2009;58:360-368.
- [Google Scholar]
- The nature of vertical natural convection flows resulting from the combined buoyancy effects of thermal and mass diffusion. Int. J. Heat Mass Transfer. 1971;14:2025-2050.
- [Google Scholar]
- Thermal analysis of a longitudinal trapezoidal fin with temperature-dependent thermal conductivity and heat transfer coefficient. Commun. Nonlinear Sci. Numer. Simulat.. 2010;15(3):590-601.
- [Google Scholar]
- A series solution of the fin problem with a temperature-dependent 3 thermal conductivity. Commun. Nonlinear Sci. Numer. Simulat.. 2009;14:3007-3017.
- [Google Scholar]
- Analytical solution for heat transfer of a third grade viscoelastic fluid in non-Darcy porous media with thermophysical effects. Commun. Nonlinear Sci. Numer. Simulat.. 2009;14(11):3867-3878.
- [Google Scholar]
- Analytical solutions and efficiency of the nonlinear fin problem with temperature-dependent thermal conductivity and heat transfer coefficient. Commun. Nonlinear Sci. Numer. Simulat.. 2009;14:3327-3338.
- [Google Scholar]
- An explicit, totally analytic approximate solution for Blasius-viscous flow problems. Int. J. Nonlinear Mech.. 1999;34(4):759-778.
- [Google Scholar]
- Beyond Perturbation: Introduction to the Homotopy Analysis Method. Boca Raton: Chapman & Hall/CRC Press; 2003.
- A new branch of solutions of boundary-layer flows over an impermeable stretched plate. Int. J. Heat Mass Transfer. 2005;48:2529-2539.
- [Google Scholar]
- Notes on the homotopy analysis method: some definitions and theorems. Commun. Nonlinear Sci. Numer. Simulat.. 2009;14(4):983-997.
- [Google Scholar]
- An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simulat.. 2010;15:2003-2016.
- [Google Scholar]
- Exponentially decaying boundary layers as limiting cases of families of algebraically decaying ones. ZAMP. 2006;57(5):777-792.
- [Google Scholar]
- A general approach to obtain series solutions of nonlinear differential equations. Stud. Appl. Math.. 2007;119:297-355.
- [Google Scholar]
- The homotopy analysis method to solve the Burgers–Huxley equation. Nonlinear Anal. Real World Appl.. 2009;10(2):589-600.
- [Google Scholar]
- Mollendorf, J.C., Gebhart, B. Axisymmetric natural convection flows resulting from combined buoyancy effects of thermal and mass diffusion, in: Proceedings Fifth International Heat Transfer Confererence, Tokyo, vol. 5, 1974, pp. 10–14.
- Interaction between heat and mass transfer in simultaneous natural convection about an isothermal vertical flat plate. Appl. Sci. Res.. 1976;32(6):599-606.
- [Google Scholar]
- Simultaneous free convection heat and mass transfer in laminar boundary layers. Chem. Eng. Sci.. 1970;25(12):1927-1937.
- [Google Scholar]







