1 Introduction

Optimization is the process of finding the point of the extreme value of a certain (target) function (Stracquadanio and Pardalos, 2019; McNaughton, 2023). It is one of the biggest cornerstones of applied mathematics, physics, engineering, economics, and industry. The scope of its application is vast and includes, for example, minimization of physical quantities at micro and macro levels, maximization of profit or efficiency of logistics chains, etc. Machine learning is also focused on optimization (Huang et al., 2022; Alexiadis, 2023): various regressions and neural networks try to minimize the discrepancy between predicted and real data.

Optimization is an active and relevant sector of scientific research. This sector includes a huge number of thematic fields and their extreme variations. The number of optimization problem statements and their solution methods has been growing like mushrooms after the rain for decades. For example, there is a huge field of Mixed-Integer Programming (Alfant et al., 2023; Zhang et al., 2023), which deals with discrete scenarios. Nondeterministic optimization (Zhang et al., 2022; Yang et al., 2019), based on stochastic principles, is known. There is robust optimization (Fransen and Langelaar, 2023; Castelli et al., 2023), in which fixed parameters are taken into account. The optimization of dynamic systems evolving in time (Yang et al., 2023; Xie et al., 2022) is known. There are various meta-heuristic methods (Marulanda-Durango and Zuluaga-Ríos, 2023; Hirsching et al., 2022): simulated annealing method, genetic algorithms, and swarm evolution methods. There are well-known approaches to optimization using fuzzy logic (Pei et al., 2023).

Let's focus on the global optimization problem of continuously differentiable functions (this will allow us to narrow the area of interest at least a little). The analysis involves evaluating the applicants in a certain quality criteria metric. In this context, first of all, we will mention such criteria as:

- global convergence (global convergence in optimization refers to the ability of an optimization algorithm to guarantee convergence to the global minimum or maximum of the objective function, regardless of the initial conditions. It ensures that the algorithm approximates the optimal solution across the entire search space, not just a local minimum or maximum. This property is crucial to avoid getting stuck in suboptimal solutions, ensuring the discovery of the best solution in the general case of the optimization problem);

- speed of local convergence (the speed of local convergence in optimization refers to the rate at which an optimization algorithm approaches the local minimum or maximum of the objective function near the convergence point. This characteristic determines how quickly the algorithm converges to the optimal solution in the vicinity of the current point, assessing the rate of decrease in the function value. A high speed of local convergence implies rapid approximation to the local optimum, which can be crucial for efficiently solving optimization problems);

- the dimension of the optimization problem, the solution of which is aimed at the method;

- the need to store matrices in the computer memory during the solution process (yes or no);

- use of the Hesse’s matrises in the solution process (yes or no);

- the need for scaling (yes or no) (scaling in optimization refers to the process of transforming variables or parameters in an optimization problem in such a way that they have a similar scale. This is important because different variables may have different orders of magnitude, which can hinder the convergence of optimization algorithms. Scaling helps balance the contribution of each variable, thereby facilitating the optimization process and enhancing the efficiency of converging to the optimal solution).

The first two criteria are analytical, the others characterize the aspects of the directly applied implementation of a particular method.

Let us pay closer attention to the first two of the mentioned criteria. An optimization method is said to have the property of global convergence if its iterations converge to a local minimizer regardless of the initial position. The speed of local convergence shows how quickly the method will find the minimizer after getting into the vicinity of the latter. Note that these two criteria are potentially competing. The so-called hybrid methods (Xu et al., 2023; Wu et al., 2023) are an actual answer to the conflict that manifests itself in an attempt to achieve simultaneous compliance with both the first and second criteria.

Now, having mentioned the main optimization method's qualitative criteria, we can go directly to the methods as such (at least, to the most used of them). Let’s recall the most used methods of smooth unconditional optimization (Ali et al., 2021; Smith and Nair, 2005): the lines method, the fastest descent method, the Newton method, quasi-Newton methods (incl, DFP, SR1, BFGS (Broyden, Fletcher, Goldfarb, Shanno) and its modifications: muffled, with limited memory, etc.), the nonlinear conjugate gradients method, the truncated Newton method. Note that from this list, only the fastest descent method and the truncated Newton method can claim (with limitations) to pass the first criterion (global convergence).

Of course, there are methods for which compliance with the first criterion was the dominant requirement at the creation time. We will distinguish three classes of such methods. The methods we refer to in the first class are focused on the configuration of the objective function and the admissible solutions domain. The most striking representative of this class is the DC functions minimizing method (Fang et al., 2012; Montano et al., 2022). In the method, both the objective function and the constraint functions for the admissible solutions domain are represented as the differences between two convex functions. A complete view of the evolution of this class of global optimization methods can be made by reading the works (Fang et al., 2012; Montano et al., 2022; Shilaja et al., 2022). Methods of the second class are focused on solving global optimization problems with simple configurations of admissible solutions regions (which have, for example, the shape of a parallelepiped) and objective functions characterized a priori by known Hölder constants (Chen and Zheng, 2021; Sovrasov, 2016). The same class can also include methods focused on reducing a multidimensional optimization problem to a one-dimensional one using Peano curves (Sovrasov, 2016). However, if the Hölder constants are unknown, the application of second-class methods is accompanied by considerable uncertainty. Finally, methods belonging to the third class focus on random search and the formalization of intellectualized heuristics to interpret its results (Gorawski et al., 2021).

We would like to separately mention Sub-gradient methods for non-smooth optimization (Tymchenko et al., 2019; Zaiats et al., 2019). Sub-gradient methods for non-smooth optimization are optimization techniques specifically designed to address problems where the objective function is not everywhere differentiable. Unlike traditional gradient methods applicable to smooth functions, sub-gradient methods use sub-gradients, a generalization of gradients, to navigate through optimization landscapes containing non-differentiable components. These methods are particularly useful in convex optimization scenarios involving functions with nonsmooth elements, such as those encountered in support vector machines and lasso regression. Sub-gradient methods iteratively adjust the solution in the direction of the sub-gradient, aiming to converge to a point where the sub-gradient approaches zero, indicating a potential solution to the non-smooth optimization problem. While they may exhibit slower convergence rates compared to methods for smooth optimization, sub-gradient methods are essential for effectively tackling problems with inherent nonsmoothness.

One of the essential problems accompanying the use of stochastic tests in the context of solving optimization problems is the generation of uniformly distributed random vectors in a certain region of the search space. Scientists are looking for ways to effectively apply this problem (Bisikalo and Kharchenko, 2023; Izonin et al., 2022). In this context, we note Hit-and-Run-like methods, Markov chains using methods, and methods that take into account relative entropy. However, a universal method has not yet been found.

Taking into account the strengths and weaknesses of the mentioned analogue methods, we will formulate the necessary attributes of scientific research.

Research object is a process of solving the global minimum finding problems, which continuous objective functions satisfy the Hölder condition, and the control parameters domain limited by continuous functions is characterized by a positive Lebesgue measure and is limited by multidimensional parallelepipeds.

Research subject includes functional analysis theory, probability theory and mathematical statistics, experiment planning theory, and computational methods.

Research aim is to formalize the process of guaranteed solutions to the optimization problems outlined by the research object in the form of a parallel computing oriented method.

Research objectives are:

- formalize the parallel computing oriented method of the guaranteed finding of the global solution of the optimization problem with the objective function and restrictions imposed by algorithmically calculated continuous functions that satisfy the Hölder condition (with a priori unknown values of the corresponding constants);

- formalize the process of generating sets of potentially global extrema as the results of simple statistical tests (as a basic element of each iteration of the method);

- formalize the probabilistic characteristics of the approximate solution, which is the result of the implementation of a finite number of iterations of the authors’ method;

- justify the adequacy of the proposed mathematical apparatus and demonstrate its functionality with an example.

Main contribution. The article proposes a parallel computing oriented method for solving the global minimum finding problems, in which continuous objective functions satisfy the Hölder condition, and the control parameters domain limited by continuous functions is characterized by a positive Lebesgue measure and is limited by multidimensional parallelepipeds. A typical example of such a task is the discrepancy minimizing problem between the left and right parts of some system of equilibrium equations. The method is based on simple statistical tests, thanks to which, at each iteration, growing sets of potential global minima and sets of decrements necessary for estimating the values of the Hölder constants are formed. The article theoretically substantiates and empirically proves the guaranteed convergence of the authors’ method to the real global minimum, which occurs at an exponential rate. For the continuous iterations number, analytical upper estimates of the spacing between the potential global minima and real global minima are formalized, as well as an estimate of the probability of overcoming this spacing is formalized. The decrements sequence approximation, estimation of a priori unknown Hölder constants, estimation of the average number of iterations of the method and probabilistic characteristics of the final solution are analytically justified.

- Statement of the research, which introduces general definitions and clarifies the purpose and objective of the research;

- Formalization of the parallel computing oriented method of the guaranteed finding of global extremum with simple statistical tests selection;

- Specific aspects of the applied application of the presented method;

- Sections devoted to demonstration and analysis of the results of the intended use of the proposed method.

2 Materials and methods

3 Results

The authors’ method is focused on finding the global minimum of the optimization problem (4), which is an adaptation of the canonical form of the optimization problem (2). We algorithmically implement the method as a composition of two functions. The function $\mathit{MinGen}\left(\right)$ implements the generation of a set of local minima $Z_i^{*}$ and a set of decrements ${\delta }_i$ , as well as checking the fulfilment of the stop condition (6). The function $\mathit{MinEst}\left(\right)$ implements the quality check of the found extrema using the probabilistic characteristic (34), which allows for determining the global minimum. The search for the extremum is implemented iteratively, and at each i-th iteration, $s$ computational operations are performed. For the convenience of readers, all variables used below are presented in the Nomenclature at the end of the article.

At each i-th iteration of the application of the function $\mathit{MinGen}\left(\right)$ , the following actions are performed:

1. Using the stochastic tests method a pool of stochastic vectors $Z_i=\left\{z^{\left(1\right)},\dots ,z^{N_i}\right\}$ , $N_i=\alpha N_{i-1}$ is formed;

2. From the pool $Z_i$ , stochastic vectors belonging to the admissible set $L$ are selected. As a result, a set $Y_i$ with capacity ${\stackrel{\sim }{N}}_i$ is formed;

3. The values of the objective function (4) on the set of admissible points $y^{\left(i\right)}\in Y$ are calculated: $F\left(y^{\left(k\right)}\right)$ , $k=\overline{1,{\stackrel{\sim }{N}}_i}$ ;

4. From the values $F\left(y^{\left(k\right)}\right)$ calculated at stage 3, the smallest one is chosen: $\underset{1⩽k⩽{\stackrel{\sim }{N}}_i}{\min }F\left(y^{\left(k\right)}\right)$ ;

5. The decrement ${\delta }_i=\left|F_i^{*}-F_{i-1}^{*}\right|$ and derived parameters $w_i=\log {\delta }_i$ , $n_i=\log N_i$ are calculated.

Stages 1–5 are repeated for $\rho$ iterations (as long as the condition $w_i<\gamma$ is fulfilled). After performing $\rho$ iterations, the function $\mathit{MinGen}\left(\right)$ completes its work. The output parameter of the function is a tuple of storage sets $〈F,\mathrm{\Delta },W,N〉$ of capacity $\rho$ each. Next, the function $\mathit{MinEst}\left(\right)$ comes into action, which for the input tuple $〈F,\mathrm{\Delta },W,N〉$ implements the following structured calculation procedure:

1. Estimates ${\widehat{C}}^{\left(i\right)}\pi$ , ${\widehat{s}}^{\left(i\right)}$ are calculated for sets $N$ , $W$ by the least squares method (see expression (24));

2. Such quality indicators of the found solution as the spacing $r_{\varphi }^{+}$ (see expression (33)) and the probability characteristic $P_{r_{\varphi }^{+}}^{*}$ (see expression (34)) are calculated.

The algorithmic constructions described above were implemented in the Python programming environment with a focus on supporting GPU Programming with Python and CUDA parallel computing technologies, the description of which is freely available at the link https://github.com/PacktPublishing/Hands-On-GPU-Programming-with-Python-and-CUDA. The created software was based on a software platform consisting of Windows, Python 2.7, Anaconda 5, CUDA 10 (incl. cuBLAS, cuSolver), PyCUDA, Scikit-CUDA. The hardware configuration of the test bench included a 64-bit Intel CPU, 32 Gigabytes of RAM, NVIDIA GPU RTX 3070.

The plan of experiments is designed to empirically confirm the adequacy of the presented method, as well as to obtain data for evaluating its effectiveness.

Empirical confirmation of the adequacy of the authors’ method was carried out based on the content of the Optimization Test Problems section of the specialized resource Virtual Library of Simulation Experiments: Test Functions and Datasets, freely available at the link https://www.sfu.ca/∼ssurjano/optimization.html.

Among the instances available in the Optimization Test Problems section, we selected ten optimization problems, the of admissible solutions domains of which are limited by ${\mathrm{P}}_x$ -shaped parallelograms. Here is a list of selected problems with the values of the corresponding controlled parameters and the output results $x^{*}$ , $f^{*}$ in the context of the terminology used in the article:

T1: $f\left(x\right)={\sum }_{i=1}^{k}1/\left(a_i+{\sum }_{j=1}^q{\left(x_j-c_{\mathit{ji}}\right)}^2\right)$ . For $k=5$ , $q=4$ , $A=\left(0,1;0,2;0,2;0,4;0,4\right)$ , $C=\left(\begin{array}{ccccc}4& 1& 6& 8& 3\\ 4& 1& 6& 8& 7\\ 4& 1& 6& 8& 3\\ 4& 1& 6& 8& 7\end{array}\right)$ we have: $x^{*}=4,000$ , $f^{*}=-10,153$ ;

T2: $f\left(x\right)=\left({\sum }_{i=1}^q{x}_i^4-16x_i^2+5x_i\right)/2$ . For $q=4$ we have: $x^{*}=2,904$ , $f^{*}=-156,664$ ;

T3: $f\left(x\right)={\sum }_{i=1}^q\left({\left(x_i-1\right)}^2+100{\left(x_{i+1}-x_i\right)}^2\right)$ . For $q=2$ we have: $x^{*}=1,000$ , $f^{*}=0,000$ ;

T4: $f\left(x\right)={\left(2,625-x_1+x_1{x}_2^3\right)}^2+{\left(2,250-x_1+x_1{x}_2^2\right)}^2+{\left(1,500-x_1+x_1{x}_2\right)}^2.$ We have: $x^{*}=\left\{3,000;0,500\right\}$ , $f^{*}=0,000$ ;

T5: $f\left(x\right)=\left(1+{\left(x_1+x_2+1\right)}^2\left(19-14x_1-14x_2+6x_1{x}_2+3x_1^2+3x_2^2\right)\right)\left(30+{\left(2x_1+3x_2\right)}^2\left(18-32x_1+48x_2-36x_1{x}_2+12x_1^2+27x_2^2\right)\right).$

We have: $x^{*}=\left\{0,000;-1,000\right\}$ , $f^{*}=3,000$ ;

T6: $f\left(x\right)=-\exp \left(0,5\left(\cos 2\pi x_1+\cos 2\pi x_2\right)\right)-20\exp \left(-0,2\sqrt{0,5\left(x_1^2+x_2^2\right)}\right)+20+\text{e}.$ We have: $x^{*}=0,000$ , $f^{*}=0,000$ ;

T7: $f\left(x\right)=-x_1\sin \sqrt{\left|x_1-x_2-47\right|}-\left(x_2+47\right)\sin \sqrt{\left|x_1/2+x_2+47\right|}$ . We have: $x^{*}=\left\{512,404;2319,000\right\}$ , $f^{*}=-959,641$ ;

T8: $f\left(x\right)={\sum }_{i=1}^{k}1/\left(a_i+{\sum }_{j=1}^q{\left(x_j-c_{\mathit{ji}}\right)}^2\right)$ . For $A=\left(0,1;0,2;0,2;0,4;0,4;0,6;0,3;0,7;0,5;0,5\right)$ , $C=\left(\begin{array}{cccccccccc}4& 1& 8& 6& 3& 2& 5& 8& 6& 7\\ 4& 1& 8& 6& 7& 9& 5& 1& 2& 3,6\end{array}\right)$ , $k=10$ , $q=2$ we have: $x^{*}=4,000$ , $f^{*}=-11,030$ ;

T9: $f\left(x\right)=1/\left(0,002+{\sum }_{j=1}^k\sqrt{j+{\sum }_{i=1}^q{\left(x_i-c_{\mathit{ji}}\right)}^6}\right)$ . For $k=25$ , $q=2$ , $c_{j1}=\left(-32;-16;0;16;32;\right.-32;-16;0;16;32;{\left.-32;-16;0;16;32;-32;-16;0;16;32;-32;-16;0;16;32\right)}^T,$ $c_{j2}=\left(-32;-32;-32;-32;-32;\right.-16;-16;-16;-16;-16;\left.0;0;0;0;0;16;16;16;16;16;32;36;32;36;32\right),$ we have: $x^{*}=-32,000$ , $f^{*}=0,998$ ;

T10: $f\left(x\right)={\sum }_{i=1}^q\left(5x_i-16x_i^2+x_i^4\right)/2$ . For $q=2$ we have: $x^{*}=2,904$ , $f^{*}=-39,166$ .

Test problems T1-T10 were solved using the authors’ method with the following initial data: $N_0=10$ , $\alpha =10$ , $\gamma ={10}^{-3}$ , $\rho =3$ , $\varphi =9$ , ${\delta }_{\varphi }=\left|f^{*}-f_{\varphi }^{*}\right|$ . The obtained empirical solutions are presented below in graphical and tabular form in Figs. 1-4. The results of the calculations are presented in the metric $\left\{{\text{P}}_x,f_{\varphi }^{*},x_{\varphi }^{*},{\delta }_{\varphi },r_{\varphi },T\right\}$ , where $f_{\varphi }^{*}$ is the optimal value of the corresponding optimization problem found on the ϕ-th iteration; $x_{\varphi }^{*}$ - the value of the argument, which corresponds to the value of $f_{\varphi }^{*}$ ; $r_{\varphi }$ - quality assessment (21); $T$ is the time spent searching for the value of $f_{\varphi }^{*}$ .

Close

Fig. 1

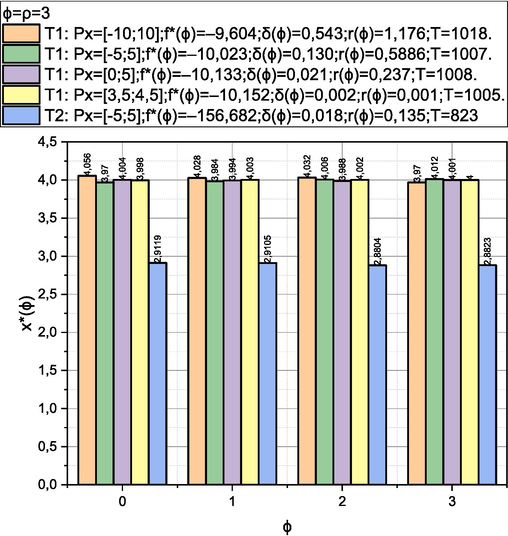
Results of solving test problems T1, T2 by the authors’ method.

Export to PPT

Close

Fig. 2

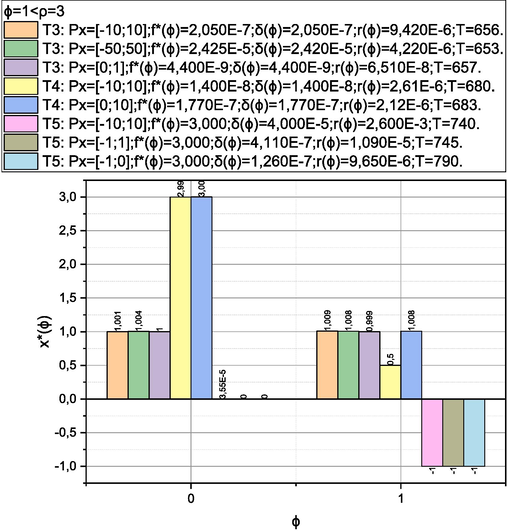
Results of solving test problems T3, T4, T5 by the authors’ method.

Export to PPT

Close

Fig. 3

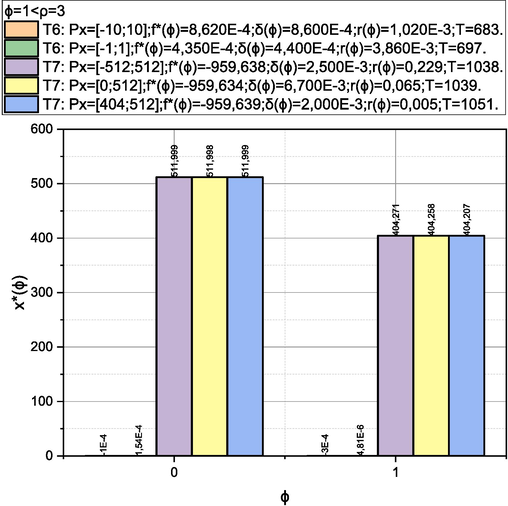
Results of solving test problems T6, T7 by the authors’ method.

Export to PPT

Close

Fig. 4

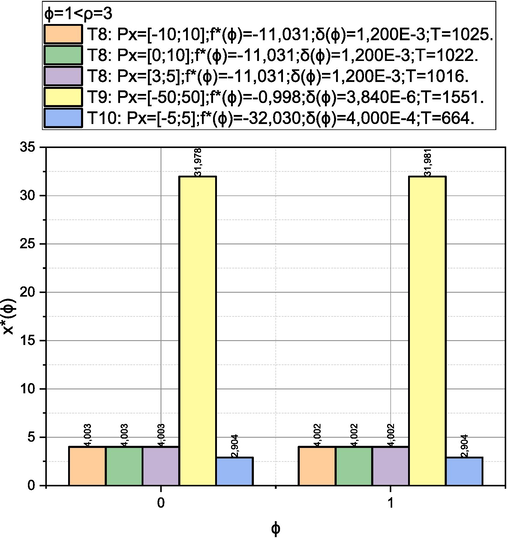
Results of solving test problems T8, T9, T10 by the authors’ method.

Export to PPT

Let's finish the experimental part by checking the adequacy of the model embodied in the expression (24). Fig. 5 presents the results of a computational experiment to identify the functional dependence of $\log {\delta }_i=\log \left(F_i^{*}-F^{*}\right)=f\left(\log \left(i\right)\right)$ at $F^{*}=0$ .

Close

Fig. 5

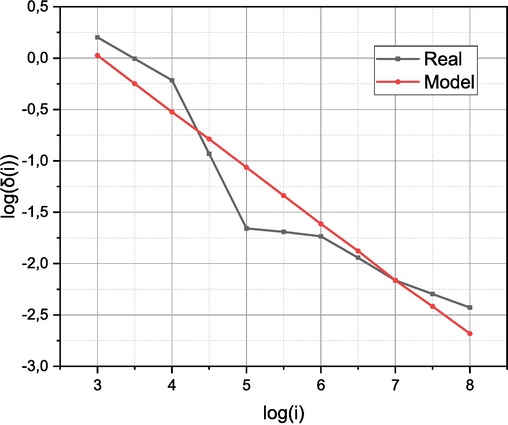
Real and simulated functional dependence of $\log {\delta }_i=f\left(\log \left(i\right)\right)$ at $F^{*}=0$ .

Export to PPT

According to the results presented in Fig. 5, the parameters and the root mean square deviation of the approximation (21) were determined by the least squares method. Note that the calculated root mean square deviation turned out to be smaller $12\%$ , which allows us to consider model (24) as adequate.

4 Discussion

Let's start the discussion by stating the empirically proven fact of the adequacy of the proposed method for solving the global optimization problems, in which continuous objective functions satisfy the Hölder condition, and the control parameters domain limited by continuous functions is characterized by a positive Lebesgue measure and is limited by multidimensional parallelepipeds. This fact is confirmed by the results of comparing the solutions obtained using the authors’ method with etalon solutions of optimization problems selected from the Optimization Test Problems section of the specialized resource Virtual Library of Simulation Experiments: Test Functions and Datasets. Figs. 1-4 shows that for all optimization test problems T1-T10, approximate values of the global minimum with an error in the range of $\left[{10}^{-9},{10}^{-2}\right]$ were found. Moreover, for test problems, T1-T7, adequate values of the upper estimates of the spacing to the exact global minimum (metric $r_{\varphi }$ ) with a probability close to one were obtained. Separately, we note that both the quality characteristics of the initial results calculated according to the authors’ method and the time to obtain them turned out to be practically independent of the size of the search area. This expected result (provided by a selection of simple statistical tests performed on iterations of the method) is a significant advantage of the authors’ method over analogues.

We will also note several theoretically grounded remarks concerning the authors’ method. In particular, the values of estimate (14) depend on the value of the established parameter $o$ , which is associated with the selected value of the unit cube (see (8)). The fact that the set $F_i^{*}$ is guaranteed to converge with an exponential rate is theoretically confirmed by the guaranteed convergence of the strictly monotonic set ${\text{F}}^{*}=\left\{F_0^{*}>F_1^{*}>\dots \right\}$ to the value of the exact global extrema with an exponential rate. Recall that the cumulative set ${\text{F}}^{*}$ grows with each transition from the i-th to the i+1-th iteration of the authors’ method (see the beginning of Section 2.2). Finally, if the admissible set is part of a unit cube (4), then when evaluating the probabilistic characteristics mentioned in Section 2.3, only the number of unit cubes in the partition of the admissible set will change. Accordingly, the estimates of the probabilistic characteristics from Section 2.3 (as well as the statements regarding the convergence of the authors’ method) are valid under the condition of compactness (4), which is characterized by the positivity of the Lebesgue measure. With this in mind, when implementing the authors’ method, at each iteration, you should check whether each stochastic point belongs to an admissible set.

5 Conclusion and future directions

The article proposes a parallel computing oriented method for solving the global minimum finding problems, in which continuous objective functions satisfy the Hölder condition, and the control parameters domain limited by continuous functions is characterized by a positive Lebesgue measure and is limited by multidimensional parallelepipeds. A typical example of such a task is the discrepancy minimizing problem between the left and right parts of some system of equilibrium equations. The method is based on simple statistical tests, thanks to which, at each iteration, growing sets of potential global minima and sets of decrements necessary for estimating the values of the Hölder constants are formed. The article theoretically substantiates and empirically proves the guaranteed convergence of the authors’ method to the real global minimum, which occurs at an exponential rate. For the continuous iterations number, analytical upper estimates of the spacing between the potential global minima and real global minima are formalized, as well as an estimate of the probability of overcoming this spacing is formalized. The decrements sequence approximation, estimation of a priori unknown Hölder constants, estimation of the average number of iterations of the method and probabilistic characteristics of the final solution are analytically justified. In addition to the theoretical proof, the adequacy of the authors’ method has been confirmed empirically. It turned out that both the quality characteristics of the initial results calculated by the authors’ method and the time to obtain them are practically independent of the size of the search area. This expected result is a significant advantage of the authors’ method over analogues.

Further research is planned to be devoted to the applied use of the proposed method, in particular, in the field of analysis of small stochastic data. The theoretical basis for these studies are articles such as (Kovtun et al., 2024; Kovtun et al., 2023).

Funding

This work was funded by Researchers Supporting Project number (RSP2024R503), King Saud University, Saudi Arabia.