Translate this page into:
Propagation of solitary waves in magnetized three-component plasmas
*Corresponding author. Tel.: +98 9113728252 Seyyed.ali.kazemipour@gmail.com (S.A. Kazemipour)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 10 August 2010
Abstract
The propagation of nonlinear ion-acoustic waves in magnetized plasma consisting of cold ions, hot electrons and positrons has been studied. It is demonstrated that in the case of weak nonlinearity the ion-acoustic waves are described by the Korteweg–de Vries (K-dV) equation. The influence of finite positron density and temperature and external magnetic field on the properties of soliton-like waves is discussed.
Keywords
Ion-acoustic waves
Electron–positron–ion plasmas
Magnetized plasmas
K-dV equation
Reductive perturbation technique
1 Introduction
Study of linear as well as nonlinear wave phenomena in electron–positron (e–p) plasmas (Tsytovich and Wharton, 1978; Berman et al., 1985; Tajima and Taniuti, 1990; Shukla and Stenflo, 1993) attracted much attention during the last decade due to their frequent occurrence in active galactic nuclei (Miller and Witta, 1987), pulsar magnetosphere (Goldreich and Julian, 1969; Michel, 1982) and in solar atmosphere (Tandberg-Hansen and Emshie, 1988). The electron–positron (e–p) plasmas are also believed to play an important role in understanding the early universe (Rees, 1983; Misner et al., 1973). An important feature of e–p plasmas is that both charged species are highly magnetized and are useful for the investigation of plasma confinement. Electron–positron plasmas have not yet been created in the laboratory but large numbers of confined positrons have also opened up a new area of positron annihilation research (Greaves et al., 1994). It is also suggested that magnetospheres of neutron stars contain e–p plasmas produced in cusp regions of stars due to intense electromagnetic radiations, where protons or other ions may be present and three-component electron–position–ion (e–p–i) plasmas can exist in such environments. Moreover, when positrons are used to probe particle transport in tokamaks, due to their sufficient lifetime, two-component electron–ion (e–i) plasma behaves as three-component e–p–i plasma (Surko and Murphy, 1990). In the presence of ions in e–p plasmas, ion-acoustic waves can exist. However, the properties of wave motion are very much different from those in e–i plasmas (Berezhiani et al., 1994).
Most of the astrophysical plasma also contains ions in addition to electrons and positrons; therefore it is important to study linear and nonlinear wave propagation in such plasmas and several authors have studied linear and nonlinear wave propagation in electron–positron–ion plasmas using different models (Nejoh, 1997; Kakati and Goswami, 2000; Gedalin et al., 1985; Jammalamadaka et al., 1996; Haque et al., 2002; Salahuddin et al., 2002).
Mahmood et al. (2003) have studied large amplitude ion-acoustic wave’s propagation in magnetized e–p–i plasma using the Sagdeev potential approach. However, it must be noticed that this method cannot yield evolution equation for plasma system. On the other hand, the study of low-frequency ion-acoustic wave propagation in plasma plays a key role through the solution of Korteweg–de Vries equation. Furthermore, the effect of the magnitude of external magnetic field on the amplitude and width of solitary waves may not be investigated.
In this paper, the properties of the nonlinear waves propagation of the small but finite-amplitude ion-acoustic solitary waves in a magnetized e–p–i plasma are studied theoretically and numerically by employing reductive perturbation method.
The manuscript is organized in the following fashion: In Section 2, we present the relevant equations for nonlinear ion-acoustic waves in magnetized e–p–i plasma and using reductive perturbation method, the K-dV equation for describe this nonlinear waves is obtained. Finally, some conclusion and discussions are given in Section 3.
2 Basic equations and K-dV equation
Let us consider an ideal homogeneous magnetized three-component (e–p–i) plasma. The external constant magnetic filed is directed along the z-axis, i.e. . Since the electrons and positrons are motive they are assumed to obey the Boltzmann distribution, while the ions are treated as a cold fluid. Furthermore, the phase velocity of ion-acoustic waves is assumed to be much larger than the characteristic ion thermal velocity but much less than the electron (positron) thermal velocities, i.e. so that .
Under these conditions the nonlinear dynamics of the low-frequency ion-acoustic waves in the three-component plasma are governed by the following equations:
We have assumed that electrons and positrons are hot and because , therefore ion Larmor radius is much larger than the Larmor radius of electrons and positrons. Therefore electrons and positrons are assumed to move almost parallel to external magnetic field and follow the Boltzmann distributions in magnetized electron–positron–ion plasma. Quantities , , and denote plasma fractional parameters, namely, electron to ion equilibrium density ratio, positron to ion equilibrium density ratio, electron to positron temperature ratio and the normalized cyclotron frequency, respectively. Furthermore, represents the unperturbed electron (positron, ion) densities. The quasineutrality condition at equilibrium situation requires that .
All parameters are normalized to relevant parameters in Eqs. (1)–(5). n is the ion number density normalized to n0; u is the ion fluid velocity normalized to the ion-acoustic speed is the electrostatic potential normalized to . The time and space variables are normalized to ion plasma period and the Debye length , respectively.
To obtain the relevant nonlinear evolution equation for small but finite-amplitude ion-acoustic solitary waves in magnetized e–p–i plasma, we define the independent variables in the stretched coordinates as (Washimi and Tanuti, 1966)
It should be noted that Eqs. (6) and (7) obtain from the expansion of the linear dispersion relation for (see Ref. Washimi and Tanuti, 1966; Infeld and Rowlands, 2000 for more details).
By using (6) and (7) in Eqs. (1)–(5), one can obtain from the first-order continuity equation z-component of the momentum equation and Poisson’s equation which, after simplification, yields
We can write the first-order x- and y-components of the momentum equation as
These, respectively, represent the x- and y-components of the electric-field drift. These equations are also satisfied by the second-order continuity equation. Again, using (6) and (7) in (2), and eliminating
, we obtain the next higher-order x- and y-components of the momentum equation as
Similarly, one can from the next higher-order continuity equation, z-component of the momentum equation and Poisson’s equation, using (8) and (10) obtain
This is the K-dV equation with the coefficients A and B given by
It is obvious that to choose , with the angle between the directions of the wave propagation vector k and the external magnetic field , as the amplitude of the soliton blows up while its width goes to zero, therefore the evolution equation is not valid at strictly perpendicular propagation. For parallel propagation results are almost similar to unmagnetized e–p–i plasma (Tiwari et al., 2007).
3 Numerical solutions and conclusions
To infer the properties of ion-acoustic solitary waves in magnetized e–p–i plasma, we have numerically solved Eq. (13) for the electrostatic potential. The numerical results are displayed in Figs. 1–3. Fig. 1 provides the form of the first–order solitary excitation – Eq. (13) – for arbitrary value of
,
,
,
and different values of
. It is found that the amplitude and the width of the ion-acoustic solitary waves decrease with increase in positrons density. Fig. 2 shows how the width and the amplitude of these solitary waves change with the temperatures ratio
. It is clear that increase in temperatures ratio decreases the amplitude and the width ion- acoustic solitary waves in magnetized e–p–i plasma.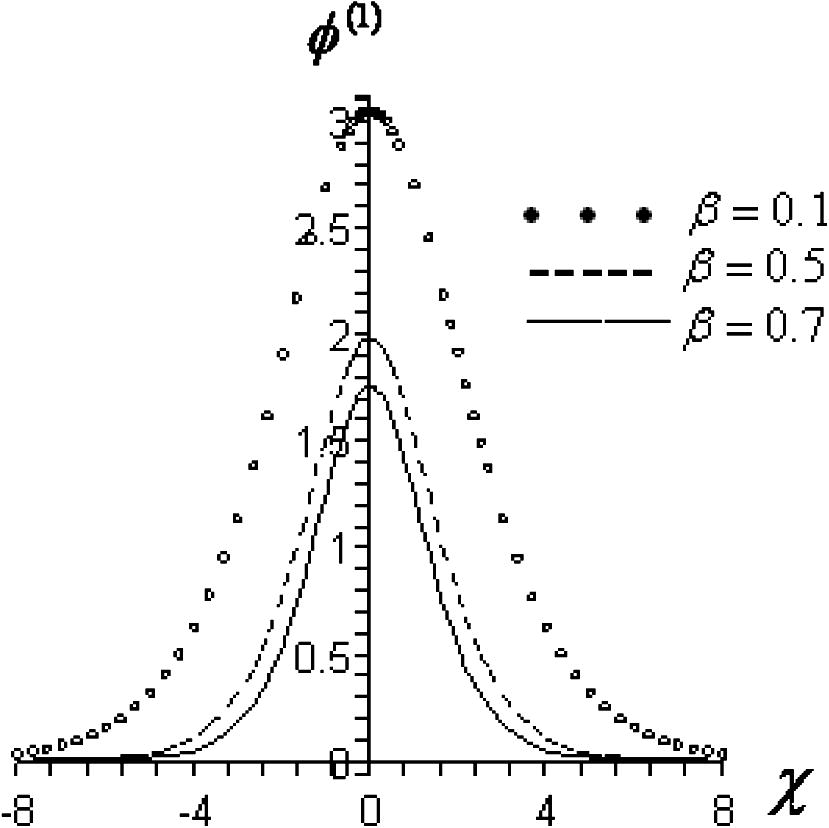
The first-order solitary excitation of the potential – Eq. (13) – for arbitrary value of
,
,
,
and different values of
.
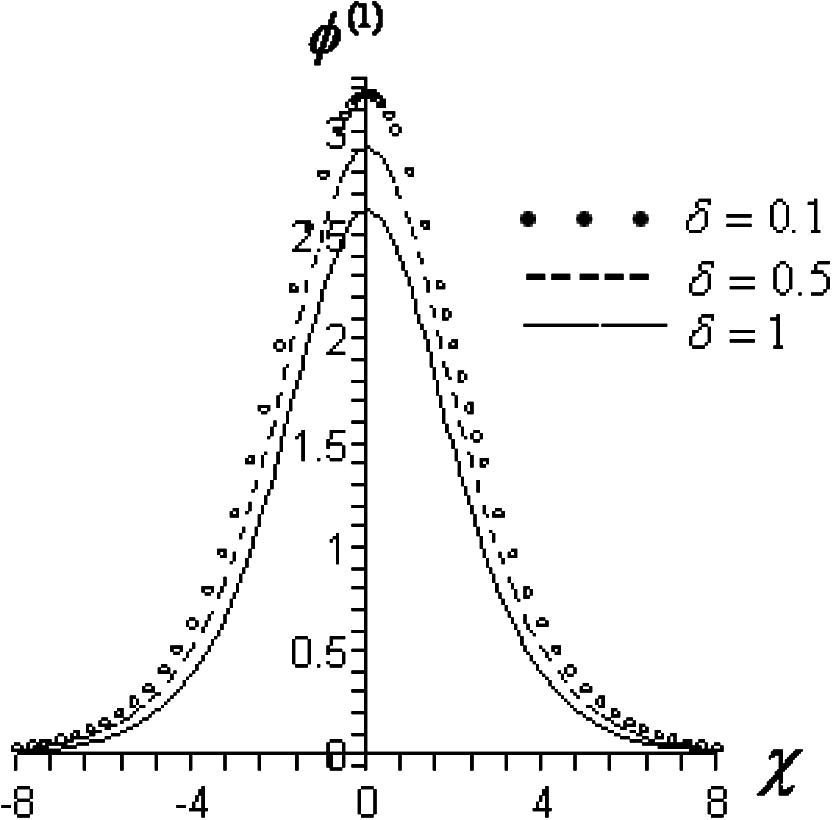
The first-order solitary excitation of the potential – Eq. (13) – for arbitrary value of
,
,
,
and different values of
.
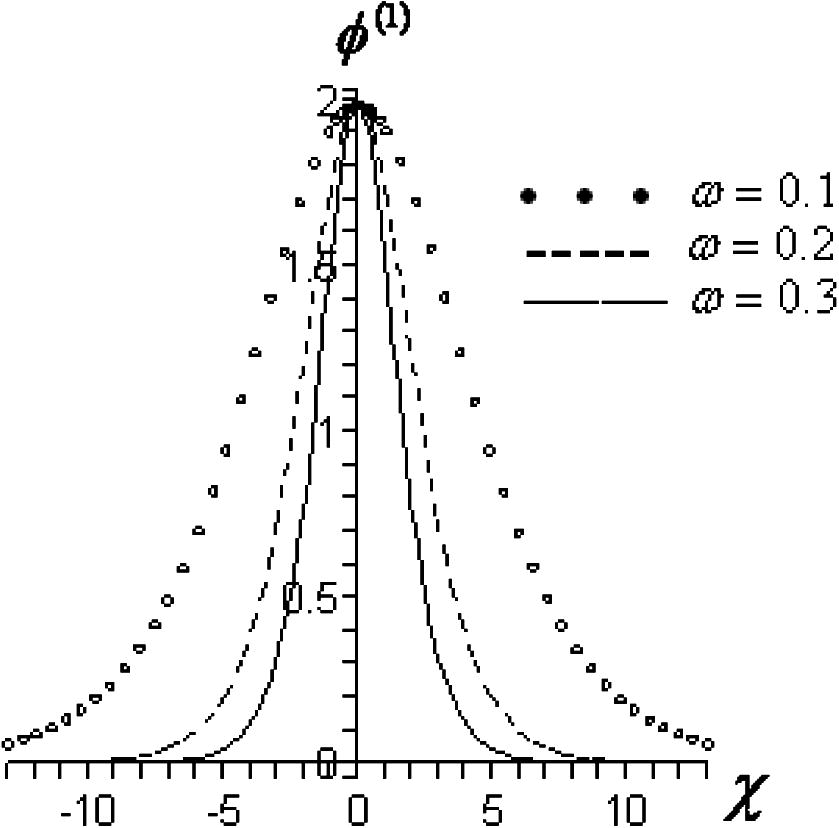
The first-order solitary excitation of the potential – Eq. (13) – for arbitrary value of
,
,
,
and different values of
.
It is seen that the magnitude of the external magnetic field has no effect on the amplitude of the solitary waves. However, it does have an effect on the width of these solitary waves. It is shown that, as we increase the magnitude of the magnetic field, the width of these solitary waves decreases, i.e. the external magnetic field makes the solitary structures more spiky (see Fig. 3).
In this paper propagation of the ion-acoustic waves in magnetized e–p–i plasma is investigated. Using reductive perturbation analysis, from basic equations a K-dV equation is obtained, however, not valid at strictly perpendicular propagation.
We think that these results will be helpful in understanding the nonlinear propagation of electrostatic perturbation in magnetized e–p–i plasmas which are believed to exist in the early universe, active galactic nuclei and the pulsar magnetospheres.
References
- Phys. Rev. E. 1994;50:448.
- Phys. Fluids. 1985;28:155.
- Astrophys. Space Sci.. 1985;108:393-400.
- Astrophys. J.. 1969;157:869.
- Phys. Plasmas. 1994;1(5):1439.
- Phys. Plasmas. 2002;9:474.
- Infeld, E., Rowlands, G., Nonlinear Waves, Solitons and Chaos, Cambridge University Press, Cambridge, England, 2000, p. 346.
- Astrophys. Space Sci.. 1996;240:39-43.
- Phys. Plasmas. 2000;7:808.
- New J. Phys.. 2003;5:28.
- Rev. Mod. Phys.. 1982;54:1.
- Active Galetic Nuclei. Berlin: Springer-Verlag; 1987. p. 202
- Gravitation. San Francisco: Freeman; 1973. p. 763
- Aust. J. Phys.. 1997;50:309.
- Gibbons G.B., Hawking S.W., Siklas S., eds. The Very Early Universe. Cambridge: Cambridge University Press; 1983.
- Phys. Rev. E. 2002;66:364.
- Astrophys. Space Sci.. 1993;209:323.
- Phys. Fluids B. 1990;2:1372.
- Phys. Rev. A. 1990;42:3587.
- The Physics of Solar Flares. Cambridge: Cambridge Univiversity Press; 1988. p. 124
- Comm. Plasma Phys. Controlled Fusion. 1978;4:91.
- Phys. Rev. Lett.. 1966;17:996.
Uncited Reference
- Eur. Phys. J. D. 2008;49:217-222.







