Parabolic curve fitting study subject to Joule heating in MHD thermally stratified mixed convection stagnation point flow of Eyring-Powell fluid induced by an inclined cylindrical surface

Khalil-Ur-Rehman; M.Y. Malik; O.D. Makinde

doi:10.1016/j.jksus.2017.02.003

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

30 (

); 440-449

doi:

10.1016/j.jksus.2017.02.003

Parabolic curve fitting study subject to Joule heating in MHD thermally stratified mixed convection stagnation point flow of Eyring-Powell fluid induced by an inclined cylindrical surface

Khalil-Ur-Rehman^{^a,⁎}, M.Y. Malik^{^a}, O.D. Makinde^{^b}

a Department of Mathematics, Quaid-i-Azam University, Islamabad 44000, Pakistan

b Faculty of Military Science, Stellenbosch University, Private Bag X2, Saldanha 7395, South Africa

⁎Corresponding author. krehman@math.qau.edu.pk (Khalil-Ur-Rehman),

Received: 2016-12-14, Accepted: 2017-2-26, Published: 2017-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

The current analysis is carried out to envision the properties of magneto-hydrodynamic boundary layer stagnation point flow of Eyring-Powell (non-Newtonian) fluid induced by an inclined stretching cylindrical surface in the presence of both mixed convection and Joule heating effects. Flow analysis is manifested with temperature stratification phenomena. The strength of temperature adjacent to the cylindrical surface is assumed to be higher in strength as compared to the ambient fluid. A suitable similarity transformations are utilized to convert the flow conducting equations (mathematically modelled) into system of coupled non-linear ordinary differential equations. A fifth order Runge-Kutta algorithm charted with shooting scheme is used to trace out the numerical additions. It was found that the velocity profile is an increasing function of both mixed convection and curvature parameters. Temperature profile show inciting nature towards Eckert number. In addition, a straight line and parabolic curve fitting way of study is executed to inspect the effect logs of mixed convection parameter, magnetic field parameter, thermal stratification parameter and heat generation parameter on skin friction coefficient and heat rate. It seems to be first attempt in this direction and will serve as a facilitating source for the preceding studies regarding fluid rheology.

Keywords

Joule heating

Stagnation point

Eyring-Powell fluid

Temperature stratification

Mixed convection

MHD

Heat generation

Parabolic curve fitting

An inclined cylindrical surface

Show Related Articles from PubMed

Nomenclature

$u,$ $v$: Velocity components
$ν$: Kinematic viscosity
$g$: Gravity
$M_{p},$ $λ$: Eyring-Powell fluid parameters
$T_{w} (x)$: Prescribed surface temperature
$T_{0}$: Reference temperature
$L$: Reference length
$α$: Thermal diffusivity
$ψ$: Stream function
$S_{T}$: Thermal stratification parameter
$Ec$: Eckert number
$F^{'} (η)$: Velocity of fluid
$k$: Thermal conductivity
$V$: Velocity vector
$I$: Identity tensor
$\vec{B}$: Magnetic field
$tr$: Trace
$u_{s}$: Free stream velocity
$T$: Fluid temperature
$R$: Radius of cylindrical surface
$Gr$: Temperature Grashof number
$b, c$: Positive constants
${Re}_{x}$: Local Reynold number
$Q_{0}$: Heat generation coefficient
$x, r$: Space variable
$ρ$: Fluid density
$μ$: Dynamic viscosity
$K_{p}$: Curvature parameter
$T_{\infty} (x)$: Variable ambient temperature
$U_{0}$: Reference velocity
$F (η)$: Dimensionless variable
$\Pr$: Prandtl number
$η$: Similarity variable
$γ_{n}$: Magnetic field parameter
$c_{p}$: Specific heat at constant pressure
$A_{p}$: Velocities ratio parameter
$N$: Cauchy stress tensor
$\vec{ϒ}$: Current density
$τ$: Deviatoric stress part
$A_{1}$: First Rivlin-Erickson tensor
$β_{T}$: Thermal expansion coefficient
$U (x)$: Stretching velocity
$λ_{p}$: Mixed convection parameter
$H_{p}$: Heat generation parameter
$B_{0}$: Uniform magnetic field
${Nu}_{x}$: Local Nusselt number

1 Literature survey

The investigation of heat transfer and boundary layer flow of non-Newtonian fluids brought by stretching surfaces are of practical importance and recognized widely by means of number of engineering applications to mention just a few, spinning of fibers, continuous casting, infinite metallic plates cooling, cylindrical wires coating, polymer fiber coating etc. Further, the fluid movement nearby stagnation zone is subjected as stagnation point flow. The heat transfer and fluid pressure are higher in strength under stagnation region. Therefore, boundary layer flows under the region of stagnation point is still a topic of great interest for scientists. Hiemenz (1911) was the earliest to mention stagnation point flow in two dimensional frame of reference by way of Navier-Stokes equations. These types of flow may be viscous or inviscid, two or three dimensional, steady or unsteady, oblique or normal, asymmetric or symmetric, reverse or forward. Furthermore, with the manifestation of stretching surfaces the stagnation point flows owned too much importance regarding industrial and engineering processes. To be more specific, hot rolling, polymer and metal extrusion, wire drawing are the few evidence of such type of flows. Furthermore, the combination of forced and natural convection is called as mixed convection. The applications of mixed convection boundary layer flow of non-Newtonian fluids includes solar power collectors, ocean and atmosphere, fans cooling devices and drying of porous solid. Therefore, it was always remain important for researchers to addressed the effect logs of mixed convection flows for both Newtonian and non-Newtonian fluids namely Gul et al. (2015a,b) discussed mixed convection effects towards MHD nanofluid (contains different shapes of nanoparticles) flow in a channel with saturated porous medium in first case. In second attempt they identified mixed convection effects on ferrofluid flow along a vertical channel. Ullah et al. (2016a) studied MHD mixed convection slip flow of Casson fluid towards stretching (non-linearly) sheet through porous medium along with chemical reaction. Magnetohydrodynamic mixed convection Poiseuille flow of nanofluid along porous medium in the presence of thermal diffusion, thermal radiation and chemical reaction was taken by Aman et al. (2016). Further, plenty of researchers performed study on forced and natural convection by considering different physical effects see (Ullah et al., 2016b; Zin et al., 2016; Sheikholeslami et al., 2016a; Sheikholeslami, 2017a; Sheikholeslami and Chamkha, 2017; Sheikholeslami and Ganji, 2017a ).

Magneto-hydrodynamic reflects the dynamic activities of fluids (Newtonian and non-Newtonian) flow over a different surfaces. Such type of fluids flow is electrically conducting and manifested with magnetic field. The heat transfer and electrically conducting flow has considerable submission in various technological and engineering fields. To mention just a few, energy extractions in geothermal field, configuration orientation regarding structure of boundary layer, MHD accelerators and power generators. In the light of above mention application the study of theory of electrically conducting flow along with heat transfer characteristics has phenomenal interest of engineers and scientists. In the presence of magnetic field Sarpkaya (1961) identified properties of non-Newtonian fluids and Pavlov (1974) discussed MHD viscous fluid flow over a stretching surface in detail. Recent studies can be encountered in Sheikholeslami and Ganji (2014, 2015, 2016, 2017b), Babu et al. (2015), Sheikholeslami et al. (2015), Ullah et al. (2016c), Ali et al. (2016), Babu and Sandeep (2016), Sheikholeslami and Shehzad (2016), Sheikholeslami et al. (2016b–d), Sheikholeslami (2017b,c), Sheikholeslami and Vajravelu (2017), Kumaran et al. (2017), Sheikholeslami and Rokni (2017).

The deposition or formation of layers in a flow regime give birth to thermal stratification phenomena. The impact of boundary layer flows along with temperature stratification is significant subject to the heat transfer analysis. The phenomena of temperature stratification arises due to alteration in temperature or combination of various fluids having different densities. As far as practical applications are concern, thermal energy storage (solar ponds system), atmosphere density stratification and production of sheeting material are the physical significances. In the light of these applications, most of the researchers and scientists probed that the boundary layer flow of Newtonian fluids are not primarily suitable in contrast to non-Newtonian fluid flows. The flow diversity of non-Newtonian fluids in nature is the source of uncertainty regarding rheological features and almost impossible to clip complete physical description by way of single constitutive expression between shear rate against stress. Due to this reason, a variety of models for non-Newtonian fluids (revealing distinct rheological impacts) are offered in the literature. Among those Eyring and Powell proposed a new fluid model in 1944, and it is known as Powell-Eyring fluid model (see Powell and Eyring (1944)). Eyring-Powell model has certain advantages over non-Newtonian model in this sense that it is derived from molecular theory of gases rather than the experimental relation and turn into Newtonian mode at low and high shear rates. Even though it is more complex but advantages of this fluid model overcomes its labouring mathematics. For example it can be used to articulate the flows of modern industrial materials such as ethylene glycol and powdered graphite. Heat diffusion through Eyring-Powell fluid plays a vital role in different geophysical, natural and industrial problems namely, moisture and temperature distribution over agricultural pitches, environmental pollution, underground energy transport etc. Although every non-Newtonian fluid model is important with respect to industrial and engineering point of view, so that the researchers identified different effects namely, magnetic field effect, unsteadiness of flow field, thermal radiation effect, heat generation phenomena, porous medium, melting heat transfer effect over a plane and cylindrical stretching geometry. The fluid flow over a cylindrical surface is treated as a two dimensional if the boundary layer thickness is small as compared to body radius. Whereas, boundary layer thickness is of same order as radius of cylinder for the case of thin or slender cylinder. This implies that fluid flow will be considered as axi-symmetric instead of two dimensional. As far as the Eyring-Powell model is concern, during past time most of the researchers owned the importance of Eyring-Powell model and so investigated diverse effects by considering flow of Eyring-Powell fluid brought by different geometries. Yoon and Ghajar (1987) wrote a note on Eyring-Powell fluid flow and concluded that Eyring-Powell is truly sensitive towards minor variations for zero shear rate viscosity and moderate sensitive for infinite shear rate viscosity. Sirohi et al. (1987) explored the Powell-Eyring fluid flow near an accelerated plate. They utilized three different methods and developed a comparison among them. Patel and Timol (2009) offered numerical solution of Powell-Eyring fluid flow. They utilized MSABC to obtained numerical computations. Rosca and Pop (2014) investigated the heat transfer effect of Eyring-Powell fluid past a shrinking surface in parallel free stream. Panigrahi et al. (2014) identified MHD impact under mixed convection flow of Eyring-Powell fluid over a non-linear stretching surface. Malik et al. (2013) pointed the Eyring-Powell fluid over a stretching cylinder with variable viscosity effect. Thermophoretic MHD Eyring-Powell fluid flow over a vertical stretching sheet with chemical reaction was investigated by Khan et al. (2015). The magnetic fields effects on Eyring-Powell fluid flow past a stretching sheet was taken by Akbar et al. (2015). Hayat et al. (2015) presented Eyring-Powell MHD nanofluid flow brought by stretching cylinder under thermal radiation impact. More recently, Khan et al. (2016) considered the unsteady Eyring-Powell nanofluid past a oscillatory stretching surface by way of generation/absorption effect. Rehman et al. (2016a) explored Eyring-Powell fluid flow over a vertical cylinder under the region of stagnation point by incorporating heat transfer. Krishna et al. (2016) discussed dual solutions for unsteady Eyring-Powell fluid flow past an inclined stretching sheet. In addition, Rehman et al. (2016b) dual convection effets for Eyring-Powell fluid flow over an inclined stretching cylinder.

The above assessed literature survey reflects that there is no reported study on magneto-hydrodynamic boundary layer flow of Eyring-Powell fluid under the region of stagnation point brought by an inclined cylindrical stretching surface along with temperature stratification, Joule heating and heat generation effects. Therefore, the aim of present work is to fulfil the gap. The temperature is supposed to be variable near the surface of the cylinder and away from it. Numerical computations of the transformed equations are presented by means of shooting technique. The achieved results shows that the fluid flow is influenced significantly against thermal stratification parameter. The effect logs for pertinent flow controlling physical parameters on dimensionless velocity and temperature distributions are inspected and plotted graphically. The estimation of local skin friction coefficient and heat transfer rate by way of straight line and parabolic curve fitting approximation is also executed in this study. It seems to be first attempt and trusted that the results found will not only offer convenient information for applications, but also serve as a complement to the preceding studies in the field of fluid science.

2 Momentum analysis

A steady non-Newtonian boundary layer incompressible fluid flow over an inclined stretching cylindrical geometry of constant radius is assumed. In a two dimensional frame of reference the fluid flow is being deliberated under the region of stagnation point manifested with magnetic field and Joule heating effects. Further, the flow regime is considered with temperature stratification phenomena. The strength of temperature near the cylindrical surface is supposed to be greater than the ambient fluid. The axial line of cylinder is presumed to be x-axis and radial direction perpendicular to x-axis is taken as r-axis. The central mathematical equation regarding momentum for Eyring-Powell fluid flow is can be written as:

(1)

ρ \frac{d \vec{V}}{dt} = \nabla \cdot N + \vec{ϒ} \times \vec{B},

(2)

N = - p I + τ, and \vec{ϒ} = σ (\vec{V} \times \vec{B}) .

Eyring-Powell fluid model stress tensor is defined as:

(3)

τ = [μ + \frac{1}{β Δ_{1}} \sinh^{- 1} (\frac{1}{c} Δ_{1}) A_{1}], where Δ_{1} = \sqrt{\frac{tr {(A_{1})}^{2}}{2}},

\sinh^{- 1}

(⧹.) function up to second order approximation is measured as:

(4)

\sinh^{- 1} (\frac{1}{c} Δ_{1}) ≅ - \frac{Δ_{1}^{3}}{6 c^{3}} + \frac{Δ_{1}}{c}, and |\frac{1}{c} Δ_{1}| ≪ 1 .

By way of boundary layer approximation and velocity field vector $V = [v (x, r), 0, u (x, r)],$ the mass conservation and momentum equations will take the form:

(5)

\frac{\partial (ru)}{\partial x} + \frac{\partial (rv)}{\partial r} = 0,

(6)

\begin{matrix} u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial r} = \frac{1}{r} (ν + \frac{1}{β ρ c}) \frac{\partial u}{\partial r} - \frac{1}{2 β c^{3} ρ} {(\frac{\partial u}{\partial r})}^{2} \frac{\partial^{2} u}{\partial r^{2}} + (ν + \frac{1}{β ρ c}) \frac{\partial^{2} u}{\partial r^{2}} - \frac{1}{6 β r ρ c^{3}} {(\frac{\partial u}{\partial r})}^{3} \\ + u_{s} \frac{\partial u_{s}}{\partial x} - \frac{σ B_{0}^{2}}{ρ} (u - u_{s}) + g (β_{T} (T - T_{\infty})) \cos ω, \end{matrix}

the relevant boundary conditions for flow model are as follows:

(7)

u = U (x) = \frac{U_{0}}{L} x, v = 0 at r = R and u \to u_{s} = a^{'} x as r \to \infty .

To find out the solution of Eq. (6) against boundary conditions given by Eq. (7), we have incorporated the following transformations:

(8)

\begin{matrix} η = \frac{r^{2} - R^{2}}{2 R} {(\frac{U_{0}}{ν L})}^{\frac{1}{2}}, ψ = {(\frac{U_{0} ν x^{2}}{L})}^{\frac{1}{2}} RF (η), \\ u = \frac{U_{0} x}{L} F^{'} (η), v = - \frac{R}{r} \sqrt{\frac{U_{0} ν}{L}} F (η), \end{matrix}

Note that the Eq. (5) identically satisfies under velocity components in terms of stream function $ψ$ , the components are defined as:

(9)

u = \frac{1}{r} (\frac{\partial ψ}{\partial r}), v = \frac{- 1}{r} (\frac{\partial ψ}{\partial x}),

by joining Eqs. (8) and (9) in Eq. (6), the resulting equations are given by:

(10)

\begin{matrix} 3 (1 + 2 K_{p} η) (1 + M_{p}) F {(η)}^{‴} + 3 F (η) F {(η)}^{″} + 6 K_{p} (1 + M_{p}) F {(η)}^{″} - 3 {(F {(η)}^{'})}^{2} - \\ 4 λ M_{p} K_{p} (1 + 2 K_{p} η) {(F {(η)}^{″})}^{3} - 3 M_{p} λ {(1 + 2 K_{p} η)}^{2} {(F^{″})}^{2} F^{‴} - 3 γ_{n}^{2} (F^{'} - A_{p}) + \\ 3 A_{p}^{2} + 3 λ_{p} (T (η)) \cos ω = 0, \end{matrix}

the transformed boundary conditions are:

(11)

F^{'} (η) = 1, F (η) = 0, as η \to 0, and F^{'} (η) \to A_{p}, as η \to \infty .

The physical parameters involved in Eq. (10) are defined as follows:

(12)

\begin{matrix} K_{p} = \frac{1}{R} \sqrt{\frac{ν}{a}}, a = \frac{U_{0}}{L}, M_{p} = \frac{1}{μ β c}, λ = \frac{a^{3} x^{2}}{2 c^{2} ν}, γ_{n} = \sqrt{\frac{σ β_{0}^{2}}{ρ a}}, \\ A_{p} = \frac{a^{'}}{a}, λ_{p} = \frac{Gr}{{Re}_{x}^{2}}, where Gr = \frac{g β_{T} (T_{w} - T_{0}) x^{3}}{ν^{2}} . \end{matrix}

The skin friction coefficient at the surface of cylinder is considered as:

(13)

C_{f} = \frac{τ_{w}}{ρ \frac{U^{2}}{2}}, τ_{w} = {[μ (\frac{\partial u}{\partial r}) + \frac{1}{β c} \frac{\partial u}{\partial r} - \frac{1}{6 β c^{3}} {(\frac{\partial u}{\partial r})}^{3}]}_{r = R},

the skin friction coefficient (dimensionless form) is prearranged as:

(14)

0.5 C_{f} {Re}_{x}^{1 / 2} = (1 + M_{p}) F^{″} (0) - \frac{M_{p} λ}{3} {(F^{″} (0))}^{3}, where {Re}_{x} = \frac{U_{0} x^{2}}{ν L} .

3 Temperature stratification analysis

The fluid flow model is supported by temperature stratification phenomena in the presence of both Joule heating and heat generation effects. The fundamental equation of energy under usual boundary layer assumption takes the form:

(15)

u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial r} = \frac{k}{ρ c_{p}} (\frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r} \frac{\partial T}{\partial r}) + \frac{Q_{0}}{c_{p} ρ} (T - T_{\infty}) + \frac{σ B_{0}^{2} u^{2}}{c_{p} ρ},

the temperature boundary conditions are prescribed as:

(16)

\begin{matrix} T (x, r) = T_{w} (x) = T_{0} + \frac{bx}{L}, at r = R, \\ T (x, r) \to T_{\infty} (x) = T_{0} + \frac{cx}{L}, as r \to \infty . \end{matrix}

To trace out the dimensionless form of Eq. (15), we incorporate the transformation given as:

(17)

η = \frac{r^{2} - R^{2}}{2 R} {(\frac{U_{0}}{ν L})}^{\frac{1}{2}}, T (η) = \frac{T - T_{\infty}}{T_{w} - T_{0}},

then, the transformed form of Eq. (15) is written as;

(18)

(1 + 2 K_{p} η) T {(η)}^{″} + 2 K_{p} T {(η)}^{'} + \Pr (F (η) T {(η)}^{'} - F {(η)}^{'} T (η) - F {(η)}^{'} S_{T} + H_{p} T (η) + Ec γ_{n}^{2} F {(η)}^{' 2}) = 0,

subjected to the transformed boundary conditions:

(19)

T (η) = 1 - S_{T}, at η = 0, and T (η) \to 0 as η \to \infty .

The physical parameters involved in Eq. (18) are defined by:

(20)

K_{p} = \frac{1}{R} \sqrt{\frac{ν}{a}}, \Pr = \frac{ν}{α}, S_{T} = \frac{c}{b}, H_{p} = \frac{{LQ}_{0}}{U_{0} ρ c_{p}}, Ec = \frac{U_{0} x}{c_{p} (T_{w} - T_{\infty}) L} .

The local Nusselt number can be prescribed as:

(21)

{Nu}_{x} = \frac{- {xq}_{w}}{k (T_{w} - T_{\infty})}, q_{w} = - k {(\frac{\partial T}{\partial r})}_{r = R},

it can be written in dimensionless form given as:

(22)

{Nu}_{x} {Re}_{x}^{- 1 / 2} = - T^{'} (0) .

4 Computational scheme

The Eq. (10), and Eq. (18) with endpoint conditions i-e Eq. (11), and Eq. (19) respectively are the system of governing coupled non-linear ODE’ s (ordinary differential equations) and this system is solved by using shooting scheme with the support of fifth order R-K (Runge-Kutta) algorithm. For this purpose as a first step, system of five first order equations are achieved and dropping independents and retain similarity variable $η$ as independent variable. So by permitting $\begin{matrix} ξ_{2} = F {(η)}^{'}, \\ ξ_{3} = ξ_{2}^{'} = F {(η)}^{″}, \\ ξ_{5} = T {(η)}^{'}, \end{matrix}$ regarding this the equivalent form of Eqs. (10) and (18) under new variables is given by:

(23)

[\begin{matrix} ξ_{1}^{'} = ξ_{2} \\ ξ_{2}^{'} = ξ_{3} \\ ξ_{3}^{'} = \frac{3 {(ξ_{2})}^{2} - 3 ξ_{1} ξ_{3} - (6 K_{p}) (1 + M_{p}) ξ_{3} + 4 λ M_{p} K_{p} (1 + 2 K_{p} η) ξ_{3}^{3} + 3 γ_{n}^{2} (ξ_{2} - A_{p}) - 3 A_{p}^{2} - 3 λ_{p} (ξ_{4}) \cos ω}{4 (1 + 2 K_{p} η) (1 + M_{p}) - 4 M_{p} λ {(1 + 2 K_{p} η)}^{2} ξ_{3}^{2}} \\ ξ_{4}^{'} = ξ_{5} \\ ξ_{5}^{'} = \frac{\Pr (ξ_{2} ξ_{4} + S_{T} ξ_{2} - ξ_{1} ξ_{5} - H_{p} ξ_{4} - Ec γ_{n}^{2} ξ_{2}^{2}) - 2 K_{p} ξ_{5}}{1 + 2 K_{p} η} \end{matrix}],

the equivalent endpoint conditions in new variables are given as follows:

(24)

\begin{matrix} ξ_{1} (0) = 0, ξ_{2} (0) = 1, ξ_{3} (0) = guess, ξ_{4} (0) = 1 - S_{T}, \\ ξ_{5} (0) = guess . \end{matrix}

The system given by Eq. (23) with endpoint condition Eq. (24) fulfil the primary criteria of shooting scheme, but for integration process of Eq. (23) as a initial valued problem (IVP) we must need $ξ_{3} (0)$ as a $F^{″} (0)$ , $ξ_{5} (0)$ as a $T^{'} (0)$ . We have additional boundary conditions:

(25)

ξ_{2} (\infty) = A_{p}, ξ_{4} (\infty) = 0 .

5 Physical outcomes

The selection of complimentary values for $F^{″} (0)$ , and $T^{'} (0)$ are estimated by keeping in mind that the integration of system of first order differential equations carried out in a such a way that the conditions in Eq. (25) holds absolutely. Note that the numerical computation up-to four decimal precision as convergence standards are obtained by maintaining $Δ η = 0.025$ as a step size.

The adopted parameter values for present computational analysis are given in Table 1. The obtained results are against these values unless indicated on graphs where needed. Table 2 is used to trace out the variations of skin friction coefficient towards Eyring-Powell fluid parameters and curvature of the cylindrical surface. It was found that the skin friction coefficient increases for increasing values of both curvature parameter $K_{p}$ and fluid parameter $M_{p}$ while it shows decline attitude for larger values of fluid parameter $λ .$ The impacts of curvature parameter, Prandtl number, an inclination and Eckert number on heat transfer rate are evaluated and given in Table 3. It was observed that the heat transfer rate is increasing function of both curvature parameter $K_{p}$ and Prandtl number Pr. 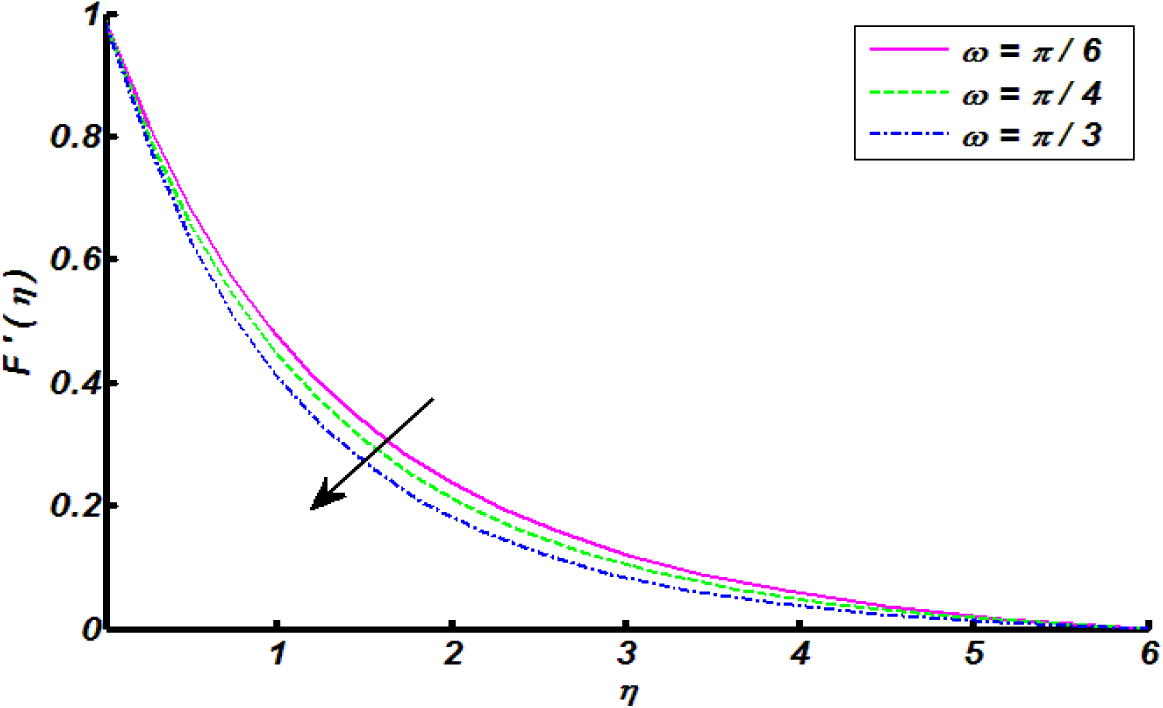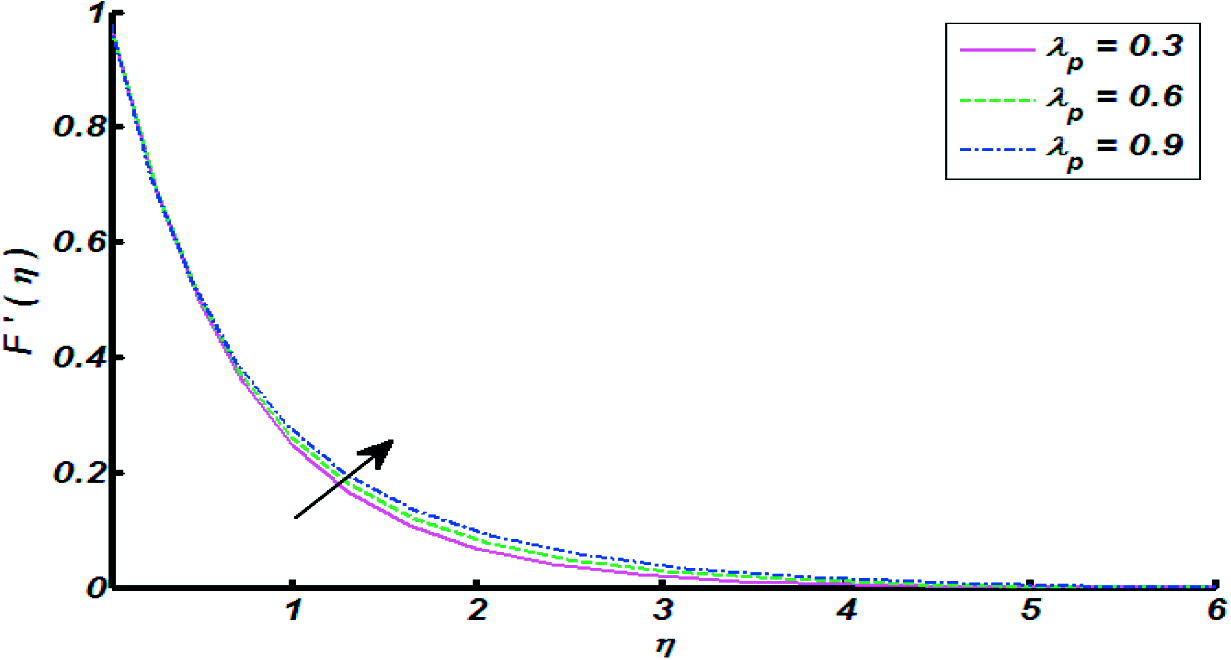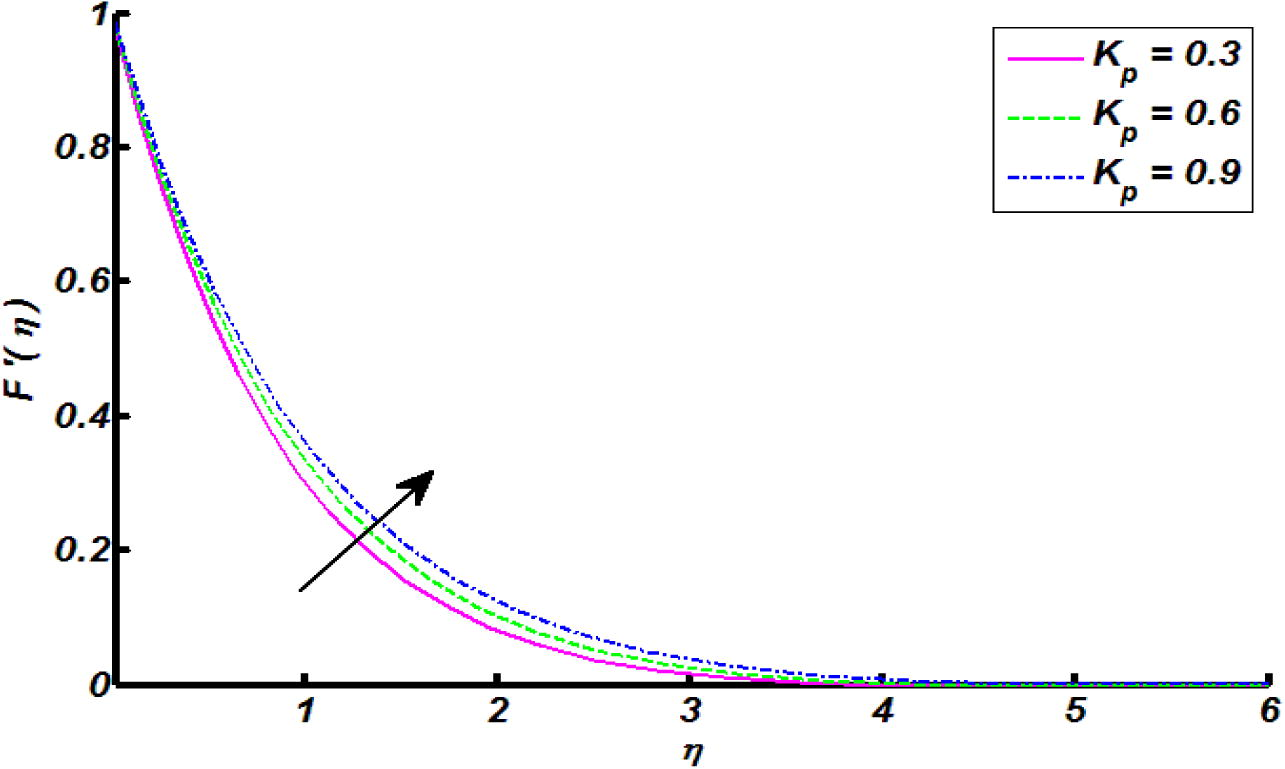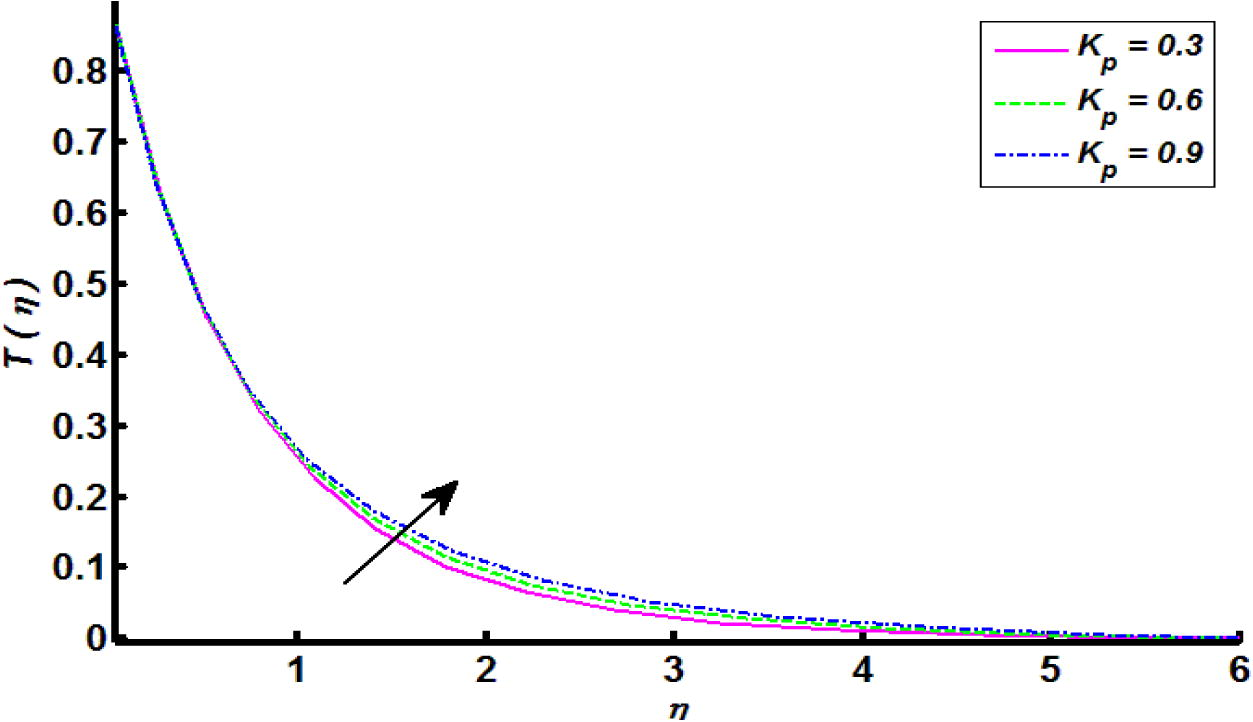Whereas, heat transfer rate shows decline nature for Eckert number $Ec$ and an inclination $ω$ of the cylindrical surface. Figs. 1 and 1a is the physical illustration of flow model and flow chart of numerical method respectively. Whereas, the Figs. 2–10 are plotted to explore the effects logs of involved physical parameters namely, velocities ratio parameter, magnetic field parameter, an inclination, mixed convection parameter, curvature parameter, thermal stratification parameter, heat generation parameter and Eckert number. Particularly, Figs. 2–6 are used demonstrate the impacts of velocities ratio parameter, magnetic field parameter, an inclination, mixed convection parameter and curvature parameter on velocity profile. Figs. 7–10 are established to identify the effects of curvature parameter, thermal stratification parameter, heat generation parameter and Eckert number over a temperature profile. Figs. 11 and 12 are sketched to identify the variation of skin friction coefficient and heat transfer rate through straight line and parabolic curve fitting analysis. To be more specific for Figs. 11 and 12, red lines curves exhibit thermal stratification and mixed convection parameter and blue dash dotted curves depicts the response of heat generation and magnetic field parameters. In detail, Fig. 2 determines the variation of fluid velocity against different values of $A_{p}$ (velocities ratio parameter). As expected by increasing the velocities ratio parameter the velocity of the fluid increase within a flow regime. The impact of magnetic field parameter over a fluid velocity is depicted in Fig. 3. The applied magnetic field is being consider perpendicular to the fluid flow and has an ability to generate the Lorentz force (drag force), which inclines to oppose the fluid flow and hence horizontal velocity shows decline attitude. Fig. 4 paints the impact of inclination on velocity of the fluid. It was observed that for larger values of an inclination $ω$ the velocity profile declines. This fact is due to influence of gravity. Because by increasing an inclination $ω$ relative to x-axis, the impact of gravity is reduced which results decline in velocity within a boundary layer. Fig. 5 determines the variation of fluid velocity against mixed convection parameter on velocity profile. It was found that for higher values of $λ_{p}$ velocity of fluid increases. Physically, it is due to inciting attitude of thermal buoyancy force. Fig. 6 shows that the higher values of curvature parameter is the cause of increase in velocity profile. The curvature parameter $K_{p}$ has inverse relation with radius of curvature. So when we increase this parameter, the radius of cylinder decreases and hence contact surface area of cylinder with fluid reduces, which offers less resistance to fluid flow. So increase in curvature parameter $K_{p}$ causes increase in velocity profile. Fig. 7 paints the temperature variation against curvature parameter. It is clearly seen that temperature distribution increases for increasing values of curvature parameter $K_{p} .$ As Kelvin temperature is defined as an average kinetic energy so when we increase curvature of cylinder, velocity of the fluid increases, resultantly kinetic energy increases and due to this temperature increases. Note that temperature of fluid start decreasing near the cylindrical.

Table 1 Adopted parameters values for computational analysis.

Magnetic field parameter	$γ_{n} = 0.1$	Thermal Stratification parameter	$S_{T} = 0.1$
Curvature parameter	$K_{p} = 0.1$	Prandtl number	$\Pr = 1.3$
Fluid parameters	$λ, M_{p} = 0.1$	Heat-generation parameter	$H_{p} = 0.1$
Velocities ratio parameter	$A_{p} = 0.1$	Mixed convection parameter	$λ_{p} = 0.1$
Inclination	$ω = \frac{π}{3}$ Eckert number $Ec = 0.1$

Table 2 Skin friction coefficient for different values of

λ, K_{p} and M_{p} .

$λ$	$K_{p}$	$M_{p}$	$F^{″} (0)$	$0.5 C_{f} \sqrt{{Re}_{x}}$
0.3			−0.9423	−1.0288
0.6			−0.9373	−1.0146
0.9			−0.9326	−1.0015
	0.3		−1.0168	−1.1150
	0.6		−1.1280	−1.2360
	0.9		−1.2243	−1.3406
		0.3	−0.8728	−1.1280
		0.6	−0.7915	−1.2565
		0.9	−0.7311	−1.3775

Table 3 Heat Transfer rate for different values of

K_{p}, \Pr and ω .

$K_{p}$	$\Pr$	$ω$	$Ec$	$- T^{'} (0)$
0.3	–	–	–	1.1683
0.6	–	–	–	1.2691
0.9	–	–	–	1.3699
–	0.3	–	–	0.4988
–	0.6	–	–	0.7290
–	0.9	–	–	0.9275
–	–	$π / 6$	–	1.1045
–	–	$π / 4$	–	1.1034
–	–	$π / 3$	–	1.1019
–	–	–	0.3	1.1009
–	–	–	0.6	1.0995
–	–	–	0.9	1.0980

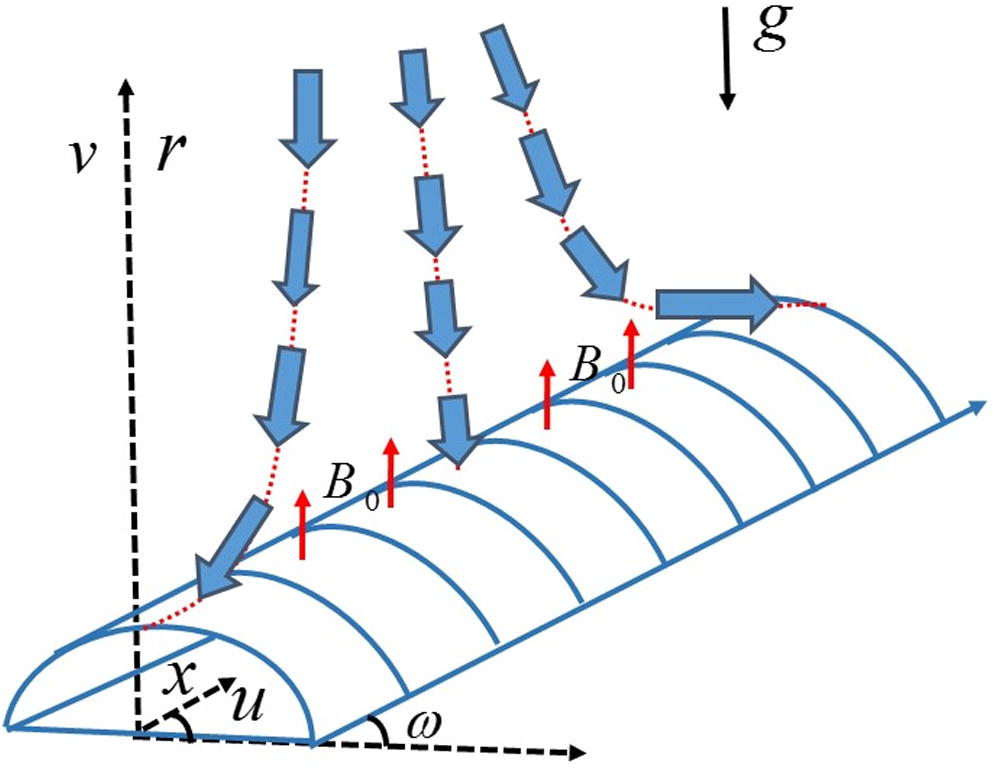
Physical illustration of fluid flow over an inclined stretching cylindrical surface.

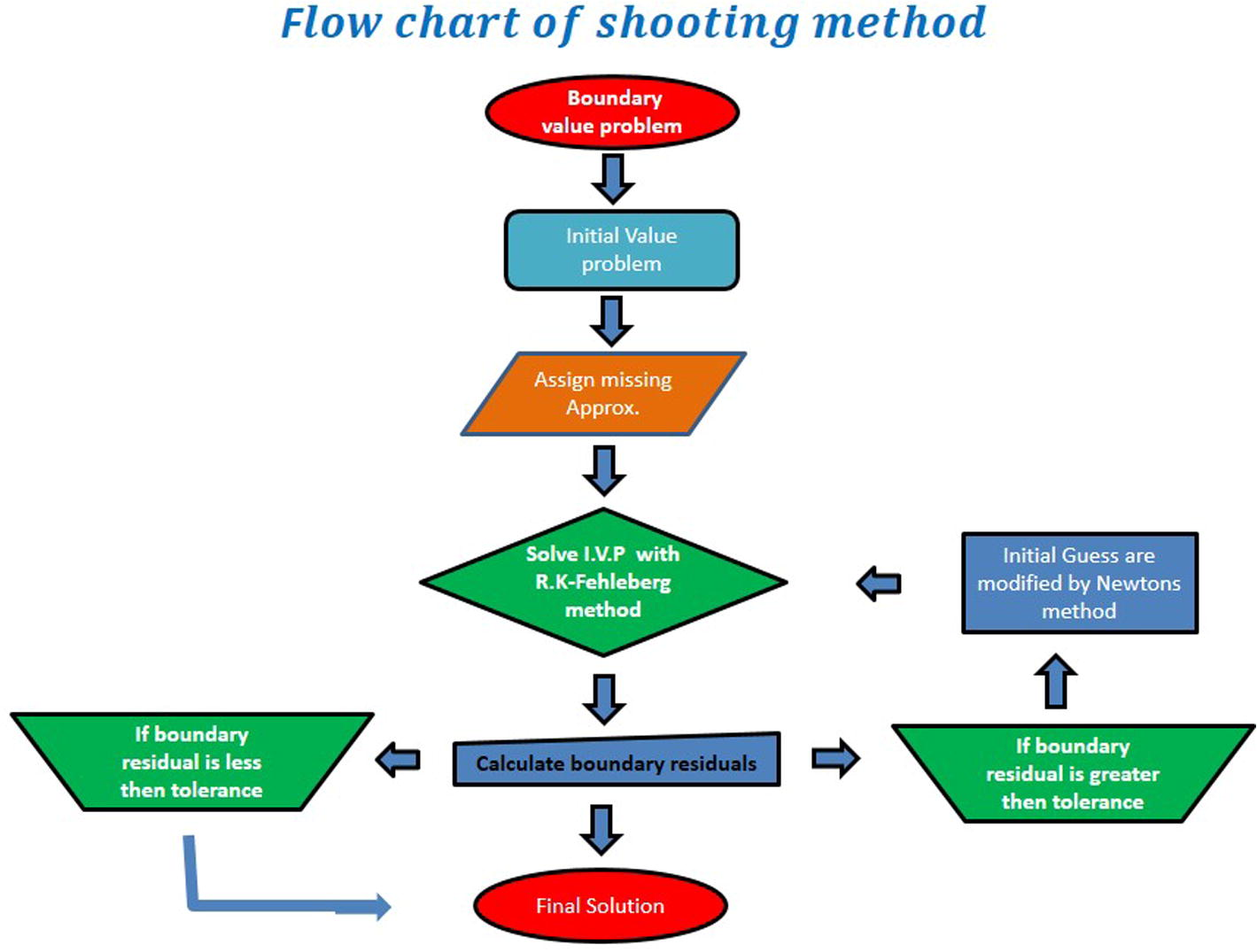
Flow chart for valuation of shooting scheme.

Effect of velocities ratio parameter A p on velocity distribution.

Effect of magnetic parameter γ n on velocity distribution.

Effect of inclination ω on velocity distribution.

Effect of mixed convection parameter λ p on velocity distribution.

Effect of curvature parameter K p on velocity distribution.

Effect of curvature parameter K p on temperature distribution.

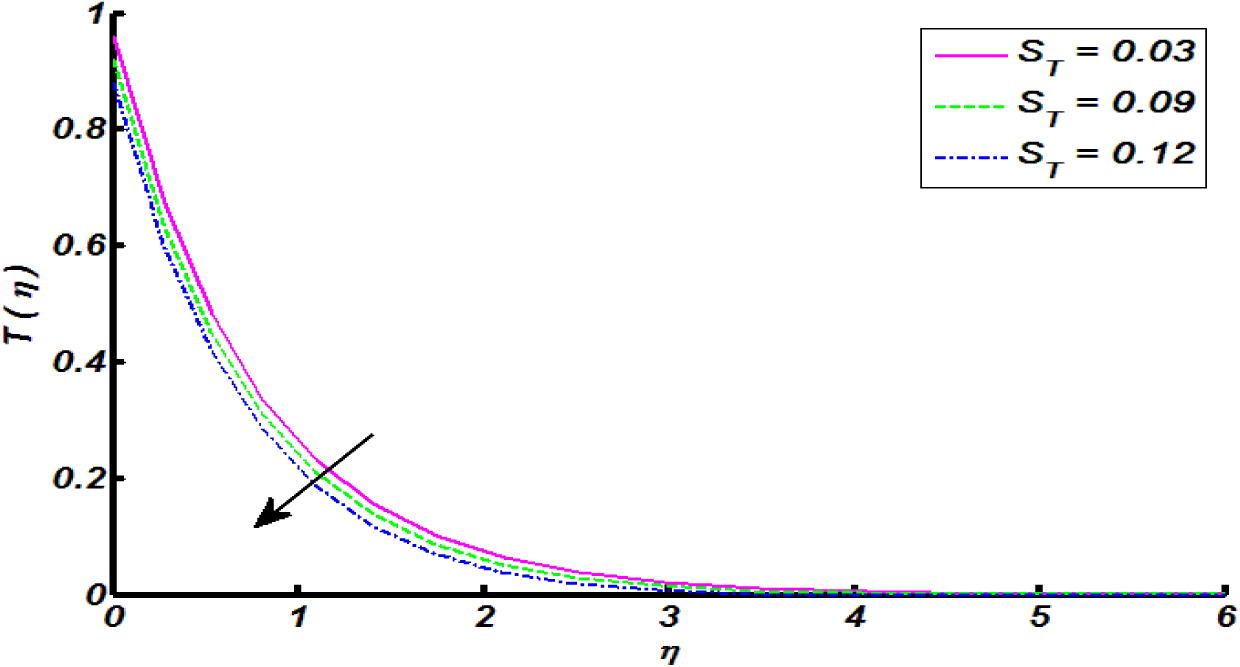
Effect of thermal stratification parameter S T on temperature distribution.

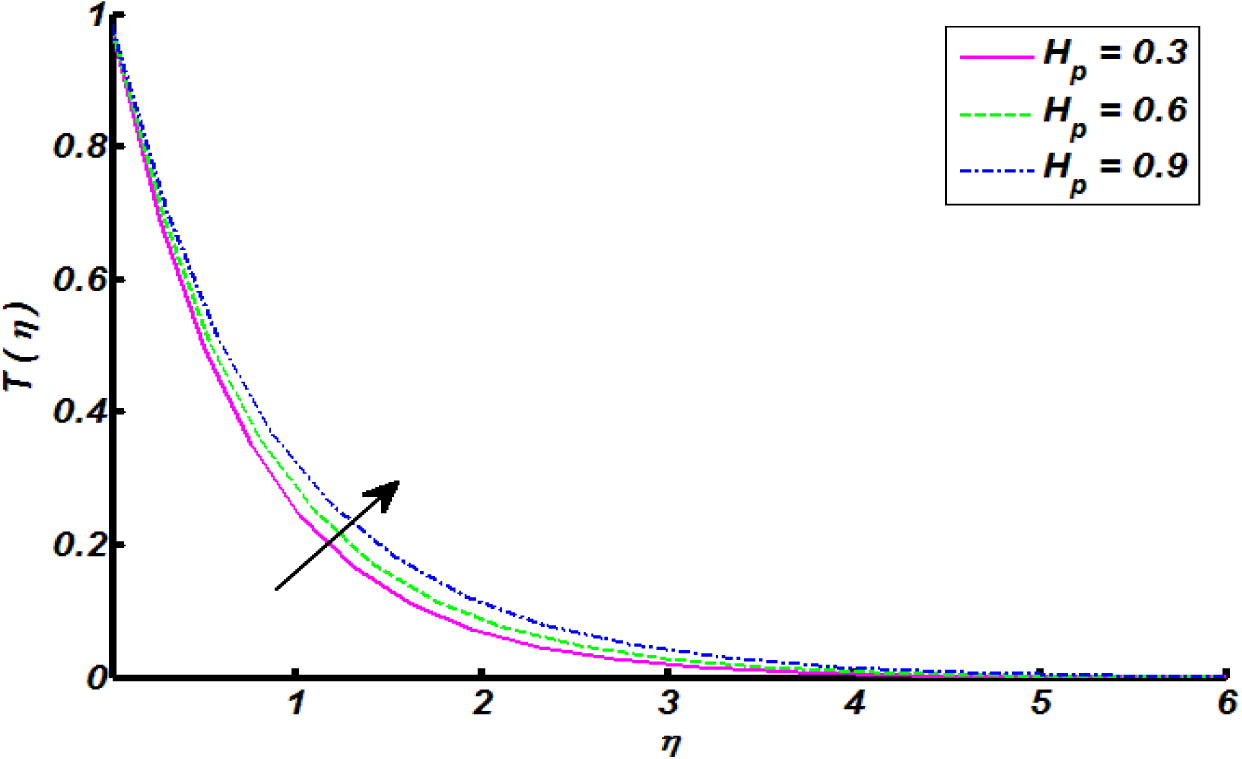
Effect of heat generation parameter H p on temperature distribution.

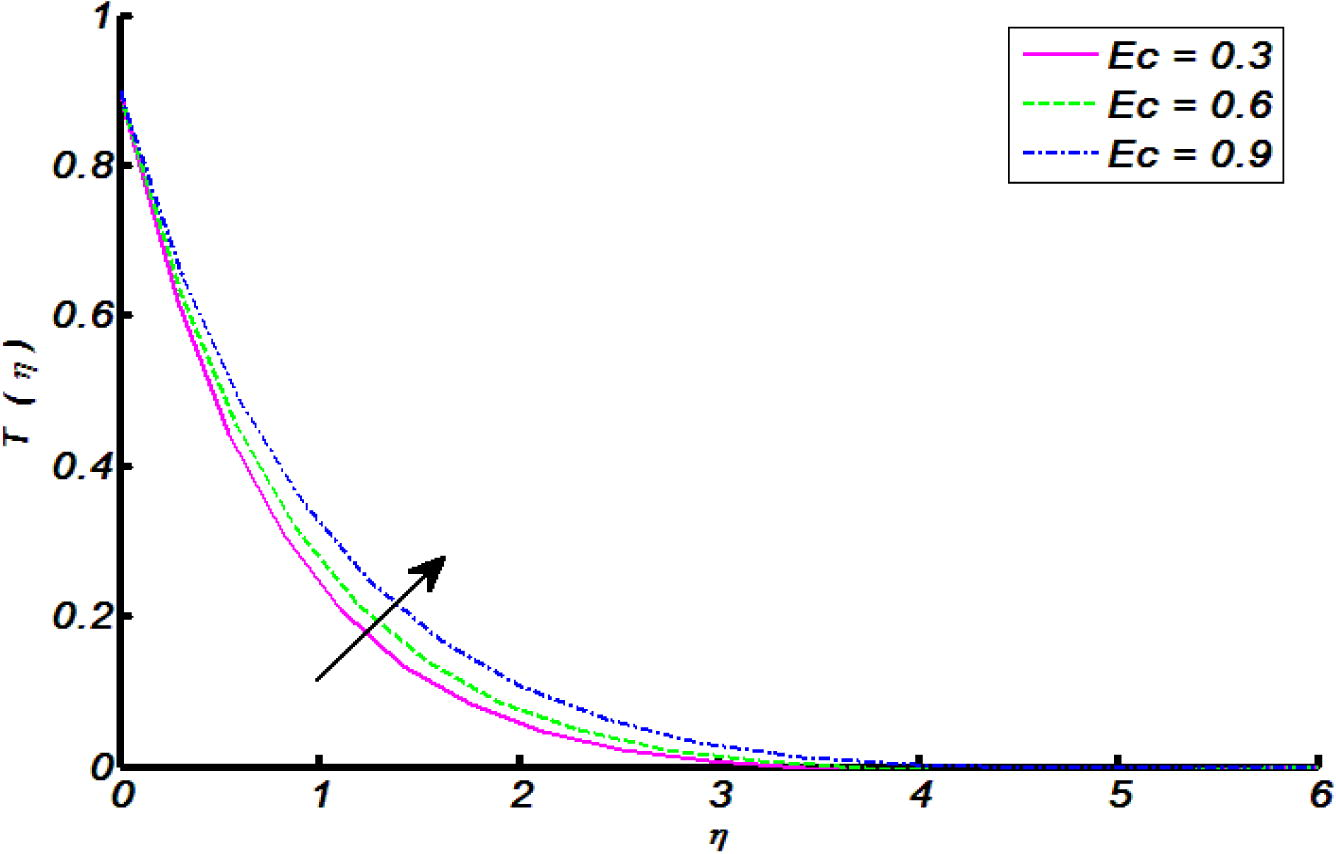
Effect of Eckert number Ec on temperature distribution.

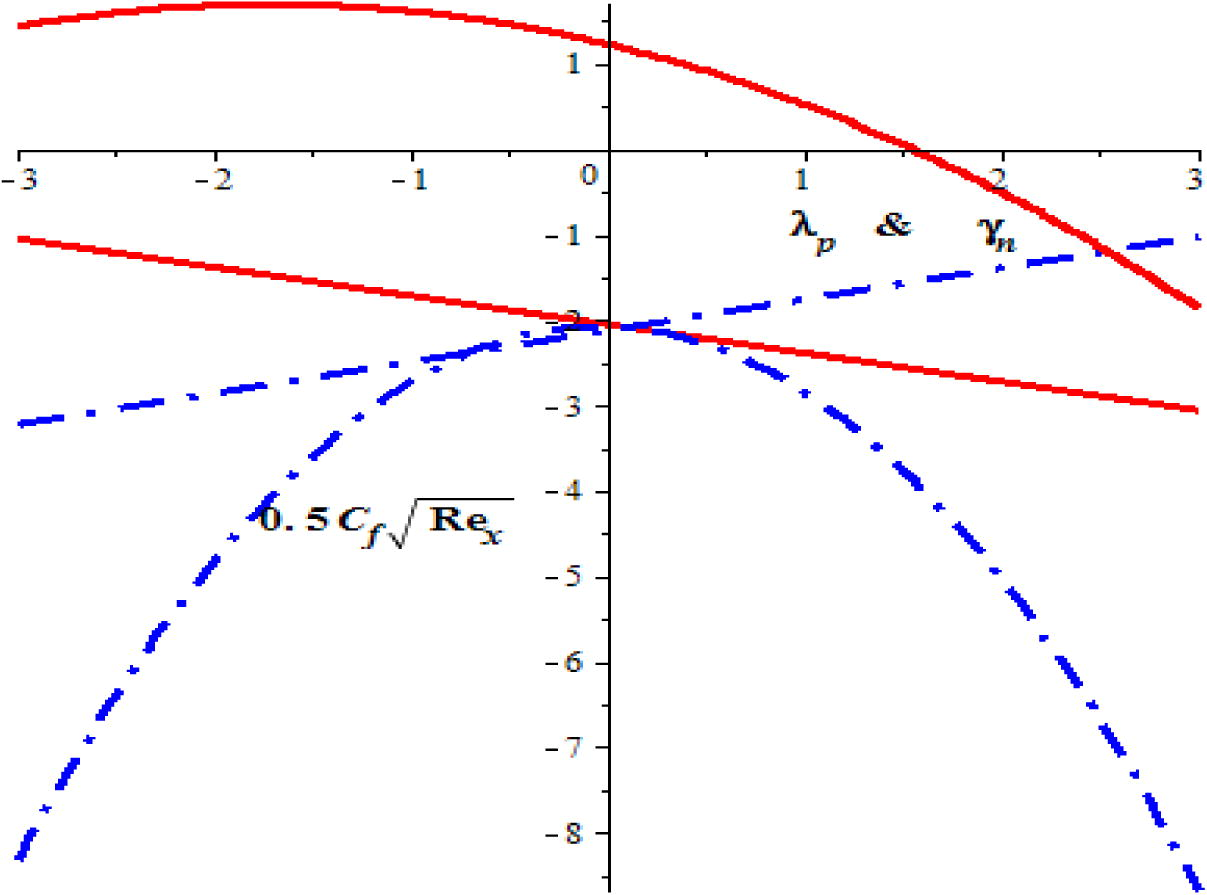
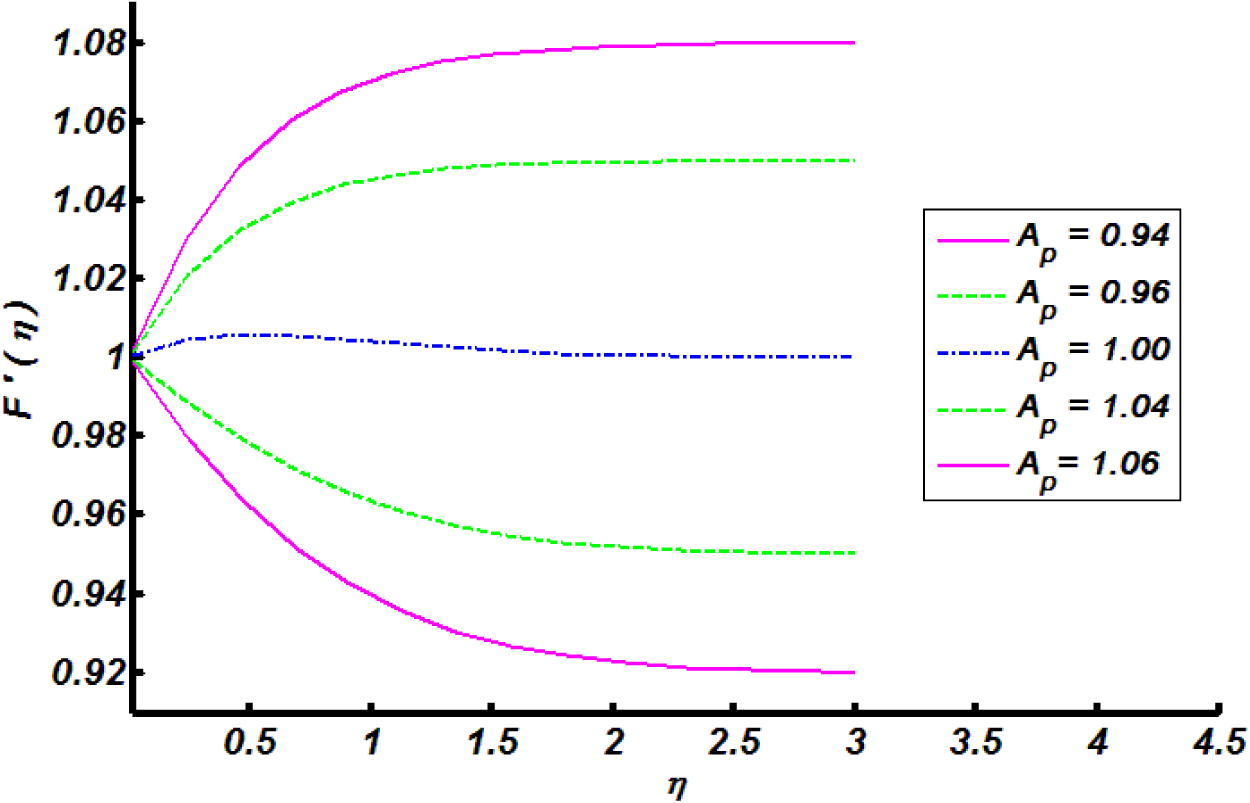
The impact of magnetic field and mixed convection parameter on skin friction coefficient.

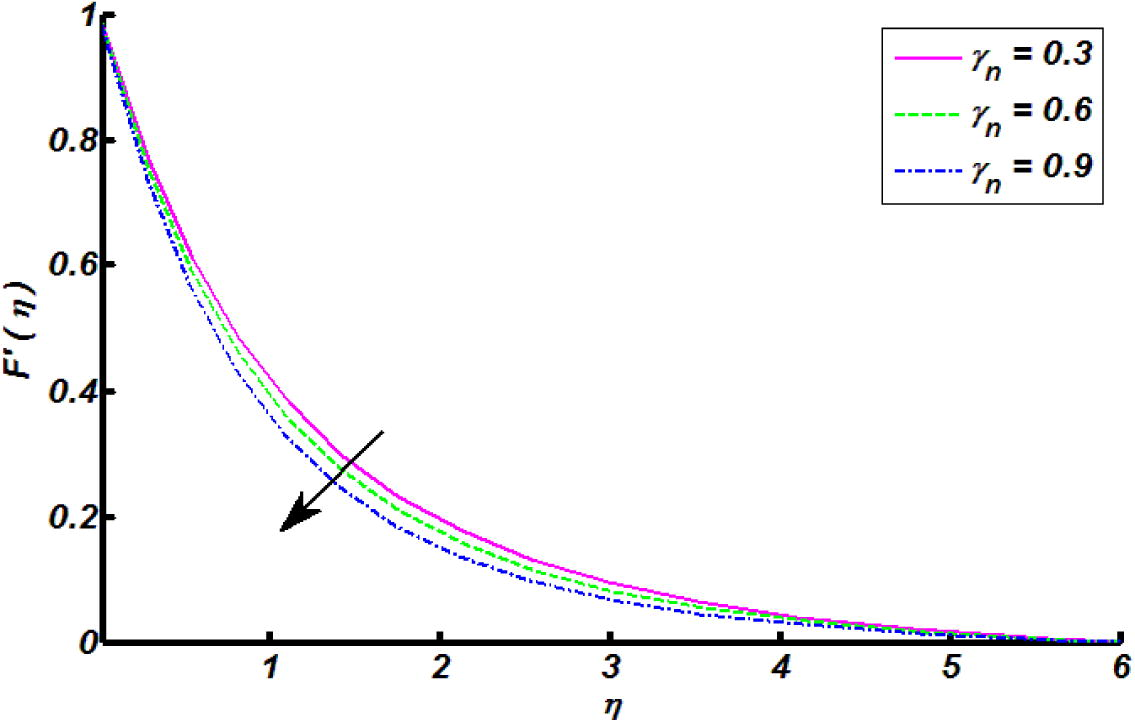
The impact of heat generation and thermal stratification parameter on heat transfer rate.

surface and increases far away with respect to surface. The influence of thermal stratification parameter on temperature of the fluid was sketched in Fig. 8. It show that temperature distribution decreases throughout the flow regime. In view of physical reasoning, this is because of decline in temperature difference between cylindrical surface and ambient fluid therefore, temperature profile decreases. In the view of Fig. 9, it is witnessed that temperature profile increases for increasing values of is heat generation parameter. This is because of production of energy by way of heat generation process, which brings enrichment in temperature distribution throughout the flow regime. Fig. 10 paints the effect of Eckert number $Ec$ on temperature profile. It was found that thermal boundary layer thickness increases for increasing values of Eckert number. Further, for increase in Eckert number the fluid particles become more energetic due to storage of energy which claims the increment in temperature of the fluid.

6 Straight line and parabolic curve fitting analysis

In this section, we have evaluated the attitude of skin friction coefficient and heat transfer rate by means of straight line and parabolic curve fitting approximation towards mixed convection parameter, magnetic field parameter, thermal stratification parameter and heat generation parameter. The least square method was utilized here and it was proposed by Guass and Legendre. The generalized curve fitting for $m$ degree polynomial is $P (X) = α_{0} + α_{1} X + \dots + α_{m} X^{m}$ , where $m ⩽ n - 1$ . Then, $Q$ takes the form $Q = \sum_{i = 1}^{n} {(Y_{i} - P (X_{i}))}^{2}$ and depends on $m + 1$ parameters namely, $α_{0}, α_{1}, \dots α_{m}$ . So, we have $m + 1$ conditions, i-e

(26)

\frac{\partial Q}{\partial α_{0}} = 0, \frac{\partial Q}{\partial α_{1}} = 0, \dots \frac{\partial Q}{\partial α_{m}} = 0,

which results a system of

m + 1

normal equations. The case of quadratic polynomial corresponds

P (X) = α_{0} + α_{1} X + α_{2} X^{2},

and normal equations for quadratic ap3proximations can be written as:

(27)

\begin{matrix} n α_{0} + α_{1} \sum X_{i} + α_{2} \sum X_{i}^{2} = \sum Y_{i} \\ α_{0} \sum X_{i} + α_{1} \sum X_{i}^{2} + α_{2} \sum X_{i}^{3} = \sum X_{i} Y_{i} \\ α_{0} \sum X_{i}^{2} + α_{1} \sum X_{i}^{3} + α_{2} \sum X_{i}^{4} = \sum X_{i}^{2} Y_{i} \end{matrix} .

To trace out straight line and parabolic curve fitting for heat transfer rate against thermal stratification and heat generation parameters i-e $S_{T}$ , and $H_{p}$ . Let $X_{i} = {(S_{T})}_{i}$ and $Y_{i} = {(- T^{'} (0))}_{i}$ we get, $\begin{matrix} \sum {(S_{T})}_{i} = 0.1, \sum {(S_{T})}_{i}^{2} = 0.01000, \\ \sum {(- T^{'} (0))}_{i} = 2.4090, \sum {(S_{T})}_{i} {(- T^{'} (0))}_{i} = 0.1184, \end{matrix}$ by incorporating these values in Eq. (27), we have

(28)

\begin{matrix} 2 a_{0} + 0.1 a_{1} = 2.4090, \\ 0.1 a_{0} + 0.01 a_{1} = 0.1184, \end{matrix}

by solving system of equations given by Eq. (28), we get

(29)

- T^{'} (0) = P (S_{T}) = a_{0} + a_{1} S_{T}

here,

a_{0} = 1.2250, and a_{1} = - 0.4099

. For parabolic curve fitting, we have

\begin{matrix} \sum {(S_{T})}_{i} = 0.4, \sum {(S_{T})}_{i}^{2} = 0.1000, \sum {(S_{T})}_{i}^{3} = 0.0280, \sum {(S_{T})}_{i}^{4} = 0.0098, \\ \sum {(- T^{'} (0))}_{i} = 3.5108, \sum {(S_{T})}_{i} {(- T^{'} (0))}_{i} = 0.4489, \sum {(S_{T})}_{i}^{2} {(- T^{'} (0))}_{i} = 0.1110, \end{matrix}

by incorporating these numeric values into Eq. (27), we obtained

(30)

\begin{matrix} 3 a_{2} + 0.4 a_{3} + 0.1000 a_{4} = 3.5108, \\ 0.4 a_{2} + 0.1000 a_{3} + 0.0280 a_{4} = 0.4489, \\ 0.1000 a_{2} + 0.0280 a_{3} + 0.0098 a_{4} = 0.1110 \end{matrix}

by common algebraic practise this system gives parabolic curve fitting relation for heat transfer rate towards thermal stratification i-e

(31)

- T^{'} (0) = P (S_{T}) = a_{2} + a_{3} S_{T} + a_{4} {(S_{T})}^{2},

where,

a_{2} = - 0.94220, a_{3} = 0.20800, and a_{4} = - 0.10000 .

Similarly, line and parabolic curve fitting for heat transfer rate for heat generation parameter is entertained as follows.

\begin{matrix} \sum {(H_{p})}_{i} = 0.4, \sum {(H_{p})}_{i}^{2} = 0.1000, \\ \sum {(- T^{'} (0))}_{i} = 2.2482, \sum {(H_{p})}_{i} {(- T^{'} (0))}_{i} = 0.4377, \end{matrix}

(32)

\begin{matrix} 2 b_{0} + 0.4 b_{1} = 2.2482, \\ 0.4 b_{0} + 0.1 b_{1} = 0.4377, \end{matrix}

then the straight line approximations towards heat generation parameter is given by:

(33)

- T^{'} (0) = P (H_{p}) = b_{0} + b_{1} H_{p},

where,

b_{0} = 1.2435 and b_{1} = - 0.5970 .

Now for parabolic curve fitting approximations is calculated as follows:

\begin{matrix} \sum {(H_{p})}_{i} = 0.9, \sum {(H_{p})}_{i}^{2} = 0.3500, \sum {(H_{p})}_{i}^{3} = 0.1530, \sum {(H_{p})}_{i}^{4} = 0.0707, \\ \sum {(- T^{'} (0))}_{i} = 3.1695, \sum {(H_{p})}_{i} {(- T^{'} (0))}_{i} = 0.8983, \sum {(H_{p})}_{i}^{2} {(- T^{'} (0))}_{i} = 0.3379, \end{matrix}

(34)

\begin{matrix} 3 b_{2} + 0.9 b_{3} + 0.3500 b_{4} = 3.1695, \\ 0.9 b_{2} + 0.3500 b_{3} + 0.1530 b_{4} = 0.8983, \\ 0.3500 b_{2} + 0.1530 b_{3} + 0.0707 b_{4} = 0.3379, \end{matrix}

than solution of system corresponds

(35)

- T^{'} (0) = P (S_{T}) = b_{2} + b_{3} H_{p} + b_{4} {(H_{p})}^{2}

here,

b_{2} = 1.23307, b_{3} = - 0.46281, and b_{4} = - 0.32343 .

Straight line and Parabolic curve fitting approximations for skin friction coefficient towards magnetic field and mixed convection parameters are processed as follows:

\begin{matrix} \sum {(γ_{n})}_{i} = 0.4, \sum {(γ_{n})}_{i}^{2} = 0.1000, \\ \sum 0.5 C_{f} \sqrt{{Re}_{x}} = - 4.2377, \sum (0.5 C_{f} \sqrt{{Re}_{x}}) γ_{n} = - 0.8542, \end{matrix}

(36)

\begin{matrix} 2 c_{0} + 0.4 c_{1} = - 4.2377, \\ 0.4 c_{0} + 0.1 c_{1} = - 0.8542, \end{matrix}

after solving this system we obtained

(37)

0.5 C_{f} \sqrt{{Re}_{x}} = P (γ_{n}) = c_{0} + c_{1} γ_{n}

here,

c_{0} = - 2.05225 and c_{1} = - 0.33299 .

Now for parabolic approximation we have,

\begin{matrix} \sum {(γ_{n})}_{i} = 0.9, \sum {(γ_{n})}_{i}^{2} = 0.3500, \sum {(γ_{n})}_{i}^{3} = 0.1530, \sum {(γ_{n})}_{i}^{4} = 0.0707, \\ \sum 0.5 C_{f} \sqrt{{Re}_{x}} = - 6.5173, \sum (0.5 C_{f} \sqrt{{Re}_{x}}) γ_{n} = - 1.9940, \sum (0.5 C_{f} \sqrt{{Re}_{x}}) γ_{n}^{2} = - 0.7844, \end{matrix}

(38)

\begin{matrix} 3 c_{2} + 0.9 c_{3} + 0.3500 c_{4} = - 6.5173, \\ 0.9 c_{2} + 0.3500 c_{3} + 0.1530 c_{4} = - 1.9940, \\ 0.3500 c_{2} + 0.1530 c_{3} + 0.0707 c_{4} = - 0.7844, \end{matrix}

by solving this system we gain

(39)

0.5 C_{f} \sqrt{{Re}_{x}} = P (γ_{n}) = c_{2} + c_{3} γ_{n} + c_{4} {(γ_{n})}^{2},

here,

c_{2} = - 2.07215, c_{3} = - 0.0563, and c_{4} = - 0.71468 .

In similar fashion, straight line and parabolic curve fitting for skin friction coefficient towards mixed convection parameter is evaluated as follows;

\begin{matrix} \sum {(λ_{p})}_{i} = 0.1, \sum {(λ_{p})}_{i}^{2} = 0.0100, \\ \sum 0.5 C_{f} \sqrt{{Re}_{x}} = - 4.2083, \sum (0.5 C_{f} \sqrt{{Re}_{x}}) λ_{p} = - 0.2086, \end{matrix}

(40)

\begin{matrix} 2 d_{0} + 0.1 d_{1} = - 4.2083, \\ 0.1 d_{0} + 0.01 d_{1} = - 0.2086, \end{matrix}

solution of this system corresponds

(41)

0.5 C_{f} \sqrt{{Re}_{x}} = P (λ_{p}) = d_{0} + d_{1} λ_{p},

here,

d_{0} = - 2.12230 and d_{1} = 0.36300 .

For parabolic relation, we have

\begin{matrix} \sum {(λ_{p})}_{i} = 0.4, \sum {(λ_{p})}_{i}^{2} = 0.1000, \sum {(λ_{p})}_{i}^{3} = 0.0280, \sum {(λ_{p})}_{i}^{4} = 0.0098, \\ \sum 0.5 C_{f} \sqrt{{Re}_{x}} = - 6.6544, \sum (0.5 C_{f} \sqrt{{Re}_{x}}) λ_{p} = - 0.8123, \sum (0.5 C_{f} \sqrt{{Re}_{x}}) λ_{p}^{2} = - 0.2020, \end{matrix}

(42)

\begin{matrix} 3 d_{2} + 0.4 d_{3} + 0.1000 d_{4} = - 6.6544, \\ 0.4 d_{2} + 0.1000 d_{3} + 0.0280 d_{4} = - 0.8123, \\ 0.1000 d_{2} + 0.0280 d_{3} + 0.0098 d_{4} = - 0.2020, \end{matrix}

after solving by common algebraic practise, we get

(43)

0.5 C_{f} \sqrt{{Re}_{x}} = P (λ_{p}) = d_{2} + d_{3} λ_{p} + d_{4} {(λ_{p})}^{2},

where,

d_{2} = - 2.44956, d_{3} = 2.23964, and d_{4} = - 2.01569 .

The variation of skin friction coefficient for the different values of both magnetic field and mixed convection parameters are presented in Fig. 11 by way of straight line and parabolic curve fitting scheme. The negative numerical values of skin friction physically reflects drag force on the fluid particles by cylindrical surface. In absolute sense, it was found that exerted drag force by cylindrical surface is increasing function of magnetic field parameter and decreasing attitude towards mixed convection parameter. Fig. 12 is sketched to study the variation heat transfer rate through straight line and parabolic approximation towards different values of both heat generation and thermal stratification parameters. Physically, the decline nature of Nusselt number represents heat transfer from cylindrical surface to the fluid (normal to the cylindrical surface). It was observed that the heat transfer rate normal to the cylindrical surface is decreasing function of both heat generation and thermal stratification parameters.

7 Results validation description

The Eqs. (10) and (18) under endpoint conditions (see Eqs. (11) and (19)) narrates the Eyring-Powell fluid flow an induced by cylindrical stretching surface along with heat transfer characteristics under thermal stratification and Joule heating phenomena. In the absence of heat transfer, if we incorporate $K_{p} = 0, λ_{p} = 0 and A_{p} = 0,$ we get

(44)

\begin{matrix} (1 + M_{p}) F^{‴} - F^{' 2} + {FF}^{″} - M_{p} λ F^{‴} F^{″ 2} - γ_{n}^{2} F^{'} = 0, \\ F (η) = 0, F^{'} (η) = 1, as η \to 0, \\ F^{'} (η) = 0, as η \to \infty . \end{matrix}

The Eq. (44) is the mathematical formulation of the physical system in which Eyring-Powell fluid flow is brought by stretching sheet in two dimensional frame, the hidden characteristics regarding this physical flow was already discussed by Akbar et al. (2015) and they justified their remarks by developing comparison with Fathizadeh et al. (2013). Table 4 is constructed to validate our obtained results with Fathizadeh et al. (2013) and Akbar et al. (2015). For this purpose we incorporate $M_{p} = λ = 0$ in Eq. (44). It is found that we have excellent match with existing values. This leads to surety of our current computations.

Table 4 Comparison of skin friction for different values of

γ_{n}

$γ_{n}$	Fathizadeh et al. (2013)	Akbar et al. (2015)	Present results
0.0	−1	−1	−1
0.5	–	−1.11803	−1.1180
1.0	−1.41421	−1.41421	−1.4142
5.0	−2.44948	−2.44949	−2.4494
10	−3.31662	−3.31663	−3.3166

8 Enumerated key findings

The magneto-hydrodynamic mixed convection boundary layer flow of Eyring-Powell fluid brought by an inclined cylindrical surface in the presence of heat generation process under the region of stagnation point was investigated theoretically. The effects logs of involved physical parameters namely, curvature parameter, magnetic field parameter, mixed convection parameter, velocities ratio parameter, thermal stratification parameter, and heat generation parameter on dimensionless velocity and temperature distributions are identified. The variation of skin friction coefficient and heat transfer rate is presented by way of straight line and parabolic curve fitting analysis. The summarized key results of current study are itemized as follows:

The velocity of fluid is found as decreasing function of angle of inclination and magnetic field parameter while it shows opposite attitude towards curvature, mixed convection and velocities ratio parameters.
Boundary layer is formed when free stream velocity is larger than stretching velocity, while inverted boundary layer is observed for case of dominancy of stretching velocity.
The temperature profile shows decline attitude towards thermal stratification parameter while it shows remarkable increment for Eckert number, curvature and heat generation parameters.
Skin friction coefficient shows decline for positive iterations of thermal stratification and heat generation parameters.
In the view of absolute frame heat transfer rate is increasing function of magnetic field parameter and paints opposite remarks for mixed convection parameter.
The impact of pertinent flow controlling parameters was studied first time by way of straight line and parabolic curve fitting approximations. It was trusted that it will serve as a helping hand for the upcoming studies.

References

Akbar N.S., Ebaid A., Khan Z.H., . Numerical analysis of magnetic field effects on Eyring-Powell fluid flow towards a stretching sheet. J. Magn. Magn. Mater.. 2015;382:355-358.
[Google Scholar]
Aman S., Khan I., Ismail Z., Salleh M.Z., . Impacts of gold nanoparticles on MHD mixed convection Poiseuille flow of nanofluid passing through a porous medium in the presence of thermal radiation, thermal diffusion and chemical reaction. Neural Comput. Appl. 2016:1-9.
[Google Scholar]
Ali F., Gohar M., Khan I., . MHD flow of water-based Brinkman type nanofluid over a vertical plate embedded in a porous medium with variable surface velocity, temperature and concentration. J. Mol. Liq.. 2016;223:412-419.
[Google Scholar]
Babu M.J., Sandeep N., Raju C.S., . Heat and mass transfer in MHD Eyring-Powell nanofluid flow due to cone in porous medium. Int. J. Eng. Res. Africa. 2015;19:57.
[Google Scholar]
Babu M.J., Sandeep N., . Three-dimensional MHD slip flow of nanofluids over a slendering stretching sheet with thermophoresis and Brownian motion effects. Adv. Powder Technol.. 2016;27(5):2039-2050.
[Google Scholar]
Fathizadeh M., Madani M., Khan Y., Faraz N., Yıldırım A., Tutkun S., . An effective modification of the homotopy perturbation method for mhd viscous flow over a stretching sheet. J. King Saud Univ. Sci.. 2013;25(2):107-113.
[Google Scholar]
Gul A., Khan I., Shafie S., . Energy transfer in mixed convection MHD flow of nanofluid containing different shapes of nanoparticles in a channel filled with saturated porous medium. Nanoscale Res. Lett.. 2015;10(1):490.
[Google Scholar]
Gul A., Khan I., Shafie S., Khalid A., Khan A., . Heat transfer in MHD mixed convection flow of a ferrofluid along a vertical channel. PLoS ONE. 2015;10(11):e0141213.
[Google Scholar]
Hiemenz, K., 1911. Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder. (Doctoral dissertation).
Hayat T., Gull N., Farooq M., Ahmad B., . Thermal radiation effect in MHD flow of Powell—Eyring nanofluid induced by a stretching cylinder. J. Aerospace Eng.. 2015;29(1):04015011.
[Google Scholar]
Khan N.A., Sultan F., Khan N.A., . Heat and mass transfer of thermophoretic MHD flow of Powell-Eyring Fluid over a vertical stretching sheet in the presence of chemical reaction and Joule heating. Int. J. Chem. Reactor Eng.. 2015;13(1):37-49.
[Google Scholar]
Khan S.U., Ali N., Abbas Z., . Influence of heat generation/absorption with convective heat and mass conditions in unsteady flow of Eyring Powell nanofluid over porous oscillatory stretching surface. J. Nanofluids. 2016;5(3):351-362.
[Google Scholar]
Krishna P.M., Sandeep N., Reddy J.R., Sugunamma V., . Dual solutions for unsteady flow of Powell-Eyring fluid past an inclined stretching sheet. J. Naval Arch. Mar. Eng.. 2016;13(1):89-99.
[Google Scholar]
Kumaran G., Sandeep N., Ali M.E., . Computational analysis of magnetohydrodynamic Casson and Maxwell flows over a stretching sheet with cross diffusion. Results Phys.. 2017;7:147-155.
[Google Scholar]
Malik M.Y., Hussain A., Nadeem S., . Boundary layer flow of an Eyring-Powell model fluid due to a stretching cylinder with variable viscosity. Scientia Iranica. 2013;20(2):313-321.
[Google Scholar]
Powell R.E., Eyring H., . Mechanism for relaxation theory of viscosity. Nature. 1944;154(55):427-428.
[Google Scholar]
Pavlov K.B., . Magnetohydrodynamic flow of an incompressible viscous fluid caused by deformation of a plane surface. Magnitnaya Gidrodinamika. 1974;4(1):146-147.
[Google Scholar]
Patel M., Timol M.G., . Numerical treatment of Powell-Eyring fluid flow using method of satisfaction of asymptotic boundary conditions (MSABC) Appl. Num. Math.. 2009;59(10):2584-2592.
[Google Scholar]
Panigrahi S., Reza M., Mishra A.K., . MHD effect of mixed convection boundary-layer flow of Powell-Eyring fluid past nonlinear stretching surface. Appl. Math. Mech.. 2014;35(12):1525-1540.
[Google Scholar]
Roşca A.V., Pop I., . Flow and heat transfer of Powell-Eyring fluid over a shrinking surface in a parallel free stream. Int. J. Heat Mass Transf.. 2014;71:321-327.
[Google Scholar]
Rehman A., Achakzia S., Nadeem S., Iqbal S., . Stagnation point flow of Eyring Powell fluid in a vertical cylinder with heat transfer. J. Power Technol.. 2016;96(1):57.
[Google Scholar]
Rehman K.U., Malik M.Y., Salahuddin T., Naseer M., . Dual stratified mixed convection flow of Eyring-Powell fluid over an inclined stretching cylinder with heat generation/absorption effect. AIP Adv.. 2016;6(7):075112.
[Google Scholar]
Sarpkaya T., . Flow of non-Newtonian fluids in a magnetic field. AIChE J.. 1961;7(2):324-328.
[Google Scholar]
Sirohi V., Timol M.G., Kalthia N.L., . Powell-Eyring model flow near an accelerated plate. Fluid Dyn. Res.. 1987;2(3):193-204.
[Google Scholar]
Sheikholeslami M., Ganji D.D., . Ferrohydrodynamic and magnetohydrodynamic effects on ferrofluid flow and convective heat transfer. Energy. 2014;75:400-410.
[Google Scholar]
Sheikholeslami M., Ganji D.D., . Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method. Physica A. 2015;417:273-286.
[Google Scholar]
Sheikholeslami M., Ganji D.D., Javed M.Y., Ellahi R., . Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magn. Magn. Mater.. 2015;374:36-43.
[Google Scholar]
Sheikholeslami M., Rashidi M.M., Hayat T., Ganji D.D., . Free convection of magnetic nanofluid considering MFD viscosity effect. J. Mol. Liq.. 2016;218:393-399.
[Google Scholar]
Sheikholeslami M., Hayat T., Alsaedi A., . Numerical study for external magnetic source influence on water based nanofluid convective heat transfer. Int. J. Heat Mass Transf. 2016
[Google Scholar]
Sheikholeslami M., Soleimani S., Ganji D.D., . Effect of electric field on hydrothermal behavior of nanofluid in a complex geometry. J. Mol. Liq.. 2016;213:153-161.
[Google Scholar]
Sheikholeslami M., Ganji D.D., Rashidi M.M., . Magnetic field effect on unsteady nanofluid flow and heat transfer using Buongiorno model. J. Magn. Magn. Mater.. 2016;416:164-173.
[Google Scholar]
Sheikholeslami M., Shehzad S.A., . Magnetohydrodynamic nanofluid convection in a porous enclosure considering heat flux boundary condition. Int. J. Heat Mass Transf. 2016
[Google Scholar]
Sheikholeslami M., Ganji D.D., . Nanofluid hydrothermal behavior in existence of Lorentz forces considering Joule heating effect. J. Mol. Liq.. 2016;224:526-537.
[Google Scholar]
Sheikholeslami M., Ganji D.D., . Transportation of MHD nanofluid free convection in a porous semi annulus using numerical approach. Chem. Phys. Lett.. 2017;669:202-210.
[Google Scholar]
Sheikholeslami M., Ganji D.D., . Numerical investigation of nanofluid transportation in a curved cavity in existence of magnetic source. Chem. Phys. Lett.. 2017;667:307-316.
[Google Scholar]
Sheikholeslami M., . Numerical simulation of magnetic nanofluid natural convection in porous media. Phys. Lett. A. 2017;381(5):494-503.
[Google Scholar]
Sheikholeslami M., . Magnetic field influence on nanofluid thermal radiation in a cavity with tilted elliptic inner cylinder. J. Mol. Liq.. 2017;229:137-147.
[Google Scholar]
Sheikholeslami M., . Influence of Lorentz forces on nanofluid flow in a porous cylinder considering Darcy model. J. Mol. Liq.. 2017;225:903-912.
[Google Scholar]
Sheikholeslami M., Chamkha A.J., . Influence of Lorentz forces on nanofluid forced convection considering Marangoni convection. J. Mol. Liq.. 2017;225:750-757.
[Google Scholar]
Sheikholeslami M., Vajravelu K., . Nanofluid flow and heat transfer in a cavity with variable magnetic field. Appl. Math. Comput.. 2017;298:272-282.
[Google Scholar]
Sheikholeslami M., Rokni H.B., . Nanofluid two phase model analysis in existence of induced magnetic field. Int. J. Heat Mass Transf.. 2017;107:288-299.
[Google Scholar]
Ullah I., Bhattacharyya K., Shafie S., Khan I., . Unsteady MHD Mixed Convection Slip Flow of Casson Fluid over Nonlinearly Stretching Sheet Embedded in a Porous Medium with Chemical Reaction, Thermal Radiation, Heat Generation/Absorption and Convective Boundary Conditions. PLoS ONE. 2016;11(10):e0165348.
[Google Scholar]
Ullah I., Khan I., Shafie S., . MHD Natural Convection Flow of Casson Nanofluid over Nonlinearly Stretching Sheet Through Porous Medium with Chemical Reaction and Thermal Radiation. Nanoscale Res. Lett.. 2016;11(1):527.
[Google Scholar]
Ullah I., Khan I., Shafie S., . Hydromagnetic Falkner-Skan flow of Casson fluid past a moving wedge with heat transfer. Alexandria Eng. J.. 2016;55(3):2139-2148.
[Google Scholar]
Yoon H.K., Ghajar A.J., . A note on the Powell-Eyring fluid model. Int. Commun. Heat Mass Transfer. 1987;14(4):381-390.
[Google Scholar]
Zin N.A.M., Khan I., Shafie S., . The impact silver nanoparticles on MHD free convection flow of Jeffrey fluid over an oscillating vertical plate embedded in a porous medium. J. Mol. Liq.. 2016;222:138-150.
[Google Scholar]