Optimisation of variance reduction techniques in EGSnrc Monte Carlo for a 6 MV photon beam of an Elekta Synergy linear accelerator

2.1 Linear Accelerator

The Elekta Synergy linear accelerator is held at Singleton Hospital, Swansea, UK (version 4.5, Elekta^TM, Crawley, West Sussex, UK). It consists of the target, primary collimator, flattening filter, chamber, backscatter plate, multi-leaf collimator (MLC), backup jaws, secondary collimator and Mylar sheet, and was modelled using the BEAMnrc user code using appropriate component modules (CMs) based on manufacturer information (Fig. 1). The validation of the model, however, is beyond the scope of this study.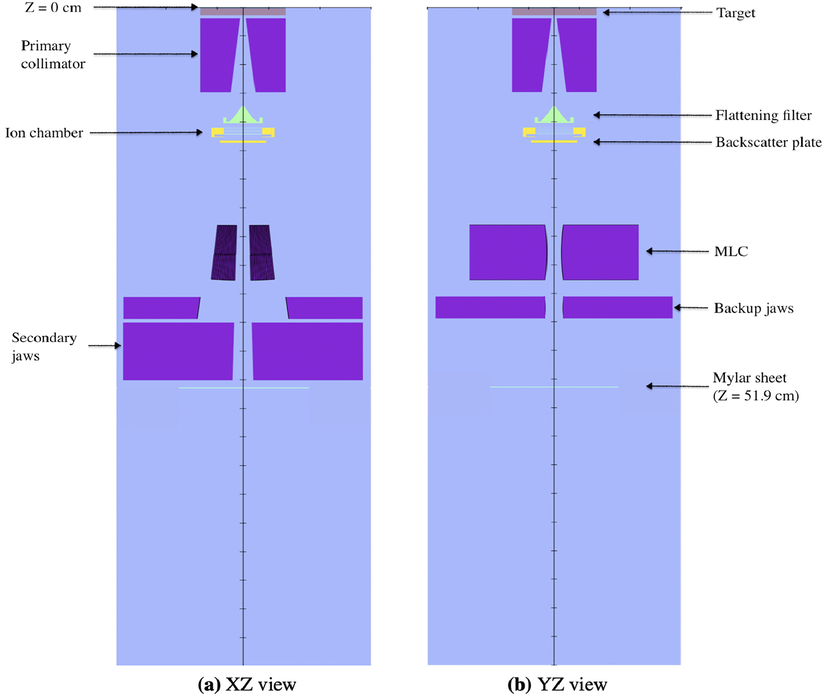

Close

Fig. 1

The MC model components of the Elekta Synergy Linac.

Export to PPT

2.2 BEAMnrc user code

In this study, the most recent version of the EGSnrc MC code was used. The BEAMnrc code was used to simulate a 10 × 10 cm² field size defined at 100 cm using source number 19 (Rogers et al., 2013). The beam intensity and the field size of the beam field were defined using MLC, backup jaws and secondary collimator components.

Most of the simulation parameters used in the BEAMnrc code were left at their recommended (default) values. The energy cut-offs for electrons and photons (ECUT and PCUT) were set to 700 keV and 10 keV, respectively. At first, each VRT was used separately and compared to the analogue method, after which the combination of different BEAMnrc VRTs that provided the most efficient simulation was investigated. Then, the combination that gave the most efficient simulation when combined with particle splitting as implemented in DOSXYZnrc (see Section 2.3.) was compared with the corresponding PHSP simulation source. In the PHSP simulation, the Linac is divided into two phases: the patient-independent and patient-dependent. Thus, it saves time to score a PHSP file just below the patient-independent part and use it as a source to avoid repeating the simulation each time. In this study, the PHSP was placed just above the MLC CM.

In the following subsection, each VRT implemented in BEAMnrc used in this study is briefly described. This includes bremsstrahlung cross-section enhancement, photon forcing, split electron or photon, range rejection and bremsstrahlung splitting, both uniform and directional.

2.3 DOSXYZnrc user code

The DOSXYZnrc code was used to model a water phantom (Walters et al., 2013). At first, all simulations were performed using a 20.25 × 20.25 × 30 cm³ water phantom, where the voxel size was 0.5 × 0.5 × 0.5 cm³ as shown in Fig. 2. The SSD was 90 cm. In combination with different BEAMnrc VRTs, the photon splitting number (n_split) implemented in DOSXYZnrc to increase the efficiency of dose calculations was investigated with and without the e−/e+ splitting option (e_split), which is available with source number 9. This technique allows splitting photons as they enter the phantom geometry. Then, after finding the most efficient combination, the photon splitting number was investigated further to find the optimum n_split.

Close

Fig. 2

Voxel water phantom modelled in DOSXYZnrc code.

Export to PPT

2.4 Efficiency calculation

The efficiency $\epsilon$ of a MC simulation can be defined as per the following equation:

3.1 Efficiency of BEAMnrc VRTs

First, each VRT implemented in BEAMnrc was investigated individually using the same number of particles, which here was 50 ×  ${10}^6$ particles. The effect of increasing the number of particles was not considered in this study as this only reduces the uncertainty, allowing better estimation, without increasing the efficiency.

Table 1 shows the effects of different VRTs on the simulation efficiency. It can be clearly seen that all the VRTs improved the simulation efficiency compared with the analogue simulation. For the range rejection technique with 2 MeV, the efficiency was improved by a factor of about 1.9 compared to the analogue simulation. Compared to the analogue calculation, the simulation was about 3.6 and 32 times more efficient when using the UBS technique without RR and with RR, respectively. The efficiency was improved by a factor of about 51 when photon splitting was applied individually. From Table 1, it appears that the most efficient VRT was the DBS technique, where the efficiency was improved by a factor of 477 compared to the analogue simulation, and 9 times compared to photon splitting. In addition, the DBS technique provided the greatest efficiency gain, with dose efficiencies a factor of up to 131 and 15 greater than for the UBS technique without RR and with RR, respectively.

Mohammed et al. (2016) found that the DBS technique improved the efficiency by a factor of 1130 compared to the analogue case for a Saturne 43 Linac with a 12 MV photon beam. Hoang et al. (2019) investigated te DBS technique with a 6 MV photon beam from a HPD Siemens Primus Linac and found that the efficiency was improved by a factor of 90 compared to the analogue simulation. The differences in results between the previous studies and the current study might be due to the differences in both photon energy and Linac geometry.

3.2 Optimisation of DBS efficiency

The results reported in the previous section showed that DBS was the most efficient VRT technique, which was therefore investigated further to find the optimum splitting numbers (NBRSPL). Fig. 3 shows the variation of simulation efficiency with DBS splitting number. The efficiency of the simulation increased with increasing splitting number until reaching a maximum at an NBRSPL of 15,000; beyond this, the efficiency decreased gradually; therefore, the optimum value of the NBRSPL was found to be 15,000.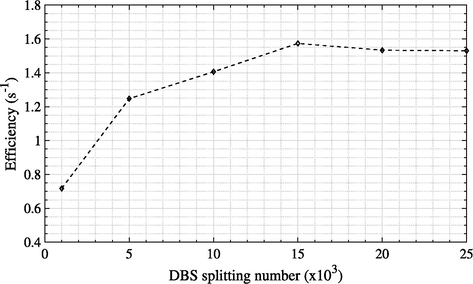

Close

Fig. 3

The effects of different DBS splitting numbers on efficiency.

Export to PPT

Hoang et al. (2019) investigated the efficiency of DBS with different splitting numbers for dose calculations. Their results showed that the optimal value was 1000. The maximum splitting number used in the study was 1500. It is worth mentioning that, in order to use high NBRSPL, the beamnrc_user_macros.mortran file has to be modified to avoid overflow.

In the DBS technique algorithm, almost all the charged particles are eliminated; few survive with a large weight (fat), thus it is very efficient with regard to photon fluence or dose. If the interest is in the charged particles’ contribution to the dose, the e−/e+ splitting option in the DBS technique should be used to recover the charged particles (Rogers et al., 2013). In this study, the DBS with e−/e+ splitting was performed for the flattening filter CM (ICM_DBS). Table 2 shows the effects of DBS splitting number with e−/e+ splitting on the efficiency. Here, the optimum NBRSPL with e−/e+ splitting was found to be 10,000. Rogers et al. (2013) suggested that, in general, a NBRSPL of around 1000 achieves peak efficiency when e−/e+ splitting is used. As mentioned in Section 1, the optimal setting for each VRT parameter depends on the energy and the details of the Linac being simulated.

Fig. 4 shows the efficiency of the DBS splitting number (15,000) with different DBS splitting field radii. It can be clearly seen that as field radius increased the efficiency decreased. This may be due to the fact that, as the field radius increases, the DBS algorithm uses more CPU time as it loops through the split photons, determining whether or not they are directed into the field of interest for each split photon. Thus the larger the radius the more photons are kept and simulated. The smallest field radius, 5 cm, that still provides adequate coverage (not diagonally) was the most efficient radius. Moving from 8 cm to 9 cm, the efficiency dropped sharply. Therefore, if there is a doubt about how far outside the edges of the beam field the splitting field of interest should go, overestimating by up to 3 cm would be sufficient for this purpose without causing a significant loss in efficiency. Moving from a 9 cm to a 10 cm radius, the efficiency decreased slightly. This might be due to the fact that not only increasing the number of histories affects the uncertainty on the efficiency estimate but also variability in the hardware performance, and other activity on the machine will also affect the estimate. However, this finding applies to DBS with e−/e+ splitting.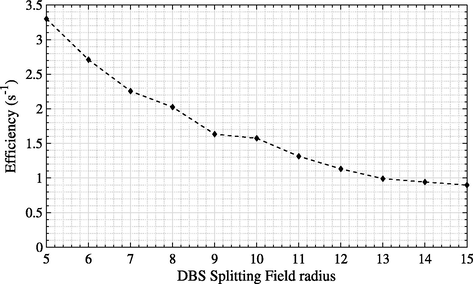

Close

Fig. 4

The effects of different DBS splitting field radii on the simulation efficiency.

Export to PPT

Zeghari et al. (2019) used BEAMnrc code to model a Saturne 43 Linac with a 12 MV photon beam. The study investigated the influence of using different splitting field radii (7, 10 and 13 cm) on the photon fluence efficiency for a 10 × 10 cm² field size. It was found that the field radius of 7 cm provided the highest efficiency. This is in agreement with the current finding results.

3.3 Efficiency of DBS combined with other BEAMnrc VRTs

Based on the previous results, the DBS technique was further investigated when it was combined with other VRTs. The results of this subsequent investigation are not shown for the sake of brevity but are provided in Appendix, Table A1. The best combination that provides the most efficient simulation was found when BCSE, range rejection with 2 MeV and splitting photons (ICM_SPLIT) were used with the DBS technique (with 15,000 NBRSPL and a 5 cm radius, as previously found). Such a combination was about 352% and892% more efficient than DBS alone, with and without optimization, respectively, thus maximising the efficiency of the BEAMnrc calculation. This means that this calculation can be done in $\approx$ 1.2 h when using this combination to obtain a 0.5% dose uncertainty.

Zeghari et al. (2019) found that using the DBS technique individually was more efficient than combining it with other VRTs. The reason behind this observation may be due to the fact that the DBS parameters were not optimized. Another possible reason is that the BCSE enhancement constant and enhancement power were set to 20 and 2, respectively. Such a configuration would invoke a different BCSE algorithm than that described in the BEAMnrc manual, and the enhancement constant is no longer straightforward (Rogers et al. 2013). Thus, this might consume more CPU time than when DBS technique is used individually. In this study, the enhancement power was set to 0 and the enhancement constant to 20, which then effectively becomes the enhancement factor.

3.4 Efficiency of DOSXYZnrc photon splitting combined with BEAMnrc VRTs

In DOSXYZnrc, as soon as the particles (photons or electrons/positrons) enter the geometry, they can be split a number of times. In this part of the study, the photon splitting (n_split) was investigated with different BEAMnrc VRTs to maximize the efficiency of the DOSXYZnrc calculation. The results are not shown for the sake of brevity (see Table A2 in the Appendix). At first, the photon splitting number (n_split) was set to 10 for all simulations in this part of the study.

The results showed that the most efficient simulation was when photon splitting was combined with DBS (with 15,000 NBRSPL and 5 cm radius), BCSE and range rejection with 2 MeV. This combination achieved an efficiency of 14.892 s⁻¹, which was about 109% greater than the best combination of BEAMnrc VRTs (without n_split) mentioned in Section 3.3. Then, for the same combination of VRTs, the efficiency of the simulation was investigated further using different photon splitting numbers, as shown in Fig. 5, for which the optimum n_split was found to be 35 where the efficiency was 20.67 s⁻¹. This is in agreement with what was generally suggested by Walters et al. (2013), which is 32. Therefore, this maximised the efficiency of the DOSXYZnrc calculation. This means that this calculation can be completed in $\approx$ 1.7 h to obtain a less than 0.3% dose uncertainty when using this combination. This increase in the efficiency is due to the efficiency inherent in the technique’s algorithm (n_split) as well as the reduction on the number of source particles needed. Therefore, the CPU time required to generate these particles is reduced, consequently avoiding the need to simulate the entire Linac head.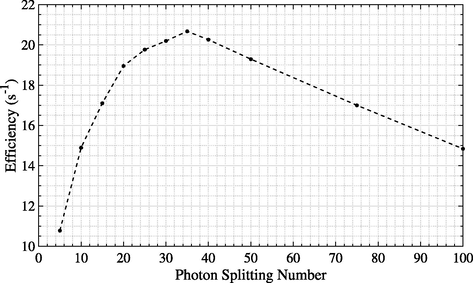

Close

Fig. 5

The effects of photon splitting number on the simulation efficiency.

Export to PPT

In addition, the charged particle split (e_split) was implemented in DOSXYZnrc in conjunction with photon splitting to prevent higher-weight charged particles from compromising the dose statistics (Rogers et al., 2013). From Section 3.2. and Section 3.3, the DBS with e−/e+ splitting (with 10,000 NBRSPL and a 5 cm radius) combined with BCSE, range rejection with 2 MeV was used to examine the e_split in DOSXYZnrc. As recommended in the DOSXYZnrc documentation, the e_split should be set equal to n_split to achieve the optimum efficiency (Walters et al., 2013). Fig. 6 shows the comparison of efficiency using different charged particle splittings. The most efficient simulation was achieved when the e_split and n_split were both set to be 55.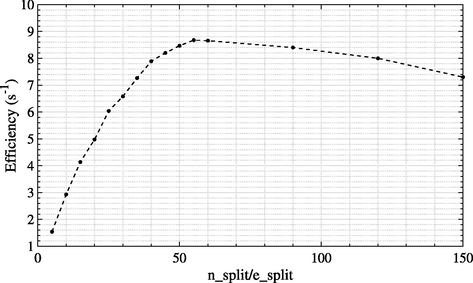

Close

Fig. 6

The effects of different photon and electron/positron splitting numbers on the simulation efficiency.

Export to PPT

3.5 Efficiency of PHSP simulation vs full beam simulation

Based on the results found in Section 3.4, a large (92 Gb) PHSP file source was generated using the same VRT combination that provided the most efficient full beam simulation. As mentioned in Section 2.2., the PHSP file was placed above the MLC CM and the number of particles collected was 1.44 ×  ${10}^9$ . Then, the PHSP was used as a source for the rest of the Linac CMs. The same number of histories in DOSXYZnrc for the full beam simulation was used. The results showed that even if the time to generate the PHSP file was omitted, the efficiency of the full beam simulation was only 8% lower than the PHSP simulation. Despite the fact that the results are comparable, the PHSP file requires a large amount of disk space, thus making it difficult to retrieve PHSP data over a network, and indeed subject to errors when transferred through networks (Alhakeem and Zavgorodni, 2018).