Translate this page into:
Operational matrix approach for approximate solution of fractional model of Bloch equation
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In present paper operational matrix of integration for Laguerre polynomial is used to solve fractional model of Bloch equation in nuclear magnetic resonance (NMR). The operational matrix converts the Bloch equation in a system of linear algebraic equations. Solving system we obtain the approximate solutions for fractional Bloch equation. Results are compared with existing methods and exact solution. Graphs are plotted for different fractional values of time derivatives.
Keywords
Fractional model of Bloch equation
Nuclear magnetic resonance
Operational matrix of integration
Laguerre polynomial
1 Introduction
The fractional Bloch equations are used in physics, chemistry, nuclear magnetic resonance (NMR), electron spin resonance (ESR) and magnetic resonance imaging (MRI). The fractional Bloch equation is generalization of standard Bloch equation and obtained by replacing integer order time derivative to fractional order Caputo derivative. Fractional calculus has many real applications in science and engineering such as fluid-dynamic traffic (He, 1999), biology (Robinson, 1981), viscoelasticity (Bagley and Torvik, 1983a,b, 1985), signal processing (Panda and Dash, 2006), bioengineering (Magin, 2004) and control theory (Bohannan, 2008). The fractional model of Bloch equation is given as,
and
Where
and
represent the system magnetization in
and
component respectively,
is the equilibrium magnetization,
is the resonant frequency given by theLarmor relationship
, where
is the static magnetic field in
-component,
is spin-lattice relaxation time,
is spin-spin relaxation time. The set of analytical solutions for integer order Bloch equation is given as,
The fraction in time derivative suggests a modulation—or weighting—of system memory (West et al., 2003; Magin et al., 2008), the assumption of fractional derivatives plays an important role affecting the spin dynamics described by the Bloch equations in Eq. (1). More recently, time fractional model of Bloch equation was resolved using Homotopy perturbation method (Kumar et al., 2014) and Petráš (2011) used iterative method to solve fractional model of Bloch equation. A generalization of the fractional Bloch equation by taking delay in the time was reported through numerical solution (Bhalekar et al., 2011). Recently Yu et al. (2014), gave an implicit numerical method to solve fractional Bloch equation in NMR. Some other existing methods to solve Bloch equation in NMR are reported in the literature (Hoult, 1979; Sivers, 1986; Yan et al., 1987; Xu and Chan, 1999; Balac and Chupin, 2008; Magin et al., 2009; Murase and Tanki, 2011; Sun et al., 2016). In this paper we are using operational matrix of fractional integration of Laguerre polynomial to solve fractional model of Bloch equation as Laguerre polynomials are more convenient for computational purpose. Recent investigations report the application of operational matrices to solve fractional differential equations (Wu, 2009; Yousefi et al., 2011; Kazem et al., 2013; Tohidi et al., 2013; Heydari et al., 2014; Zhou and Xu, 2014; Bhrawy and Zaky, 2015; Singh and Singh, 2016). Using operational matrix we convert the Bloch equation into a system of linear algebraic equation whose solution gives approximate solution for Bloch equation in NMR.
2 Preliminaries and operational matrix
In this paper, the fractional order differentiations and integrations are in well-known Caputo and Riemann-Liouville sense respectively (Miller and Ross, 1993; Diethelm et al., 2005).
The Riemann-Liouville fractional order integral operator is given by
The Caputo fractional derivative of order are defined as
The Laguerre polynomial is defined by Ali et al. (2015) and Bhrawy et al. (2014)
The set of Laguerre polynomial
forms an orthonormal basis with respect to weight function
on the interval [0, ∞) with the following property,
A function
, square integrable in [0, ∞) may be expressed as sum of Laguerre polynomial as follows:
If the series is truncated at
, then we have
Let
be Laguerre vector and consider
then
Pl see (Bhrawy and Taha, 2012). □
3 Outline of method
In this section, we describe the outline of the method for the construction of approximate solution of the Bloch equation.
Consider the following approximations:
Taking integral of order
and
in component
and
respectively in Eq. (9) we get,
Let
From Eqs. (10)–(13) we get,
Using Eqs. (9), (14), (15) and (16) in Eq. (1) we get following equations,
On solving Eqs. (17) and (18) we get,
From Eq. (19), we can write
Using Eqs. (20)–(22) in Eqs. (14)–(16) respectively, we get approximate solution for Bloch equations in NMR.
4 Numerical results and discussion
In all the figures given below we have taken and .
Figs. 1–3, represent comparison of exact and approximate solution for
and
at n = 15 respectively.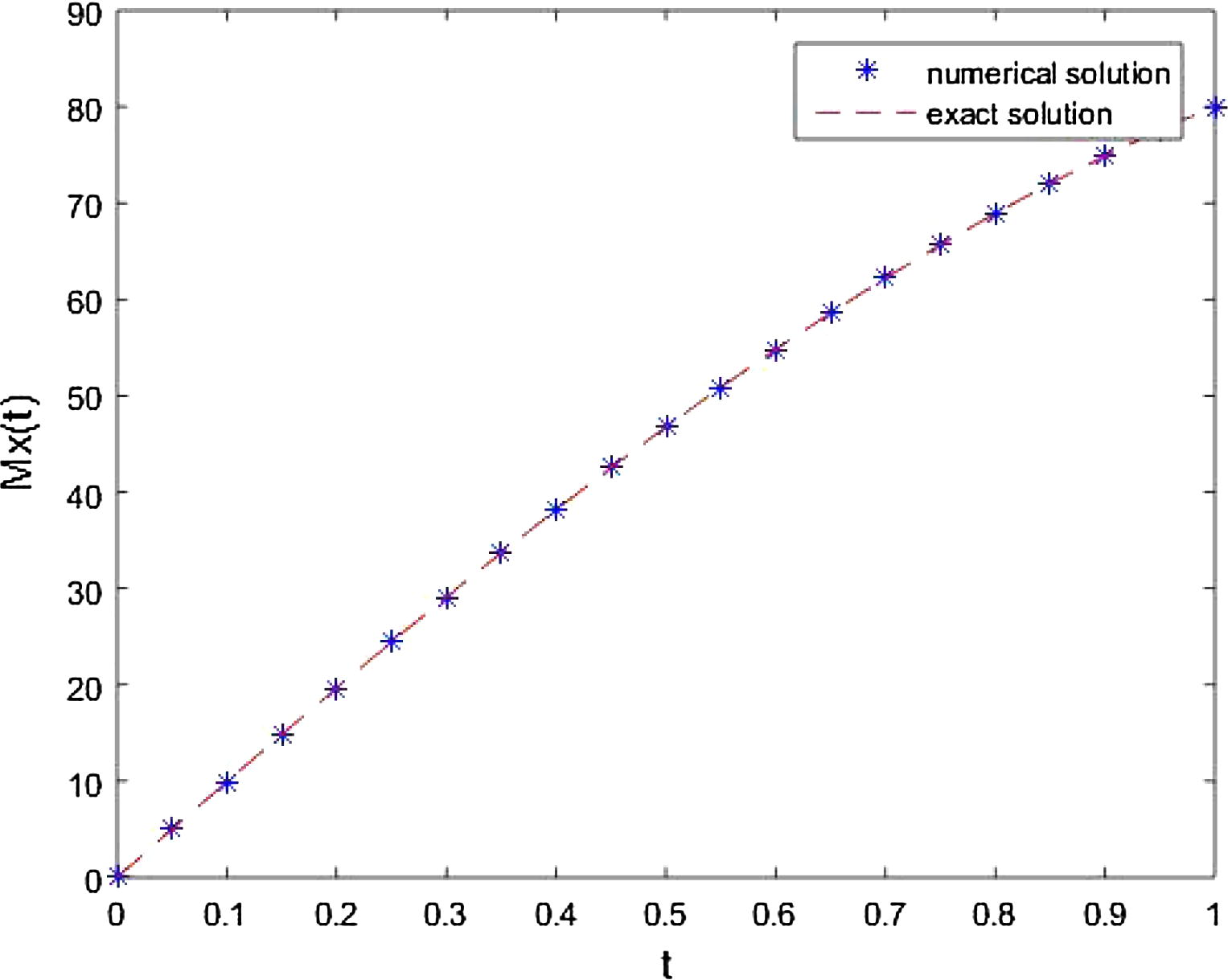
Comparison of exact and approximate solution for
at n = 15.
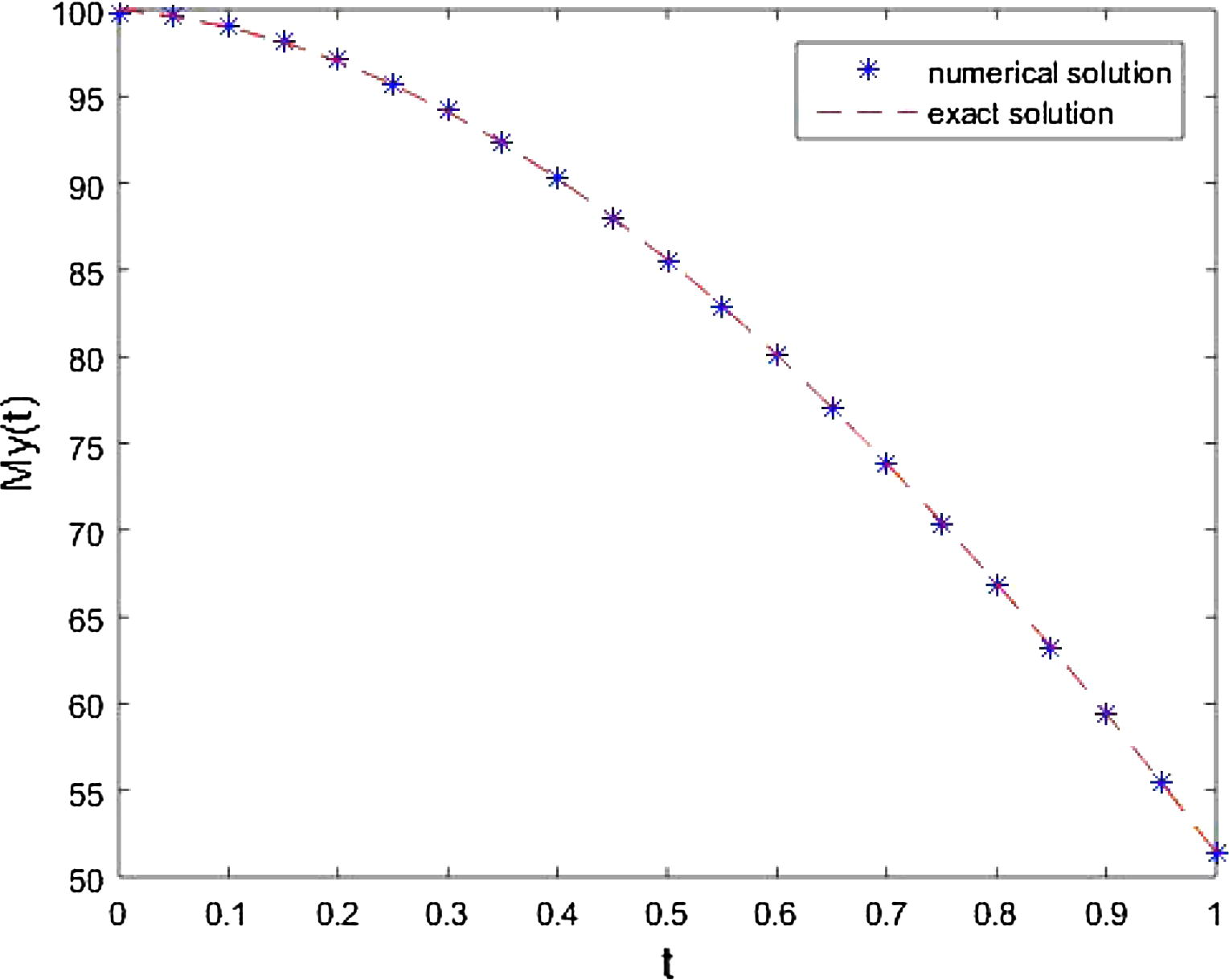
Comparison of exact and approximate solution for
at n = 15.
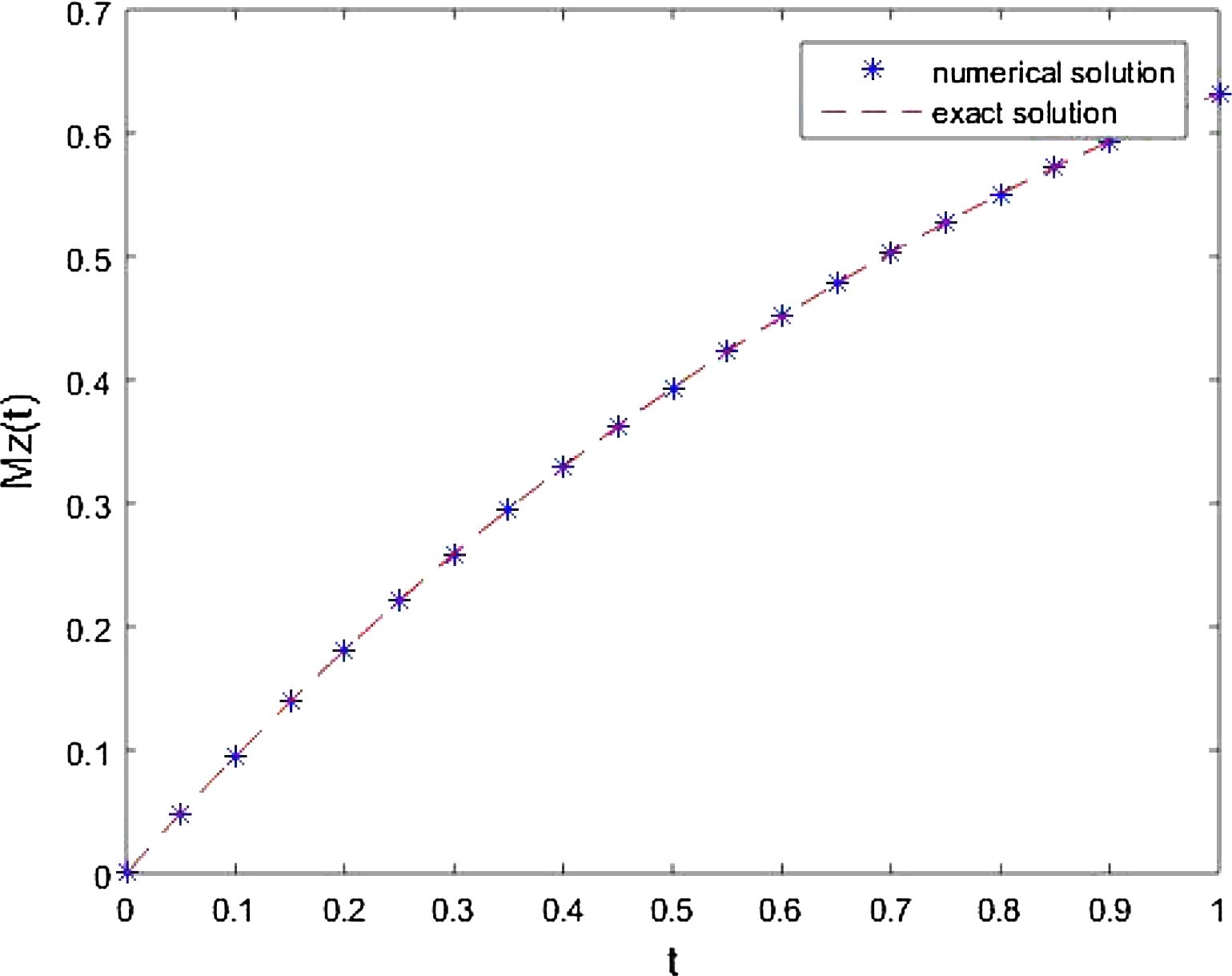
Comparison of exact and approximate solution for
at n = 15.
Figs. 4–6, show the behaviour of approximate solutions at values of n = 10, 15, 20, 25 and exact solution for
and
respectively. From Figs. 4–6, it is observed that approximate solution comes close to the exact solution with the increasing n.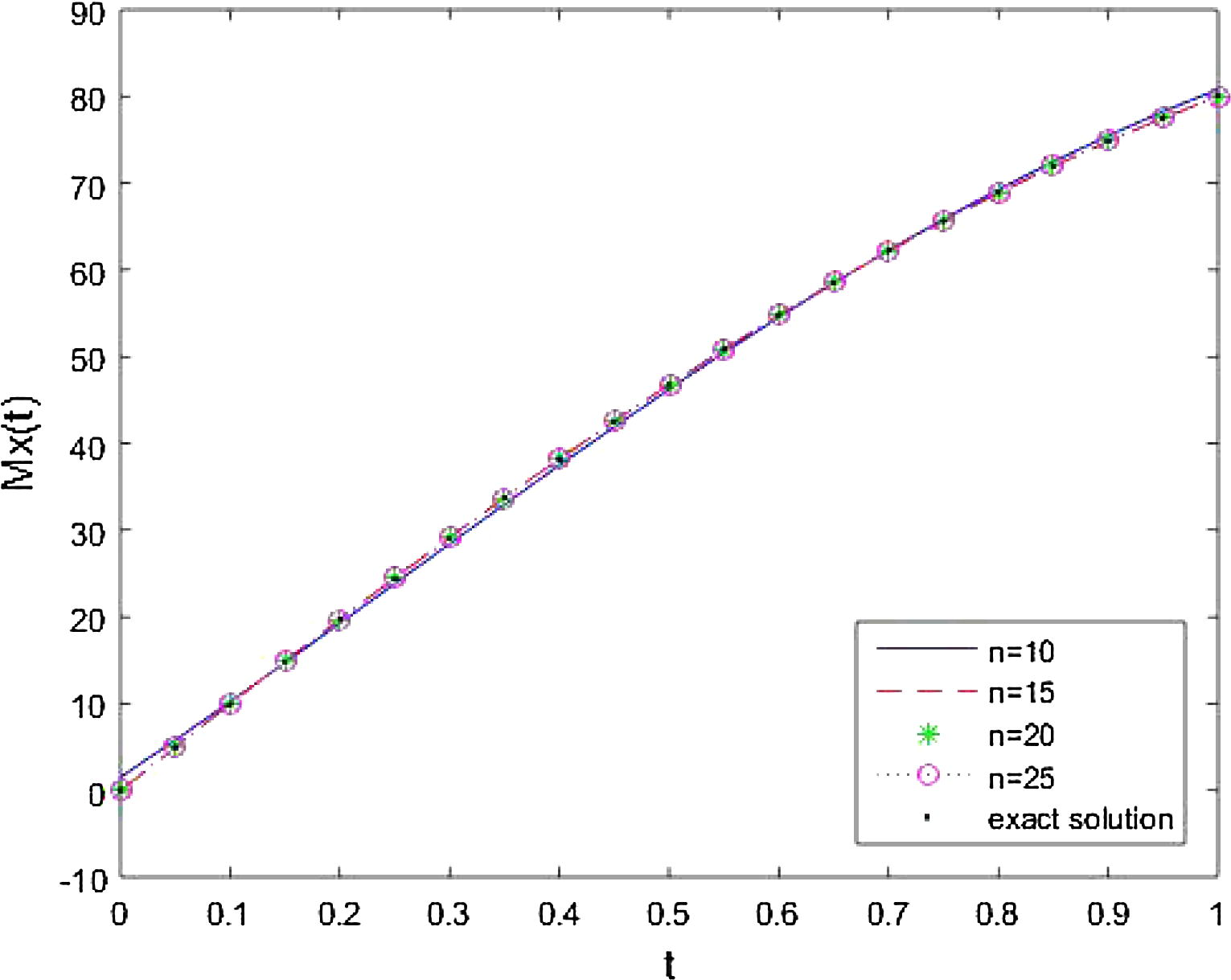
Comparison of approximate solution at different values of n = 10, 15, 20, 25 and exact solution for
.
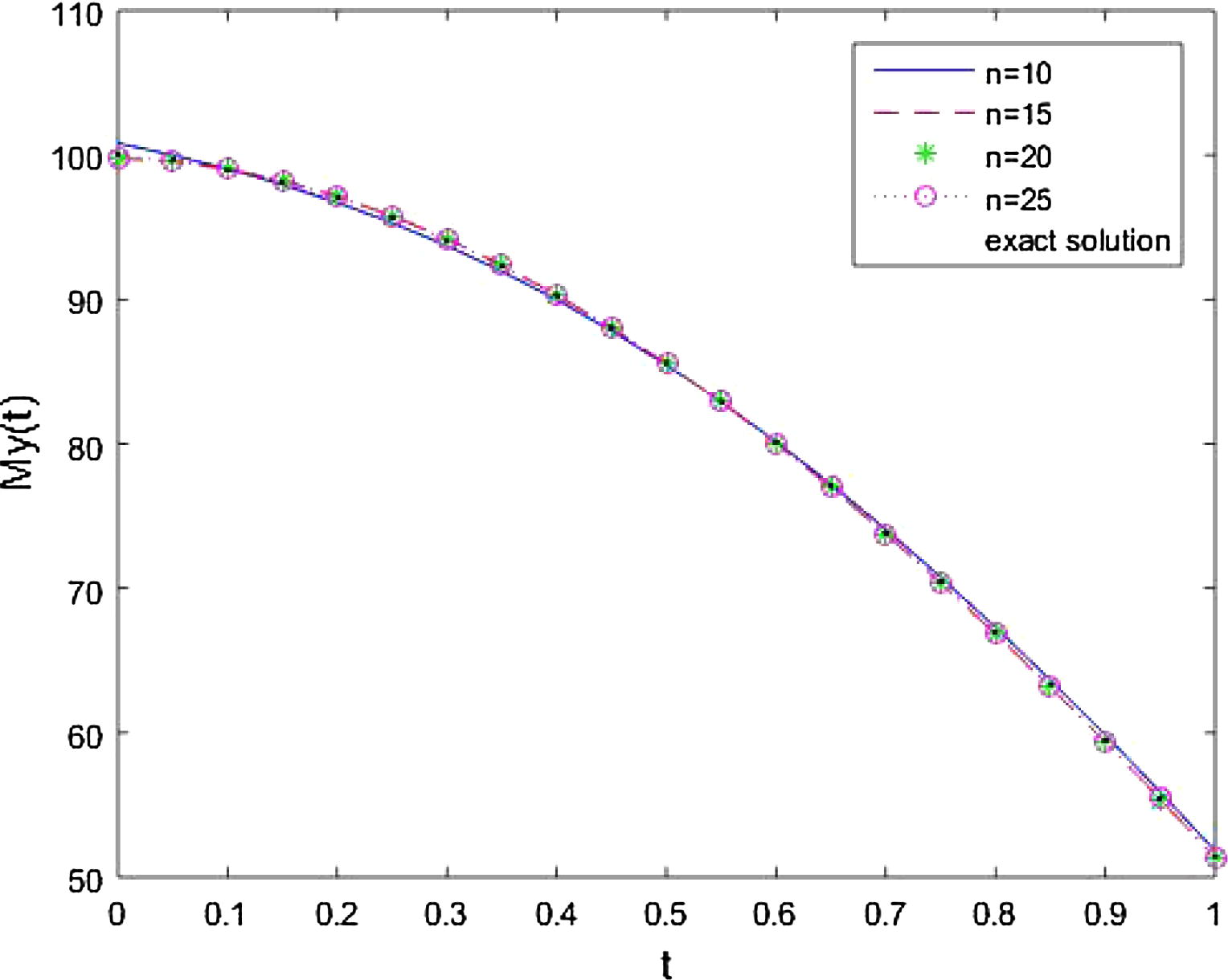
Comparison of approximate solution at different values of n = 10, 15, 20, 25 and exact solution for
.
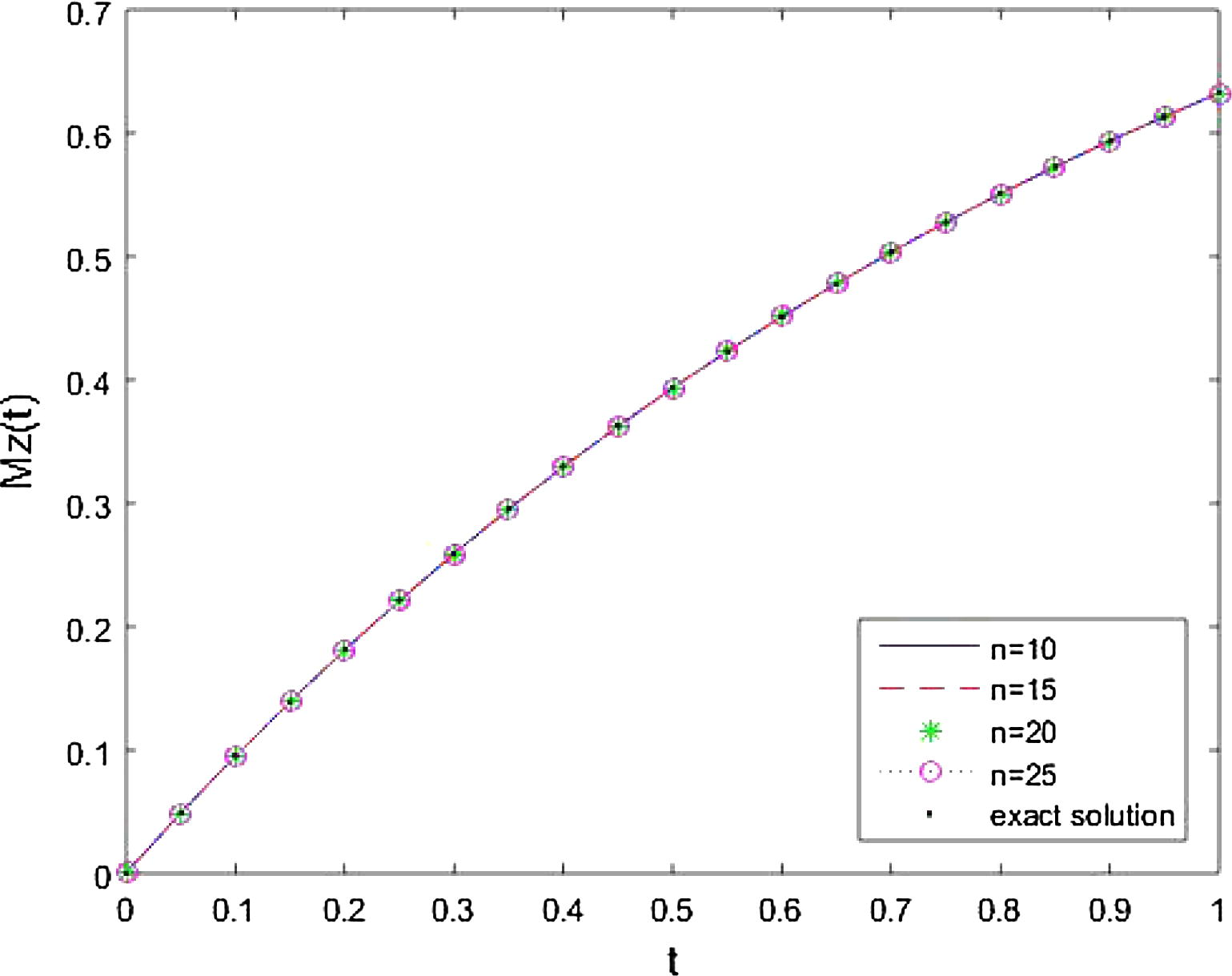
Comparison of approximate solution at different values of n = 10, 15, 20, 25 and exact solution for
.
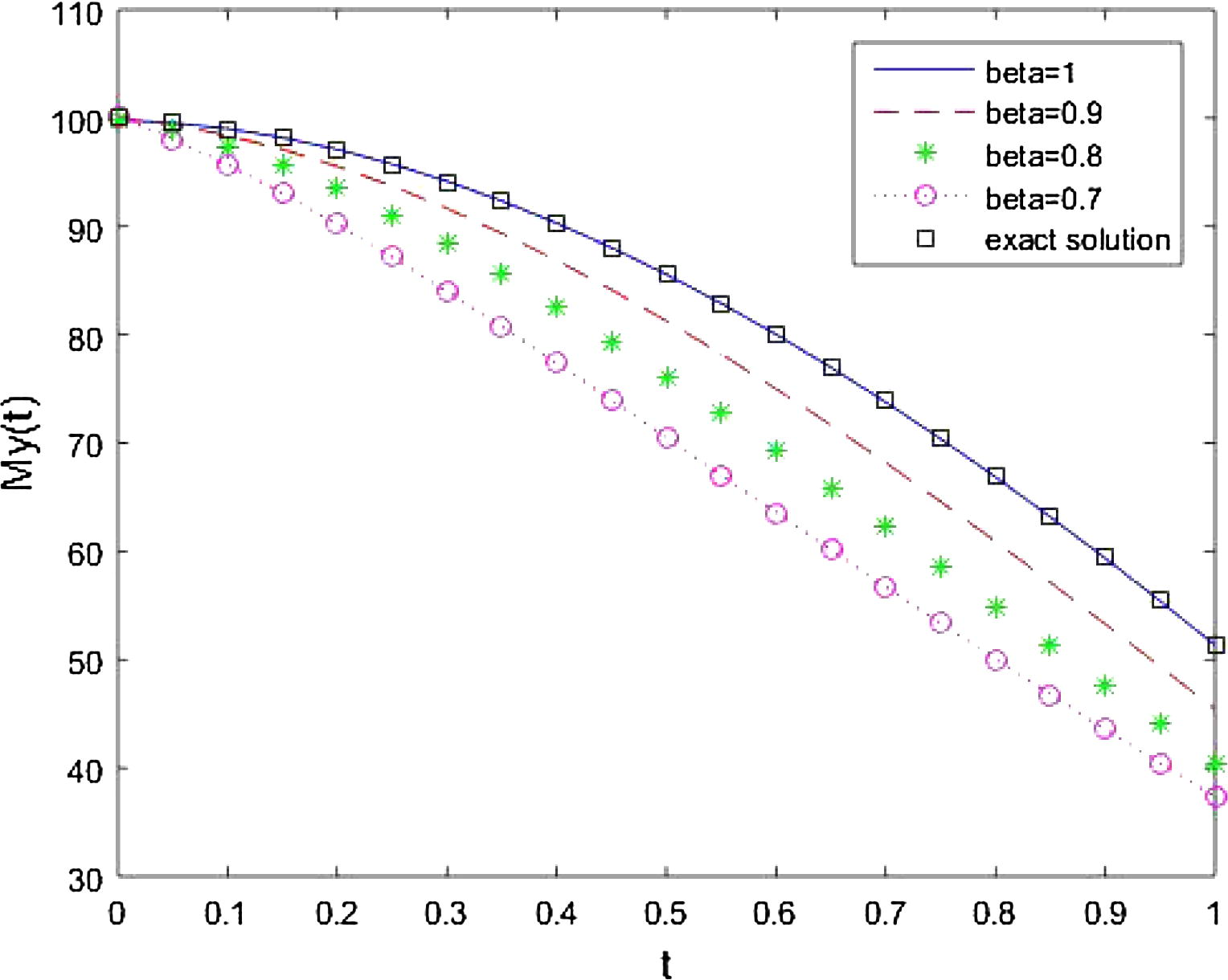
The behaviour of approximate solutions with time for different values of fractional order time derivatives
and
is shown from Figs. 7–9, respectively. It is clear that the solution varies continuously with fractional values of time derivatives for fractional Bloch equation in NMR and for
solution for standard Bloch equation is obtained. In Figs. 7 and 9 the approximate solution for
and
increases with the increasing of time for different value of
and 1. In Fig. 8 the approximate solution for
decreases with the increasing of time for different value of
and 1.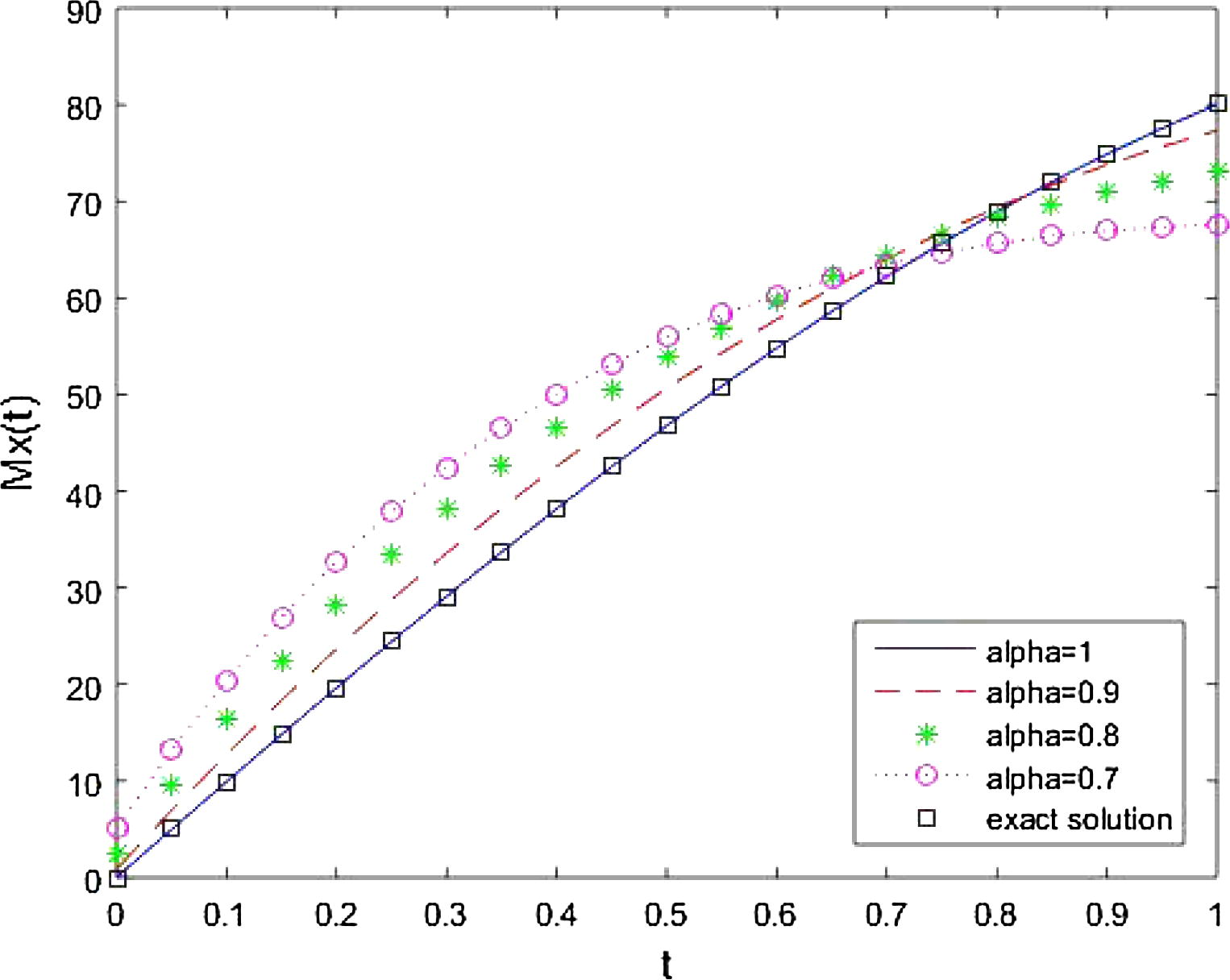
Approximate solution for
at different values of
and exact solution.
Approximate solution for
at different values of
and exact solution.
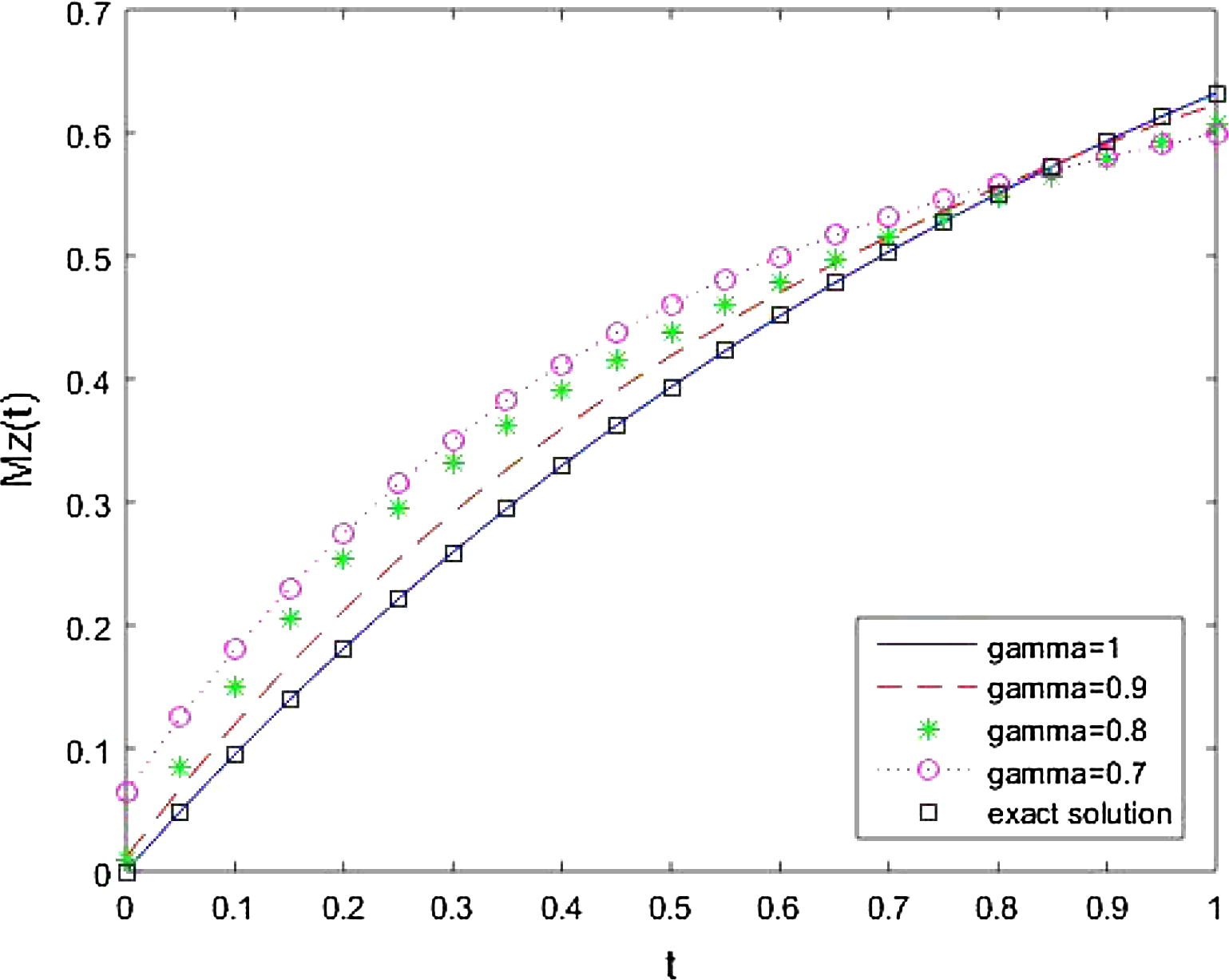
Approximate solution for
at different values of
and exact solution.
To show the accuracy of the proposed method we have compared our results from existing methods and exact solution. In Table 1 comparison of our results from the Homotopy Perturbation Method (HPM) (Kumar et al., 2014), iterative method (Petráš, 2011) and exact solution is given.
M
t
Exact solution
Present method
Kumar et al. (2014)
Petráš (2011)
0.1
9.9335
9.9245
9.9335
9.2237
0.3
29.1120
29.1080
29.1034
29.0937
0.5
46.7588
46.7732
46.6823
46.7507
0.7
62.2060
62.2180
61.8762
62.1921
0.9
74.8859
74.8814
73.8911
74.8806
0.1
99.0042
99.0213
99.0187
99.0051
0.3
94.1113
94.1645
94.1837
94.1166
0.5
85.5915
85.5689
85.5518
85.5942
0.7
73.8536
73.7886
73.1630
73.8635
0.9
59.4258
59.3782
57.0572
59.4296
0.1
0.0952
0.0952
0.0952
0.0952
0.3
0.2592
0.2592
0.2592
0.2590
0.5
0.3935
0.3935
0.3935
0.3934
0.7
0.5034
0.5034
0.5034
0.5033
0.9
0.5934
0.5934
0.5934
0.5934
In Table 2, we have listed maximum absolute errors and root mean square errors of
and
for different values of n = 15, 20.
M
n
Maximum absolute error (MAE)
Root mean square error (RMSE)
1.5
20
1.5
20
1.5
20
From Table 2, it is clear that as the value of n increases maximum absolute errors and root mean square decreases.
In Table 3, we have listed root mean square at different points from our method and Homotopy Perturbation Method (HPM) (Kumar et al., 2014), iterative method (Petráš, 2011).
M
t
Present Method
Kumar et al. (2014)
Petráš (2011)
0.2
0.4
0.6
0.8
1.0
1.5849
0.2
0.4
0.6
0.8
1.0
0.2
0.4
0.6
0.8
1.0
The computational order for the numerical results are given as (Dehghan et al., 2015; Singh and Singh, 2016)
Order = where is maximum absolute error for approximation having n number of basis elements.
In Table 4, we list the computational order for the numerical results.
M
n
Computational order
5
10.71300
–
10
1.49014
2.8458
20
5.9592
5
2.784942
–
10
0.82201
1.7604
20
2.2073
5
0.01563
–
10
5.0000
20
5.4122
From Table 4, it is clear that our method is good for computational purposes in comparison to iterative method (Petráš, 2011) in which we take thousands of iterations to achieve the desired accuracy.
5 Conclusions
Our method is easy for computation purposes because we are approximating time derivatives first. Our numerical algorithm is easy to implement in compare to existing methods because construction of operational matrix is very easy. It is presented how the approximate solution varies continuously for different values of fractional time derivatives and for integer order approximate solution coinciding with the exact solution for Bloch equation.
Acknowledgements
The author acknowledges the financial support from Ministry of Human Resource Development, Indian Institute of Technology, Banaras Hindu University, Varanasi, India under the SRF scheme. The author is very grateful to the referees for their constructive comments and suggestions for the improvement of the paper.
References
- Tau method for the numerical solution of a fuzzy fractional kinetic model and its application to the Oil Palm Frond as a promising source of xy lose. J. Comput. Phys.. 2015;294:562-584.
- [Google Scholar]
- A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol.. 1983;27:201-210.
- [Google Scholar]
- Fractional calculus a differential approach to the analysis of viscoelasticity damped structures. AIAA J.. 1983;21(5):741-748.
- [Google Scholar]
- Fractional calculus in the transient analysis of viscoelasticity damped structures. AIAA J.. 1985;23:918-925.
- [Google Scholar]
- Fast approximate solution of Bloch equation for simulation of RF artifacts in Magnetic Resonance Imaging. Math. Comput. Model.. 2008;48:1901-1913.
- [Google Scholar]
- An operational matrix of fractional integration of the Laguerre polynomials and its application on a semi-infinite interval. Math. Sci.. 2012;6:41.
- [Google Scholar]
- A method based on Jacobi tau approximation for solving multi-term time-space fractional partial differential equations. J. Comput. Phys.. 2015;281:876-895.
- [Google Scholar]
- New spectral techniques for systems of fractional differential equations using fractional-order generalized Laguerre orthogonal functions. Fract. Calc. Appl. Anal.. 2014;17:1137-1157.
- [Google Scholar]
- Analog fractional order controller in temperature and motor control applications. J. Vib. Control. 2008;14:1487-1498.
- [Google Scholar]
- Error estimate for the numerical solution of reaction-sub diffusion process based on a mesh less method. J. Comput. Appl. Math.. 2015;280(15):14-36.
- [Google Scholar]
- Algorithms for fractional calculus: a selection of numerical methods. Comput. Methods Appl. Mech. Eng.. 2005;194:743-773.
- [Google Scholar]
- Some applications of nonlinear fractional differential equations and their approximations. Bull. Sci. Technol.. 1999;15(2):86-90.
- [Google Scholar]
- A new approach of the Chebyshev wavelets method for partial differential equations with boundary conditions of the telegraph type. Appl. Math. Model.. 2014;38:1597-1606.
- [Google Scholar]
- The solution of the Bloch equation in presence of varying B 1 field – An approach to selective pulse analysis. J. Magn. Reson.. 1979;35:69-86.
- [Google Scholar]
- Fractional order Legendre functions for solving fractional-order differential equations. Appl. Math. Model.. 2013;37:5498-5510.
- [Google Scholar]
- A fractional model of Bloch equation in NMR and its analytic approximate solution. Walailak J. Sci. Technol.. 2014;11(4):273-285.
- [Google Scholar]
- Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J. Magn. Reson.. 2008;190:255-270.
- [Google Scholar]
- An introduction to fractional calculus and fractional differential equations. New York: John Wiley & Sons Inc; 1993.
- Numerical solution to the time dependent Bloch equations revisited. J. Magn. Reson.. 2011;29:126-131.
- [Google Scholar]
- Fractional generalized splines and signal processing. Signal process. 2006;86:2340-2350.
- [Google Scholar]
- Modeling and numerical analysis of fractional-order Bloch equations. Comput. Math. Appl.. 2011;61:341-356.
- [Google Scholar]
- The use of control systems analysis in neurophysiology of eye movements. Ann. Rev. Neurosci.. 1981;4:462-503.
- [Google Scholar]
- Stable numerical solutions of fractional partial differential equations using Legendre scaling functions operational matrix. Ain Shams Eng. J. 2016
- [CrossRef] [Google Scholar]
- Approximate solution to the Bloch equation with symmetric RF pulses and flip angles less than TT/2. J. Magn. Reson.. 1986;69:28-40.
- [Google Scholar]
- Some high order difference schemes for the space and time fractional Bloch-Torrey equations. Appl. Math. Comput.. 2016;281:356-380.
- [Google Scholar]
- A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model.. 2013;37:4283-4294.
- [Google Scholar]
- Physics of Fractal Operators. New York: Springer-Verlag; 2003.
- A wavelet operational method for solving fractional partial differential equations numerically. Appl. Math. Comput.. 2009;214:31-40.
- [Google Scholar]
- A near-resonance solution to the Bloch equations and its application to RF pulse design. J. Magn. Reson.. 1999;138:225-231.
- [Google Scholar]
- Approximate solutions of the Bloch equations for selective excitation. J. Magn. Reson.. 1987;75:83-95.
- [Google Scholar]
- The operational matrices of Bernstein polynomials for solving the parabolic equation subject to the specification of the mass. J. Comput. Appl. Math.. 2011;235:5272-5283.
- [Google Scholar]
- Numerical simulation of the fractional Bloch equations. J. Comput. Appl. Math.. 2014;255:635-651.
- [Google Scholar]
- Numerical solution of convection diffusions equations by the second kind Chebyshev wavelets. Appl. Math. Comput.. 2014;247:353-367.
- [Google Scholar]







