One and two spin-1/2 particle systems under the Lorentz transformations

1 Introduction

In quantum mechanics, systems may blurt a non-local behavior from themselves (Einstein et al., 1935). Bohm and Aharanov provided a spin version for exhibiting this behavior (Bohm and Aharonov, 1957). In their setup, non-locality leads to entanglement, i.e. the state of the system is not equal to the product of its constituent particles' states (Moradpour et al., 2015). Firstly, Bell tried to get a criterion for distinguishing the local and non-local phenomenon from each other (Bell, 1964). His work leads to a well-known inequality called the Bell inequality which may be violated by non-local states. In fact, there are various models for this inequality (Clauser et al., 1969; Audretsch, 2008; Brunner et al., 2014; Bertlmann, 2014). In the two-particle systems, the Bell operator is defined as

Spin is a quantum mechanical property of systems which was exhibited in investigating the relativistic quantum mechanical systems. Pauli derived an operator for describing the spin of particles in the low-velocity limit. By considering the low-velocity limit, Pauli got 2 × 2 matrixes, called the Pauli matrixes or operator ${\sigma }_i$ , and the corresponding spin operator for spin- $1/2$ particles (Greiner, 1990). Nowadays, it is believed that the predictions from the Pauli spin operator ( $S_i$ ) about the spin of systems are in line with the Stern-Gerlach type experiments in the lab frame, a frame in which the particle's velocity is not relativistic (Sakurai and Napolitano, 2014). But, is it the only candidate for the spin operator which leads to the consistent results with a Stern-Gerlach type experiment in the lab frame? Moreover, what is the result of a Stern-Gerlach type experiment, if it is observed by a moving observer which moves with respect to the lab frame with a constant velocity (β)? Indeed, there are various attempts to get a candidate for describing spin and thus the results of applying a Stern-Gerlach type experiment on a system which is in relative motion with respect to observer (Bauke et al., 2014a,b; Caban, 2012; Caban et al., 2013; Czachor, 1997a,b; Terno, 2003), where Czachor followed the Pryce (1948) and Fleming (1965) arguments to get the spin operator as

In addition, the normalized spin operator can be obtained by dividing the above operator into its Eigenvalues and the following normalized operator is achieved for the spin-½ particle which commutes with the Hamiltonian (Czachor, 1997a,b)

Based on this result, this operator may be used instead of the Pauli operator along the $\overrightarrow{A}$ vector $(\overrightarrow{A}·\overrightarrow{\sigma })$ whenever, states with zero momentum uncertainty are taken into account. It is easy to check that, independent of $\overrightarrow{A}$ , the Pauli spin operator along the $\overrightarrow{A}$ vector is recovered by substituting ${\beta }_0=0$ . Here, $\sigma$ and $\widehat{e}$ are the Pauli operator and the unit vector along the ${\beta }_0$ direction, respectively (Moradpour et al., 2015). In fact, ${\beta }_0$ represents the particle's velocity, but, since the lab frame is a frame in which the particle's velocity is not relativistic, the Pauli operators are suitable operators to describe the system's spin in the lab frame and thus, we can consider ${\beta }_0=0$ in the lab frame (Doyeol et al., 2003; Kim and Son, 2005; Moradi, 2008). We should also mention here that, for a moving observer which moves with respect to the lab frame with velocity $\beta$ , since motion is a relative concept, we have ${\beta }_0=\beta \ne 0$ (Friis et al., 2010; Moradi, 2009; Moradi and Aghaee, 2010; Moradi et al., 2014; Saldanha and Vedral, 2012a,b; Saldanha and Vedral, 2013). Therefore, from now we consider ${\beta }_0=\beta$ as the boost velocity and $\widehat{e}$ as the unit vector directed along the boost direction. It is worthwhile mentioning that the subscripts $\perp$ and $\parallel$ denote the perpendicular and parallel components of the vector $\overrightarrow{A}$ to the boost direction, respectively (Moradpour and Montakhab, 2016). This operator also supports the Pauli spin operator either ${\overrightarrow{A}}_{\perp }=0$ or ${\overrightarrow{A}}_{\parallel }=0$ ( $\widehat{A}=\overrightarrow{A}·\overrightarrow{\sigma }$ ). It is worth to note that the uncertainty principle leads to $\mathrm{\Delta }\beta \ne 0$ and therefore, this principle prevents such possibility in a realistic experiment (Czachor, 1997a,b), where its generalization to the wave-packets can be found. Some of the shortcomings and strengths of Czachor's and the Pauli operators are investigated in (Bauke et al., 2014a,b). Although, just the same as the Pauli operator, Czachor's spin operator should indeed be defined as $\hslash \widehat{A}/2$ to coverer the spin-½ particles, we should note that the eigenvalues of Czachor's spin operator are not always equal to $\pm \hslash /2$ . Whenever the effects of considering high velocities such as the probability of pair production are ignored, the phenomena interpretations made by quantum mechanics are satisfactory and the lab frame is connected to the moving frame, which moves with a constant velocity with respect to the lab frame, by a LT (Halpern, 1968). Therefore, one may apply LT on the system state in the lab frame to get state seen by the moving observer. By this approach, the spin state of the system is affected by a rotation of the Wigner angle (Wigner and Halpern, 1939). The effects of LT on the single-particle entangled states are investigated by Palge et al. (2011). It is shown that such rotations may also affect the spin entropy of one spin-½ particle as well as the two spin-½ entangled particles systems (Dunningham et al., 2009; Peres et al., 2002; Nishikawa, 2008). There are also various attempts in which authors investigate the behavior of non-locality under LT. Their results can also be used to get some theoretical predictions about the outcome of a Stern-Gerlach type experiment which may lead to getting a more suitable spin operator. The acceleration effects on non-locality are also investigated in León and Martín-Martínez (2009), Mann and Villalba (2009), Smith and Mann (2012), Terashima and Ueda (2004).

Some authors have used the Pauli spin operator to generate the Bell operator and considered bipartite pure entangled state (Terashima and Ueda, 2002, 2003). Thereinafter, they considered a special set of measurement directions which leads to violating Bell's inequality to its maximum violation amount $2\sqrt{2}$ in the lab frame. In addition, they have been considered a moving observer connected to the lab frame by an LT, and applied an LT on the system state in the lab frame to get the corresponding state in the moving frame. They took into account the same set of measurement directions for the moving frame as the lab frame, and investigate the behavior of Bell's inequality in the moving frame. In fact, they use Bell's inequality as a witness for the bi-partite non-locality. Finally, they find that the violation of Bell's inequality in the moving frame is decreased as a function of the boost velocity and the particle energy in the lab frame. It should be noted that if one applies LT on both of the Bell operator and the system state, Bell's inequality is violated to the same value as the lab frame. The generalization of this work to three-particle non-local systems can be found in Moradpour et al. (2015), Moradpour and Montakhab (2016).

In a similar approach, Ahn et al. have been considered the Bell states and used Czachor's operator to construct the Bell operator (Doyeol et al., 2003; Moradpour and Montakhab, 2016). Bearing in mind this fact that Czachor's and the Pauli operators are the same operators in the lab frame $(\beta =0)$ , authors have considered the special set of spin measurements which violates Bell's inequality to its maximum violation amount in the lab frame. They applied LT on the system state in the lab frame to get the corresponding state in the moving frame. They also assumed that the moving frame uses the same set of spin measurements as the lab frame for evaluating Bell's inequality. Therefore, their setup has some similarity with those of Terashima and Ueda (2002, 2003). There are also some differences between setups investigated in these papers. Their LT differs from each other, and they used the different spin operator to build the Bell operator. Finally, Ahn et al. found out that the expectation value of the Bell operator in the moving frame is decreased as a function of the boost velocity and the energy of particles in the lab frame. It should be noted again that Bell's inequality will be violated in the moving frame to the same value as the lab frame, if one applies LT on both of the Bell operator and the system state (Friis et al., 2010). It means that, the moving observer can obtain the maximum amount of violation for the Bell’s inequality provided that, in the moving frame, the LT has been applied to both Bell’s states and Bell’s operator (Doyeol et al., 2003). More studies on this subject and its generalization to the three-particle non-local systems can be found in Moradi (2008), Moradpour and Montakhab (2016).

In fact, both of the mentioned approaches found out that the expectation value of the Bell operator in the moving frame is decreased by increasing the boost velocity and the energy of particles in the lab frame. Although it seems that this conclusion is a common result of the mentioned attempts, but they are completely different from each other. For example, based on the results obtained in Terashima and Ueda (2002, 2003), Bell's inequality, in the moving frame and the $(\beta \to 0)$ limit, is violated to its maximum violation amount for the low energy particles, whilst the results observed by Ahn et al. suggest that this inequality is preserved at this limit independent of the particle energy. However, the question is which view is correct? Here we used the Stern-Gerlach type experiment as an appropriate approach to solve this problem. Is it possible to get more theoretical information about this inconsistency appeared in these studies? Indeed, this inconsistency between the results of considering Czachor's operator and those of considered the Pauli operator will be more complicated in the three-particle non-local systems. It is reported that the Pauli operator and its corresponding spin operator lead to better agreement with the behavior of the spin state of the three-particle non-local systems under an LT compared with Czachor's operator. Moreover, the Pauli-Lubanski spin operator is not suitable to describe the spin interaction with a magnetic field in the moving frame connected to the lab frame by an LT (Saldanha and Vedral, 2012a,b). Indeed, authors took into account the Pauli-Lubanski definition of spin operator and introduced a Hamiltonian for the spin interaction with the magnetic field. In continue, they considered the effects of LT on the reduced spin density matrix of one spin- $1/2$ particle and the results of applying a Stern-Gerlach experiment on the system in various frames by focusing on the quantization axes in the various frames. Finally, they concluded that the Pauli-Lubanski spin operator (and similar operators such as Czachor's operator) is not suitable for describing the system, which includes one spin-½ particle interacting with the magnetic field in the lab frame, in all inertial frames connected to each other by LT. Hence, what is the origin of these differences between the results of considering the Pauli operator and that of Czachor? Loosely speaking, which one of these operators is in better agreement with the spin states of one and two-particle systems, and helps us get more suitable predictions about the results of applying a Stern-Gerlach type experiment on a system which is in relative motion with respect to the observer?

In this paper, we study the differences between the results of considering the Pauli operator for describing spin and those of used Czachor's operator to investigate spin. Unlike Refs (Saldanha and Vedral, 2012a,b), we do not consider any magnetic field. Moreover, in order to avoid any paradoxes due to apply an LT on the system, we consider a situation in which the particles momentums are specified with zero uncertainty, in the lab frame. In addition, we focus on the behavior of the system state and spin operator, and show that, even in the absence of the magnetic fields, Czachor's spin operator is not probably suitable to describe spin. We start from the one particle system and consider a moving observer connected to the lab frame by a LT. By studying the behavior of spin state in the lab and moving frames, we try to establish a theoretical criterion to decide about the validity of spin behavior predicted by either using Czachor's or the Pauli spin operators. In addition, we generalize our study to the two-particle non-local system. Our results indicate that the predicted result by Pauli operator is more compatible to the behavior of spin state in both of the moving and labs frames compared with Czachor's operator. We also address some results of considering Pauli-Lubanski operator (Bogolubov et al., 2012; Terno, 2003).

The paper is organized as follows. In the next section, we focus on the one particle system and investigate the behavior of expectation values of Czachor's and the Pauli spin operators under LT. We also point to the behavior of the spin state under LT, and compared the results with the behavior of expectation values of Czachor's and the Pauli spin operators under LT to get the better spin operator. In section (III), we focus on the two-particle non-local system including two purely entangled spin-½ particles which move away from each other along the $Z$ direction with the same momentum. In addition, we point to the above-mentioned inconsistency and try to eliminate that by considering the behavior of the system state under LT. In the fourth section, some results of Pauli-Lubanski operator are investigated. The last section is devoted to the summary and concluding remarks. Throughout this paper we set $c=1$ for simplicity.

2 Quantum mechanics under LT

In the lab frame (S) for a spin-½ particle, with the momentum state $\left|\overrightarrow{P}\rangle \right.$ and the spin state $\left|\mathrm{\Sigma }\rangle \right.$ (Moradpour and Montakhab, 2016), the state of system is written as (Moradpour et al., 2015)

Here, we take into account that $\overrightarrow{p}=p_0\widehat{z}$ . The state of particle is viewed by an observer which moves along the $x$ axis $\overrightarrow{\beta }=\beta \widehat{x}$ as [3]

where ${\left|\overrightarrow{P}\rangle \right.}^{\mathrm{\Lambda }}$ shows the particle momentum state at moving frame (S′), and Wigner representation in the Lorentz group for the spin-½ particles is given by $D\left(W\left(\mathrm{\Lambda }\text{,}{p}_1\right)\right)$ (Halpern, 1968; Wigner and Halpern, 1939)

In this equation, ${\sigma }_y$ and ${\mathrm{\Omega }}_p$ are the y-component of Pauli matrix and the Wigner angle, respectively, evaluated as (Halpern, 1968; Wigner and Halpern, 1939)

$\cosh \delta =\frac{p_0}{m}$ and $\cosh \alpha =\sqrt{1-{\beta }^2}$ are related to the particle energy in the lab frame and the boost effects, respectively. Bearing Eq. (6) in mind, one can easily get

which finally leads to

for the moving frame. Here, $\left|+\rangle \right.$ and $\left|-\rangle \right.$ denote the up and down spin states along the $z$ direction in the lab frame, respectively. Moreover, the superscript $\mathrm{\Lambda }$ is used to specify the corresponding spin state at the moving frame. In the $\beta \to 1$ limit, $\sin \frac{{\mathrm{\Omega }}_p}{2}\approx \sqrt{\frac{\mathrm{\Gamma }-1}{2\mathrm{\Gamma }}}$ where $\mathrm{\Gamma }=\frac{1}{\sqrt{1-{\beta }_1^2}}$ and ${\beta }_1$ are the energy factor and the velocity of the particle in the lab frame, respectively. Using Eq. (9) to get

for a low energy particle $(\mathrm{\Gamma }\to 1)$ and

for a high energy particle $(\mathrm{\Gamma }\to \infty )$ Now, consider a situation in which the lab and moving observers apply a Stern-Gerlach experiment in the same direction $\overrightarrow{A}$  =  $\frac{1}{\sqrt{2}}(1\text{,}0\text{,}1)$ while, $\left|+\rangle \right.$ is the spin state of the particle in the lab frame. Therefore, the spin state of the system in the moving frame can be found in Eq. (9). Let us focus on the results obtained by taking into account Czachor's and the Pauli spin operators. In case of using the moving and lab frames with the Pauli spin operator and the same spin measurement direction ( $\overrightarrow{A})$ , simple calculations lead to

and

for the lab and moving frames, respectively. Here, the subscript 1 and 2 are also used to denote the lab and moving frames, respectively. In addition, $S=\frac{\hslash }{2}(\overrightarrow{A.}\overrightarrow{\sigma })=\frac{\hslash }{2\sqrt{2}}({\sigma }_x+{\sigma }_z)$ is the spin operator along the $\overrightarrow{A}$ direction. It is easy to check that Eq. (13) is in line with the asymptotic behavior explained in Eqs. (10) and(11). In fact, using the ${\left|+\rangle \right.}^{\mathrm{\Lambda }}$ expression in Eq. (11) and the relation $S=\frac{\hslash }{2\sqrt{2}}({\sigma }_x+{\sigma }_z)$ one can easily find that $\langle S{\rangle }_1\approx \frac{\hslash }{2\sqrt{2}}$ for the high energy particle at the $\beta \to 1$ limit. Additionally, since for the high energy particle at $\beta \to 1$ limit we have $({\mathrm{\Omega }}_p\approx \pi /2)$ , it is obvious that Eq. (13) leads also to $\langle S{\rangle }_2\approx \frac{\hslash }{2\sqrt{2}}$ for the high energy particle at the $\beta \to 1$ limit. Thus, the prediction made by the Pauli operator for the spin in the moving frame is in line with behavior of the system’s state under the LT. It is also useful to mention here that, in the $\beta \to 1$ limit, Eq. (13) leads to $(\frac{\hslash }{2\sqrt{2}})$ for both of the low $({\mathrm{\Omega }}_p\approx 0)$ and high $({\mathrm{\Omega }}_p\approx \pi /2)$ energy particles. These results are in agreement with the asymptotic behaviors addressed in Eqs. (10) and (11). If Czachor's spin operator together with the vector $\overrightarrow{A}$  = ( $\frac{1}{\sqrt{2}}\text{,}0\text{,}\frac{1}{\sqrt{2}}$ ) are considered, one can use Eq. (3) in order to evaluate the spin operator in the lab and moving frame as

and

respectively. In these equations, the subscripts 1 and 2 denote the lab and moving frames, respectively. Since $\left|+\rangle \right.$ is the spin state of particle in the lab frame, by using Eq. (14) we get

which is the same as the previous results achieved using the Pauli spin operator. For the moving frame, using Eqs. (9) and (15) to obtain

which differs from the result obtained by using the Pauli operator, Eq. (13). But which approach is right? In order to check this prediction, we focus on the $\beta \to 1$ limit. For the low energy particle ${\mathrm{\Omega }}_p\to 0$ and we get $\langle C_2\rangle \to 0$ which is fully inconsistent with Eq. (10). Additionally, considering ${\mathrm{\Omega }}_p\to \pi /2$ leads to $\langle C_2\rangle \to \frac{\hslash }{2}$ which is again in contrast with the result predicted by Eq. (13). All in all, using both of these operators lead to the same predictions for the spin in the lab frame but, in the moving frame the results obtained using Czachor's spin operator differ from that of considered the Pauli spin operator. Our approach shows that the predictions made by considering the Pauli spin operator is in agreement with the behavior of the spin state in the lab and moving frames. The same conclusion is not accessible by considering Czachor's spin operator which indicates that our approach is in full agreement with previous results obtained in Moradpour et al. (2015), Saldanha and Vedral (2012a,b). The Stern-Gerlach type experiment is required to identify the correct result between Eqs. (13) and (17). Based on Eq. (3), in the moving frame, $C=\frac{\hslash \widehat{A}}{2}=S$ under one of the following conditions $(\widehat{e}.\widehat{A}=0\text{,}{\overrightarrow{A}}_{\parallel }=0)$ or $(\widehat{e}.\widehat{A}=1\text{,}{\overrightarrow{A}}_{\perp }=0)$ . Under these conditions Czachor's operator is the same as the Pauli operator and the results lead to the same predictions in the lab and moving frames.

3 Pure bi-partite entangled states under LT

In order to investigate the LT effects on the pure bipartite non-locality, the above arguments are required to be generalized to the two-particle system. This generalization is as follows. For a system, including two spin-½ particles, in the lab frame (S), with the spin state $\left|\psi \rangle \right.$ and the momentum state $\left|{\overrightarrow{P}}_1{\overrightarrow{P}}_2\rangle \right.$ , the state of system is (Moradpour et al., 2015)

Now, consider a moving frame (S′) which moves along the $x$ axis $({\overrightarrow{\beta }}_1=\beta \widehat{x}$ ). In the S′ frame, the state of the system is [3]

${\left|{\overrightarrow{P}}_1{\overrightarrow{P}}_2\rangle \right.}^{\mathrm{\Lambda }}$ is the system’s momentum state in the moving frame, and as stated in Eq. (6) the $D(W\left(\mathrm{\Lambda }\text{,}{\text{p}}_i)\right)$ is the Wigner representation for the i^th particle. Consider a system, including two particles which move away from each other along the z direction

in the lab frame, with the total state as

The maximum violation of Bell's inequality in the lab frame ( $B=2\sqrt{2})$ is obtainable by choosing the

for the directions of Pauli's operators applying on the first and second particles, respectively (Doyeol et al., 2003; Kim and Son, 2005). As noted in the introduction, since $\beta$ meets the $\beta =0$ condition in the lab frame, Czachor's operator is compatible with the Pauli operator in the lab frame. Therefore, this result is also obtainable in the lab frame if Czachor's operator is used to generate the Bell operator. Let us focus on the moving observer. If the Czachor's operator being used by moving observer and the distinctive set of measurement directions, given in Eqs. (22) and (23), then (Doyeol et al., 2003)

here C index indicates the consideration of Czachor's operator. The lab frame result is obtainable by inserting $\beta =0$ and ${\mathrm{\Omega }}_p=0$ simultaneously. It is obvious that $B_C\le 2$ for the $\beta \to 1$ limit, which means that Bell's inequality is preserved in the moving frame and is independent from the particle energy in the lab frame. This behavior indicates that non-locality has vanished in this limit if the moving frame uses the same set of measurements as the lab frame violating the Bell inequality to its maximum violation amount in the lab frame (Doyeol et al., 2003; Moradpour and Montakhab, 2016). From Eq. (21), we see that, in the $\beta \to 1$ limit and for the low energy particles system ( ${\mathrm{\Omega }}_p\sim 0$ ), ${\left|\xi \right.}^{\mathrm{\Lambda }}\sim {\left|{\overrightarrow{P}}_1{\overrightarrow{P}}_2\right.〉}^{\mathrm{\Lambda }}\frac{1}{\sqrt{2}}\left(\left|++\rangle \right.+\left|--\rangle \right.\right)$ which is the same as the system state in the lab frame. Therefore, the bi-partite non-locality does not completely disappear at this limit. We believe a true Bell operator should show this behavior. Therefore, we see that, once again, Czachor's operator does not lead to the results compatible with the behavior of the spin state of system. This weakness of Czachor's operator was also reported in the multi-particle non-local systems. Using the Pauli operators to form the Bell’s operator together with Eqs. (19), (20) and (21), we get

for the expectation value of Bell’s operator in the moving frame. Here, l index denotes that the Pauli operators are used to build the Bell operator. Moreover, we took into account the special directions explained in Eqs. (22) and (21). $\langle B_l\rangle$ is displayed in Fig. 1.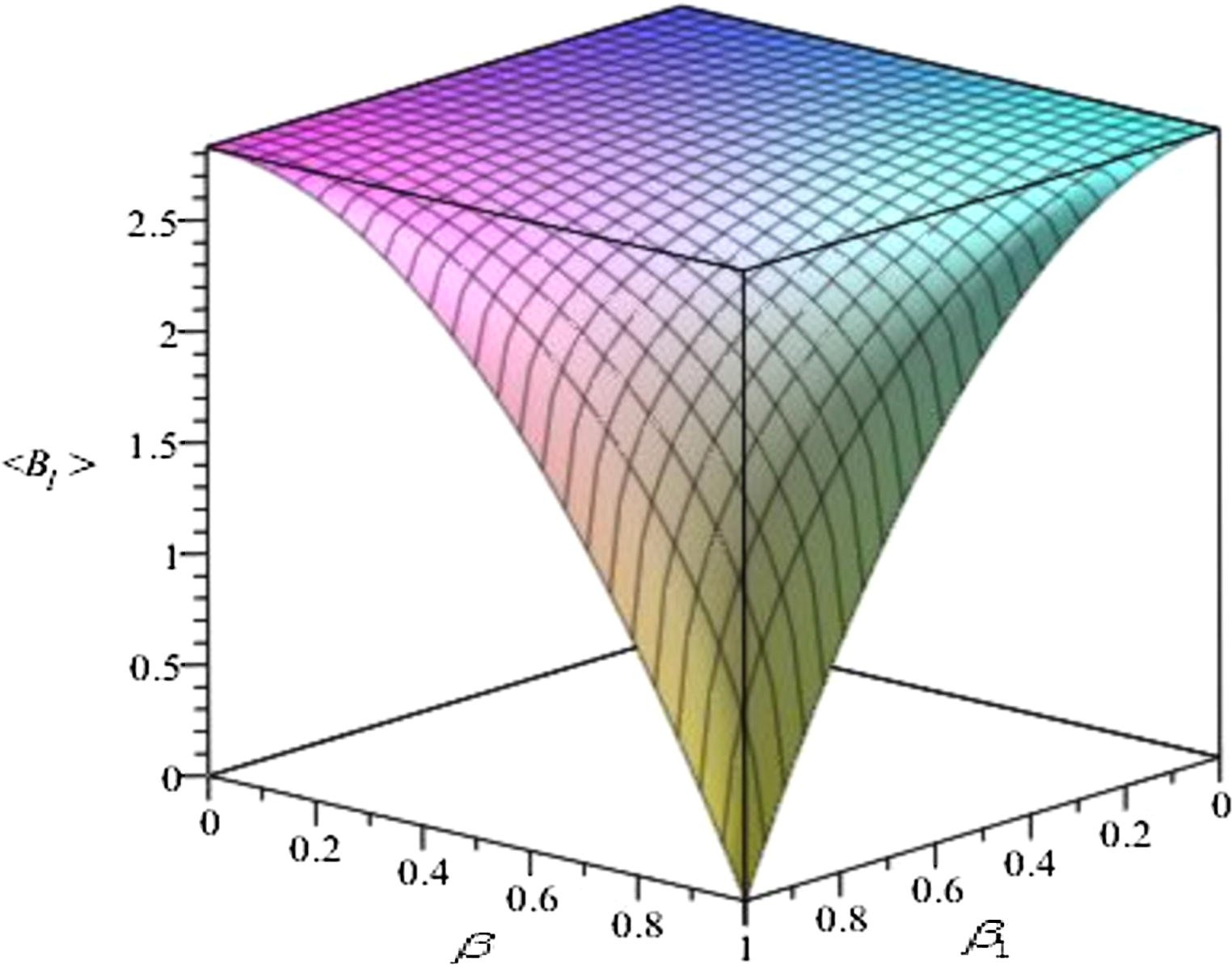

Close

Fig. 1

The plot depicts $\langle B_l\rangle$ . Here, $\beta$ and ${\beta }_1$ point to the boost velocity and the velocity of particles in the lab frame, respectively.

Export to PPT

In the non-relativistic limit $({\mathrm{\Omega }}_p\to 0)$ , the result of lab frame is obtainable. In addition, for the low energy particles in the $\beta \to 1$ limit, the $({\mathrm{\Omega }}_p\to 0)$ and therefore, Bell's inequality is maximally violated which is in agreement with the asymptotic behavior of the system state. For the high energy particles in the $\beta \to 1$ limit, $({\mathrm{\Omega }}_p\to \pi /2)$ which leads to ${\left|\xi \rangle \right.}^{\mathrm{\Lambda }}\sim {\left|{\overrightarrow{P}}_1{\overrightarrow{P}}_2\right.〉}^{\mathrm{\Lambda }}\frac{1}{\sqrt{2}}\left(\left|-+\rangle \right.-\left|+-\rangle \right.\right)$ . The latter points that since the spin measurement directions have not been changed in our setup, Bell's inequality should be satisfied in the $\beta \to 1$ limit by the high energy particles system. It is easy to check that this expectation is satisfied by both of $\langle B_C\rangle$ and $\langle B_l\rangle$ . Finally, we found that, independent of using either Czachor's or the Pauli spin operators to describe the spin, the expectation amount of the Bell operator is decreased as a function of the boost velocity and the particles energy if the moving and lab frames use the same set of measurement directions for the Bell operator violating Bell's inequality to its maximum violation amount in the lab frame. Another special case is

which means that the considered LT leaves this state unchanged. Therefore, it is crystal clear that when the moving observer uses the Pauli spin operator and identical set of measurements as the lab frame to get the Bell operator and Bell's inequality, Bell's inequality is violated to the same value as the lab frame. The latter means that, in the moving frame, this inequality violated to its maximum violation amount of ( $2\sqrt{2}$ ) in this situation. If the moving observer uses Czachor's operator to construct the Bell operator and investigates the behavior of Bell's inequality and thus the corresponding non-locality, then (Doyeol et al., 2003)

which claims that non-locality is decreased by increasing the boost velocity and thus, in the $\beta \to 1$ limit, Bell's inequality is marginally satisfied in the moving frame (Doyeol et al., 2003). This result is in contrast with the invariant form of this state under LT Eq. (27) and the results made by considering the Pauli operator. Once again, It is figured out that, whenever the lab and moving frames use the same set of measurements which violate Bell's inequality to its maximum violation amount in the lab frame (Moradpour and Montakhab, 2016), the behavior of the bi-partite pure entangled state Eq. (27) under LT is fully consistent with the behavior of the Bell operator under LT if the Pauli operator applied to form the Bell operator. Loosely speaking, the same as the results of the previous section and the three-particle non-local systems, the predictions of Czachor's spin operator about the spin differ from those of the Pauli operator and the system state. It is useful to note here that a Stern-Gerlach type experiment is required to experimentally distinguish these results. Finally, we should again note that since LT introduced in this paper is a unitary operator, it should be possible to get the same violation amount as the lab frame for Bell's inequality in the moving frame. Indeed, if one applies LT on both of the system state and the Bell operator, Bell's inequality is also maximally violated in the moving frame (Terashima and Ueda, 2002, 2003).

4 Pauli-Lubanski operator

For a system with four-momentum operator ( $P^{\tau }$ ) and the relativistic angular momentum tensor ( $J^{\lambda \eta }$ ), the Pauli-Lubanski spin vector is given by (Bogolubov et al., 2012)

Here, $S_i$ is Pauli operator (the indices i = 1, 2,3 show the directions), $E=P^2+m^2$ , and $P$ denote the particle energy and the absolute value of its momentum, respectively. Therefore, it is obvious that the spin measurements along the $x$ and $y$ axis are not be affected by the relative motion. Considering the conditions led to Eqs. (12) and (13), one can use the Pauli-Lubanski vector to find

and

like before $\mathrm{\Gamma }=1/\sqrt{1-{\beta }_1^2}$ shows the energy factor and ${\beta }_1$ is the velocity of the particle in the lab frame. In addition $E^{\prime }$ is particle’s energy in moving frame thus $E^{\prime }=\gamma E=\gamma \mathrm{\Gamma }m$ where $\gamma =1/\sqrt{1-{\beta }^2}$ and $\beta$ denotes the boost velocity. The key point in obtaining the above results is this fact that the x component of the particle’s momentum in lab frame is zero. It is obvious that in the absence of any boost ( $\gamma \to 1$ ) the Wigner angle is vanished meaning that $\langle W_2\rangle \to \langle W_1\rangle$ . Moreover, from Eq. (31), it is apparent that for low energy particle in the lab frame where $\langle W\rangle \to 1$ then we have $\langle W_1\rangle \to \frac{m\hslash }{2\sqrt{2}}$ . In fact, in this situation lab frame and rest frame are identical. Here, it is also interesting to note that in case of considering the rest frame of particle $\langle W\rangle =\frac{m\hslash }{2\sqrt{2}}$ which is independent of energy and is in full agreement with the rest frame relation discussed after Eq. (29) $(\langle \overrightarrow{W}\rangle =m\overrightarrow{S})$ , and also the low energy limit Eq. (31).

As we mentioned previously, the set of (a, a′, b, b′) operators are used as Yes or No operators with the eigenvalues of ±1 in order to get the $\langle B\rangle \le 2$ result (Clauser et al., 1969). Since this is the specific property of Pauli operator, it can be used to study the Bell’s inequality. Therefore, in order to form the Bell operator, using the set of (a, a′, b, b′) operators with eigenvalues of $\pm \alpha$ leads to the limit of $\langle B\rangle \le 2{\alpha }^2$ for the local states. In these situations, we have a shift as large as ${\alpha }^2$ in the behavior of $\langle B\rangle$ . In fact, the possibility of violation of Bell’s inequality depends on the non-local feature of system and it is independent of the value of $\alpha$ . Bearing Eq. (30) in mind, one can easily find that for $(a\text{,}{a}^{\prime }\text{,}b\text{,}{b}^{\prime })\in \left\{W_1\text{,}{W}_2\right\}\text{,}$ , we have $\alpha =m\hslash /2$ and thus $\langle B\rangle \le (m^2{\hslash }^2)/2$ . Dividing $\langle B\rangle$ to $(m^2{\hslash }^2)/4$ , we reach $\langle B\rangle \le 2$ which is the familiar form of Bell’s inequality. Moreover, in case of using $(a\text{,}{a}^{\prime }\text{,}b\text{,}{b}^{\prime })\in \left\{\frac{2W_1}{\hslash }\text{,}\frac{2W_2}{\hslash }\right\}\text{,}$ to form the Bell operator we have $\langle B\rangle \le 2m^2$ . It is also obvious that by dividing this result into $m^2$ we can again reach the $\langle B\rangle \le 2$ .

Now, just the same as the procedure led to Eq. (25) we consider $\langle \left|\xi \rangle \right.=\left|{\overrightarrow{P}}_1{\overrightarrow{P}}_2\right.〉\frac{1}{\sqrt{2}}\left(\left|++\rangle \right.+\left|--\rangle \right.\right)$ in the lab frame were as mentioned before ${\overrightarrow{P}}_1=-{\overrightarrow{P}}_2={\widehat{P}}_z$ . Using the set of measurements introduced in Eqs. (22) and (23) it is easy to find that $\langle {\beta }_w{\rangle }_1=2\sqrt{2}{m}^2$ . Moreover, for the moving observer using Eq. (21) and following the recipe lead to Eq. (25) we reach to $\langle {\beta }_w{\rangle }_2=2\sqrt{2}{m}^2{\mathit{cos}}^2{\mathrm{\Omega }}_p$ . Here, again in the absence of Wigner angle $\langle B{\rangle }_{w_2}\to \langle B{\rangle }_{w_1}$ and $\langle B_w\rangle$ shows the Bell operator in which the Pauli-Lubanski operator are used to form it. Since $m$ is a constant and positive quantity the behavior of $\langle B_w{\rangle }_2$ is similar to that of $\langle B_{\mathit{wl}}\rangle$ plotted in Fig. 1. Finally, it is also worthwhile mentioning that the calculations for the rest frame, by using Eqs. (22) and (23), will also lead to $\langle {\beta }_w\rangle =2\sqrt{2}{m}^2$ which is similar to the result obtained in lab frame. This similarity in results stems in this fact that in the rest frame the momentum is zero and in the lab frame x and y components of $W_v$ are used which are independent of the momentum of particles.

5 Discussion and conclusion

Spin is a quantum mechanical property of systems. It has vast implications for the spectroscopy, quantum information theory and etc. Therefore, it is necessary to find a suitable operator to describe this property. Indeed, there are various operators suggested for this aim (Bauke et al., 2014a,b; Terno, 2003). We believe that our approach potentially can be used to study the relation between the various spin operators and the effects of LT on the system state, provides a frame to get some predictions about the outcomes of a Stern-Gerlach type experiment in the relativistic situations. Here, we focused on the two spin operators, including Czachor's and the Pauli spin operators. Firstly, we saw that Czachor's operator is in agreement with the Pauli operator in the limit of low velocity, both of them predict the same outcome for a Stern-Gerlach type experiment, applied on a spin-½ particle, in the lab frame. In continue, we considered a moving frame which moves along the x direction and is connected to the lab frame by an LT. It means that we discard the relativistic effects such as the pair productions, and in fact, one should use relativistic quantum mechanics or quantum field theory to get more precise results (Friis et al., 2010; Moradi et al., 2014). Moreover, the lab and moving frames use the same set of measurement directions in our setup. We found that the Pauli spin operator predictions about the spin of a particle are compatible with the behavior of the system state in the moving frame, whiles, Czachor's spin operator predictions differ from those of the Pauli spin operator and the behavior of system state under LT. In addition, we focused on the two purely bipartite entangled states, known as the Bell states, which include two spin- $1/2$ particles moving away from each other along the $z$ direction with the same momentum in the lab frame. Bearing LT in mind, we evaluated the corresponding system states in the previously mentioned moving frame. Thereinafter, we used the Pauli operator to construct the Bell operator and the special set of measurement directions which violates Bell's inequality in the lab frame to its maximum violation amount. In continue, by taking into account the same directions as the lab frame for the Bell operator in the moving frame, we have investigated the expectation value of the Bell operator in the moving frame. For a Bell state introduced in Eq. (20), the expectation value of the Bell operator in the moving frame is decreased as a function of the boost velocity together with the energy of particles in the lab frame. It is also found that, for particles with low energy in the lab frame, Bell's inequality in the moving frame is violated to the same value as the lab frame (the maximum violation amount) in the limit, which is the same as the lab frame. We also addressed another Bell state Eq. (26) which is invariant under LT, and found out that the expectation of the Bell operator is also invariant under LT which is in agreement with the behavior of the system state. In addition, the same as the one-particle system, our study shows that the predictions of the Pauli spin operator are in line with the behavior of system state in both of the lab and moving frames. We have also pointed to the results obtained by considering Czachor's operator and compared them with ours (Fleming, 1965). The results for Pauli-Lubanski operator were also discussed. Finally, we found out that the Pauli spin operators are in better agreement with the behavior of spin system in these situations. Our study helps us make clearer the origin of differences between the predictions about the spin behavior made by considering Czachor's and the Pauli spin operators. It is useful to note that although our results are in agreement with those of three-particle non-local systems (Moradi et al., 2014), but a Stern-Gerlach type experiment is needed to get a decision about the quality of validity of these results in nature.