Translate this page into:
On the exponential solutions to three extracts from extended fifth-order KdV equation
⁎Corresponding author. aly742001@yahoo.com (Aly R. Seadawy),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
An extended fifth order Korteweg-de-Vries (efKdV) equation is an important equation in fluids dynamics for the description of nonlinear wave processes, and contains quite a number of KdV-type equations including the Sawada-Kotera equation, the Caudrey-Dodd-Gibbon equation, the Lax equation, the Kaup-Kuperschmidt equation and the Ito equation among others. However, in this paper, we examine the efKdV by extracting three different fifth order Korteweg-de-Vries (fKdV) equations. Solitary wave solutions to the extracts are found by means of an exponential function ansatz specifically constructed for the study. The obtained solutions can be used in description of shallow-water waves.
Keywords
Fifth order KdV equation
KdV equations
Exponential function ansatz
Solitary wave
1 Introduction
Nonlinear partial differential equations are known for their roles in many nonlinear science applications including the hydrodynamics, fluid dynamics and mechanics, plasma physics and nonlinear dispersive wave among others. An important model in this regard is the Korteweg-de-Vries (KdV) equation (Olver, 1984) that has many applications such as in description of shallow water waves and ion-acoustic waves in plasmas. The KdV equation has undergone several modifications and extensions leading to various forms of KdV equations appearing in three, five, seven or more order forms and different dimensions; read (Hereman, 2000; Hereman, 2009; Helal and Seadawy, 2009; Bakodah, 2013; Adomian, 1996; Nuruddeen, 2018; Djidjeli et al., 1995; Kaya, 2005; Khater et al., 2000; Khater et al., 2006; Lei et al., 2002; Sawada and Kotera, 1974; El-Wakil et al., 2011; Pandir et al., 2013; Islam et al., 2015) for various forms and methods.
Further, of recent, Yun-hu and Yong (Yun-hu and Yong, 2013) analyzed the extended fifth order Korteweg-de-Vries (efKdV) equation of the form
However in this study, we aim to study three different fKdV equations to be extracted from the efKdV equation given in Eq. (1) as follows:
1). The first one is obtained by setting
in Eq. (1), to yields
2). The second by setting
in Eq. (1), which gives
3). The third by setting
in Eq. (1), that reads
2 The methodology
In constructing exact solutions to the extracrted equations in Eqs. (2)–(4), we devise an exponential function ansatz and presented here by considering the general form of differential equation below:
Thus, substituting Eq. (6) and its possible derivatives into Eq. (5) gives a polynomial in for . Equating the coefficient of each power of to zero, we obtain a system of algebraic equations which will then be solved for the unknowns (we use Mathematica software) to obtain the solution of Eq. (5).
3 Application
In this section, we present exact exponential function traveling wave solutions to the three extracts given in Eqs. (2)–(4) which we extracted from the extended fifth-order KdV (efKdV) equation given in (1) as follows:
3.1 The first extract
We consider the first extract of the extended fifth-order KdV (efKdV) equation given in Eq. (2);
, and
, where, .
The first set gives the exact solution
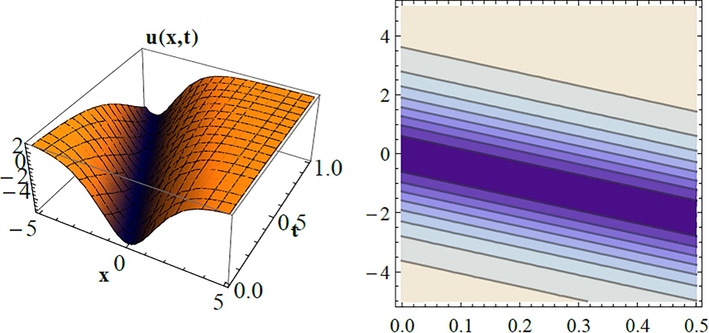
The 3D and the contour plots for Eq. (8).
Further, the second set gives the solution:
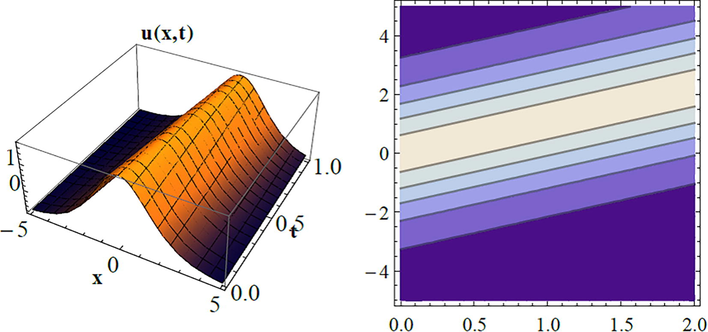
The 3D and the contour plots for Eq. (9).
3.2 The second extract
We consider the second extract of the extended fifth-order KdV (efKdV) equation given in Eq. (3);
; which produces a solution:
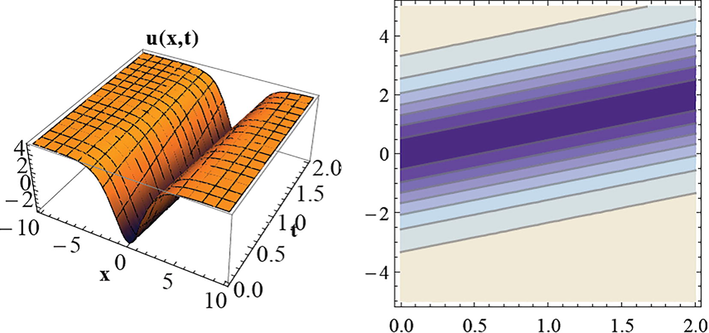
The 3D and the contour plots for Eq. (11).
3.3 The third extract
We consider the third extract of the extended fifth-order KdV (efKdV) equation given in Eq. (4);
; which produces a solution:
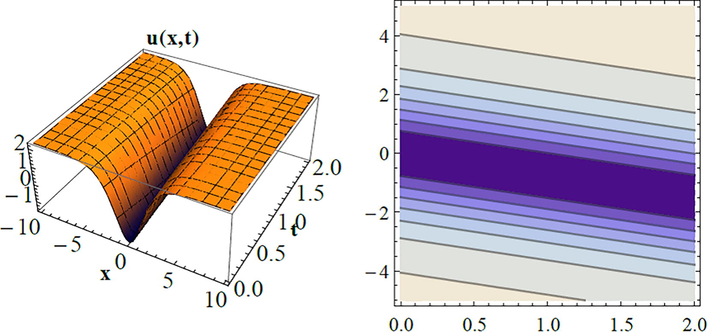
The 3D and the contour plots for Eq. (13).
4 Results and discussion
The present study effectively constructs exponential traveling wave solutions to three different fifth order Korteweg-de-Vries equations (fKdV) extracted from the extended fifth order Korteweg-de-Vries equation (efKdV) that has recently been studied by Yun-hu and Yong in Yun-hu and Yong (2013). The first extract Eq. (1) which was once numerically considered by Bakodah (2013) was found to have two different exponential function exact solutions. The fractional version of the second extract Eq. (2) was also recently studied by Khalid et al. (2018) using generalized exp expansion method, while the third extract Eq. (3) is first extracted and studied in this study to our knowledge with one exponential function exact solutions each. Since KdV equations play vital roles in the study of shallow-water waves, thus the present obtained traveling wave solutions would not be an exception in the description of shallow-water waves and other nonlinear wave processes. Finally, Three-dimensional (3D) and contour plots are given for the obtained solution.
5 Conclusion
In conclusion, exponential functions traveling wave solutions to three different fifth order Korteweg-de-Vries equations have been constructed. The three fKdV equations considered are extracted from the extended fifth order Korteweg-de-Vries equation that has recently been studied in the literature and found to be of various applications in nonlinear sciences. Interesting and reliable exponential function ansatz was proposed and implemented on Mathematica software in the study. We provide three-dimensional and contour plots for the obtained solutions for easier interpretations of results.
References
- On the formulation of mass, momentum and energy conservation in the KdV equation. Acta Appl. Math.. 2014;133:113-131.
- [Google Scholar]
- Analytical solution of the time-fractional Phi-4 equation using modified power series method. Nonlinear Dyn. 2017
- [Google Scholar]
- Modified Adomain decomposition method for the generalized fifth order KdV equations. Am. J. Comput. Math.. 2013;3:53-58.
- [Google Scholar]
- Decomposition method for solving Burger’s equation with Dirichlet and Neumann boundary conditions. Int. J. Light Electron Opt.. 2016;30
- [Google Scholar]
- Numerical methods for the soltution of the third and fifth-order disprsive Korteweg-De Vries equations. J. Comput. Appl. Math.. 1995;58:307-336.
- [Google Scholar]
- Time-fractional KdV equation: formulation and solution using variational methods. Nonlinear Dyn.. 2011;65:55-63.
- [Google Scholar]
- Gevrey regularity for a class of water-wave models. Nonlinear Anal.: Theory Methods Appl.. 2009;71(3–4):1160-1170.
- [Google Scholar]
- Variational method for the derivative nonlinear Schr-dinger equation with computational applications. Phys. Scr.. 2009;80:350-360.
- [Google Scholar]
- Exact soliton solutions of an D-dimensional non- linear Shrodinger equation with damping and difusive terms. Z. Angew. Math. Phys.. 2011;62:839-847.
- [Google Scholar]
- Hereman, W., 2000. Wolfram Research Academic Intern Program Inc., Champaign. Illinois, pp. 1–14.
- Hereman, W., 2009. Springer Verlag. Heibelberg, Germany, pp. 1620–1536.
- A rational (G/G)-expansion method and its application to modified KdV-Burgers equation and the (2+1)-dimensional Boussineq equation. Nonlinear Stud.. 2015;6:4.
- [Google Scholar]
- An Application for the higher order modified KdV equation by decomposition method. Commun. Nonlinear Sci. Numer. Simul.. 2005;10:693-702.
- [Google Scholar]
- Analytical treatment for the conformable space-time fractional Benney-Luke equation via two reliable methods. Int. J. Phys. Res.. 2017;5:109-114.
- [Google Scholar]
- New structures for the space-time fractional simplified MCH and SRLW equations. Chaos Solitons Fractals. 2018;106:304-309.
- [Google Scholar]
- New exact solitary wave solutions for the extended (3+1)-dimensional Jimbo-Miwa equations. Results Phys.. 2018;9:12-16.
- [Google Scholar]
- New hyperbolic structures for the conformable time-fractional variant bussinesq equations. Opt Quant Electron.. 2018;50
- [Google Scholar]
- General soliton solutions of an n-dimensional Complex Ginzburg-Landau equation. Phys. Scr.. 2000;62:353-357.
- [Google Scholar]
- Variational method for the nonlinear dynamics of an elliptic magnetic stagnation line. Eur. Phys. J. D. 2006;39:237-245.
- [Google Scholar]
- The homogeneous balance method, Lax Pair Hirota transformation and a general fifth order KdV equation. Chaos Solutions Fractals. 2002;13
- [Google Scholar]
- On solutions of generalized modified Korteweg-de-Vries equation of the fifth order with dissipation. Appl. Math. Comput.. 2016;230:39-45.
- [Google Scholar]
- Multiple soliton solutions for the (3+1) conformable space-time fractional modified Korteweg-de-Vries equations. Ocean J. Eng. Sci.. 2018;3:11-18.
- [Google Scholar]
- Exact solutions of wave-type equations by the Aboodh decomposition method. Stochastic Model Appl.. 2017;21:23-30.
- [Google Scholar]
- Hamiltonian and non-Hamiltonian models for water waves. In: Lecture Notes in Physics. Vol 195. New York: Springer-Verlag; 1984. p. :273-290.
- [Google Scholar]
- New exact solutions of the time fractional nonlinear dispersive KdV equation. Int. J. Model. Optim.. 2013;3
- [Google Scholar]
- A method for finding N-soliton solutions of the KdV equation and the KdV-like equation. Progr. Theor. Phys.. 1974;51:1355-1367.
- [Google Scholar]
- Two-dimensional interaction of a shear flow with a free surface in a stratified fluid and its a solitary wave solutions via mathematical methods. Eur. Phys. J. Plus. 132 2017,;518(12):1-11.
- [Google Scholar]
- Fractional solitary wave solutions of the nonlinear higher-order extended KdV equation in a stratified shear flow: Part I. Comp. Math. Appl.. 2015;70:345-352.
- [Google Scholar]
- Ion acoustic solitary wave solutions of two-dimensional nonlinear Kadomtsev-Petviashvili-Burgers equation in quantum plasma. Math. Methods Appl. Sci.. 2017;40(5):1598-1607.
- [Google Scholar]
- Ionic acoustic solitary wave solutions of two-dimensional nonlinear Kadomtsev-Petviashvili Burgers equations in quantum plasma. Math. Methods Appl. Sci.. 2017;40:1598-1607.
- [Google Scholar]
- Three-dimensional weakly nonlinear shallow water waves regime and its travelling wave solutions. Int. J. Comput. Methods. 2018;15(1)
- [Google Scholar]
- Bright and dark solitary wave soliton solutions for the generalized higher order nonlinear Shrodinger equation and its stability. Results Phys.. 2017;7:43-48.
- [Google Scholar]
- Stability analysis of new exact traveling Wave Solutions of new coupled KdV and new coupled Zakharov-Kuznetsov systems. Eur. Phys. J. Plus. 2017;132(162):1-20.
- [Google Scholar]
- The integrability of an extended fifth-order KdV equation with Riccati-type pseudopotential. Pramana-J. Phys.. 2013;81:737-746.
- [Google Scholar]







