Translate this page into:
Numerical solutions of two-dimensional nonlinear fractional Volterra and Fredholm integral equations using shifted Jacobi operational matrices via collocation method
⁎Corresponding author. rashidinia@iust.ac.ir (Jalil Rashidinia),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this paper, an efficient numerical method is presented to approximate solutions of two-dimensional nonlinear fractional Volterra and Fredholm integral equations. We derive new operational matrices of fractional-order integration and product based on two-variable shifted Jacobi polynomials. These operational matrices via shifted Jacobi collocation method are utilized to reduce the understudy equations to systems of linear or nonlinear algebraic equations. Then, the arising systems can be solved by the Newton method. Discussion on the error bound and convergence analysis of the proposed method is presented. The efficiency, accuracy, and validity of the presented method are demonstrated by its application to three test examples and by comparing our results with the results obtained by existing methods in the literature.
Keywords
Two-dimensional nonlinear fractional Volterra and Fredholm integral equations
Two-variable shifted Jacobi polynomials
Collocation method
Operational matrices
Convergence analysis
1 Introduction
Fractional calculus is the generalization of calculus, in which the order of derivatives and integrals can be arbitrary numbers. The history of fractional calculus is more than three centuries old; however, only in the last two decades, the field has received practical attention and interest. Many researchers have shown with the applications of fractional calculus to groundwater flow problems and groundwater pollution (Atangana and Kılıçman, 2013a; Benson et al., 2000; Caputo, 1967; Cloot and Botha, 2006; Meerschaert and Tadjeran, 2004), acoustic wave problems (Atangana and Kılıçman, 2013b), and others (Chen et al., 2007; Mainardi, 1997; Yuste and Acedo, 2005; Zhuang et al., 2009). Moreover, advances in sciences have led to the formation of many physical and engineering problems that can be mathematically represented by fractional integro-differential equations (FIDEs). For example, problems from rheology, porous media, electrochemistry, control, electromagnetism fluid structure, viscoelasticity, coupling and particle mechanics (see e.g. Carpinteri and Mainardi, 1997; Metzler et al., 1995; Oldham and Spanier, 1974; Thomas and Fehmi, 2010). In recent years, numerical methods for solving FIDEs have attracted the attention of a large number of researchers. Such as, Ma and Huang (2013) have proposed a hybrid collocation method for solving FIDEs. Mohammed (2014) has developed an approximate scheme based on least squares method with aid of shifted Chebyshev polynomial to solve linear FIDEs. Alkan (2015) has obtained numerical solutions of a class of nonlinear Fredholm FIDEs by using sinc–collocation method. Maleknejad et al. (2020a) have proposed operational matrix method based on the hybrid of two-dimensional block-pulse functions and two-variable shifted Legendre polynomials (2D-HBPSLs) to solve nonlinear two-dimensional FIDEs of the general form. Nemati et al. (2020) have presented a collocation method based on the Legendre wavelet combined with the Gauss-Jacobi quadrature formula for calculating the numerical solution of a class of delay-type FIDEs. For a review on numerical techniques, proposed to solve other different problems, see for instance Kumar et al., 2017, 2018, 2020, Maleknejad et al., 2018, 2021; Mirzaee et al., 2018; Mirzaee and Alipour, 2018, 2019a, 2019b, Mirzaee and Samadyar, 2018a, 2018b; Samadyar and Mirzaee, 2019; Singh, 2020a, 2020b, Singh et al., 2019, 2020; Singh and Srivastava, 2020; Yadav et al., 2019 and references therein.
In this paper, the following fractional integral equations of the second kind are considered:
Two-dimensional nonlinear fractional Volterra integral Eqs. (2D-NFVIEs):
Two-dimensional nonlinear fractional Fredholm integral Eqs. (2D-NFFIEs):
Najafalizadeh and Ezzati (2016) constructed operational matrices of fractional-order integration and product for two-dimensional block pulse functions (2D-BPFs) and applied them to solve Eqs. (1) and (2). Jabari Sabeg et al. (2017) derived the operational matrix of two-dimensional orthogonal triangular functions (2D-TFs) for two-dimensional fractional integrals. Then, they applied this operational matrix and properties of two-dimensional orthogonal triangular functions to solve Eq. (1). Hesameddini and Shahbazi (2018) used the operational matrix method based on two-dimensional shifted Legendre polynomials (2D-SLPOM) for the numerical solution of Eqs. (1) and (2). Mirzaee and Samadyar (2019) developed a numerical scheme based on two-dimensional orthonormal Bernstein polynomials (2D-OBPs) for solving Eqs. (1) and (2). Maleknejad et al. (2020b) have provided sufficient conditions for the local and global existence of solutions for Eqs. (1) and (2), based on the Schauder’s and Tychonoff’s fixed-point theorems. Also, they have provided sufficient conditions for the uniqueness of the solutions. Moreover, they have used operational matrix method based on the 2D-HBPSLs via collocation method to find approximate solutions of the mentioned equations in a Banach space. Moreover, Maleknejad et al., 2020 applied a new and efficient numerical method based on shifted fractional-order Jacobi operational matrices for solving Eqs. (1) and (2). In this research study, we present an efficient numerical method, based on two-variable shifted Jacobi polynomials (SJPs), to approximate the solutions of (1) and (2) using operational matrices of fractional-order integration and product via shifted Jacobi collocation method. The main advantage of the proposed technique is that the problems under consideration are reduced to systems of linear or nonlinear algebraic equations. Then, the arising systems can be solved by the Newton method.
The outline of this paper is organized as follows. In Section 2, a review of fractional calculus and also one-variable SJPs is given. In Section 3, we introduce two-variable SJPs and then we derive operational matrices of fractional-order integration and product based on these polynomials. In Section 4, we explain the numerical solutions of 2D-NFVIEs and 2D-NFFIEs, respectively, by using what was introduced in Section 3. Also, in Section 5, the error bound and convergence analysis of the presented method are studied. Moreover, three test examples are given in Section 6 to demonstrate the effectiveness of the method. Finally, a conclusion is given in Section 7.
2 Preliminary knowledge
2.1 Fractional calculus
Definition 1 (Podlubony, 1999)
The Riemann–Liouville fractional integral of order is defined by where is the gamma function.
Definition 2 (Abbas and Benchohra, 2014)
The left-sided mixed Riemann–Liouville integral of order of f is defined by
2.2 One-variable SJPs and their properties
The one-variable SJPs are defined on the interval
by
with the following orthogonality property on the interval
:
where
is Kronecker delta,
is weight function, and
Another property of one-variable SJPs is as follows:
3 Two-variable SJPs and their operational matrices of fractional-order integration and product
3.1 Two-variable SJPs and function approximation
The two-variable SJPs are defined on the domain by for i,j = 0,1,2,…,N, with the following orthogonality property on the domain : where is weight function.
A two-variable continuous function
in the domain
can be approximated by using the two-variable SJPs as follows:
3.2 Operational matrices of fractional-order integration
Khalil and Khan (2014) defined an operational matrix of one-dimensional integration of fractional order in the Riemann–Liouville sense by with the entries where .
Let
and
be the vector of two-variable SJPs defined in (6). Then
Since , we have
Let
. Suppose that
is the vector of two-variable SJPs defined in (6). Then, we have
From the definition of one-variable SJPs, we have
3.3 Operational matrix of product
Let
be the vector of two-variable SJPs defined in (6). Borhanifar and Sadri (2016) obtained the operational matrix of product for
. In a similar way, we can compute this operational matrix for
as follows:
4 The method of solution
In this section, we use two-variable SJPs and their operational matrices for solving Eqs. (1) and (2).
4.1 The method for 2D-NFVIEs
Here, we are going to convert Eq. (1) to a nonlinear system by using two-variable SJPs. First, we can write
4.2 The method for 2D-NFFIEs
Now we want to convert Eq. (2) to a nonlinear system by using the two-variable SJPs. For this purpose, we apply (5), (7), (9)–(13) in (2) and therefore we obtain
So, we have
5 Error bound for the approximation
Let and the weighted space be the space of square integrable functions in . To verify the convergence of the presented method first we define the following inner product and norm on :
Let
be the finite-dimensional polynomial space. Suppose that
If
be the best approximate solution from N to
and
be the Taylor expansion of
, then
By considering the Taylor expansion of gabout , we have Therefore, we obtain where , and is defined in (17). Since is the best approximation to g, we have Now we can take the square roots and therefore we conclude the proof of the theorem. □
Suppose that
for 0⩽i1⩽N,0⩽i2⩽i1,0⩽i3⩽i2,0⩽i4⩽i3. If
be the best approximate solution to
obtained by the proposed method and
be the Taylor expansion of
, then
By considering the Taylor expansion of about , we have Therefore, we obtain where , and is defined in (19). Since is the best approximation to k, we have Now we can take the square roots and therefore the proof is completed. □
Let be the exact solution of Eq. (2) and be its approximate solution obtained by the presented method. Suppose that for the following assumptions hold:
-
and ,
-
There exists a Lipschitz constant such that ,
-
,
-
.
Considering the two-variable SJPs expansions of
and
leads to
It is clear that
Obviously the right hand side of the inequality (20) tends to zero as , so and this proves convergence of the proposed method.
For the 2D-NFVIE, since , we can use similar way which has been used in Theorem 5.
6 Illustrative examples
Here, three test examples are presented by using Maple 2018 software to examine numerical results of the proposed method. In all of this section, denotes the number of bases that used for solving these problems. To show the accuracy and computational efficiency of our method, we use and which are, respectively, the absolute errors in the solutions and the maximum absolute errors, where points are roots of two-variable SJPs in the domain for different values of and .
Also, graphs of maximum absolute errors are plotted by using where points are roots of one-variable SJPs in the interval .
Consider the following 2D-NFFIEs studied by Najafalizadeh and Ezzati (2016): with the exact solution .
Tables 1 and 2, respectively, report the exact and approximate solutions and also absolute errors in the solutions at selected points in the domain with and . Also, Table 3 report the maximum absolute errors with and different values of and . From these tables, we see that by using numbers of two-variable SJPs, we obtain more accurate results than the methods reported in Hesameddini and Shahbazi (2018), Maleknejad et al. (2020a) and Najafalizadeh and Ezzati (2016) that respectively used 2D-SLPOM, 2D-HBPSLs, and 2D-BPFs for solving this problem. Figs. 1 and 2 illustrate the efficiency and accuracy of our method.
Consider the following 2D-NFVIEs studied by Najafalizadeh and Ezzati (2016): with the exact solution . Tables 4 and 5, respectively, report the exact and approximate solutions and also absolute errors in the solutions at selected points in the domain with and . Also, Table 6 report the maximum absolute errors with and different values of and . From these tables, we see that by using numbers of two-variable SJPs, we obtain more accurate results than the methods reported in Mirzaee and Samadyar (2019) and Najafalizadeh and Ezzati (2016) that respectively used 2D-OBPs and 2D-BPFs for solving this problem. Figs. 3 and 4 illustrate the efficiency and accuracy of our method.
Consider the following 2D-NFFIEs studied by Maleknejad et al. (2020a): where The exact solution of this equation is . Note that .
Tables 7 and 8, respectively, report the exact and approximate solutions and also absolute errors in the solutions at selected points in the domain with and . Also, Table 9 report the maximum absolute errors with and different values of and . From these tables, we see that by using numbers of two-variable SJPs, we obtain more accurate results than the method reported in Maleknejad et al. (2020a) that used 2D-HBPSLs for solving this problem. Figs. 5 and 6 illustrate the efficiency and accuracy of our method.
| Exact solution | Present method | 2D-HBPSLs method | 2D-SLPOM method | 2D-BPFs method | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ||||||
| Max error | 0 | ||||||||
| Present method | 2D-HBPSLs method | 2D-BPFs method | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ||||
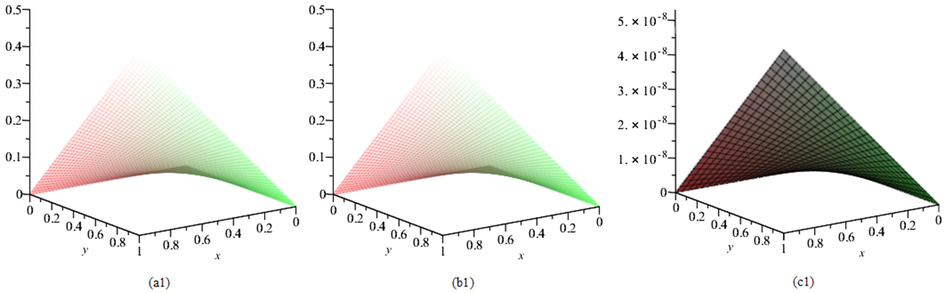
- Plots of: (a1) the exact solution, (b1) the approximate solution, (c1) the absolute error with
and
for Example 1.
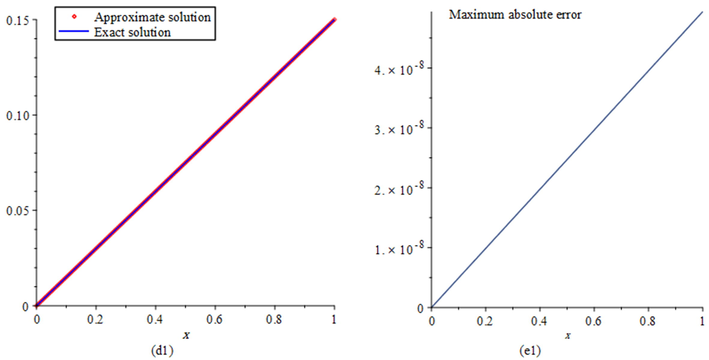
- Plots of: (d1) the comparison of the exact and approximate solutions, (e1) the maximum absolute error at
with
and
for Example 1.
| Exact solution | Present method | 2D-OBPs method | 2D-BPFs method | ||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | ||||||
| Max error | 0 | ||||||
| Present method | 2D-OBPs method | 2D-BPFs method | ||||
|---|---|---|---|---|---|---|
| 0 | ||||||
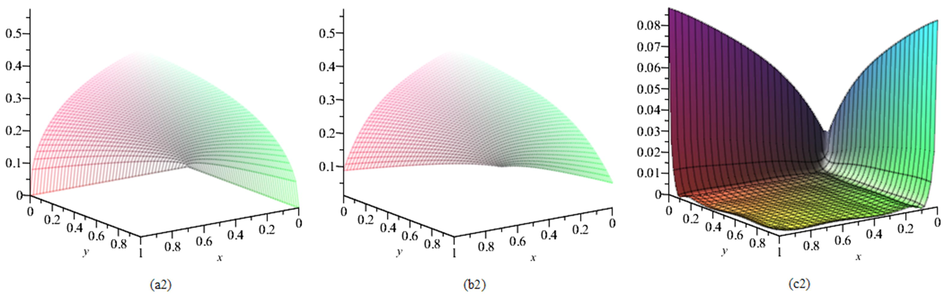
- Plots of: (a2) the exact solution, (b2) the approximate solution, (c2) the absolute error with
and
for Example 2.
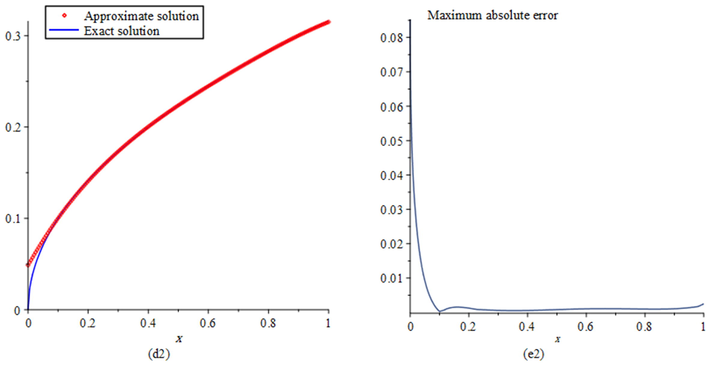
- Plots of: (d2) the comparison of the exact and approximate solutions, (e2) the maximum absolute error at
with
and
for Example 2.
| Exact solution | Present method | 2D-HBPSLs method | |||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | ||||||
| 1 | 1 | ||||||
| Max error | 0 | ||||||
| Present method | 2D-HBPSLs method | |||||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | ||||||
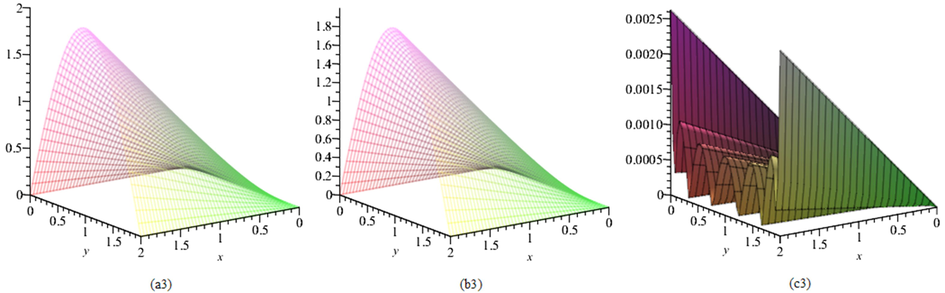
- Plots of: (a3) the exact solution, (b3) the approximate solution, (c3) the absolute error for
for Example 3.
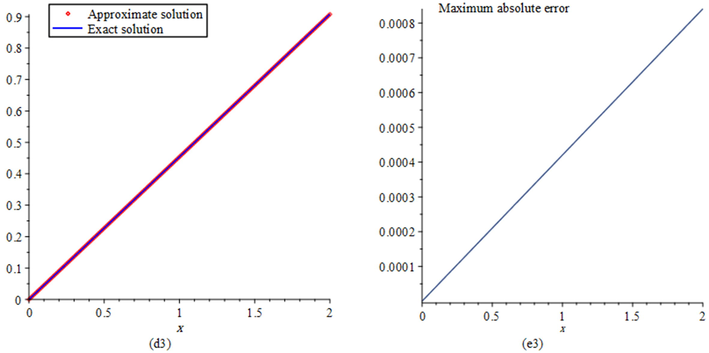
- Plots of: (d3) the comparison of the exact and approximate solutions, (e3) the maximum absolute error for
at
for Example 3.
7 Conclusion
In this paper, we derived new operational matrices of fractional-order integration and product based on two-variable shifted Jacobi polynomials. These operational matrices utilized for solving the two-dimensional nonlinear fractional Fredholm and Volterra integral equations. Also, the error bound and convergence analysis for the proposed method were discussed. Moreover, the proposed method was evaluated by solving three numerical examples. Throughout the experimental examples, one can observe that the small size of operational matrices and basis functions are required to obtain a favorable approximate solution. The operational matrices obtained in this paper can be useful for numerically solving problems involving the left-sided mixed Riemann–Liouville integral operator of fractional order.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Fractional order integral equations of two independent variables. Applied Mathematics and Computation. 2014;227:755-761.
- [Google Scholar]
- A new solution method for nonlinear fractional integro-differential equations. American Institute of Mathematical Sciences. 2015;8(6):1065-1077.
- [Google Scholar]
- Analytical solutions of the spacetime fractional derivative of advection dispersion equation. Mathematical Problems in Engineering. 2013;2013:9.
- [CrossRef] [Google Scholar]
- A possible generalization of acoustic wave equation using the concept of perturbed derivative order. Mathematical Problems in Engineering. 2013;2013:6.
- [CrossRef] [Google Scholar]
- Application of a fractional advection-dispersion equation. Water Resources Research. 2000;36(6):1403-1412.
- [Google Scholar]
- A generalized operational method for solving integro-partial differential equations based on Jacobi polynomials. Hacettepe Journal of Mathematics and Statistics. 2016;45(2):311-335.
- [Google Scholar]
- Linear models of dissipation whose Q is almost frequency independent-part II. Geophysical Journal International. 1967;13(5):529-539.
- [Google Scholar]
- Fractals and Fractional Calculus in Continuum Mechanics. New York: Springer-Verlag; 1997. p. :223-276.
- A Fourier method for the fractional diffusion equation describing sub-diffusion. Journal of Computational Physics. 2007;227(2):886-897.
- [Google Scholar]
- A generalised groundwater flow equation using the concept of non-integer order derivatives. Water SA. 2006;32(1):55-78.
- [Google Scholar]
- Two-dimensional shifted Legendre polynomials operational matrix method for solving the two-dimensional integral equations of fractional order. Applied Mathematics and Computation. 2018;322:40-54.
- [Google Scholar]
- A new operational matrix for solving two-dimensional nonlinear integral equations of fractional order. Cogent Mathematics. 2017;4(1):1347017.
- [CrossRef] [Google Scholar]
- Khalil, H., Khan, R.A., 2014. The use of Jacobi polynomials in the numerical solution of coupled system of fractional differential equations, International Journal of Computer Mathematics, doi: 10.1080/00207160.2014.945919.
- Effect of Hall current and wall conductance on hydromagnetic natural convection flow between vertical walls. International Journal of Industrial Mathematics.. 2017;9(4):289-299.
- [Google Scholar]
- Effect of Hall current on the magnetohydrodynamic free convective flow between vertical walls with induced magnetic field. European Physical Journal Plus. 2018;133:207.
- [CrossRef] [Google Scholar]
- Influence of heat source/sink on MHD flow between vertical alternate conducting walls with Hall effect. Physica A. 2020;544:123562
- [CrossRef] [Google Scholar]
- Numerical solution of fractional integro-differential equations by a hybrid collocation method. Applied Mathematics and Computation. 2013;219:6750-6760.
- [Google Scholar]
- Fractional calculus: Some basic problems in continuum and statistical mechanics. In: Carpinteri A., Mainardi F., eds. Fractals and Fractional Calculus in Continuum Mechanics. New York: Springer; 1997. p. :291-348.
- [Google Scholar]
- Numerical solution of three-dimensional Volterra-Fredholm integral equations of the first and second kinds based on Bernstein’s approximation. Applied Mathematics and Computation. 2018;339:272-285.
- [Google Scholar]
- Operational matrices based on hybrid functions for solving general nonlinear two-dimensional fractional integro-differential equations. Computational and Applied Mathematics. 2020;39(2):1-34.
- [CrossRef] [Google Scholar]
- Existence, uniqueness, and numerical solutions for two-dimensional nonlinear fractional Volterra and Fredholm integral equations in a Banach space. Computational and Applied Mathematics. 2020;39(4):1-22.
- [CrossRef] [Google Scholar]
- Numerical solutions of distributed order fractional differential equations in the time domain using the Müntz-Legendre wavelets approach. Numer Methods Partial Differential Eq.. 2021;37(1):707-731.
- [CrossRef] [Google Scholar]
- Finite difference approximations for fractional advection-dispersion flow equations. Journal of Computational and Applied Mathematics. 2004;172(1):65-77.
- [Google Scholar]
- Relaxation in filled polymers: A fractional calculus approach. Journal of Chemical Physics. 1995;103:7180-7186.
- [Google Scholar]
- Numerical solution of nonlinear partial quadratic integro-differential equations of fractional order via hybrid of block-pulse and parabolic functions. Numerical Methods for Partial Differential Equations. 2018;35(3):1134-1151.
- [Google Scholar]
- Solving two-dimensional nonlinear quadratic integral equations of fractional order via operational matrix method. Multidiscipline Modeling in Materials and Structures. 2019;15(6):1136-1151.
- [Google Scholar]
- Fractional-order orthogonal Bernstein polynomials for numerical solution of nonlinear fractional partial Volterra integro-differential equations. Mathematical Methods in the Applied Sciences. 2019;42(6):1870-1893.
- [Google Scholar]
- Convergence of 2D-orthonormal Bernstein collocation method for solving 2D-mixed Volterra-Fredholm integral equations. Transactions of A. Razmadze Mathematical Institute. 2018;172(3):631-641.
- [Google Scholar]
- Application of hat basis functions for solving two-dimensional stochastic fractional integral equations. Computational and Applied Mathematics. 2018;37(4):4899-4916.
- [Google Scholar]
- Numerical solution based on two-dimensional orthonormal Bernstein polynomials for solving some classes of two-dimensional nonlinear integral equations of fractional order. Applied Mathematics and Computation. 2019;344–345:191-203.
- [Google Scholar]
- A numerical approach for solving weakly singular partial integro-differential equations via two-dimensional-orthonormal Bernstein polynomials with the convergence analysis. Numerical Methods for Partial Differential Equations. 2018;35(2):615-637.
- [Google Scholar]
- Maleknejad, K., Rashidinia, J., Eftekhari, T., 2020. A new and efficient numerical method based on shifted fractional-order Jacobi operational matrices for solving some classes of two-dimensional nonlinear fractional integral equations, submitted to Numer Methods Partial Differential Eq.
- Mohammed, D. Sh., 2014. Numerical solution of fractional integro-differential equations by least squares method and shifted Chebyshev polynomial. Mathematical Problems in Engineering, 2014, Article ID 431965, 5 pages. doi: 10.1155/2014/431965.
- Numerical methods for solving two-dimensional nonlinear integral equations of fractional order by using two-dimensional block pulse operational matrix. Applied Mathematics and Computation. 2016;280:46-56.
- [Google Scholar]
- Legendre wavelet collocation method combined with the Gauss-Jacobi quadrature for solving fractional delay-type integro-differential equations. Applied Numerical Mathematics. 2020;149:99-112.
- [Google Scholar]
- The Fractional Calculus. New York, London: Academic Press; 1974.
- Fractional Differential Equations. San Diego: Academic Press; 1999.
- Numerical scheme for solving singular fractional partial integro-differential equation via orthonormal Bernoulli polynomials. International Journal of Numerical Modelling. 2019;32(6):e2652
- [Google Scholar]
- Analysis for fractional dynamics of Ebola virus model. Chaos Solitons & fractals. 2020;138:109992
- [Google Scholar]
- Numerical simulation for fractional delay differential equations. International Journal of Dynamic and Control 2020
- [CrossRef] [Google Scholar]
- Numerical Simulation for Fractional-Order Bloch Equation Arising in Nuclear Magnetic Resonance by Using the Jacobi Polynomials. Applied Science. 2020;10:2850.
- [Google Scholar]
- Solving non-linear fractional variational problems using Jacobi polynomials. Mathematics. 2019;7:224.
- [Google Scholar]
- Legendre spectral method for the fractional Bratu problem. Mathematical Methods in the Applied Sciences. 2020;43(9):5941-5952.
- [CrossRef] [Google Scholar]
- An immersed finite element method with integral equation correction. International Journal for Numerical Methods in Engineering. 2010;86:93-114.
- [Google Scholar]
- Magnetohydrodynamic flow in horizontal concentric cylinders. International Journal of Industrial Mathematics. 2019;11(2):89-98.
- [Google Scholar]
- An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equations. SIAM Journal on Numerical Analysis. 2005;42(5):1862-1874.
- [Google Scholar]
- Numerical methods for the variable-order fractional advection-diffusion equation with a nonlinear source term. SIAM Journal on Numerical Analysis. 2009;47:1760-1781.
- [Google Scholar]







