Nonlinear optimization in bi-level selective maintenance allocation problem

1 Introduction

Nowadays, engineers design highly complex systems to function reasonably without failure for some time and meet their functional requirements. The absence of complete failure of the system components during its mission cannot be guaranteed. However, its reliability can be measured and ascertain based on the operational lifetime. The reliability of a system component is its failure-free probability during the operational face up to a specific period under certain conditions. Recently, this area is receiving attention from several researchers because of its importance in all real-life operational systems such as manufacturing, transportation, power, telecommunication, and exploration Rausand (2014) and Muhuri et al. (2019).

Several systems have different configurations, and maximizing their overall performance requires Reliability Optimization (RO). The RO problems are of three categories (i) “redundancy allocation problem (RAP)”, (ii) “reliability allocation problem”, and (iii) “Reliability-Redundancy Allocation Problem (RRAP)” Modibbo et al. (2021).The RO has a different view regarding the system structure, which could be series, parallel, series–parallel, k-out-of n system, etc. The Reliability Block Diagram (RBD) of some system structures is shown in Fig. 1.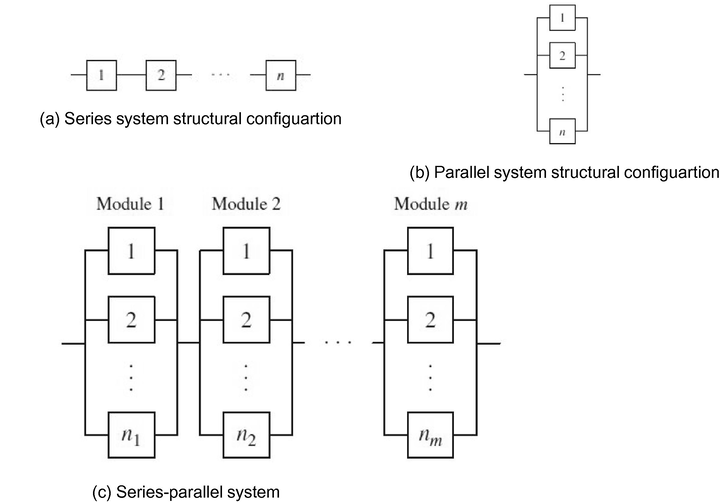

Close

Fig. 1

Some systems structural configuration.

Export to PPT

The importance of reliability and maintenance theory is significantly increasing in recent times. Engineers, scientists, researchers and industrial managers realized the importance of this topic now more than anytime in history, especially with the advent of advanced technology and soft-computing power. A reliable system optimizes cost and guarantees a design for high-quality products. As a result, it optimizes profit, increases product durability and market acceptability.

Most of the researches in RO concentrate on single optimization of the system reliability; however, there is no significant attention to Bi-level Optimization (BO) of the problem, and the problem can perfectly fit bi-level optimization. Motivated by this fact, this study seeks to present a BO in addressing the selective maintenance allocation problem in RO using bi-level programming. There are many real-life situations where decision-making takes place at levels. In BO, it involves only two levels-the upper and lower. Each level may have a different objective function with decision space in part of the other levels.

Additionally, one level‘s decision may influence the decisions at the other levels; as a result, the objective function of the other level improves. For instance, allocating resources or selective maintenance of some lower components of a system may directly confer benefits on the other levels of the system. The common feature of these systems is that they have an interactive decision-making unit within their structure hierarchically. Each lower-level subsystem executes its function after and following the upper-level subsystem actions. Each subsystem optimizes its reliability independently with other subsystems but may be affected by the performance of those subsystems. The decision-makers problem‘s external effect reflects both the objective function and the feasible solution sets. These processes and procedures are well-explained in Section 3.1. The related literature is reviewed in the following section, and the research gap is established.

2 Literature review and research gap

Several studies use the concept of bi-level programming in different sectors. For instance, Sadati et al. (2013) uses BLPP to optimize the random portfolio under a fuzzy environment based on possibility and necessity models. They used newly generated stock market information to calculate the objective function’s upper bound (level) while the lower level is calculated based on historical data. Kornai et al. (1965) applied the concept as a two-level planning problem in game-theoritical model involving two players’ team. Similarly, Bialas et al. (1984) formulated BLPP to decentralized planning as a decision-making process with geometric characteristics and algorithms. Nath et al. (2017), Muhuri et al. (2019) and Sinha et al. (2014) studied a reliability redundancy allocation problem of a series–parallel system and formates a mixed-integer non-linear model based on the bi-level programming concept-the solution to the optimization problem obtained with the help of an evolutionary algorithm using quadratic approximations. In the study, they considered two objective functions as reliability weight and cost.

Nath et al. (2019) conducted similar research to study the effect of “BrainStorm Optimization Algorithm (BSOA) and ”Brainstorm Optimization algorithm in Objective Space (BSOA-OS)”. The study compares these algorithms with ”genetic algorithm (GA) and self-organizing migrating algorithm (SOMA)” and concluded that BSO-OS converges faster. Most recently, Ghasemi et al. (2021) formulated a bi-level mathematical model in response to the COVID-19 pandemic for logistic management considering the evolutionary game with environmental feedback. Similarly, Li et al. (2021) proposed a stochastic bi-level model for the facility location and protection problem having a probabilistic interdiction strategy. Candler et al. (1982) formulated a Stackelberg game as a linear two-level programming problem where the first player optimizes his objective function. However, the constraints are under the control of the second player. The study uses a necessary condition to show that a local optimum exists in the game. Sakawa et al. (2012) extended the Stackelberg solution to consider decision-makers fuzzy goals in a randomized fashion and solve the problem via maximizing the probability with possibility.Gupta et al. (2018) also applied a bi-level concept in studying supply chain network order allocation problem under fuzziness. The authors formulated the problem as multi-objective bi-level optimization. Fortuny-Amat et al. (1981) presented an economic interpretation of a two-level programming problem in which the Khun-Tucker conditions replace the lower level problem and transformed using mixed-integer quadratic programming problem exploring and demonstrating the complementary slackness conditions. Sakawa et al. (2002) formulated decentralized BLPP using an interactive fuzzy programming approach. Similarly, Wen et al. (1990) formulated BLPP in which the yes or no high-level decision-makers control combined with the real-valued lower-level decision control as a mixed-integer programming problem. The study provides both exact and heuristics algorithms for solving such models.

Christiansen et al. (2001) developed a bi-level stochastic model to optimize the cost of a structural topology design problem. The study considered a trust topology under unilateral frictionless contact and when the load conditions data are uncertain. The scenario is one in which structural failure can only lead to reconstruction cost and not loss of life. Casas-Ramírez et al. (2018) applied the bi-level programming concept in facility location problem. The model comprises minimizing the facility cost of location and distribution by the company, which serve as the upper-level problem and maximize the facility preference by customers, which serve as the lower level problem. The cross-entropy method and the randomized greedy algorithm are used to solve the model. Wen et al. (1991) presents a comprehensive review of the BLPP applied to government policies, agriculture, economic system, financial model and transportation; however, it does not consider reliability areas. The study also analysed the geometric properties of the linear BLPP and outlined the approaches used in solving BLPP, such as vertex enumeration and its variants and the Khun-Tucker approach.

Recently, Kamal et al. (2021) studied a selective maintenance problem under a neutrosophic condition, where the authors formulated the model with fuzzy parameters. They considered a replaceable and repairable component of the system and optimized the reliability. Of all the literature on BLPP, only very few applied in reliability optimization. None of them uses the Khun-Tucker optimality conditions in maximizing the reliability of a series–parallel system. Hence, this paper aims to bridge the existing gap by demonstrating the applicability of BLPP using the Khun-Tucker approach. Therefore, the research contributes to the bank of reliability literature concerning the methodologies and techniques.

3 Methodology

This section presents an overview of the philosophy, concepts, origin and mathematical model of BLPP. It also discusses the concept of the Khun-Tucker optimality conditions as a solution approach to a BLPP. The following section discusses the BLPP.

3.1

3.1 Bi-level programming problem

The BLPP is a two-person non-zero-sum game in which the first player can influence but not control the action of the second. The BLPP is a model for a leader–follower game in which the two players try to maximize (or minimize) their objective functions. The BLPP has been developed and studied by many authors including Bialas et al. (1982), Bialas et al. (1984); Candler et al. (1982), Wen et al. (1990), Wen et al. (1991), Bard (1984) and Bard (1983). According to Nath et al. (2019), the concept is divided into two optimization levels- upper-level decision making (ULDM) and lower-level decision making (LLDM) [see Fig. 2]. At each level, decisions are taken independently; however, actions and inactions of LLDM may affect the decision-making process as a result of dissatisfaction with the ULDM outcomes. In other words, LLDM obtained its optimal solutions which satisfy its constraints as a result, create a feasible region for the ULDM who eventually make decision with its own characteristics variables with the feasible solution space created by the LLDM units.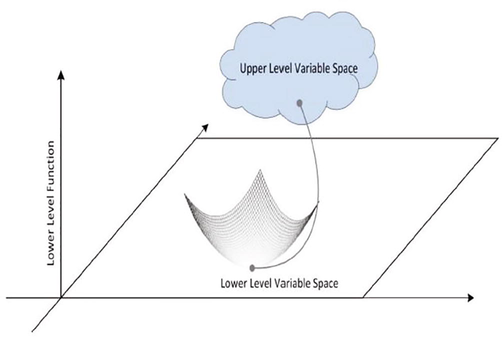

Close

Fig. 2

Overview of bi-level optimization.

Export to PPT

Outline required to construct the BLPP.

1. There exist interacting decision-making units within a predominantly hierarchical structure.

2. The execution of decisions is sequential from higher to lower levels. The lower level decision maker executes its policies after and based on the decision of the higher levels.

3. Each decision-making unit optimizes its objective function independently of other units but is affected by the actions and reactions of other units.

4. The external effect on a decision-makers problem can be reflected in both his objective function and his set of feasible decisions. see Fig. 3.

Close

Fig. 3

Constraint diagram for inequality optimization problems.

Export to PPT

Further, assume that there are two levels in a hierarchy with higher and lower level decision-makers. Let a vector of decision variables $(x,y)\in {\mathbb{R}}^{\mathbb{n}}$ be partitioned among the two planners. The higher-level decision maker has control over the vector ${\mathbb{R}}^{{\mathbb{n}}_{\mathbb{1}}}$ , and the lower-level decision-maker has control over the vector ${\mathbb{R}}^{{\mathbb{n}}_{\mathbb{2}}},{\mathbb{n}}_{\mathbb{1}}+{\mathbb{n}}_{\mathbb{2}}=\mathbb{n}$ . Furthermore, assuming that $$F,f:{\mathbb{R}}^{{\mathbb{n}}_{\mathbb{1}}}\times {\mathbb{R}}^{{\mathbb{n}}_{\mathbb{2}}}\in {\mathbb{R}}^{\mathbb{n}}$$ are convex and bounded, the non-linear BLPP can mathematically be stated as follows:

(1)

$$\begin{array}{c}{P}_1:{\max }_{x}F(x,y),\mathit{where}y\mathit{solves}\hfill \\ P_2:{\max }_{y}f(x,y),\hfill \\ \mathit{subject}\mathit{to}:\hfill \\ \mathit{Ax}+\mathit{By}⩽r\hfill \end{array}$$

Where $x\in {\mathfrak{R}}^{n_1}$ is a vector of leader’s problem variables, $y\in {\mathfrak{R}}^{n_2}$ vector of follower’s problem, $r\in {\mathfrak{R}}^m,A$ is a $m\times n_1$ matrix, B is a $m\times n_2$ matrix, and $F(x,y)$ and $f(x,y)$ are convex functions. Let S denotes the problem constraint region

(2)

$$S=\left\{(x,y)|\mathit{Ax}+\mathit{By}\right\}$$

Hence for each value of x, the lower level will react with a corresponding value of y. This induces a functional relationship between the decisions of the leader and the reactions of the follower. For a given x, let $Y\left(x\right)$ denote the set of the optimal solution to the inner problem $P_2$ ,

(3)

$${\max }_{y\in Q\left(x\right)}\stackrel{\sim }{f}\left(y\right)=\mathit{dy},\mathit{where}Q\left(x\right)=\left\{y|\mathit{By}⩽b-\mathit{Ax}\right\}$$

And ${\mathbf{\Psi }}_f\left(S\right)$ represent the higher-level decision-makers solution space or the set of the rationale of the f over S, as

(4)

$${\mathbf{\Psi }}_f\left(S\right)=\left\{(x,y)\left|\right(x,y)\in S,y\in Y(x)\right\}$$

We assume that S is closed, bounded and non-empty with $Q\left(x\right)$ as bounded and non-empty and a unique solution exists for $P_2$ for any feasible x. The definitions of feasibility and optimality for the BNLPP are then given by the following:

Definition 1

A point $(x,y)$ is called feasible if $(x,y)\in {\mathbf{\Psi }}_f\left(S\right)$ .

Definition 2

A feasible point $(x^{\ast },y^{\ast })$ is called optimal if $F^{\ast }(x,y)$ is unique for all $y^{\ast }\in Y\left(x^{\ast }\right)$ and $F^{\ast }(x,y)⩾F(x,y)$ for all feasible pairs $(x,y)\in {\mathbf{\Psi }}_f\left(S\right)$ .

Thus the BLPP can mathematically be formulated as:

(5)

$$\begin{array}{c}{P}_1:{\max }_{x}F(x,y),\mathit{where}y\mathit{solves}\hfill \\ P_2:{\max }_{y}f(x,y),\hfill \\ \mathit{subject}\mathit{to}:\hfill \\ \mathit{Ax}+\mathit{By}⩽r\hfill \\ x,y⩾0\hfill \end{array}$$

4 Bi-level Selective Maintenance Allocation Problem

Now, suppose we encounter a reliability problem of a system consisting of subsystems where it is given that a certain subsystem must be given priority over other subsystems and has control over a particular repairable component. In that case, the problem can be solved using BLPP.

Let us consider a reliability problem of a system consisting of two subsystems where the reliability of one subsystem is given priority over the other and controls specific repairable components. This way, the reliability problem can be solved by a bi-level programming problem of which two cases can be formed:

$R_1$ is the reliability of first subsystem.

$R_2$ is the reliability of second subsystem.

$d_1$ is the first repairable component and.

$d_2$ is the second repairable component.

• Case 1: Here $R_1$ is given priority over $R_2$ .

  $R_1$ is the reliability of the first subsystem that is considered as the leader’s problem where $d_2$ solves.

  (16)

  $$\begin{array}{c}{\displaystyle \underset{d_1}{\max }}{R}_1=\left\{1-{(1-r_1)}^{n_1-a_1+d_1}\right\}\mathit{where}{d}_2\mathit{solves}\hfill \\ {\displaystyle \underset{d_2}{\max }}{R}_2=\left\{1-{(1-r_2)}^{n_2-a_2+d_2}\right\}\hfill \\ \hfill & \hfill \\ \mathit{subject}\mathit{to}:\hfill \\ {\displaystyle \sum _{i=1}^m}{t}_i{d}_i⩽T_o\hfill \\ {\displaystyle \sum _{i=1}^m}{c}_i{d}_i⩽C_o\hfill \\ \mathit{and}0⩽d_i⩽a_i,i=1,2,\mathit{and}\mathit{integers}\text{.}\hfill \end{array}$$

• Case 2: Here $R_2$ is given priority over $R_1$ .

  $R_2$ is the reliability of the second subsystem that is considered as the leader’s problem where $d_1$ solves.

  (17)

  $$\begin{array}{c}{\displaystyle \underset{d_2}{\max }}{R}_2=\left\{1-{(1-r_2)}^{n_2-a_2+d_2}\right\}\mathit{where}{d}_1\mathit{solves}\hfill \\ {\displaystyle \underset{d_1}{\max }}{R}_1=\left\{1-{(1-r_1)}^{n_1-a_1+d_1}\right\}\hfill \\ \hfill & \hfill \\ \mathit{subject}\mathit{to}:\hfill \\ {\displaystyle \sum _{i=1}^m}{t}_i{d}_i⩽T_o\hfill \\ {\displaystyle \sum _{i=1}^m}{c}_i{d}_i⩽C_o\hfill \\ \mathit{and}0⩽d_i⩽a_i,i=1,2,\mathit{and}\mathit{integers}\text{.}\hfill \end{array}$$

• Procedure In the Kuhn-Tucker approach, the rational reaction set of the follower is replaced by Kuhn-Tucker optimality conditions. The leader takes into account the follower’s optimality conditions while solving its own problem. Thus, by taking the Kuhn-Tucker transformation to the inner problem, we get the resulting equivalent problem. Consider non-linear bi-level programming problem Eq. (16), and apply the K-T conditions on the inner problem $${\displaystyle \underset{d_2}{\max }}{R}_2=\left\{1-{(1-r_2)}^{n_2-a_2+d_2}\right\}$$ subject to the same set of constarints. Here the objective is nonlinear whereas the constarints are linear. The necessary and sufficient K-T conditions for the above problem can be obtain as:

  (18)

  $$\begin{array}{c}\varphi (d,\lambda )=\left\{1-{(1-r_2)}^{n_2-a_2+d_2}\right\}+\hfill \\ {\lambda }_1(T_o-t_1{d}_1-t_2{d}_2)+\hfill \\ {\lambda }_2(C_o-c_1{d}_1-c_2{d}_2)+{\lambda }_3(a_1-d_1)+{\lambda }_4(a_2-d_2)\hfill \\ {\nabla }_{\underline{d}}\varphi (\underline{d},\underline{\lambda })=\hfill \\ \left[\begin{array}{c}-{\lambda }_1{t}_1-{\lambda }_2{c}_1-{\lambda }_3\hfill \\ -\log (1-r_2){(1-r_2)}^{n_2-a_2+d_2}-{\lambda }_1{t}_2-{\lambda }_2{c}_2-{\lambda }_4\hfill \end{array}\right]\hfill \\ ⩽0\hfill \\ \underline{d\prime }{\nabla }_{\underline{d}}\varphi (\underline{d},\underline{\lambda })=d_1(-{\lambda }_1{t}_1-{\lambda }_2{c}_1-{\lambda }_3)+\hfill \\ d_2(-\log (1-r_2){(1-r_2)}^{n_2-a_2+d_2}-{\lambda }_1{t}_2-{\lambda }_2{c}_2-{\lambda }_4)\hfill \\ =0\hfill \\ {\nabla }_{\underline{\lambda }}\varphi (\underline{d},\underline{\lambda })=\left[\begin{array}{c}{T}_o-t_1{d}_1-t_2{d}_2\hfill \\ C_o-c_1{d}_1-c_2{d}_2\hfill \\ a_1-d_1\hfill \\ a_2-d_2)\hfill \end{array}\right]⩾0\hfill \\ \lambda \prime {\nabla }_{\underline{\lambda }}\varphi (\underline{d},\underline{\lambda })=\hfill \\ {\lambda }_1(T_o-t_1{d}_1-t_2{d}_2)+\hfill \\ {\lambda }_2(C_o-c_1{d}_1-c_2{d}_2)+{\lambda }_3(a_1-d_1)+\hfill \\ {\lambda }_4(a_2-d_2)=0\hfill \\ \underline{d}⩾0,\underleftarrow{\lambda }⩾0\text{.}\hfill \end{array}$$

  Now using slack and surplus variables in the above Eq. (18), we get the KT conditions in light of Eqs. (6)–(10). $$\begin{array}{c}-{\lambda }_1{t}_1-{\lambda }_2{c}_1-{\lambda }_3+u_1=0\hfill \\ \mathit{or}{u}_1={\lambda }_1{t}_1+{\lambda }_2{c}_1+{\lambda }_3=-{\nabla }_{d_1}\varphi (\underline{d},\underline{\lambda })\hfill \\ \mathit{or}{d}_1{u}_1=-\left[{\nabla }_{d_1}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ -\log (1-r_2){(1-r_2)}^{n_2-a_2+d_2}\hfill \\ -{\lambda }_1{t}_2-{\lambda }_2{c}_2-{\lambda }_4+u_2=0\hfill \\ \mathit{or}{d}_2{u}_2=-\left[{\nabla }_{d_2}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ T_o-t_1{d}_1-t_2{d}_2-s_1=0\mathit{or}{t}_1{d}_1+t_2{d}_2+s_1=T_o\hfill \\ \mathit{or}{s}_1=T_o-t_1{d}_1-t_2{d}_2\mathit{or}{s}_1=\left[{\nabla }_{{\lambda }_1}\varphi (\underline{d},\underline{\lambda })\right]\hfill \\ \mathit{or}{\lambda }_1\prime s_1={\lambda }_1\prime \left[{\nabla }_{{\lambda }_1}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ C_o-c_1{d}_1-c_2{d}_2-s_2=0\mathit{or}{c}_1{d}_1+c_2{d}_2+s_2=C_o\hfill \\ \mathit{or}{\lambda }_2\prime s_2={\lambda }_2\prime \left[{\nabla }_{{\lambda }_2}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ a_1-d_1-s_3=0\mathit{or}{d}_1+s_3=a_1\hfill \\ \mathit{or}{\lambda }_3\prime s_3={\lambda }_3\prime \left[{\nabla }_{{\lambda }_3}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ a_2-d_2-s_4=0\mathit{or}{d}_2+s_4=a_2\hfill \\ \mathit{or}{\lambda }_4\prime s_4={\lambda }_4\prime \left[{\nabla }_{{\lambda }_4}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ d,\lambda ,u,s,⩾0\hfill \end{array}$$

  Now the non-linear BLPP is converted into a single non-linear optimization problem is:

  (19)

  $$\begin{array}{c}{\displaystyle \underset{d_1}{\max }}{R}_1=\left\{1-{(1-r_1)}^{n_1-a_1+d_1}\right\}\hfill \\ \mathit{subject}\mathit{to}:\hfill \\ -{\lambda }_1{t}_1-{\lambda }_2{c}_1-{\lambda }_3+u_1=0\hfill \\ -\log (1-r_2){(1-r_2)}^{n_2-a_2+d_2}\hfill \\ -{\lambda }_1{t}_2-{\lambda }_2{c}_2-{\lambda }_4+u_2=0\hfill \\ t_1{d}_1+t_2{d}_2+s_1=T_o\hfill \\ c_1{d}_1+c_2{d}_2+s_2=C_o\hfill \\ d_1+s_3=a_1\hfill \\ d_2+s_4=a_2\hfill \\ d,\lambda ,u,s,⩾0\hfill \\ d_1\prime u_{=}{d}_2\prime u_2=0\hfill \\ {\lambda }_1\prime s_1={\lambda }_2\prime s_2={\lambda }_3\prime s_3={\lambda }_4\prime s_4=0\hfill \end{array}$$ It is clear that Eq. (19) comprises of the linear equations, the non-negativity restriction, and the complementary slackness condition of KKT, while the objective function is non-linear. Now, this resulting NLPP can be solved with a variety of techniques.

5 Numerical Example

Consider a system consisting of two subsystems. The available time between two production runs for repairing and replacing back the components is 30-time units. Let the given maintenance cost of the system be 50 units. The other parameters for the various subsystems are given in Table 1. These parameters can be estimated using the process described in Section 3.3.

To solve the above NLPP example, two cases of the problem formulated as follows:

• Case 1: Here $R_1$ is given priority over $R_2$ .

  $R_1$ is the reliability of the first subsystem that is considered as the leader’s problem where $d_2$ solves.

  (20)

  $$\begin{array}{c}{\displaystyle \underset{d_1}{\max }}{R}_1=\left\{1-{\left(0.1\right)}^{2+d_1}\right\}\mathit{where}{d}_2\mathit{solves}\hfill \\ {\displaystyle \underset{d_2}{\max }}{R}_2=\left\{1-{\left(0.15\right)}^{3+d_2}\right\}\hfill \\ \mathit{subject}\mathit{to}:\hfill \\ 3d_1+4d_2⩽30\hfill \\ 8d_1+7d_2⩽50\hfill \\ d_1⩽5\hfill \\ d_2⩽7\hfill \\ {\mathit{andd}}_1,d_2⩾0,\mathit{and}\mathit{integers}\text{.}\hfill \end{array}$$

Now non-linear BLPP Eq. (20) can be solved by the procedure discussed above as follows:

Consider the lower level problem as:

Now, applying the K-T conditions in Eq. (21), we get

Now using slack and surplus variables in the above Eq. (22), we get the KT conditions in light of Eqs. (6)–(10). $$\begin{array}{c}-3{\lambda }_1-8{\lambda }_2-{\lambda }_3+u_1=0,\mathit{or}{u}_1=3{\lambda }_1+8{\lambda }_2+{\lambda }_3\hfill \\ =-{\nabla }_{d_1}\varphi (\underline{d},\underline{\lambda })\hfill \\ \mathit{or}{d}_1\prime u_1=-\left[d_1\prime {\nabla }_{d_1}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ -\log \left(0.15\right){\left(0.15\right)}^{3+d_2}-4{\lambda }_1-7{\lambda }_2-{\lambda }_4+u_2=0\hfill \\ \mathit{or}{u}_2=\log \left(0.15\right){\left(0.15\right)}^{3+d_2}+4{\lambda }_1+7{\lambda }_2+{\lambda }_4\hfill \\ =-{\nabla }_{d_1}\varphi (\underline{d},\underline{\lambda })\hfill \\ \mathit{or}{d}_2\prime u_2=-\left[d_2\prime {\nabla }_{d_2}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ 30-3d_1-4d_2-s_1=0,\mathit{or}3d_1+4d_2+s_1=30\hfill \\ \mathit{or}{s}_1=30-3d_1-4d_2=\left[{\nabla }_{{\lambda }_1}\varphi (\underline{d},\underline{\lambda })\right]\hfill \\ \mathit{or}{\lambda }_1\prime s_1={\lambda }_1\prime \left[{\nabla }_{{\lambda }_1}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ 50-8d_1-7d_2-s_2=0,\mathit{or}8d_1+7d_2+s_2=50\hfill \\ s_2=50-8d_1-7d_2=\left[{\nabla }_{{\lambda }_2}\varphi (\underline{d},\underline{\lambda })\right]\hfill \\ \mathit{or}{\lambda }_2\prime s_2={\lambda }_2\prime \left[{\nabla }_{{\lambda }_2}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ 5-d_1-s_3=0,\mathit{or}{d}_1+s_3=5\hfill \\ \mathit{or}{\lambda }_3\prime s_3={\lambda }_3\prime \left[{\nabla }_{{\lambda }_3}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ 7-d_2-s_4=0,\mathit{or}{d}_2+s_4=7\hfill \\ \mathit{or}{\lambda }_4\prime s_4={\lambda }_4\prime \left[{\nabla }_{{\lambda }_4}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ d,\lambda ,u,s,⩾0\hfill \end{array}$$

Now we get the resulting single-level optimization problem as

Where I-II are the linear equations, III is the non-negativity restriction, IV is a complementary slackness condition, and the objective function is non-linear. Now, this resulting NLPP can be solved with a variety of techniques. We solve this problem with the help of a software called LINGO and get the optimal solution as $\max R_1=0.99999,d_1=5,\mathit{and}{d}_2=1$ .

• Case 2: Here $R_2$ is given priority over $R_1$ .

  $R_2$ is the reliability of the second subsystem that is considered as the leader’s problem where $d_1$ solves.

  (24)

  $$\begin{array}{c}{\displaystyle \underset{d_2}{\max }}{R}_2=\left\{1-{\left(0.15\right)}^{3+d_2}\right\}\mathit{where}{d}_1\mathit{solves}\hfill \\ {\displaystyle \underset{d_1}{\max }}{R}_1=\left\{1-{\left(0.1\right)}^{2+d_1}\right\}\hfill \\ \mathit{subject}\mathit{to}:\hfill \\ 3d_1+4d_2⩽30\hfill \\ 8d_1+7d_2⩽50\hfill \\ d_1⩽5\hfill \\ d_2⩽7\hfill \\ {\mathit{andd}}_1,d_2⩾0,\mathit{and}\mathit{integers}\text{.}\hfill \end{array}$$

Now non-linear BLPP (24) can be solved by the procedure discussed above as follows: Consider the lower level problem as:

Now, applying the K-T conditions in Eq. (25), we get

Now using slack and surplus variables in the above Eq. (26), we get $$\begin{array}{c}-\log \left(0.1\right){\left(0.1\right)}^{2+d_1}-3{\lambda }_1-8{\lambda }_2-{\lambda }_3+u_1=0\hfill \\ \mathit{or}{u}_1=\log \left(0.15\right){\left(0.15\right)}^{2+d_1}+3{\lambda }_1+8{\lambda }_2+{\lambda }_3\hfill \\ =-{\nabla }_{d_1}\varphi (\underline{d},\underline{\lambda })\hfill \\ \mathit{or}{d}_1\prime u_1=-\left[d_1\prime {\nabla }_{d_1}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ -4{\lambda }_1-7{\lambda }_2-{\lambda }_4+u_2=0\hfill \\ \mathit{or}{u}_2=4{\lambda }_1+7{\lambda }_2+{\lambda }_4=-{\nabla }_{d_2}\varphi (\underline{d},\underline{\lambda })\hfill \\ \mathit{or}{d}_2\prime u_2=-\left[d_2\prime {\nabla }_{d_2}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ 30-3d_1-4d_2-s_1=0\mathit{or}3d_1+4d_2+s_1=30\hfill \\ \mathit{or}{s}_1=30-3d_1-4d_2=\left[{\nabla }_{{\lambda }_1}\varphi (\underline{d},\underline{\lambda })\right]\hfill \\ \mathit{or}{\lambda }_1\prime s_1={\lambda }_1\prime \left[{\nabla }_{{\lambda }_1}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ 50-8d_1-7d_2-s_2=0,\mathit{or}8d_1+7d_2+s_2=50\hfill \\ s_2=50-8d_1-7d_2=\left[{\nabla }_{{\lambda }_2}\varphi (\underline{d},\underline{\lambda })\right]\hfill \\ \mathit{or}{\lambda }_2\prime s_1={\lambda }_2\prime \left[{\nabla }_{{\lambda }_2}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ 5-d_1-s_3=0,\mathit{or}{d}_1+s_3=5\hfill \\ \mathit{or}{\lambda }_3\prime s_3={\lambda }_3\prime \left[{\nabla }_{{\lambda }_3}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ 7-d_2-s_4=0,\mathit{or}{d}_2+s_4=7\hfill \\ \mathit{or}{\lambda }_4\prime s_4={\lambda }_4\prime \left[{\nabla }_{{\lambda }_4}\varphi (\underline{d},\underline{\lambda })\right]=0\hfill \\ d,\lambda ,u,s,⩾0\hfill \end{array}$$

Now we get the resulting single-level optimization problem as