Nonlinear optical properties of LLDPE composites with titanium dioxide anatase phase

Nafeesah Yaqub; W.A. Farooq; M.S. AlSalhi

doi:10.1016/j.jksus.2021.101723

View/Download PDF

Buy Reprints

PDF

Translate this page into:

01 2021

:34;

101723

doi:

10.1016/j.jksus.2021.101723

Nonlinear optical properties of LLDPE composites with titanium dioxide anatase phase

Nafeesah Yaqub^⁎, W.A. Farooq, M.S. AlSalhi

Department of Physics and Astronomy College of Science King Saud University, Riyadh 11451, Saudi Arabia

⁎Corresponding author. 437203488@student.ksu.edu.sa (Nafeesah Yaqub)

Received: 2021-5-26, Accepted: 2021-11-15,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In this research work, the linear and nonlinear optical properties of linear low-density polyethylene (LLDPE) composites with anatase phase of titanium dioxide nanoparticles in different weight percentages are investigated. Solvent casting method have been used to synthesize the thin film of LLDPE/anatase nanocomposites. Thin films are characterized via XRD technique and field emission scanning electron microscope (FESEM). Wrinkles formed on the surface of thin films by adding the titanium dioxide. Linear optical and electrical parameters such as linear absorption coefficient, extinction coefficient, refractive indices, optical conductivity, and dielectric constants at various wavelengths from 190 nm to 2700 nm are determined for different weight percentages of nanoparticles in polymer nanocomposites. Z-scan technique has been employed to explore the nonlinear optical properties using CW laser at 532 nm wavelength. The nonlinearity is examined at various irradiance of laser to study the effect of irradiance on nonlinear optical properties. Pure LLDPE has saturable absorption (SA) at low laser irradiance. As the laser irradiance increases, the nonlinearity behavior turns from SA to reverse saturable absorption (RSA). The results show the suitability of the thin films for the applications in optical devices that involve the use of optical limiting properties of materials.

Keywords

LLDPE polymer

Linear optical

Z-scan

Show Related Articles from PubMed

1 Introduction

Linear low density polyethylene (LLDPE) is related to the polyethylene polymer family which is classified as thermoplastic. LLDPE is usually referred to the ethylene copolymers in the density range of 0.915–0.925 gcm⁻³, with a co-monomer (butene, hexene or octene or butene) (Carraher, 2016), The molecular formula of LLDPE is (C₂H₄)_n, the chain of LLDPE is primarily consisted of CH₂CH₂ repeating units with intermittent branches obtain from a comonomer (Holding, 2010).

The comonomers are also named as short-chain branches of the polymer and their physical and mechanical properties vary accordingly. Mechanical properties such as tear, tensile and impact are strongly reliant on the chemical nature of the comonomer type (Mark, 2009). Almost research about the LLDPE are focused in the mechanical, electrical and the thermal properties of the polymers and its composites (Hotta and Paul, 2004). The dielectric of LLDPE composites with ground tire rubber particles are studied by Genesca (Marín-Genescà et al., 2020). In other research, LLDPE polymer were filled with ground tire rubber and polyester recycled to study the mechanical properties of it (Moghaddamzadeh and Rodrigue, 2018). Also LLDPE was filled by copper powder (Luyt et al., 2006), aluminum nitride (Zhou, 2011), and filled with silicon nitride to enhanced thermal conductivity (Zhou et al., 2009). LLDPE has an absorbance of the UV light and it is transparency in the visible light, it transmittance about 92% at 439 nm (Xie et al., 2016). Other linear optical and nonlinear optical properties of the LLDPE are not searched so far, as in literature review.

Z-scan technique(Sheik-Bahae et al., 1990) depend on the spatial distortion of a laser beam, interacting with a nonlinear optical material, is exceedingly utilized to examine the nonlinear optical properties of materials due to their easiness, high sensitivity and well-established theory (Thilak et al., 2013).

In this paper, linear and nonlinear optical properties of LLDPE/TiO₂ anatase phase are explored by synthesizing a film of LLDPE/anatase via simple casting method. The investigation of nonlinear properties of LLDPE/TiO₂ has not been carried out by any researcher. The present investigations are important for many applications in switching, generation of lasers, aerospace, automotive and marine industries. Particularly the use of polymeric materials in electrical engineering for improvements in operating voltages, performance, reliability, and size reduction are increasing tremendously.

2 Methodology

2.1

2.1 Materials

TiO₂ anatase phase having average particle size of 10–30 nm with 99% purity, purchased from Nanostructured & Amorphous Materials Inc., USA, was mixed with LLDPE (SABIC, Saudi Arabia), and dissolved in Xylene (Fisher Chemical).

2.2

2.2 Preparation of LLDPE doped TiO₂ films

LLDPE polymer is dissolved in xylene by stirring and heating the solution at 90° and stirred by magnetic stirrer for an hour until the solvent is totally dissolved. Then different amount of anatase nanoparticles are prepared to make different weight percentage of nanoparticles corresponding to the weight of polymer (0.5, 0.75, 1, 1.25 and 1.8 wt% anatase nanoparticles). The polymer nanocomposites solution is placed into the ultra-sonication machine. In order to achieve homogeneous dispersion, magnetic stirrer is used for two hours. Subsequently the solutions are transferred into a petri dish and leave to dry for at least 48 h. When all the solvent is evaporated, the thin films are peeled off from the petri dish. It is pertinent to mention that the amount of diluent in the solution is adjusted such that the prepared films had thicknesses in the range of 0.04 mm.

2.3

2.3 Characterization

The crystal structure of LLDPE/anatase nanocomposites films is conformed using X-ray diffraction (XRD) technique, (XRD- Bruker D8 advance, Germany). The morphology of LLDPE/TiO₂ nanocomposites is observed by FESEM, model JEOL-JSM‐7600F; manufactured by JEOL Ltd., Akishima, Tokyo, Japan.

To examine the linear optical properties of the prepared films o nanocomposites, JASCO V-770 spectrophotometer is employed to estimate the reflectance R (λ), transmittance T (λ), and the absorbance abs (λ) in 190 nm to 2700 nm range at the normal incidence. All the optical parameters such as optical band gap (Eg), absorption coefficient (α), linear refractive index, extinction coefficient (k), real and imaginary part of dialectical constant are calculated.

Z-scan technique is utilized to evaluate the third order nonlinear optical properties of the films like magnitude and sign of nonlinear refractive index, nonlinear absorption coefficient and real and imaginary parts of the susceptibilities. To calculate the these mentioned nonlinear optical parameters: to types of Z-scan technique are used; open aperture and close aperture Z-scan technique. In our Z-scan system we have used (HO-ED-LOE-03, Holmarc, India) that is used a Diode-Pumped Solid State CW laser with wavelength 532 nm and has Gaussian profile. The laser beam power has changed to see the effect of irradiance on the nonlinearity.

3 Results and discussion

3.1

3.1 X-ray diffraction

X-ray diffraction pattern for TiO₂ nanoparticles, pure LLDPE and 1.23 wt% of anatase nanoparticles in the LLDPE matrix is depicted in Fig. 1. The peaks in XRD pattern of LLDPE matches with COD card no. 1514536 for LLDPE polymer (Yu et al., 2013). In the figure three diffraction peaks centered at 2θ = 19.18°, 30.7° and 40.93° assigned to (1 1 0), (2 0 0) and (0 0 2) plans respectively. The XRD pattern of TiO₂ confirms that the TiO₂ has anatase tetragonal structure of the particles according to the COD card no. 5000223 related to anatase tetragonal nanoparticles (Horn et al., 1972) with space group 14-1/amd (1 4 1). The lattice plane indices (hkl) correspond to various diffraction peaks of TiO₂ are noted from its COD files and marked in Fig. 1. The Lattice parameters are calculated using equation (1) of tetragonal crystal system.

(1)

\frac{1}{d_{hkl}^{2}} = \frac{h^{2} + k^{2}}{a^{2}} + \frac{l^{2}}{c^{2}}

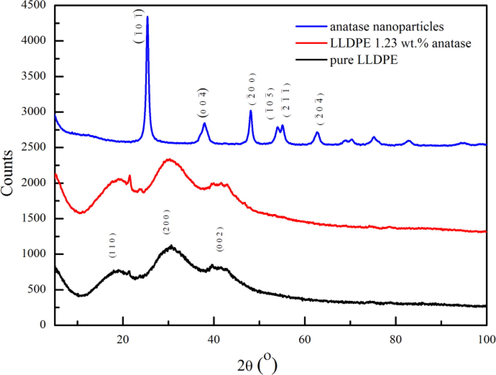
XRD patterns of anatase nanoparticles, pure LLDPE polymer, and LLDPE/anatase nanocomposites.

The value of a and c are 3.7814 and 9.4788 Å respectively, and the unit volume is 135.5372 Å³.

FESEM is employed for studying the surface morphology of LLDPE composites with anatase nanoparticles. Fig. 2 exhibits the surface images related to LLDPE/TiO₂ composite films. As evident from the figure, a wrinkle on the surface formed by adding titanium dioxide. The wrinkles increase with increasing the amount of titanium. At first, the surface is quite smooth and by increase doping the roughness increases. The surface morphology is greatly altered with the amount of anatase in composite structure. The wrinkle formation on the surface might be due to that the TiO2 nanoparticles correlated to the LLDPE polymer chain and effect of the solvent evaporation process (Visaveliya et al., 2017). During evaporation if lower surface is somehow contracted then the top layer might ultimately deform to produce wrinkles.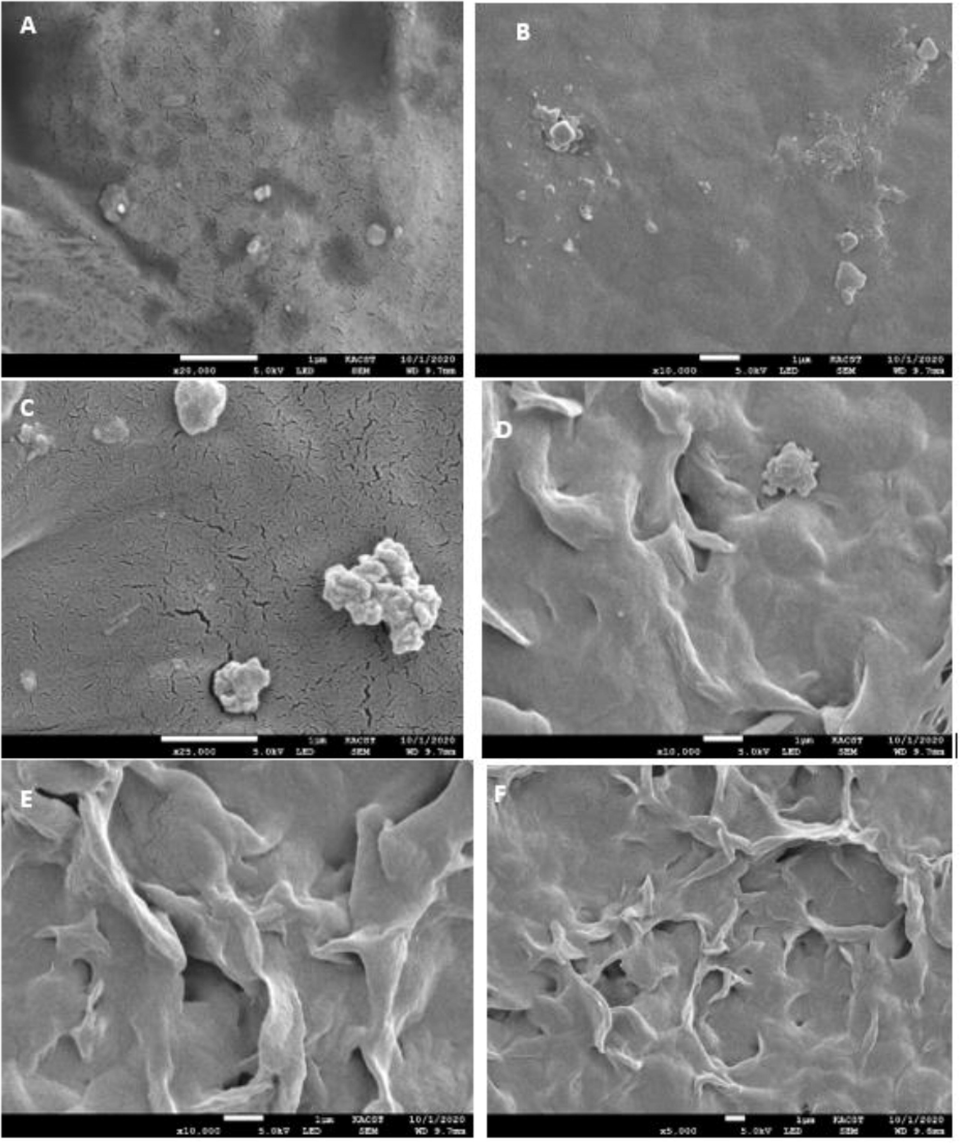

FESEM images of A). pure LLDPE and B–F). LLDPE/anatase nanocomposites of 0.5, 0.75, 1, 1.25, and 1.8 wt%.

3.2

3.2 Linear optical parameters

Transmittance and reflectance spectra of LLDPE/anatase nanocomposites as a function of wavelength are presented in Fig. 3 (B and C). The transmittance of pure LLDPE is very low, it decreases gradually from longer-wavelength so that it has the lowest values in the visible and UV regions. With adding TiO₂ anatase nanoparticles there is corresponding decreasing trend in the transmittance, however, in nanocomposite with 0.75 and 1.25 wt% of anatase the transmittance is found to be higher.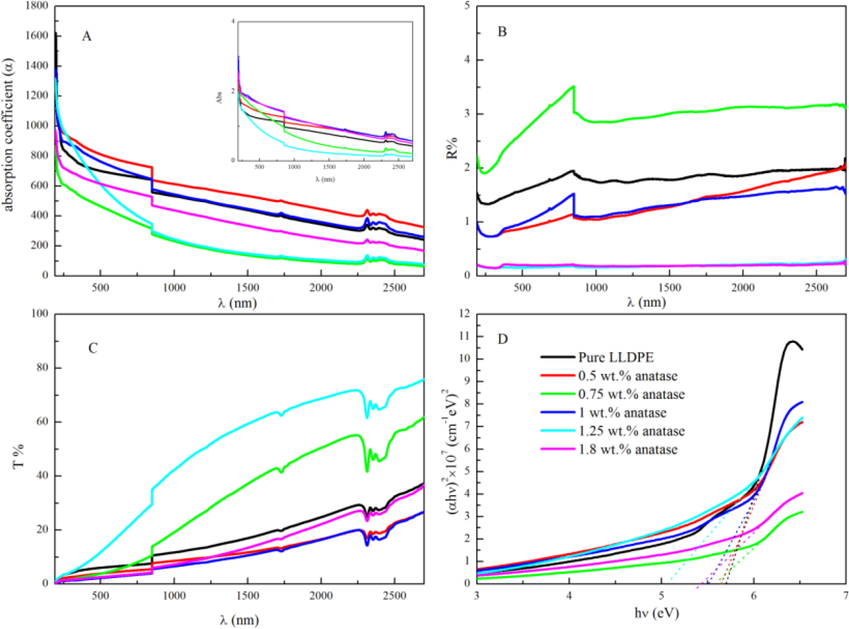

A). Absorption spectra (inset) and absorption coefficient B) Transmittance C). reflectance spectra, and D) Tauc's plot for direct optical band gap energy of pure and anatase composites LLDPE at various amount of anatase.

Variation of reflectance of LLDPE/anatase nanocomposite and pure LLDPE with wavelength is depicted in Fig. 3-C. It is observed that the reflectance is low, below 3 %. Pure LLDPE is approximately around 1.8% for long-wavelength and begin to decrease gradually from 840 nm to UV range, where it has its minimum value around 1.3%. With Incorporating TiO₂ anatase into the LLDPE, the reflectance has overall decreased tend.

Linear absorption variation in terms of the wavelength of pure LLDPE and LLDPE doped with different contents of anatase are depicted in the inset of Fig. 3-A. The observed spectrum of pure LLDPE has high absorption which is around 12% in the visible region. Adding TiO₂ anatase structure to the LLDPE increases its absorption slightly, around 15%, as the weight percentage of anatase nanoparticles is increased, the absorption increases specifically in UV region. The linear absorption coefficient of nanocomposites is calculated using equation (2) (Darwish et al., 2017) where d is the thickness of the sample. The variation of linear absorption coefficient with wavelength is shown in Fig. 3-A

(2)

α = \frac{1}{d} l n [\frac{(1 - R^{2})}{2 T} + \sqrt{\frac{(1 - R^{2})}{4 T^{2}} + R^{2}}]

Direct optical band gap energy of LLDPE/anatase nanocomposites are calculated from transmittance and reflectance spectrum using Tauc's plot as in this equation (3) (Al-Ghamdi, 2017; Hendi and Rashad, 2018)

(3)

{(α h ν)}^{2} = A (h ν - E_{g})

The Tauc’s plots of LLDPE/anatase nanocomposites are shown in Fig. 3-D. The values of band gap energy are 5.87, 5.64, 5.60, 5.51, 5.06, and 5.42 for 0, 0.5, 0.75, 1, 1.25, 1.8 wt% of anatase respectively. It observed that by adding anatase nanoparticles there is an overall decrease in the optical band gap energy. The reduction in the value of band gap might be due to the splitting of each level into many levels equal to number of interacting atoms according to the energy band theory (Li, 1993). So, the bands come closer or overlapped which reduce the energy gap between the levels.

Refractive indices are calculated using Fresnel’s Formula (Aksoy and Ruzgar, 2017; Yaqub et al., 2020) given in equation (5) and its variation with wavelength is shown in Fig. 4-A. Pure LLDPE has a low refractive index which is around 1.3 and with adding TiO₂, it has overall decreasing trend because it depends on reflectance of the samples.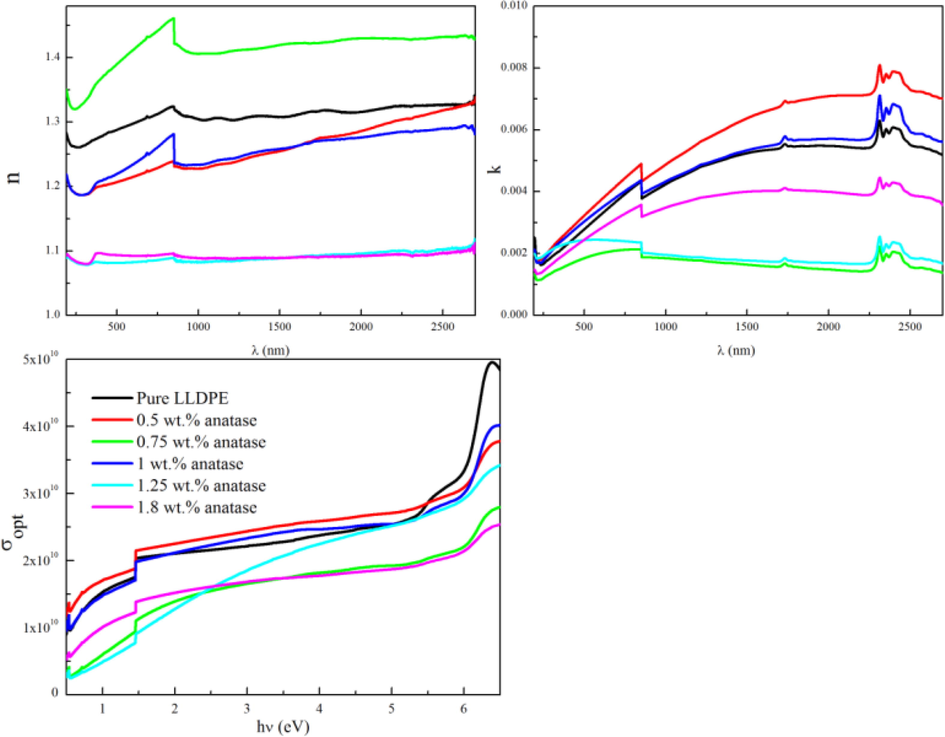

Refractive index (A), extinction coefficient (B), and optical conductivity (C)) of LLDPE/anatase for various amount of anatase nanoparticles.

The extinction coefficient of LLDPE/anatase nanocomposite are calculated using equation (4) (Dere, 2020). The variation of extinction coefficient of LLDPE/anatase nanocomposite with wavelength is shown in the Fig. 4-B. In general, LLDPE/anatase nanocomposites with various weight percentages have close values of extinction coefficient in the visible and UV regions, but it varies a lot in the infrared region. There is no regular pattern of extinction coefficient with changing amount of TiO₂ nanoparticles which might be due to irregular distribution of nanoparticles in polymer nanocomposites.

(4)

k = \frac{λ α}{4 π}

(5)

n = \frac{1 + R}{1 - R} + \sqrt{\frac{4 R}{{(1 - R)}^{2}} - k^{2}}

Optical conductivity is calculated using equation (6) (Pankove and Kiewit, 1972) and its variation with energy of incident photon is shown in Fig. 4-C.

(6)

σ_{opt} = \frac{α n c}{4 π}

Optical conductivity is caused with the diffusion current in the material, this current arises under optical excitation without the presence of applied electrical field, so in the LLDPE/anatase nanocomposites the optical conductivity has low value when the photon has low energy, by increasing the energy of the incident photon $σ_{opt}$ slightly increase and at E = 6 eV. $σ_{opt}$ It increases rapidly, this is due to that at this energy the electron has absorb the energy and translate to higher band of energy.

3.3

3.3 Open aperture Z-scan

The open aperture Z-scan technique is utilized to manifest the nonlinear absorption coefficient of pure LLDPE and LLDPE/ anatase nanocomposites. Figs. 5 and 6 show the measured values of the normalized transmittance as a function of the distance from the beam focus in the open aperture z-scan for pure LLDPE and 1 wt% anatase nanoparticle in the LLDPE matrix. Other concentrations of LLDPE/anatase are shown the same traces but ΔT differ with changing the concentration of nanoparticles in which that ΔT increased with increasing the concertation at fixed irradiance. For all the concentrations the transmittance is measured for the different laser irradiance (8, 5.6, 4, 2.8, and 2 kW/cm²). In the pure LLDPE at low laser excitations levels, the open aperture curve demonstrates the presence of saturable absorption (SA) that the transmittance increases at the focus. As the laser irradiance is increased, the data is characteristic of reverse saturation absorption (RSA) in the film, that is, the transmission at the focus decreases with increase in intensity. Due to the changing behavior of nonlinearity from SA to RSA. The nonlinear absorption coefficient changes from negative to positive with increasing irradiance. The such influence of nonlinearity are observed before in PANI-Ag film (Sezer et al., 2009) and linear polymer in dimethylformamide (Gao et al., 2007) and others. It can be seen in Fig. 6 that the nonlinear absorption behavior is strongly affected by the irradiance. The dependance of nonlinear absorption coefficient on the intensity of the laser is illustrated in the Fig. 7.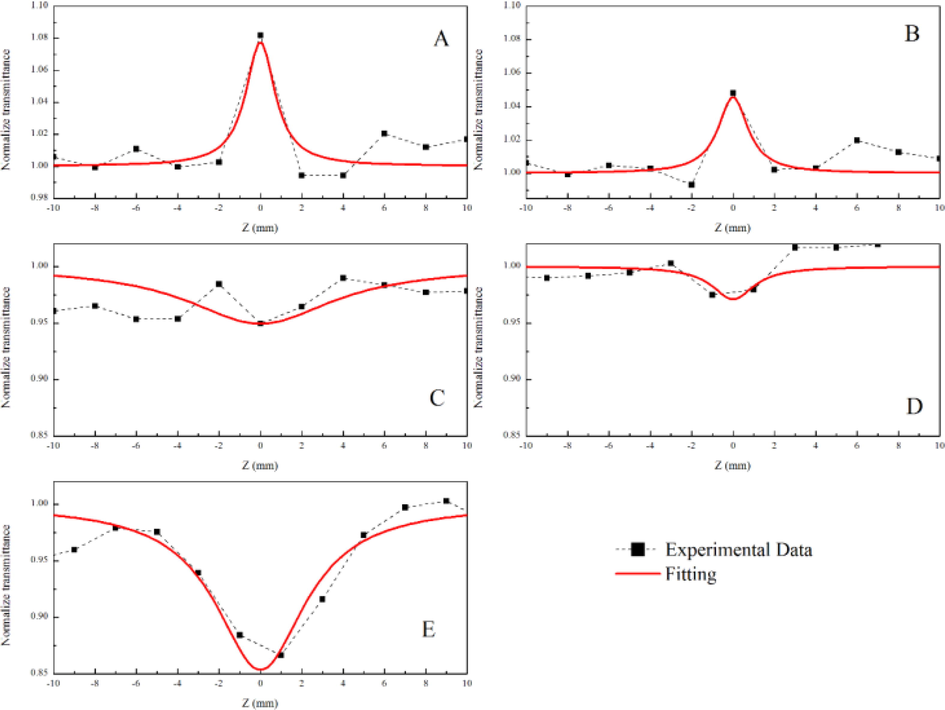

Open aperture Z-scan of pure LLDPE polymer in the different laser output power; 25, 35, 50, 75, and 100 mW for A-F.

Open aperture Z-scan of LLDPE/anatase (1 wt%) nanocomposites in the different laser output power; 25, 35, 50, 75, and 100 mW for A-F.

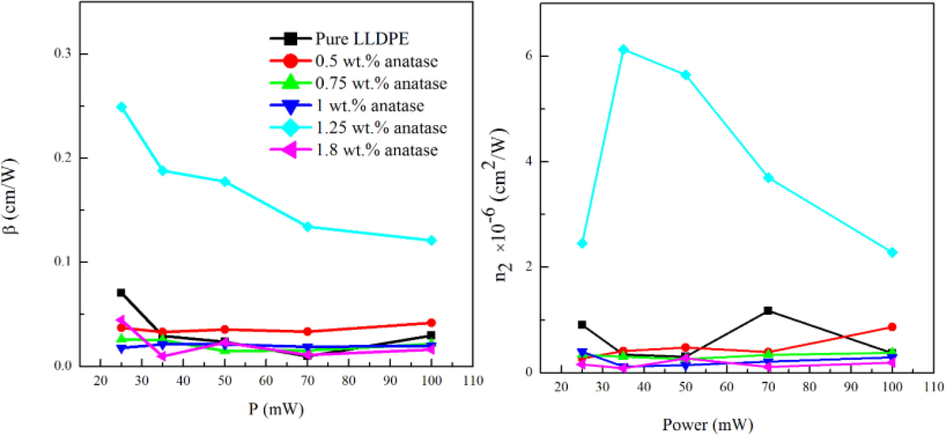
Dependence of the nonlinear optical parameters on the laser output power of LLDPE/anatase nanocomposites.

The nonlinear absorption coefficient β is obtained by fitting the experimental data of open aperture measurement with equation (9) (Sheik-Bahae et al., 1990)

(9)

T (z) = \sum_{m = 0}^{\infty} \frac{{[- q_{0} (z)]}^{m}}{{(m + 1)}^{3 / 2}}

where

q_{0} (z) = \frac{β I_{0} L_{eff}}{[1 + \frac{Z^{2}}{Z_{0}^{2}}]}

$Z_{0}$ is Rayleigh range of laser, $L_{eff} = \frac{1 - e^{- α L}}{α}$ is the effective length of the films, α is the linear absorption coefficient, I_o is he intensity of the laser power at the focus. From the fitting curve we calculate the nonlinear absorption coefficient using equation (10) (Vinitha and Ramalingam, 2010).

(10)

β = \frac{2 \sqrt{2} Δ T}{I_{0} L_{eff}}

The nonlinear absorption process has different mechanisms to occur (Nagaraja et al., 2013). In the current case, were CW laser used, the mechanisms of nonlinear absorption are competing, and more than one mechanism will occur in a time (Sezer et al., 2009). As in Fig. 7, it is clearly that β depends on the intensity of laser output power, in which the values of nonlinear absorption coefficient decrease with increasing in the laser power for LLDPE/anatase films, this indicates two photon absorption induced free carrier absorption (Nagaraja et al., 2013) has the dominated mechanism in the LLDPE/anatase nanocomposites. These samples can be used for optical limiting applications, because all films show a decrease in transmission with increase in the laser power.

3.4

3.4 Close aperture Z-scan

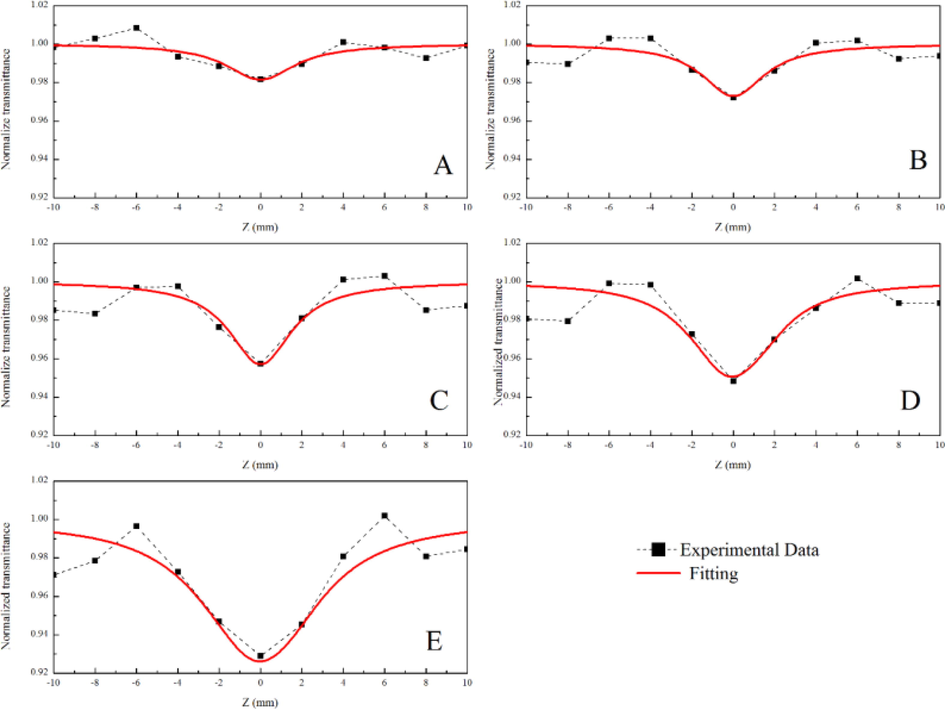
To determine the nonlinear refractive index of LLDEP/anatase nanocomposites, close aperture z-scan technique is performed. The thickness of the films in the range of 0.04 mm, which is satisfy criterion for diffraction L < z₀ for close aperture Z-scan (Sheik-Bahae et al., 1990). Figs. 8 and 9 demonstrate the closed aperture z scan profiles of pure LLDPE and LLDPE/anatase 0.5 wt% nanocomposites, and similar results are obtained in the other concentrations of anatase nanoparticles, but different values of ΔT_p-v obtained with changing the concentration of anatase nanoparticles. The closed aperture Z-scan curve exhibit peak followed by valley transmittance for all pure LLDPE and LLDPE/anatase films. Which is mean these films have negative nonlinear refractive indices.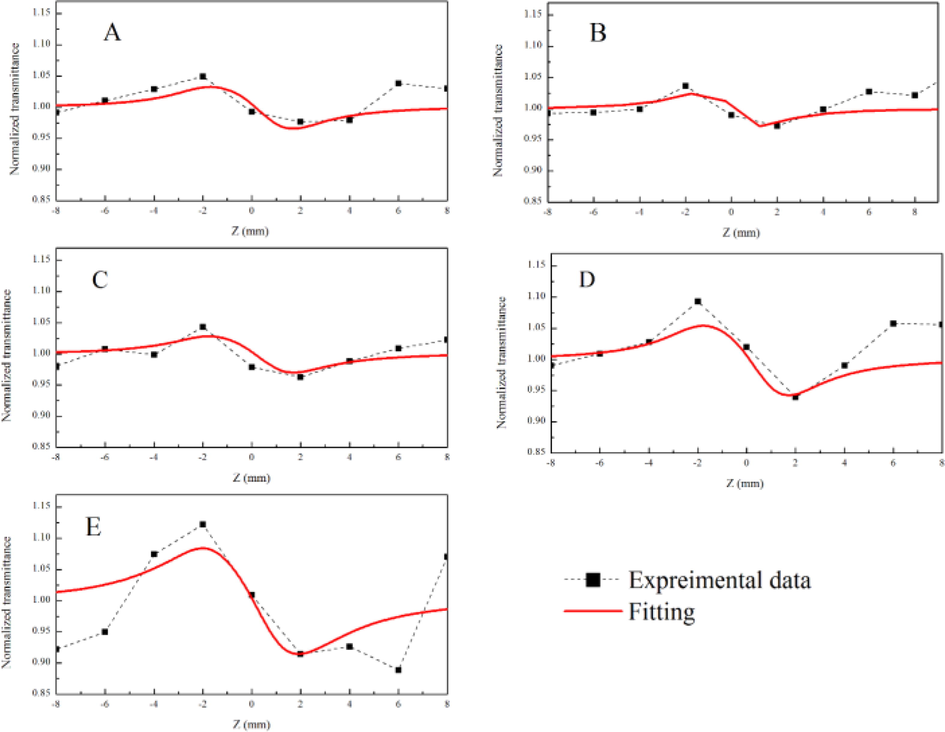

Close aperture Z-scan of pure LLDPE in the different laser output power; 25, 35, 50, 75, and 100 mW for A-F.

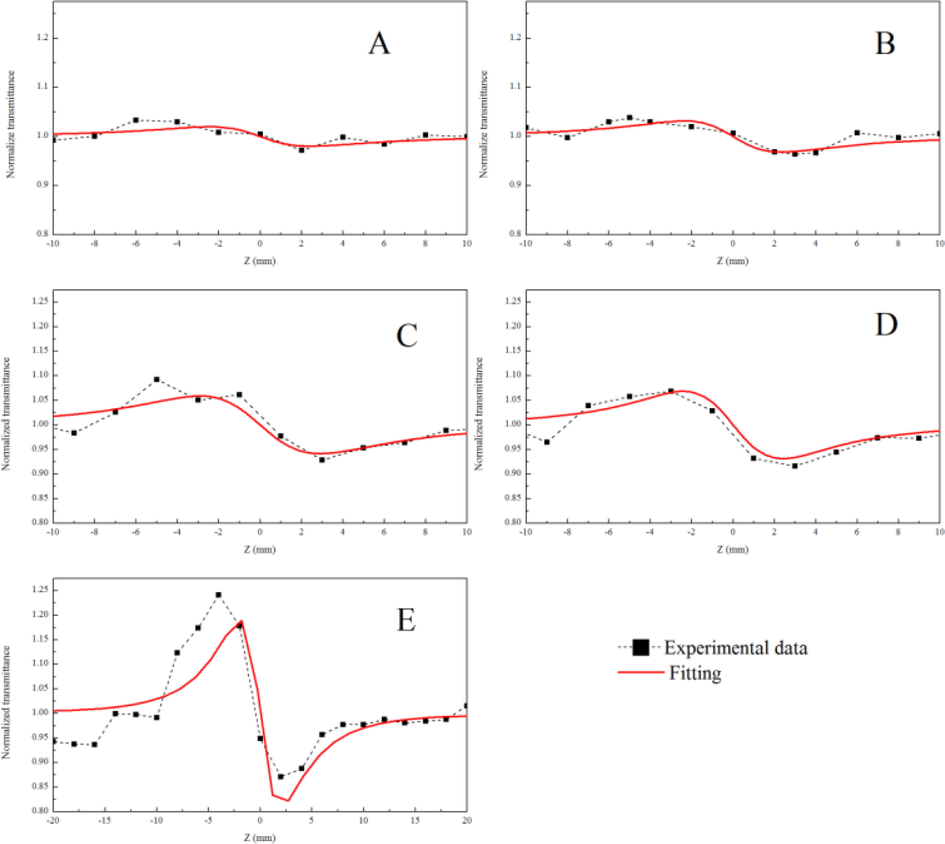
Close aperture Z-scan of LLDPE composite with 0.5 wt% anatase, in the different laser output power; 25, 35, 50, 75, and 100 mW for A-F.

Nonlinear refractive index n₂ is calculated after fitted the experimental data using equation (11) (Sheik-bahae et al., 1989; Sheik-Bahae et al., 1990)

(11)

T ((z) = 1 + \frac{4 x Δ Φ_{0}}{(x^{2} + 1) (x^{2} + 9)}

where

= \frac{z}{z_{0}}

{Δ Φ}_{0}

is the on-axis phase shift represented by following relation

{Δ Φ}_{0} = \frac{Δ T_{p - v}}{0.406 {(1 - S)}^{0.25}}

S is the linear aperture transmittance, and it is equal to 0.3 in our experiments, $Δ T_{p - v}$ is the difference between the peak-valley normalized transmittance. To calculate n₂ equation (12) used (Chapple et al., 1997)

(12)

{Δ Φ}_{0} = k n_{2} I_{0} L_{eff}

The ΔT_p-v of close aperture Z-scan curve differs as the anatase nanoparticles concentration is changed resulting from the modification in the nonlinear phase shift which leads to a change in the value of the nonlinear refractive index n₂ with changing the amount of nanoparticles. The magnitude of n₂ depends on the concentrations of anatase nanoparticles in the nanocomposites, is shown in the Fig. 7.

The close aperture z-scan data is used to calculate the nonlinear refractive index n₂, and it is important to note that usually nonlinear refraction conjunction with nonlinear absorption. This implies that the closed aperture data will contain both nonlinear refraction and nonlinear absorption components. By dividing the closed aperture z-scan trace by the open aperture z-scan trace, one can extract pure nonlinear refraction (Chapple et al., 1997).

The ΔZ_p-v separation distance between valley and peak of LLDPE/anatase nanocomposites for all films are approximately 1.7z₀. Which is mean these nanocomposites have Kerr nonlinearity concluding from satisfy the condition of Kerr nonlinearity (Kumar et al., 2007). In case 1.8 wst.%; ΔZ_p-v is more than 1.7z₀ that mean it assign to the thermal nonlinearity (Sheik-bahae et al., 1989).

3.5

3.5 Third-order nonlinear optical properties

Nonlinear optical materials can be beneficial for all optical switching, wavelength manipulation and signal processing. The third-order optical nonlinearities of LLDPE/anatase nanocomposites are investigated by Z-scan technique to examine the influence of various amount of nanoparticles in nanocomposites and laser intensity on the cubic nonlinear response. The third-order nonlinear properties of materials are described as the nonlinear susceptibility, the nonlinear absorption coefficient or nonlinear refractive index.

Third-order nonlinear optical susceptibility is complex quantity, the real part depends on nonlinear refractive index n₂, while the imaginary part depends on β as in the equations 13–15

(13)

R e (χ^{(3)}) (e s u) = 10^{- 4} \frac{ε_{0} c^{2} n_{0}^{2}}{π} n_{2} ({cm}^{2} / W)

(14)

I m (χ^{(3)}) (e s u) = 10^{- 2} \frac{ε_{0} c^{2} n_{0}^{2} λ}{4 π^{2}} β (c m / W)

(15)

χ^{(3)} = \sqrt{{(R e (χ^{(3)}))}^{2} + {(I m (χ^{(3)}))}^{2}}

where

ε_{0}

represents the dielectric constant in a vacuum, n_o denotes the linear refractive index, c is the speed of light in a vacuum and λ symbolize the laser wavelength(Shanshool et al., 2017). The imaginary, real and the absolute values of χ(3) for LLDPE/TiO₂ anatase nanocomposites are listed in Table 1. LLDEP/anatase polymer nanocomposites have high values of χ(3) that is in the order 10⁻⁵ e s u.

Table 1 Values of χ(3) for LLDPE/TiO₂ anatase nanocomposites.

C%	Io KW/cm²	χ_R⁽³⁾10⁻⁵ e s u	χ_Im⁽³⁾ 10⁻⁵ e s u	χ⁽³⁾10⁻⁵ e s u
pure	8	1.58	0.53	1.66
	5.6	4.95	0.18	4.95
	4	1.29	0.42	1.36
	2.8	1.47	0.53	1.56
	2	3.84	1.26	4.04
0.5	8	3.21	0.66	3.28
	5.6	1.45	0.53	1.55
	4	1.77	0.56	1.86
	2.8	1.53	0.52	1.62
	2	1.02	0.59	1.18
0.75	8	1.89	0.46	1.95
	5.6	1.70	0.33	1.73
	4	1.28	0.32	1.32
	2.8	1.52	0.54	1.62
	2	1.71	0.55	1.79
1	8	1.10	0.32	1.14
	5.6	0.81	0.30	0.86
	4	0.54	0.34	0.64
	2.8	0.46	0.34	0.57
	2	1.52	0.29	1.54
1.25	8	18.75	4.21	19.21
	5.6	30.37	4.68	30.73
	4	46.41	6.18	46.82
	2.8	50.32	6.54	50.75
	2	20.17	8.68	21.95
1.8	8	0.58	0.21	0.61
	5.6	0.33	0.14	0.36
	4	0.82	0.29	0.87
	2.8	0.27	0.12	0.30
	2	0.48	0.57	0.74

4 Conclusion

Pure LLDPE film as its nonlinearity properties change from SA to RSA at the same wavelength by changing the irradiance suggests the film can be used in sensor application for optical limiting as sensor protection from high laser power, and in the low power it is used for magnification of transmitted signal. LLDPE/anatase nanocomposites have a high value of third order nonlinear optical susceptibility required to use in manufacturing of optical devices.

Declarations of interest

None.

Acknowledgements

The authors would like to thank Deanship of scientific research in King Saud University for funding and supporting this research through the initiative of DSR Graduate Students Research Support (GSR).

References

Aksoy S., Ruzgar S., . Effect of Nitrogen on optical properties of ZnO film deposited by sol gel method. J. Mater. Electron. Devices. 2017;1:1-4.
[Google Scholar]
Al-Ghamdi A., . Optical constants and dispersion energy parameters of gallium phosphide. J. Mater. Electron. Devices. 2017;1:1-5.
[Google Scholar]
Carraher Jr., C.E., Carraher’s Polymer Chemistry, 2016. https://doi.org/10.1201/b15405.
Chapple P.B., Staromlynska J., Hermann J.A., Mckay T.J., Mcduff R.G., . Single-beam Z-scan: measurement techniques and analysis. J. Nonlinear Opt. Phys. Mater.. 1997;06:251-293.
[CrossRef] [Google Scholar]
Darwish A.A.A., Rashad M., Bekheet A.E., El-Nahass M.M., . Linear and nonlinear optical properties of GeSe2-xSnx (0 ≤ x ≤ 0.8) thin films for optoelectronic applications. J. Alloys Compd.. 2017;709:640-645.
[CrossRef] [Google Scholar]
Dere, A, Refractive index dispersion and determination of the optical constants of BaTiO3 thin film prepared by sol gel, 6 (2020) 1–5.
Gao Y., Chang Q., Ye H., Jiao W., Song Y., Wang Y., Qin J., . Saturable and reverse saturable absorption of a linear polymer in dimethylformamide. Appl. Phys. B Lasers Opt.. 2007;88:255-258.
[CrossRef] [Google Scholar]
Hendi A.A., Rashad M., . Photo-induced changes in nano-copper oxide for optoelectronic applications. Phys. B Condens. Matter.. 2018;538:185-190.
[CrossRef] [Google Scholar]
Holding, S. Polymers: A Property Database, 2010. https://doi.org/10.1365/s10337-010-1620-z.
Horn M., Schwerdtfeger C.F., Meagher E.P., . Refinement of the structure of anatase at several temperatures. Zeitschrift Fur Krist. - New Cryst. Struct.. 1972;136:273-281.
[CrossRef] [Google Scholar]
Hotta S., Paul D.R., . Nanocomposites formed from linear low density polyethylene and organoclays. Polymer (Guildf). 2004;45:7639-7654.
[CrossRef] [Google Scholar]
Kumar G.S., Milka B.V., Muneera C.I., Sathiyamoorthy K., Vijayan C., . Nonlinear refraction and optical limiting in solid films of amido black dye under CW laser illumination. Opt. Mater. (Amst). 2007;30:311-313.
[CrossRef] [Google Scholar]
Li S.S., . Energy Band Theory. In: Semicond. Phys. Electron.. Boston, MA: Springer US; 1993. p. :55-85.
[CrossRef] [Google Scholar]
Luyt A.S., Molefi J.A., Krump H., . Thermal, mechanical and electrical properties of copper powder filled low-density and linear low-density polyethylene composites. Polym. Degrad. Stab.. 2006;91:1629-1636.
[CrossRef] [Google Scholar]
Marín-Genescà M., García-Amorós J., Mujal-Rosas R., Massagués L., Colom X., . Study and characterization of the dielectric behavior of low linear density polyethylene composites mixed with ground tire rubber particles. Polymers (Basel). 2020;12
[CrossRef] [Google Scholar]
Mark J.E., . Polymer Data Handbook, 2nd ed. J. Am. Chem. Soc.. 2009;131:16330.
[CrossRef] [Google Scholar]
Moghaddamzadeh S., Rodrigue D., . The effect of polyester recycled tire fibers mixed with ground tire rubber on polyethylene composites. Part I: Morphological analysis. Prog. Rubber, Plast. Recycl. Technol.. 2018;34:200-220.
[CrossRef] [Google Scholar]
Nagaraja K.K., Pramodini S., Santhosh Kumar A., Nagaraja H.S., Poornesh P., Kekuda D., . Third-order nonlinear optical properties of Mn doped ZnO thin films under cw laser illumination. Opt. Mater. (Amst).. 2013;35:431-439.
[CrossRef] [Google Scholar]
Pankove J.I., Kiewit D.A., . Optical processes in semiconductors. J. Electrochem. Soc.. 1972;119:156C.
[CrossRef] [Google Scholar]
Sezer A., Gurudas U., Collins B., Mckinlay A., Bubb D.M., . Nonlinear optical properties of conducting polyaniline and polyaniline-Ag composite thin films. Chem. Phys. Lett.. 2009;477:164-168.
[CrossRef] [Google Scholar]
Shanshool H.M., Yahaya M., Yunus W.M.M., Abdullah I.Y., . Influence of CuO nanoparticles on third order nonlinearity and optical limiting threshold of polymer/ZnO nanocomposites. Opt. Quantum Electron.. 2017;49
[CrossRef] [Google Scholar]
Sheik-bahae M., Said A.A., Van Stryland E.W., . High-sensitivity, single-beam n_2 measurements. Opt. Lett.. 1989;14:955.
[CrossRef] [Google Scholar]
Sheik-Bahae M., Said A.A., Wei T.H., Hagan D.J., Van Stryland E.W., . Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron.. 1990;26:760-769.
[CrossRef] [Google Scholar]
Thilak T., Ahamed M.B., Vinitha G., . Third order nonlinear optical properties of potassium dichromate single crystals by Z-scan technique. Optik (Stuttg).. 2013;124:4716-4720.
[CrossRef] [Google Scholar]
Vinitha G., Ramalingam A., . Optical limiting characteristics of core-shell nanoparticles. World Acad. Sci. Eng. Technol.. 2010;40:699-701.
[Google Scholar]
Visaveliya N.R., Leishman C.W., Ng K., Yehya N., Tobar N., Eisele D.M., Köhler J.M., . Surface wrinkling and porosity of polymer particles toward biological and biomedical applications. Adv. Mater. Interfaces. 2017;4
[CrossRef] [Google Scholar]
Xie J., Zhang K., Zhao Q., Wang Q., Xu J., . Large-scale fabrication of linear low density polyethylene/layered double hydroxides composite films with enhanced heat retention, thermal, mechanical, optical and water vapor barrier properties. J. Solid State Chem.. 2016;243:62-69.
[CrossRef] [Google Scholar]
Yaqub N., Farooq W.A., AlSalhi M.S., . Delving into the properties of polymer nanocomposites with distinctive nano-particle quantities, for the enhancement of optoelectronic devices. Heliyon. 2020;6
[CrossRef] [Google Scholar]
Yu J., Sun J., Niu Y., Li R., Liao J., Zhang F., Yu B., . Synthetic access toward the diverse ginsenosides. Chem. Sci.. 2013;4:3899-3905.
[CrossRef] [Google Scholar]
Zhou W., . Thermal and dielectric properties of the AlN particles reinforced linear low-density polyethylene composites. Thermochim. Acta. 2011;512:183-188.
[CrossRef] [Google Scholar]
Zhou W., Wang C., Ai T., Wu K., Zhao F., Gu H., . A novel fiber-reinforced polyethylene composite with added silicon nitride particles for enhanced thermal conductivity. Compos. Part A Appl. Sci. Manuf.. 2009;40:830-836.
[CrossRef] [Google Scholar]

Introduction

Methodology

Materials
Preparation of LLDPE doped TiO2 films
Characterization

Results and discussion

X-ray diffraction
Linear optical parameters
Open aperture Z-scan
Close aperture Z-scan
Third-order nonlinear optical properties

Conclusion

Declarations of interest

Fulltext Views
28

PDF downloads
24

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Aksoy S., Ruzgar S., . Effect of Nitrogen on optical properties of ZnO film deposited by sol gel method. J. Mater. Electron. Devices. 2017;1:1-4.
[Google Scholar]

[2] Al-Ghamdi A., . Optical constants and dispersion energy parameters of gallium phosphide. J. Mater. Electron. Devices. 2017;1:1-5.
[Google Scholar]

[3] Carraher Jr., C.E., Carraher’s Polymer Chemistry, 2016. https://doi.org/10.1201/b15405.

[4] Chapple P.B., Staromlynska J., Hermann J.A., Mckay T.J., Mcduff R.G., . Single-beam Z-scan: measurement techniques and analysis. J. Nonlinear Opt. Phys. Mater.. 1997;06:251-293.
[CrossRef] [Google Scholar]

[5] Darwish A.A.A., Rashad M., Bekheet A.E., El-Nahass M.M., . Linear and nonlinear optical properties of GeSe2-xSnx (0 ≤ x ≤ 0.8) thin films for optoelectronic applications. J. Alloys Compd.. 2017;709:640-645.
[CrossRef] [Google Scholar]

[6] Dere, A, Refractive index dispersion and determination of the optical constants of BaTiO3 thin film prepared by sol gel, 6 (2020) 1–5.

[7] Gao Y., Chang Q., Ye H., Jiao W., Song Y., Wang Y., Qin J., . Saturable and reverse saturable absorption of a linear polymer in dimethylformamide. Appl. Phys. B Lasers Opt.. 2007;88:255-258.
[CrossRef] [Google Scholar]

[8] Hendi A.A., Rashad M., . Photo-induced changes in nano-copper oxide for optoelectronic applications. Phys. B Condens. Matter.. 2018;538:185-190.
[CrossRef] [Google Scholar]

[9] Holding, S. Polymers: A Property Database, 2010. https://doi.org/10.1365/s10337-010-1620-z.

[10] Horn M., Schwerdtfeger C.F., Meagher E.P., . Refinement of the structure of anatase at several temperatures. Zeitschrift Fur Krist. - New Cryst. Struct.. 1972;136:273-281.
[CrossRef] [Google Scholar]

[11] Hotta S., Paul D.R., . Nanocomposites formed from linear low density polyethylene and organoclays. Polymer (Guildf). 2004;45:7639-7654.
[CrossRef] [Google Scholar]

[12] Kumar G.S., Milka B.V., Muneera C.I., Sathiyamoorthy K., Vijayan C., . Nonlinear refraction and optical limiting in solid films of amido black dye under CW laser illumination. Opt. Mater. (Amst). 2007;30:311-313.
[CrossRef] [Google Scholar]

[13] Li S.S., . Energy Band Theory. In: Semicond. Phys. Electron.. Boston, MA: Springer US; 1993. p. :55-85.
[CrossRef] [Google Scholar]

[14] Luyt A.S., Molefi J.A., Krump H., . Thermal, mechanical and electrical properties of copper powder filled low-density and linear low-density polyethylene composites. Polym. Degrad. Stab.. 2006;91:1629-1636.
[CrossRef] [Google Scholar]

[15] Marín-Genescà M., García-Amorós J., Mujal-Rosas R., Massagués L., Colom X., . Study and characterization of the dielectric behavior of low linear density polyethylene composites mixed with ground tire rubber particles. Polymers (Basel). 2020;12
[CrossRef] [Google Scholar]

[16] Mark J.E., . Polymer Data Handbook, 2nd ed. J. Am. Chem. Soc.. 2009;131:16330.
[CrossRef] [Google Scholar]

[17] Moghaddamzadeh S., Rodrigue D., . The effect of polyester recycled tire fibers mixed with ground tire rubber on polyethylene composites. Part I: Morphological analysis. Prog. Rubber, Plast. Recycl. Technol.. 2018;34:200-220.
[CrossRef] [Google Scholar]

[18] Nagaraja K.K., Pramodini S., Santhosh Kumar A., Nagaraja H.S., Poornesh P., Kekuda D., . Third-order nonlinear optical properties of Mn doped ZnO thin films under cw laser illumination. Opt. Mater. (Amst).. 2013;35:431-439.
[CrossRef] [Google Scholar]

[19] Pankove J.I., Kiewit D.A., . Optical processes in semiconductors. J. Electrochem. Soc.. 1972;119:156C.
[CrossRef] [Google Scholar]

[20] Sezer A., Gurudas U., Collins B., Mckinlay A., Bubb D.M., . Nonlinear optical properties of conducting polyaniline and polyaniline-Ag composite thin films. Chem. Phys. Lett.. 2009;477:164-168.
[CrossRef] [Google Scholar]

[21] Shanshool H.M., Yahaya M., Yunus W.M.M., Abdullah I.Y., . Influence of CuO nanoparticles on third order nonlinearity and optical limiting threshold of polymer/ZnO nanocomposites. Opt. Quantum Electron.. 2017;49
[CrossRef] [Google Scholar]

[22] Sheik-bahae M., Said A.A., Van Stryland E.W., . High-sensitivity, single-beam n_2 measurements. Opt. Lett.. 1989;14:955.
[CrossRef] [Google Scholar]

[23] Sheik-Bahae M., Said A.A., Wei T.H., Hagan D.J., Van Stryland E.W., . Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron.. 1990;26:760-769.
[CrossRef] [Google Scholar]

[24] Thilak T., Ahamed M.B., Vinitha G., . Third order nonlinear optical properties of potassium dichromate single crystals by Z-scan technique. Optik (Stuttg).. 2013;124:4716-4720.
[CrossRef] [Google Scholar]

[25] Vinitha G., Ramalingam A., . Optical limiting characteristics of core-shell nanoparticles. World Acad. Sci. Eng. Technol.. 2010;40:699-701.
[Google Scholar]

[26] Visaveliya N.R., Leishman C.W., Ng K., Yehya N., Tobar N., Eisele D.M., Köhler J.M., . Surface wrinkling and porosity of polymer particles toward biological and biomedical applications. Adv. Mater. Interfaces. 2017;4
[CrossRef] [Google Scholar]

[27] Xie J., Zhang K., Zhao Q., Wang Q., Xu J., . Large-scale fabrication of linear low density polyethylene/layered double hydroxides composite films with enhanced heat retention, thermal, mechanical, optical and water vapor barrier properties. J. Solid State Chem.. 2016;243:62-69.
[CrossRef] [Google Scholar]

[28] Yaqub N., Farooq W.A., AlSalhi M.S., . Delving into the properties of polymer nanocomposites with distinctive nano-particle quantities, for the enhancement of optoelectronic devices. Heliyon. 2020;6
[CrossRef] [Google Scholar]

[29] Yu J., Sun J., Niu Y., Li R., Liao J., Zhang F., Yu B., . Synthetic access toward the diverse ginsenosides. Chem. Sci.. 2013;4:3899-3905.
[CrossRef] [Google Scholar]

[30] Zhou W., . Thermal and dielectric properties of the AlN particles reinforced linear low-density polyethylene composites. Thermochim. Acta. 2011;512:183-188.
[CrossRef] [Google Scholar]

[31] Zhou W., Wang C., Ai T., Wu K., Zhao F., Gu H., . A novel fiber-reinforced polyethylene composite with added silicon nitride particles for enhanced thermal conductivity. Compos. Part A Appl. Sci. Manuf.. 2009;40:830-836.
[CrossRef] [Google Scholar]

Nonlinear optical properties of LLDPE composites with titanium dioxide anatase phase

Abstract

Keywords

LLDPE polymer

Linear optical

Z-scan

1 Introduction

2 Methodology

2.1 Materials

2.2 Preparation of LLDPE doped TiO2 films

2.3 Characterization

3 Results and discussion

3.1 X-ray diffraction

3.2 Linear optical parameters

3.3 Open aperture Z-scan

3.4 Close aperture Z-scan

3.5 Third-order nonlinear optical properties

4 Conclusion

Declarations of interest

Acknowledgements

References

Suggested read for related articles:

2.2 Preparation of LLDPE doped TiO₂ films