New operational matrix of derivative for solving non-linear fractional differential equations via Genocchi polynomials

Abdulnasir Isah; Chang Phang

doi:10.1016/j.jksus.2017.02.001

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

31 (

); 1-7

doi:

10.1016/j.jksus.2017.02.001

New operational matrix of derivative for solving non-linear fractional differential equations via Genocchi polynomials

Abdulnasir Isah^{^a,^b}, Chang Phang^{^a,⁎}

a Department of Mathematics and Statistics, University Tun Hussein Onn Malaysia, 86400, Batu Pahat, Johor, Malaysia

b Department of Mathematics, Ahmadu Bello University, Zaria, Nigeria

⁎Corresponding author. pchang@uthm.edu.my (Chang Phang)

Received: 2017-1-24, Accepted: 2017-2-8, Published: 2017-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In this research, new operational method based on Genocchi polynomials for numerical solutions of non-linear fractional differential equations (NFDEs) is proposed. The Genocchi operational matrix of fractional derivative is first constructed by using some important properties of Genocchi polynomials. These operational matrices together with the collocation method are used to reduce the NFDEs into a system of non-linear algebraic equations. The error bound for this proposed method is shown. Some examples are given to display the simplicity and accuracy of the proposed technique.

Keywords

Genocchi polynomials

Operational matrix of fractional derivatives

Fractional differential equations

Collocation points

0096-3003

1 Introduction

In this article, we consider NFDEs of the form:

(1)

D^{α_{i}} y_{n} (x) = f_{n} (x, y_{1}, y_{2} . \dots, y_{n}),

where,

D^{α_{i}}

is the fractional derivative of order

α_{i}

in Caputo sense and

α_{i}

is an arbitrary order, subject to initial conditions

y_{i} (0) = d_{i}, i = 1, 2, \dots, n

Fractional calculus as a generalization of integer order differentiation and integration to an arbitrary order or fractional order, has been the focus of many studies because it was proved to be more realistic in modeling many physical phenomena. Modeling and simulation of systems or processes by using fractional derivatives will lead to the formation of fractional differential equations (FDEs). Naturally, these FDEs are difficult to solve. Hence, numerical methods are always needed. The numerical methods for solving FDEs are including the Adomian decomposition method (Hosseini and Abbasbandy (2015)), variational iteration method (Jafari et al. (2014, 2015)), homotopy perturbation method (Odibat, 2011; Johnston et al., 2016) and predictor–corrector method (Diethelm et al., 2002). On top of that, the idea of approximating the solution of FDEs using a family of basis functions is now being widely used. The most commonly used functions include block pulse functions (Mollahasani et al., 2016), Legendre polynomials (Bhrawy et al., 2016), Chebyshev polynomials (Sweilam et al., 2016), Laguerre polynomials (Gürbüz and Sezer, 2016) and etc. Different than the previous studies, in this research, we use a semi-orthogonal polynomial which also is an important member of Appell polynomials called the Genocchi polynomials. This Genocchi polynomials share some sound advantages with other members such as Bernoulli polynomials, over other classical orthogonal polynomials when approximating an arbitrary function. These advantages are stated in Loh et al. (2017) and Isah and Phang (2016). Motivated by these advantages, we attempt to introduce a new operational matrix of fractional order derivative based on Genocchi polynomials to provide approximate solutions of NFDEs (1) through collocation method. In this research direction, some numerical schemes involving operational matrix of non-orthogonal or semi-orthogonal polynomials had been developed for solving fractional calculus problems, which including Bernoulli polynomials (Keshavarz et al., 2016), Fibonacci Polynomials (Abd-Elhameed and Youssri, 2016), Lucas polynomials (Abd-Elhameed and Youssri, 2016), Boubaker Polynomials (Bolandtalat et al., 2016; Rabiei et al., 2016). Here, we compared our results with existing standard results to clearly demonstrate the simplicity, applicability and accuracy of our method.

The rest of the paper is organized as follows: Section 2, introduces some preliminaries of fractional calculus. In Section 3, Genocchi polynomials and their important properties, arbitrary function approximation and error bound are discussed. In Section 4, we derive the Genocchi operational matrix of fractional order derivative, whereas the collocation method is applied to solve NFDEs using the Genocchi operational matrix of fractional derivative in Section 5. In Section 6, the proposed method is applied to some examples. Finally, Section 7 concludes the paper.

2 Preliminaries

2.1

2.1 Fractional derivative and integration

Here, we give a recap of some definitions and properties of fractional calculus that are used in this article. There are many definitions for fractional differentiation (Kilbas et al., 2006; Podlubny, 1998). The Riemann–Liouville definition has certain disadvantages when it comes to modelling a real-world phenomenon (Kilbas et al., 2006). However, the Caputo’s definition is more reliable in application. However, the most often used definition of fractional order integral is the Riemann–Liouville integral, in which the fractional integral operator $I$ of a function $f (t)$ is defined as:

Definition 1

The Riemann–Liouville fractional integral of order $α$ of $f (t)$ is given by

(2)

I^{α} f (t) = \frac{1}{Γ (α)} \int_{0}^{t} {(t - τ)}^{α - 1} f (τ) d τ, t > 0, α \in R^{+}

where

Γ (.)

is the well known gamma function. The Riemann–Liouville fractional derivative of order

α > 0

is also defined by

$(D_{l}^{α} f) (t) = {(\frac{d}{dt})}^{m} (I^{m - α} f) (t), (α > 0, m - 1 < α < m)$

Some properties of $I^{α}$ are as follows:

(3)

I^{α} I^{β} f (t) = I^{α + β} f (t), α > 0, β > 0

(4)

I^{α} t^{β} = \frac{Γ (β + 1)}{Γ (β + α + 1)} t^{β + α}

Definition 2

The Caputo fractional derivative $D^{α}$ of a function $f (t)$ is defined as:

(5)

D^{α} f (t) = \frac{1}{Γ (n - α)} \int_{0}^{t} \frac{f^{(n)} (τ)}{{(t - τ)}^{α - n + 1}} d τ, n - 1 < α ⩽ n, n \in N .

Below are some properties of Caputo fractional derivatives;

(6)

D^{α} C = 0,

where, C is a constant.

(7)

D^{α} t^{β} = \{\begin{matrix} 0, β \in N \cup {0} & and β < ⌈ α ⌉ \\ \frac{Γ (β + 1)}{Γ (β + 1 - α)} t^{β - α}, & β \in N \cup {0} and β ⩾ ⌈ α ⌉ or β \notin N \\ and β > ⌊ α ⌋, \end{matrix}

where,

⌊ α ⌋

denotes the largest integer less than or equal to

α

and

⌈ α ⌉

is the smallest integer greater than or equal to

α

The operator $D^{α}$ is a linear operator, since,

(8)

D^{α} (λ f (t) + μ g (t)) = λ D^{α} f (t) + μ D^{α} g (t)

where

λ

and

μ

are constants.

3 Genocchi polynomials and some properties

Genocchi numbers and polynomials have been widely studied in a wide range of settings in many branches of mathematics such as elementary number theory, complex analytic number theory, homotopy theory, differential topology (differential structures on spheres) and quantum physics (quantum groups). The Genocchi numbers $G_{n}$ and polynomials $G_{n} (x)$ are usually defined respectively, by means of the exponential generating functions (Araci, 2012; Araci, 2014; Bayad and Kim, 2010 ).

(9)

Q (t) = \frac{2 t}{e^{t} + 1} = \sum_{n = 0}^{\infty} G_{n} \frac{t^{n}}{n!}, (| t | < π)

(10)

Q (t, x) = \frac{2 {te}^{xt}}{e^{t} + 1} = \sum_{n = 0}^{\infty} G_{n} (x) \frac{t^{n}}{n!}, (| t | < π)

where

G_{n} (x)

is the Genocchi polynomial of degree n and is given by

(11)

G_{n} (x) = \sum_{k = 0}^{n} (\binom{n}{k}) G_{n - k} x^{k}

G_{n - k}

here is the Gennochi number which can also be obtained from

(12)

G_{n} = 2 (1 - 2^{n}) B_{n},

where

B_{n}

is the well-known Bernoulli number. The first few Genocchi polynomials are;

$G_{0} (x) = 0$

$G_{1} (x) = 1$

$G_{2} (x) = 2 x - 1$

$G_{3} (x) = 3 x^{2} - 3 x$

$G_{4} (x) = 4 x^{3} - 6 x^{2} + 1$

$G_{5} (x) = 5 x^{4} - 10 x^{3} + 5 x$ .

Some of the important properties of Genocchi polynomials are:

(13)

\int_{0}^{1} G_{n} (x) G_{m} (x) dx = \frac{2 {(- 1)}^{n} n! m!}{(m + n)!} G_{m + n}, n, m ⩾ 1

(14)

\frac{{dG}_{n} (x)}{dx} = {nG}_{n - 1} (x), n ⩾ 1

(15)

G_{n} (1) + G_{n} (0) = 0, n > 1

From (12) and (14) it is obvious that:

(16)

G_{n} (t) = \int_{0}^{t} {nG}_{n - 1} (x) dx + G_{n}, n ⩾ 1 .

We refer the readers to Araci et al. (2014a); Araci et al. (2014b) for more properties of Genocchi polynomials and higher order Genocchi polynomials.

3.1

3.1 Function approximation

Suppose that $\{G_{1} (t), G_{2} (t), \dots, G_{N} (t)\} \subset L^{2} [0, 1]$ is the set of Genocchi polynomials and $Y = Span \{G_{1} (t), G_{2} (t), \dots, G_{N} (t)\}$ . Let $f (t)$ be arbitrary element of $L^{2} [0, 1]$ , since Y is a finite dimensional subspace of $L^{2} [0, 1]$ space, then, $f (t)$ has a unique best approximation in Y, say $f^{*} (t)$ such that

(17)

\forall y (t) \in Y, ‖ f (t) - f^{*} (t) ‖_{2} ⩽ ‖ f (t) - y (t) ‖_{2}

This implies that $\forall y (t) \in Y$

(18)

〈 f (t) - f^{*} (t), y (t) 〉 = 0

where

〈 . 〉

denotes inner product. Since

f^{*} (t) \in Y

, then there exist the unique coefficients

c_{1}, c_{2}, \dots, c_{N}

such that

(19)

f (t) \approx f^{*} (t) = \sum_{n = 1}^{N} c_{n} G_{n} (t) = C^{T} G (t)

where

C = {[c_{1}, c_{2}, \dots, c_{N}]}^{T}, G (t) = {[G_{1} (t), G_{2} (t), \dots, G_{N} (t)]}^{T}

Using (18), we have $〈 f (t) - C^{T} G (t), G_{i} (t) 〉 = 0 i = 1, 2, \dots, N$ for simplicity we write

(20)

C^{T} 〈 G (t), G (t) 〉 = 〈 f (t), G (t) 〉 .

where

〈 G (t), G (t) 〉

is an

N \times N

matrix.

Let $D = 〈 G (t), G (t) 〉 = \int_{0}^{1} G (t) G^{T} (t) dt$ , the entries of the matrix D can be calculated from (13). Therefore, any function $f (t) \in L^{2} [0, 1]$ can be expanded by Genocchi polynomials as $f (t) = C^{T} G (t)$ , where

(21)

C = D^{- 1} 〈 f (t), G (t) 〉 .

3.2

3.2 Error bound

In this section we provide the error bound for the approximated function $f (t)$ . It is important to note that, in general, $f (t)$ might fail to have a bounded derivative at certain points of the considered domain. But in our case, the smoothness of solutions of fractional differential equations in Caputo derivative sense is shown in Diethelm (2010), where a full characterization of the situation where smooth solutions exist is proven and very good results concerning the differentiability of the solution in the interval $[0, X]$ are also shown. Therefore, we suppose that $f (t) \in C^{n + 1} [0, 1]$ and $Y = Span \{G_{1} (t), G_{2} (t), \dots, G_{N} (t)\}$ if $C^{T} G (t)$ is the best approximation of $f (t)$ out of Y then $‖ f (t) - C^{T} G (t) ‖ ⩽ \frac{h^{\frac{2 n + 3}{2}} R}{(n + 1)! \sqrt{2 n + 3}}, t \in [t_{i}, t_{i + 1}] \subseteq [0, 1]$ where $R = \max_{t \in [t_{i}, t_{i + 1}]} ∣ f^{(n + 1)} (t) ∣$ and $h = t_{i + 1} - t_{i}$

To see this, we set $y_{1} (t) = f (t_{i}) + f^{'} (t_{i}) (t - t_{i}) + f^{″} (t_{i}) \frac{{(t - t_{i})}^{2}}{2!} + \dots + f^{(n)} (t_{i}) \frac{{(t - t_{i})}^{n}}{n!} .$

From Taylor’s expansion it is clear that $∣ f (t) - y_{1} (t) ∣ ⩽ ∣ f^{(n + 1)} (ξ_{t}) ∣ \frac{{(t - t_{i})}^{n + 1}}{(n + 1)!},$ where $ξ_{t} \in [t_{i}, t_{i + 1}]$ .

Since $C^{T} G (t)$ is the best approximation of $f (t)$ out of Y and $y_{1} (t) \in Y$ , then from (17), we have $‖f (t) - C^{T} G (t) ‖_{2}^{2} ⩽‖ f (t) - y_{1} (t) ‖_{2}^{2} = \int_{t_{i}}^{t_{i + 1}} ∣ f (s) - y_{1} (s) ∣^{2} ds ⩽ \int_{t_{i}}^{t_{i + 1}} {‖f^{(n + 1)} (ξ_{t})‖}^{2} \frac{{(s - t_{i})}^{n + 1}}{(n + 1)!} ds ⩽ \frac{h^{2 n + 3} R^{2}}{{((n + 1)!)}^{2} (2 n + 3)} .$

Taking the square root of both sides, we have $‖f (t) - C^{T} G (t)‖ ⩽ \frac{h^{\frac{2 n + 3}{2}} R}{(n + 1)! \sqrt{2 n + 3}}$ which is the desired result. Hence we conclude that at each sub interval $[t_{i}, t_{i + 1}], i = 1, 2, \dots, n . f (t)$ has a local error bound of $O (h^{\frac{2 n + 3}{2}})$ . Thus, $f (t)$ has a global error of $O (h^{\frac{2 n + 1}{2}})$ on the whole interval $[0, 1]$ .

The following lemma is also of great importance.

Lemma 1

Let $G_{i} (t)$ be the Genocchi polynomial then, $D^{α} G_{i} (t) = 0$ , for $i = 1, \dots, ⌈ α ⌉ - 1, α > 0$ .

The proof of this Lemma is obvious, one can use (6)–(8) on (11).

4 Genocchi operational matrix of fractional derivative

If we consider the Genocchi vector $G (t)$ given by $G (t) = [G_{1} (t), G_{2} (t), \dots, G_{N} (t)]$ , then the derivative of $G (t)$ with the aid of (14) can be expressed in the matrix form by $\frac{d G {(t)}^{T}}{dt} = M G {(t)}^{T}$ . where $M = [\begin{matrix} 0 & 0 & 0 & \dots & 0 & 0 & 0 \\ 2 & 0 & 0 & \dots & 0 & 0 & 0 \\ 0 & 3 & 0 & \dots & 0 & 0 & 0 \\ 0 & 0 & 4 & \dots & 0 & 0 & 0 \\ ⋮ & ⋮ & ⋮ & \dots & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & \dots & N - 1 & 0 & 0 \\ 0 & 0 & 0 & \dots & 0 & N & 0 \end{matrix}]$

Thus, M is $N \times N$ operational matrix of derivative.

It is not difficult to show inductively that, the $k^{th}$ derivative of $G (t)$ is given by $\frac{d^{k} G {(t)}^{T}}{{dt}^{k}} = G (t) {(M^{T})}^{k} .$

In the following theorem, we derive the operational matrix of fractional order derivative for the Genocchi polynomials.

Theorem 1

Suppose $G (t)$ is the Genocchi vector given in (19) and let $α > 0$ . Then,

(22)

D^{α} G {(t)}^{T} = P^{α} G {(t)}^{T}

where

P^{α}

N \times N

operational matrix of fractional derivative of order

α

in Caputo sense and is defined as follows:

P^{(α)} = [\begin{matrix} 0 & 0 & \dots & 0 \\ ⋮ & ⋮ & \dots & ⋮ \\ 0 & 0 & \dots & 0 \\ \sum_{k = ⌈ α ⌉}^{⌈ α ⌉} ρ_{⌈ α ⌉, k, 1} & \sum_{k = ⌈ α ⌉}^{⌈ α ⌉} ρ_{⌈ α ⌉, k, 2} & \dots & \sum_{k = ⌈ α ⌉}^{⌈ α ⌉} ρ_{⌈ α ⌉, k, N} \\ ⋮ & ⋮ & \dots & ⋮ \\ \sum_{k = ⌈ α ⌉}^{i} ρ_{i, k, 1} & \sum_{k = ⌈ α ⌉}^{i} ρ_{i, k, 2} & \dots & \sum_{k = ⌈ α ⌉}^{i} ρ_{i, k, N} \\ ⋮ & ⋮ & \dots & ⋮ \\ \sum_{k = ⌈ α ⌉}^{N} ρ_{N, k, 1} & \sum_{k = ⌈ α ⌉}^{N} ρ_{N, k, 2} & \dots & \sum_{k = ⌈ α ⌉}^{N} ρ_{N, k, N} \end{matrix}]

where

ρ_{i, k, j}

is given by:

(23)

ρ_{i, k, j} = \frac{i! G_{i - k}}{(i - k)! Γ (k + 1 - α)} c_{j}

$G_{i - k}$ is the Genocchi number and $c_{j}$ can be obtained from (21).

Proof

From (11) we have

(24)

D^{α} G_{i} (t) = \sum_{k = 1}^{i} \frac{i! G_{i - k}}{(i - k)! k!} D^{α} t^{k} = \sum_{k = ⌈ α ⌉}^{i} \frac{i! G_{i - k}}{(i - k)! Γ (k + 1 - α)} t^{k - α}

Let $f (t) = t^{k - α}$ , then if we approximate $f (t)$ using truncated Genocchi series, we have $f (t) = \sum_{j = 1}^{N} c_{j} G_{j} (t)$ .

Therefore, putting this in (24), we have

(25)

\begin{matrix} D^{α} G_{i} (t) & = \sum_{j = 1}^{N} (\sum_{k = ⌈ α ⌉}^{i} \frac{i! G_{i - k}}{(i - k)! Γ (k + 1 - α)} c_{j}) G_{j} (t) \\ = \sum_{j = 1}^{N} (\sum_{k = ⌈ α ⌉}^{i} ρ_{i, k, j}) G_{j} (t) \end{matrix}

where

ρ_{i, k, l}

is given in (23). Rewriting (25) in vector form, we have

(26)

\begin{matrix} D^{α} G_{i} (t) & = [\sum_{k = ⌈ α ⌉}^{i} ρ_{⌈ α ⌉, k, 1} \sum_{k = ⌈ α ⌉}^{i} ρ_{⌈ α ⌉, k, 2} \dots \sum_{k = ⌈ α ⌉}^{i} ρ_{⌈ α ⌉, k, N}] G (t) \\ i = ⌈ α ⌉ \dots N . \end{matrix}

Also according to Lemma 1, we can write

(27)

D^{α} G_{i} (t) = [0, 0, \dots 0] G (t) i = 1, \dots, ⌈ α ⌉ - 1

Thus, combining (26) and (27) leads to the desired result.

5 Collocation method based on Genocchi operational matrix of fractional derivative

In this section, we use the collocation method based on the Genocchi operational matrix of fractional derivatives to solve the NFDEs (1) numerically. To do this, we first approximate $y_{j} (t)$ for $j = 1, 2, \dots, n$ , by Genocchi polynomials as follows:

(28)

y_{j} (t) = \sum_{k = 1}^{N} c_{j, k} G_{k} (t) = C_{j} G {(t)}^{T} j = 1, 2, \dots, n

where,

C_{j} = [c_{j, 1}, c_{j, 2}, \dots, c_{j, N}]

is an unknown vector. Now employing (22) in (28), we have

(29)

D^{α} y_{j} (t) ≃ C_{j} P^{(α)} G {(t)}^{T}, j = 1, 2, \dots, n .

Therefore, substituting (28) and (29) in (1), we have

(30)

\begin{matrix} C_{j} P^{(α)} G {(t)}^{T} & = f_{j} (t, C_{1} G {(t)}^{T} C_{2} G {(t)}^{T}, \dots, C_{n} G {(t)}^{T}) \\ j = 1, 2, \dots, n . \end{matrix}

From the initial conditions we have

(31)

C_{j} G {(0)}^{T} = d_{j} j = 1, 2, \dots, n .

To find the solution of (1), we collocate (30) at the collocation points $t_{i} = \frac{i}{N - 1}, i = 1, 2, \dots, N - 1$ to obtain

(32)

\begin{matrix} C_{j} P^{(α)} G {(t_{i})}^{T} & = f_{j} (t_{i}, C_{1} G {(t_{i})}^{T} C_{2} G {(t_{i})}^{T}, \dots, C_{n} G {(t_{i})}^{T}) \\ i = 1, 2, \dots, N - 1, j = 1, 2, \dots, n . \end{matrix}

Thus, (32) contains $n (N - 1)$ algebraic equations. These equations together with (31) make $n (N)$ algebraic equations which can be solved through Newton’s iterative method. Thus, $y_{j} (t)$ given in (28) can be calculated.

The procedure can be easily extend to solve the nonlinear system of fractional differential equations (NSFDEs).

6 Numerical examples

In this section, we solve some examples to illustrate the applicability and accuracy of the proposed method. All the numerical computations are carried out using Maple 18.

Example 1

First let’s consider the following fractional differential equation solved using B spline operational method in Lakestani et al. (2012).

(33)

D^{2} y (t) + Γ (\frac{4}{5}) t^{\frac{6}{5}} D^{\frac{6}{5}} y (t) + \frac{11}{9} Γ (\frac{5}{6}) t^{\frac{1}{6}} D^{\frac{1}{6}} y (t) - {(y^{'} (t))}^{2} = 2 + \frac{1}{10} t^{2}

subject to,

y (0) = 1, y (1) = 2

. The exact solution is given by

y (t) = t^{2} + 1

We consider this problem when $N = 3, 4, 5, 6$ and 7. The $L^{2}$ and $L^{\infty}$ errors of the results obtained are compared with that obtained using B-spline operational method (Lakestani et al., 2012) as shown in Table 1. From this table one can observe that despite the simplicity of our operational method, we are able to get a more accurate result than that obtained using B spline operational method in Lakestani et al. (2012).

Example 2

We consider the following system of fractional differential equations as in Chen et al. (2010).

(34)

\begin{matrix} D^{\frac{3}{2}} y_{1} (t) = \frac{2 Γ (8) t^{\frac{1}{2}}}{Γ (\frac{13}{2})} y_{2} (t) - \frac{2 Γ (8) t^{\frac{1}{2}}}{Γ (\frac{13}{2})} - \frac{Γ (3) t^{\frac{1}{2}}}{Γ (\frac{3}{2})} \\ D^{\frac{5}{3}} y_{2} (t) = \frac{Γ (6) t^{- \frac{11}{3}}}{2 Γ (\frac{13}{3})} y_{1} (t) + \frac{Γ (6) t^{- \frac{5}{3}}}{2 Γ (\frac{13}{3})} \end{matrix}

subject to,

y_{1} (0) = 0, y_{1} (1) = 1 y_{2} (0) = 1, y_{2} (1) = 2

Table 1 Comparison of the

L^{2}

and

L^{\infty}

errors obtained by the present method and that in Lakestani et al. (2012) for numerical solution

y (t)

for Example 1.

$L^{2}$ Error		$L^{\infty}$ Error
Lakestani et al. (2012)	Present method	Lakestani et al. (2012)	Present method
1.9E−3 $(J = 3)$	1.323E−4 $(N = 3)$	5.1E−3 $(J = 3)$	1.8119E−4 $(N = 3)$
4.7E−4 $(J = 4)$	3.377E−5 $(N = 4)$	1.2E−3 $(J = 4)$	5.5528E−5 $(N = 4)$
1.2E−4 $(J = 5)$	1.698E−5 $(N = 5)$	3.3E−4 $(J = 5)$	1.8466E−5 $(N = 5)$
3.0E−5 $(J = 6)$	9.990E−6 $(N = 6)$	8.1E−5 $(J = 6)$	1.3312E−5 $(N = 6)$
7.6E−6 $(J = 7)$	9.262E−6 $(N = 7)$	2.1E−5 $(J = 7)$	1.4556E−5 $(N = 7)$

The exact solutions of this system are given by $y_{1} (t) = 2 t^{7} - t^{2}$ and $y_{2} (t) = t^{5} + 1$ This example is solved in Chen et al. (2010) using Legendre wavelets method, with $M = 4$ and different values of k. We used Genocchi polynomials operational method and compared the absolute errors obtained with Legendre wavelets method and that of our method for $y_{1} (t)$ and $y_{2} (t)$ . The results are shown in Table 2 and 3 respectively.

Example 3

Consider the following NSFDE.

(35)

\begin{matrix} D^{\frac{3}{2}} y_{1} (t) = - 8 y_{1} (t) + y_{2}^{2} (t) - 4 t^{6} + 4 t^{3} + \frac{8 t^{\frac{3}{2}}}{\sqrt{π}} - 1 \\ D^{\frac{1}{2}} y_{2} (t) = t^{2} D^{1} y_{1} (t) + y_{2} (t) - 3 t^{4} - 2 t^{3} + \frac{32 t^{\frac{5}{2}}}{5 \sqrt{π}} - 1 \end{matrix}

subject to,

y_{1} (0) = 0, y_{2} (0) = 1, y_{1} (1) = 1, y_{2} (1) = 3, y_{1}^{'} (0) = 0, y_{1}^{'} (1) = 3

Table 2 Comparison of the absolute errors obtained by the present method and that in Chen et al. (2010) for numerical solution

y_{1} (t)

for Example 2.

t	Chen et al. (2010) $k = 3$	Present method $N = 8$	Chen et al. (2010) $k = 4$	Present method $N = 16$	Chen et al. (2010) $k = 5$	Present method $N = 20$
0.2	5.4189E−5	1.90235E−5	5.4369E−6	8.95309E−8	2.7929E−6	2.48113E−7
0.4	2.1851E−4	3.42767E−5	1.1205E−4	1.47111E−5	7.1572E−5	1.04730E−5
0.6	3.9439E−3	2.72428E−4	2.5271E−3	3.02569E−4	1.2697E−3	1.88619E−4
0.8	3.7760E−2	3.77612E−4	1.9787E−2	2.25477E−3	5.4447E−3	1.41045E−3

Table 3 Comparison of the absolute errors obtained by the present method and that in Chen et al. (2010) for numerical solution

y_{2} (t)

, for Example 2.

t	Chen et al. (2010) $k = 3$	Present method $N = 8$	Chen et al. (2010) $k = 4$	Present method $N = 16$	Chen et al. (2010) $k = 5$	Present method $N = 20$
0.2	7.3753E−4	3.64710E−4	2.0239E−4	4.20073E−6	4.6757E−5	3.93829E−6
0.4	7.2903E−4	2.93359E−4	4.5844E−4	6.05796E−5	8.2082E−5	3.47028E−5
0.6	6.1980E−3	1.21135E−4	3.4222E−3	4.21201E−4	7.6776E−4	2.61086E−4
0.8	2.9120E−2	2.09568E−4	8.4107E−3	1.77011E−3	2.9426E−3	1.10169E−3

The exact solution of this system is known to be $y_{1} (t) = t^{3}, y_{2} (t) = 2 t^{3} + 1$ . We solve this problem using the present method. The absolute error for solutions $y_{1} (t)$ and $y_{2} (t)$ obtained with different values of N are shown in Table 4.

Example 4

Consider the following NSFDE (Wu and Xia, 2001; Dixit et al., 2011).

(36)

\begin{matrix} D^{α} y_{1} (t) = - 1002 y_{1} (t) + 1000 y_{2}^{2} (t) \\ D^{α} y_{2} (t) = y_{1} (t) - y_{2} (t) - y_{2}^{2} (t) \end{matrix}

subject to,

y_{1} (0) = 1, y_{2} (0) = 1

Table 4 Absolute errors obtained by the present method for numerical solution

y_{1} (t)

and

y_{2} (t)

, for Example 3.

	$N = 6$		$N = 10$		$N = 15$
t	$y_{1} (t)$	$y_{2} (t)$	$y_{1} (t)$	$y_{2} (t)$	$y_{1} (t)$	$y_{2} (t)$
0.2	8.34845E−5	2.65555E−4	3.17722E−5	2.97062E−5	9.53891E−6	4.67442E−6
0.4	6.77277E−5	2.39200E−4	1.99578E−5	3.78689E−5	6.37208E−6	6.73884E−6
0.6	5.23846E−5	3.81107E−4	3.29544E−6	6.70313E−5	5.36904E−7	1.33571E−5
0.8	7.66654E−5	4.24562E−4	2.70757E−5	1.16860E−4	6.23829E−6	2.74888E−5

The exact solution of this system when $α = 1$ is known to be $y_{1} (t) = e^{- 2 t}$ and $y_{2} (t) = e^{- t}$ . This example is solved by our method with $N = 10$ when $α = 0.9, 0.75, 0.5, 0.25$ . The results are compared with the exact solution $(α = 1)$ in Fig. 1 in which the figures affirm that when $α$ approaches 1, our results approach the exact solution. The results obtained when $α = 0.25, 0.5, 0.9$ for $y_{1} (t)$ and $y_{2} (t)$ are also shown in Table 5. We also compared the absolute error obtained by our method and that in Wu and Xia (2001) when $t = 1$ in Table 6.

Example 5

Here we consider the following NSFDE (Zurigat et al., 2001; Dixit et al., 2011).

(37)

\begin{matrix} D^{α} y_{1} (t) = \frac{y_{1} (t)}{2} \\ D^{α} y_{2} (t) = {(y_{1} (t))}^{2} + y_{2} (t) \end{matrix}

subject to,

y_{1} (0) = 1, y_{2} (0) = 0

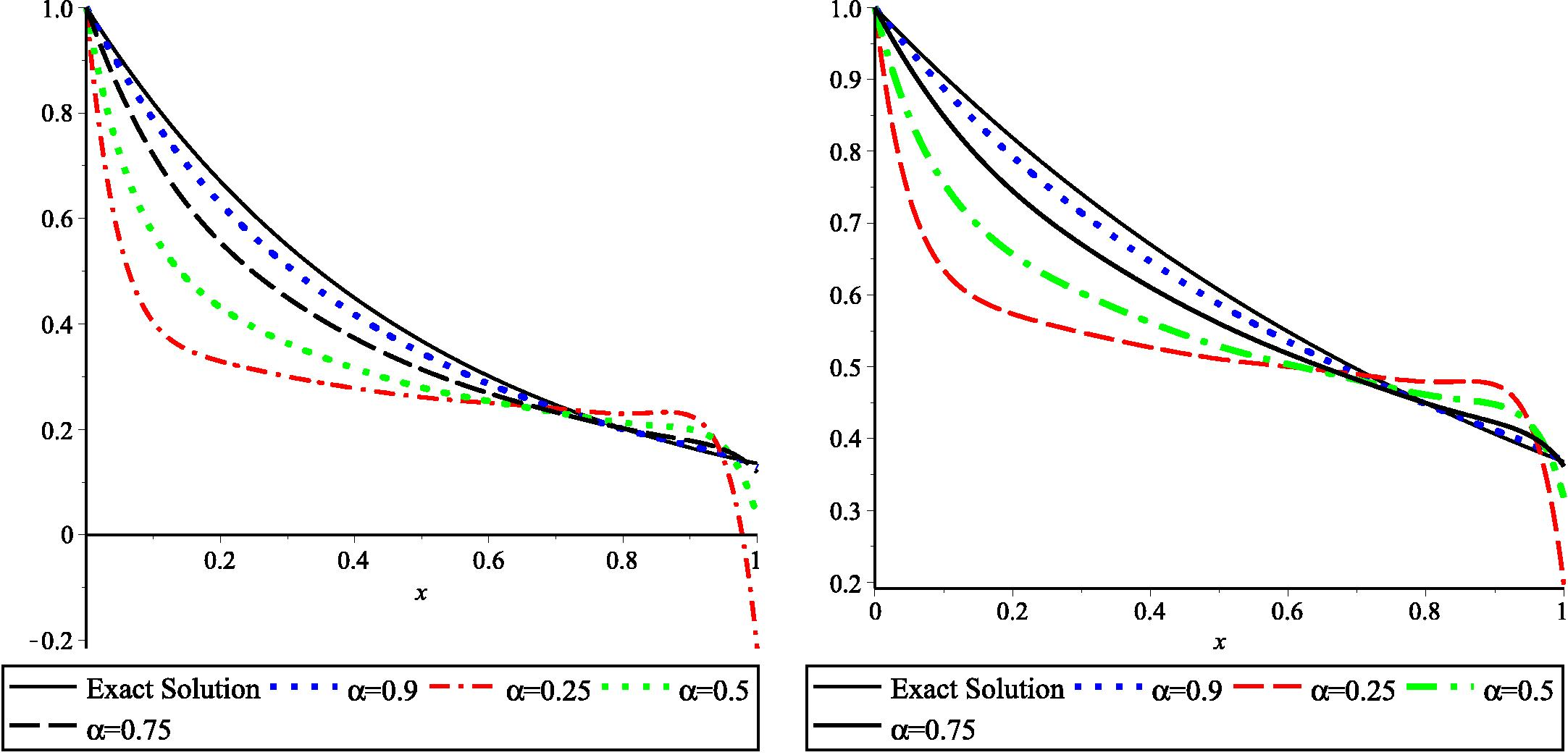
Comparison of our solutions y 1 ( x ) and y 2 ( x ) respectively, when α = 1 , 0.9 , 0.75 , 0.5 and 0.25 for Example 4.

Table 5 Numerical solutions

y_{1} (t)

and

y_{2} (t)

, when

α = 0.25, 0.5, 0.9

obtained by the present method for Example 4.

	$α = 0.25$		$α = 0.5$		$α = 0.9$
t	$y_{1} (t)$	$y_{2} (t)$	$y_{1} (t)$	$y_{2} (t)$	$y_{1} (t)$	$y_{2} (t)$
0.2	0.3292530	0.5736073	0.4312529	0.6565720	0.6283094	0.7926404
0.4	0.2781248	0.5271530	0.3157611	0.5617578	0.4179744	0.6464731
0.6	0.2503713	0.5001338	0.2537459	0.5035336	0.2863979	0.5351088
0.8	0.2299841	0.4793216	0.2128393	0.4611347	0.2007005	0.4479343

Table 6 Absolute errors obtained by the present method and that in Wu and Xia (2001) at

t = 1

for Example 4.

t	$Y (t)$	Error Wu and Xia (2001) $h = 0.002$	Our Error $N = 10$
1	$y_{1} (t)$	2.5606E−7	3.70730E−08
	$y_{2} (t)$	8.0150E−8	2.09476E−11

The exact solution of this system when $α = 1$ is known to be $y_{1} (t) = e^{\frac{t}{2}}$ and $y_{2} (t) = {te}^{t}$ . We consider this example when $N = 10$ and $α = 0.95, 0.9, 0.7, 0.5$ and the results are compared with the exact solution when $α = 1$ as shown in Fig. 2. The figures affirm that when $α$ approaches 1, our results approach the exact solution. We also reported the numerical results for $y_{1} (t)$ and $y_{2} (t)$ when $α = 0.5, 0.7, 0.9$ in Table 7.

Example 6

Lastly, we consider the following NSFDE (Zurigat et al., 2001; Dixit et al., 2011).

(38)

\begin{matrix} D^{α} y_{1} (t) = y_{1} (t) \\ D^{α} y_{2} (t) = 2 {(y_{1} (t))}^{2} \\ D^{α} y_{3} (t) = 3 y_{1} (t) y_{2} (t) \end{matrix}

subject to,

y_{1} (0) = 1, y_{2} (0) = 1 y_{3} (0) = 0

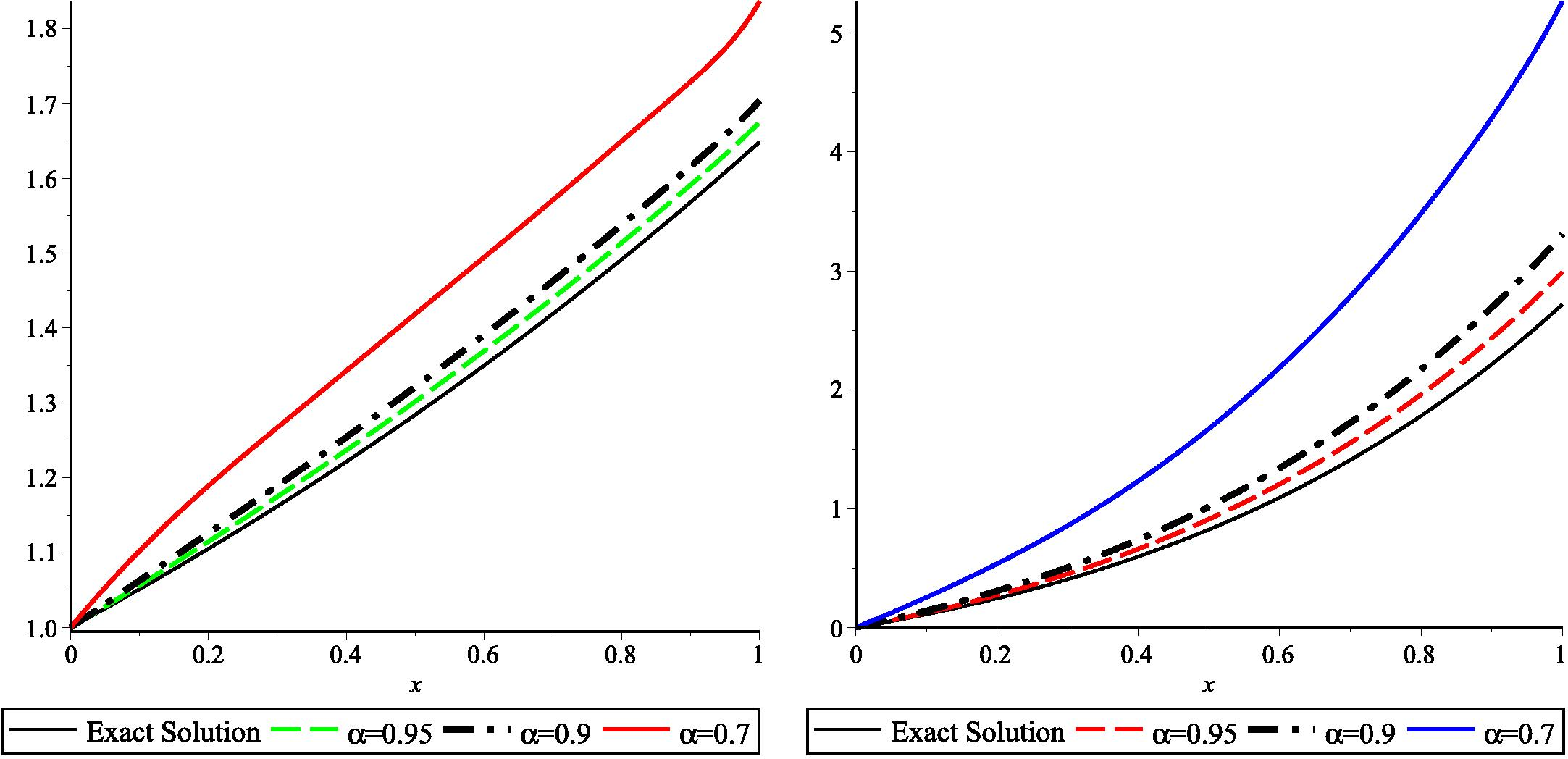
Comparison of our solutions y 1 ( x ) and y 2 ( x ) respectively, when α = 0.95 , 0.9 , 0.7 and 1 for Example 5.

Table 7 Numerical solutions

y_{1} (t)

and

y_{2} (t)

, when

α = 0.5, 0.7, 0.9

obtained by the present method for Example 5.

	$α = 0.5$		$α = 0.7$		$α = 0.9$
t	$y_{1} (t)$	$y_{2} (t)$	$y_{1} (t)$	$y_{2} (t)$	$y_{1} (t)$	$y_{2} (t)$
0.2	1.2931031230	1.0835866399	1.1892580591	0.5361674631	1.1260021754	0.3073945918
0.4	1.4695250791	2.3646303626	1.3428046690	1.2320138557	1.2541212454	0.7383813062
0.6	1.6293827449	4.0691446057	1.4944201345	2.1872479471	1.3906810301	1.3411957180
0.8	1.7841485799	6.3194120920	1.6499360492	3.4822704268	1.5380075467	2.1711230181

The exact solution of this system when $α = 1$ is known to be $y_{1} (t) = e^{t}$ , $y_{2} (t) = e^{2 t}$ and $y_{3} (t) = e^{3 t} - 1$ . The example is solved using our method with $N = 10$ . The absolute errors obtained for $y_{1} (t), y_{2} (t)$ and $y_{3} (t)$ are shown in Table 8.

Table 8 Absolute errors obtained by the present method for numerical solution

y_{1} (t), y_{2} (x)

and

y_{3} (t)

, for Example 6.

t	Abs. Err $y_{1} (t)$	Abs. Err $y_{2} (t)$	Abs. Err $y_{3} (t)$
0.2	0.00000E+00	7.10000E−08	6.66760E−06
0.4	0.00000E+00	7.30000E−08	6.74900E−06
0.6	1.00000E−09	7.30000E−08	6.82000E−06
0.8	0.00000E+00	7.20000E−08	6.88000E−06

This example is also solved when $α = 0.9, 0.7, 0.5$ and the results are compared with the exact solution when $α = 1$ as shown in Fig. 3 and it affirms that when $α$ approaches 1, our results approach the exact solution.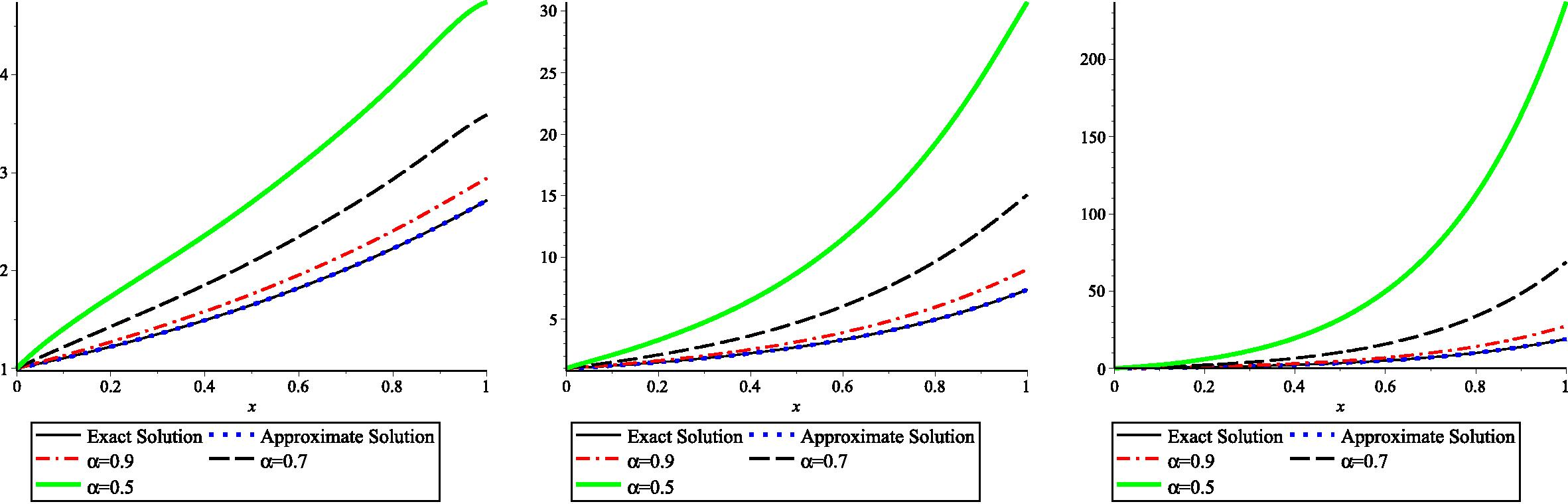

Comparison of our solutions y 1 ( t ) , y 2 ( t ) and y 3 ( t ) respectively, when α = 0.9 , 0.7 , 0.5 and 1 for Example 6.

7 Conclusion

In this paper, a new operational matrix based on the Genocchi polynomials is derived and applied together with the collocation method to numerically solve the NFDEs. The comparison of the results shows that the present method is a simple and good mathematical tool for finding the numerical solutions of NFDEs. The advantage of this operational matrix over others is that it has less computational complexity because every operational matrix of differentiation involves more numbers of zeros and thus, reduces the run time and provides the solution with high accuracy.

Acknowledgment

This work was supported in part by FRGS Grant Vot 1433. We also thank for financial support from UTHM through GIPS U060.

References

Abd-Elhameed W., Youssri Y., . Spectral solutions for fractional differential equations via a novel Lucas operational matrix of fractional derivatives. Rom. J. Phys.. 2016;61:795-813.
[Google Scholar]
Abd-Elhameed W.M., Youssri Y.H., . A novel operational matrix of Caputo fractional derivatives of Fibonacci polynomials: Spectral solutions of fractional differential equations. Entropy. 2016;18:345.
[Google Scholar]
Araci S., . Novel identities for q-Genocchi numbers and polynomials. Journal of Function Spaces and Applications. 2012;2012
[Google Scholar]
Araci S., . Novel identities involving Genocchi numbers and polynomials arising from applications of umbral calculus. Appl. Math. Comput.. 2014;233:599-607.
[Google Scholar]
Araci S., Acikgoz M., Sen E., . Some new formulae for Genocchi numbers and polynomials involving Bernoulli and Euler polynomials. Internat. J. Math. Math. Sci.. 2014;2014
[Google Scholar]
Araci S., Sen E., Acikgoz M., . Theorems on Genocchi polynomials of higher order arising from Genocchi basis. Taiwanese J. Math.. 2014;18:473.
[Google Scholar]
Bayad A., Kim T., . Identities for the Bernoulli, the Euler and the Genocchi numbers and polynomials. Adv. Stud. Contemp. Math.. 2010;20:247-253.
[Google Scholar]
Bhrawy A., Doha E., Ezz-Eldien S., Abdelkawy M., . A numerical technique based on the shifted Legendre polynomials for solving the time-fractional coupled KdV equations. Calcolo. 2016;53:1-17.
[Google Scholar]
Bolandtalat A., Babolian E., Jafari H., . Numerical solutions of multi-order fractional differential equations by Boubaker polynomials. Open Physics. 2016;14:226-230.
[Google Scholar]
Chen Y., Ke X., Han X., Sun Y., Liu L., . Wavelets methods for solving system of fractional differential equations and the convergence analysis. J. Shandong Univ.. 2010;50:67-74.
[Google Scholar]
Diethelm K., . The analysis of fractional differential equations: An application-oriented exposition using differential operators of Caputo type. Springer; 2010.
Diethelm K., Ford N.J., Freed A.D., . A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn.. 2002;29:3-22.
[Google Scholar]
Dixit S., Singh O., Kumar S., . An analytic algorithm for solving system of fractional differential equations. J. Mod Meth Numer Math.. 2011;1:12-26.
[Google Scholar]
Gürbüz B., Sezer M., . Laguerre polynomial solutions of a class of initial and boundary value problems arising in science and engineering fields. Acta Phys. Pol., A. 2016;130:194-197.
[Google Scholar]
Hosseini S.G., Abbasbandy S., . Solution of Lane-Emden type equations by combination of the spectral method and Adomian decomposition method. Math Probl Eng. 2015;2015
[Google Scholar]
Isah A., Phang C., . Genocchi wavelet-like operational matrix and its application for solving non-linear fractional differential equations. Open Physics. 2016;14:463-472.
[Google Scholar]
Jafari H., Kadem A., Baleanu D., . Variational iteration method for a fractional-order Brusselator system. In: Abstr. Appl. Anal.. Hindawi Publishing Corporation; 2014.
[Google Scholar]
Johnston S., Jafari H., Moshokoa S., Ariyan V., Baleanu D., . Laplace homotopy perturbation method for Burgers equation with space-and time-fractional order. Open Physics. 2016;14:247-252.
[Google Scholar]
Keshavarz E., Ordokhani Y., Razzaghi M., . A numerical solution for fractional optimal control problems via Bernoulli polynomials. J. Vib. Control. 2016;22:3889-3903.
[Google Scholar]
Kilbas A.A.A., Srivastava H.M., Trujillo J.J., . Theory and applications of fractional differential equations. volume 204. Elsevier Science Limited; 2006.
Lakestani M., Dehghan M., Irandoust-Pakchin S., . The construction of operational matrix of fractional derivatives using B-spline functions. Commun. Nonlinear Sci. Numer. Simul.. 2012;17:1149-1162.
[Google Scholar]
Loh J.R., Phang C., Isah A., . New operational matrix via Genocchi polynomials for solving Fredholm-Volterra fractional integro-differential equations (FIDEs) Adv. Math. Phys.. 2017;2017 12 pages
[CrossRef] [Google Scholar]
Mollahasani N., Moghadam M.M.M., Afrooz K., . A new treatment based on hybrid functions to the solution of telegraph equations of fractional order. Appl. Math. Model.. 2016;40:2804-2814.
[Google Scholar]
Odibat Z., . On Legendre polynomial approximation with the VIM or HAM for numerical treatment of nonlinear fractional differential equations. J. Comput. Appl. Math.. 2011;235:2956-2968.
[Google Scholar]
Podlubny I., . Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. volume 198. Academic press; 1998.
Rabiei K., Ordokhani Y., Babolian E., . The Boubaker polynomials and their application to solve fractional optimal control problems. Nonlinear Dyn. 2016:1-14.
[Google Scholar]
Sweilam N., Nagy A., El-Sayed A.A., . On the numerical solution of space fractional order diffusion equation via shifted Chebyshev polynomials of the third kind. J. King Saud Univ. Sci.. 2016;28:41-47.
[Google Scholar]
Wazwaz A.M., . Solving two Emden-Fowler type equations of third order by the variational iteration method. Appl. Math. Inf. Sci.. 2015;9:2429-2436.
[Google Scholar]
Wu X.Y., Xia J.L., . Two low accuracy methods for stiff systems. Appl. Math. Comput.. 2001;123:141-153.
[Google Scholar]
Zurigat M., Momani S., Odibat Z., Alawneh A., . The homotopy analysis method for handling systems of fractional differential equations. Appl. Math. Model.. 2001;34:24-35.
[Google Scholar]