Translate this page into:
New extension of Burr type X distribution properties with application
⁎Corresponding author. fmerovci@yahoo.com (Faton Merovci)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
We introduce a new distribution named Exponentiated Generalized Burr type X (EGBX) distribution with four parameters. This new model can be expressed as a mixture of Burr type X (BX) distribution with different parameters. Several sub models are investigated and also some important structure properties of new model are derived including the quantile function, limit behavior, the rth moment, the moment-generating function, Rényi entropy, and order statistics. We estimate the parameters using the maximum likelihood estimation. Finally, simulation study is carried at under varying sample size to assess the performance of this model, the flexibility of EGBX distribution is illustrated by using real data set.
Keywords
Burr type X
Exponentiated generalized
Quantile function
Moment
Estimation
1 Introduction
Recently, several attempts have been established and studied to define new models that extend the baseline distributions. Burr (1942) introduced twelve distributions using differential equation. Burr type X with one parameter (BX1) and Burr type XII distributions have received much attention in the literatures. Surles and Padgett (2001) proposed a new extension for Burr type X one parameter by adding scale parameter named Burr type X with two parameters or Burr type X (BX) distribution. Many authors have studied widely BX distribution and applied them in different areas such as Burr (1942), Merovci et al. (2016),Raqab and Kundu (2006), Shayib and Haghighi (2011) and Merovci et al. (2016) and many others. The cumulative distribution function (cdf) of BX is given by:
The hazard rate functions of the BX distribution is: and the r th moment for BX distribution is given as:
Many families have been established in recent years, Eugene et al. (2002) proposed and study a general class of distributions based on the logic of a beta random variable named Beta-G family distribution and added two shape parameters. Zografos and Balakrishnan (2009) and Ristic and Balakrishnan (2012) used gamma class of family. In Cordeiro et al. (2013) proposed the Exponentiated Generalized (EG) class of distribution with two extra shape parameters. The term of “Exponentiated” and “Generalized” are mean the process of transforming a quantity to some positive real number. The new class of distribution gives more flexibility for the baseline of distribution. The cumulative distribution function of EG is given by:
The first motivation is based on the two extra shape parameters of EG family which place a very important role in generating a distribution with heavier tail. The second motivation is the EG family can be applied more effectively on censored incomplete data because its more tractable the beta-G family. Therefore, the new model can analyze continuous univariate and multivariate sets.
In this paper, we propose a new extension of Burr type X distribution with more flexibility than the baseline (2). The new distribution can be applied to different kind of data because the three shape parameters can control the tail of data. The new distribution has more sub-models when compared with baseline distribution and hence it allows us to study more comprehensive structural properties.
Thus, the aims of this work are to explore and study the mathematical properties of the new distribution, which is an extended BX distribution and to prove the new model is more flexible than other models by applying it to real data using a goodness of fit test for real data.
The rest of this paper is arranged as follows: In Section 2, The cumulative function, density function and hazard function of the new distribution are defined. The expansion including the pdf and cdf are provided in Section 3. In Section 4, some mathematical properties of the new model are studied and discussed, such as the quantile function, limit behavior, the r th moment, the moment-generating function, Rényi entropy and order statistics. The parameters of new distribution are estimated using the maximum likelihood method in Section 5. In Section 6, two real datasets are used to illustrate the usefulness of the new model. Finally, concluding remarks are presented in Section 7.
2 Exponentiated Generalized Burr type X
In this section, the four parameter Exponentiated Generalized Burr type X (EGBX) distribution is examined. Several authors have used the EG method to study and explore many distributions. Exponentiated Generalized Inverse Weibull (EGIW) distribution is proposed by using the cdf of Inverse Weibull distribution. In Oguntunde et al. (2015) used the cdf of Weibull distribution to propose the Exponentiated Generalized Weibull (EGW) distribution by applying the Eq. (3). Andrade et al. (2015) used cdf of Gumbel distribution to find a new generalization of Gumbel distribution named Exponentiated Generalized Gumbel (EGGu) distribution.
Let
be the cdf of Burr type X distribution. Inserting (1) in (3) we have the cdf of the new extension of Burr type X distribution named Exponentiated Generalized Burr type X (EGBX) distribution as given in Eq. (5)
X EGBX denotes a random variable with the pdf (6).
The hazard function of X is given by:
The survival function of X is given by:
Figs. 1 and 2 display a variety of possible shapes of pdf and cdf of EGBX distribution for selected values of parameters
, and
. In Fig. 3. the hazard function of the EGBX distribution are shown and it can be seen that the hazard function can take many different shapes like bathtub,inverted bathtub and monotonically increasing or decreasing depending on the parameter values and a such can be useful for modeling different types of data.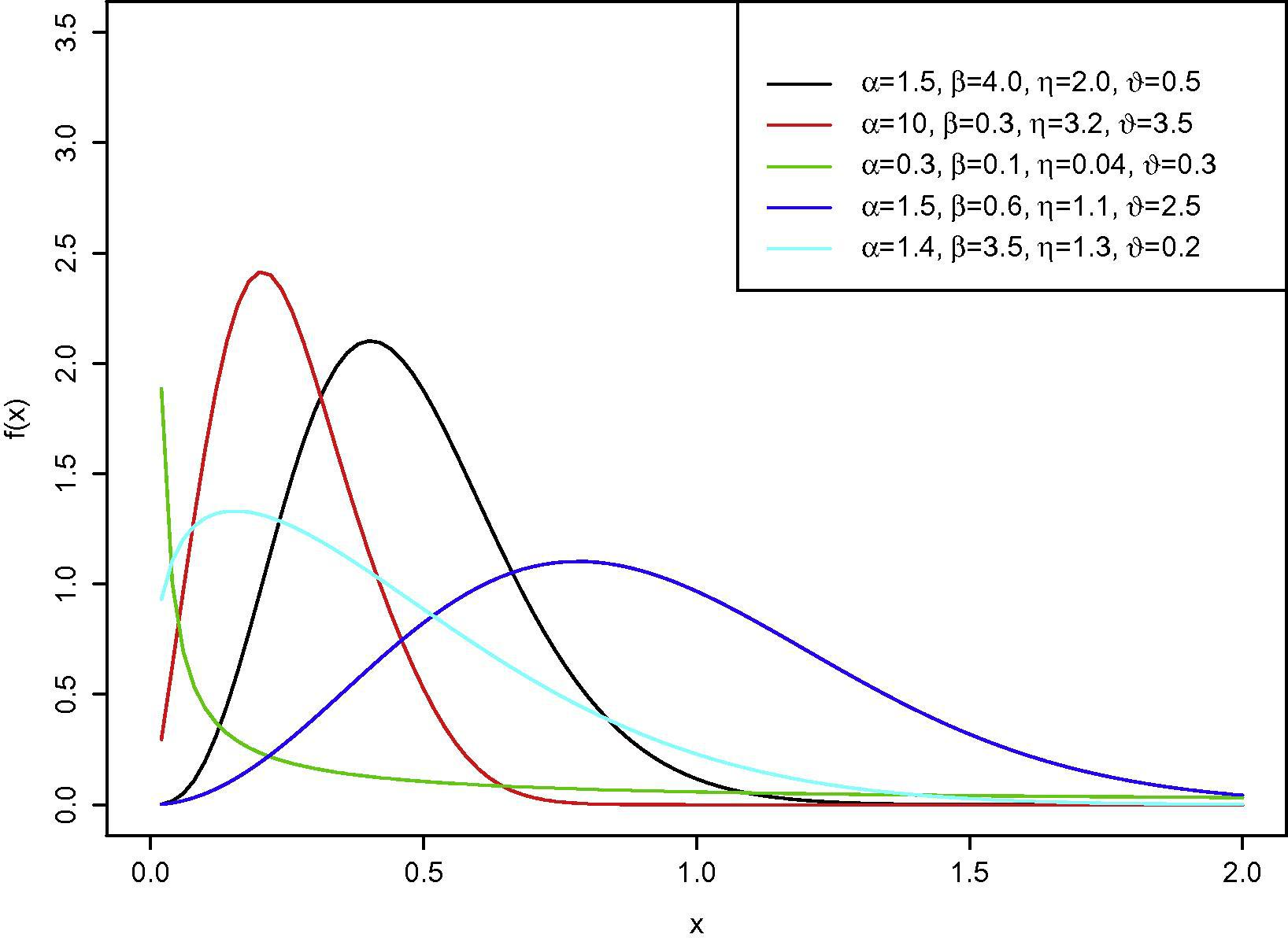
Plot of the EGBX density function for different values of
and
.
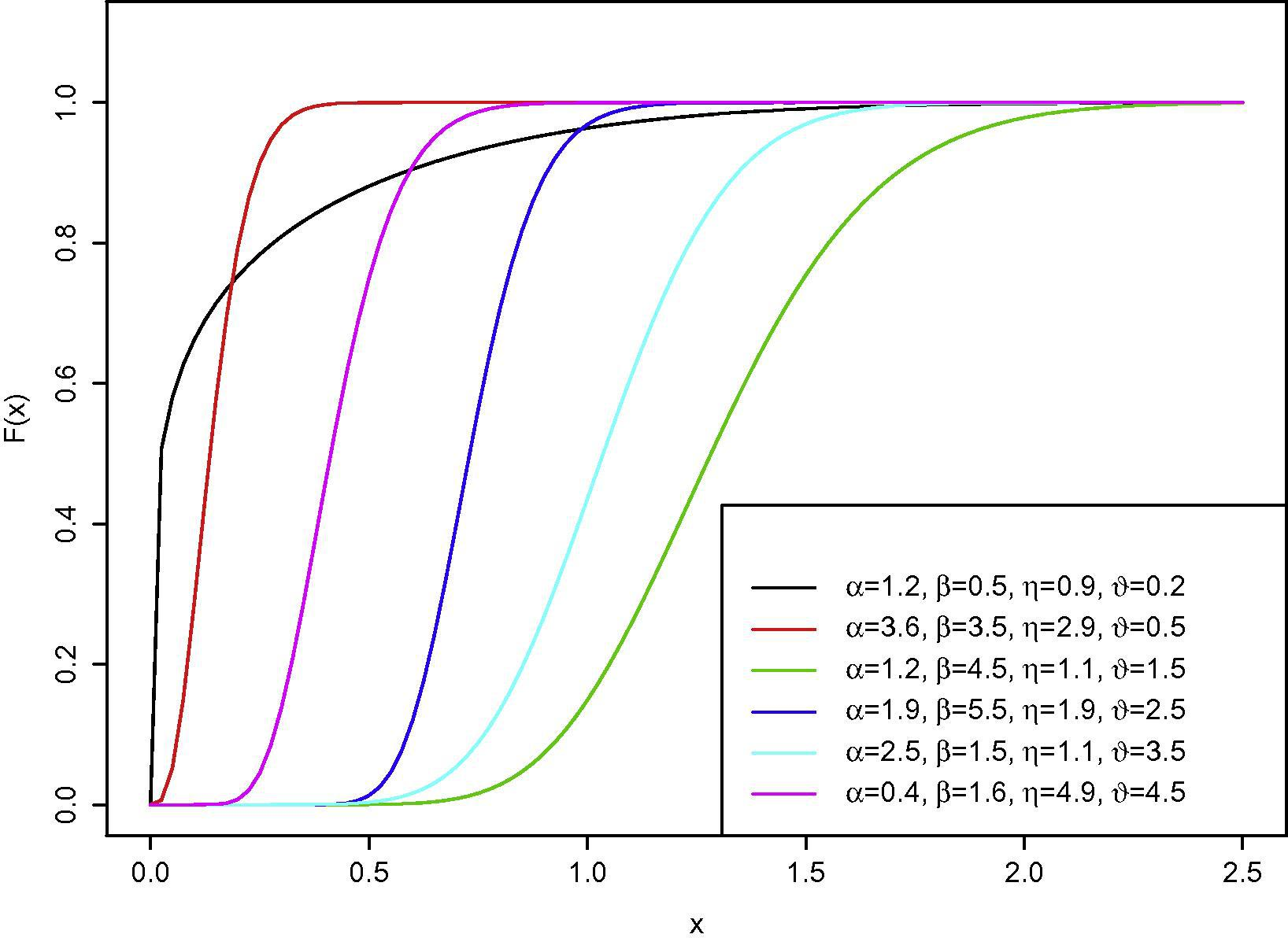
Plot of the EGBX cumulative function for different values of
and
.
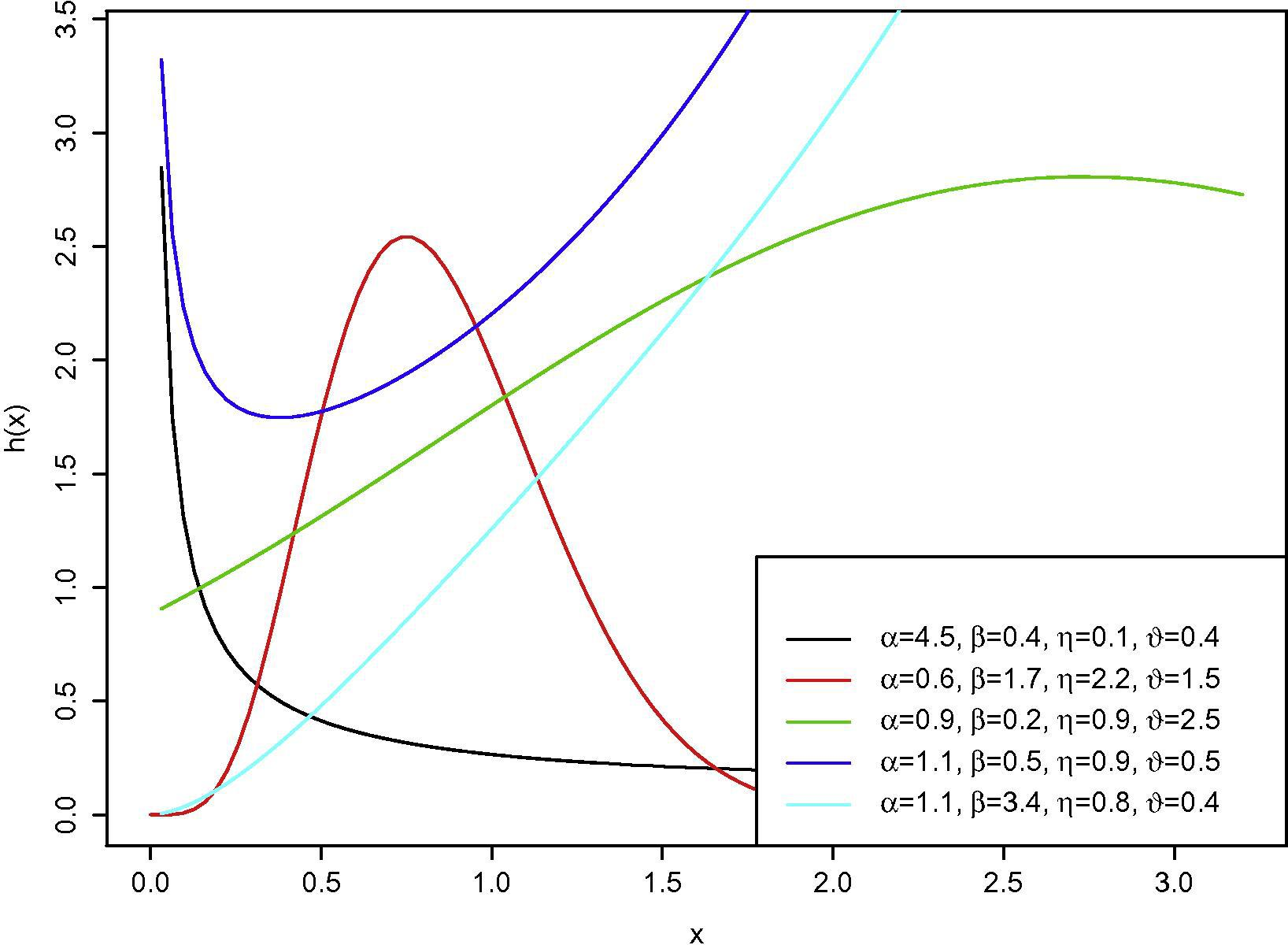
Plot of the EGBX hazard function for some different values of of
and
.
2.1 Sub-models
It is worth noting that many sub-models can be obtained as special cases of the EGBX distribution by selecting specific values of parameters in Eq. (6). such as Exponentiated Generalized Rayleigh (EGR), Exponentiated Generalized Burr type X with one parameter (EGBX1), Generalized Burr type X (GBX), Generalized Burr type X with one parameter (GBX1), Exponentiated Burr type X (EBX), Exponentiated Rayleigh (ER) distributions and others distributions. Table 1 summarize some sub-models of EGBX distribution by equit the parameters to number 1.
Parameters
Distribution
Exponentiated Burr type X (EBX)
1
Exponentiated Burr type X with one parameter (EBX1)
1
1
Exponentiated Rayleigh (ER)
1
1
Generalized Burr type X (GBX)
1
Generalized Burr type X with one parameter (GBX1)
1
1
Generalized Rayleigh (GR)
1
1
Burr type X(BX)
1
1
Burr type X with one parameter (BX1)
1
1
1
Rayleigh (R)
1
1
1
3 Expansion of pdf and cdf
In this section, expansion for the pdf and cdf of the EGBX distribution are derived, which are useful to study several statistical properties of EGBX distribution. The generalized binomial is used to find the expression of the pdf and cdf. For any positive real non-integer
, the generalized binomial is giving by (see Jeffrey and Zwillinger, 2007):
by repeated application of the generalized binomial to Eq. (6) we obtain the Eq. (6) of EGBX:
Eq. (8) can be expressed as an infinite weighted linear combination of Burr type X ( )) distribution random variable.
The expansion of cdf can be found by applying the binomial expansion also twice for positive real number and we have:
Eqs. (8) and (9) would be useful in deriving some mathematical properties of the EGBX distribution like the moments and moment generation function directly.
4 Mathematical properties
In this section, some important mathematical properties of the EGBX distribution are explored, specifically the quantile function, limit behavior, the rth moment, the moment-generating function, Rényi entropy, and order statistics.
4.1 Quantile function
Quantile function (qf) of continuous distribution are usefull in many application like Bowley’s skewness and Moor’s kurtosis and generated frequency of occurrence of the distribution.
The cdf of the EGBX distribution (5) is inverted to obtain the qf which is given as follows:
In particular the EGBX median of X is .
Simulating the EGBX random variable is straightforward if U is a continuous uniform variable on the unit interval
. By using the inverse transformation method, the random variable X is given by:
Eq. (11) is used to generate random numbers from the EGBX distribution when the parameters and are known.
4.2 Limit behavior
In this sub section, we investigate the limit behavior of the pdf of EGBX distribution as and .
The because the because
4.3 Moments
In this sub section, we try to find the r th moment for EGBX distribution. Moments are very necessary and significant in any statistical analysis, especially for application studies. Several important features can be studied using moments, such as mean, median, tendency, skewness and kurtosis. The rth moment for EGBX can be defined as:
Using the pdf of the EGBX distribution in Eq. (8) gives:
Eq. (14) is also important for finding many measures, such as the mean, coefficient of central moments, variance, cumulants, skewness and kurtosis, or anthers properties. Setting in Eq. (14) gives the mean of X. Similarly, the central moment and the cumulants of X are obtained from (14) as: and respectively, where , and
. The Coefficient of variation (CV), Skewness ( ), and Kurtosis ( ) can be determined from the above forms as: respectively. Furthermore, Eq. (14) can be used to find the moment-generating function (mgf).
4.4 Moment generating function
The moment generating function for EGBX distribution is given by:
The well-known definition of for the random variable X starts with probability density function given by: By using the representation Then (see Jeffrey and Zwillinger (2007)), and by using the Eq. (14), is found as follows: where which completes the proof. □
4.5 Rényi entropy
Rényi entropy is a measure of variation or uncertainty of random variable. It is a very popular entropy measure in many fields of science such as engineering, theory of communication, and probability. The Rényi entropy for a random variable with pdf of EGBX distribution is as follows:
4.6 Order Statistics
In this subsection, we drive the order statisics of EGBX distribution. Let
be a random sample from EGBX and let
be the corresponding order statistics. The pdf of ith order statistics
is given by:
5 Parameter estimation
In this section, the unknown parameters of the EGBX distribution are estimated using the method maximum likelihood estimation.
5.1 Maximum likelihood function
Let
be a random sample of size n from the EGBX distribution with parameter
and
. The logarithm of likelihood function for vector of parameters
is given by:
The first partial derivative of the log likelihood function with respect the vectors of parameters and by equating the derivative to zero, we obtain:
Note that Eqs. (22)–(25) its very difficult to solve analytically. However, there is a range of statistical software that can be used to maximize the likelihood function by using for example the Package in R . Also, solving can be done numerically using iterative methods such as the Newton–Raphson method for interval estimation of the model parameter.
5.2 Simulation study
Next, we conducted a small simulation study based on 1000 replications to evaluate the performance of Maximum Likelihood Estimation (MLE) of the parameters of EGBX distribution. We took u as a Uniform random variable in (0,1) and set
and 100. We computed the mean of 1000 replications of the estimations, Biases and mean squared errors (MSEs) for the parameters are set1
and
and set2
and
. The simulation results are listed in Table 2. From Table 2 we find that the bias and MSEs of the estimation parameters decrease toward zero when the sample size increase as we expected. Also the Average of MLEs (AvE) of parameters tend to be close from true value of parameter when n is increasing.
Set1
n
AvE
Bias
MSE
AvE
Bias
MSE
10
4.2992
0.2992
1.5696
2.4553
0.4553
1.8187
20
4.1800
0.1800
0.8983
2.2736
0.2736
1.0245
30
4.1415
0.1415
0.5722
2.1690
0.1690
0.6359
50
4.1020
0.1020
0.5060
2.1299
0.1299
0.4361
100
4.0859
0.0859
0.2981
2.0799
0.0799
0.1696
n
AvE
Bias
MSE
AvE
Bias
MSE
10
6.0623
0.5623
1.9740
1.8415
0.3415
0.6041
20
5.7954
0.2954
0.8152
1.6659
0.1659
0.2368
30
5.6642
0.1642
0.4514
1.6011
0.1011
0.1353
50
5.6058
0.1058
0.5060
1.5548
0.0548
0.0810
100
5.5236
0.0236
0.2981
1.5134
0.0134
0.0298
Set2
n
AvE
Bias
MSE
AvE
Bias
MSE
10
2.8274
0.6274
2.5306
3.5582
0.5582
3.4377
20
2.5143
0.3143
0.8748
3.3404
0.3404
1.6914
30
2.4392
0.2392
0.5881
3.1278
0.1278
1.1501
50
2.3416
0.1416
0.3354
3.1132
0.1132
0.6965
100
2.2433
0.0433
0.1245
3.0954
0.0954
0.4137
n
AvE
Bias
MSE
AvE
Bias
MSE
10
2.5460
0.0460
0.0870
4.7533
0.7533
3.0079
20
2.5267
0.0267
0.0492
4.3928
0.3928
1.2864
30
2.5109
0.0109
0.0366
4.3578
0.3578
0.9056
50
2.5082
0.0082
0.0242
4.2000
0.2000
0.4680
100
2.5035
0.0035
0.0125
4.1016
0.1016
0.2837
6 Application to real data set
In this section, we consider a real data set to illustrate the potentiality of the new model. The real data set from Smith and Naylor (1987). consist of 63 observations of strengths of 1.5 cm glass fibers, originally obtained by workers at the UK National Physics Laboratory. We estimated the unknown parameters for each distribution using the method of maximum likelihood. We compare the fit of the EGBX distribution with sub-models such as Exponentiated Generalized Rayleigh (EGR), Burr type X (BX) and non-nested Beta Burr type X with one parameter (BBX1) distributions. In order to select the best model we used criteria like Log Likelihood (l), Akaike information criterion (AIC), corrected Akaike information criterion (AICC), and Bayesian information criterion (BIC) statistics which are defined as fellows, and where k is the number of parameters in the statistical model, n the sample size and is the maximized value of the log-likelihood function. Smaller values of these statistics indicate a better fit.
The results of model fitting are listed in Tables 3. According to the criterion
, and BIC, we found that EGBX distribution is the best fitted model than the sub models EGRe, BX and non nested BBX distributions for the strengths of 1.5 cm glass fibers data set. So, the EGBX model could be chosen as the best model. The
confidence intervals for
and
are [−81.239, 179.981], [−0.0186, 0.91212], [0.1729, 0.8380] and [−0.8181, 14.0402] respectively.
Model
ML Estim
l
AIC
AICC
BIC
EGBX
= 47.826
14.963
37.92
38.61
46.49
= 0.4467
= 0.5054
= 6.6110
EGRe
= 0.9869
23.928
53.85
54.26
60.28
= 5.4860
= 0.9870
BBX1
= 79.7074
21.6064
48.012
48.4196
54.442
= 0.0797
= 2.9480
BX
= 0.9869
23.928
51.857
52.057
56.143
= 5.4859
The histogram of strengths of 1.5 cm glass fibers data set and the estimated PDFs, CDFs for the fitted data model are displayed in Figs. 4 and 5 which are the fitted histogram comparing the new propose model EGBX with its sub-models. It is clear from Tables 3 and Figs. 4 and 5 thatthe EGBX provides a better fit to the histogram and therefore it could be chosen as the best model based on the dataset used, because in histogram graph any model with the highest peak is the best one among others.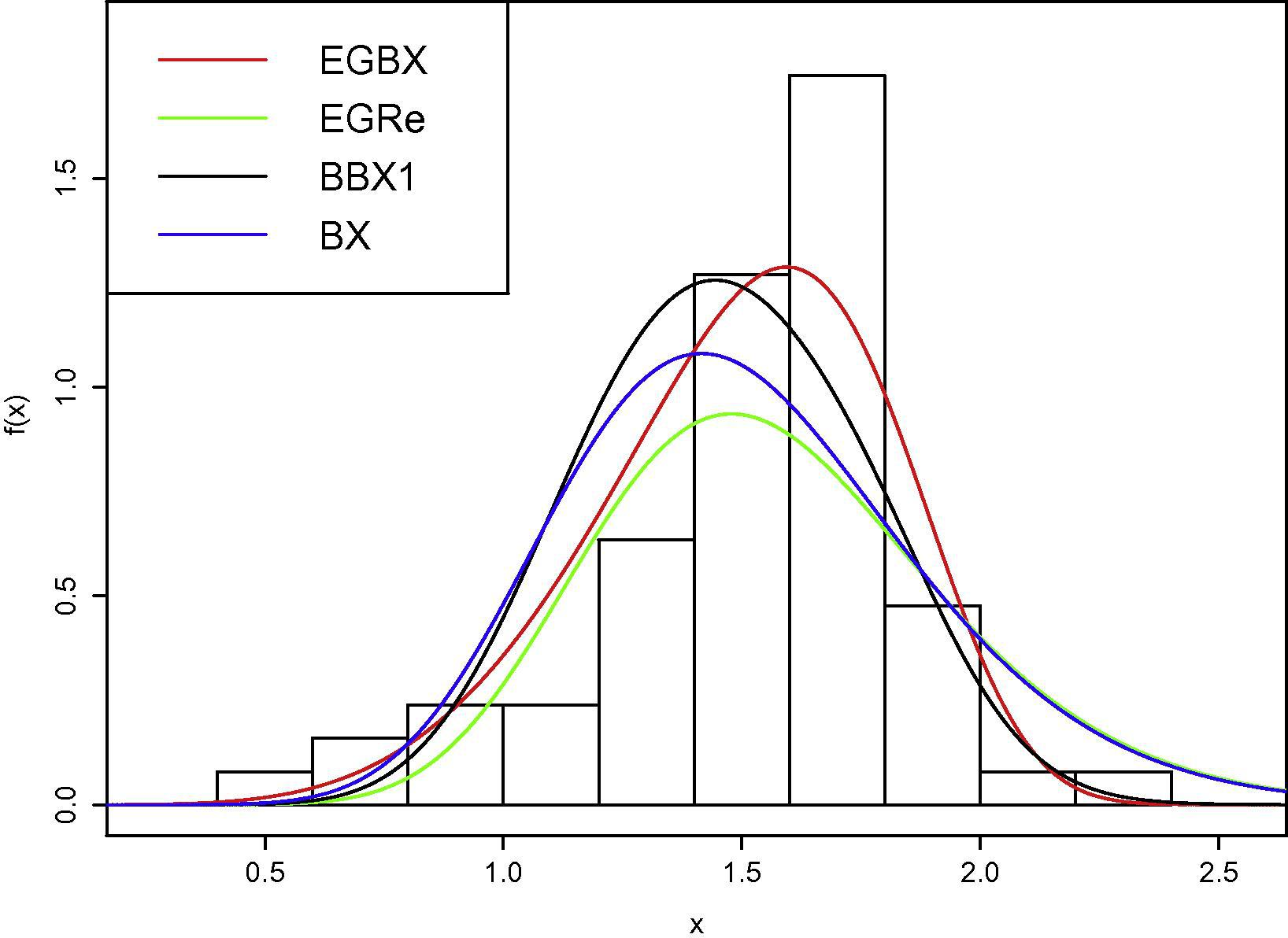
Estimated densities of four models fitted to data.
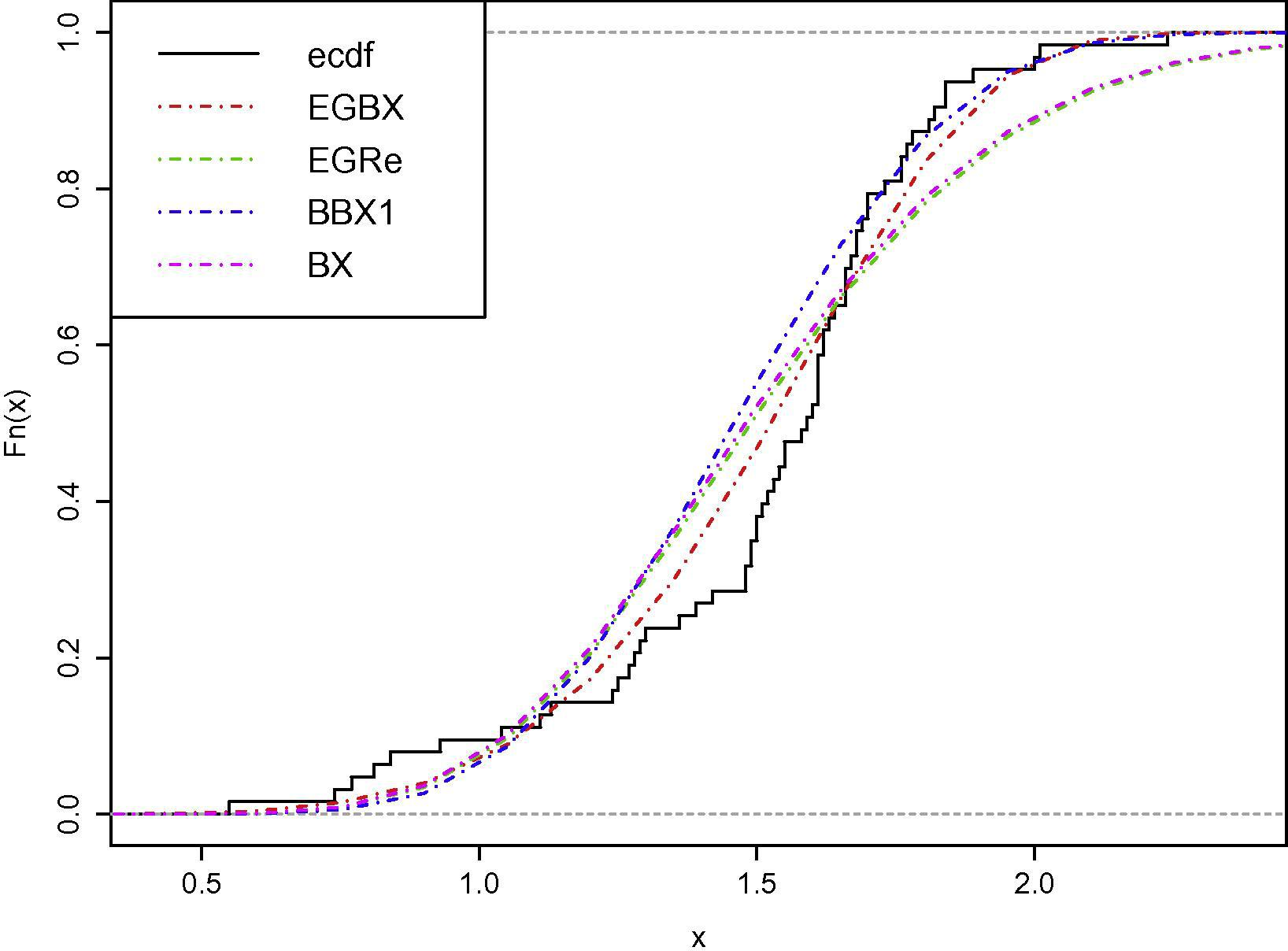
Estimated CDFs for data set.
7 Conclusion
In this study, a new four-parameter model was proposed and studied, called the Exponentiated Generalized Burr type X, which is an extension of the Burr type X distribution and many others distribution as a sub-models. The cumulative function and the probability density function of EGBX were expressed as a mixture of BX distribution with different parameters. It was observed that the hazard function has various shapes, such as increasing, decreasing and bathtub. Several of its mathematical properties were derived such as the quantile function, limit behavior, moments, moment-generating function and the Rényi entropy and order statistics. The unknown parameter was estimated using maximum likelihood function. Simulation study is carried at under varying sample size to assess the performance of this model. Finally, numerical examples were presented in order to demonstrate the usefulness of the new model with real data set. The EGBX distribution provides a better fit than other sub-models.
References
- The exponentiated generalized Gumbel distribution. Rev. Colomb. Estadística. 2015;38(1):123-143.
- [Google Scholar]
- The exponentiated generalized class of distributions. J. Data Sci.. 2013;11(1):1-27.
- [Google Scholar]
- Beta-normal distribution and its applications. Commun. Stat. Theory Methods. 2002;31(4):497-512.
- [Google Scholar]
- Jeffrey A., Zwillinger D., eds. Table of Integrals, Series, and Products. Academic Press; 2007.
- The beta Burr type X distribution properties with application. SpringerPlus. 2016;5(1):1-18.
- [Google Scholar]
- On the exponentiated generalized weibull distribution: a generalization of the Weibull distribution. Indian J. Sci. Technol.. 2015;8(35)
- [Google Scholar]
- The gamma-exponentiated exponential distribution. J. Stat. Comput. Simul.. 2012;82(8):1191-1206.
- [Google Scholar]
- An estimation of reliability: case of one-parameter Burr Type X distribution. Int. J. Stat. Econ.. 2011;6(S11):1-19.
- [Google Scholar]
- A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distribution. Appl. Stat. 1987:358-369.
- [Google Scholar]
- Inference for reliability and stress-strength for a scaled Burr Type X distribution. Lifetime Data Anal.. 2001;7(2):187-200.
- [Google Scholar]
- On families of beta-and generalized gamma-generated distributions and associated inference. Stat. Methodol.. 2009;6(4):344-362.
- [Google Scholar]







