New approach of soft M-open sets in soft topological spaces

1 Introduction

Soft set was created by Molodtsov (1999) in order to deal with challenges arising from incomplete information. He had indicated a few applications of soft theory for finding solutions of problems in economics, medical science and so on. Recently, there has been a significant increase in the number of papers published on soft sets and their applications in various fields (Al-Shami and Abo-Tabl, 2021, Alzahrani et al., 2022). Soft sets and their applications have advanced significantly in recent years (Alzahrani et al., 2022; Fatimah and Alcantud, 2021). The concept of S $\tau s$ was introduced by Shabir and Naz (2011), who study them as existing in an initial universe with a fixed set of parameters. Furthermore, (Maji et al., 2003) presented various operations on soft sets, and so far, several of the fundamental features of these operations have been exposed. Soft open ( $\mathcal{S}$ o) sets, soft interior, soft closed sets, soft closure, and soft separation axioms were defined by the authors. M-open sets were introduced into general topology by (EL-Maghrabi and AL-Juhani, 2011). The purpose of this article is to conduct a theoretical investigation of the new set termed $\mathcal{S}$ Mo and $\mathcal{S}$ Mc sets over $\mathcal{S}$ τs and to analysis some of their properties. Also, in this research, we express soft operations by ‘∼’, soft closed ( $\mathcal{S}$ c) set, soft open cover by $\mathcal{S}$ o cover.

Throughout this entire article, we will refer to ${\mathrm{U}}_1$ as an initial universal set, ( $U_1$ , τ, H) is a $\mathcal{S}$ τs and $(F_1,H_1$ ) is a soft set over $U_1$ .

2 Preliminaries

Except where else stated, $U_1$ and W denoted a $\mathcal{S}\tau s$ with ( $U_1$ , τ, S) and (W,ν, T). Additionally, a soft mapping f: $U_1$  → W, since f: ( $U_1$ , τ, S) →(W,ν, T), u: $U_1$  → W and p:S → T denote assumed mappings.

$\mathit{And}$ ( $F_1,H_1$ ) $\stackrel{\sim }{\cap }$ ( $F_2$ , D) =(V,J) is a soft sets defined as J = $H_1$ $\stackrel{\sim }{\cap }$ D, and V(s) = $F_1$ (s) $\stackrel{\sim }{\cap }$ $F_2$ (s), $\forall$ s ∈ J.

(i) The soft closure of ( $F_2$ , $H_1$ ) is $\stackrel{\sim }{s}$ cl( $F_2$ , $H_1$ ) = $\stackrel{\sim }{\cap }$ {(D, $H_1$ ): (D, $H_1$ ) is $\mathcal{S}$ c set and ( $F_2$ , $H_1$ ) $\stackrel{\sim }{\subseteq }$ (D, $H_1$ }.

(ii) The soft interior of ( $F_2$ , $H_1$ ) is s̃int( $F_2$ , $H_1$ ) = $\stackrel{\sim }{\cup }$ {(D, $H_1$ ): (D, $H_1$ ) is $\mathcal{S}$ o set and (D, $H_1$ ) $\stackrel{\sim }{\subseteq }$ ( $F_2$ , $H_1$ )}.

(i) ( $F_1,H_1$ ) is $\mathcal{S}$ c set iff ( $F_1,H_1$ ) = s̃cl( $F_1,H_1$ ).

(ii) ( $F_2$ , $H_1$ ) is $\mathcal{S}$ o set iff ( $F_2$ , $H_1$ ) = s̃int( $F_2$ , $H_1$ ).

Akdağ and Özkan (2014a,b) defined soft (pre-open(closed), α-open(closed), Chen (2013)​ defined soft (semi-open(closed)) and Arockiarani and Arokialancy (2013) defined soft (regular open(closed), β-open(closed)) sets, for example.

3 M-open and M-closed soft sets

We define soft θ-semi-open and $\mathcal{S}$ Mo sets in $\mathcal{S}\tau s$ and study some of their characteristics.

Mukherjee and Debnath (2017) defined soft (δ-pre open (closed), δ-pre interior and δ-pre closure) sets, for example.

(i) soft θ-semi ( $\mathcal{S}$ θ-semi) open set iff ( $F_1$ , H) $\stackrel{\sim }{\subseteq }$ cl(int_θ ( $F_1$ , H)).

(ii) $\mathcal{S}$ θ-semi ( $\mathcal{S}$ θ-semi) closed set iff ( $F_1$ , H) $\stackrel{\sim }{\supseteq }$ int(cl_θ ( $F_1$ , H)).

(i) soft M-open (briefly, $\mathcal{S}$ Mo) set if ( $F_1,H$ ) $\stackrel{\sim }{\subseteq }$ cl(int_θ( $F_1,H$ )) $\stackrel{\sim }{\cup }$ int(cl_δ( $F_1,H$ )),

(ii) soft M-closed (briefly, $\mathcal{S}$ Mc) set if (( $F_1,H$ ) $\stackrel{\sim }{\supseteq }$ int(cl_θ( $F_1,H$ )) $\stackrel{\sim }{\cap }$ cl(int_δ( $F_1,H$ )).

Close

Fig. 1

Export to PPT

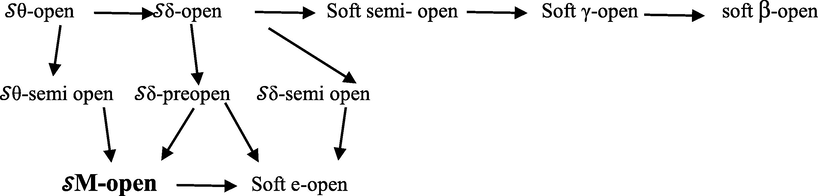
In the next example, we will prove that $\mathcal{S}$ Mo se is not $\mathcal{S}$ δ-preopen.

F₁(s₁) = {u₁, u₂} F₁(s₂) = {u₁, u₂}.

F₂(s₁) = {u₂} F₂(s₂) = {u₁, u₃}.

F₃(s₁) = {u₂, u₃} F₃(s₂) = {u₁}.

F₄(s₁) = {u₂} F₄(s₂) = {u₁}.

F₅(s₁) = {u₁, u₂} F₅(s₂) = U.

F₆(s₁) = U F₆(s₂) = {u₁, u₂}.

F₇(s₁) = {u₂, u₃} F₇(s₂) = {u₁, u₃}.

( $U_1$ , τ, S) is a $\mathcal{S}$ τs, and $\mathcal{S}$ c sets are $\stackrel{\sim }{U_1}$ , $\stackrel{\sim }{\varphi }$ , (F₁, S)^c, (F₂, S)^c, (F₃, S)^c, …., (F₇, S)^c.

Let ( $F_{1,}{H}_1$ )= {(h₁, {u₁, u₂}, (h₂, {u₂}), (h₃, {u₁, u₃})}. Then.

cl(int_θ ( $F_1$ , $H_1$ )) $\stackrel{\sim }{\cup }$ int(cl_δ ( $F_1$ , $H_1$ )) =  $\stackrel{\sim }{U_1}$ and ( $F_1,H_1$ ) $\stackrel{\sim }{\subseteq }$ cl(int_θ( $F_1,H_1$ )) $\stackrel{\sim }{\cup }$ int(cl_δ( $F_1,H_1$ )), therefore, ( $F_1$ , $H_1$ ) is $\mathcal{S}$ Mo set but not $\mathcal{S}$ δ-preopen.

(i) ( $F_1,K$ ) is a $\mathcal{S}$ Mo set iff ( $F_1,K$ )^c is a $\mathcal{S}$ Mc set.

(ii) ( $F_1,K$ ) is a $\mathcal{S}$ Mc set iff ( $F_1,K$ )^c is a $\mathcal{S}$ Mo set.

Proof. Obvious.

1. $\mathcal{S}$ M-closure of a soft set is defined as $\mathcal{S}$ Mcl( $F_1,H_1$ ) = $\stackrel{\sim }{\cap }$ {(V, $H_1$ )⊇^̃ ( $F_1,H$ ): (V,H) is a $\mathcal{S}$ Mc set of $U_1$ }.

2. $\mathcal{S}$ M-interior of a soft set is defined as $\mathcal{S}$ Mint( $F_1,H_1$ ) = $\stackrel{\sim }{\cup }$ {( $F_2$ , $H_1$ ) $\stackrel{\sim }{\subseteq }$ ( $F_1,H_1$ ):( $F_2$ , $H_1$ ) is a $\mathcal{S}$ Mo set of $U_1$ }.

1. $\mathcal{S}$ Mcl( $F_1,H_1$ )^c =  $\stackrel{\sim }{U_1}$ - $\mathcal{S}$ Mint( $F_1,H_1$ ),

2. $\mathcal{S}$ Mint( $F_1,H_1$ )^c =  $\stackrel{\sim }{U_1}$ - $\mathcal{S}$ Mcl( $F_1,H_1$ ).

(ii) Let ( $F_2$ , $H_1$ ) be a $\mathcal{S}$ Mo set. Then for a $\mathcal{S}$ Mc set ( $F_1,H_1$ ) $\stackrel{\sim }{\subseteq }$ ${(F}_2$ , $H_1$ )^c,

${(F}_2$ , $H_1$ ) $\stackrel{\sim }{\subseteq }$ ( $F_1,H_1$ )^c. Now, $\mathcal{S}$ Mcl( $F_1,H_1$ ) = $\stackrel{\sim }{\cap }$ {( $F_2$ , $H_1$ )^c: $(F_2$ , $H_1$ ) is a $\mathcal{S}$ Mo set ,( $F_2$ , $H_1$ ) $\stackrel{\sim }{\subseteq }$ ( $F_1$ , $H_1$ )^c = $\stackrel{\sim }{U_1}$ - $\stackrel{\sim }{\cup }$ {( $F_2$ , $H_1$ ): ( $F_2$ , $H_1$ ) is a $\mathcal{S}$ Mo set and ( $F_2$ , $H_1$ ) $\stackrel{\sim }{\subseteq }$ ( $F_1,H_1$ )^c }= $\stackrel{\sim }{U_1}$ - $\mathcal{S}$ Mint( $F_1,H_1$ )^c. So, $\mathcal{S}$ Mint( $F_1,H_1$ )^c =  $\stackrel{\sim }{U_1}$ - $\mathcal{S}$ Mcl( $F_1,H_1$ ).

Proof. Obvious.

1. $\mathcal{S}$ Mcl( $\stackrel{\sim }{\varphi }$ ) =  $\stackrel{\sim }{\varphi }$ ,

2. $\mathcal{S}$ Mint( $\stackrel{\sim }{\varphi }$ ) =  $\stackrel{\sim }{\varphi }$ ,

3. $\mathcal{S}$ Mcl( $F_1,H$ ) is a $\mathcal{S}$ Mc set,

4. $\mathcal{S}$ Mint( $F_1,H$ ) is a $\mathcal{S}$ Mo set,

5. $\mathcal{S}\mathrm{M}cl(F_1,H)\stackrel{\sim }{\subseteq }\mathcal{S}\mathrm{M}cl(F_2,H)if(F_1,H)\stackrel{\sim }{\subseteq }(F_2,H),$

6. $\mathcal{S}\mathrm{M}int(F_1,H)\stackrel{\sim }{\subseteq }\mathcal{S}\mathrm{M}int(F_2,H)if(F_1,H)\stackrel{\sim }{\subseteq }(F_2,H),$

7. $\mathcal{S}$ Mcl( $\mathcal{S}$ Mcl( $F_1,H$ )) =  $\mathcal{S}$ Mcl( $F_1,H$ ),

8. $\mathcal{S}$ Mint( $\mathcal{S}$ Mint( $F_1,H$ )) =  $\mathcal{S}$ Mint( $F_1,H$ ).

1. $\mathcal{S}$ Mcl (( $G_1,K_1$ ) $\stackrel{\sim }{\cup }$ ( $G_2$ , $K_1$ )) $\stackrel{\sim }{\supseteq }$ $\mathcal{S}$ Mcl( $G_1,K_1$ ) $\stackrel{\sim }{\cup }$ $\mathcal{S}$ Mcl( $G_2$ , $K_1$ ).

2. $\mathcal{S}$ Mcl(( $G_1,K_1$ ) $\stackrel{\sim }{\cap }$ $(G_2$ , $K_1$ )) $\stackrel{\sim }{\subseteq }$ $\mathcal{S}$ Mcl( $G_1,K_1$ ) $\stackrel{\sim }{\cap }$ $\mathcal{S}$ Mcl( $G_2$ , $K_1$ ).

Therefore, $\mathcal{S}$ Mcl(( $G_1,K_1$ ) $\stackrel{\sim }{\cup }$ ${(G}_2$ , $K_1$ )) $\stackrel{\sim }{\supseteq }$ $\mathcal{S}$ Mcl( $G_1,K_1$ ) $\stackrel{\sim }{\cup }$ $\mathcal{S}$ Mcl( $G_2$ , $K_1$ ).

(ii)Similar to (i).

1. $\mathcal{S}$ Mint( $L_1,H$ ) $\stackrel{\sim }{\cup }$ ${(L}_2$ , H)) $\stackrel{\sim }{\supseteq }$ $\mathcal{S}$ Mint( $L_1,H$ ) $\stackrel{\sim }{\cup }$ $\mathcal{S}$ Mint( $L_1,H$ )

2. $\mathcal{S}$ Mint(( $L_1,H$ ) $\stackrel{\sim }{\cap }$ ${(L}_2$ , H)) $\stackrel{\sim }{\subseteq }$ $\mathcal{S}$ Mint( $L_1,H$ ) $\stackrel{\sim }{\cap }$ $\mathcal{S}$ Mint( $L_2$ , H)

Proof. Obvious.

(i) If int_θ( $F_1,H$ ) =  $\stackrel{\sim }{\varphi }$ , then ( $F_1,H$ ) is a $\mathcal{S}$ δ-preopen set.

(ii) If cl_δ( $F_1,H$ ) =  $\stackrel{\sim }{\varphi }$ , then ( $F_1,H$ ) is a $\mathcal{S}$ θ-semiopen set.

Proof. Obvious.

(i) The union of any $\mathcal{S}$ Mo sets is a $\mathcal{S}$ Mo set,

(ii) The intersection of any $\mathcal{S}$ Mc sets is a $\mathcal{S}$ Mc set.

[cl(int_θ( $\stackrel{\sim }{\cup }$ ( $F_1,H$ ) _α)) $\stackrel{\sim }{\cup }$ int(cl_δ( $\stackrel{\sim }{\cup }$ ( $F_1,H$ ) _α))]. Thus $\stackrel{\sim }{\cup }$ ( $F_1,H$ ) _α is $\mathcal{S}$ Mo set.

(ii) As (i) by taking the complements.

(F₁, S) = {(s₁,{u₁}), (s₂, {u₂})}, (F₂, S) = {(s, U), (s₂, { u₂})}.

(F₃, S) = {(s₁,{u₁}), (s₂, $U_1$ )}.

( $U_1$ , τ, S) is a $\mathcal{S}$ τs. So, the soft sets (G₁, S), (G₂, S) which defines as (G₁, S) = {(s₁,{u₂}), (s₂, {u₁})} and (G₂, S) ={(s₁,{u₁, u₂}), (s₂, {u₁})} are $\mathcal{S}$ Mo sets, but (G₁, S) $\stackrel{\sim }{\cap }$ (G₂, S)=(K, S) is not a $\mathcal{S}$ Mo set.

And, the soft sets (G₃, S) and (G₄, S) which defines as(G₃, S) = {(s₁,{u₁}), (s₂, {u₁})} and (G₄, S) ={((s₂, {u₂})} are $\mathcal{S}$ Mc sets, but (G₃, S) $\stackrel{\sim }{\cup }$ (G₄, S)= {(s₁,{u₁}), (s₂, {u₁, u₂})} =(M, S) is not a $\mathcal{S}$ Mc set.

1. Each $\mathcal{S}$ δ-preopen set is $\mathcal{S}$ Mo.

2. Every $\mathcal{S}$ θ-semi-open set is $\mathcal{S}$ Mo.

( $F_1,H$ ) $\stackrel{\sim }{\subseteq }$ int(cl_δ ( $F_1,H$ )), therefore ( $F_1,H$ ) $\stackrel{\sim }{\subseteq }$ [int(cl_δ ( $F_1,H$ )) $\stackrel{\sim }{\cup }$ int_δ ( $F_1,H$ ))] $\stackrel{\sim }{\subseteq }$ [int(cl_δ ( $F_1,H$ )) $\stackrel{\sim }{\cup }$ cl(int_δ ( $F_1,H$ ))]. Hence, ( $F_1,H$ ) is a $\mathcal{S}$ Mo set.

(ii) Suppose that ( $F_1,H$ ) is a $\mathcal{S}$ θ-semio-penset in a $\mathcal{S}$ τs. Then, ( $F_1,H$ ) $\stackrel{\sim }{\subseteq }$ cl(int_θ( $F_1,H$ )) which implies that ( $F_1,H$ ) $\stackrel{\sim }{\subseteq }$ [cl(int_θ( $F_1,H$ )) $\stackrel{\sim }{\cup }$ int( $F_1,H$ )] $\stackrel{\sim }{\subseteq }$ [cl(int_θ( $F_1,H$ )) $\stackrel{\sim }{\cup }$ int(cl_δ ( $F_1,H$ ))]. Thus ( $F_1,H$ ) is a $\mathcal{S}$ Mo set.

4 Soft M-continuity and soft M-functions

In this section, we define $\mathcal{S}$ M-continuous functions, $\mathcal{S}$ M-irresolute functions, $\mathcal{S}$ M-open function ( $\mathcal{S}$ Mof) and $\mathcal{S}$ M- closed function ( $\mathcal{S}$ Mcf). Also, we study some of their characteristics and separation axioms by using $\mathcal{S}$ Mo sets.

u: $U_1$  → W, p: S → T are functions, for soft sets ( $F_1$ , H), ( $F_2$ , B) and a family of soft sets {( $F_{1\alpha }$ , H _α):α ∈ Λ, an index set} in the soft class ( $U_1$ , S), then:

(1) f ( $\stackrel{\sim }{\varphi }$ ) =  $\stackrel{\sim }{\varphi }$ ,

(2) f ( $\stackrel{\sim }{U_1}$ ) =  $\stackrel{\sim }{W}$ and $f^{-1}$ ( $\stackrel{\sim }{W}$ ) = $\stackrel{\sim }{U_1}$ ,

(3) f (U _α∈Λ ( $F_{1\alpha }$ ,H _α)) = (U _α∈Λ f ( $F_{1\alpha }$ , H _α)),

(4) f (∩_α∈Λ ( $F_{1\alpha }$ , H _α)) $\stackrel{\sim }{\subseteq }$ (∩_α∈Λ f ( $F_{1\alpha }$ _α, H_α)),

(5) If ( $F_1$ , H) $\stackrel{\sim }{\subseteq }$ ( $F_2$ , B), then f ( $F_1$ , H) $\stackrel{\sim }{\subseteq }$ f ( $F_2$ , B),

(i) a $\mathcal{S}$ δ-precontinuous (Anjan Mukherjee and Bishnupada Debnath, 2017).

if $f^{-1}$ ( $F_1$ , H) is $\mathcal{S}$ δ-preopen in $U_1,$ for each $\mathcal{S}$ o set ( $F_1,$ H) in W,

(ii) a $\mathcal{S}$ θ-semi continuous if $f^{-1}$ ( $F_1$ , H) is $\mathcal{S}$ θ-semi-open in $U_1,$ for each $\mathcal{S}$ o set ( $F_1$ , H) in W.

1. a $\mathcal{S}$ M-continuous if $f^{-1}$ ( $F_1$ , H) is a $\mathcal{S}$ Mo in $U_1,$ for each $\mathcal{S}$ o set ( $F_1$ , H) in W.

2. a $\mathcal{S}$ M-irresolute if $f^{-1}$ ( $F_1$ , H) is a $\mathcal{S}$ Mo set in $U_1,$ for each $\mathcal{S}$ Mo set ( $F_1$ , H) in W.

1. f is a $\mathcal{S}$ M-continuous.

2. For each soft singleton $P_{\lambda }^{F_1}$  ∈  $U_1$ and each $\mathcal{S}$ o set ( $F_1$ , H) in W, where f ( $P_{\lambda }^{F_1}$ ) $\stackrel{\sim }{\subseteq }$ ( $F_1$ , H) ∃ a $\mathcal{S}$ Mo set ( $F_2$ , H) in U, since $P_{\lambda }^{F_1}$ ∈( $F_2$ , H) and f (( $F_2$ , H)) $\stackrel{\sim }{\subseteq }$ ( $F_1$ , H)

3. $f^{-1}$ ( $F_1$ , H) = cl(int_θ( $f^{-1}$ ( $F_1$ , H))) $\stackrel{\sim }{\cup }$ int(cl_δ ( $f^{-1}$ ( $F_1$ , H))), for each $\mathcal{S}$ o set ( $F_1$ , H) in E.

4. The inverse image of every $\mathcal{S}$ c set in E is $\mathcal{S}$ Mc set.

5. cl(int_θ( $f^{-1}$ ( $F_1$ , H))) $\stackrel{\sim }{\cap }$ int(cl_δ ( $f^{-1}$ ( $F_1$ , H))) $\stackrel{\sim }{\subseteq }$ $f^{-1}$ ((cl ( $F_1$ , H))) for every soft set ( $F_1$ , H) $\stackrel{\sim }{\subseteq }$ W.

6. f [cl(int_θ( $F_2$ , H)) $\stackrel{\sim }{\cap }$ int(cl_δ ( $F_2$ , H))] $\stackrel{\sim }{\subseteq }$ cl(f( $F_2$ , H)), for each soft set ( $F_2$ , H) in $U_1$ .

$f^{-1}$ ( $F_1$ , H). Suppose that ( $F_2$ , H) = $f^{-1}$ ( $F_1$ , H) which is a $\mathcal{S}$ Mo set in $U_1$ . So, we have $P_{\lambda }^{F_1}$ ∈( $F_2$ , H). Now, f( $F_2$ , H) = f ( $f^{-1}$ ( $F_1$ , H)) ⊆̃ ( $F_1$ , H) .

(ii)⇒(iii). Consider ( $F_1$ , H) is an arbitrary $\mathcal{S}$ o set in W, let $P_{\lambda }^{F_1}$ be an arbitrary soft point in $U_1,$ since f (Ρ^F_λ) $\stackrel{\sim }{\subseteq }$ ( $F_1$ , H), then $P_{\lambda }^{F_1}$ ∈ $f^{-1}$ ( $F_1$ , H). By (ii), there is a $\mathcal{S}$ Mo set( $F_2$ , H) in $U_1$ , where $P_{\lambda }^{F_1}$ ∈( $F_2$ , H) and f (( $F_2$ , H)) $\stackrel{\sim }{\subseteq }$ ( $F_1$ , H). Therefore, $P_{\lambda }^{F_1}$ ∈( $F_2$ , H) $\stackrel{\sim }{\subseteq }$ $f^{-1}$ (f (( $F_2$ , H))) $\stackrel{\sim }{\subseteq }$ $f^{-1}$ ( $F_1$ , H) $\stackrel{\sim }{\subseteq }$ cl(int_θ( $f^{-1}$ ( $F_1$ , H))) $\stackrel{\sim }{\cup }$ int(cl_δ ( $f^{-1}$ ( $F_1$ , H))).

(iii)⇒(iv). Suppose that ( $F_1$ , H) is an arbitrary $\mathcal{S}$ c set in W. Then $\stackrel{\sim }{W}$ - ( $F_1$ , H) is a $\mathcal{S}$ o set in W. By (iii), ( $f^{-1}$ ( $\stackrel{\sim }{W}$ - ( $F_1$ , H))) $\stackrel{\sim }{\subseteq }$ cl(int_θ( $f^{-1}$ ( $\stackrel{\sim }{W}$ - ( $F_1$ , H)))) $\stackrel{\sim }{\cup }$ int(cl_δ ( $f^{-1}$ ( $\stackrel{\sim }{W}$ - ( $F_1$ , H)))). This implies $\stackrel{\sim }{U_1}$ -( $f^{-1}$ ( $F_1$ , H)) $\stackrel{\sim }{\subseteq }$ cl(int_θ( $\stackrel{\sim }{U}$ - $f^{-1}$ ( $F_1$ , H))) $\stackrel{\sim }{\cup }$ int(cl_δ ( $\stackrel{\sim }{U_1}$ - $f^{-1}$ ( $F_1$ , H))) $\stackrel{\sim }{\subseteq }$ cl( $\stackrel{\sim }{U_1}$ -int_θ( $f^{-1}$ ( $F_1$ , H))) $\stackrel{\sim }{\cup }$ int( $\stackrel{\sim }{U_1}$ - cl_δ ( $f^{-1}$ ( $F_1$ , H))) $\stackrel{\sim }{\subseteq }$ [ $\stackrel{\sim }{U_1}$ -cl(int_θ( $f^{-1}$ ( $F_1$ , H)))] $\stackrel{\sim }{\cup }$ .