Neutronic feasibility study of (





Th
-

233

U)-Zr

H

1.65






 fuel in a modelled TRIGA research reactor

Fadi El Banni; Ouadie Kabach; Aka A. Koua; Bogbe L.H. Gogon; Georges A. Monnehan; Abdelfettah Benchrif; Hamid Amsil; Abdelouahed Chetaine

doi:10.1016/j.jksus.2021.101769

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

02 2021

:34;

101769

doi:

10.1016/j.jksus.2021.101769

Neutronic feasibility study of ( ${Th -}^{233} U)-Zr H_{1.65}$ fuel in a modelled TRIGA research reactor

Fadi El Banni^{^a}, Ouadie Kabach^{^b,⁎}, Aka A. Koua^{^a}, Bogbe L.H. Gogon^{^a}, Georges A. Monnehan^{^a}, Abdelfettah Benchrif^{^c}, Hamid Amsil^{^c}, Abdelouahed Chetaine^{^b}

a LASMES, SSMT, Felix Houphouet Boigny University, Abidjan, Cote d’Ivoire

b PRESN, Department of Physics, FSR, Mohammed V University, Rabat, Morocco

c National Centre of Nuclear Energy Sciences and Techniques, Rabat, Morocco

⁎Corresponding author at: Mohammed V University, Faculty of Science, 4 Avenue Ibn Battouta B.P. 1014 RP, Rabat 10000, Morocco. ouadie.kabach10@gmail.com (Ouadie Kabach) ouadie_kabach@um5.ac.ma (Ouadie Kabach)

Received: 2021-5-17, Accepted: 2021-12-10,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

This paper presents a comparative analysis when transitioning from fuel meat based on uranium zirconium hydride ( $U-Zr H_{1.65}$ ) to one based on thorium-uranium-233 zirconium hydride ( $({Th -}^{233} U)-Zr H_{1.65}$ ) as an alternative option for TRIGA reactors. The aim of this study was to investigate the neutronic characteristics of ( ${Th -}^{233} U)-Zr H_{1.65}$ fuels with two different Th-²³³U weight contents (i.e., 8.5 wt% and 12 wt%) and various U-233 enrichment levels. Using MCNP6.2 computer code based on the Monte Carlo method, a three-dimensional (3D) hypothetical TRIGA model was developed to investigate various neutronic parameters, such as the effects of U-233 enrichment and different ( ${Th -}^{233} U)$ weight contents on the effective multiplication factor, burnup behavior, spent fuel composition, neutron flux, and fission product poison concentration. Since fuel temperature coefficients of reactivity and effective delayed neutron fractions play important roles in the reactor’s kinetics, these were also investigated, and the results were compared to the model with $U-Zr H_{1.65}$ fuel. The obtained results revealed that the presence of Th-232 in the fuels did not drastically reduce the fuel temperature coefficients due to the zirconium hydride within the fuels providing most of the feedback in a TRIGA reactor. In contrast, the presence of U-233 in the ( ${Th -}^{233} U)-Zr H_{1.65}$ fuels did reduce the effective delayed neutron fraction. Despite this, the lower transuranic generation in cores fueled by $({Th -}^{233} U)-Zr H_{1.65}$ make this fuel advantageous in terms of achieving longer cycle lengths and less-hazardous nuclear waste for disposal.

Keywords

Neutronic analysis

TRIGA reactor

Fuel

Burnup characteristics

MCNP6.2

Show Related Articles from PubMed

1 Introduction

Research reactors like TRIGA (Training, Research and Isotopes production, General Atomic) reactors have a wide range of applications, such as neutron activation analysis, education, laboratory radioisotope production, and neutron beam implementation (Amsil et al., 2021; Vignolo et al., 2014). They are also useful for training in terms of acquiring practical experience and becoming familiar with the key parameters of reactor physics. These potential applications make them attractive to countries interested in researching nuclear technology. Currently, most TRIGA reactors use the standard TRIGA fuel manufactured by General Atomic (GA) by homogeneously mixing zirconium hydride with U-235-enriched fuel (8.5 wt%, 12 wt%, etc.). This fuel is primarily responsible for the high degree of inherent safety that is associated with TRIGA reactors (IAEA, 2016; Matsumoto, 1998; Huda, 2006; Borio di Tigliole et al., 2010 ). After the Fukushima accident, however, the Company for the Study of Atomic Fuel Creation France (CERCA), which is charged with providing fuel elements, suspended fuel production in order to implement safety improvements that were demanded by the French Nuclear Safety Authority and the European Commission. Consequently, many TRIGA reactors around the world are now experiencing fuel shortages (Böck et al., 2016; Office of Nuclear Energy, 2017).

Research into new fuel mixtures, such as thorium-based fuels, has been widely conducted recently to enhance the safety and sustainability of nuclear energy. Thorium and thorium-based fuels enjoy many advantages, such as natural abundance, low-radiotoxicity waste, chemical inertness, a low thermal expansion coefficient, proliferation resistance, and so on. Natural thorium, mostly in the form of the Th-232 isotope (fertile), is three to four times more abundant than uranium. Furthermore, Th-232 has a greater capture cross-section for thermal neutrons than U-238, so it has a higher conversion ratio when converted to U-233, compared with when U-238 is converted to Pu-239. Another major advantage of using thorium is that the spent fuel is unsuitable for the development of weapons due to the limited production of plutonium isotopes in burned thorium-based fuels (Mirvakili et al., 2015). What is more, U-233 is advantageous as a fissile nucleus in a thermal reactor for several reasons. For example, it has the lowest $α$ value (the capture-to-fission ratio) of the various fissile nuclides, and this is responsible for the highest thermal value of $η$ (Bourquin, 2016) (Table 1). Consequently, Th-²³³U fuel may represent a feasible alternative option for use in nuclear reactors (Adams et al., 2020; IAEA, 2006; Nuclear Energy Agency, 2015; Kabach et al., 2020 ).

Table 1 Comparison of nuclear properties for the relevant (U-233 and U-235) and fertile (Th-232 and U-238) isotopes in thermal and epithermal regions (IAEA, 2005).

	Th-232	U-233	U-235	U-238
Thermal
$σ c a p t u r e (b a r n s)$	4.62	364	405	1.73
$σ f i s s i o n (b a r n s)$	0	332	346	0
$α = σ_{c} / σ_{f}$	–	0.096	0.171	–
$η_{t h}$	–	2.26	2.08	–
Epithermal resonance	–	764	–	275
I.R: Integral resonance in infinite dilution
$R I c a p t u r e$	85.6	882	405	278
$R I f i s s i o n$	–	746	272	–
$α = {R I}_{c} / {R I}_{f}$	–	0.182	0.489	–
$η_{e p i}$	–	2.1	1.63	–
Neutron yield υ	–	2.48	2.43	–
Delayed neutron yield β	–	0.0031	0.0069	–
Capture:
2 200 m/s value	7.6	54	100	2.7
Resonance integral	85	140	144	275
Neutron/fission	–	2.5	2.4	–

To integrate the thorium fuel cycle into research reactors, new core designs are needed, because fuel core configurations must be optimized to meet future needs. Furthermore, before integrating new fuels into reactors, several preparatory activities must be performed, such as conceptual studies, neutronic and physical studies, and feasibility studies. Hence, this paper aims to investigate, from a neutronic point of view, the possibility of improving the performance of a hypothetical TRIGA core by using $({Th -}^{233} U)-Zr H_{1.65}$ instead of the widely used $U-Zr H_{1.65}$ fuel. In this study, two different Th-²³³U contents for the $({Th -}^{233} U)-Zr H_{1.65}$ fuel (8.5 wt% and 12 wt%) were considered for the modeled core. Extending the operation time of the core was considered the primary measure of performance. To investigate the effect of the proposed $({Th -}^{233} U)-Zr H_{1.65}$ fuels on the neutronic performances of the modeled core, the following neutronic parameters were also evaluated: the fuel temperature coefficients of reactivity and effective delayed neutron fractions. Burnup simulations were performed at 2 MW power using the BURN option of the MCNP code.

2 Description of the TRIGA reactor and the 3D model

The TRIGA reactor was originally designed and developed by the GA Corporation in the 1960s to serve as a reliable reactor for research and training. The reactor was designed to be inherently safe with a large prompt negative temperature coefficient of reactivity (IAEA, 2016; Chiesa et al., 2015; General Atomics, 2021; Fouquet et al., 2003 ). In general, the TRIGA fuel rod is an alloy of zirconium hydride (ZrH_1.x, with x, the atomic ratio between hydrogen and zirconium, usually being between 1.2 and 1.8 (Simnad, 1981)) and uranium metal-enriched to 20 wt% with U-235 with different weights (Kabach et al., 2020). Four TRIGA reactor models have been developed over the years: the Mark I, Mark F, Mark II (which varies slightly from the Mark I), and Mark III with its movable core (IAEA, 2016).

Since the TRIGA core and rod dimensions are not standardized and differ slightly from reactor to reactor, the basic parameters for a typical TRIGA Mark II reactor were used in this study to build our hypothetical TRIGA reactor model. In this model, the core of the reactor is 21.0 cm wide and 88.4 cm deep in a water-filled tank. It contains 126 fuel holes located across the central thimble, and these are divided into six circular rings (B to G), where ring B is closest to the central thimble, while ring G is located at the outer edge of the core. The number of holes in each ring increases by six with each increase in radius, such that the innermost ring has six holes, while the outer ring has 36 holes. The core is surrounded by an annular graphite reflector that has been designed to reduce neutron leakage from the sides of the reactor. The outer side of the reflector is surrounded by an aluminum structure (type 6061) with a thickness of 2 cm (Böck and Villa, 2005). The fuel element has a radius of 1.82769 cm and a length of 38.1 cm, and it is surrounded by 0.054-cm-thick stainless-steel cladding with a zirconium plug in the middle of the fuel rod (Table 2 and 3). In addition, the analysis was performed by filling all the holes with fuel rods and withdrawing all the control rods. Figs. 1 and 2 provide an overview of the model’s reactor core and fuel rods, respectively, and convey all the important aspects of the model’s geometry.

Table 2 Fuels’ material and geometric specifications for the hypothetical TRIGA core.

Fuel meat composition	$U-Zr H_{1.65}$	$({Th -}^{233} U)-Zr H_{1.65}$
Content (wt.%)	8.5 (U-235 & U-238)	8.5 or 12 (Th-232 & U-233)
Diameter of zirconium rod (cm)	0.635	0.635
Diameter of fuel meat (cm)	3.655	3.655
Length of fuel meat (cm)	38.1	38.1
Cladding material (Table 3)	SS-304L	SS-304L
Cladding thickness (cm)	0.054	0.054
Graphite reflector thickness (cm)	30	30

Table 3 Atomic density for stainless steel 304L cladding.

	Atomic density (atoms.b^-1.c^-1)
C	0.0003021
Si	0.0001715
Cr	0.0175939
Mn	0.0017540
Fe	0.0592637
Ni	0.0075942
Co	0.0001200

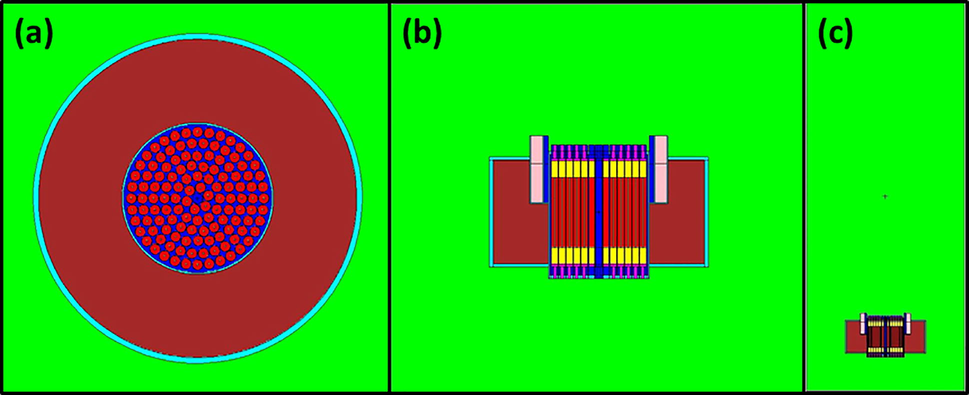
(a) x-y plane and (b) x-z plane cross-sectional views of the MCNP model of the TRIGA core used in this study; (c) a view of the reactor core in water.

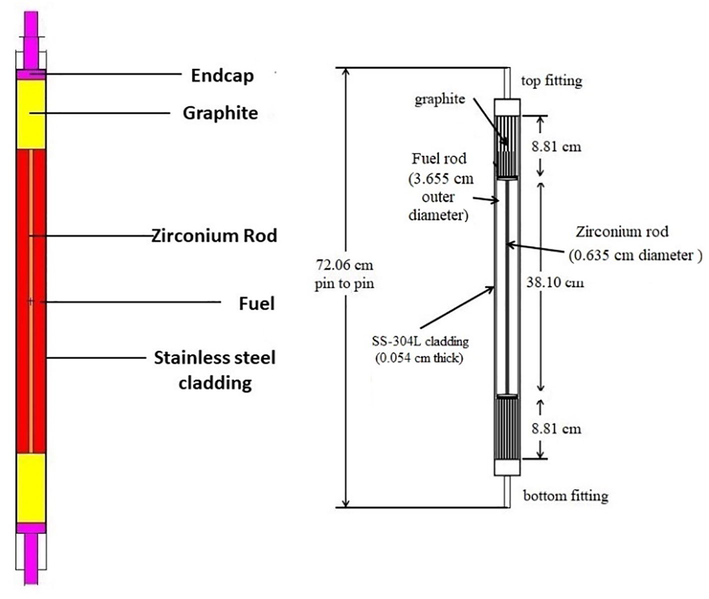
Schematic of a typical TRIGA fuel rod with SS-304L cladding (dimensions are given in centimeters) (Shugart, 2013).

3 Description of computational code and research method

The geometry of our TRIGA model, as shown in Figs. 1 and 2, was modeled through the Monte Carlo method using MCNP 6.2 code (Werner, 2017). MCNP6 is a general-purpose, continuous-energy, generalized-geometry, time-independent, depletion/burnup, and coupled neutron/photon/electron transport code. In this study, a burnup card was used in the MCNP model and enabled in order to evaluate how long the reactor core could support sustained criticality. In addition, the Tier 3 fission products (i.e., all the fission products for which CINDER90 has fission-yield data) was used to track the products at a realistic power of 2 MW. To determine the effective multiplication factors (keff) for each burnup step calculation, all the control rods were completely removed and the KCODE criticality calculation was defined using 30,000 particles per cycle over 500 active cycles, with the initial 100 cycles being skipped before tally accumulation. All the data came from the ENDF/B-VIII.0 (Brown et al., 2018) data library and were processed using NJOY (Macfarlane et al., 2017; Kabach et al., 2021), and the required $S (α, β)$ models were used for the moderator, reflector, and zirconium hydride (Kabach et al., 2019).

4 Results and discussion

4.1

4.1 Parametric study: Selecting potential $({Th -}^{233} U)-Zr H_{1.65}$ fuel mixtures for the TRIGA model

This preliminary phase of the investigation aimed to compare the criticality behavior of $({Th -}^{233} U)-Zr H_{1.65}$ fuel with two proposed contents (8.5 wt% and 12 wt%) and enrichments at beginning of the cycle (BOC) that differed from that of the reference $U-Zr H_{1.65}$ fuel.

The first scenario, which is depicted in Fig. 3 (a), uses ( ${Th -}^{233} U)-Zr H_{1.65}$ (8.5 wt%) fuel with U-233 enrichment increasing from 5% to 90%. From the figure, we can see that after 10% enrichment, the criticality increases quickly in line with the increasing U-233 enrichment, and the reactor becomes critical at 11.3 % enrichment, while at 15 % enrichment, ${k e f f}_{({Th -}^{233} U) - Z r H_{1.65}} \approx {k e f f}_{U-Zr H_{1.65}}$ . The second scenario calculations were performed with a different ( ${Th -}^{233} U)$ content (12 wt%), and the outcome is shown in Fig. 3 (b). In this case, at 8.6% U-233 enrichment, the reactor becomes critical, while at 11.3% enrichment, ${k e f f}_{({Th -}^{233} U) - Z r H_{1.65}} \approx {k e f f}_{U-Zr H_{1.65}}$ . Fig. 4 illustrates the correlated densities as a function of U-233 enrichment and temperature.

(1)

ρ_{({Th -}^{233} U) - Z r H_{1.65}} = {(\frac{w_{{Th -}^{233} U}}{ρ_{{Th -}^{233} U}} + \frac{1 - w_{{Th -}^{233} U}}{ρ_{Z r H_{1.65}}})}^{- 1}

where

w_{{Th -}^{233} U}

is the weight fraction of

{Th -}^{233} U

ρ_{{Th -}^{233} U}

is the density of the

({Th -}^{233} U)

mixture calculated as a function of temperature, as described in (IAEA, 2008), while

ρ_{Z r H_{x}}

can be calculated as follows (Simnad, 1981):

(2)

ρ_{Z r H_{x}} [g / {c m}^{3}] = {(0.171 + 0.0042 x)}^{- 1} f o r x > 1.6

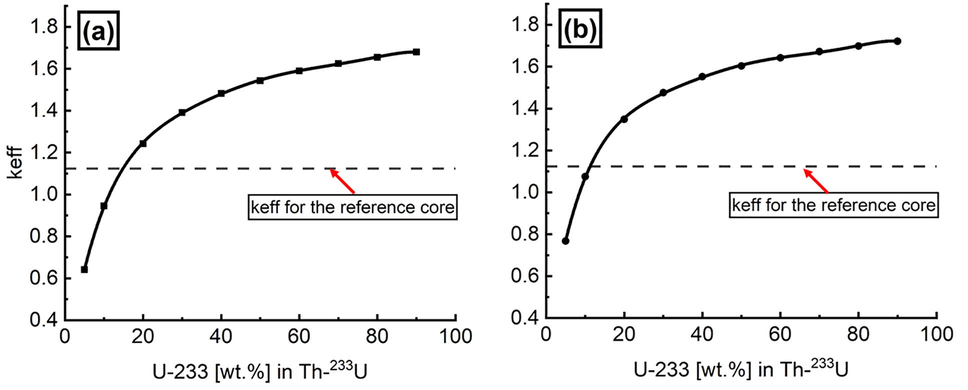
Evolution of the effective multiplication factor depending on fuel enrichment and heavy metal weight contents ((a) 8.5 wt% and (b) 12 wt%) for the TRIGA model.

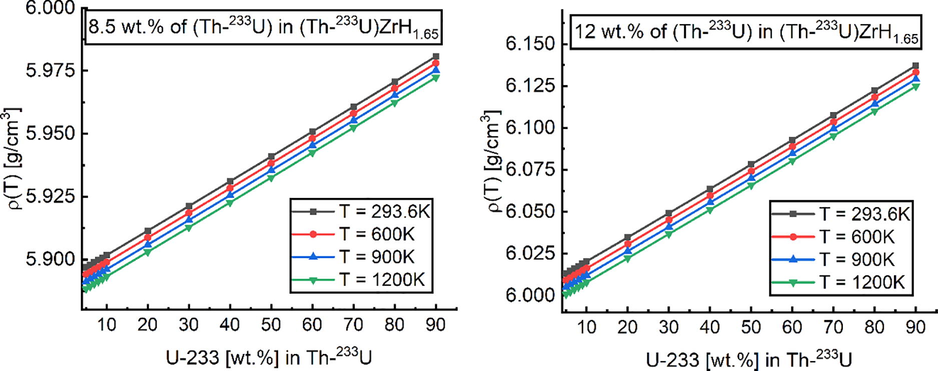
Density of ( Th - 233 U )-Zr H 1.65 fuel depending on U-233 enrichment in Th-233U, Th-233U content (wt.%) in ( Th - 233 U )-Zr H 1.65 and fuel temperature; the alloy density can be calculated using Eqs. (1 and 2).

4.2

4.2 Time-dependent calculations and burnup

4.2.1

4.2.1 Reactivity behavior of the ( ${Th -}^{233} U)-Zr H_{1.65}$ cores as a function of burnup

In this section, we load the modeled reactor core with six different fuel mixtures (core-2 to core −7) with the enrichment and weight fractions described in Table 4. These mixtures were selected based on the results of the previous section, beginning with the enrichment whose excess reactivity reached the $U-Zr H_{1.65}$ value with an estimated difference smaller than 0.3% and then increasing the enrichment by approximately 1% until we reached mixtures with a higher discharge burnup (in days) than that of $U-Zr H_{1.65}$ (core-1 [i.e., the reference fuel]).

Table 4 Characteristics of the fuels chosen for further investigation in this study.

Case name	Description
Case name	Fuel meat type	Heavy metal content	Enrichment
Core-1 [Reference core]	$U-Zr H_{1.65}$	8.5 wt% (U-235 & U-238)	20% (U-235)
Core-2	( ${Th -}^{233} U)-Zr H_{1.65}$	8.5 wt% (Th-232 & U-233)	15% (U-233)
Core-3			16% (U-233)
Core-4			17% (U-233)
Core-5		12 wt% (Th-232 & U-233)	11.3% (U-233)
Core-6			12% (U-233)
Core-7			13% (U-233)

The effective multiplication factor (keff) values depend on both the U-233 enrichment and heavy metal content ( ${Th -}^{233} U)$ in the assembly, and these are illustrated in Fig. 5. In all cases, the keff values decrease over two stages. In the first stage, the keff values decrease rapidly due to the buildup of fission product poisons (i.e., Xenon-135 and Samarium-149). In the second stage, the keff values decrease more gradually with burnup due to the consumption of fissile material. According to the burnup calculations, core-7, core-6, and core-4 have longer cycles than the reference core-1, primarily due to the higher reactivity values at BOC, while core-2, core-3, and core-5 have the shortest cycles. The initial load of core-1, however, was 4,851 g of U-235, while the initial loads of core-7, core-6, and core-4 were 4,591 g, 4,237 g, and 4,171 g of U-233, respectively. Figs. 6 and 7 show the mass variation of the fissile isotopes with burnup. The lower initial loads that are needed for the $({Th -}^{233} U)-Zr H_{1.65}$ fuels, when compared to $U-Zr H_{1.65}$ , are clearly due to U-233′s lower capture-to-fission ratio (Table 1) and higher average number of neutrons emitted per fission (ν). Furthermore, a fundamental benefit of the $({Th -}^{233} U)-Zr H_{1.65}$ fuels is the higher reactivity that is obtained at end of life (EOL) for core-7, core-6, and core-4.

Evolution of the keff values with burnup (days) for the examined fuels. Standard deviation lower than 20 pcm.

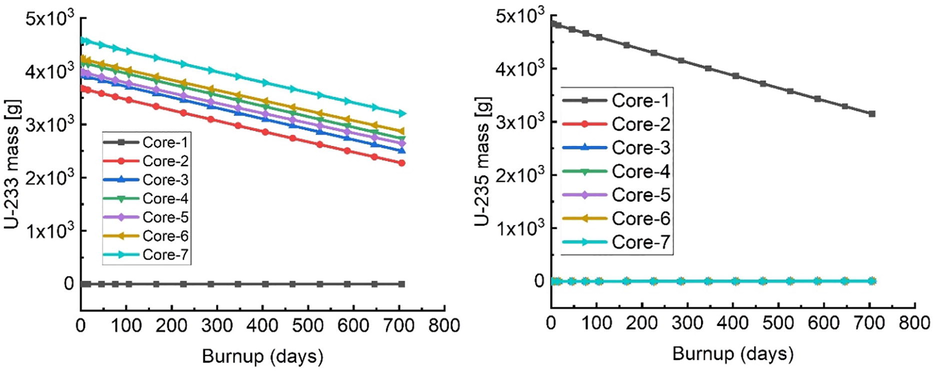
Mass degradation of U-233 and U-235 isotopes in different cases.

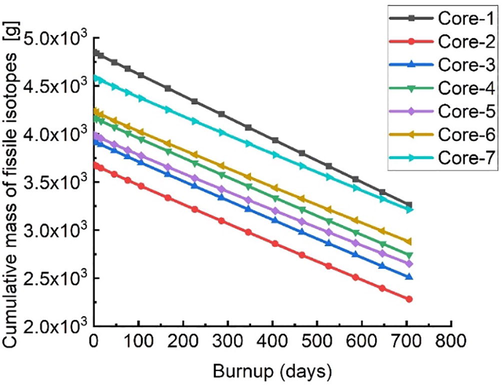
Mass variation of the accumulated fissile isotopes with burnup.

Fig. 8 illustrates how the average number of neutrons emitted per fission tends to vary with burnup (ν). The figure indicates that the ν values in the ( ${Th -}^{233} U)-Zr H_{1.65}$ cases are greater than the value in the $U-Zr H_{1.65}$ case because the ν value of U-233 in the thermal region is 2.4968 while the value of U-235 is 2.4355 (Nichols et al., 2007; Galahom et al., 2021). In the $U-Zr H_{1.65}$ case, the ν value increases linearly with burnup, which is due to fissile material formed with burnup, primarily Pu-239 and Pu-241, which were formed from U-238 (the ν values of Pu-239 and Pu-241 are 2.8836 and 2.9479, respectively). However, in the case of ( ${Th -}^{233} U)-Zr H_{1.65}$ , the smaller formation of U-235 does not contribute to the change in ν value.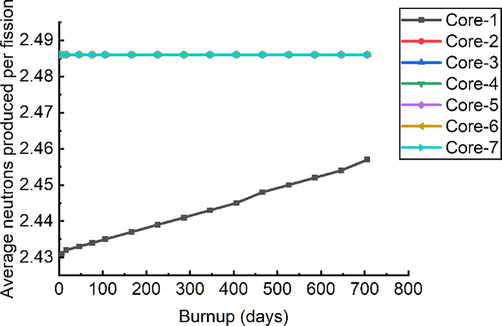

Variation in the average number of neutrons emitted per fission with burnup.

4.2.2

4.2.2 Actinide inventory

A comparative analysis of the actinides produced in all of the investigated cases was also performed. Table 5 shows the mass of these actinides at the same burnup step (466 days), which is approximately the stage at which the reference core reaches a critical condition (keff = 1). Fig. 9, meanwhile, depicts the evolution of the accumulated actinide inventories over time.

Table 5 Mass inventory of actinides for different spent fuels (burnup = 466 days).

Mass inventory [g]
Isotope	Zaid	Core-1	Core-2	Core-3	Core-4	Core-5	Core-6	Core-7
Th-229	90229	–	1.628E-02	1.757E-02	1.887E-02	1.802E-02	1.932E-02	2.120E-02
Th-230	90230	–	2.598E-03	2.534E-03	2.541E-03	3.342E-03	3.313E-03	3.252E-03
Th-231	90231	1.548E-08	7.827E-04	7.480E-04	7.174E-04	1.154E-03	1.111E-03	1.059E-03
Th-232	90232	4.844E-06	2.073E + 04	2.048E + 04	2.025E + 04	3.114E + 04	3.091E + 04	3.058E + 04
Th-233	90233	4.223E-12	6.889E-03	6.382E-03	5.941E-03	9.028E-03	8.436E-03	7.733E-03
Th-234	90234	3.210E-07	1.431E-15	1.281E-15	1.072E-15	1.359E-15	1.127E-15	9.132E-16
Pa-230	91230	–	3.171E-08	2.981E-08	2.797E-08	4.710E-08	4.435E-08	4.137E-08
Pa-231	91231	–	2.010E-01	1.939E-01	1.874E-01	3.016E-01	2.921E-01	2.811E-01
Pa-232	91232	3.363E-09	1.578E-04	1.423E-04	1.292E-04	2.169E-04	1.978E-04	1.759E-04
Pa-233	91233	6.565E-08	1.184E + 01	1.098E + 01	1.023E + 01	1.555E + 01	1.454E + 01	1.334E + 01
U-232	92232	–	2.061E-02	1.923E-02	1.804E-02	2.771E-02	2.588E-02	2.384E-02
U-233	92233	–	2.738E + 03	2.974E + 03	3.213E + 03	3.085E + 03	3.323E + 03	3.665E + 03
U-234	92234	2.713E-02	9.025E + 01	9.087E + 01	9.147E + 01	9.157E + 01	9.215E + 01	9.292E + 01
U-235	92235	3.715E + 03	3.343E + 00	3.181E + 00	3.038E + 00	3.160E + 00	3.021E + 00	2.846E + 00
U-236	92236	1.811E + 02	6.649E-02	5.861E-02	5.206E-02	5.653E-02	5.040E-02	4.328E-02
U-237	92237	6.725E-02	–	–	–	–	–	–
U-238	92238	1.991E + 04	–	–	–	–	–	–
U-239	92239	5.861E-03	–	–	–	–	–	–
U-240	92240	6.942E-18	–	–	–	–	–	–
Np-235	93235	1.465E-09	3.677E-12	3.075E-12	2.544E-12	3.028E-12	2.542E-12	2.017E-12
Np-236	93236	5.814E-07	2.634E-11	2.211E-11	1.868E-11	2.215E-11	1.880E-11	1.521E-11
Np-237	93237	1.580E + 00	–	–	–	–	–	–
Np-238	93238	1.154E-03	–	–	–	–	–	–
Np-239	93239	8.465E-01	–	–	–	–	–	–
Pu-236	94236	4.468E-08	5.717E-12	4.706E-12	3.901E-12	4.672E-12	3.900E-12	3.086E-12
Pu-237	94237	8.540E-08	1.015E-12	7.918E-13	6.244E-13	7.741E-13	6.149E-13	4.545E-13
Pu-238	94238	5.595E-02	–	–	–	–	–	–
Pu-239	94239	8.275E + 01	–	–	–	–	–	–
Pu-240	94240	7.291E + 00	–	–	–	–	–	–
Pu-241	94241	1.098E + 00	–	–	–	–	–	–
Pu-242	94242	4.983E-02	–	–	–	–	–	–
Totals		2.390E + 04	2.357E + 04	2.356E + 04	2.357E + 04	3.434E + 04	3.434E + 04	3.435E + 04

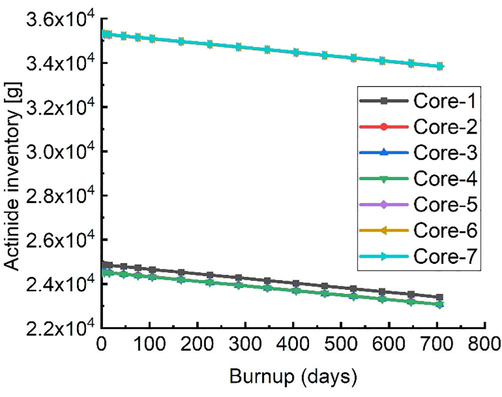
Evolution of the cumulative inventory of actinides in the core over time.

According to the table, there was no production of plutonium isotopes in the $({Th -}^{233} U)-Zr H_{1.65}$ fuels. Conversely, due to the presence of U-238 in the reference $U-Zr H_{1.65}$ fuel, plutonium isotopes were formed during the burnup process. Among these were 82.75 g of Pu-239, which is produced through the capture of a neutron in U-238 and two subsequent β decays of U-239.

Neptunium isotopes, primarily Np-235 and Np-236, were produced in small quantities for both the $U-Zr H_{1.65}$ and $({Th -}^{233} U)-Zr H_{1.65}$ fuels. As U-233 enrichment in the $({Th -}^{233} U)-Zr H_{1.65}$ fuels increases, however, the masses of Np-235 and Np-236 decrease. In the $U-Zr H_{1.65}$ fuel, the mass of the Np-237 isotope is greater, which may be attributed to the presence of U-235 in the $U-Zr H_{1.65}$ fuel. In contrast, there was no Np-237 production in the $({Th -}^{233} U)-Zr H_{1.65}$ fuels.

Other radionuclides, such as protactinium (Pa-233, 27-day half-life) and U-232 (a gamma emitter), may have long-term radiological effects in the case of $({Th -}^{233} U)-Zr H_{1.65}$ fuels. What is more, as shown in Fig. 9, increasing the $({Th -}^{233} U)$ content increases the total mass of actinide, although this is due to the augmented Th-232 charge in the fuels.

4.2.3

4.2.3 Fission product poisons

Fission product poisons are nuclei with a large absorption cross-section and a considerable ability to capture neutrons without contributing to the fission process. Xenon-135 and samarium-149 are the most significant poisons (2.7E + 06 barns and 4.2E + 06 barns, respectively) that may affect the safety of the reactor due to their ability to extract neutrons from the reactor and thus impact reactivity (Galahom, 2017; Uguru et al., 2020). Fig. 10 illustrates how Xe-135 and Sm-149 masses vary with burnup over all the investigated cases. This reveals that the production of Xe-135 and Sm-149 during the burnup of the $({Th -}^{233} U)-Zr H_{1.65}$ fuels are lower and decrease in line with decreasing U-233 enrichment, while the isotope concentrations are the highest with $U-Zr H_{1.65}$ fuel. This is because when U-235 fissions, it yields significantly more fission products that cause reactor poisoning during operation compared to when U-233 fissions.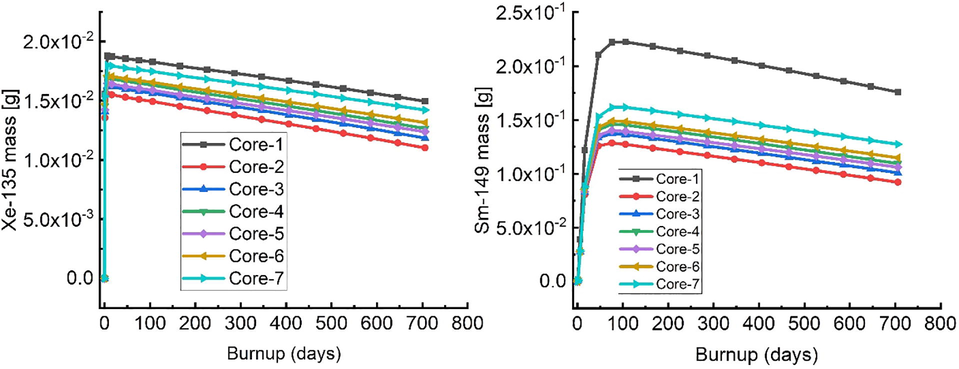

Comparison of Xe-135 and Sm-149 buildup as a function of core burnup.

4.2.4

4.2.4 Neutron energy spectra

It is important that transitioning from $U-Zr H_{1.65}$ to $({Th -}^{233} U)-Zr H_{1.65}$ fuel in a TRIGA reactor does not dramatically change the neutron energy spectrum of the core. Fig. 11 depicts the neutron spectra for the various investigated cases at BOC and burnup (466 days). The calculations revealed that the neutron spectra for core-7 and the reference fuel are virtually identical, while in the other cases, the neutron spectrum becomes even more thermal as the Th-232 content increases (and the U-233 enrichment decreases). This phenomenon may be explained by the fact that the neutron capture cross-section of Th-232 in the thermal and epithermal neutron spectra is approximately two and a half times greater than that of U-238 (Kabach et al., 2020). In the cases of high U-233 enrichment, meanwhile, the nearly equivalent neutron spectra can be attributed to the fact that both U-233 and U-235 have similar capture resonance integral values of 138 and 133, respectively (Attom et al., 2019).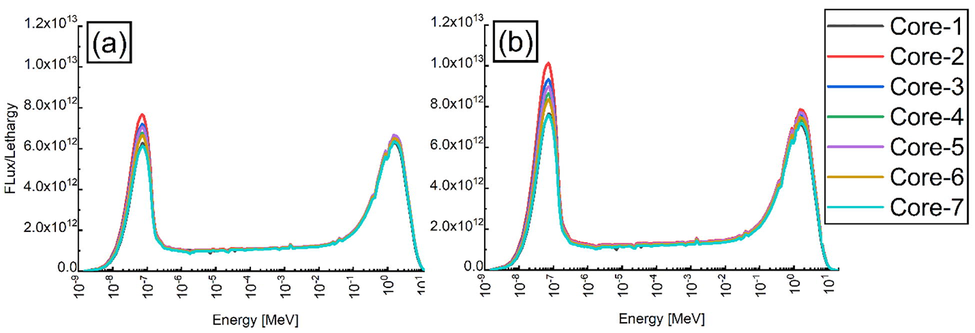

Neutron spectra for the investigated cases at (a) BOC and (b) burnup (466 days).

Fig. 12 illustrates the variation in thermal neutron flux with burnup for the analyzed cases. In all these cases, the neutron fluxes increased in a similar manner. Furthermore, in the neutron spectrum, a specific feature indicates that the neutron flux increases proportionally with the Th-232 content of the fuel.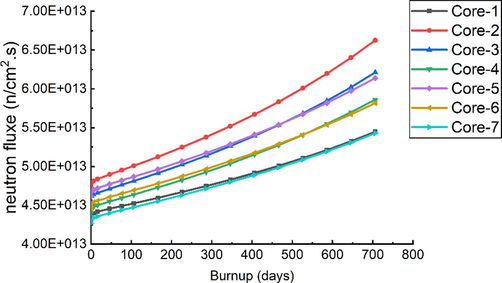

Variation of thermal neutron fluxes with burnup.

4.2.5

4.2.5 Fuel temperature coefficients

The fuel temperature coefficient (FTC) is a critical safety parameter that affects a core’s reactivity, with a change in fuel temperature inducing a change in reactivity because the latter causes a variation in the fuel absorption cross-section (Abdelghafar Galahom, 2020). If the reactivity is negative, the reactor will tend to stabilize, but if the reactivity is positive, the reactor’s state tends to escalate out of control, necessitating an external intervention to preserve its stability. This section, therefore, looks into how the FTC values of the core change in line with burnup, U-233 enrichment, and ${Th -}^{233} U$ content as a result of two different operating states: cold and warm. The cold state means that the temperatures of the Zr rod, cladding, and moderator are set to be the same as the fuel temperature (room temperature or 293.6 K). In the warm state, meanwhile, the temperature of the fuel and the Zr rod is raised to 600 K, while the temperature of the moderator remains at 293.6 K. The FTCs were determined using Equation (3) (Kabach et al., 2021; Mosteller et al., 1991), evaluated by performing sixth-order polynomial fitting, and plotted as reactivity versus burnup. Fig. 13 shows the temperature coefficients as calculated across the temperature range. The first thing that can be gleaned from this figure is that all the FTCs are negative. Moreover, with increased fuel burnup, the coefficient curves show a more negative trend. However, the cores fueled by $({Th -}^{233} U)-Zr H_{1.65}$ have marginally lower negative FTC values due to the lower neutron capture resonance of Th-232 when compared to U-238. Furthermore, increasing the U-233 enrichment of the fuel has a positive effect due to the fission cross-section broadening in the Doppler Effect.

(3)

F T C = \frac{Δ ρ}{Δ T_{F u e l}} = (\frac{ρ (W a r m s t a t e) - ρ (C o l d s t a t e)}{Δ T_{F u e l}}) * 10^{5} [p c m / K]

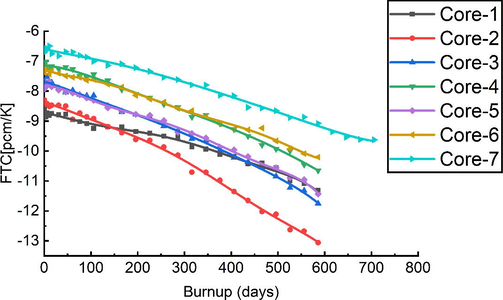
Fitted curves for fuel temperature coefficients as a function of burnup. The 1σ statistical uncertainty bars range from around 0.0015 to 0.0033 pcm.

4.2.6

4.2.6 Effective delayed neutron fraction

The effective delayed neutron fraction (βeff) is the second safety parameter that was calculated. βeff is an important parameter to investigate because it is a kinetics parameter that determines the time-dependent response of a reactor. A higher βeff value means that a smaller proportion of the fission neutrons appear as prompt neutrons, and the core responds more slowly. A lower βeff value, on the other hand, means that a greater proportion of fission neutrons appear as prompt neutrons, so the reactor’s kinetic response is quicker (Carbajo, 2005). We therefore calculated the βeff values using MCNP code for each case by using the prompt method, which requires two simulations. In the first simulation, both delayed neutrons and prompt neutrons were counted, resulting in a total multiplication factor ( $k_{e f f, (t o t a l)}$ ). In the second simulation, only the prompt neutrons were counted (TOTNU data mode with entry NO after KCODE), resulting in the prompt multiplication factor ( $k_{e f f, (p r o m p t)}$ ). Based on the results of these two simulations, the βeff values could be estimated using Equation (4) (Kabach et al., 2020; Kabach et al., 2019; Tucker and Usman, 2018 ).

Based on the simulation results shown in Fig. 14, the βeff values of the modeled cores fueled with $({Th -}^{233} U)-Zr H_{1.65}$ were lower at every stage than those of the core fueled with $U-Zr H_{1.65}$ . This is unsurprising given that the delayed neutron fraction of U-233 (0.0031) is lower than that of U-235 (0.0069) (IAEA, 2005), something that is undesirable from a reactor safety viewpoint. Furthermore, the U-233 isotope clearly makes the greatest contribution to the effective delayed neutron fraction values, while thorium makes virtually no contribution, and this happens because the fission rate of U-233 in the thermal core is noticeably higher than that of Th-232 (Mirvakili et al., 2015).

(4)

β_{e f f} ≅ (1 - \frac{k_{e f f, (p r o m p t)}}{k_{e f f, (t o t a l)}}) {* 10}^{5} [p c m]

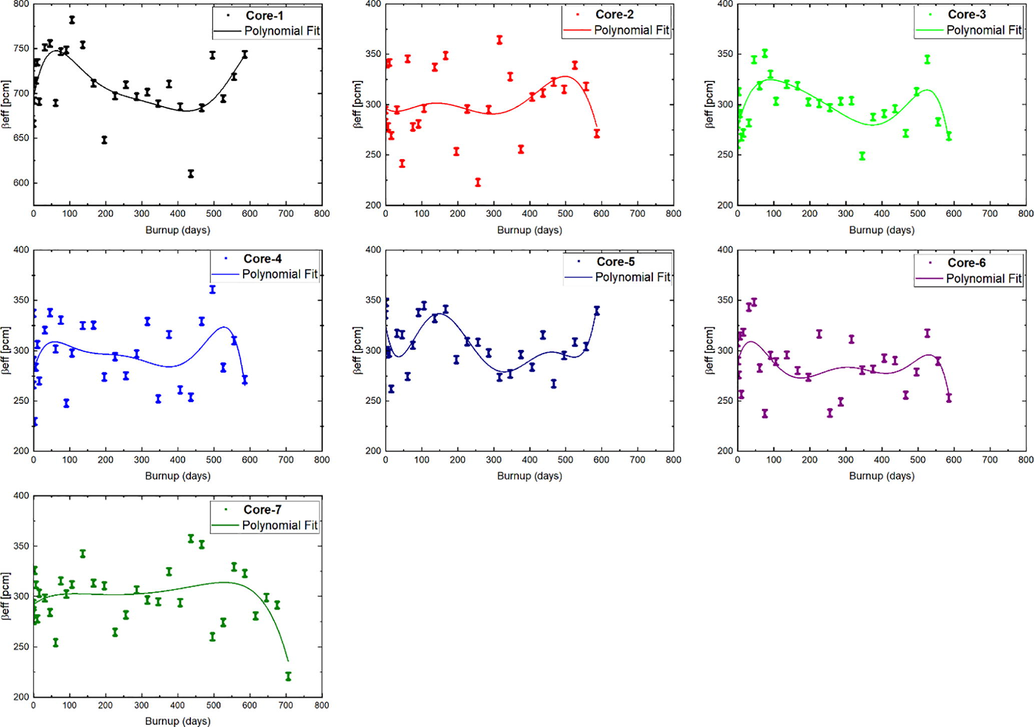
Effective delayed neutron fraction versus burnup. The 1σ statistical uncertainty bars range from around 3 to 4 pcm.

5 Conclusion and future work

This study investigated the consequences of transitioning from $U-Zr H_{1.65}$ fuel to $({Th -}^{233} U)-Zr H_{1.65}$ fuel in a TRIGA reactor core by simulating two different Th-²³³U weight contents (i.e., 8.5 wt% and 12 wt%) and various U-233 enrichment levels. According to the results, the U-238 isotope was found to be the primary source of plutonium isotopes and actinides, so replacing $U-Zr H_{1.65}$ with $({Th -}^{233} U)-Zr H_{1.65}$ would greatly reduce the actinides in spent fuel because the plutonium content in the spent form of the latter fuel is virtually zero. Furthermore, fission product poisons were produced in much lower concentrations in the $({Th -}^{233} U)-Zr H_{1.65}$ fuels. It was observed, however, that replacing U (i.e., U-235 and U-238) with ${Th -}^{233} U$ requires a higher excess reactivity at BOC to achieve the same discharge burnup. Consequently, at this level of reactivity, a burnable absorber would be needed to control the excess reactivity. The findings of this study also revealed that the fuel temperature coefficients for the $({Th -}^{233} U)-Zr H_{1.65}$ fuels were slightly less negative than those for the reference $U-Zr H_{1.65}$ fuel. Moreover, due to the lower delayed neutron fraction of U-233, the effective delayed neutron fractions for $({Th -}^{233} U)-Zr H_{1.65}$ fuels are noticeably lower at all-time steps when compared to $U-Zr H_{1.65}$ fuel, which is not desirable from the reactor safety point of view. It is possible; however, that bringing about more favorable temperature coefficient values could ameliorate the controllability issues suggested by its lower delayed neutron fractions.

Overall, using $({Th -}^{233} U)-Zr H_{1.65}$ fuel in a TRIGA reactor seems feasible from a neutronics perspective due to its numerous advantages. Even so, a complete thermal fluid analysis in combination with a neutronic analysis is needed to fully understand the impact of this change of fuel. Future research could also focus on other neutronic properties and safety parameters for $({Th -}^{233} U)-Zr H_{1.65}$ fuels, such as incorporating a burnable absorber to control core excess reactivity, improve core lifetime, and bring about more-negative fuel temperature coefficients that in turn will reduce the impact of the lower delayed neutron fraction.

6 Data availability statement

This paper and the references therein contain all the data needed to reproduce and validate the presented results.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

A.L. Nichols, D.L. Aldama, Verpelli, M., 2007. Handbook of Nuclear Data for Safeguards, International Atomic Energy Agency.
Abdelghafar Galahom A., . Investigate the possibility of burning weapon-grade plutonium using a concentric rods BS assembly of VVER-1200. Ann. Nucl. Energy. 2020;148:107758.
[CrossRef] [Google Scholar]
Adams F.P., Yaraskavitch L., Atfield J.E., . Measurements on (233U, Th)O2 fuel by substitution experiments in the ZED-2 critical facility. Ann. Nucl. Energy. 2020;148:107709.
[CrossRef] [Google Scholar]
Amsil H., Jalil A., Kabach O., Chahidi H., Bounouira H., Elyounoussi C., Chetaine A., . Neutron beam characterization for the Moroccan TRIGA Mark II reactor. J. Radioanal. Nucl. Chem.. 2021;327(3):1063-1072.
[CrossRef] [Google Scholar]
Attom A.M., Wang J., Yan C., Ding M., . Neutronic analysis of thorium MOX fuel blocks with different driver fuels in advanced block-type HTRs. Ann. Nucl. Energy. 2019;129:101-109.
[CrossRef] [Google Scholar]
Böck, H., Villa, M., 2005. TRIGA reactor characteristics, International Atomic Energy Agency.
Böck H., Villa M., Bergmann R., . Five decades of TRIGA reactors. In: 25th Int. Conf. Nucl. Energy New Eur.. 2016. p. :1-8.
[Google Scholar]
Borio di Tigliole A., Cammi A., Clemenza M., Memoli V., Pattavina L., Previtali E., . Benchmark evaluation of reactor critical parameters and neutron fluxes distributions at zero power for the TRIGA Mark II reactor of the University of Pavia using the Monte Carlo code MCNP. Prog. Nucl. Energy. 2010;52(5):494-502.
[CrossRef] [Google Scholar]
Bourquin, M., 2016. Thorium Energy for the World, in: Revol, J.-P., Bourquin, M., Kadi, Y., Lillestol, E., de Mestral, J.-C., Samec, K. (Eds.), Thorium Energy for the World. Springer International Publishing, Cham. https://doi.org/10.1007/978-3-319-26542-1.
Brown D.A., Chadwick M.B., Capote R., Kahler A.C., Trkov A., Herman M.W., Sonzogni A.A., Danon Y., Carlson A.D., Dunn M., Smith D.L., Hale G.M., Arbanas G., Arcilla R., Bates C.R., Beck B., Becker B., Brown F., Casperson R.J., Conlin J., Cullen D.E., Descalle M.A., Firestone R., Gaines T., Guber K.H., Hawari A.I., Holmes J., Johnson T.D., Kawano T., Kiedrowski B.C., Koning A.J., Kopecky S., Leal L., Lestone J.P., Lubitz C., Márquez Damián J.I., Mattoon C.M., McCutchan E.A., Mughabghab S., Navratil P., Neudecker D., Nobre G.P.A., Noguere G., Paris M., Pigni M.T., Plompen A.J., Pritychenko B., Pronyaev V.G., Roubtsov D., Rochman D., Romano P., Schillebeeckx P., Simakov S., Sin M., Sirakov I., Sleaford B., Sobes V., Soukhovitskii E.S., Stetcu I., Talou P., Thompson I., van der Marck S., Welser-Sherrill L., Wiarda D., White M., Wormald J.L., Wright R.Q., Zerkle M., Žerovnik G., Zhu Y., . ENDF/B-VIII.0: the 8th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data. Nucl. Data Sheets. 2018;148:1-142.
[CrossRef] [Google Scholar]
Carbajo, J., 2005. Issues in the use of Weapons-Grade MOX Fuel in VVER-1000 Nuclear Reactors: Comparison of UO2 and MOX Fuels, ORNL/TM-2004/223, Oak Ridge National Laboratory. Oak Ridge, TN. https://doi.org/10.2172/885998.
Chiesa D., Clemenza M., Nastasi M., Pozzi S., Previtali E., Scionti G., Sisti M., Prata M., Salvini A., Cammi A., . Measurement and simulation of the neutron flux distribution in the TRIGA Mark II reactor core. Ann. Nucl. Energy. 2015;85:925-936.
[CrossRef] [Google Scholar]
Fouquet D.M., Razvi J., Whittemore W.L., . TRIGA research reactors: a pathway to the peaceful applications of nuclear energy. Nucl. News. 2003;46:46-56.
[Google Scholar]
Galahom A.A., . Minimization of the fission product waste by using thorium based fuel instead of uranium dioxide. Nucl. Eng. Des.. 2017;314:165-172.
[CrossRef] [Google Scholar]
Galahom, A.A., Mohsen, M.Y.M., Amrani, N., 2021. Explore the possible advantages of using thorium-based fuel in a pressurized water reactor (PWR) Part 1: Neutronic analysis. Nucl. Eng. Technol. https://doi.org/10.1016/j.net.2021.07.019.
General Atomics, 2021. No Title [WWW Document]. URL http://triga.ga.com.
Huda M.Q., . Computational analysis of Bangladesh 3 MW TRIGA research reactor using MCNP4C, JENDL-3.3 and ENDF/B-Vl data libraries. Ann. Nucl. Energy. 2006;33:1072-1078.
[CrossRef] [Google Scholar]
IAEA, 2016. History, Development and Future of TRIGA Research Reactors. Tech. Reports Ser. No. 482.
IAEA, . Summary for Policymakers, Climate Change 2013 - The Physical Science Basis. Cambridge: Cambridge University Press; 2008.
IAEA, 2006. Thermophysical Properties Database of Materials for Light Water Reactors and Heavy Water Reactors, IAEA-TECDOC-1496.
IAEA, . Thorium Fuel Cycle - Potential Benefits and Challenges IAEA. IAEA Publication; 2005.
Kabach O., Chetaine A., Benchrif A., . Processing of JEFF-3.3 and ENDF/B-VIII.0 and testing with critical benchmark experiments and TRIGA Mark II research reactor using MCNPX. Appl. Radiat. Isot.. 2019;150:146-156.
[CrossRef] [Google Scholar]
Kabach O., Chetaine A., Benchrif A., Amsil H., . An inter-comparison between ENDF/B-VIII.0-NECP-Atlas and ENDF/B-VIII.0-NJOY results for criticality safety benchmarks and benchmarks on the reactivity temperature coefficient. Nucl. Eng. Technol.. 2021;53(8):2445-2453.
[CrossRef] [Google Scholar]
Kabach O., Chetaine A., Benchrif A., Amsil H., . Neutronic investigation of the thorium-based mixed-oxide as an alternative fuel in the TRIGA Mark-II research reactor – Part I: A beginning of life calculations. Ann. Nucl. Energy. 2020;140:107075.
[CrossRef] [Google Scholar]
Macfarlane, R., Muir, D.W., Boicourt, R.M., Kahler, III, A.C., Conlin, J.L., 2017. The NJOY Nuclear Data Processing System, Version 2016. https://doi.org/10.2172/1338791.
Matsumoto T., . Benchmark analysis of criticality experiments in the TRIGA mark II using a continuous energy monte carlo code MCNP. J. Nucl. Sci. Technol.. 1998;35(9):662-670.
[CrossRef] [Google Scholar]
Mirvakili S.M., Alizadeh Kavafshary M., Joze Vaziri A., . Comparison of neutronic behavior of UO 2, (Th- 233 U)O 2 and (Th- 235 U)O 2 fuels in a typical heavy water reactor. Nucl. Eng. Technol.. 2015;47:315-322.
[CrossRef] [Google Scholar]
Mosteller, R.D., Eisenhart, L.D., Little, R.C., Eich, W.J., Chao, J., 1991. Benchmark calculations for the doppler coefficient of reactivity. Nucl. Sci. Eng. 107, 265–271. https://doi.org/10.13182/NSE91-A23789.
Nuclear Energy Agency, . Introduction of Thorium in the Nuclear Fuel Cycle. Nuclear Energy Agency; 2015. 10.1787/9789264241732-en
Office of Nuclear Energy, 2017. Nuclear Fuel from Idaho Now Benefiting University of Maryland Reactor, https://www.energy.gov/ne/articles/nuclear-fuel-idaho-now-benefiting-university-maryland-reactor (accessed 4.25.19).
Shugart, N., 2013. Neutronic and thermal hydraulic analysis of the geological survey TRIGA REACTOR.
Simnad M.T., . The UZrHx alloy: Its properties and use in TRIGA fuel. Nucl. Eng. Des.. 1981;64(3):403-422.
[CrossRef] [Google Scholar]
Tucker L.P., Usman S., . Thorium-based mixed oxide fuel in a pressurized water reactor: a burnup analysis with MCNP. Ann. Nucl. Energy. 2018;111:163-175.
[CrossRef] [Google Scholar]
Uguru E.H., Sani S.F.A., Khandaker M.U., Rabir M.H., . Investigation on the effect of 238U replacement with 232Th in small modular reactor (SMR) fuel matrix. Prog. Nucl. Energy. 2020;118:103108.
[CrossRef] [Google Scholar]
Vignolo R., Villarino E., Hergenreder D., . Conceptual design of a compact nuclear reactor core conceptual design of a compact nuclear reactor core. In: IGORR Conference. 2014. p. :1-11.
[Google Scholar]
Werner, C.J., 2017. MCNP® USER’S MANUAL Code Version 6.2.

Introduction

Description of the TRIGA reactor and the 3D model

Description of computational code and research method

Results and discussion

Parametric study: Selecting potential ( Th - 233 U )-Zr H 1.65 fuel mixtures for the TRIGA model
Time-dependent calculations and burnup

Conclusion and future work

Data availability statement

Fulltext Views
34

PDF downloads
22

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] A.L. Nichols, D.L. Aldama, Verpelli, M., 2007. Handbook of Nuclear Data for Safeguards, International Atomic Energy Agency.

[2] Abdelghafar Galahom A., . Investigate the possibility of burning weapon-grade plutonium using a concentric rods BS assembly of VVER-1200. Ann. Nucl. Energy. 2020;148:107758.
[CrossRef] [Google Scholar]

[3] Adams F.P., Yaraskavitch L., Atfield J.E., . Measurements on (233U, Th)O2 fuel by substitution experiments in the ZED-2 critical facility. Ann. Nucl. Energy. 2020;148:107709.
[CrossRef] [Google Scholar]

[4] Amsil H., Jalil A., Kabach O., Chahidi H., Bounouira H., Elyounoussi C., Chetaine A., . Neutron beam characterization for the Moroccan TRIGA Mark II reactor. J. Radioanal. Nucl. Chem.. 2021;327(3):1063-1072.
[CrossRef] [Google Scholar]

[5] Attom A.M., Wang J., Yan C., Ding M., . Neutronic analysis of thorium MOX fuel blocks with different driver fuels in advanced block-type HTRs. Ann. Nucl. Energy. 2019;129:101-109.
[CrossRef] [Google Scholar]

[6] Böck, H., Villa, M., 2005. TRIGA reactor characteristics, International Atomic Energy Agency.

[7] Böck H., Villa M., Bergmann R., . Five decades of TRIGA reactors. In: 25th Int. Conf. Nucl. Energy New Eur.. 2016. p. :1-8.
[Google Scholar]

[8] Borio di Tigliole A., Cammi A., Clemenza M., Memoli V., Pattavina L., Previtali E., . Benchmark evaluation of reactor critical parameters and neutron fluxes distributions at zero power for the TRIGA Mark II reactor of the University of Pavia using the Monte Carlo code MCNP. Prog. Nucl. Energy. 2010;52(5):494-502.
[CrossRef] [Google Scholar]

[9] Bourquin, M., 2016. Thorium Energy for the World, in: Revol, J.-P., Bourquin, M., Kadi, Y., Lillestol, E., de Mestral, J.-C., Samec, K. (Eds.), Thorium Energy for the World. Springer International Publishing, Cham. https://doi.org/10.1007/978-3-319-26542-1.

[10] Brown D.A., Chadwick M.B., Capote R., Kahler A.C., Trkov A., Herman M.W., Sonzogni A.A., Danon Y., Carlson A.D., Dunn M., Smith D.L., Hale G.M., Arbanas G., Arcilla R., Bates C.R., Beck B., Becker B., Brown F., Casperson R.J., Conlin J., Cullen D.E., Descalle M.A., Firestone R., Gaines T., Guber K.H., Hawari A.I., Holmes J., Johnson T.D., Kawano T., Kiedrowski B.C., Koning A.J., Kopecky S., Leal L., Lestone J.P., Lubitz C., Márquez Damián J.I., Mattoon C.M., McCutchan E.A., Mughabghab S., Navratil P., Neudecker D., Nobre G.P.A., Noguere G., Paris M., Pigni M.T., Plompen A.J., Pritychenko B., Pronyaev V.G., Roubtsov D., Rochman D., Romano P., Schillebeeckx P., Simakov S., Sin M., Sirakov I., Sleaford B., Sobes V., Soukhovitskii E.S., Stetcu I., Talou P., Thompson I., van der Marck S., Welser-Sherrill L., Wiarda D., White M., Wormald J.L., Wright R.Q., Zerkle M., Žerovnik G., Zhu Y., . ENDF/B-VIII.0: the 8th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data. Nucl. Data Sheets. 2018;148:1-142.
[CrossRef] [Google Scholar]

[11] Carbajo, J., 2005. Issues in the use of Weapons-Grade MOX Fuel in VVER-1000 Nuclear Reactors: Comparison of UO2 and MOX Fuels, ORNL/TM-2004/223, Oak Ridge National Laboratory. Oak Ridge, TN. https://doi.org/10.2172/885998.

[12] Chiesa D., Clemenza M., Nastasi M., Pozzi S., Previtali E., Scionti G., Sisti M., Prata M., Salvini A., Cammi A., . Measurement and simulation of the neutron flux distribution in the TRIGA Mark II reactor core. Ann. Nucl. Energy. 2015;85:925-936.
[CrossRef] [Google Scholar]

[13] Fouquet D.M., Razvi J., Whittemore W.L., . TRIGA research reactors: a pathway to the peaceful applications of nuclear energy. Nucl. News. 2003;46:46-56.
[Google Scholar]

[14] Galahom A.A., . Minimization of the fission product waste by using thorium based fuel instead of uranium dioxide. Nucl. Eng. Des.. 2017;314:165-172.
[CrossRef] [Google Scholar]

[15] Galahom, A.A., Mohsen, M.Y.M., Amrani, N., 2021. Explore the possible advantages of using thorium-based fuel in a pressurized water reactor (PWR) Part 1: Neutronic analysis. Nucl. Eng. Technol. https://doi.org/10.1016/j.net.2021.07.019.

[16] General Atomics, 2021. No Title [WWW Document]. URL http://triga.ga.com.

[17] Huda M.Q., . Computational analysis of Bangladesh 3 MW TRIGA research reactor using MCNP4C, JENDL-3.3 and ENDF/B-Vl data libraries. Ann. Nucl. Energy. 2006;33:1072-1078.
[CrossRef] [Google Scholar]

[18] IAEA, 2016. History, Development and Future of TRIGA Research Reactors. Tech. Reports Ser. No. 482.

[19] IAEA, . Summary for Policymakers, Climate Change 2013 - The Physical Science Basis. Cambridge: Cambridge University Press; 2008.

[20] IAEA, 2006. Thermophysical Properties Database of Materials for Light Water Reactors and Heavy Water Reactors, IAEA-TECDOC-1496.

[21] IAEA, . Thorium Fuel Cycle - Potential Benefits and Challenges IAEA. IAEA Publication; 2005.

[22] Kabach O., Chetaine A., Benchrif A., . Processing of JEFF-3.3 and ENDF/B-VIII.0 and testing with critical benchmark experiments and TRIGA Mark II research reactor using MCNPX. Appl. Radiat. Isot.. 2019;150:146-156.
[CrossRef] [Google Scholar]

[23] Kabach O., Chetaine A., Benchrif A., Amsil H., . An inter-comparison between ENDF/B-VIII.0-NECP-Atlas and ENDF/B-VIII.0-NJOY results for criticality safety benchmarks and benchmarks on the reactivity temperature coefficient. Nucl. Eng. Technol.. 2021;53(8):2445-2453.
[CrossRef] [Google Scholar]

[24] Kabach O., Chetaine A., Benchrif A., Amsil H., . Neutronic investigation of the thorium-based mixed-oxide as an alternative fuel in the TRIGA Mark-II research reactor – Part I: A beginning of life calculations. Ann. Nucl. Energy. 2020;140:107075.
[CrossRef] [Google Scholar]

[25] Macfarlane, R., Muir, D.W., Boicourt, R.M., Kahler, III, A.C., Conlin, J.L., 2017. The NJOY Nuclear Data Processing System, Version 2016. https://doi.org/10.2172/1338791.

[26] Matsumoto T., . Benchmark analysis of criticality experiments in the TRIGA mark II using a continuous energy monte carlo code MCNP. J. Nucl. Sci. Technol.. 1998;35(9):662-670.
[CrossRef] [Google Scholar]

[27] Mirvakili S.M., Alizadeh Kavafshary M., Joze Vaziri A., . Comparison of neutronic behavior of UO 2, (Th- 233 U)O 2 and (Th- 235 U)O 2 fuels in a typical heavy water reactor. Nucl. Eng. Technol.. 2015;47:315-322.
[CrossRef] [Google Scholar]

[28] Mosteller, R.D., Eisenhart, L.D., Little, R.C., Eich, W.J., Chao, J., 1991. Benchmark calculations for the doppler coefficient of reactivity. Nucl. Sci. Eng. 107, 265–271. https://doi.org/10.13182/NSE91-A23789.

[29] Nuclear Energy Agency, . Introduction of Thorium in the Nuclear Fuel Cycle. Nuclear Energy Agency; 2015. 10.1787/9789264241732-en

[30] Office of Nuclear Energy, 2017. Nuclear Fuel from Idaho Now Benefiting University of Maryland Reactor, https://www.energy.gov/ne/articles/nuclear-fuel-idaho-now-benefiting-university-maryland-reactor (accessed 4.25.19).

[31] Shugart, N., 2013. Neutronic and thermal hydraulic analysis of the geological survey TRIGA REACTOR.

[32] Simnad M.T., . The UZrHx alloy: Its properties and use in TRIGA fuel. Nucl. Eng. Des.. 1981;64(3):403-422.
[CrossRef] [Google Scholar]

[33] Tucker L.P., Usman S., . Thorium-based mixed oxide fuel in a pressurized water reactor: a burnup analysis with MCNP. Ann. Nucl. Energy. 2018;111:163-175.
[CrossRef] [Google Scholar]

[34] Uguru E.H., Sani S.F.A., Khandaker M.U., Rabir M.H., . Investigation on the effect of 238U replacement with 232Th in small modular reactor (SMR) fuel matrix. Prog. Nucl. Energy. 2020;118:103108.
[CrossRef] [Google Scholar]

[35] Vignolo R., Villarino E., Hergenreder D., . Conceptual design of a compact nuclear reactor core conceptual design of a compact nuclear reactor core. In: IGORR Conference. 2014. p. :1-11.
[Google Scholar]

[36] Werner, C.J., 2017. MCNP® USER’S MANUAL Code Version 6.2.

Neutronic feasibility study of ( Th - 233 U)-Zr H 1.65 fuel in a modelled TRIGA research reactor