Modal treatment in two dimensions theoretical foundations of VLF-radio wave propagation using the normalized airy functions

Data availability

Data sharing not applicable to this article as no data-sets were generated or analyzed during the current study.

1 Introduction

Beginning in the first decade of the 20th century, conformal mappings were first used to solve Laplace’s equation and other steady-state issues in mathematical physics. All integral equations found in any conformal mapping problem are Fredholm integral equations of the second type with a limited kernel, with the exception of Symm’s integral equation, which is of the first kind with a kernel that contains a logarithmic singularity. The second class of Fredholm integral equations are never ill-conditioned, and accurate error estimates are available for them (Kythe, 2019). Assuring that the solution is periodic and singular is the ideal approach for creating a computational technique based on an integral equation formulation. This allows for the efficient use of the extremely precise trapezoid rule on smooth contours. It is also important to search for the fact that the mapping onto canonical areas (such as the unit disk, annuls, or slit disks) results in systems of linear equations rather than systems of nonlinear equations that must be solved.

The Earth-ionosphere waveguide pattern propagation of VLF (Very Low Frequency) radio waves is an enthralling phenomenon that is important for communications over long distances and for the research of electromagnetic wave propagation in the Earth’s atmosphere. Let us divide this notion down into its key elements to better comprehend it:

• The Earth-Ionosphere waveguide is a geological route that connects the Earth’s surface to the ionosphere, a layer of electrons in the Earth’s outer atmosphere. The ionosphere is a layer of electrically charged particles that exists between 30 miles (50 km) and 600 miles (1000 km) beyond the Earth’s surface and can absorb and distort radio signals.

• VLF radio waves are electromagnetic waves with frequencies ranging from 3 kHz to 30 kHz; however, the actual frequency range might vary significantly. Although they are capable of traversing the Earth’s atmosphere and transmitting faraway information with very minimal power, these waves are frequently utilized for communication over long distances.

• VLF radio waves may propagate in a special mode known as the “ground wave” or “surface wave” pattern in the Earth-ionosphere waveguide. This type of radiation includes VLF waves interacting with the Earth’s surface and ionosphere.

The Earth is shown as a spherical entity in the theory of radio transmission, and layers of the atmosphere are frequently deified as spheres. In order to investigate the geoenvironmental issues in shallow, low-conductivity sedimentary layers, explore the groundwater, and pinpoint the location of anomalous source bodies underneath, VLF electromagnetic technology is applied. The frequency region between 15 and 30 kHz is where VLF electromagnetic technology is applied. The carrier waves of long-distance, strong communications transmission used by military groups are also used by VLF. When a VLF transmitter travels across the surface of the Earth, strong signals transported over the resistible section of the crystalline rock mass will be picked up. In addition to water-bearing cracks, VLF technique may identify any linear conductive substance. The aerial use of VLF methods is particularly well-liked. Both conductive and resistible objects may be effectively searched for using this technique (Gandhi and Sarkar, 2016).

The propagating spherical wave functions are typically substituted by the Airy functions (AFs) and Legendre functions in the approximate outcome because of their asymptotic expansions. The solutions to the Airy differential equation ${\varphi }^{\prime \prime }\left(\zeta \right)-\zeta \varphi \left(\zeta \right)=0$ are known as the Air functions (AFs). Two essays by G. B. Airy included the first integral representation of the function Ai( $\zeta$ ). Olivier and Soares presented a study on the optics of a raindrop containing a detailed explanation of the Airy hypothesis (Olivier and V, 2010). The AFs have a significant role in electromagnetism, the propagation of radio waves, the study of electromagnetic diffraction, the propagation of light and optical studies. They are also extensively used in research in Olivier (2002). The applications of AFs are presented depending on two properties of these functions, symmetry and convexity. Symmetry property is used in radial studies (see Anikin et al. (2019), Minin et al. (2021), Chen et al. (2019)). While the convexity property is employed in the lenses investigations (see Suarez and Gesualdi (2020), Len (2022), Indenbom (2022)).

In this effort, we employ the properties of Airy functions to determine the solution of a complex variable wave equation. To discuss the behavior of the solution of the wave equation, we firstly present the Airy functions in the normalized form (NAFs). This will help us to investigate the geometric properties. We prove that the normalized formula involves some interesting special functions. To examine the propagation of 2D-waves in a complex domain, we proceeded to find the symmetry-convex depiction of the NAFs. Our aim is to illustrate a set of sufficient conditions to obtain the one-one (univalent) outcome, which is very important in the complex wave equation. The basic working formula for the VLF-Radio-mode theory is shown to be easily derivable from orthogonality considerations without the requirement for in-depth justification in the open unit disk. By considering the symmetry-convex behavior of the NAFs, the expression is combined. Section 2 presents the methodology, Section 3 indicates the results with the discussion and Section 4 involves the final conclusion.

2 Methodology

This section deals with different concepts that will be used in the outcome.

2.2

2.2 Airy symmetric-convex differential operator

We proceed to define the symmetric-convex differential operator using the above normalized Airy functions. Consider the analytic function $\aleph \left(\zeta \right)\in \Delta ≔\{\zeta \in ℂ:\left|\zeta \right|<1\}$ with the power series $$\aleph \left(\zeta \right)=\zeta +\sum _{n=2}^{\infty }{a}_n{\zeta }^n.$$ Thus, the convoluted operator ( $\ast$ ) with the normalized Airy function ${\mathbb{A}}_1\left(\zeta \right)$ brings the following power series $$(\aleph \ast {\mathbb{A}}_1)\left(\zeta \right)=({\mathbb{A}}_1\ast \aleph )\left(\zeta \right)=\zeta +\sum _{n=2}^{\infty }{a}_n{\lambda }_n{\zeta }^n,\zeta \in \Delta .$$ By using the Airy convoluted operator, we formulate the normalization structure of Airy symmetric-convex differential operator (ASCDO): $${\Omega }_{\alpha }\left(\zeta \right)=(1-\alpha )\zeta {(\aleph \ast {\mathbb{A}}_1)}^{\prime }\left(\zeta \right)-\alpha \zeta {(\aleph \ast {\mathbb{A}}_1)}^{\prime }(-\zeta )=(1-\alpha )\left(\zeta +\sum _{n=2}^{\infty }n{a}_n{\lambda }_n{\zeta }^n\right)-\alpha \left(-\zeta +\sum _{n=2}^{\infty }n{a}_n{\lambda }_n{(-1)}^n{\zeta }^n\right)=\zeta +\sum _{n=2}^{\infty }n{a}_n{\lambda }_n[(1-\alpha )+\alpha {(-1)}^{n+1}]{\zeta }^n≔\zeta +\sum _{n=2}^{\infty }n{a}_n{\lambda }_n{\omega }_n\left(\alpha \right){\zeta }^n\zeta \in \Delta ,$$ where $${\omega }_n\left(\alpha \right)≔[(1-\alpha )+\alpha {(-1)}^{n+1}].$$ In general, ASCDO can be recognized by $${\Omega }_{\alpha }^2\left(\zeta \right)={\Omega }_{\alpha }\left({\Omega }_{\alpha }\right)\left(\zeta \right)=(1-\alpha )\zeta {\left({\Omega }_{\alpha }\right)}^{\prime }\left(\zeta \right)-\alpha \zeta {\left({\Omega }_{\alpha }\right)}^{\prime }(-\zeta )=(1-\alpha )\left(\zeta +\sum _{n=2}^{\infty }{n}^2{a}_n{\lambda }_n{\omega }_n\left(\alpha \right){\zeta }^n\right)-\alpha \left(-\zeta +\sum _{n=2}^{\infty }{n}^2{a}_n{\lambda }_n{\omega }_n\left(\alpha \right){(-1)}^n{\zeta }^n\right)=\zeta +\sum _{n=2}^{\infty }n{a}_n{\lambda }_n{\omega }_n\left(\alpha \right)[(1-\alpha )+\alpha {(-1)}^{n+1}]{\zeta }^n=\zeta +\sum _{n=2}^{\infty }{n}^2{a}_n{\lambda }_n{\omega }_n^2\left(\alpha \right){\zeta }^n\zeta \in \Delta .$$ In general, we have the following $k-$ formula (see Fig. 2)

(2.1)

$${\Omega }_{\alpha }^k\left(\zeta \right)=\zeta +\sum _{n=2}^{\infty }{n}^k{a}_n{\lambda }_n{\omega }_n^k\left(\alpha \right){\zeta }^n\zeta \in \Delta .$$ Note that, when $\alpha =0$ and ${\lambda }_n\approx 1$ , when obtain the Salagean differential operator (Salagean, 2006).

Close

Fig. 1

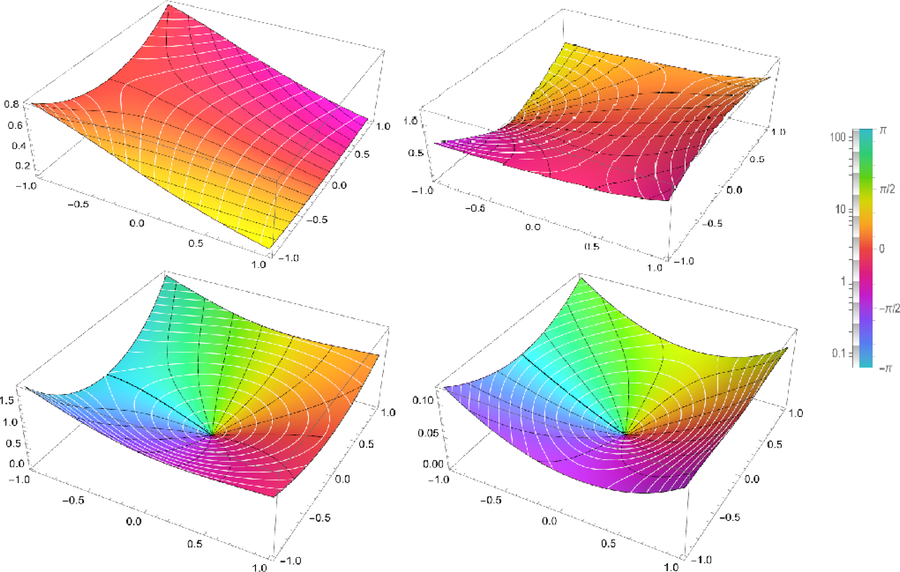
The ComplexPlot3D of the Airy functions ${\Lambda }_1,{\Lambda }_2$ (the first row) and the normalized Airy functions ${\mathbb{A}}_1,{\mathbb{A}}_2$ (the second row) respectively using MATHEMATICA 13.3.

Export to PPT

Close

Fig. 2

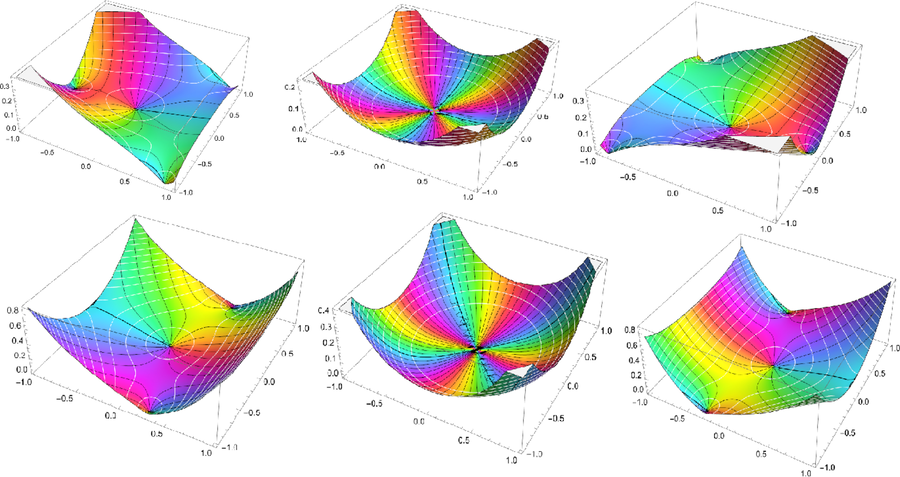
The ComplexPlot3D of ASCDO, which is acting on $\zeta /(1-\zeta )$ with ${\mathbb{A}}_1$ in the first row and ${\mathbb{A}}_2$ in the second row, when $k=1,\alpha =0.25,0.5,0.75$ .

Export to PPT

2.3

2.3 Wave equation with a univalent solution

We recommend using the parametric Koebe function in this endeavor to define the wave equation. The convex univalent function family includes an extreme function known as the Koebe function. The Koebe function $\kappa \left(\zeta \right)=\zeta /{(1-\zeta )}^2$ extends a slit along the ray from the point with radius 1/4 to the point $\zeta =0$ and translates $\Delta$ onto the complex plane. Using the rotate Koebe function of the form (see Fig. 3) $${\kappa }_{\tau }\left(\zeta \right)=\frac{\zeta }{{(1-e^{i\tau }\zeta )}^2}=\zeta +\sum _{n=2}^{\infty }n{e}^{i(n-1)\tau }{\zeta }^n,\zeta \in \Delta .$$ The suggested functional operator ${\Omega }_{\alpha }^k$ can be acted on $\kappa \left(\zeta \right)$ to obtain the generalized series

(2.2)

$${\Omega }_{\alpha }^k(\zeta ;\tau )=\zeta +\sum _{n=2}^{\infty }{n}^{k+1}{e}^{i(n-1)\tau }{\lambda }_n{\omega }_n^k\left(\alpha \right){\zeta }^n\zeta \in \Delta .$$ We then use the proposed operator to solve the wave equation of a complex variable. This equation is of the form

(2.3)

$$\left(\frac{{\partial }^2}{\partial {\tau }^2}+{\varepsilon }^2\frac{{\partial }^2}{\partial {\zeta }^2}\right){\Omega }_{\alpha }^k(\zeta ;\tau )=\Psi \left(\zeta \right),$$ where ${\Omega }_{\alpha }^k(\zeta ;\tau )$ is the $k-$ iterative wave amplitude in $\Delta$ joining the convex factor $\alpha \in [0,1]$ and $\Psi$ is the nonlinear functional of the wave satisfying $\Psi \left(0\right)=0$ and ${\Psi }^{\prime }\left(0\right)=1$ . A special case is studied in Wait (1964), when $\Psi \left(\zeta \right)=0$ and ${\Omega }_{\alpha }(\zeta ;\tau )=\Lambda (\zeta ;\tau )$ .

We will propose a univalent result to our wave equation. In wave equations, the univalent solution is crucial (see Broer and Sarluy (1964), Ibrahim et al. (2020), Ibrahim and Baleanu (2021), Hadid and Ibrahim (2022)). The outcomes of the wave equations are assumed to be incorrect for infinite layers because they are not univalent functions; hence, the wave’s peaks will invariably move more quickly than the through and eventually reach these levels. In the next section, we deal with the main sufficient condition to obtain an analytic univalent solution satisfying the inequality $\Re \left({\Omega }_{\alpha }^k{(\zeta ;\tau )}^{\prime }\right)>0$ where ${}^{\prime }=(d/d\zeta );$ or in other words, the solution is a bounded turning function in the complex domain $\Delta$ . In this case, the gradients keep growing, but gradually these effects start to take effect and this expansion is slowed down.

Close

Fig. 3

The plot on the left is the real part and the right is the imaginary part of ${\kappa }_{\tau }\left(\zeta \right)$ .

Export to PPT

3 Results and discussions

The recent section admits the results regarding the univalent outcome of Eq. (2.3) for different suggestions on $\Psi \left(\zeta \right)$ .

More conditions on $\left[{\Omega }_{\alpha }^k(\zeta ;\tau )\right]$ to be univalent solution in the next results.

Proceeding to discover more condition on $\left[{\Omega }_{\alpha }^k(\zeta ;\tau )\right]$ to be univalent. The next result is a connection between $\left[{\Omega }_{\alpha }^k(\zeta ;\tau )\right]$ and $\Psi \left(\zeta \right)$ in Eq. (2.3).

There are some special cases of Proposition 3.3, as follows:

By Corollary 3.4, we have

We have the final remarks on this study.

4 Conclusion

In the above study, we formulated a symmetric-convex differential expression normalized Airy functions in a complex domain. We considered this formula as a differential operator acting on a normalized class of analytic functions. In the next step of this investigation, we illustrated a wave equation involving the suggested operator (ASCDO) as a solution. Since we aimed to study the behavior of the solution geometrically, we presented the most sufficient conditions on ASCDO to be univalent solved. Univalent solution is a very delicate property on the theory of the wave equation of a complex variable. This property brings a lot of geometric presentations for the solution based on the geometric function theory.

Funding

No funding was used in this study.