Modal parameters of resonant spruce wood (Picea abies L.) after thermal treatment

1 Introduction

Acoustic properties of musical instruments depend on the effectiveness of stimulation of wooden element vibrations (e.g. top boards of violins or guitars) by vibrations of air. This effectiveness depends on the construction of the instruments and the properties of the materials used. A violin of the same construction but made of wood of different properties will give different sound. The most important parameters of wood determining its acoustic properties include: density, elasticity modulus and damping (Bucur, 2006). The effectiveness of stimulation of the resonant boards is the greater the lower the wood density and the higher its elasticity modulus. These demands are contradictory because the wood elasticity modulus is proportional to its density (Kollmann and Côté, 1968; Bucur, 2006; Wegst, 2006). This is one of the reasons why it is so difficult to find good resonant wood. Much effort has been devoted to explain the excellent sound of antique violin instruments and find methods of wood modification reducing the wood inhomogeneities and improving the relation between the elasticity modulus and density (E/ρ) (Hunt and Balsan, 1996; Nagyvary et al., 2006; Spycher et al., 2008; Schwarze et al., 2008; Stoel and Borman, 2008).

Thermal modification of wood is known to decrease its density and, in mild conditions of the process, it can lead to increase in the linear elasticity modulus and hardness. Increased ratio of E/ρ (elasticity modulus/ density) known also as the specific elasticity modulus, improves the wood acoustic properties, in particular: sound propagation velocity, acoustic resistance, musical constant and damping through radiation. Thermal treatment can also have negative effect on these properties as it can lead to cracks between cells and microcracking in the cell wall. Then, although the specific elasticity modulus is improved, these defects cause an increase in the internal damping (logarithmic decrement), which can disqualify the usability of the modified wood for production of resonant boards. For this reason, the logarithmic decrement seems to be a particularly important parameter describing the suitability of wood for making musical instruments, more important than the propagation rate of acoustic wave, acoustic constant and acoustic resistance (Ono and Norimoto, 1984; Yano et al., 1993).

Logarithmic decrement describes the dissipation of energy of vibrations, so it characterizes the internal damping of absorbed sound (Bucur and Böhnke, 1994; Gough, 2000). This parameter has not been sufficiently understood for thermally modified wood used for making top boards of violins. Thermal degradation of hemicellulose, which is a kind of linking agent between cellulose and lignin in the cell wall, can lead to the appearance of new voids in this substance, which can change the internal damping of acoustic waves.

The aim of the study was to determine and compare modal frequencies and logarithmic decrements before and after thermal modification at 160 °C.

2 Material and methods

The study was performed for 8 radially cut out planks from spruce wood of different suitability for resonant boards production, obtained from trees growing in Eastern Romanian Carpathians near Maramureș. All planks were classified by luthiers to three groups of resonant wood quality, classes I, II and III, according to BN-70/9221-06. The planks were also characterized by different widths of annual rings and different contribution of latewood in them. These macrostructural differences were responsible for different densities and elasticity of the planks. The samples density was determined according to the method recommended by ISO 13061-2:2014. Moisture content of all samples was 9.5%.

Modal analysis was performed on samples of the size 350 (in longitudinal direction) × 130 (in radial direction) × 5 mm (in tangential direction). On the surface of the wood samples 330 measuring points, separated by the distances 12 × 12 mm, were chosen (Fig. 1). For modal experiment the samples were mounted in a box with a mass of 940 g by clamping longer sides in the direction perpendicular to the main surface.

Close

Fig. 1

Measuring points for modal analysis of a wood sample and the site of accelerometer attachment – a black dot.

Export to PPT

Similarly as in other papers (Mania et al., 2017, 2015; Skrodzka et al., 2013), in this study the experimental modal analysis with a fixed point of response and varied point of excitation was made. The response signal of the structure was measured by an accelerometer NP – 2910 made by Ono Sokki, Tokio, Japan, of 2 g in mass, attached to the sample’s surface with the use of bee wax (Fig. 1). The sample was excited by an impact hammer with a force transducer, (PCB Piezoelectronics Impact Hammer Model 086C05, New York). The impact of this hammer gives a signal of a wide spectrum to the object studied. The impact force is measured by a piezoelectric force transducer. The accelerometer and impact hammer were connected to Ono Sokki analyzer CF 5210. The modal parameters were calculated using the software packet SMS STAR Modal. Measurements were made for the frequencies 0 – 6800 Hz with the spectral resolution of 3 Hz. At one measuring site, 10 impacts were made by the impact hammer and then the computer program gave averaged results in the frequency domain. Each measurement was controlled by the coherence function. On the basis of these signals, the Frequency Response Functions (FRFs) were calculated between all the measuring points excited by the hammer and the fixed response point at which the acceleration was measured.

The damping factor δ was defined as: $$\delta =\frac{\mathrm{\Pi }\mathrm{\Delta }f}{\sqrt{3}{f}_0}$$

where: f₀ – resonant frequency (Hz),

Δf – the width of the peak at the amplitude 3 dB below the resonant frequency (Hz).

After modal analysis, all samples were subjected to thermal modification by the most often used method, in the steam atmosphere, according to the procedure ThermoWood (Viitaniemi et al., 1997; González-Peña and Hale, 2007; Boonstra, 2008; Moliński et al., 2010). Wood modification was carried out in laboratory conditions at 160 °C, applied for 8 h. After thermal treatment, the samples were conditioned in laboratory conditions. When the samples reached the equilibrium moisture content the same as before the modification, the samples were subjected to modal analysis in the same conditions.

3 Results and discussion

The samples density slightly decreased as a result of thermal treatment, which confirms earlier reports (Gündüz et al., 2008; González-Peña and Hale, 2009). The mean values of wood density before and after thermal treatment are given in Table 1.

According to the data presented in Table 1, the thermal treatment at 160 °C caused slight decrease in wood density, by about 3.3%.

In Table 2 the results of modal analysis of spruce wood samples before thermal treatment are shown; only characteristic and best pronounced modes obtained in the studied frequency range are listed. The Table gives the resonant frequency (f, [Hz]) of the modes showing modal damping not higher than 10%. Systems or materials with the percentage of critical damping lower than 10% can be classified as linear (Ewins, 1995; Skrodzka et al., 2009, 2013) and only linear materials can be subjected to modal analysis.

As follows from Table 2, the number of modes in the analyzed range of frequencies was not the same for all spruce wood samples. Only for two samples 12 different modes were observed and these results were treated as reference for the results obtained for the other samples. All planks were subjected to thermal modification and then the modal analysis was repeated. Table 3 presents the modal frequencies determined for the samples after thermal modification.

Analysis of the data presented in Table 3 shows that thermal modification had ambiguous effect on modal frequencies. In the range of low frequencies 0–1600 Hz, the frequency of modes increased on average by about 3.5%. In the range of higher frequencies 2300–3500 Hz the modal frequency decreased by about 10%. The most pronounced changes were noted in the frequencies of modes number 4 and 6, whose frequency decreased by 15 and 12%, respectively. In the range of the highest frequencies (4400–6800 Hz) the modal frequency increased by about 4%. Reduction of the modal frequency was also observed for the wood samples selected for production of xylophone keys (Kang et al., 2016), subjected to thermal modification. In all studies mentioned the modal frequency decreased in the entire band. The change in modal frequency was also observed as result of other methods of wood modification. Yano et al. (1993) have found that a small change in frequency after the process of acetylation was caused mainly by the change in the equilibrium moisture content in the samples conditioned in the same conditions. Changes were also noted in the sound propagation rate.

Fig. 2 presents the example frequency response function (FRF) for the untreated and thermal treated wood samples.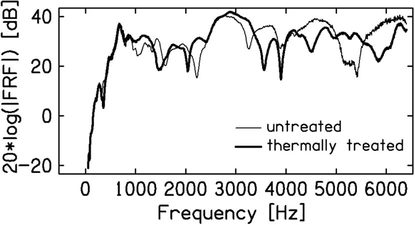

Close

Fig. 2

Examples of the FRFs measured for spruce samples before and after thermal treatment.

Export to PPT

In both curves the number of peaks corresponding to the characteristic modes is similar, but frequencies of modal peaks differ for thermally treated and not thermally treated samples, as could be expected. For details see Tables 2 and 3. Another analyzed parameter was logarithmic decrement. In Table 4 the experimentally determined logarithmic decrement for spruce wood before thermal modification is presented. To give some insight to obtained values comparison of logarithmic decrement of samples no. 2, 3 and 5 before and after thermal modification are shown in Fig. 3.

Close

Fig.3

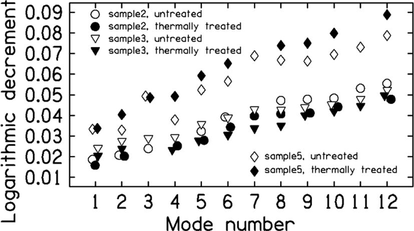
Comparison of logarithmic decrement before and after thermal modification for samples no.2, 3 and 5.

Export to PPT

In the entire range of frequencies considered and for each sample studied, the logarithmic decrement increased with increasing resonant frequency. The average logarithmic decrement for all samples was 0.0473. The lowest average values of 0.0387 and 0.0377 were obtained for samples number 2 and 3, respectively. Moreover, the same samples showed the lowest densities 400 and 360 kg/m³. According to literature, the logarithmic decrement of wood suitable for construction of musical instruments should take the lowest possible values (Holz, 1984; Bucur and Böhnke, 1994; Beldan and Pescaru, 1996; Gough, 2000). Thus, it can be concluded that samples no. 2 and 3 belonged to a higher class of wood than the other ones. The highest average logarithmic decrement of 0.0572 was obtained for sample no. 5.

The results are not much different than the literature data. For instance, Buksnowitz (2006) who studied resonant wood in a wide range of resonant frequencies obtained the logarithmic decrement of 0.0404. Haines et al. (1977) who studied the properties of Sitka spruce wood for construction of guitars reported the logarithmic decrement varying in the range 0.025–0.075. Spycher et al. (2008) has reported obtaining the experimental logarithmic decrement of 0.043, while Halachan et al. (2017) who has reported modal analysis of resonant spruce wood obtained the value of 0.026.

Table 5 presents logarithmic decrement determined for spruce wood after thermal modification and after reaching equilibrium moisture content at the same level as before modification.

Thermal modification at 160 °C caused changes in the logarithmic decrement for each mode and for each sample. For each frequency certain fluctuations of this parameter were observed. The greatest changes were noted for samples no. 2 and 3 for whose logarithmic decrement was reduced on average by 13 and 12%, respectively from 0.0387 to 0.0337 and from 0.0377 to 0.0331. For sample no. 8 this parameter decreased from 0.0484 to 0.0456, so by about 6%. In some samples thermal modification led to an increase in logarithmic decrement, for samples no. 4 and 5 by 8%, while for sample 7 by 6%. For samples no. 1 and 6, the average value of logarithmic decrement did not change. As follows from the above, the process of thermal modification had different effects on logarithmic decrement value. Similar results have been obtained by Kang et al. (2016) who thermally modified for the wood chosen for production of xylophone keys also reported that logarithmic decrement increased or decreased for different samples. Wu et al. (2016) has described similar changes in logarithmic decrement of samples from dawn redwood (Metasequoia glyptostroboides). Different methods of modification can bring different changes in this parameter. For instance Kubojima et al. (1998) have modified the wood for piano boards in nitrogen atmosphere and reported that for each variant analyzed, the logarithmic decrement decreased. Čulík et al. (2014) who modified resonant wood with fluid glass have obtained the opposite results as the logarithmic decrement values significantly increased.

However, some tendency can be observed: logarithmic decrement decreased, which means that from the acoustic point of view – was improved for the samples of the lowest density, samples no. 2 and 3 (400 kg/m³ and 360 kg/m³ before modification; 390 kg/m³ 350 kg/m³ after modification). These two samples were classified by luthiers as good and very good. The logarithmic decrement increased (its average value increased) for the samples of the highest density, no. 4 and 5 (480 kg/m³ and 500 kg/m³ before modification; 465 kg/m³ 480 kg/m³ after modification), classified by luthiers as of average quality.

One of possible reasons for this phenomenon can be the microcrackings appearing in wood tissue upon its modification. In the process of thermal modification, besides relaxation of growth stress, new stress appears in particular in close vicinity of anatomical elements differing in the thickness of cell walls, so also in the wood density. The tissue of higher density shows greater stiffness and lower deformability, so has a lower tendency to energy dissipation. The stiff elements are characterized by the highest stress because of the tissue coherence, which means that showing lower deformability they are the sites at which microcrackings are likely to form. This mechanism often leads to the cracking of wood at the borders of annual rings (Boonstra et al., 2006; Welzbacher et al., 2011). Other sites of potential wood cracking are the borders between the radial and axial tissues, at which radial cracks may appear. The formation of such structural defects is fostered by different anisotropy of moisture-related deformations of earlywood and latewood; the latewood tracheids undergo almost isotropic shrinking, while the earlywood ones show clearly anisotropic shrinking (Patera et al., 2011; Rafsanjani et al., 2012).

The resonant spruce wood that should show low density and its lowest possible gradient in individual annual rings, should also be less susceptible to developing these defects than the wood of high density and greater density gradient in annual rings. The appearance of additional discontinuities in wood tissue, e.g. crackings, contributes to increasing damping of sound waves.

4 Conclusions

The results of modal analysis of resonant spruce wood samples before and after thermal treatment lead to the following conclusions.

1. Thermal modification of spruce wood has brought about insignificant changes in the mean resonant frequency values. However, analysis of changes in particular frequency ranges revealed that in the range ∼2.3–3.5 kHz, the resonant frequency decreased by over 10%.

2. No significant differences in the number of modes of vibrations for particular resonant boards were found.

3. Thermal modification has different effect on the logarithmic decrement, however, the results show a tendency to improve the acoustic properties of wood samples classifies as of the highest quality.