Mapping structural features of the Wadi Umm Dulfah area using aeromagnetic data

1 Introduction

The Wadi Umm Dulfah area lies in the Egyptian North Eastern Desert (ENED) to the west of Hurghada city. The area is covered by sediments in its central and eastern parts and with basement in the western part. The basements represent the northeastern portion of the Pan-African orogenic-belt that reveals evidence of a complicated crustal evolution that took place in many stages during the time from 1100 Ma to around 450 Ma age (Kennedy, 1964; Kroner, 1983). Tectonic and Igneous events in this Wadi Umm Dulfah region resulted in the action of primitive-ensimatic crustal terrains, which were created collapsed together, and were swallowed by granites through the last 400 Ma of the Precambrian (Engel et al., 1980). Hamimi et al. (2019) analyzed the structure regimes in the ENED. They noted that the intersection of NE-SW and NNW-SSE faults is followed by the late tectonic granite masses intrusions. Despite the structural importance of the Wadi Umm Dulfah area due to its proximity to the Gulf of Suez and Gulf os Aqaba rifts, there are no extensive studies to explain the tectonic situation of the region and delineate the dominant structures. Our study aims to produce a new and accurate structural map for the Wadi Umm Dulfah area using a sharp edge detector of aeromagnetic data.

Detection of the edges and depth of anomalous bodies is one of the most important aims in magnetic and gravity interpretation (Ghomsi et al., 2020, 2021; Hang et al, 2019; Eldosouky and Saada, 2020; Pham et al., 2019, 2021a,b; Eldosouky et al., 2021a; Hoang et al., 2021; Duong et al., 2021; Eldosouky and Mohamed, 2021; Melouah et al., 2021). The information of the edges is important in estimating the boundaries of geology formations (Pham et al., 2018a; Eldosouky et al., 2021b). There are a great number of edge detection methods developed for interpreting the potential field data (Eldosouky et al., 2020a,b; Pham, 2020). The total gradient method (TG) is one of the conventional methods that are commonly used for outlining the edges (Roest et al., 1992). Although this method is a very popular method used to interpret magnetic data, it also has some limitations (Pham et al., 2021c, 2021d). Hsu et al. (1996) suggested using an enhancement of the TG method (ETG) to increase the resolution of the result. These methods use the maximum location to extract the source edges. Miller and Singh (1994) proposed the tilt derivative method to balance the different anomalies. This method detects the edges of the geological structures by the zero contours. Wijns et al. (2005) proposed the theta map method that normalizes the TG by the total horizontal gradient. The negative contours of the theta map are located over the edges of magnetic structures. Cooper and Cowan (2006) proposed the normalized version of the horizontal gradient that normalizes the vertical derivative amplitude by the gradient amplitude. The method uses the maximum location to detect the edges of the geology structures. Pham et al. (2018b, 2020a) developed some methods based on hyperbolic tangent and logistic functions that provide the maximum values over the edges of the sources. These methods bring the edges with higher resolution compared to the conventional methods. Melouah and Pham (2021) proposed an improved version of the logistic method that is based on the derivatives of the total horizontal gradient of the vertical derivative of the potential field. Oksum et al. (2021) presented a new method that uses the fast-sigmoid function of the gradients of the gradient amplitude. Similar to the logistic filters, this method provides an image with high resolution for the source edges, and it uses the maximum values to outline the edges. In addition to the above-mentioned filters, there are many other methods based on the derivatives of magnetic and gravity data in the literature (Beiki, 2010; Cordell and Grauch; 1985; Ferreira et al., 2013; Pham et al., 2020b, 2021e; Pham, 2021).

In this paper, the methods such as the enhanced total gradient (ETG), normalized horizontal gradient (TDX), theta map (TM) and fast sigmoid (FSED) have been applied to aeromagnetic data to extract geology features of the Wadi Umm Dulfah area. Moreover, the depth to the magnetic sources in the area were also estimated by the tilt depth method.

2 Geological setting

The Egyptian Eastern Desert (EED) is divided into three main territories. These main parts are South (ESED), Central (ECED), and North (ENED). These three domains were generated in different tectonic frameworks in an independent, but in a very similar style and exhibit a specific younging from ESED to ENED (Abd El-Wahed and Hamimi, 2021). Geologically, these three domains differ from each other to their foremost revealed rock types (Kroner et al., 1987). The ENED, to the north of 27° 00′ lat., is distinguished by the presence of younger rocks (e.g., Dokhan volcanics, younger Gattarian granites, and Hammamat sediments), while the older types of the rocks rarely occur like the granodiorites, 610–680 Ma (Stern and Hedge, 1985).

The Wadi (W) Umm Dulfah area is located in the Egyptian North-Eastern Desert (ENED). The main wadis cutting the area are W Faliq, W Umm Dulfah, W Umm Duhaysi, and W Umm Kharazah (EGSMA, 2005). The area reaches the coast of the red sea from its north-eastern side and is covered by various rock units of different ages (Precambrian to Recent) (Fig. 1). The basements of the ENED are a part of the Arabian Nubian Shield (ANS) which were created throughout the Pan-African era (900–600 Ma) in a marine setting (Kroner, 1985; Shackleton et al., 1980). The eastern and central parts of W Umm Dulfah area are covered by the recent Holocene deposits (Wadi deposits, Coral Reefs, Sabkha, and Alluvial wadi deposits, Pleistocene deposits, Gabir formation (F) of Pliocene age, and Samh F and Gharamul F (Miocene) (Conoco, 1987; EGSMA, 2005). The basements (western part of W Umm Dulfah area) acidic-to-intermediate metavolcanics, Gabbro-Diorite, Granodiorite-Tonalite, Monzogranie, and Alkali feldspar granite (El-Gaby et al., 1990; EGSMA, 2005).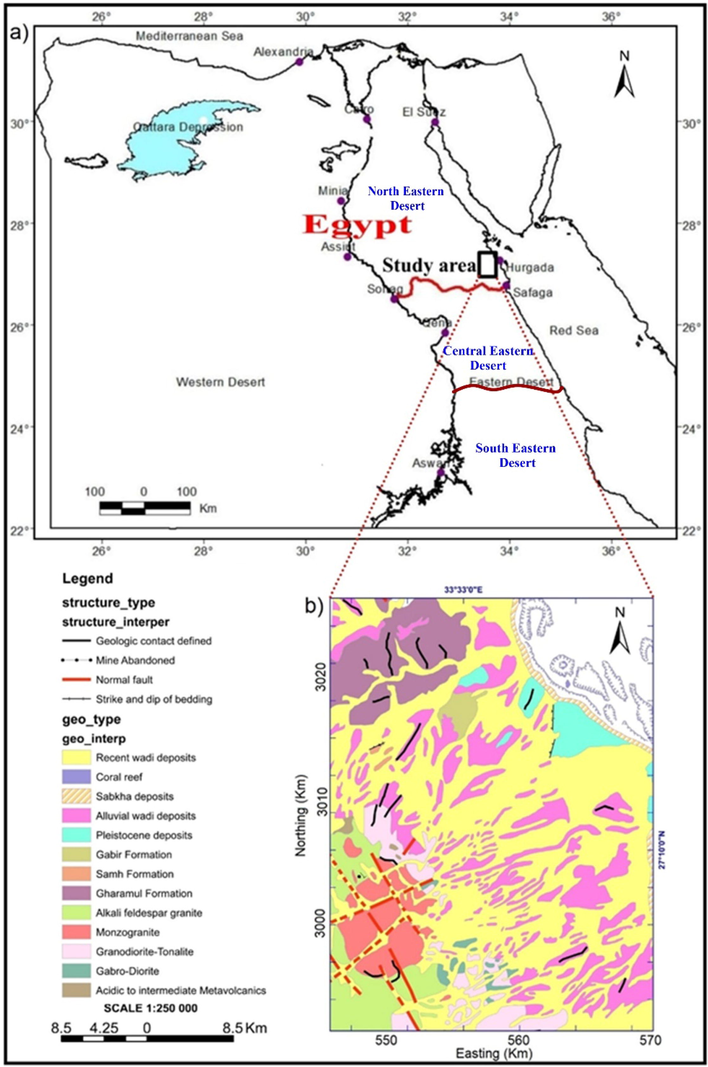

Close

Fig. 1

a) Geographical location (Abd El-Wahed and Hamimi, 2021), b) The geology of the Wadi Umm Dulfah area (modified after EGSMA, 2005).

Export to PPT

3 Data

The studied area was operated by Aero-Service-Aircraft, Cessna-Titan, type 404. The separation of traverse lines was 1 km and 10 km, and tie-line separation was at 120 m altitude (terrain clearance). The traverse lines were situated in a north-east:south-west (NE-SW) direction and perpendicular tie lines to the traverse direction, north-west:south-east (NW-SE) (Aero-Service-Report, 1984). The data is obtained in the form of total magnetic intensity (TMI). The TMI data is digitized and gridded after subtracting the IGRF (=42425 nT). Then, the TMI is reduced to the north magnetic pole (RTP). The parameters employed for the reduction are an inclination of 39.5˚N and declination of 2˚E which express the mean value for the area. The RTP data range from 395 nT to 690 nT with high amplitude anomalies that appear in the southeastern region of the Wadi Umm Dulfah area (Fig. 2).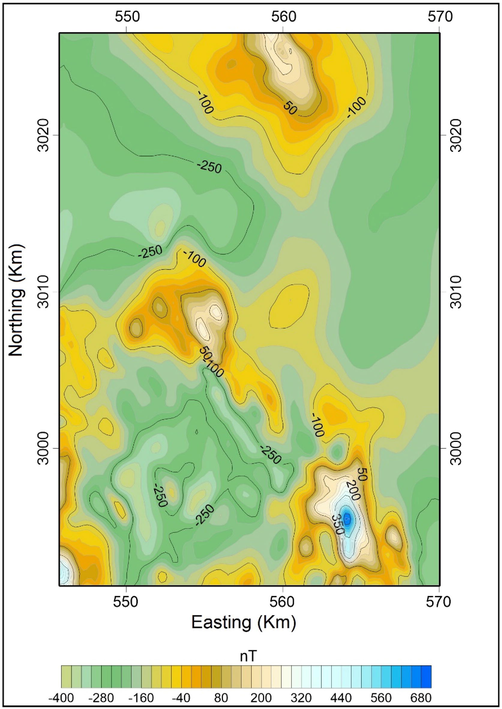

Close

Fig. 2

RTP aeromagnetic data of the Wadi Umm Dulfah area.

Export to PPT

4 Methods

The ETG method is one of the high-resolution methods for enhancing the edges of the geology structures. The ETG of the field F is defined by the following equation (Hsu et al., 1996):

The TM method is defined by Wijns et al. (2005). It uses the ratio of the derivatives to balance the different anomalies. Its equation is given as:

The TDX is another balanced method, proposed by Cooper and Cowan (2006). The equation of the TDX is given as the following equation:

Another method for enhancement of the edges is introduced by Oksum et al. (2021), which is based on the gradients of the gradient amplitude. The method can enhance the edges of the shallow and deep bodies at the same time. Its equation is given by:

and

The FSED function provides maximum amplitudes over the source edges. Since the method design is based on the ratio of the derivatives of the total horizontal gradient, it can balance anomalies from shallow and deep sources simultaneously (Oksum et al., 2021).

The tilt depth method is introduced by Salem et al. (2007) for detecting the depth to the top of magnetic sources. The method uses the RTP data and derives the relationship between the tilt angle, horizontal location and depth of a vertical 2D contact model as

Equation (7) indicates the tilt angle value above the edges of the contact is 0° (h = 0) and equal to 45° when ${h=z}_c$ and –45° when ${h=-z}_c$ . This suggests that contours of the tilt angle can identify both the horizontal location (θ = 0°) and depth (half distance between ±45° contours) of magnetic sources (Salem et al., 2007).

5 Test study

Initially, we generated a synthetic magnetic model to study the effectiveness of the methods, and their enhanced versions. The three-dimensional view of the model is displayed in Fig. 3a. This model consists of three prismatic sources, whose parameters are given in Table 1. The computed magnetic anomaly over the model is displayed in Fig. 3b. Fig. 4a shows the ETG of data in Fig. 3b. We can see that, the ETG method can bring clear images for the edges for the body A, but responses from the bodies B and C are blurred. Fig. 4b shows the TM of magnetic data in Fig. 3b. Although the TM can equalize the signals from shallow and deep sources, it brings the false boundaries around the body B. Fig. 4c shows the result of application of the TDX method to magnetic data in Fig. 3b. As can be seen from this figure, the TDX is more effective in determining all the edges than the ETG method. Similar to the TM method, the ETG method uses the ratio of the gradients, thus it can equalize the signals from shallow and deep bodies. However, the TDX method also brings the false boundaries around the body B. Fig. 4d displays the boundaries obtained from applying the FSED method to magnetic data in Fig. 3b. It is clearly seen that the peaks of the FSED are located directly over the source boundaries, and this method provides sharper responses over the source boundaries than ETG, TM and TDX methods.

Close

Fig. 3

Three-dimensional view of the model (a) and its magnetic anomaly (b). The dashed lines show the true edges of the prismatic sources.

Export to PPT

Close

Fig. 4

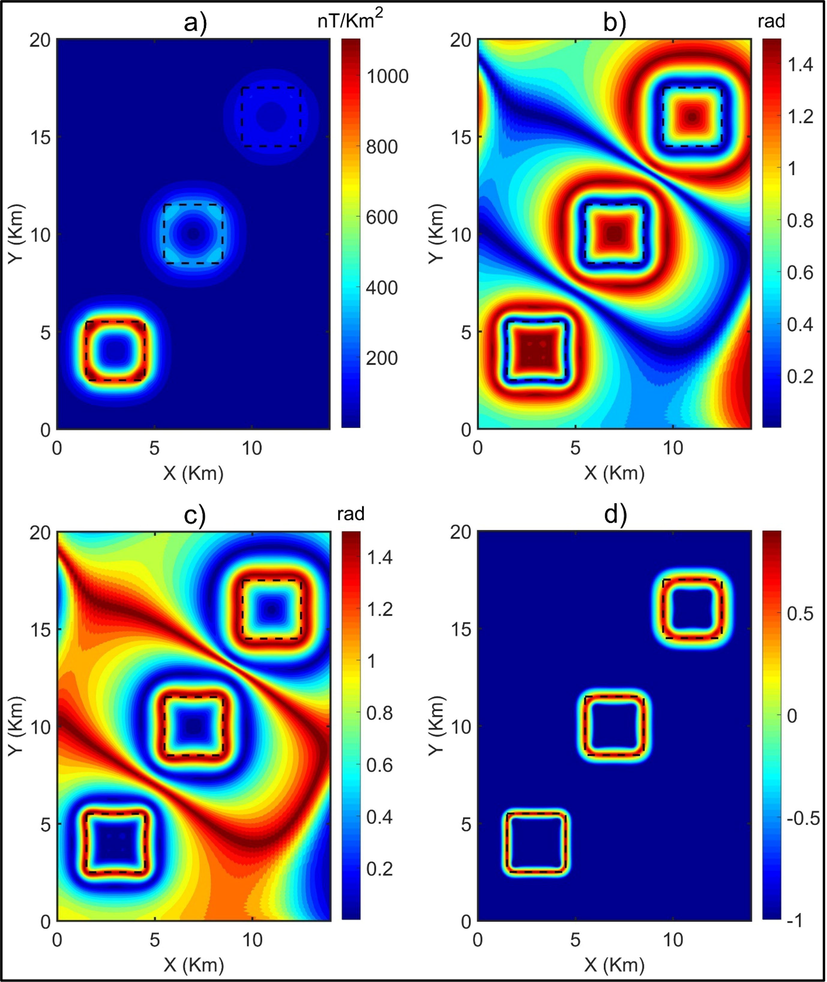
a) ETG, b) TM, c) TDX, d) FSED. The dashed lines show the true boundaries of the prismatic sources.

Export to PPT

6 Results and discussion

We have applied the RAPS (radially averaged power spectrum) method to separate residual anomaly from RTP data. The amplitude spectrum of The RTP anomalies was computed using MagB_inv software that was developed by Pham et al. (2020c). A plot of the logarithm power spectrum versus wavenumber usually shows several straight-line segments that decrease in slope with increasing wavenumber. Fig. 5 shows a plot of the radially averaged amplitude spectrum of the RTP anomaly versus wavenumber. Here, the linear segment S₁ relates to deep sources, linear segment S₂ relates to intermediate sources, while the other linear segment S₃ relates to shallower sources. The regional anomalies of deep structures were calculated by applying a low-pass filter to the RTP data using a cut-off wavenumber 0.2 km⁻¹ at which the low wavenumber segment intercepts the intermediate segment (Fig. 5). Then the residual anomaly caused by localized magnetic effects was calculated by removing the regional anomaly from the observed anomaly. The calculated regional field and the residual field anomaly maps are shown in Fig. 6a and b, respectively.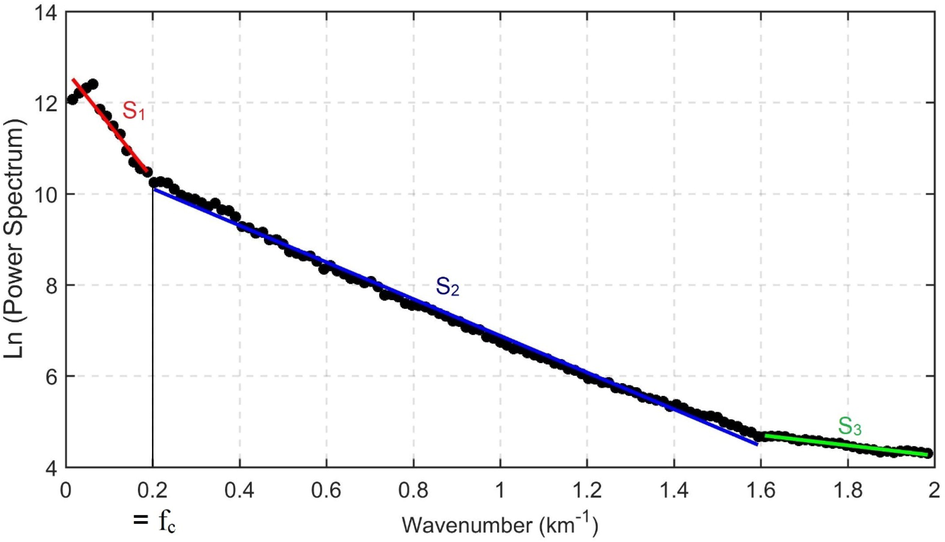

Close

Fig. 5

Radially averaged amplitude spectrum (Spector and Grant 1970) of the RTP data in Fig. 2 with three linear segments related to deep sources, intermediate sources, and shallower sources.

Export to PPT

Close

Fig. 6

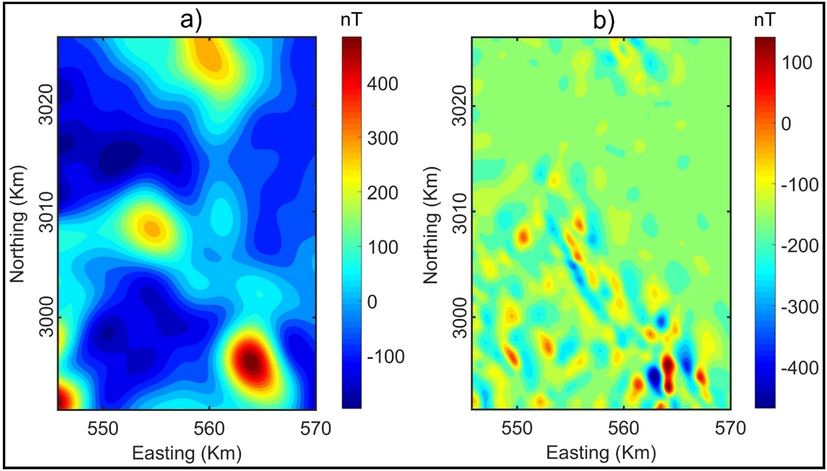
Regional field and the residual field anomaly maps.

Export to PPT

We used the residual map (Fig. 6b) to extract the structural features of the Wadi Umm Dulfah area. Fig. 7a shows the boundaries determined by applying the ETG filter to the RTP data. We can see that the ETG filter is dominated by the anomalies with larger amplitudes in the southeastern region, and it cannot outline the edges of the small anomalies clearly. Fig. 7b shows the result obtained by applying the TM method to the RTP data. It is clearly seen that the TM method is very effective in balancing magnetic anomalies with different amplitudes, and it provides clearer geological features compared to the ETG. Fig. 7c shows the result obtained by applying the TDX method to the RTP data. Similar to the TM method, the TDX method is also effective in bringing a balanced image of the edges, and it provides clearer lineaments compared to the ETG. Fig. 7b and 7c show that both the TM and TDX methods gave the same result. Although the TM and TDX methods are not dominated by the anomalies with larger amplitudes in the southeastern part of the area, the boundaries determined by these methods are connected, making it hard for extracting structural features of the Wadi Umm Dulfah area. The reason is that the TM and TDX methods are based on the zero values of the vertical gradient that produces the false zero contours around the sources (Pham et al., 2021). Fig. 7d shows the result obtained from applying the FSED method to the RTP data. Clearly, the FSED method cannot only delineate the edges of strong and weak amplitude signals at the same time, but also brings sharp responses over geological features of the Wadi Umm Dulfah area.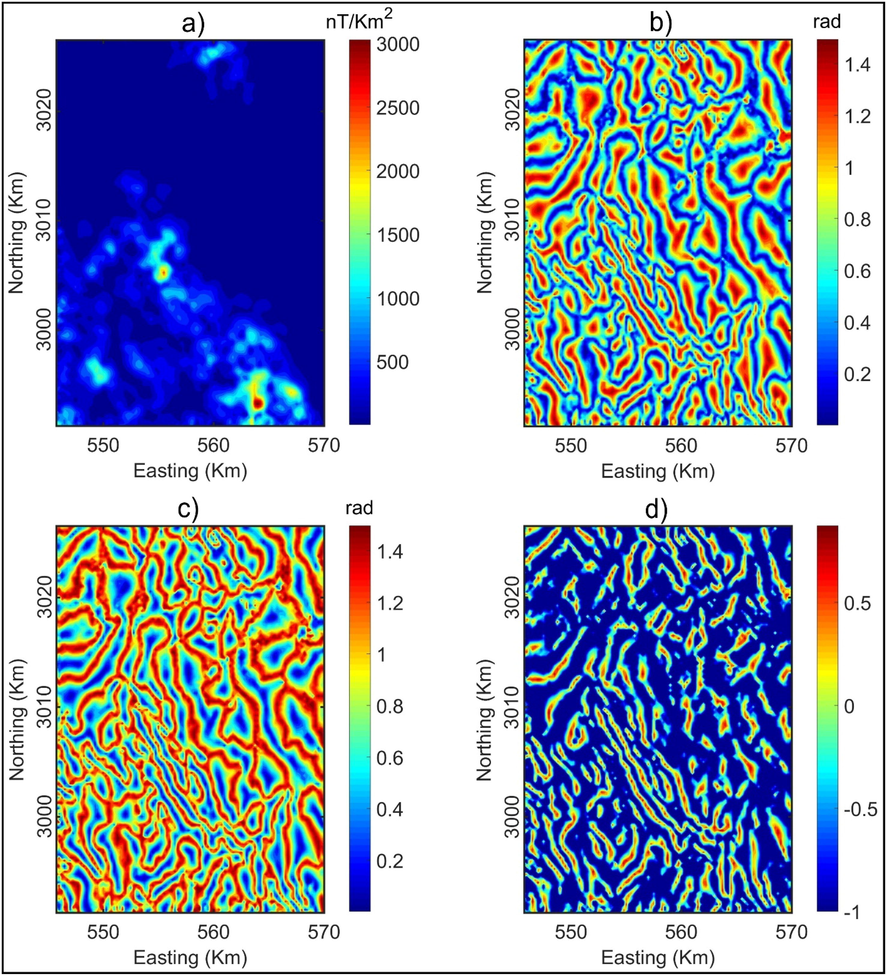

Close

Fig. 7

a) ETG, b) TM, c) TDX, d) FSED.

Export to PPT

To estimate the depths to magnetic sources in the Wadi Umm Dulfah area, the tilt depth method (Salem et al., 2007) was be used. The best advantage of this method is that it does not need to use magnetization, window size or structure index. Fig. 8a shows the depths of magnetic structures in the area. The obtained result shows that most of the depth of magnetic structures ranges from 0.1 to 1 km. Here, we used the FSED map to extract the lineaments of geological features of the Wadi Umm Dulfah area. These lineaments are superimposed on the tilt depth map (Fig. 8b). The synoptic Rose diagrams of the lineaments delineated from the FSED method is shown in Fig. 8c. As can be seen from this figure, the main structures of the study area are NW–SE, N-S and NE–SW trending structures. In addition, most of the lineaments determined from the FSED method are verified by the magnetic sources in Fig. 8a.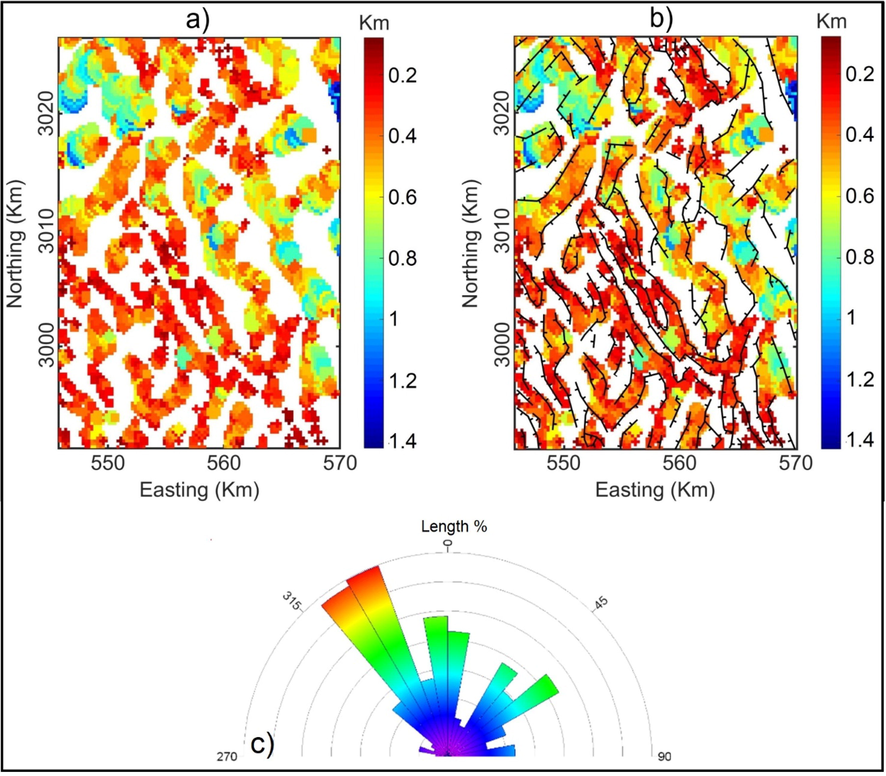

Close

Fig. 8

(a) Tilt depth contour map, (b) Lineaments from the FSED map superimposed on Tilt depth contour map, (c) Synoptic rose diagram for the lineaments in Fig. 8b.

Export to PPT

We also compared the structures interpreted from the FSED map with the geologic structures of Fig. 1b (Fig. 9). The lineaments of the FSED method show that the Wadi Umm Dulfah area was affected by the Gulf of Suez rifting (GOSR) system. This can be notified by the excess of the NW-SE trends related to the GOSR system in the central and western parts bounding the basement blocks. The E-W (Tethyan or Mediterranean) trend is absent in the obtained lineaments map (Fig. 9).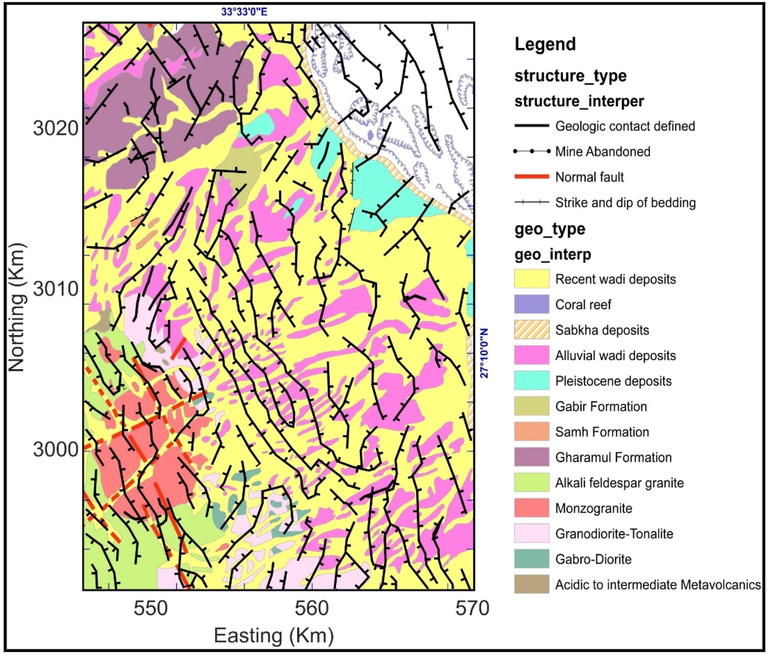

Close

Fig. 9

Lineaments from the FSED map superimposed on the geological map.

Export to PPT

The NW-SE (Gulf of Suez-Red Sea, Erythrean or Clysmic) direction appeared as the main structural trend controlling the study area (Figs. 8 and 9). Our results agree with Meshref and El-Sheikh (1973) whose concluded that the NW-SE is the complementary shear fracture system that might result from a northern compressive force. El-Shazly (1966) defined the NE-SW trend as a transverse fracture to the dominant NW-SE fractures along which huge intrusions were emplaced. Fig. 7d shows that the NW-SE structural trend is dissected and being cut by the recent NE-SW trend.

NW-SE (Gulf of Suez) and NE-SW are the main trends affecting the area. On this Closed alternative elongated anomalies (negative and positive) have a NW-SE trend. We can presume that the NW-SE (younger) trend is dominant in the Wadi Umm Dulfa area (Meshref et al., 1980) and the area is affected by the GOSR system during Miocene. The NW-SE faults of the study area are aligned with main basement lineaments that may have developed preexisting basement structures during the rifting (Moustafa and El Shaarawy, 1987; Saada, 2016).

7 Conclusions

The aeromagnetic data interpretation allowed us to highlight the geological features of the Wadi Umm Dulfah area. This study is based on the use of the enhanced total gradient (ETG), normalized horizontal gradient (TDX), theta map (TM), fast sigmoid (FSED) and tilt depth methods. Findings show that the FSED method has permit to clearly identify the lineaments of geological features, while the tilt depth method can provide the information on the depth of structures in the Wadi Umm Dulfah area, which ranges 0.1 to 1 km. It is observed from the FSED map that the lineaments show three major trends in NW–SE, N-S, and NE–SW directions. These results are a very useful document in better understanding of the capability of the edge detecting methods, as well as the geological structures of the Wadi Umm Dulfah area.