Machine learning approaches to genome-wide association studies

2.1 Information sources and search strategy

We carried out a search for relevant studies from 2015 to 2021 using online databases such as ScienceDirect and PubMed. This was done to extract relevant research articles that apply machine learning algorithms to genome-wide association studies. The keywords used for the search was done with the query strings “(Machine learning) AND (genome-wide association studies)” both on the PubMed and Science Direct databases. Pubmed retrieved n = 453 articles while Science Direct retrieved n = 378, giving a total number of 827 articles. Duplicate records numbering 20 articles were removed manually while the rest n = 807 were further screened to 122 records after excluding 685 records that did not meet the required criteria as depicted in the model shown in Fig. 1. Finally 22 records were included and reported in the study.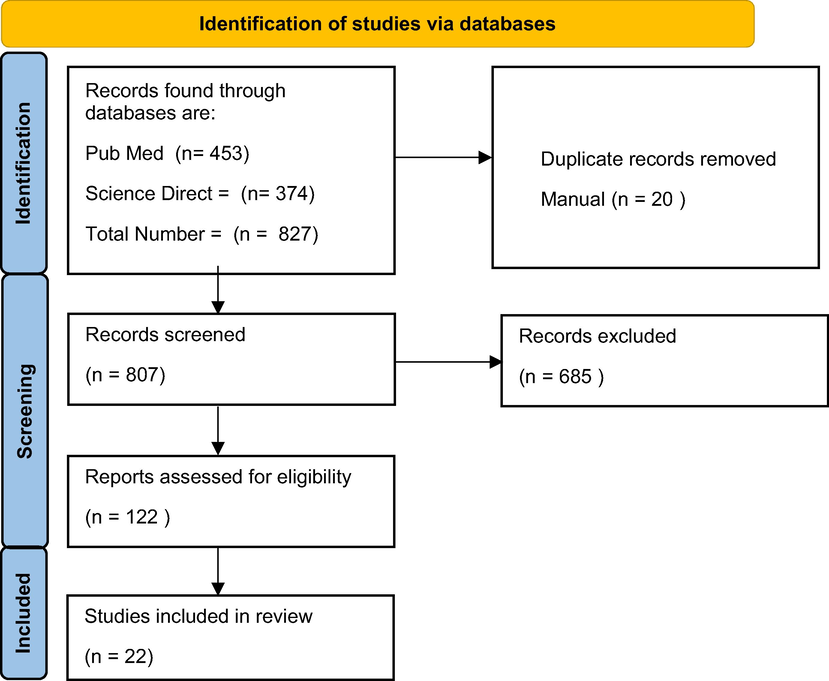

Close

Fig. 1

Identification, screening and inclusion of studies.

Export to PPT

2.2 Eligibility criteria

The inclusion criteria entails selection for articles that are research articles and not review articles. This is because the focus of the review is for machine learning research articles in genome-wide association studies. Therefore, articles that applied machine learning algorithms in the methodology of the work were included. Additionally, articles that are based on human research were included. The exclusion criteria include the removal of articles that did not relate to the specific research subject in question (Falola et al., 2017). Furthermore, review articles and articles that do not specifically apply ML to their GWASbased work were excluded. The methodology in each of these articles was analysed to identify the specific applications of machine learning to the genome-wide association analysis. From this set of articles, we rigorously reviewed the contributions to the subject of our study with 22 included articles.

3.1 Supervised machine learning approaches

The supervised machine learning target in this scenario is developing a genotype-phenotype model. This is done by building the patterns from a labelled set of training datasets. The aim is that the model will accurately predict the phenotype in new cases with related genetic backgrounds (Kruppa et al., 2012; Okser et al., 2014). The approaches which have been reviewed include regression, classification, ensemble learning, and neural networks.

3.2 Classification

Mieth et al. (2016) developed an SVM algorithm to predict an unknown phenotype of an unseen genotype x. Consequently, the SNPs that correspond to the greatest values of the SVM weighting are selected and the rest are discarded. A chi-squared test was then performed on the selected SNPs where SNPs with a p-value lesser than the significance threshold were selected. The COMBI method which they developed outperformed Raw P-value thresholding (RPVT). The comparison figure stood at a gain in true positive rate up to 80%. Additionally, their method identified 12 more SNPs. Among these SNPs, 10 have already been replicated in later GWAS and/or meta-analyses. The principle of SVMs is to separate labelled data points into two groups, with a large difference between them (Mittag et al., 2012; Roshan et al., 2011). Mittag et al. (2012) also used the SVM in genetic risk prediction. They developed the method to conduct genome-wide risk profiling for Parkinson’s Disease and Type 1 Diabetes. The algorithm was applied to train models based on GWAS SNP data, which could perform binary classification on a test dataset. Compared to Parkinson’s disease, their method reached satisfactory performance on application to type 1 diabetes datasets. They approached AUC scores in the range of 0.81 to 0.88. For validation they performed within study cross validation and between study validation. Hajiloo et al. (2013) used a simple K-Nearest Neighbours (KNN) learning algorithm to classify breast cancer patients according to their SNPs as having breast cancer or not. They used two strategies for evaluating the classification algorithm viz, Leave-One-Out Cross Validation (LOOCV) strategy and external hold-out (validation). Their LOOCV strategy estimated the accuracy, precision, sensitivity and specificity of the model to be 59.55%, 50.40%, 61.92% & 57.32% respectively.

3.3 Ensemble learning algorithms

The Random Forest is an example of the ensemble machine learning (ML) algorithm. It comprises an ensemble (collection) of decision trees. Each is developed with a bootstrapped subsample of the entire training dataset. Hence, it is anticipated that the ensemble algorithms are well fit for modelling the non-linear biological dependencies apparent in genetic data such as the GWAS SNP data (Lee et al., 2020). This is because the multi-variate and non-linear characteristics of tree-based ensemble learning algorithms have been shown to be a robust analytic tool in detection of genes’ interaction in GWAS (Dorani et al., 2018). Furthermore, ML algorithms have been utilized successfully in GWAS to identify genetic variants which have relatively large consequences in complex disease states. Random forest is one of them (Nguyen et al., 2015). Dorani et al. (2018) utilized random forests and gradient boosting machine to find 44 possibly susceptible SNPs that were ranked most significantly. For the random forests, AUC of 0.84 was achieved when number of predicted variables of 100 and number of trees of 2000 were applied. This means that the algorithm performed best when the number of trees were set to maximum and the number of predictor variables were set to the minimum. Nguyen et al. (2015) focused on a method for choosing informative SNPs with the use of the Random Forest method. They used a new approach in learning Random Forest’s model (ts-RF) with a two-stage quality-based method for subspace selection of SNPs. This method is precisely fit for the high dimensional nature of GWAS data. The fivefold cross-validation was also applied in evaluating the predictive performance of the model on GWAS datasets. Gradient boosting of decision trees was also applied to GWAS datasets. Behravan et al. (2018) developed a SNP selection process with an XGBoost model. Next, there was a repetitive SNP search to get the optimal SNP groups interacting and having a high breast cancer risk potential. This model was developed as a surrogate to the polygenic risk scoring model and included the SVM classifier in its backend for classification of SNPs.

Oh et al. (2017) developed a model called preconditioned random forest regression (PRFR). They converted a binary variable viz toxicity and non-toxicity into a continuous variable. This was achieved with principal component analysis and logistic regression. López et al. (2018) used the Random Forest algorithm to find the most important SNPs related to diabetes. They assigned the weights as values that range between 0 and 1, to each attribute. Lee et al. (2020) applied the preconditioned random forest regression method to predict the risk of contralateral breast cancer. Using a 5-fold cross validation, the PRFR model on 712 SNPs achieved an average AUC of 0.57 (95% confidence interval: 0.57–0.58) on the validation data.

3.4 Neural networks

Liu et al. (2019) proposed an independent deep Convoluted Neural Network (CNN) model to predict phenotypes information from data on SNPs. They were also the first to apply a saliency map deep learning visualization method to select significant biomarkers (SNPs) from their trained model. They were compared against other statistical methods viz Best Linear Unbiased Prediction (BLUP), Bayesian ridge regression (BRR), Bayesian A, and Bayesian Lasso. The design was to associate quantitative traits of soybean with the SNP dataset. Neural networks were applied in a comparative work with other machine learning algorithms. Specifically, Dense neural networks with one fully connected layer, with different numbers of fully connected hidden layer and with varying odd numbers of fully connected hidden layer. They achieved mean AUC scores in the range of 0.80 with the model (Romagnoni et al., 2019). In the neural networks, work done by Romagnoni et al. (2019) noted that an increase in the number of hidden neurons did not significantly increase the performance of the model in terms of classification of cases and controls. The deep mixed model (composed of Convoluted neural network and Long Term Short Term Memory model) was compared against such methods as standard univariate testing & standard linear mixed model (with Benjamini Hochberg procedure) (Wang et al., 2019). However, the results of this method when verified in literature search. seem not verifiable in the GWAS catalogue. The SNP reported by this method are linked to the disease in question-Alzheimer's disease. In predicting the risk for Age-related Macular Degeneration, Neural Networks were also used although it did not show a great advantage over the other methods applied (AUC = 0.82 ∼ 0.83) (Yan et al., 2019).

4.1 Identification of significant SNPs

A problem with the current methods of GWAS analysis is the dependence on testing each SNP individually. Consequently, this leads to the disregard for any biological correlation structures between the SNPs understudied. These structures are introduced by both population genetics (linkage disequilibrium) and other biological effects (Mieth et al., 2016). The approach by Nguyen et al. (2015) with Random Forest has shown to have effectivity in selecting SNPs that are possibly associated with diseases. Where they succeed, the authors posit that traditional statistical approaches might fail. The machine learning approaches thrive in the high dimensionality problem where the number of sample subjects is notably less than that of the SNPs. Mieth et al. (2016) was also able to combine the Support vector machine classifier with the standard statistical testing, RPVT (Raw P-value thresholding), to identify significant SNPs associated with the WTCCC data. They called their method COMBI. Behravan et al. (2018) developed a gradient tree boosting method to capture the complex non-linear SNP-SNP interactions. Eventually, the method obtains a group of significant SNPs which have high Breast Cancer predictive potential. They also developed a support vector machine classifier formed by the identified SNPs to classify Breast Cancer cases and controls. They achieved approximate precision (mAP) scores of 73, 67, and 69 in classifying Breast Cancer cases and controls on three datasets (individual and merged datasets). Dorani et al. (2018) had used the plink software for prior quality control on the total GWAS data set. They then focused the next stage of their work on the application of two ensemble learning algorithms, random forests, and gradient boosting machine, in identifying the interacting and significant SNPs correlated with colorectal cancer.

4.2 Disease risk assessment and prediction

SNPs from GWAS have been shown to be valuable in estimating the risk of developing the disease phenotype (Kooperberg et al. 2010; Wang et al., 2016). The computational methods are useful to analyse the impact of the identified variants on the disease risk (Vihinen, 2013). In a study on prediction of the risk of an individual sensitivity to radiotherapy, Oh et al. (2017) developed an innovative multi-SNP predictive model based on ML algorithms namely preconditioned random forest regression (PRFR). They concluded that GWAS SNPs can yield useful risk stratification models and identify important biological processes in radiation damage and tissue repair processes. Mittag et al. (2012) applied a SVM model to Parkinson's disease and type 1 diabetes. This was to reveal that apart from effect sizes of risk variants, disease heritability is also important in disease risk prediction. This points to the effects that each disease variant has a role to play in disease risk assessment and prediction. Gaudillo et al. (2019) also built a novel machine learning model to quantify an individual's risk of developing asthma based on SNP data. Maciukiewicz et al. (2018) studied the potential of ML models using GWAS data to predict duloxetine outcomes in major depressive disorders. SVM and classification & regression trees' based models were the models developed and they had a promising sensitivity scores. Oh et al. (2017) have been able to predict the risk of individual radio sensitivity with novel multi-SNP predictive framework dependent on ML algorithms. Their approach outperformed other methods in predicting the risk of erectile dysfunction and late rectal bleeding after prostate cancer radiotherapy. Similarly in the area of radio genomics, Lee et al. (2018) also applied a preconditioned random forest regression method to genome-wide data. This was done to combine the effects of multiple SNPs to predict patients with high late genitourinary toxicity risk. Lee et al. (2020) also predicted the risk of developing radiation associated contralateral breast cancer (RCBC). Wei et al. (2019) used a six SNPs as classifier (LASSO-Cox Regression) and predictor where the latter may assist the current staging system for predicting localised renal cell carcinoma recurrence after surgery. This helps clinicians make better informed decisions about treatment in adjuvant therapy. Yan et al. (2019) also used four Neural networks, lasso regression, support vector machine, and random forest on GWAS data to predict the risk of developing Age-related macular degeneration. It is a neurodegenerative disease with no known cure but can be adequately managed with diagnosis and risk prediction. Fukaya et al. (2018) applied a gradient boosting machine (GBM) model for the agnostic discovery of novel risk factors in varicose vein development.

4.3 Epistasis (non-linear SNPs) detection

The concept of epistasis is simply the interactions among genetic loci. It has been constantly restated as a major factor contributing to the missing heritability in complex diseases (Okser et al., 2013). Seldomly considered is the non-linear interactions between many genetic factors that play an important role in identifying the genetic variations (Dorani and Hu, 2018). Residual feed intake in dairy were studied by Yao et al. (2013) and epistasis was detected and analysis of tree structures was produced with Random Forest. Finally, the 25 most occurring pairwise SNP interactions were reported as potential epistatic interactions. Wu et al. (2010) developed a method called screen and clean to identify liability loci, including SNPs interactions, with the use of LASSO which is a model selection tool for regression in high dimensional data. Recently, a neural network technique was suggested that could theoretically model arbitrary interactions in GWAS between SNPs as an addendum to the mixed models to correct confounder's effect (Wang et al., 2019). The goal was the investigation of marginal epistasis, for which a deep learning-based method was developed to model arbitrary high-level interactions among genetic variants. The deep mixed model was applied to Alzheimer's disease in order to understand the genetic architecture of the disease. The method reported the top 20 SNPs associated with the disease. A deep learning framework for analysis of epistasis and heterogeneity (Li et al., 2018) called DPEH was developed. The 3-stage framework involves detection of epistasis in the first stage, clustering in the second stage, and prediction in the final stage. Prediction deals with developing a diagnosis model for complex diseases.

In the step of epistasis detection, DPEH searches. Candidate epistatic combinations based on multi-objective optimization and chi-square tests are used to filter false-negative epistatic interaction through filtering based on significance levels. Furthermore, Fergus et al. (2020) combined the GWAS quality control and logistic regression with deep learning stacked autoencoders to develop an approach to extract epistatic interactions among SNPs. The complete framework models the effects of epistasis on minor and major SNP interactions. To essentially capture the epistatic interactions a softmax classifier model pre-initialized with the stacked autoencoder was applied. This approach was eventually applied for the classification of preterm birth risk in mothers within the population of African ancestry. Their model achieved a Sensitivity of 0.96, Specificity of 0.88, and AUC score of 0.97.

A summary of existing machine learning methods and their inferences as applicable to Genome-wide association studies are listed in Table 2.

5.1 Challenges in GWAS

Traditional statistical methods that apply linear mixed models and logistic regression in case control datasets are not well suited for detecting interactive and non-linear effects. This is especially when there is a large number of predictors. Additionally, when higher level and non-linear interactions are present. The linear modelling method used in GWAS frequently considers only one SNP, thereby ignoring the environmental and genetic context (Moore et al., 2010). It is well known that one of the most significant difficulties to be solved in the detection of GWAS-associated SNPs is in the modelling of complex interactions like higher-level non-linear interactions between SNPs and a given biological phenotype (Behravan et al., 2018). Population stratification causes false positive outcomes in genetic association studies, especially in case-control studies (Menting et al., 2014). Until this moment, genomic data has been explored on the premise of single-locus statistical analyses. The approach is able to identify variant with large effects within a population. However, it is unable to capture variants with smaller effects which may have larger effect sizes when in joint interaction with other SNPS. Detection of SNP interactions remains a significant problem because of the high-dimensionality of genomic data, including the GWAS datasets. This is due to such characteristics as biomolecular complexity, lack of marginal effects, missing heritability, and the limits of computational capacities (Gusareva et al., 2014; Padyukov, 2013; Uppu and Krishna, 2018).

5.2 African genetic diversity

There is relative low number of genetic studies that involve people of African ancestry (Benafif et al., 2018; Gurdasani et al., 2015; Mulder et al., 2018; Radouani et al., 2020). For instance neurogenetic studies of people of African ancestry only account for 11.1 percent in the GWAS catalogue (Quansah and McGregor, 2018). Popejoy and Fullerton (2016) further deliberated on the gross underrepresentation of people of non-European ancestry in Genome-wide Association studies. H3Africa projects have continuously played a role in advancing research bioinformatic capacity and output from African nations (Mulder et al., 2017). African and admixed populations have a more complex haplotype block structure and, as such, will benefit from a broader reference dataset containing more genetic diversity (Schurz et al., 2019). African populations are also characterized by extensive population structure and lower LD among loci relative to non-African population (Campbell and Tishkoff, 2008). Consequently, a larger number of SNPs is required in order to capture the genetic variation within the African genome. It is known that the African population is the most genetically diverse in the world (Bentley et al., 2020). Gurdasani et al. (2015) further reiterated that this haplotype diversity would affect the design of genomics studies. The diversity of the African genome (Choudhury et al., 2018; Ramsay et al., 2011) gives more reason to develop methodologies that can capture non-linear interaction of SNPs, such as the machine learning algorithms described in Section 3.

5.3 Challenges with the adoption of Machine learning in GWAS

Romagnoni et al. (2019) also stated that after training the model, the performance of the model should be estimated on a completely different dataset. This is done in a bid toward evaluation of the ability proposed algorithm to be generalizable. This is similar to the case of having a validation dataset. This is tedious because of the large amount of data that would be generated and the complexity of the entire work. The major weakness of the machine learning model in GWAS is the difficulty in application of the algorithm and difficulty in interpretation of the underlying genetic effects from the results (Ho et al., 2019). The nature of the GWAS dataset is also challenging to pre-process before the eventual model is built. Grinberg et al. (2020) suggested that there is room for the development of new machine learning approaches that make better use of prior knowledge of population structure. They further proposed better collaboration between the machine learning and statistical genetics communities. This is because machine learning suffers from a source of technically interesting and societally important problems which could be gained from the latter.