Local and regional earthquake magnitude calibration of Tabuk analog sub-network, Northwest of Saudi Arabia

1 Introduction

Magnitude is a term normally used to describe the size of an earthquake based on instrument measurements. Richter (1935) first introduced it. He proposed a magnitude scale based solely on amplitudes of ground motion recorded by seismographs. Richter’s procedure to estimate earthquake magnitude followed the practice by Wadati (1931) in which the calculated ground amplitudes for various Japanese stations were plotted against their epicentral distances. Richter (1935) took several bold steps to simplify the estimation of earthquake magnitude.

The magnitude is a quantity, which is a characteristic of an earthquake and can be determined from different recording stations within accepted error limits. Even in the best conditions, errors of 0.2–0.3 units are expected in a calculated magnitude. So far, the magnitude concept appears simple and relatively free from complications. However, this is not the case, as evidenced by the three different scales commonly in use: Local magnitude (ML) is the original magnitude introduced by Richter (1935) for local earthquakes in Southern California. ML was defined by Richter as the logarithm of the maximum recorded trace amplitude (expressed in microns) by a Wood–Anderson Torsion Seismograph at an epicentral distance of 100 km with specified constants. Gutenberg (1945a) developed the concept of a magnitude scale (later on called Surface Wave Magnitude (Ms)) that was applicable to any epicentral distance and to any type of seismograph. This magnitude required a better knowledge of the variation of wave amplitudes with distance. It was necessary to use ground amplitudes instead of trace amplitudes in order to use different seismograph types. The first generalization was made for Rayleigh surface waves, by limiting the period range considered to 20 ± 2.0 s. Further, by including only earthquakes of normal depth (constant h) and finally by stating that the function f for surface waves is proportional to the logarithm of the epicentral distance. The amplitude refers to the horizontal component of Rayleigh surface waves and similar formulas for the vertical component of Rayleigh surface waves have been developed. Gutenberg (1945b,c) extended magnitude determinations to body waves (later on called Body Wave Magnitude (mb)) and to earthquakes at any depth.

However, magnitudes given by the three scales do not agree with each other, which mean the same earthquake will have different magnitude values on the different scales.

Magnitude can be calculated from the maximum amplitude on the seismogram (Eaton et al., 1970) or from the length of time from the P-wave arrival to the end of coda (signal duration). Lee et al. (1972) established an empirical formula for estimating magnitudes of local earthquakes using signal durations.

However, the main purpose of most micro-earthquake networks, which operate short period, high-gain instruments, is to locate every small event, using the arrival times of P-waves and S-waves. In these networks, it is often impracticable to establish a suitable magnitude scale based on amplitude measurements because of the instrument’s limited dynamic range, which often results in even relatively small events overloading the recorders.

Tabuk seismographic sub-network operates analog basic equipment (Sinno et al., 1988; Al-Arifi and Gharib, 1994) so this necessitates the establishment of a simple and easy-to-apply magnitude scale, which has no recording problems. It consists of eight seismic stations (Fig. 1), namely, Haql (HQL), Al-Ouyannah (AYN), Al-Sharaf (SRFA), Al-Sultania (SALT), Bir-El-Mashi (BMSH), Al-Bada (BADA), and Maqna (MKNA). See Table 1 for the station information, such as, geographical location, means of data relay and date of operation of the Tabuk sub-network, Saudi Arabia.

Close

Figure 1

Map showing the seismicity of the study area and the location of each seismic station used in this study.

Export to PPT

2 Method and result

Estimating magnitudes from signal duration is an empirical correlation between the magnitudes of the earthquakes and the duration of its recorded signal. This correlation has been consistently observed in different parts of the world. A partially satisfactory theoretical basis for this correlation has been sought in terms of the properties of coda waves (Suteau and Whitcomb, 1979; Lee and Stewart, 1981).

Bisztricsany (1958) was the first to use signal duration in estimating magnitudes by establishing a relationship between the magnitudes of teleseismic events at epicentral distances between 4 û and 160 û recorded in eastern Europe (Budapest, Prague and Warsaw) and the logarithm of the duration of their surface wave train. He suggested that:

where M is magnitude (mainly in the range of 5–8). τ is the duration of the surface wave in seconds. Δ is the epicentral distance in degrees.

Sole’vev (1965) and Tsumura (1967) derived empirical relationships between the total signal duration of local earthquakes and magnitude for the areas of Sakhalin, USSR, and Kii Peninsula, Japan, respectively. The Tsumura empirical formula was:

The studies of Lee et al. (1972) for central California, USA, and Crosson (1972) for the Puget Sound region of Washington State, USA, have subsequently led to the widespread use of signal duration in estimating magnitudes (for a list of examples, see Adams, 1977; Lee and Wetmiller, 1978; Bath, 1981).

According to Lee and Stewart (1981), the duration magnitude (MD) is usually given in the form:

The coefficients in Eq. (3) are usually determined by correlating signal duration for a chosen number of events with their magnitudes, using some other accepted magnitude scale taking into account the epicentral distance and focal depth. Since no dependence of duration magnitude on depth (range 0.0–60.0 km) has ever been conclusively found anywhere, the depth dependent term has been omitted. Eq. (3) is therefore reduced to:

In this study, signal duration is arbitrarily defined as the time interval in seconds between the first onset of the first P-wave and the point where the signal (peak-to-peak amplitude) no longer exceeds 2 mm as it appears on a TELEDYNE GEOTECH helicorder model RV301B, Portacorder model RV-320B. This is for a recording system consisting of TELEDYNE GEOTECH S-13 Seismometer (Natural period = 1.0 s/cycle), amp-mod (gain ≈ 84 dB), Portacorder (gain ≈ 54 dB), and Helicorder (gain = 24 dB). In Fig. 2 signal duration (τ) with background noise on the portacorder records.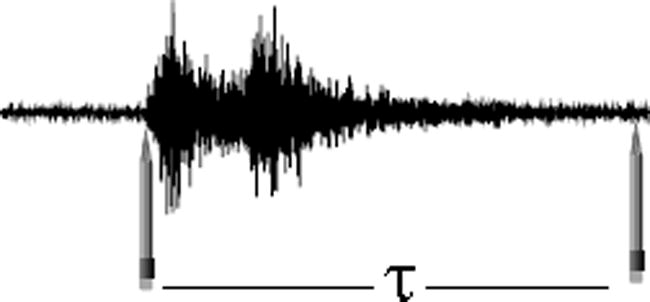

Close

Figure 2

Signal duration (τ) as defined in this study with background noise on the portacorder records.

Export to PPT

There are three reasons why total duration is defined in this study:

1. This method enables signal duration to be defined independent of the particular recording device,

2. neither of the seismic stations in this study operate at unusually high gain which would tend to make the total duration inconveniently long, or the amplitude of the background noise excessively large, presenting practical difficulties in the measurement of duration, and

3. the network is large in aperture, and, hence, for small earthquakes, the more distant stations may record very small amplitudes (<2.0 mm), which makes it difficult to assign an arbitrary cut-off amplitude but, on the other hand, more practical to read the entire duration. Another point of interest is that defining the end of the record in terms of the background noise makes the duration somewhat independent of a subsequent change in the instrument gain since increasing the magnification would amplify the noise as well as the earthquake signal.

There are also four reasons why duration magnitude is used in this study:

1. It does not require any amplitude calibration of the seismograph,

2. it is not affected by instrument saturation (record clipping) or too faint traces at the largest amplitudes,

3. the often negligible distance-dependence makes the method applicable also when the epicentral locations are only approximate, and

4. this method has an extensive application, especially in micro-earthquake surveys, notably in the U.S.A. since around 1972.

This method may break down when a new shock occurs on the tail of a preceding event. 194 earthquakes (506 observations) recorded from January 1986 to December 1991 by the Tabuk Sub-network (Table 1) were sampled to study the duration magnitude. Signal durations of 104, 98, 60, and 44 selected earthquakes recorded by HQL, AYN, BADA and SRFA seismic stations, respectively, are plotted against their ML (Fig. 3a–e).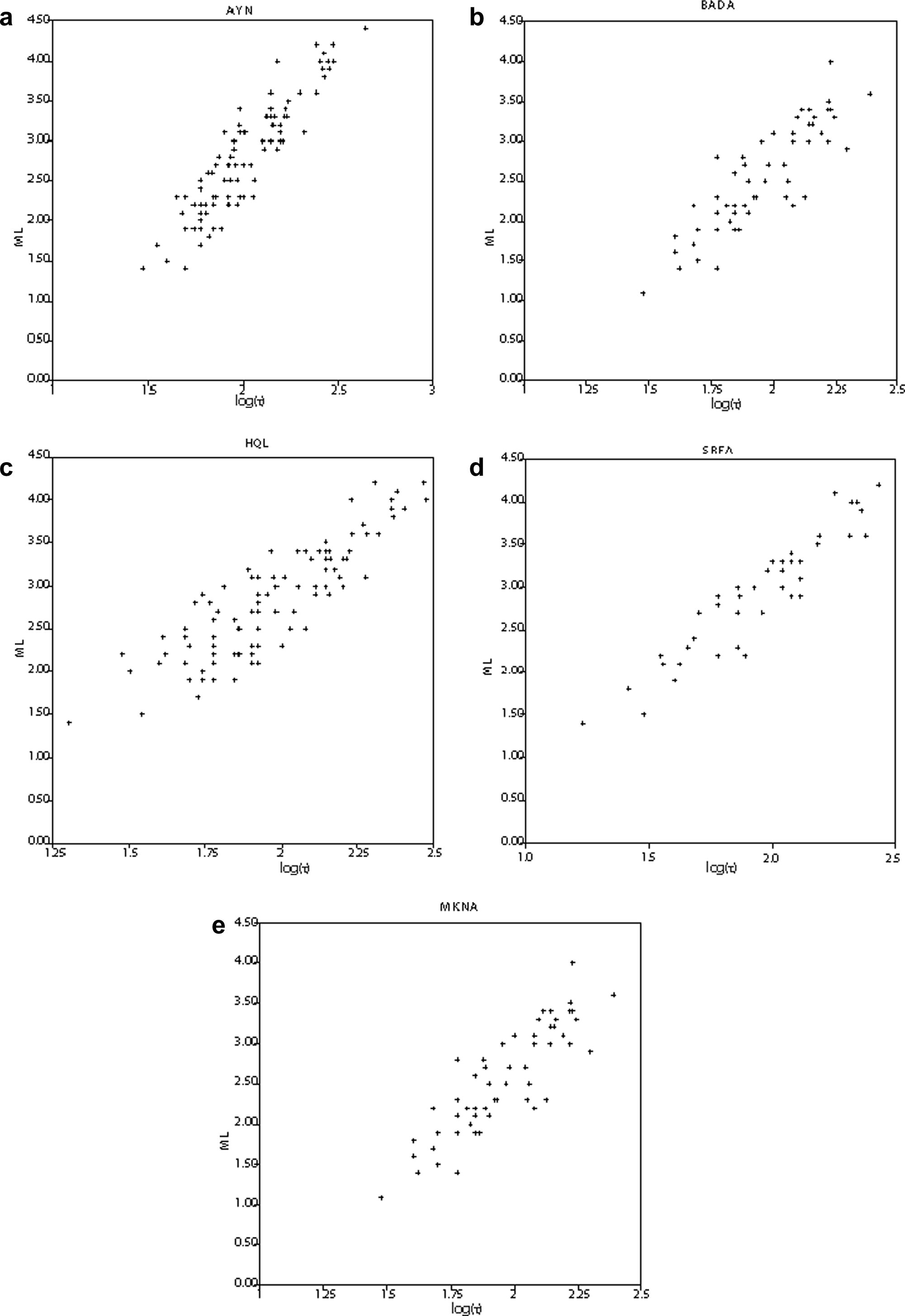

Close

Figure 3

Correlation between ML and the common logarithm of the signal duration (τ) for: (a) 98 earthquakes recorded by AYN station, (b) 60 earthquakes recorded by BADA station, (c) 60 earthquakes recorded by BADA station, (d) 104 earthquakes recorded by HQL station, and (e) 44 earthquakes recorded by SRFA station.

Export to PPT

If the duration magnitude is to be both practical and reliable, it is essential that data be sampled over a wide range of magnitude. The highest magnitude used in this study (4.8) was limited by practical difficulties encountered in reading the duration of large earthquakes, which were almost invariably followed by immediate aftershocks.

The reduction of data was accomplished by a sequence of steps that allowed an examination of the effects of the secondary variables at various stages of the process. The analytical procedure may be outlined as follows:

3 Discussion and conclusion

Results of the regression for each station are summarized in Table 2. The slight variation of constants among stations presumably arises from the effect of local site geology.

The adjusted R square values show that 91.26%, 88.53%, 90.25%, and 93.81% of the variations of the local magnitude are explained by the effect of the three independent variables (log τ, Δ, and focal depth) of the AYN, BADA, HQL, and SRFA stations, respectively. The remaining percentages (8.74%, 11.47%, 9.75%, and 6.19%) are due to error, while the F-test shows that the reliability of the cause and effect between the dependent variable and the independent variables are highly significant F = 507.50, 228.90, 477.94, and 327.02 for the AYN, BADA, HQL and SRFA stations, respectively. Furthermore, these significant F’s values show that the probability of rejecting such relationships is negligible. However, by applying the t-test which defines the degree of reliability between each of the independent variables and the dependent variable, the following results emerged:

1. the common logarithm of the signal duration (log τ) t-test shows that it is the most reliable result since the t-test values are 28.18, 18.78, 25.52, and 22.72 for the AYN, BADA, HQL and SRFA stations, respectively, with a negligible probability of rejecting this relationship (0.0 for all stations).

2. Epicentral distance (Δ) t-test shows that it gives less reliable results since the t-test values are 9.99, 8.85, 12.71, and 6.30 for the AYN, BADA, HQL and SRFA stations, respectively, with a negligible probability of rejecting this relationship (0.0 for all stations).

3. Focal depth (h) t-test shows that it produces results of very low reliability since the t-test values are −0.936, −0.496, 0.873, and −1.490 for the AYN, BADA, HQL, and SRFA stations, respectively, with a high probability of rejecting this relationship (35.18%, 62.19%, 38.49%, 14.41%, for the AYN, BADA, HQL, and SRFA stations, respectively). Therefore, this variable was not included in the equation. Then the magnitude equations were written for the four seismic stations (Eq. (5) for AYN, Eq. (6) for BADA, Eq. (7) for HQL, Eq. (8) for SRFA) as follows:

   (5)
   $${\text{MD}}_{\text{AYN}}=-3.01+2.57\text{log}\tau +0.003\mathrm{\Delta }$$
   (6)
   $${\text{MD}}_{\text{BADA}}=-3.05+2.61\text{log}\tau +0.004\mathrm{\Delta }$$
   (7)
   $${\text{MD}}_{\text{HQL}}=-1.92+2.17\text{log}\tau +0.004\mathrm{\Delta }$$
   (8)
   $${\text{MD}}_{\text{SRFA}}=-1.68+2.19\text{log}\tau +0.003\mathrm{\Delta }$$