Translate this page into:
Kumaraswamy generalized Kappa distribution with application to stream flow data
⁎Corresponding author. tahir.nawaz@gcuf.edu.pk (Tahir Nawaz),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Recently in literature many families of distributions have been introduced to study the skewness, kurtosis and to explore the shape of the distribution more intensely. These families of distribution have wider applicability in variety of fields. In this paper, we introduce a five-parameter distribution, called the Kumaraswamy generalized Kappa distribution which extends the three-parameter Kappa distribution. The new distribution is more flexible and is applicable in the study of the highly-skewed data. Some mathematical properties of the proposed distribution are studied that includes the explicit expression for generating functions, moments, inequality indices, and entropies. The maximum likelihood estimates are computed using the numerical procedure. An application of the Kumaraswamy generalized Kappa distribution is illustrated using a real data set on stream flow.
Keywords
Entropy
Inequality indices
Kumaraswamy distribution
Kappa distribution
Maximum likelihood
1 Introduction
Many families of distribution have been recently proposed which are more flexible and have wider applicability ranging from survival analysis, reliability engineering, and related fields. Classical distributions do not provide adequate fits to the real data which are highly skewed. To overcome this drawback numerous methods of introducing additional shape parameters, and generating new families of distributions are available in the statistical literature.
Some well-known generators are the Marshall and Olkin (1997), exponentiated generalized (exp-G) class of distributions based on Lehmann-type alternatives suggested by Gupta et al. (1998), generalized-exponential (GE) also known as exponentiated exponential (EE) distributions introduced by Gupta and Kundu (1999), beta-generated distributions proposed by Eugene et al. (2002) and Jones (2004), Kumaraswamy generalized (Kum-G) distribution suggested by Cordeiro and de Castro (2011), McDonald generalized (Mc-G) distribution introduced by Alexander et al. (2012), gamma-generated type-1 distributions proposed by Zografos and Balakrishnan (2009) and Amini et al. (2014), gamma-generated type-2 distributions by Ristic and Balakrishnan (2012) and Amini et al. (2014), exponentiated generalized (exp-G) distribution introduced by Cordeiro et al. (2013) and odd Weibull-generated distribution proposed by Bourguignon et al. (2014). The induction of one, two or three more shape parameters to the base-line distribution increases the chances to investigate skewness and vary tail weights. The earlier mentioned generalizations also help to deduce sub-model of generalized distributions that greatly enhances the applicability.
There is no general class of distribution to model skewed data in every practical situation. Mielke (1973) presented a class of asymmetric positively skewed distributions, known as the Kappa distribution, for explaining and examining rainfall data and weather modification. Mielke and Johnson (1973) presented the maximum likelihood estimates and the likelihood ratio tests for the three-parameter Kappa distribution. The Kappa distribution has obtained attention from the hydrologic experts. Conventionally, the log normal and gamma distributions are fitted to precipitation data but these distributions have their own limitations due to non-existence of closed forms of the cdfs and quantile functions. The class of Kappa distribution have closed algebraic expressions that can easily be analysed.
Let
be a three-parameter Kappa random variable, then the pdf and cdf of the Kappa distribution are given by
Parameter is scale while parameters and are shape.
In this paper [deduced from Hussain (2015)], we have extended the three parameter Kappa distribution, namely the Kumaraswamy generalized Kappa (KGK) distribution by introducing additional shape parameters. The paper is organized as follows. In Section 2 we have defined KGK distribution, its sub-models and the behaviour of its pdf. The mathematical properties such as: quantile functions, moments, and generating functions are derived in Section 3. The Reliability properties are presented in Section 4. Some inequality indices are given in Section 5. Entropies are discussed in Section 6. Maximum likelihood estimation of the parameters of the distribution is presented in Section 7. The application on real life data set of stream flows amount is provided in Section 8. Finally, Section 9 concludes the manuscript.
2 Kumaraswamy generalized Kappa distribution
Cordeiro and de Castro (2011) defined a general class of general distributions for double-bounded random process based on Kumaraswamy (1980) which is known as the Kumaraswamy generalized (Kum-G) distribution.Let X be a random variable, the cdf of Kum-G class of distribution is given by
2.1 Special sub-models
The KGK has the following distributions as special sub-models.
-
Exponentiated Kappa Lehmann type II (EK-L2) distribution: If , the KGK reduces to the exponentiated Kappa (Lehmann type II) distribution with parameters and .
-
Exponentiated Kappa Lehmann type I (EK-L1) distribution: If , the KGK reduces to the exponentiated Kappa (Lehmann type I) distribution with parameters and .
-
Three-parameter Kappa distribution: If , the KGK reduces to three-parameter Kappa distribution with parameter and .
-
Two-parameter Kappa distribution: If , the KGK reduces to two-parameter Kappa distribution with parameter and .
-
One-parameter Kappa distribution: If , the KGK reduces to one-parameter Kappa distribution with parameter .
2.2 A useful representation of KGK density function
Using the binomial expansion, , where is real non-integer and .
The KGK density given in (2.4) in more simplified form can be expressed as
Graphical representation of the density function for various values of the parameters selected arbitrarily provided in Fig. 1. It can be observed from the Fig. 1 that increasing the value of the shape parameters
the peakedness of the density function tends to increase. Similarly, the increase in the value of the scale parameter
shifts the density function away from the origin.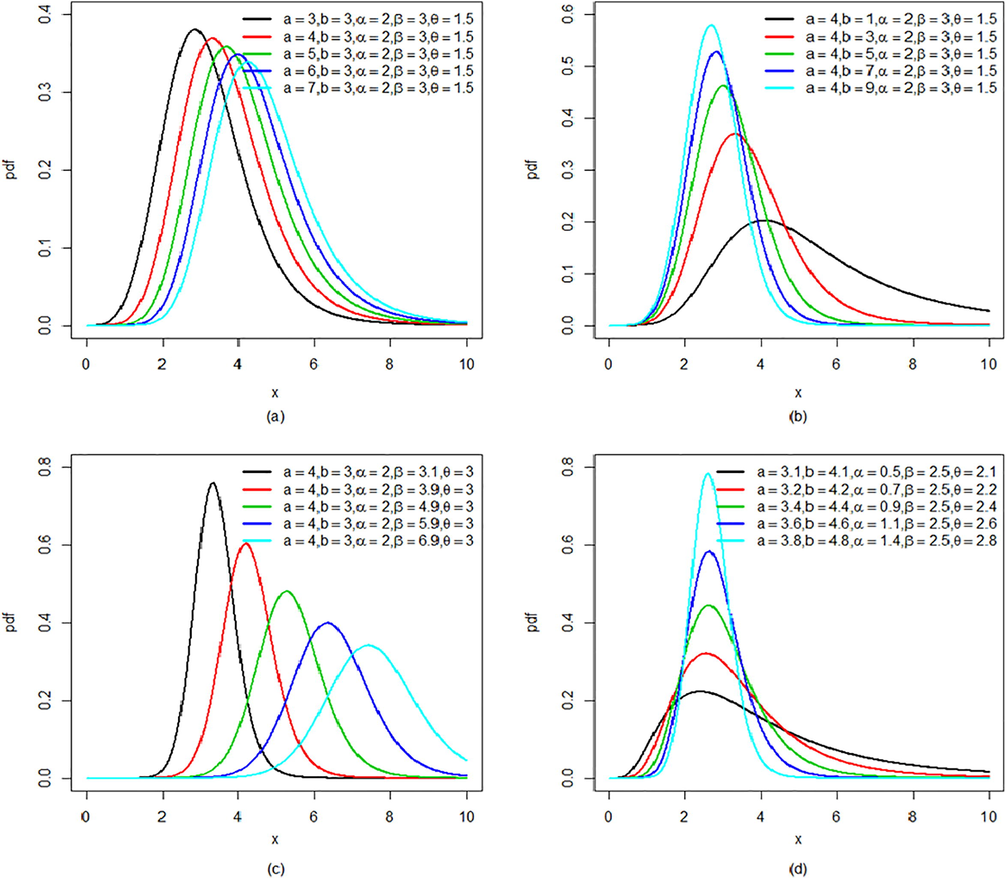
Plots of density function of KGK distribution by varying the parameter values.
3 Statistical properties
In this section, various statistical properties of the KGK distribution, viz. Quantile function, median, random number generation, mode, moments, moment generating function (mgf), characteristic function (cf), mean deviation from mean and mean deviation from median.
3.1 Quantile function and random number generation
The qth quantile,
, of the KGK distribution can be obtained by
Now, for solving
, gives us quantile function of the Kum generalized Kappa (KGK) distribution.
3.2 Mode
The mode of the KGK is obtained as
The first derivative of
for the KGK distribution is
. So, the modes of the KGK distribution are the roots of the following equation
which gives
3.3 rth moment
The moment for KGK random variable is given by using (2.6), we have Let then After simplification, we get Let and
After simplification, we get
Using beta function,
The mean and the variance of the KGK distribution are, respectively, given by
3.4 Moment generating function and characteristic function
The moment generating function and characteristic function of the KGK distribution are given by
4 Reliability properties
In this section, we have derived the reliability properties such as survival (or reliability) function, hazard rate, reversed hazard rate, cumulative hazard rate, mean residual life and mean waiting time for the Kumaraswamy generalized Kappa distribution.
A life time random variable
is said to have KGK
distribution, when its
and
are represented as follows
The survival (or reliability) function,
, is given by
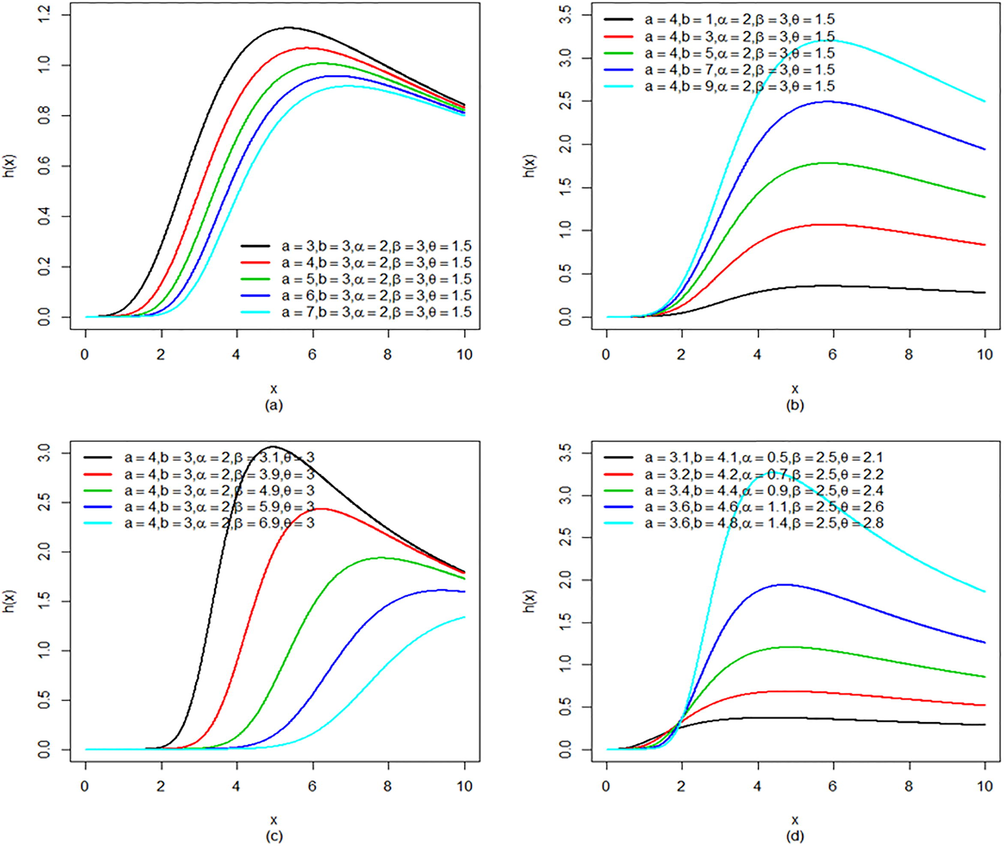
Plots of hazard rate of KGK distribution by varying the parameter values.
It is observable from Fig. 2 that the hazard rate of the KGK distribution tends to increase initially, and then after reaching a certain level it starts decreasing. This indicates that the KGK distribution can be useful to model first increasing then decreasing hazard rate.
The cumulative hazard rate function,
, and reversed hazard rate,
, of KGK distribution are given respectively as
Using the results of (4.8) in (4.7), the MRL of the KGK distribution obtained as
5 Inequality measures
In this section, inequality measures such as Gini index, Lorenz curve, Bonferroni curve, Zenga index, Atkinson index, Pietra index and generalized entropy for the KGK distribution have been obtained.
5.1 Gini index
The most well-known inequality index is Gini index, suggested by Gini (1914), is defined as
Now simplifying further, we have
5.2 Lorenz curve
Lorenz (1905) provided a curve,
, which is defined as
The
for KGK distribution is given as
5.3 Bonferroni curve
The curve suggested by Bonferroni (1930) based on partial means for inequality measure can be determined through the relation
5.4 Zenga index
Zenga (1984, 1990) provided the following income inequality index
5.5 Atkinson index
Atkinson (1970) presented a family of subjective indices, is defined as
5.6 Pietra index
Pietra (1915) offered an index, which is also known as Schutz index or half the relative mean deviation is defined as
5.7 Generalized entropy (GE)
Cowell (1980) and Shorrocks (1980) introduced the generalized entropy (GE) index and is defined as
Using (3.5), we get
6 Entropies
The most essential entropies of are Shannon entropy, Rényi entropy, -entropy. Here we consider two entropy measures: the Rényi entropy, -entropy. Entropies and kurtosis measures play the same role in comparing the shape of various densities and measuring heaviness of tails.
6.1 Rényi entropy
Rényi (1961) provided an extension of the Shannon entropy which is defined as:
Applying binomial expansion on KGK
given by (2.4), we get
in more simple form
6.2 -entropy
Havrda and Charvát (1967) presented -entropy and later Tsallis (1988) applied it to physical problems. Furthermore, one-parameter generalization of the Shannon entropy is -entropy which can lead to models or statistical results that are different from those acquired by using the Shannon entropy.
For a continuous random variable
having
, the
-entropy is defined by
Using the result of (6.5), we get
7 Estimation of parameters of KGK distribution
This section considers the estimation of the model parameters of the KGK distribution by using the method of maximum likelihood.
We assume that
follows the KGK distribution and let
be the parameter vector of interest. The log-likelihood function
for a random sample
is given by
To check KGK distribution is strictly superior to the Kappa distribution for a given data set the likelihood ratio (LR) statistic can be used. Then, the test of versus is equivalent to compare the KGK and Kappa distributions and the LR statistic becomes , where and are the MLEs under and and are the estimates under .
8 Empirical illustration
In this section, real data set is examined for illustration purpose. The MLEs are calculated and the measures of goodness of fit are used to compare the proposed model Kumaraswamy generalized Kappa distribution with the other competing models. We computed log-likelihood , AIC (Akaike information criterion), BIC (Bayesian information criterion) and CAIC (consistent Akaike information criterion): where signifies the log-likelihood function examined at the maximum likelihood estimates, is the number of parameters, and is the sample size. We also used conventional goodness-of-fit tests in order to check which distribution fits better to this data set. We look at the Cramer-von Mises and Anderson-Darling statistics. In general, the smaller the values of these statistics, the better the fit to the data.
The following data set from Mielke and Johnson (1973) consists of Stream flow amounts (1000 acre-feet) for 35 year (1936–70) at the U.S. Geological Survey (USGS) gaging station number 9-3425 for April 1–August 31 of each year:
192.48, 303.91, 301.26, 135.87, 126.52, 474.25, 297.17, 196.47, 327.64, 261.34, 96.26, 160.52, 314.60, 346.30, 154.44, 111.16, 389.92, 157.93, 126.46, 128.58, 155.62, 400.93, 248.57, 91.27, 238.71, 140.76, 228.28, 104.75, 125.29, 366.22, 192.01, 149.74, 224.58, 242.19, 151.25.
Table 1 presents the estimated values of the MLEs of the parameters of the distributions and their standard errors. Estimated values for AIC, BIC, CAIC,
and
against all the fitted distributions are provided in Table 2. The histogram of the data set and the estimated pdfs and cdfs for the fitted models are displayed in Fig. 3. It is evident from the lower value of the statistics
and
for KGK distribution in comparison to the rest of the fitted distributions that it is the best fit distribution in the given circumstances. These findings are further supplemented by the estimated pdf and cdf plots given in Fig. 3 which clearly depicts that KGK distribution is a better fitted model as compared to others.
Distribution
KGK
37.6739
(563.6182)4.8300
(9.7572)0.1678
(1.0243)17.3661
(219.7929)7.2191
(44.7869)
EK (Lehmann type-I)
58.6622
(1716.8957)–
–0.2164
(1.6786)32.0895
(373.3277)11.7289
(91.2334)
EK (Lehmann type-II)
–
–8.3742
(36.9606)0.0629
(0.1273)515.3789
(1623.1231)16.8224
(26.8103)
Kappa3
–
––
–0.0457
(0.2369)161.5442
(15.9801)56.7357
(287.0343)
Kappa2
–
––
–10.7420
(5.9393)312.1797
(46.5958)–
–
Distribution
KGK
206.4671
422.9343
430.7110
425.0033
0.4555
0.0788
EK (Lehmann type-I)
207.0059
422.0117
428.2331
423.3450
0.4931
0.0794
EK (Lehmann type-II)
206.6339
421.2678
427.4892
422.6011
0.4867
0.0844
Kappa3
207.0037
420.0074
424.6735
420.7816
0.4919
0.0799
Kappa2
214.1449
432.2899
435.4006
432.6649
1.0876
0.1802
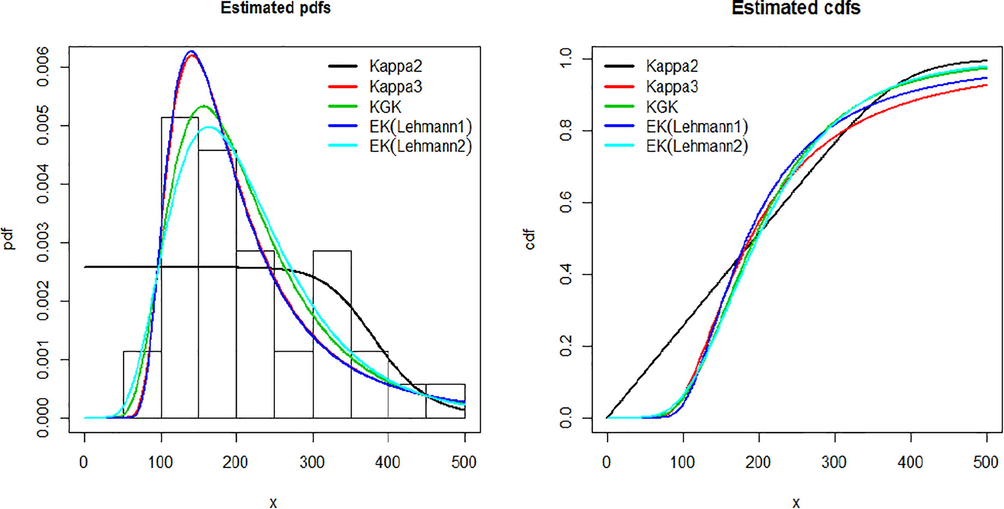
Plot of estimated pdf and cdf for stream flow amounts.
9 Conclusion
In this paper, we propose a five-parameter Kumaraswamy generalized Kappa distribution. Algebraic expressions for various properties of the proposed distribution are provided. The method of maximum likelihood is employed to estimate the parameters along with an empirical illustration expressing the application by using stream flow amount data set. The proposed distribution is compared with some similar existing distributions by using Cramer-von Mises and Anderson-Darling statistics as measure of goodness of fit. It is concluded that KGK distribution is good competitive model for stream flow data set. The proposed distribution KGK has the potential to attract wider application in various areas such as hydrology, reliability and survival analysis.
Acknowledgment
The authors are grateful to the anonymous learned reviewers for their valuable suggestions which have greatly helped in improving the presentation of the manuscript.
References
- Generalized beta-generated distributions. Comput. Stat. Data Anal.. 2012;56(6):1880-1897.
- [CrossRef] [Google Scholar]
- Log-gamma-generated families of distributions. Statistics. 2014;48(4):913-932.
- [CrossRef] [Google Scholar]
- On the measurement of th inequality. J. Econ. Theory. 1970;2(3):244-263.
- [CrossRef] [Google Scholar]
- Elementi Di Statistica Generale. Firenze: Libreria Seeber; 1930.
- The Weibull-G family of probability distributions. J. Data Sci.. 2014;12(1):53-68. www.jds-online.com/files/JDS-1210.pdf·2013-10-21
- [Google Scholar]
- A new family of generalized distributions. J. Stat. Comput. Simul.. 2011;81(7):883-898.
- [CrossRef] [Google Scholar]
- The exponentiated generalized class of distributions. J. Data Sci.. 2013;11(1):1-27.
- [Google Scholar]
- On the structure of additive inequality measures. Rev. Econ. Stud.. 1980;47(3):521-531. Oxford University Press
- [Google Scholar]
- Beta-normal distribution and its applications. Commun. Statist. Theory Methods. 2002;31(4):497-512.
- [CrossRef] [Google Scholar]
- Gini, C., 1914. Sulla Misura della concentrazione e della variabilit’a dei caratteri. Attidel regio Istituto Venteto di SS. LL.AA.,a.a. 1913-14, tomo LXXIII, parte II, pp. 1203–1248.
- Modeling failure time data by Lehmann alternatives. Commun. Statist. Theory Methods. 1998;27(4):887-904.
- [CrossRef] [Google Scholar]
- Generalized exponential distribution. Austral. New Zealand J. Statist.. 1999;41(2):173-188.
- [CrossRef] [Google Scholar]
- Quantification method in classification processes: concept of structural alpha-entropy. Kybernetika. 1967;3(1):30-35.
- [Google Scholar]
- Hussain, S., 2015. Properties, Extension and Application of Kappa Distribution. Unpublished M.Phil thesis submitted to Government College University, Faisalabad, Pakistan.
- Families of distributions arising from the distributions of order statistics. Test. 2004;13(1):1-43.
- [CrossRef] [Google Scholar]
- A generalized probability density function for double-bounded random processes. J. Hydrol.. 1980;46(1–2):79-88.
- [CrossRef] [Google Scholar]
- Methods of measuring the concentration of wealth. Publ. Am. Statist. Assoc.. 1905;9(70):209-219.
- [CrossRef] [Google Scholar]
- A new method for adding a parameter to a family of distributions with applications to the exponential and weibull families. Biometrika. 1997;84(3):641-652.
- [CrossRef] [Google Scholar]
- Another family of distributions for describing and analyzing precipitation data. J. Appl. Meteorol.. 1973;12(2):275-280.
- [Google Scholar]
- Three parameter Kappa distribution maximum likelihood estimations and likelihood ratio tests. Monthly Weather Rev.. 1973;101:701-707. ftp://ftp.library.noaa.gov/docs.lib/htdocs/rescue/mwr/101/mwr-101-09-0701.pdf
- [Google Scholar]
- Pietra, G., 1915. Delle relazioni tra indici di variabilità, note I e II. Atti del Reale Istituto Veneto di Scienze, Lett ere ed Arti, a.a. 1914–15, LXXIV, 775–804.
- On Measures of Entropy and Information. University of California Press 1961:547-561.
- [Google Scholar]
- The gamma-exponentiated exponential distribution. J. Statist. Comput. Simul.. 2012;82(8):1191-1206.
- [CrossRef] [Google Scholar]
- The class of additively decomposable inequality measures. Econometrica. 1980;48(3):613-625.
- [Google Scholar]
- Possible generalization of Boltzmann-Gibbs statistics. J. Statist. Phys.. 1988;52(1–2):479-487.
- [CrossRef] [Google Scholar]
- Zenga, M., 1984. Proposta per un indice di concentrazione basto sui rapporti fraquantili di populizone e quantili di reddito. Giornale degli Economisti e Annali di Economia Nuova Serie, Anno 43, No. 5/6 (Maggio-Giugno 1984), pp. 301–326. http://www.jstor.org/stable/23246074.
- Concentration curves and concentration indexes derived from them. In: Dagum C., Zenga M., eds. Income and Wealth Distribution, Inequality and Poverty. Studies in Contemporary Economics. Berlin, Heidelberg: Springer; 1990. p. :94-110.
- [Google Scholar]
- On families of beta- and generalized gamma-generated distributions and associated inference. Statist. Method.. 2009;6(4):344-362.
- [CrossRef] [Google Scholar]
Appendix A
The elements of the observed information matrix where are given by where







