Ion-acoustic waves in an inhomogeneous plasma with negative ions

A.E. Mowafy; W.M. Moslem

doi:10.1016/j.jksus.2012.01.001

View/Download PDF

Buy Reprints

PDF

Translate this page into:

ORIGINAL ARTICLE

24 (

); 343-349

doi:

10.1016/j.jksus.2012.01.001

Ion-acoustic waves in an inhomogeneous plasma with negative ions

A.E. Mowafy^a,*, W.M. Moslem^b,c

a Physics Department, Faculty of Science, Hail University, Saudi Arabia

b International Centre for Advanced Studies in Physical Sciences, Faculty of Physics and Astronomy, Ruhr University Bochum, D-44780 Bochum, Germany

c Department of Physics, Faculty of Science, Port Said University, Port Said, Egypt

*Corresponding author. Tel.: +966 592024955. aemowafy@yahoo.com (A.E. Mowafy)

Received: 2011-11-2, Accepted: 2012-1-12, Published: 2012-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 24 January 2012

Peer review under responsibility of King Saud University.

Abstract

The propagation of the ion-acoustic waves (IAWs) in a collisionless, unmagnetized inhomogeneous plasma composed of warm positive and negative ions with different masses and isothermal electrons is investigated. The reductive-perturbation method is employed to reduce the basic set of fluid equations to the variable coefficients Korteweg–de Varies (KdV) equation. It is found that both compressive and rarefactive solitons can propagate in the system. Below (above) certain values of positive ions densities the system supports rarefactive (compressive) solitons. The dependence of solitons amplitude and width on the system parameters is investigated.

Keywords

Inhomogeneous plasma

Ion acoustic waves

Variable coefficient KdV equation

Solitary wave solution

Show Related Articles from PubMed

1 Introduction

Negative ion plasma can be defined as plasma that contains both negative and positive ion species, as well as electrons. Negative ion plasma can appear as a result of elementary processes, such as dissociative or non-dissociative electron attachment to neutrals when an electronegative gas, such as halogens and hexafluorides, is introduced into an electrical gas discharge or injected from the external sources (Vladimirov et al., 2003; Mamun and Shukla, 2003; Djebli, 2003 ). Furthermore, negative ion plasma can be created in the plasma processing reactors (Gottscho and Gaebe, 1986), low-temperature laboratory experiments (Jacquinot et al., 1977; Nakamura et al., 1997; Weingarten et al., 2001; Ichiki et al., 2002 ), and neutral beam sources (Bacal and Hamilton, 1979). Also, negative ion plasma can be found in many space observations such as the D-region of the ionosphere (Massey, 1976; Portnyagin et al., 1991), cometary comae (Chaizy et al., 1991), etc.

The presence of the negative ion in a plasma modifies the charge neutrality condition i.e., n_e = n_p−n_n, where n_e, n_p, and n_n are the electron, positive ion, and negative ion number densities, respectively. It is clear that as the number density of the negative ions increases, the electrons’ number density decreases. The result is a decrease of the shielding effect produced by the electrons, which is one of the main effects governing the behavior of plasmas. From this perspective, it seems to follow that the negative ions only influence plasmas secondarily. Although this is a fact, most of the phenomena are actually affected by the negative ions themselves, as well as by the lack of electrons (Ichiki et al., 2002).

In the absence of dissipation or if the dissipation is weak, the balance between the nonlinear and the dispersion effects can result in the formation of symmetrical solitary waves – soliton. The IAWs and their attributes have been the subject of many researches in plasma physics and complex (dusty) plasma as well. There has been considerable interest (see, for example, Das and Tagare, 1975; Nakamura, 1982; Watanabe, 1984; Tajiri and Tuda, 1985; Ludwig et al., 1984; Moslem, 1999; El-Labany et al., 2000, 2011a,b ) in the investigation of nonlinear IAWs in plasmas with positive–negative ions and Boltzmann distributed electrons. Extensive work has been devoted to the study of IAWs in plasmas with positive–negative ions. For example, The propagation of IAWs in a multi-species plasma consisting of positive ions, electrons and negative ions have been investigated theoretically by Das and Tagare (1975), Watanabe (1984), Tagare (1986), and experimentally by Cooney et al. (1991), etc. and their studies showed the rarefactive solitary waves owing to the presence of negative ions. Chakraborty et al. (1992), Chakraborty et al. (1993), Chakraborty et al. (1994), Chattopadhyay et al. (2002), considered the effect of negative ions on the formation of ion acoustic solitons in relativistic plasmas. They have numerically estimated the width, amplitude and phase velocity of IAWs for a model plasma having the negative ions which have short lifetimes (or small probability of existence). Chattopadhyay et al. (2002), found that drift motion of ions has a significant contribution on the excitation of IAWs in the presence of negative ions in plasma. Chattopadhyay et al. (2009), studied warm positive and negative ions with two-temperature isothermal electrons using the pseudopotential method. They found that the concentration of negative ions, drift velocities, mass ratios, equal temperatures of ions (particular case) and presence of two groups of electrons and their ratios modify the profiles of the Sagdeev pseudopotential curves of the solitary waves in the plasma. Das and Nag (2010), used reductive-perturbation technique to study the propagation of IAWs in the vicinity of KdV equation in magnetized plasma with negative ions. They found that the presence of negative ions changes the nonlinearity as a result of which the formation of soliton exhibits different nature on soliton propagation. Furthermore, several authors (Das and Singh, 1992; Malik and Dahiya, 1994; Das and Devi, 2006; Malik and Stroth, 2008; Singh and Malik, 2008 ) have focused their attention on the investigation of IAWs in inhomogeneous plasmas with positive–negative ions. Since the propagation characteristics of IAWs may be modified by the effects of the presence of negative ion, the main concern of this paper is to study the IAWs in multicomponent inhomogeneous plasma consisting of warm positive- and negative ion species along with isothermal electrons. The salient feature is to demonstrate the existence of compressive and rarefactive IAWs in inhomogeneous plasma with two-ion species having different masses, concentrations, and temperatures. The two types of ions are assumed to have the same charge number = 1. Using the reductive-perturbation method, we have derived a KdV equation that admits a soliton solution. We have investigated the effect of mass, concentration, and temperature of different ion species on the characteristics of IAWs in detail. Furthermore, for numerical illustrations, we take a realistic example of plasma containing the ions $({Ar}^{+}, {SF}_{6}^{-})$ . The $({Ar}^{+}, {SF}_{6}^{-})$ plasma composition has been used in the experimental investigation of strong double layers by Merlino and Loomis (1990).

The present paper is organized as follows. In Section 2, the basic set of fluid equations for the IAWs in positive–negative ion plasma with isothermal electrons is presented. The well known KdV equation is derived. In Section 3, the KdV equation is solved and analyzed to study the profiles of the nonlinear IAW. Section 4 is devoted to a concluding discussion.

2 Basic equations and derivation of the KdV equation

Let us consider a medium of an unmagnetized, collisionless, warm, adiabatic inhomogeneous plasma containing mixture of positive and negative ions and isothermal electrons. The fluid equations of motion governing the system can be expressed as follows (Kalita et al., 1996; Moslem et al. 2009):

(1)

\frac{\partial}{\partial t} n_{p} + \frac{\partial}{\partial x} (n_{p} u_{p}) = 0,

(2)

(\frac{\partial}{\partial t} + u_{p} \frac{\partial}{\partial x}) u_{p} + 3 σ_{p} n_{p} \frac{\partial}{\partial x} n_{p} + \frac{\partial}{\partial x} ϕ = 0,

(3)

\frac{\partial}{\partial t} n_{n} + \frac{\partial}{\partial x} (n_{n} u_{n}) = 0,

(4)

(\frac{\partial}{\partial t} + u_{n} \frac{\partial}{\partial x}) u_{n} + \frac{3 σ_{n}}{q} n_{n} \frac{\partial}{\partial x} n_{n} - \frac{1}{q} \frac{\partial}{\partial x} ϕ = 0,

(5)

n_{e} = e^{ϕ},

(6)

\frac{\partial^{2}}{\partial x^{2}} ϕ = - n_{p} + n_{n} + n_{e} .

Here, u_p and u_n are the velocities of the positive and negative ions, respectively,

ϕ

the electrostatic potential, x the space coordinate, and t the time variable. Furthermore, σ_P = T_P/T_e and σ_n = T_n/T_e are the ratios of the temperatures of positive ions (T_p) and negative ions (T_n) to the electron temperature (T_e), and q = m_n/m_p is the ratio of the negative ion mass (m_n) to the positive ion mass (m_p).

We normalized all the physical quantities as follows. The background electron density $n_{e}^{(0)}$ normalizes the densities, u_p_,_n by the ion sound speed (KT_e/m_p)^1/2, $ϕ$ by KT_e/e, t by the inverse of the plasma frequency $ω_{pi}^{- 1} = (m_{p} / 4 π e^{2} n_{e})^{1 / 2}$ , x by the electron Debye length λ_D = KT_e/4πe²n_e)^1/2, where K is Boltzmann's constant. The independent variables can be stretched as (Asano, 1974)

(7)

ξ = ɛ^{1 / 2} - (\int \frac{dx}{λ (x)} - t), s = ɛ^{3 / 2} x,

where ɛ is a small parameter less than one and λ is the wave propagation speed to be determined later. The dependent variables are expanded as

(8)

(\begin{matrix} n_{n, p} \\ u_{n, p} \\ ϕ \end{matrix}) = (\begin{matrix} n_{n, p}^{(0)} \\ u_{n, p}^{(0)} \\ ϕ^{(0)} \end{matrix}) + (\begin{matrix} ɛ n_{n, p}^{(1)} + ɛ^{2} n_{n, p}^{(2)} + \dots \\ ɛ u_{n, p}^{(1)} + ɛ^{2} u_{n, p}^{(2)} + \dots \\ ɛ ϕ^{(1)} + ɛ^{2} ϕ^{(2)} + \dots \end{matrix}),

where

n_{n, p}^{(0)}

are the unperturbed densities, which satisfy the neutrality condition

(9)

n_{p}^{(0)} = n_{n}^{(0)} + 1 + ϕ^{(0)},

for simplicity we shall consider the ionic charge number of positive and negative ions equal unity.

Using the stretching (7) and the expansion (8) into Eqs. (1)–(6), and assuming the gradients is in the spatial only, it follows that

(10)

\frac{\partial}{\partial ξ} n_{n, p}^{(0)} = \frac{\partial}{\partial ξ} u_{n, p}^{(0)} = \frac{\partial}{\partial ξ} λ .

In equilibrium, Eqs. (1)–(6) give the following relations:

(11)

\frac{\partial}{\partial s} (u_{p}^{(0)} u_{p}^{(0)}) = 0,

(12)

3 σ_{p} n_{p}^{(0)} \frac{\partial}{\partial s} n_{p}^{(0)} + u_{p}^{(0)} \frac{\partial}{\partial s} u_{p}^{(0)} + \frac{\partial}{\partial s} ϕ^{(0)} = 0,

(13)

\frac{\partial}{\partial s} (u_{n}^{(0)} u_{n}^{(0)}) = 0,

(14)

3 σ_{p} n_{p}^{(0)} \frac{\partial}{\partial s} n_{p}^{(0)} + u_{p}^{(0)} \frac{\partial}{\partial s} u_{p}^{(0)} + \frac{\partial}{\partial s} ϕ^{(0)} = 0,

(15)

\frac{3 σ_{n} n_{n}^{(0)}}{q} \frac{\partial}{\partial s} n_{n}^{(0)} + u_{n}^{(0)} \frac{\partial}{\partial s} u_{n}^{(0)} - \frac{1}{q} \frac{\partial}{\partial s} ϕ^{(0)} = 0 .

The zero order of ɛ gives

(16)

n_{p}^{(0)} - n_{n}^{(0)} - 1 - ϕ^{(0)} - \frac{ϕ^{(0)^{2}}}{2} = 0,

The first order in ɛ yields the following relations:

(17)

n_{p}^{(1)} = - \frac{n_{p}^{(0)} ϕ^{(1)}}{C_{p}},

(18)

u_{p}^{(1)} = - \frac{λ ϕ^{(1)}}{C_{p}},

(19)

n_{n}^{(1)} = \frac{n_{n}^{(0)} ϕ^{(1)}}{C_{n}},

(20)

u_{n}^{(1)} = \frac{λ ϕ^{(1)}}{C_{n}},

(21)

1 + \frac{n_{p}^{(0)}}{C_{p}} + \frac{n_{n}^{(0)}}{C_{n}} + ϕ^{(0)} = 0,

In deriving Eqs. (17)–(21), it has been assumed that the equilibrium flow velocity of positive and negative ions are neglected by assuming them to be much smaller than DIAW phase speed

(λ ≫ u_{p, n}^{(0)})

. From Eq. (21), we obtain the linear phase velocity, which is equivalent to the linear wave dispersion relation

(22)

λ = {(\frac{R_{1} + \sqrt{(- R_{1})^{2} - 4 (q + ϕ^{(0)} q) (R_{2})}}{2 (q + ϕ^{(0)} q)})}^{1 / 2},

where

R_{1} = n_{n}^{(0)} + n_{p}^{(0)} q + (3 n_{n}^{(0)^{2}} σ_{n} + 3 n_{p}^{(0)^{2}} q σ_{p}) (1 + ϕ^{(0)}),

R_{2} = 3 n_{n}^{(0)} n_{p}^{(0)} (n_{n}^{(0)} σ_{n} + n_{p}^{(0)} σ_{p} + 3 n_{n}^{(0)} n_{p}^{(0)} σ_{n} σ_{p} (1 + ϕ^{(0)})),

C_{p} = 3 σ_{p} n_{p}^{(0)^{2}} - λ^{2}, C_{n} = 3 σ_{n} n_{n}^{(0)^{2}} - q λ^{2} .

The second-order in ɛ yields

(23)

u_{p}^{(1)} \frac{\partial}{\partial s} n_{p}^{(0)} + n_{p}^{(1)} \frac{\partial}{\partial s} u_{p}^{(0)} + \frac{u_{p}^{(1)}}{λ} \frac{\partial}{\partial ξ} n_{p}^{(1)} - \frac{\partial}{\partial ξ} n_{p}^{(2)} + \frac{u_{p}^{(0)}}{λ} \frac{\partial}{\partial ξ} n_{p}^{(2)} + \frac{n_{p}^{(1)}}{λ} \frac{\partial}{\partial ξ} u_{p}^{(1)} + \frac{n_{p}^{(0)}}{λ} \frac{\partial}{\partial ξ} u_{p}^{(2)} + u_{p}^{(0)} \frac{\partial}{\partial s} n_{p}^{(1)} + n_{p}^{(0)} \frac{\partial}{\partial s} u_{p}^{(1)} = 0,

(24)

3 σ_{p} n_{p}^{(1)} \frac{\partial}{\partial s} n_{p}^{(0)} + u_{p}^{(1)} \frac{\partial}{\partial s} u_{p}^{(0)} + \frac{3 σ_{p} n_{p}^{(1)}}{λ} \frac{\partial}{\partial ξ} n_{p}^{(1)} + \frac{3 σ_{p} n_{p}^{(0)}}{λ} \frac{\partial}{\partial ξ} n_{p}^{(2)} + \frac{u_{p}^{(1)}}{λ} \frac{\partial}{\partial ξ} u_{p}^{(1)} - \frac{\partial}{\partial ξ} u_{p}^{(2)} + \frac{u_{p}^{(0)}}{λ} \frac{\partial}{\partial ξ} u_{p}^{(2)} + \frac{1}{λ} \frac{\partial}{\partial ξ} ϕ^{(2)} + 3 σ_{p} n_{p}^{(0)} \frac{\partial}{\partial s} n_{p}^{(1)} + u_{p}^{(0)} \frac{\partial}{\partial s} u_{p}^{(1)} + \frac{\partial}{\partial s} ϕ^{(1)} = 0,

(25)

u_{n}^{(1)} \frac{\partial}{\partial s} n_{n}^{(0)} + n_{n}^{(1)} \frac{\partial}{\partial s} u_{n}^{(0)} + \frac{u_{n}^{(1)}}{λ} \frac{\partial}{\partial ξ} n_{n}^{(1)} - \frac{\partial}{\partial ξ} n_{n}^{(2)} + \frac{u_{n}^{(0)}}{λ} \frac{\partial}{\partial ξ} n_{n}^{(2)} + \frac{n_{n}^{(1)}}{λ} \frac{\partial}{\partial ξ} u_{n}^{(1)} + \frac{n_{n}^{(0)}}{λ} \frac{\partial}{\partial ξ} u_{n}^{(2)} + u_{n}^{(0)} \frac{\partial}{\partial s} n_{n}^{(1)} + n_{n}^{(0)} \frac{\partial}{\partial s} u_{n}^{(1)} = 0,

(26)

\frac{3 σ_{n} n_{n}^{(1)}}{q} \frac{\partial}{\partial s} n_{n}^{(0)} + u_{n}^{(1)} \frac{\partial}{\partial s} u_{n}^{(0)} + \frac{3 σ_{n} n_{n}^{(1)}}{q λ} \frac{\partial}{\partial ξ} n_{n}^{(1)} + \frac{3 σ_{n} n_{n}^{(0)}}{q λ} \frac{\partial}{\partial ξ} n_{n}^{(2)} + \frac{u_{n}^{(1)}}{λ} \frac{\partial}{\partial ξ} u_{n}^{(1)} - \frac{\partial}{\partial ξ} u_{n}^{(2)} + \frac{u_{n}^{(0)}}{λ} \frac{\partial}{\partial ξ} u_{n}^{(2)} - \frac{1}{q λ} \frac{\partial}{\partial ξ} ϕ^{(2)} + \frac{3 σ_{n} n_{n}^{(0)}}{q} \frac{\partial}{\partial s} n_{n}^{(1)} + u_{n}^{(0)} \frac{\partial}{\partial s} u_{n}^{(1)} - \frac{1}{q} \frac{\partial}{\partial s} ϕ^{(1)} = 0,

(27)

\frac{1}{λ^{2}} \frac{\partial^{2}}{\partial ξ^{2}} ϕ^{(1)} + n_{p}^{(2)} - n_{n}^{(2)} - (1 + ϕ^{(0)}) ϕ^{(2)} - \frac{1}{2} ϕ^{(1)^{2}} = 0 .

Eliminating the second-order perturbed quantities and making use of the first-order results, we finally get the following nonlinear partial differential equation with variable coefficients:

(28)

\frac{\partial}{\partial s} ϕ^{(1)} + \frac{a_{3}}{a_{2}} ϕ^{(1)} \frac{\partial}{\partial s} ϕ^{(0)} + \frac{a_{1}}{a_{2}} ϕ^{(1)} \frac{\partial}{\partial ξ} ϕ^{(1)} + \frac{1}{a_{2}} \frac{\partial^{3}}{\partial ξ^{3}} ϕ^{(1)} = 0,

where

\begin{matrix} a_{1} = - 1 + \frac{3 n_{n}^{(0)} q λ^{2}}{C_{n}^{3}} - \frac{3 n_{p}^{(0)} λ^{2}}{C_{p}^{3}} + \frac{3 n_{n}^{(0)^{3}} σ_{n}}{C_{n}^{3}} - \frac{3 n_{p}^{(0)^{3}} σ_{p}}{C_{p}^{3}}, \\ a_{2} = \frac{n_{n}^{(0)} u_{n}^{(0)} q λ^{2}}{C_{n}^{2}} + \frac{n_{n}^{(0)} q λ^{3}}{C_{n}^{2}} - \frac{n_{n}^{(0)} λ}{C_{n}} - \frac{n_{p}^{(0)} λ}{C_{p}} + \frac{3 n_{n}^{(0)^{3}} λ σ_{n}}{C_{n}^{2}}, \\ a_{3} = \frac{2 n_{n}^{(0)} u_{n}^{(0)} q^{2} λ^{3}}{C_{1} C_{n}^{3}} + \frac{2 n_{n}^{(0)} q^{2} λ^{4}}{C_{1} C_{n}^{3}} + \frac{n_{n}^{(0)} q λ^{2}}{C_{1} C_{n}^{2}} - \frac{2 n_{n}^{(0)^{2}} u_{n}^{(0)} q^{3} λ^{5}}{C_{1} C_{n}^{5} ν_{n}} - \frac{2 n_{n}^{(0)^{2}} q^{3} λ^{6}}{C_{1} C_{n}^{5} ν_{n}} \\ - \frac{n_{n}^{(0)^{2}} q^{2} λ^{4}}{C_{1} C_{n}^{4} ν_{n}} - \frac{n_{n}^{(0)} u_{n}^{(0)} q λ^{2}}{C_{n}^{2} ν_{n}} + \frac{n_{n}^{(0)} q λ^{3}}{C_{n}^{2} ν_{n}} + \frac{2 n_{p}^{(0)} u_{p}^{(0)} λ^{2}}{C_{p}^{2} ν_{p}} - \frac{n_{p}^{(0)} λ^{3}}{C_{p}^{2} ν_{p}} \\ + \frac{2 n_{n}^{(0)} n_{p}^{(0)} u_{n}^{(0)} q^{2} λ^{5}}{C_{1} C_{n}^{3} C_{p}^{2} ν_{p}} + \frac{2 n_{n}^{(0)} n_{p}^{(0)} q^{2} λ^{6}}{C_{1} C_{n}^{3} C_{p}^{2} ν_{p}} + \frac{n_{n}^{(0)} n_{p}^{(0)} q λ^{4}}{C_{1} C_{n}^{2} C_{p}^{2} ν_{p}} \\ + \frac{6 n_{n}^{(0)^{3}} q λ^{2} σ_{n}}{C_{1} C_{n}^{3}} - \frac{6 n_{n}^{(0)^{4}} u_{n}^{(0)} q^{2} λ^{3} σ_{n}}{C_{1} C_{n}^{5} ν_{n}} - \frac{12 n_{n}^{(0)^{4}} q^{2} λ^{4} σ_{n}}{C_{1} C_{n}^{5} ν_{n}} \\ - \frac{3 n_{n}^{(0)^{4}} q λ^{2} σ_{n}}{C_{1} C_{n}^{4} ν_{n}} - \frac{6 n_{n}^{(0)^{3}} u_{n}^{(0)} q λ^{2} σ_{n}}{C_{n}^{3} ν_{n}} - \frac{6 n_{n}^{(0)^{3}} q λ^{3} σ_{n}}{C_{n}^{3} ν_{n}} \\ + \frac{6 n_{n}^{(0)^{3}} λ σ_{n}}{C_{n}^{2} ν_{n}} + \frac{6 n_{n}^{(0)^{3}} n_{p}^{(0)} q λ^{4} σ_{n}}{C_{1} C_{n}^{3} C_{p}^{2} ν_{p}} - \frac{18 n_{n}^{(0)^{6}} q λ^{2} σ_{n}^{2}}{C_{1} C_{n}^{5} ν_{n}} - \frac{18 n_{n}^{(0)^{5}} λ σ_{n}^{2}}{C_{n}^{3} ν_{n}} - \frac{3 n_{p}^{(0)^{3}} λ σ_{p}}{C_{p}^{2} ν_{p}} \\ + \frac{6 n_{n}^{(0)} n_{p}^{(0)^{3}} u_{n}^{(0)} q^{2} λ^{3} σ_{p}}{C_{1} C_{n}^{3} C_{p}^{2} ν_{p}} + \frac{6 n_{n}^{(0)} n_{p}^{(0)^{3}} q^{2} λ^{4} σ_{p}}{C_{1} C_{n}^{3} C_{p}^{2} ν_{p}} \\ + \frac{3 n_{n}^{(0)} n_{p}^{(0)^{3}} q λ^{2} σ_{p}}{C_{1} C_{n}^{2} C_{p}^{2} ν_{p}} + \frac{18 n_{n}^{(0)^{3}} n_{p}^{(0)^{3}} q λ^{2} σ_{n} σ_{p}}{C_{1} C_{n}^{3} C_{p}^{2} ν_{p}}, \\ C_{1} = - \frac{2 {qn}_{n}^{(0)} λ}{C_{n}^{2}} - \frac{2 n_{p}^{(0)} λ}{C_{p}^{2}}, ν_{n} = 3 σ_{n} n_{n}^{(0)^{2}} - {qu}_{n}^{(0)^{2}}, ν_{p} = 3 σ_{p} n_{p}^{(0)^{2}} - u_{p}^{(0)^{2}} \end{matrix}

3 The stationary solutions

In order to obtain the solitary wave solutions, one can use the following transformation:

(29)

ϕ^{(1)} = Ψ \exp (- \frac{a_{3}}{a_{2}} ϕ^{(0)}) .

In order to recast Eq. (28) to the standard form of Korteweg–de Vries (KdV) equation with variable coefficients,

(30)

\frac{\partial}{\partial s} Ψ + B Ψ \frac{\partial}{\partial ξ} Ψ + A \frac{\partial^{3}}{\partial ξ^{3}} Ψ = 0,

where

A = \frac{1}{a_{2}}, B = \frac{a_{1}}{a_{2}} \exp (- \frac{a_{3}}{a_{2}} ϕ^{(0)}) .

However, the nonlinear coefficients functionally depend on the space of the plasma, for the sake of simplicity for mathematical development, the variations are assumed negligibly as compared to the scale length or it is assumed that all parameters are locally constant. This equation, as is well known, has the following solution given by Kodama and Taniuti (1978).

(31)

Ψ = Ψ_{m} {Sech}^{2} (\frac{X}{W}),

where the amplitude Ψ_m = 3U/B, the width W = (4A/U)^1/2, and X is the transformed coordinate with respect to a frame moving with velocity U (i.e.

X = ξ - Us

4 Results and discussion

We have presented a study of the weakly nonlinear IAWs in plasma with two distinct ion species (i.e., positive and negative ions) and isothermal electrons. By employing the two-fluid equations for the ions and isothermal electron distribution, we have derived the KdV equation. The latter is used to examine the width and the amplitude of IAWs.

The dependence of the soliton amplitude Ψ_m on the ion density $n_{p}^{(0)}$ is depicted in Fig. 1. It is found that the soliton amplitude Ψ_m can be positive (a₁/a₂ > 0) or negative (a₁/a₂ < 0), indicating thereby that both rarefactive and compressive solitons can exist in the present system. It is seen that, the rarefactive amplitude increases as $n_{p}^{(0)}$ increases for its lower range (i.e. $n_{p}^{(0)} < 3.16)$ , on the other hand the compressive amplitude decreases with $n_{p}^{(0)}$ (i.e. $n_{p}^{(0)} > 3.16)$ . From Fig. 2, it is obvious that the soliton phase velocity gradually decreases with the increase of $n_{p}^{(0)}$ . Fig. 3 shows that both the amplitude and width of the compressive (rarefactive) solitons increase (decrease) with the negative ion density $n_{n}^{(0)}$ . The effect of the ratio of the negative ion mass to the positive ion mass (q) on the compressive soliton amplitude is depicted in Fig. 4. It is clear that the amplitude of the compressive soliton increases rapidly with q. Fig. 5 reveals how the compressive soliton amplitude decreases with the increase of the ratio of the negative ions temperature to the electron temperature σ_n. It is obvious from Fig. 6 that the amplitude of compressive soliton decreases sharply by increasing σ_p for σ_p < 0.02, but for σ_p > 0.02 the amplitude decreases gradually.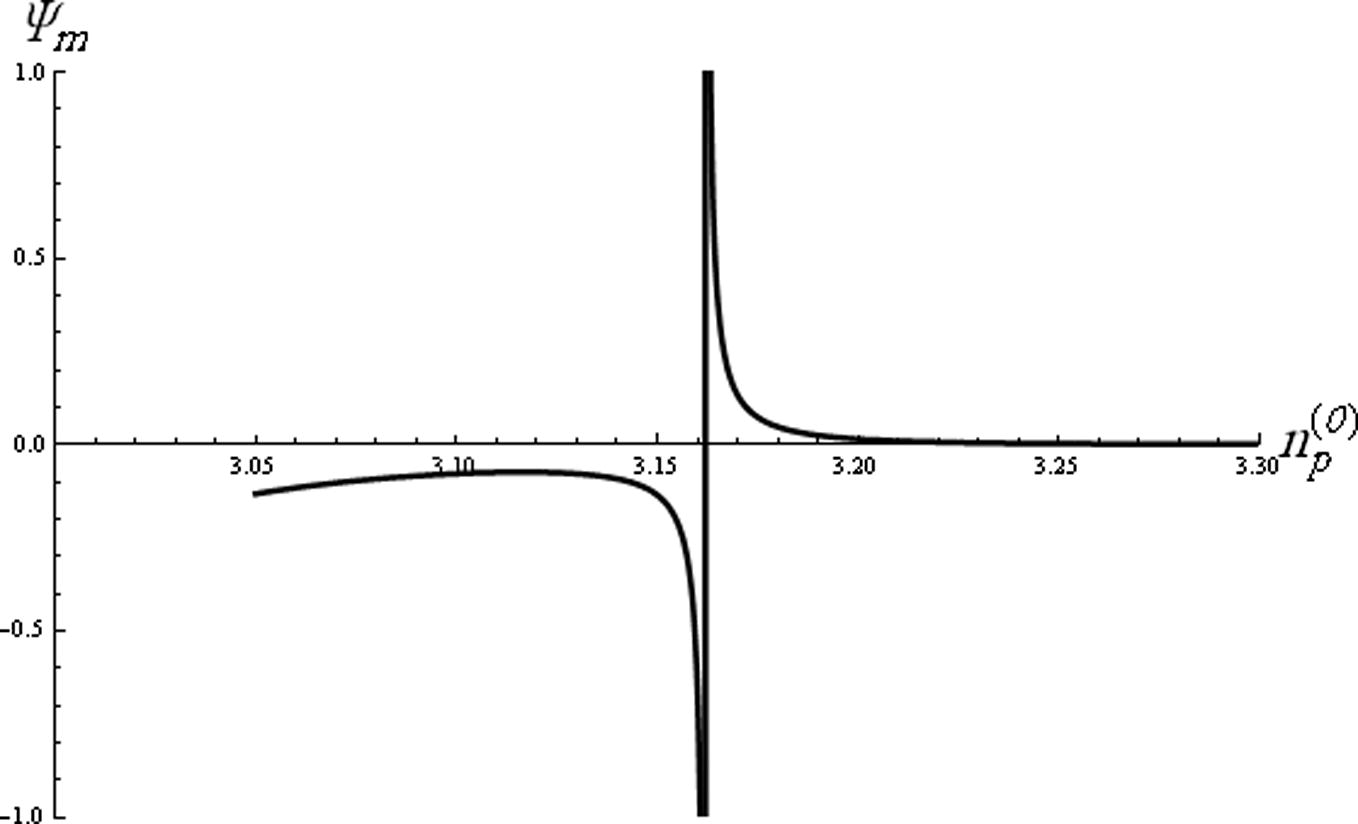

The variation of solitons amplitude (Ψm) against ion density ( n p ( 0 ) ) for n e ( 0 ) = 1.8 , q = 1.7 , σ p = 0.01 , and σn = 0.001.

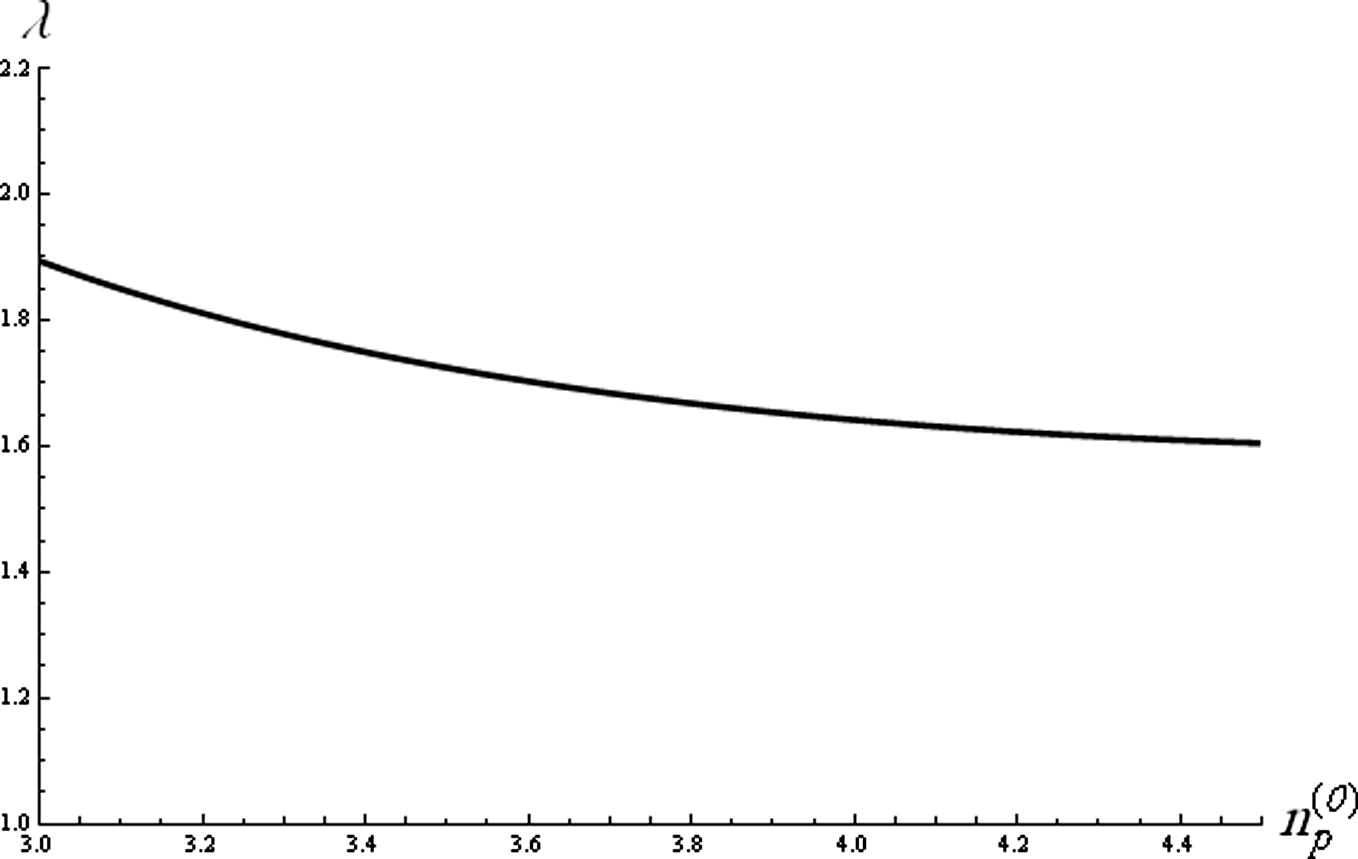
Graph of soliton velocity (λ) soliton against n p ( 0 ) for n e ( 0 ) = 1.8 q = 1.7, σp = 0.01 and σn = 0.001.

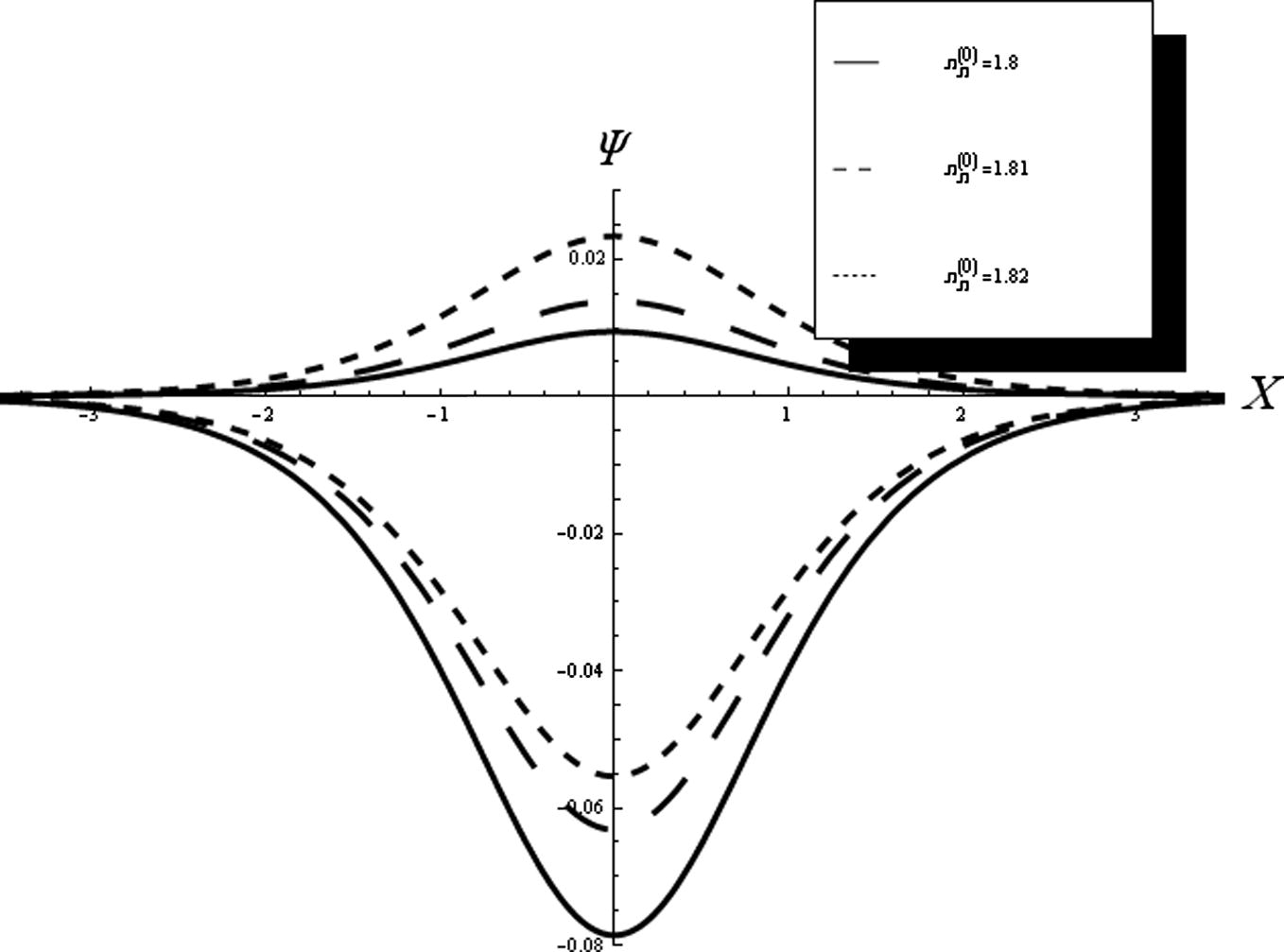
Graph of compressive (rarefactive) soliton at n p ( 0 ) = 3.21 ( 3.13 ) against x for q = 1.7, σp = 0.01 and σn = 0.001.

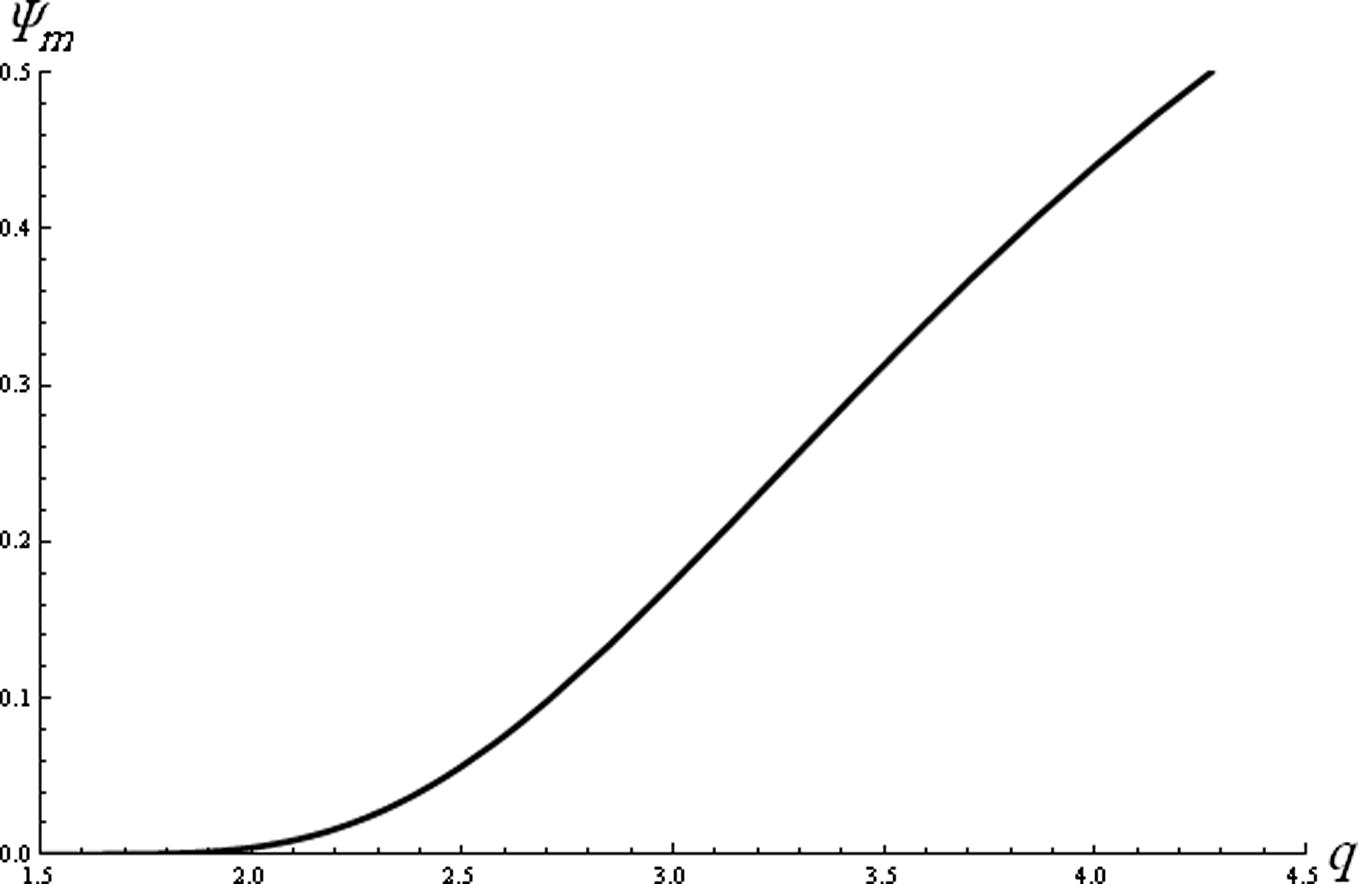
The compressive amplitude (Ψm) is plotted against q for ( n p ( 0 ) ) for n e ( 0 ) = 3.35 , n n ( 0 ) = 1.8 , σ p = 0.01 and σn = 0.001.

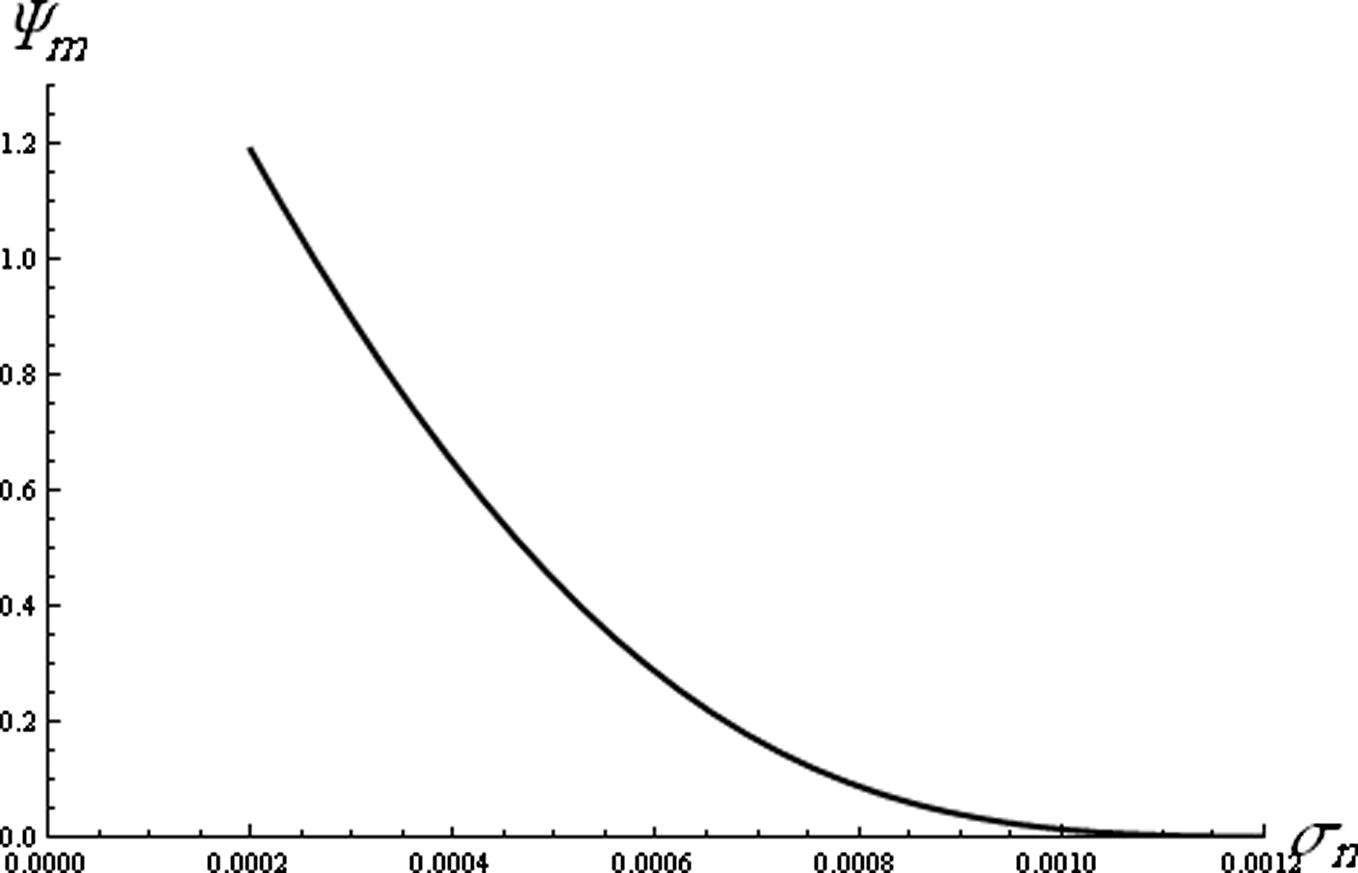
The variation of compressive amplitude (Ψm) against the ratio of the negative ions temperature to the free electron temperature (σn) for n p ( 0 ) = 3.2 , n n ( 0 ) = 1.8 , p = 1.7 and σp- = 0.01.

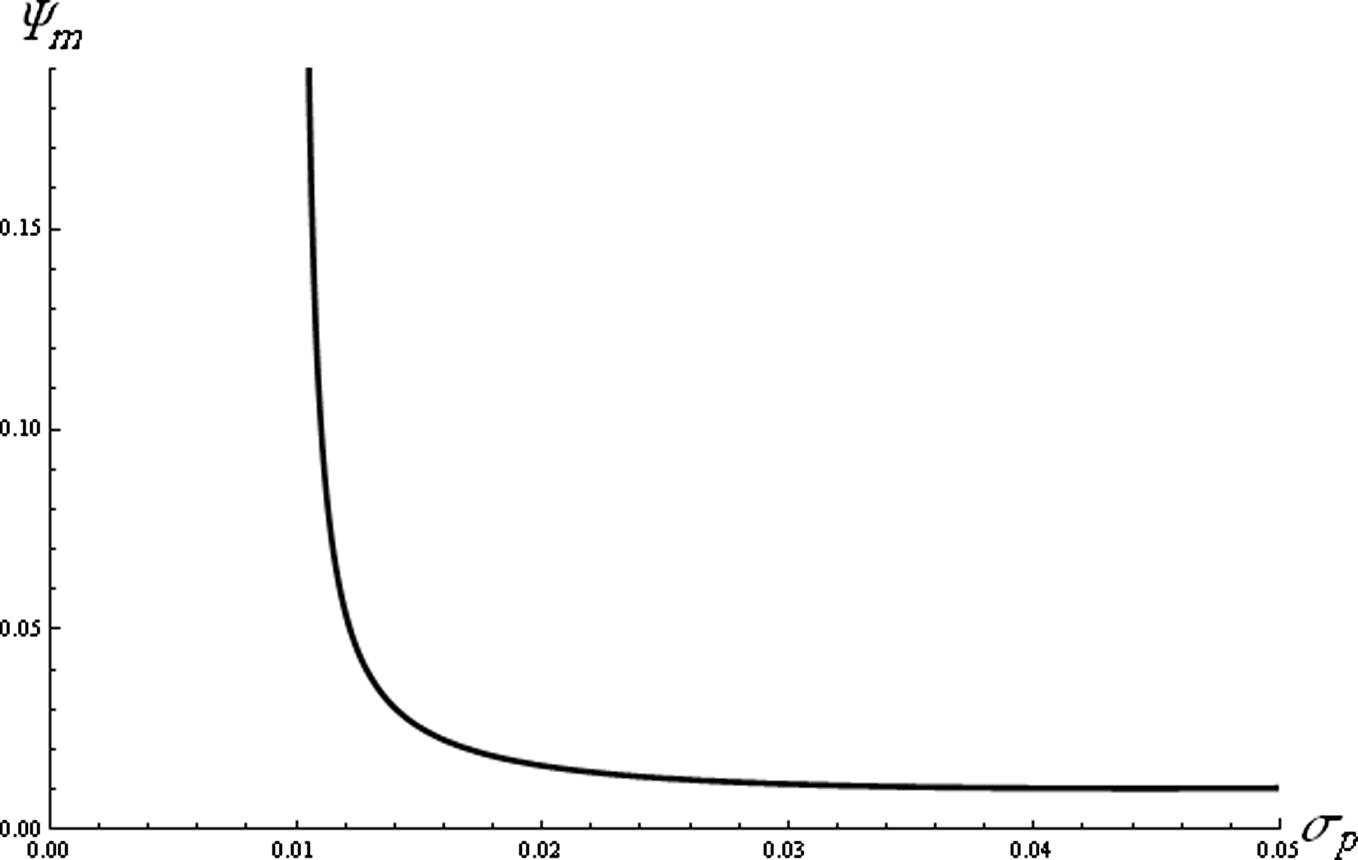
The compressive soliton amplitude (Ψm) is depicted against σp for n p ( 0 ) = 1.7 , n n ( 0 ) = 1.8 , p = 1.7 and σn = 0.001 .

The present study is applied to examine the nonlinear IAWs excitations for the $({Ar}^{+}, {SF}_{6}^{-})$ plasma, which has been used in the experimental investigation of strong double layers by Merlino and Loomis (1990). Finally, this investigation should be helpful in understanding the salient features of the nonlinear IAWs both in space and in laboratory experiments where two distinct groups of ions and isothermal electrons are present.

References

Asano N.B., . Wave propagations in non-uniform media. Prog. Theor. Phys. Suppl.. 1974;55:52-79.
[Google Scholar]
Bacal M., Hamilton G.W., . H⁻ and D⁻ production in plasmas. Phys. Rev. Lett.. 1979;42:1538.
[Google Scholar]
Chaizy P.H., Rème H., Sauvaud J.A., D’uston C., Lin R.P., Larson D.E., Mitchell D.L., Anderson K.A., Carlson C.W., Korth A., Mendis D.A., . Negative ions in the coma of comet Halley. Nature (London). 1991;349:393.
[Google Scholar]
Chakraborty S., Chowdhury A.R., Paul S.N., . Ion acoustic solitons in a streaming relativistic plasma with negative ions. Inter. J. Theor. Phys.. 1992;31:343.
[Google Scholar]
Chakraborty S., Roychowdhury A., Paul S.N., . Ion-acoustic wave in relativistic nonisothermal plasma with negative ions. Inter. J. Theor. Phys.. 1993;32:1465.
[Google Scholar]
Chakraborty S., Paul S.N., Chowdhury A.R., . On the formation of solitons in an isothermal relativistic plasma with positive and negative ions. Fizika A. 1994;3:97.
[Google Scholar]
Chattopadhyay S., Bhattacharya S.K., Paul S.N., . On the effects of drift motion and negative ions on ion-acoustic solitary waves and double-layers in plasmas. Indian J. Phys. B. 2002;76:59.
[Google Scholar]
Chattopadhyay S., Paul S.N., Ray D., . Influence of negative ions on ion-acoustic solitary waves in a two-electron-temperature plasma. Fizika A. 2009;18(3):89.
[Google Scholar]
Cooney J.L., Gavin M.T., Lonngren K.E., . Experiments on Korteweg–de Vries solitons in a positive ion–negative ion plasma. Phys. Fluids B. 1991;3:2758.
[Google Scholar]
Das G.C., Devi K., . Propagation of soliton and its radiation in inhomogeneous discharge plasma. Indian J. Pure Phys.. 2006;44:31.
[Google Scholar]
Das G.C., Nag A., . Transient behaviours of ion-acoustic waves in magnetized plasma with negative ions. Assam Univ. J. Sci. Technol.. 2010;5:169.
[Google Scholar]
Das G.C., Singh S.S., . Ion-acoustic solitons in an inhomogeneous multicomponent plasma with negative ions. IEEE-Plasma Sci.. 1992;20(1):13-18.
[Google Scholar]
Das G.C., Tagare S.G., . Propagation of ion-acoustic waves in a multi-component plasma. Plasma Phys.. 1975;17:1025.
[Google Scholar]
Djebli M., . Charge evolution in dusty plasma expansion with negative ions. Phys. Plasmas. 2003;10:4910.
[Google Scholar]
El-Labany S.K., El-Warraki S.A., Moslem W.M., . Cylindrical ion-acoustic waves in a warm multicomponent plasma. J. Plasma Phys.. 2000;63:343.
[Google Scholar]
El-Labany S.K., Moslem W.M., Shnishin Kh.A., El-Tantawy S.A., . Plasma with two negative ions and immobile dust particles: planar and non-planar ion-acoustic wave propagation. Eur. Phys. J. D. 2011;61:409.
[Google Scholar]
El-Labany S.K., Moslem W.M., Shnishin Kh.A., El-Tantawy S.A., Shukla P.K., . Fully nonlinear solitary waves in a dusty electronegative multispecies plasmas. Phys. Plasmas. 2011;18:042306.
[Google Scholar]
Gottscho R.A., Gaebe C.E., . Negative ion kinetics in rf glow discharges. IEEE Trans. Plasma Sci.. 1986;14:92.
[Google Scholar]
Ichiki R., Yoshimura S., Watanabe T., Nakamura Y., Kawai Y., . Experimental observation of dominant propagation of the ion-acoustic slow mode in a negative ion plasma and its application. Phys. Plasmas. 2002;9:4481.
[Google Scholar]
Jacquinot J., McVey B.D., Scharer J.E., . Mode conversion of the fast magnetosonic wave in a deuterium-hydrogen tokamak plasma. Phys. Rev. Lett.. 1977;39:88.
[Google Scholar]
Kalita B.C., Barman S.N., Goswami G., . Weakly relativistic solitons in a cold plasma with electron inertia. Phys. Plasmas. 1996;3:145.
[Google Scholar]
Kodama Y., Taniuti T.J., . Higher-order approximation in the reductive perturbation method. Phys. Soc. Jpn.. 1978;45:298.
[Google Scholar]
Ludwig G.O., Ferreira J.L., Nakamura Y., . Observation of ion-acoustic rarefaction solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett.. 1984;52:275.
[Google Scholar]
Malik H.K., Dahiya R.P., . Ion acoustic solitons in finite ion temperature inhomogeneous plasmas having negative ions. Phys. Plasmas. 1994;1:2872.
[Google Scholar]
Malik H.K., Stroth U., . Nonlinear solitary waves (solitons) in inhomogeneous magnetized warm plasma with negative ions and nonisothermal electrons. Plasma Sources Sci. Technol.. 2008;17:035005.
[Google Scholar]
Mamun A.A., Shukla P.K., . Charging of dust grains in a plasma with negative ions. Phys. Plasmas. 2003;10:1518.
[Google Scholar]
Massey H., . Negative Ions (third ed). Cambridge, England: Cambridge University Press; 1976. p. 663
Merlino R.L., Loomis J.J., . Double layers in a plasma with negative ions. Phys. Fluids B. 1990;2:2865.
[Google Scholar]
Moslem W.M., . Propagation of ion acoustic waves in a warm multicomponent plasma with an electron beam. J. Plasma Phys.. 1999;61:177.
[Google Scholar]
Moslem W.M., Sabry R., Abdelsalam U.M., Kourakis I., Shukla P.K., . Solitary and blow-up electrostatic excitations in rotating magnetized electron-positron-ion plasmas. New J. Phys.. 2009;11:033028.
[Google Scholar]
Nakamura Y., . Experiments on ion-acoustic solitons in plasmas invited review article. IEEE Trans. Plasma Sci.. 1982;10:180.
[Google Scholar]
Nakamura Y., Odagiri T., Tsukabayashi I., . Ion-acoustic waves in a multicomponent plasma with negative ions. Plasma Phys. Controlled Fusion. 1997;39:105.
[Google Scholar]
Portnyagin Yu.I., Klyuev O.F., Shidlovsky A.A., Evdokimov A.N., Buzdigar T.W., Matukhin P.G., Pasynkov S.G., Shamshev K.N., Sokolov V.V., Semkin N.D., . Simulation of cosmic man-made dust effects on space vehicle elements in rocket and laboratory experiments. Adv. Space Res.. 1991;11:89.
[Google Scholar]
Singh D.K., Malik H.K., . Solitons in inhomogeneous magnetized negative ion containing plasma with two temperature nonisothermal electrons. 2008;2:462.
Tagare S.G., . Effect of ion temperature on ion-acoustic solitons in a two-ion warm plasma with adiabatic positive and negative ions and isothermal electrons. J. Plasma Phys.. 1986;36:301.
[Google Scholar]
Tajiri M., Tuda M., . Large amplitude ion acoustic solitons in plasma with negative ions. J. Phys. Soc. Jpn.. 1985;54:19.
[Google Scholar]
Vladimirov S.V., Ostrikov K., Yu M.Y., Morfill G.E., . Ion-acoustic waves in a complex plasma with negative ions. Phys. Rev. E. 2003;67:036406.
[Google Scholar]
Watanabe S.S., . Ion acoustic soliton in plasma with negative ion. J. Phys. Soc. Jpn.. 1984;53:950.
[Google Scholar]
Weingarten A., Arad R., Maron Y., Fruchtman A., . Ion separation due to magnetic field penetration into a multispecies plasma. Phys. Rev. Lett.. 2001;87:115004.
[Google Scholar]

Introduction

Basic equations and derivation of the KdV equation

The stationary solutions

Results and discussion

Fulltext Views
6

PDF downloads
8

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Asano N.B., . Wave propagations in non-uniform media. Prog. Theor. Phys. Suppl.. 1974;55:52-79.
[Google Scholar]

[2] Bacal M., Hamilton G.W., . H⁻ and D⁻ production in plasmas. Phys. Rev. Lett.. 1979;42:1538.
[Google Scholar]

[3] Chaizy P.H., Rème H., Sauvaud J.A., D’uston C., Lin R.P., Larson D.E., Mitchell D.L., Anderson K.A., Carlson C.W., Korth A., Mendis D.A., . Negative ions in the coma of comet Halley. Nature (London). 1991;349:393.
[Google Scholar]

[4] Chakraborty S., Chowdhury A.R., Paul S.N., . Ion acoustic solitons in a streaming relativistic plasma with negative ions. Inter. J. Theor. Phys.. 1992;31:343.
[Google Scholar]

[5] Chakraborty S., Roychowdhury A., Paul S.N., . Ion-acoustic wave in relativistic nonisothermal plasma with negative ions. Inter. J. Theor. Phys.. 1993;32:1465.
[Google Scholar]

[6] Chakraborty S., Paul S.N., Chowdhury A.R., . On the formation of solitons in an isothermal relativistic plasma with positive and negative ions. Fizika A. 1994;3:97.
[Google Scholar]

[7] Chattopadhyay S., Bhattacharya S.K., Paul S.N., . On the effects of drift motion and negative ions on ion-acoustic solitary waves and double-layers in plasmas. Indian J. Phys. B. 2002;76:59.
[Google Scholar]

[8] Chattopadhyay S., Paul S.N., Ray D., . Influence of negative ions on ion-acoustic solitary waves in a two-electron-temperature plasma. Fizika A. 2009;18(3):89.
[Google Scholar]

[9] Cooney J.L., Gavin M.T., Lonngren K.E., . Experiments on Korteweg–de Vries solitons in a positive ion–negative ion plasma. Phys. Fluids B. 1991;3:2758.
[Google Scholar]

[10] Das G.C., Devi K., . Propagation of soliton and its radiation in inhomogeneous discharge plasma. Indian J. Pure Phys.. 2006;44:31.
[Google Scholar]

[11] Das G.C., Nag A., . Transient behaviours of ion-acoustic waves in magnetized plasma with negative ions. Assam Univ. J. Sci. Technol.. 2010;5:169.
[Google Scholar]

[12] Das G.C., Singh S.S., . Ion-acoustic solitons in an inhomogeneous multicomponent plasma with negative ions. IEEE-Plasma Sci.. 1992;20(1):13-18.
[Google Scholar]

[13] Das G.C., Tagare S.G., . Propagation of ion-acoustic waves in a multi-component plasma. Plasma Phys.. 1975;17:1025.
[Google Scholar]

[14] Djebli M., . Charge evolution in dusty plasma expansion with negative ions. Phys. Plasmas. 2003;10:4910.
[Google Scholar]

[15] El-Labany S.K., El-Warraki S.A., Moslem W.M., . Cylindrical ion-acoustic waves in a warm multicomponent plasma. J. Plasma Phys.. 2000;63:343.
[Google Scholar]

[16] El-Labany S.K., Moslem W.M., Shnishin Kh.A., El-Tantawy S.A., . Plasma with two negative ions and immobile dust particles: planar and non-planar ion-acoustic wave propagation. Eur. Phys. J. D. 2011;61:409.
[Google Scholar]

[17] El-Labany S.K., Moslem W.M., Shnishin Kh.A., El-Tantawy S.A., Shukla P.K., . Fully nonlinear solitary waves in a dusty electronegative multispecies plasmas. Phys. Plasmas. 2011;18:042306.
[Google Scholar]

[18] Gottscho R.A., Gaebe C.E., . Negative ion kinetics in rf glow discharges. IEEE Trans. Plasma Sci.. 1986;14:92.
[Google Scholar]

[19] Ichiki R., Yoshimura S., Watanabe T., Nakamura Y., Kawai Y., . Experimental observation of dominant propagation of the ion-acoustic slow mode in a negative ion plasma and its application. Phys. Plasmas. 2002;9:4481.
[Google Scholar]

[20] Jacquinot J., McVey B.D., Scharer J.E., . Mode conversion of the fast magnetosonic wave in a deuterium-hydrogen tokamak plasma. Phys. Rev. Lett.. 1977;39:88.
[Google Scholar]

[21] Kalita B.C., Barman S.N., Goswami G., . Weakly relativistic solitons in a cold plasma with electron inertia. Phys. Plasmas. 1996;3:145.
[Google Scholar]

[22] Kodama Y., Taniuti T.J., . Higher-order approximation in the reductive perturbation method. Phys. Soc. Jpn.. 1978;45:298.
[Google Scholar]

[23] Ludwig G.O., Ferreira J.L., Nakamura Y., . Observation of ion-acoustic rarefaction solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett.. 1984;52:275.
[Google Scholar]

[24] Malik H.K., Dahiya R.P., . Ion acoustic solitons in finite ion temperature inhomogeneous plasmas having negative ions. Phys. Plasmas. 1994;1:2872.
[Google Scholar]

[25] Malik H.K., Stroth U., . Nonlinear solitary waves (solitons) in inhomogeneous magnetized warm plasma with negative ions and nonisothermal electrons. Plasma Sources Sci. Technol.. 2008;17:035005.
[Google Scholar]

[26] Mamun A.A., Shukla P.K., . Charging of dust grains in a plasma with negative ions. Phys. Plasmas. 2003;10:1518.
[Google Scholar]

[27] Massey H., . Negative Ions (third ed). Cambridge, England: Cambridge University Press; 1976. p. 663

[28] Merlino R.L., Loomis J.J., . Double layers in a plasma with negative ions. Phys. Fluids B. 1990;2:2865.
[Google Scholar]

[29] Moslem W.M., . Propagation of ion acoustic waves in a warm multicomponent plasma with an electron beam. J. Plasma Phys.. 1999;61:177.
[Google Scholar]

[30] Moslem W.M., Sabry R., Abdelsalam U.M., Kourakis I., Shukla P.K., . Solitary and blow-up electrostatic excitations in rotating magnetized electron-positron-ion plasmas. New J. Phys.. 2009;11:033028.
[Google Scholar]

[31] Nakamura Y., . Experiments on ion-acoustic solitons in plasmas invited review article. IEEE Trans. Plasma Sci.. 1982;10:180.
[Google Scholar]

[32] Nakamura Y., Odagiri T., Tsukabayashi I., . Ion-acoustic waves in a multicomponent plasma with negative ions. Plasma Phys. Controlled Fusion. 1997;39:105.
[Google Scholar]

[33] Portnyagin Yu.I., Klyuev O.F., Shidlovsky A.A., Evdokimov A.N., Buzdigar T.W., Matukhin P.G., Pasynkov S.G., Shamshev K.N., Sokolov V.V., Semkin N.D., . Simulation of cosmic man-made dust effects on space vehicle elements in rocket and laboratory experiments. Adv. Space Res.. 1991;11:89.
[Google Scholar]

[34] Singh D.K., Malik H.K., . Solitons in inhomogeneous magnetized negative ion containing plasma with two temperature nonisothermal electrons. 2008;2:462.

[35] Tagare S.G., . Effect of ion temperature on ion-acoustic solitons in a two-ion warm plasma with adiabatic positive and negative ions and isothermal electrons. J. Plasma Phys.. 1986;36:301.
[Google Scholar]

[36] Tajiri M., Tuda M., . Large amplitude ion acoustic solitons in plasma with negative ions. J. Phys. Soc. Jpn.. 1985;54:19.
[Google Scholar]

[37] Vladimirov S.V., Ostrikov K., Yu M.Y., Morfill G.E., . Ion-acoustic waves in a complex plasma with negative ions. Phys. Rev. E. 2003;67:036406.
[Google Scholar]

[38] Watanabe S.S., . Ion acoustic soliton in plasma with negative ion. J. Phys. Soc. Jpn.. 1984;53:950.
[Google Scholar]

[39] Weingarten A., Arad R., Maron Y., Fruchtman A., . Ion separation due to magnetic field penetration into a multispecies plasma. Phys. Rev. Lett.. 2001;87:115004.
[Google Scholar]