Intelligent neuro-computing to analyze the awareness programs of fractional epidemic system outbreaks
⁎Corresponding author. n.sooppy@psau.edu.sa (Kottakkaran Sooppy Nisar), ksnisar1@gmail.com (Kottakkaran Sooppy Nisar),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
A new model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI) is described in this research. The fractional Caputo operator (FCO) is used to expand this system to the typical awareness program model (ICIEI-FCO). Analytically and quantitatively, the properties of the new system are investigated. This article presents an artificial neural network-based fractional model (ANN-FM) for estimating the efficacy of epidemic outbreak awareness initiatives. The reliability, resolution, durability, and robustness of the proposed model are examined using the suggested ANN-BLM approach for five distinct situations. The population of the model is created by utilizing the power of the explicit Runge-Kutta numerical approach, and it is represented by a system of nonlinear ordinary differential equations. The Grunwald–Letnikov (GL) technique is used to numerically evaluate the modeled differential system of the physical issue for multiple scenarios to anticipate numerical data, and these results are utilized as a reference dataset of the networks. The data needed to answer the fractional model's questions on how awareness campaigns affect epidemic outbreaks is broken down as follows: training takes up 80% of the time, testing 10%, and authorization 10%. There are two aspects to the strategy: First, the fundamental ANN-BLM operator performances are displayed. In the meantime, the ANN-BLM execution approach is used to address the fractional-order problem. The GL-mathematical system was used to compare the numerical findings. The TSs, regression, correlation, EHs, and MSE are used to demonstrate the dependability and competency of ANN-BLM as well as their numerical performances in the presented numerical findings, which were developed using ANN-BLM to lower the MSE. The Levenberg-Marquart training (LMT) algorithm is used to optimize network results in terms of mean-square errors, training states graphs, errors of the histogram, recession analysis, auto-correlation and time series responses, which demonstrates the system's accurate and proficient trend acknowledgment. The mean-square error fitness analysis in the ranges of 10-6 to 10-11 validates the authenticity and effectiveness of the designed solver. The suggested AI-based study is expected to pave the way for new, creative approaches to fractional order modeling and analysis of naturally unpredictable dynamic systems.
Keywords
Fractional Caputo operator
Grunwald–Letnikov
Levenberg–Marquardt backpropagation technique
Caputo fractional derivative
Intelligent networks
1 Introduction
(Raja et al., 2021) It is common knowledge that precise models have shown to be useful in understanding the crescendos of infectious disease transmission in populations (Borrelli et al., 2004). Traditional models rely on interactions between susceptible and infected individuals. Other variables, such as the media and population immigration, have an impact on the spread of infectious illnesses. Media awareness initiatives such as posters, television messages, and social media sources are utilized daily to alert the public about current fitness concerns to lessen the risk of infection. Nonlinear mathematical modeling of the effect of awareness programs on the spread of epidemics was given by Misra et al. (Misra et al., 2011) and is called the Influence of Consciousness Initiatives on Epidemic Incidences (ICIEI), based on the assumption that the growth rate of awareness programs is directly related to the number of people exposed to an outbreak. The model research revealed that while awareness efforts can help to restrict the spread of an infectious illness, the disease stays common owing to immigration. Assuming that diseases spread only through direct contact between susceptible and infective people, Lixia Zuo et al. established a nonlinear model including delay time and the effects of media-driven awareness campaigns on infection transmission. (Zuo and Liu, 2014).
To comprehend how infectious diseases affect a population, epidemiological research is crucial. In mathematical modeling, we validate models, calculate their numerical simulations by constructing models, estimate parameters, evaluate sensitivity through various parameters, and compute their sensitivity. Through this kind of study, it is possible to comprehend the disease's control factors and the ratio of spread. These kinds of disease models are sometimes referred to as infectious diseases or diseases that spread from one person to another. Measles, rubella, chicken pox, mumps, HIV/AIDS, gonorrhea, and syphilis are all examples of infectious diseases (Farman et al., 2021; Khan et al., 2021; Azam et al., 2021; Akgül et al., 2021; Hussain et al., 2021).
We are interested in fractional calculus in this study because it is a potent new apparatus that has recently been used to simulate biological systems with non-linear behavior. Integer order differential equations are generalized to produce fractional order differential equations. Where the consequences of prior values (memory) are relevant, they are more suited and precise than integer order. The term “memory” assures the preservation of the past and its influence (Nagy and Sweilam, 2014; Sweilam et al., 2012; Sweilam and Al-Mekhlafi, 2016).
This research examines numerical fractional model solutions. We use the Levenberg-Marquardt algorithm to optimize a neural network (Zúñiga-Aguilar et al., 2021; ur Rehman et al., 2023; Khan et al., 2021). Furthermore, the results of various mathematical models involving epidemic illnesses are presented analytically. As a result, obtaining numerical designs for such situations is critical. To solve the suggested model, computational approaches based on the artificial neural network (ANN) with innovative backpropagation Levenberg-Marquardt (BLM) features, i.e., ANN-BLM, are used. ANNs are machine learning algorithms used in pattern recognition, image and signal processing, classification, disease diagnosis, and human-robot cooperation (See (Solís-Pérez et al., 2022; Viera-Martin et al., 2022). For the suggested model, the ANN-BLM techniques were used to solve it. For preparation, challenge, and authentication, the data proportion is modified for three examples of epidemic breakouts fractional model are 80 percent, 10%, and 10%, respectively. For solving the coronavirus spreading model, numerical measurements are taken using the ANN-BLM, and comparisons are made using the reference dataset-based GL scheme (Umar et al., 2021; Bhattacharyya et al., 2022).
The goal of this research is to propose a computational framework for coronavirus spreading model analysis based on an artificial neural network trained using backpropagation Levenberg-Marquardt (ANN-BLM). While there is a wealth of material available on the internet that may be utilizing advanced computer paradigms like NN, deep learning (Khalid et al., 2016), and transfer learning, there is still a need for more research. However, for a better understanding of the contribution, the potentials of the suggested ANN-BLM to solve the epidemic outbreak fractional model are provided as follows:
-
AI skills based on a computational approach using network models learned with the Levenberg-Marquardt algorithm are given and applied to solve a proposed model with 5 classes of ordinary distinction equations. (ODEs).
-
Based on absolute error s (AEs) values, the outcomes obtained by considering computing ANN-BLM with numerical solutions are found to be in excellent agreement, approving the value, worth, and importance of the ANN-BLM to solve the epidemic fractional model.
-
The dependability and consistency of the ANN-BLM scheme are further supported by the performance or convergence curves on mean square errors (MSEs), accuracy (Scherer et al., 2011), progression metric computations of correlation index, and error histograms (EHs) obtained from exhaustive simulations.
The following are the key points of this paper: In Sec. 2, we review several fractional calculus definitions. Section 3 contains the developed approach based on ANN-BLM, Section 4 contains Mathematical formulation, Section 5 is constructed for analysis of the results, and Section 6 contains concluding observations (Sabir et al., 2020).
2 Fractional calculus
The R-L (Riemann–Liouville) (Xiong et al., 2021) and Caputo sense definitions of derivatives of fractional and integrals are the most commonly used, so here's a little primer on them:
For a function Cµ,µ>-1, the R-L fractional integral operator of order α > 0 is defined as:
The following are some of the features of the operator
A existent valued function x(u), u > 0 is said to be in space Cµ,µ
In the Caputo notion, the fractional derivative (Iqbal et al., 2023) of x(t) is described as.
Caputo fractional derivative analyses just an ordinary derivative before obtaining the requisite fractional derivative through fractional integral. This R-L fractional integral operator is a linear operation because it closely approaches integer order integration (Zúñiga-Aguilar et al., 2021; Shoaib et al., 2022; Coronel-Escamilla et al., 2022; Ilyas et al., 2021; Sabir et al., 2022; Sabir et al., 2022).
2.1 Grünwald–Letnikov (GL)
For our purposes, the Caputo operator D in fractional differential equations is important. The Caputo definition is equal to the R-L definition, as well as the G-L definition in the case of a consistent starting value. However, if the beginning value is inhomogeneous, the correction term is required. Using the Caputo operator, consider the fractional differential equation.
and suppose that in the range [0, T], there is only one solution y = y(
Where,
When
3 Suggested methodology
This section discusses how to solve the model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI) using the recommended ANN-BLM structure. The strategy is separated into two parts. The basic ANN-BLM operator performances are shown first. Meanwhile, to tackle the fractional-order problem, the ANN-BLM execution strategy is applied.
The dataset being used is randomly divided into three groups: 10% validation, 10% testing, and 80% training. During training, the dataset must meet any stopping requirements in order to get the data output that was planned. To get the right data output during training, the data set needs to meet any stopping constraints. The most logical way to solve the problem is to reduce the mean square error as much as possible. This means that as the error gets closer to zero, a more accurate answer appears. Fig. 1 depicts the fundamental structure of ANN-BLM.(See Fig. 2).
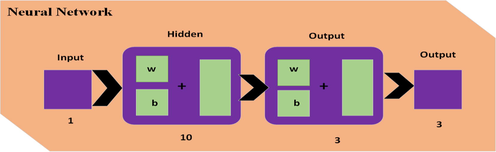
- ICIEI-FCO model schematic neural network layout.

- ANN-BLM flow mechanism to resolve model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI).
4 Mathematical modeling
A new model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI) is described in this section. The whole population is separated into three programs: vulnerable X(t), aware population Y (t), and infested M(t).
The model's new parameters are listed in Table 1. It's worth noting that all of these metrics are based on the fractional order α.
| Parameters | Definition | Value |
|---|---|---|
| t | Time | t ≥ 0 |
|
|
The percentage of persons who have recovered will rise, and they will join the conscious vulnerable class. | 0:85α |
|
|
The remainder of the population will become vulnerable., where pα + qα = 1: | 0:15α |
|
|
The proportion of conscious susceptibles who come into touch with infective people. The remainder of the population will become vulnerable. | 0:2α |
|
|
The rate at which unaware susceptible persons come into contact with the infected population. | Assumed |
|
|
The rate at which the ignorant vulnerable class becomes conscious. | 0:08α |
|
|
The pace at which conscious susceptibles become unaware. | 0:02α |
|
|
The recovery rate. | 0:43α |
|
|
The Death rate. | 0:002α |
|
|
proportional to the infection population rate. | 0:002α |
|
|
The pace at which conscious susceptibles become unaware. | 0:02α |
5 Analysis of results obtained by employing a methodology
Various kinds of mathematical with their graphical outputs are generated and shown in Figs. 3, 4, and 5 and Tables 1 and 2 to examine the influence of all relevant restrictions after resolving the resulting set of ODEs.. The non-integer order derivative is used to investigate the dynamic behaviour of the fractional order (FO) model. Because most FO differential systems lack accurate analytical solutions, a arithmetic solver based on the G-L approach, is used to estimate the model's solution.
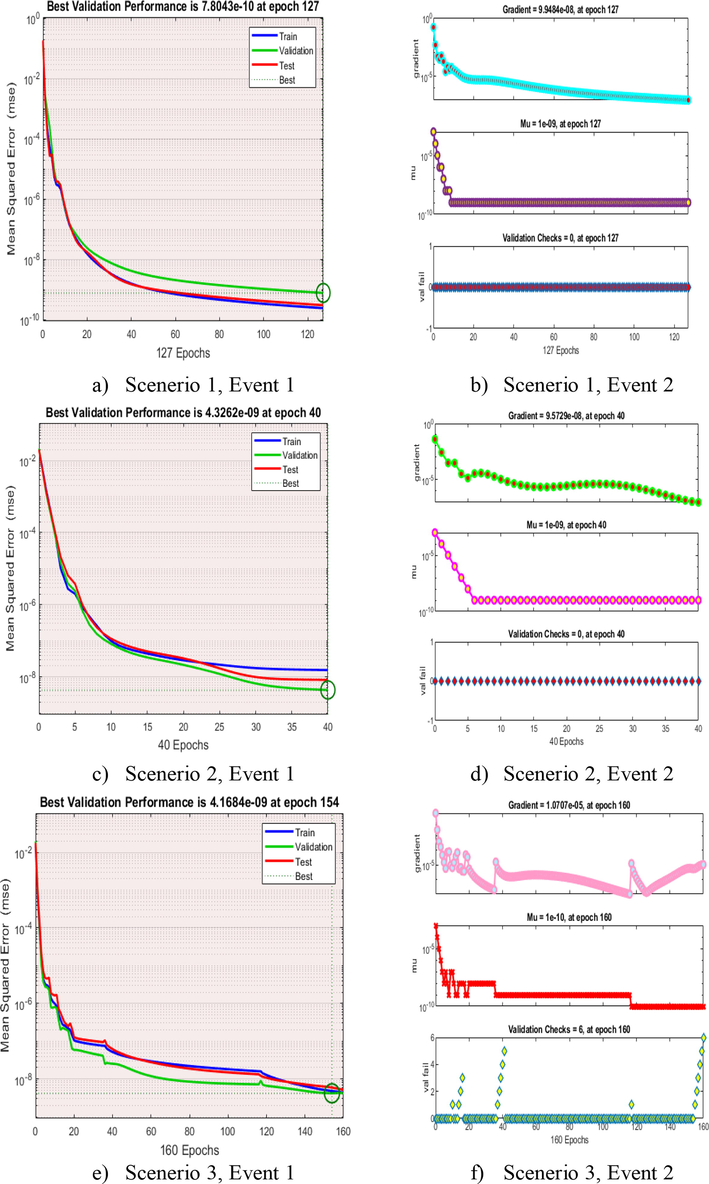
- Performance and TS of AIEO-FCO model.
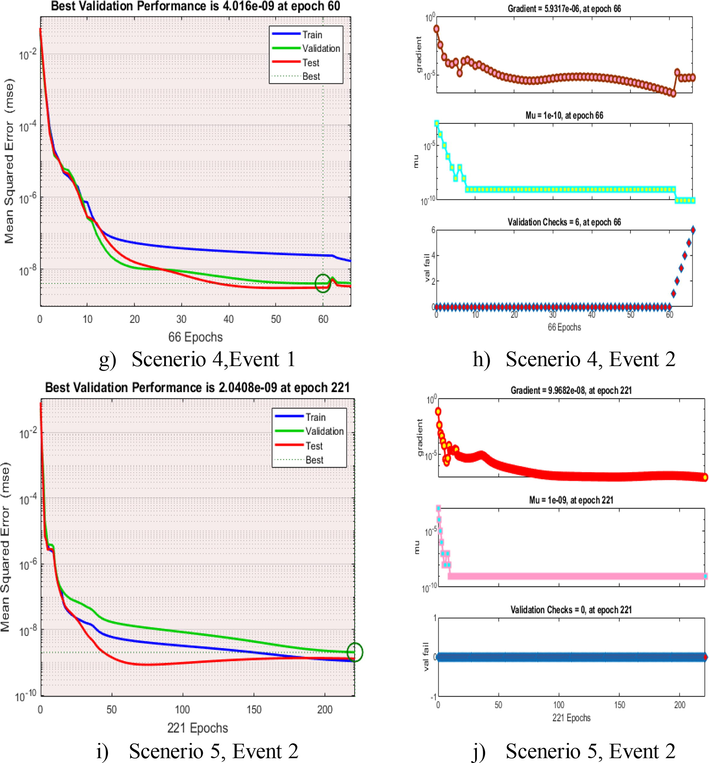
- Performance and TS of AIEO-FCO model.
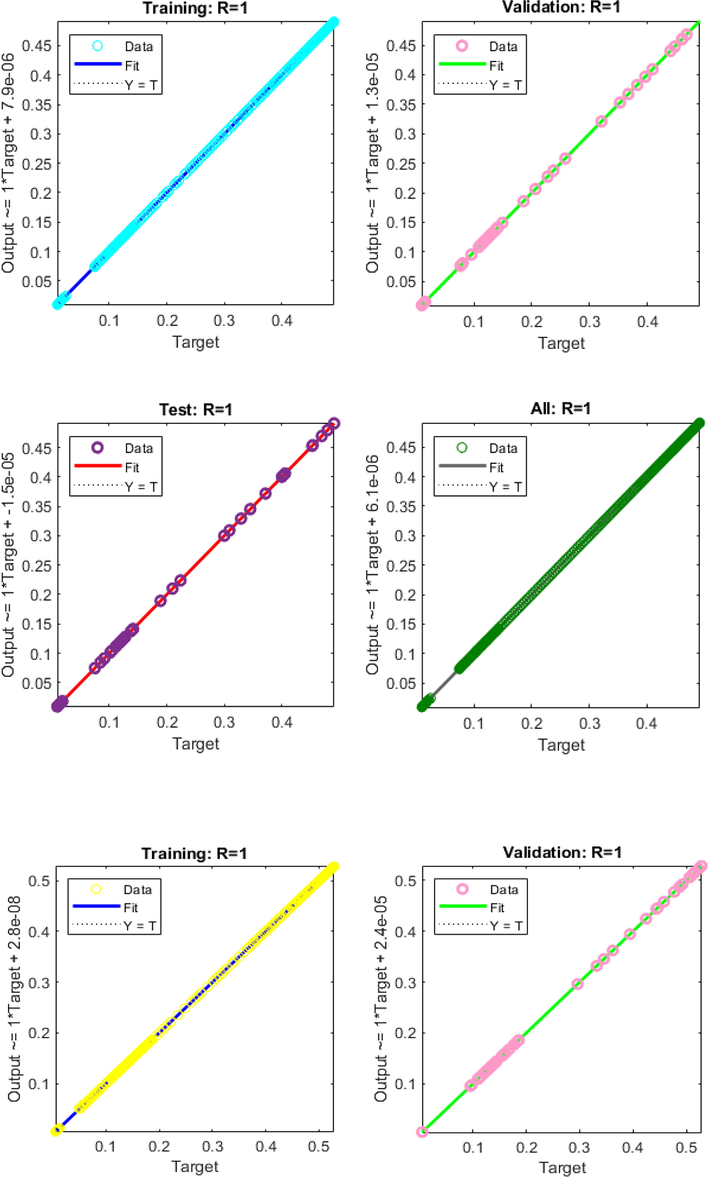
- Regression plots of AIEO-FCO model.
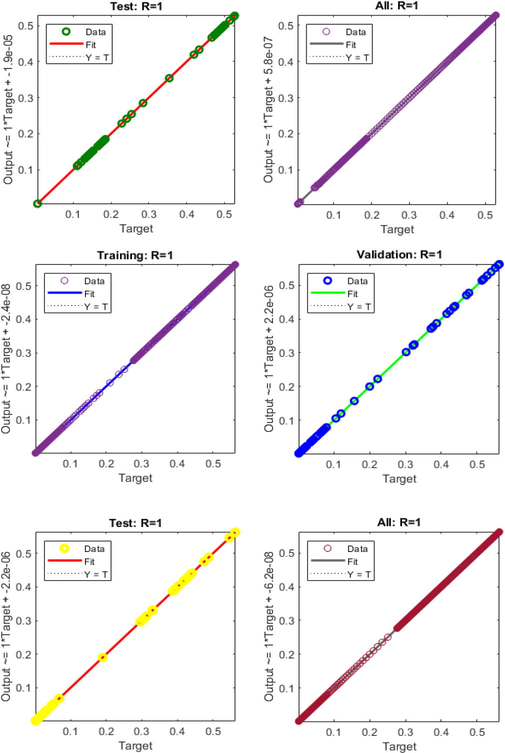
- Regression plots of AIEO-FCO model.
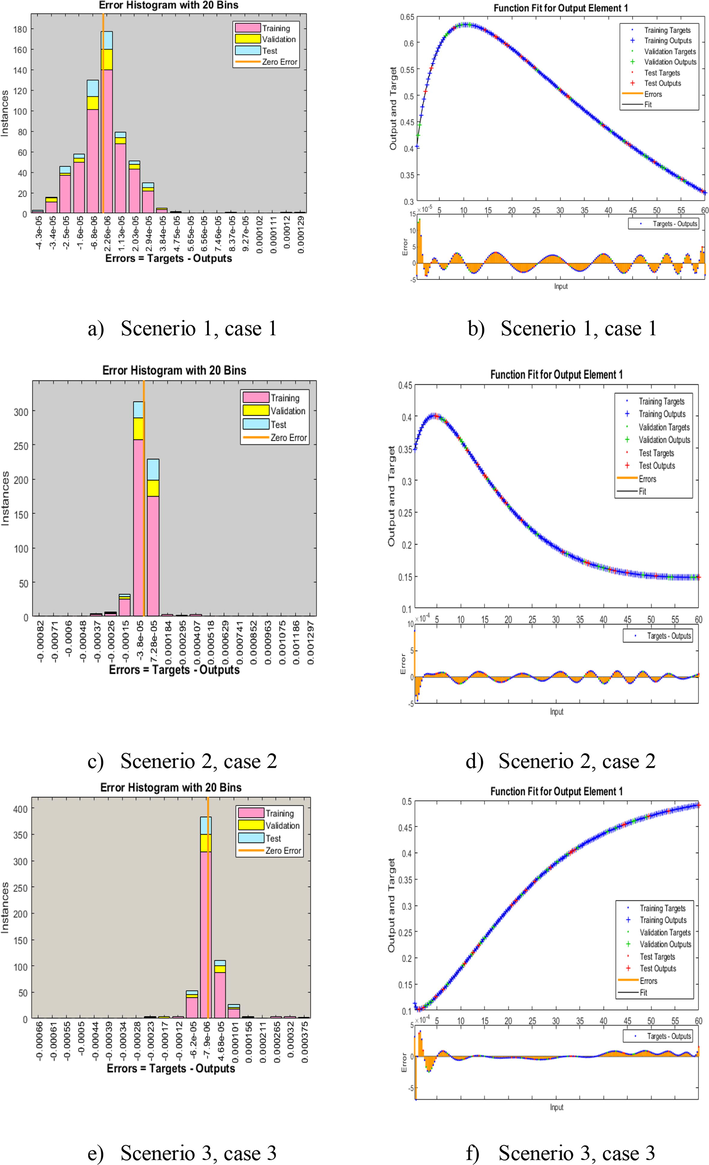
- EHs and fitness plots of AIEO-FCO model.
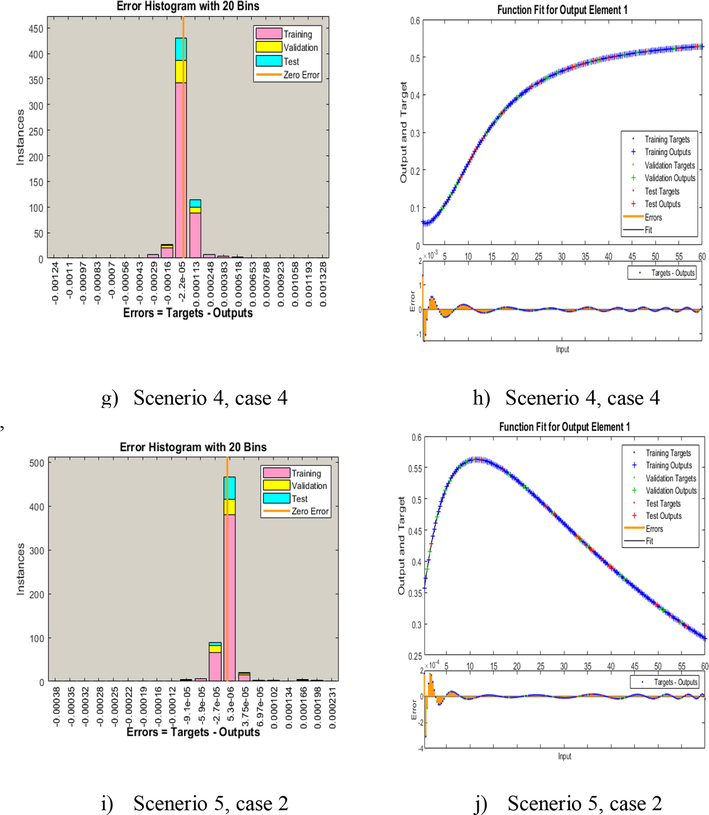
- EHs and fitness plots of AIEO-FCO model.
| Scenarios | Cases | MSE | Performance | Gradient | Mu | Epochs | Time (s) | ||
|---|---|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | |||||||
| 1 | 1 | 2.44E-10 | 7.80E-10 | 3.06E-10 | 2.44E-10 | 9.95E-08 | 1.00E-09 | 127 | < 1s |
| 2 | 2.47E-8 | 1.22E-9 | 4.00E-9 | 4.01E-09 | 9.55E-08 | 1.00E-09 | 61 | < 1s | |
| 3 | 1.11E-9 | 3.23E-8 | 2.87E-10 | 1.11E-09 | 9.99E-08 | 1.00E-10 | 88 | < 1s | |
| 4 | 5.58E-10 | 3.81E-7 | 1.87E-10 | 5.59E-10 | 8.86E-08 | 1.00E-11 | 21 | < 1s | |
| 2 | 1 | 5.57E-9 | 6.42E-9 | 8.82E-9 | 5.57E-09 | 9.91E-08 | 1.00E-08 | 130 | < 1s |
| 2 | 1.54E-08 | 4.32E-9 | 8.23E-9 | 1.54E-08 | 9.57E-08 | 1.00E-09 | 40 | < 1s | |
| 3 | 1.82E-9 | 8.21E-9 | 1.69E-7 | 1.82E-09 | 9.85E-08 | 1.00E-09 | 119 | < 1s | |
| 4 | 2.39E-9 | 1.13E-9 | 3.85E-8 | 2.40E-09 | 9.96E-08 | 1.00E-11 | 16 | < 1s | |
| 3 | 1 | 1.13E-9 | 9.92E-10 | 1.82E-9 | 1.14E-09 | 9.92E-08 | 1.00E-09 | 73 | < 1s |
| 2 | 4.45E-8 | 3.22E-8 | 2.78E-8 | 4.22E-08 | 8.16E-07 | 1.00E-08 | 31 | < 1s | |
| 3 | 4.78E-9 | 4.16E-9 | 5.90E-9 | 4.28E-09 | 1.07E-05 | 1.00E-10 | 160 | < 1s | |
| 4 | 2.72E-9 | 2.47E-9 | 6.66E-7 | 2.73E-09 | 9.67E-08 | 1.00E-09 | 63 | < 1s | |
| 4 | 1 | 5.89E-10 | 5.56E-9 | 5.53E-10 | 5.89E-10 | 9.98E-08 | 1.00E-09 | 154 | 1 s |
| 2 | 5.13E-9 | 3.37E-8 | 3.19E-9 | 4.72E-09 | 2.30E-07 | 1.00E-09 | 65 | < 1s | |
| 3 | 2/34E-8 | 1.63E-8 | 6.08E-8 | 2.22E-08 | 2.41E-06 | 1.00E-09 | 210 | 1 s | |
| 4 | 2.42E-8 | 4.01E-9 | 3.06E-9 | 1.69E-08 | 5.93E-06 | 1.00E-10 | 66 | < 1s | |
| 5 | 1 | 1.44E-11 | 3.81E-9 | 1.87E-11 | 1.45E-11 | 9.83E-08 | 1.00E-10 | 89 | < 1s |
| 2 | 1.09E-9 | 2.04E-9 | 1.31E-9 | 1.10E-09 | 9.97E-08 | 1.00E-09 | 221 | 9 s | |
| 3 | 7.70E-10 | 7.33E-10 | 5.42E-7 | 7.71E-10 | 9.51E-08 | 1.00E-10 | 88 | < 1s | |
| 4 | 3.46E-10 | 6.01E-8 | 1.87E-10 | 3.47E-10 | 8.96E-08 | 1.00E-11 | 25 | < 1s | |
Fig. 3 shows fractional model gradient measurements for awareness initaitive and epidemic outbreaks (AIEO) using ANN-BLM. The gradient performances for Scenarios 1, 2, 3,4, and 5 were determined to be 7.8043E-10 at 127 epochs,4.3262E-09 at 40 epochs,4.168E-09 at epochs 154,4.016E-09 at epochs and 2.0408E-09 at epochs respectively. The convergence of recommended ANN-BLM to solve the model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI) using ANN-BLM is shown in these graphical depictions.
The correlation has been shown in Fig. 4 to corroborate the regression performance. The recommended ANN-BLM is effective for modelling on training, testing, and validation data in order to resolve the AIEO-FCO since the correlation value R is nearly equal to the ideal value of unity. The training, testing, and authentication expressions show that the ANN-BLM approach used to solve the model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI) is valid (Sabir et al., 2021).
The values of the appropriate curves utilized to address each scenario in the proposed model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI) are shown in Fig. 5(b-j), to solve the functional order system (Shoaib et al., 2021);.
The performance of the reference and the results obtained are compared in these visuals. The substantiation, testing, and training for all scenarios of the model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI) are shown by error graphs. Fig. 5(a–i) shows several EHs, The top overall bins' accuracy ranges, or the bins with the most entries and the near to zero error lines, show how well ANN-BLM solve the AIEO-FCO model, as well as accompanying regression measures, based on a model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI). The EHs for instances 1, 2,3,4 and 5 are estimated to be2.26E-05, −3.8E-05,-7.8E-06,-2.2E-05 and 5.3E-05, respectively. More fractional derivatives demonstrate real and authentic implementations (Shoaib Anwar and Rasheed, 2017).
The charting for their outcome comparisons as well as AE values is shown in Figs. 6 and 7. It is clear that the AE for the AIEO-FCO model's parameter fluctuation is situated in
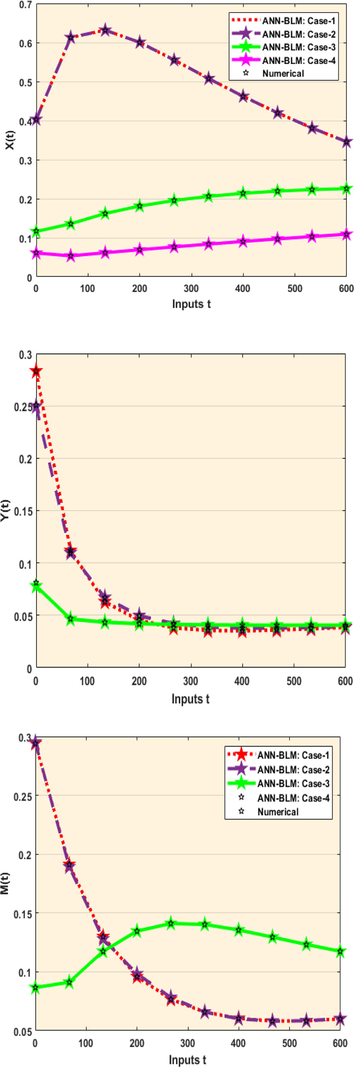
- Result analysis of AIEO-FCO model for the variation of a1, a2,b1,b2,d1,d2,f1,f2,s.
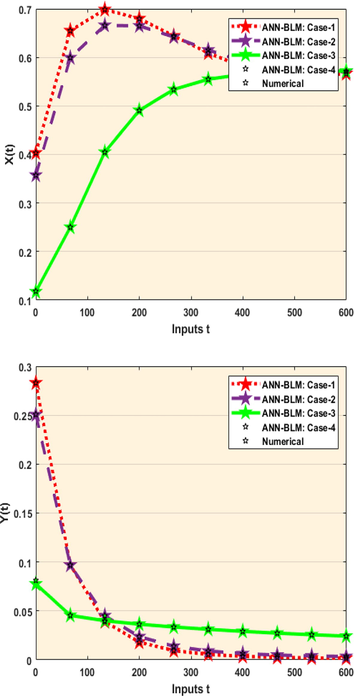
- Result analysis of AIEO-FCO model for the variation of a1, a2,b1,b2,d1,d2,f1,f2,s.
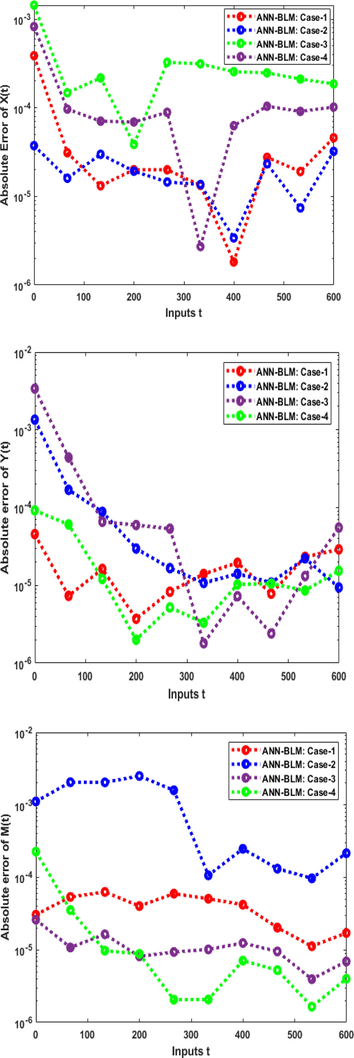
- AEs plots founded upon an AIEO-FCO model for the variation of a1, a2,b1,b2,d1,d2,f1,f2,s.
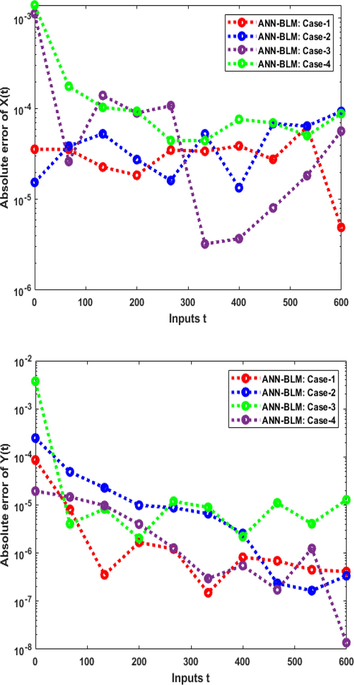
- AEs plots founded upon an AIEO-FCO model for the variation of a1, a2,b1,b2,d1,d2,f1,f2,s.
6 Conclusion
A new fractional model for the influence of consciousness initiatives on epidemic incidences (ICIEI) is described in this article. This study shows that the fraction model outperforms the integral order model in explaining memory-enhanced biotic phenomena, and that it can easily incorporate the memory effects observed in many real-world events. Four instances with varied fractional-order values have been provided to solve the fractional model for the influence of consciousness initiatives on epidemic incidences. The following is a breakdown of the data required to provide numerical answers for the proposed model for the impact of AIEO: 80% of the time is spent on training, 10% on testing, and 10% on the authorization. The numerical results were compared to the GL- mathematical system. To reduce the MSE, the provided numerical findings were created using ANN-BLM, to illustrate the dependability and competency of ANN-BLM, as well as their numerical performances, the TSs, regression, correlation, EHs, and MSE are employed. The proposed method ANN-BLM appears to be capable of solving differential equations with fractional and integer derivatives, such as the model of fractional for the influence of consciousness initiatives on epidemic incidences (ICIEI). The following are the novelty, significance and main conclusions reached by the AIEO-FCO model as a result of the numerical simulation and analysis:
-
The model AIEO-FCO is successfully used to identify an approximation of the solution. The dynamics of the AIEO-FCO are greatly affected by changes in the parameters.
-
Studies comparing suggested ANN-BLM findings to referenced numerical results generated by the GL-mathematical system showed the designed technique's accuracy and convergence as well as the size of AE lies
-
The developed ANN-BLM is efficient, reliable, and resilient as shown by histogram error infographics, regression indices, and MSE acquisition curves for lengthy computations.
7 Future work
Future study may make use of the development of the fractional computing paradigms for the influence of consciousness initiatives on epidemic incidences (ICIEI) and its deep variants to handle numerical models for computational fluid dynamics (Anwar et al., 2022), bio-informatics [41], and computer virus model [42]. Also, the design process will enable future engineering and technological fields to benefit from nonlinear differential systems.
Acknowledgement
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IF2/PSAU/2022/01/21873)
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Optimal existence of fractional order computer virus epidemic model and numerical simulations. Math. Methods Appl. Sci.. 2021;44(13):10673-10685.
- [Google Scholar]
- Intelligent predictive stochastic computing for nonlinear differential delay computer virus model. Waves Random Complex Media 2022:1-29.
- [Google Scholar]
- Structure preserving numerical scheme for spatio-temporal epidemic model of plant disease dynamics. Results Phys.. 2021;30:104821
- [Google Scholar]
- Stochastic forecasting of COVID-19 daily new cases across countries with a novel hybrid time series model. Nonlinear Dyn. 2022:1-16.
- [Google Scholar]
- Borrelli, R.L., Coleman, C.S. and Switkes, J., 2004. Differential Equations: A Modeling Perspective, Mathematica Technology Resource Manual. Wiley
- Intelligent computing with Levenberg–Marquardt artificial neural networks for a nonlinear system of COVID-19 epidemic model for future generation disease control. Eur. Phys. J. Plus. 2020;135(11):1-35.
- [Google Scholar]
- Dynamics and synchronization of a fractional conformable neural network with power-law. Eur. Phys. J. Special Topics. 2022;231(10):1771-1788.
- [Google Scholar]
- System analysis of HIV infection model with 4 under non-singular kernel derivative. Appl. Math. Nonlinear Sci.. 2020;5(1):139-146.
- [Google Scholar]
- Modeling of fractional-order COVID-19 epidemic model with quarantine and social distancing. Math. Methods Appl. Sci.. 2021;44(11):9334-9350.
- [Google Scholar]
- Modeling the dynamics of novel coronavirus (COVID-19) via stochastic epidemic model. Alex. Eng. J.. 2021;60(4):4121-4130.
- [Google Scholar]
- Intelligent networks for crosswise stream nanofluidic model with Cu–H2O over porous stretching medium. Int. J. Hydrogen Energy. 2021;46(29):15322-15336.
- [Google Scholar]
- A finite difference scheme to solve a fractional order epidemic model of computer virus. AIMS Math.. 2023;8:2337-2359.
- [Google Scholar]
- A highly accurate numerical method for solving a time-fractional partial differential equation. Prog. Fract. Diff. Appl. Int. J.. 2016;2:227-232.
- [Google Scholar]
- Stochastic COVID-19 SEIQ epidemic model with time-delay. Results Phys.. 2021;30:104775
- [Google Scholar]
- Stochastic COVID-19 SEIQ epidemic model with time-delay. Results Phys.. 2021;30:104775
- [Google Scholar]
- Design of fractional order epidemic model for future generation tiny hardware implants. Futur. Gener. Comput. Syst.. 2020;106:43-54.
- [Google Scholar]
- Modeling and analysis of effects of awareness programs by media on the spread of infectious diseases. Math. Comput. Model.. 2011;53(5–6):1221-1228.
- [Google Scholar]
- An efficient method for solving fractional Hodgkin-Huxley model. Phys. Lett. A. 2014;378(30–31):1980-1984.
- [Google Scholar]
- Bio-inspired heuristics hybrid with sequential quadratic programming and interior-point methods for reliable treatment of economic load dispatch problem. Neural Comput. Applic.. 2019;31(1):447-475.
- [Google Scholar]
- Integrated intelligent computing application for the effectiveness of Au nanoparticles coated over MWCNTs with velocity slip in curved channel peristaltic flow. Sci. Rep.. 2021;11(1):1-20.
- [Google Scholar]
- Neuro-swarming intelligence-based computing for second-order singular periodic non-linear boundary value problems. Front. Phys.. 2020;8:224.
- [Google Scholar]
- Computational intelligence approach using Levenberg–Marquardt backpropagation neural networks to solve the fourth-order nonlinear system of the Emden-Fowler model. Eng. Comput. 2021:1-17.
- [Google Scholar]
- FMNSICS: fractional Meyer neuro-swarm intelligent computing solver for nonlinear fractional Lane-Emden systems. Neural Comput. Applic.. 2022;34(6):4193-4206.
- [Google Scholar]
- FMNSICS: fractional Meyer neuro-swarm intelligent computing solver for nonlinear fractional Lane–Emden systems. Neural Comput. Applic.. 2022;34(6):4193-4206.
- [Google Scholar]
- Scherer, R., Kalla, S.L., Tang, Y. and Huang, J., 2011. The Grünwald–Letnikov method for fractional differential equations. Computers & Mathematics with Applications, 62(3), pp.902-917. [.2641-2659
- Heat transfer at the microscopic level in an MHD fractional inertial flow confined between non-isothermal boundaries. Eur. Phys. J. Plus. 2017;132(7):1-17.
- [Google Scholar]
- A stochastic numerical analysis based on hybrid NAR-RBFs networks nonlinear SITR model for novel COVID-19 dynamics. Comput. Methods Programs Biomed.. 2021;202:105973
- [Google Scholar]
- A design of predictive computational network for transmission model of lassa fever in Nigeria. Results Phys.. 2022;39:105713
- [Google Scholar]
- Artificial neural networks with conformable transfer function for improving the performance in thermal and environmental processes. Neural Netw.. 2022;152:44-56.
- [Google Scholar]
- Numerical study for multi-strain tuberculosis (TB) model of variable-order fractional derivatives. J. Adv. Res.. 2016;7(2):271-283.
- [Google Scholar]
- Sweilam, N.H., Khader, M.M. and Mahdy, A.M., 2012. Numerical studies for fractional-order Logistic differential equations with two different delays. Journal of Applied Mathematics, 2012.
- Numerical investigations through ANNs for solving COVID-19 model. Int. J. Environ. Res. Public Health. 2021;18(22):12192.
- [Google Scholar]
- ur Rehman, M.A., Kazim, M., Ahmed, N., Raza, A., Rafiq, M., Akgül, A., Inc, M., Park, C. and Zakarya, M., 2023. Positivity preserving numerical method for epidemic model of hepatitis B disease dynamic with delay factor. Alexandria Engineering Journal, 64, pp.505-515
- Anti-synchronization of a M-Hopfield neural network with generalized hyperbolic tangent activation function. Eur. Phys. J. Special Topics. 2022;231(10):1801-1814.
- [Google Scholar]
- Spectral entropy analysis and synchronization of a multi-stable fractional-order chaotic system using a novel neural network-based chattering-free sliding mode technique. Chaos Solitons Fract.. 2021;144:110576
- [Google Scholar]
- Numerical solution of fractal-fractional Mittag-Leffler differential equations with variable-order using artificial neural networks. Eng. Comput. 2021:1-14.
- [Google Scholar]
- Fractal-fractional neuro-adaptive method for system identification. Eng. Comput. 2021:1-24.
- [Google Scholar]
- Zuo, L. and Liu, M., 2014, January. Effect of awareness programs on the epidemic outbreaks with time delay. In Abstract and Applied Analysis (Vol. 2014). Hindawi
Appendix A
Supplementary material
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jksus.2023.102691.
Appendix A
Supplementary material
The following are the Supplementary data to this article:







