Influence of dipole interaction on the quantum correlation detection and teleportation in a qubit-field system
⁎Corresponding author at: Department of Mathematics, College of Science, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia. eiedkhalil@tu.edu.sa (E.M. Khalil)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
This study examines the analysis of the teleportation process in a two-qubit state, particularly scrutinizing the interplay of atomic dipole coupling interaction, the detuning parameter, photon count, and the surrounding environment. Our investigation assumes the existence of a teleportation channel comprising two-qubit systems interacting with a photon field enveloped by the dephasing environment. Within this framework, we closely examine the quantum correlations exhibited by the teleported state, encompassing dimensions of entanglement, steering, and non-locality. Our results underscore the pivotal role played by the initial state of the atomic and field subsystems in shaping quantum relations. The dipole coupling has a profound impact, significantly enhancing the three quantifiers. Particularly, the entanglement changes from a de-entangled state to a partially entangled state. On the other hand, the detuning parameter introduces distortion in the quantum correlations, a phenomenon that can be effectively mitigated by controlling the dipole coupling.
Keywords
Dipole interaction
Teleportation
Steering
Entanglement
Non-locality
1 Introduction
Realistic experiments demonstrate that open quantum systems inevitably exchange energy with their surrounding environment during interactions. This energy exchange gradually erodes the system’s quantum properties, even at specific instances, potentially hindering their exploitation for practical applications (Yu and Eberly, 2009; Almeida et al., 2007). The detrimental effects of decoherence are particularly pronounced in the context of independent qubits, each embedded in its environment, which is essential for implementing quantum communication and information protocols with distant, individually addressable particles (Ladd et al., 2010; Abd-Rabboul et al., 2021). In response to the detrimental effects of decoherence on quantum correlations, researchers are exploring the possibility of designing effective and feasible quantum models that can safeguard these delicate correlations from the harmful influence of noise (Gisin and Thew, 2007). Conversely, significant attention has been devoted to Markovian designs, which involve crafting appropriate quantum systems capable of preserving quantum memory effects (Man et al., 2018). The non-Markovian systems exhibit fundamental characteristics that are essential for reviving quantum entanglement, regardless of whether they possess a bosonic or fermionic quantum nature (Fanchini et al., 2010; Rahman et al., 2023) or a classical nature (e.g., random noise, random field, noisy phase laser) (Abd-Rabbou et al., 2023c). In quantum systems, the presence of a thermal environment, characterized by its temperature, poses a significant challenge as it can induce decoherence, ultimately leading to the degradation of quantum correlations (Bellomo et al., 2008; Yan and Yue, 2013). This phenomenon has garnered considerable attention in recent research efforts, particularly in understanding its impact on entanglement dynamics. Moreover, the entanglement of multi-qubit quantum systems under the influence of both thermal and dephasing environments has been a subject of investigation (Hu et al., 2009; Hu, 2012). Additionally, quantum systems are often subjected to various noisy channels, such as amplitude damping, depolarizing, and phase damping channels, which disrupt quantum correlations, leading to information loss and diminished entanglement (Abd-Rabbou et al., 2019, 2023a). Therefore, this paper aims to explore the effects of the thermal environment and common dephasing environment on entanglement dynamics, particularly in the presence of n-sequential sin
Quantum information theory was adopted to study the entanglement of quantum systems because of its key role in knowing the main characteristics in the interaction process between parts of the system, such as quantum encryption (Bouwmeester et al., 2013), quantum computations, geometric quantum computation (Wang, 2009; Guo et al., 2019), and dense cryptography (Hiroshima, 2001). Quantum correlations underpin the fundamental principles of quantum information processing. These correlations, including entanglement, nonlocality, steering, and discord, arise from interactions between parts of complex quantum systems (Abd-Rabbou et al., 2022; Youssef et al., 2023). Attention has been paid to studying the features of quantum correlations in encryption and teleportation on a large scale, both theoretically and experimentally (Mirmasoudi and Ahadpour, 2018). Using the previous quantum entanglement in which the sender and receiver participated, quantum teleportation and dense cryptography were implemented (Omri et al., 2022; Abd-Rabbou and Khalil, 2022). Therefore, many different quantum models have been designed to generate quantum correlation theoretically and experimentally. For example, a surface polariton-supporting method has been proposed to generate dually entangled electrons (Asban and García de Abajo, 2021). A shared phonon tank was designed to form non-classical correlations between two excited qubits (Krzywda and Roszak, 2016). The entanglement and discord periods generated from an unbound system when exposed to a combined thermal or pressurized tank are investigated in Gallego et al. (2012). A laboratory-viable scheme for generating a multi-mode quantum light source using a non-degenerate four-wave mixing procedure in a thermally controlled atomic vapor cell was designed in Cao et al. (2017). In addition, another practical scheme has been proposed, therefore, to generate quantum correlations and experimentally control the parameters of the quantum system to study entanglement periods (Ding et al., 2012).
The central aim of this study is to explore the viability of teleporting a pair of quantum qubits through an atom-field interaction within a dephasing environment. Teleported qubits undergo instantaneous exposure to various effects originating from the teleportation channel, encompassing factors such as the channel’s initial state, photon count, detuning, dipole coupling, and the decay rate of the dephasing environment. These factors can exert either augmenting or diminishing influences on the teleported quantum correlations. Prior research has indicated that dipole coupling has the potential to enhance quantum correlations (Khalil and Abd-Rabbou, 2022; Abd-Rabbou and Khalil, 2022). Our objective is to ascertain whether this enhancement extends to teleported quantum correlations and whether it can ameliorate the adverse effects of the dephasing environment and detuning. To address these inquiries, we will scrutinize the entanglement, steering, and nonlocality of the teleported state. This paper is structured as follows: Section 2 introduces the Hamiltonian model of the quantum channel and its density operator, incorporating the effects of the dephasing environment. Sections 3 and 4 provide a concise overview of the teleportation process and quantum correlation quantifiers, including entanglement, steering, and nonlocality. Section 5 presents our results, exploring the impact of teleportation channel parameters on quantum correlations. Finally, Section 6 summarizes our findings and concludes the paper.
2 Physical model of channel
Consider two partners, referred to as Jon in lab (a) and Rob in lab (b), who share a quantum channel comprising a two-qubit system with a frequency
Now, we direct our focus toward determining the dynamic operators governing the current system. To achieve this, the application of well-established principles, such as the Heisenberg equations of motion, becomes imperative
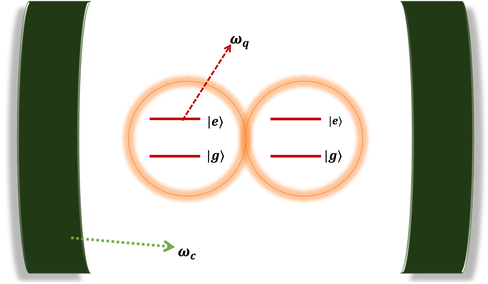
- A Sketch of a two-qubit system located inside a cavity field. Here,
To get
According to Eqs. (5) and (6), we can get the following system of ordinary differential equations (ODE)
3 Teleportation process
The phenomenon of teleporting an entangled state between two distinct labs through a quantum channel has been introduced in the work of Lee and Kim (2000). Our methodology involves the utilization of the decayed density operator
Hereinafter, we employ the concurrence, 3-steering, and Bell non-locality to examine the quantum correlation of the teleported state.
4 Quantum correlation measure
The fundamental concepts of quantum entanglement, steering, and non-locality are presented in this section as potent expressions of quantum correlations. States demonstrating entanglement and steerability can be quantified via metrics like concurrence and 3-steering, respectively. Notably, states that transgress Bell inequalities exemplify the most formidable correlations, signifying inherent non-locality between qubits when subjected to optimal measurement procedures.
4.1 Entanglement by concurrence
The degree of entanglement existing between two qubits can be effectively quantified through a well-established metric known as concurrence (Coffman et al., 2000). Concurrence serves as a reliable indicator of the entanglement strength within the quantum system, offering valuable insights into the interconnection between qubits. This quantification enables a more precise assessment of the quantum correlations and their potential impact on the system’s overall behavior. The quantification of entanglement, whether in pure or mixed quantum states, is conducted through the evaluation of eigenvalues (
4.2 Steering
In quantum information theory, 3-steering represents a concept that delves into the phenomenon of steering, which is a manifestation of quantum correlations. Steering involves the possibility of one quantum system indirectly influencing the state of another. In terms of three observable measurements on the two qubits (a) and (b), say
4.3 Bell non-locality
For deep investigation, we shall use the Bell non-locality, which is a phenomenon wherein entangled states correlations that cannot be elucidated by any local hidden variable theory (Clauser et al., 1970). This concept provides us with profound insights into the intricate nature of quantum correlations. In the case of a two-qubit state with X-shaped, the Bell non-locality is given by
5 Results and discussion
Fig. 2 provides a comprehensive visualization of the quantum correlations characterizing the teleported state through a damped atomic-field channel. In this study, we consider two distinct initial scenarios for the channel, one with
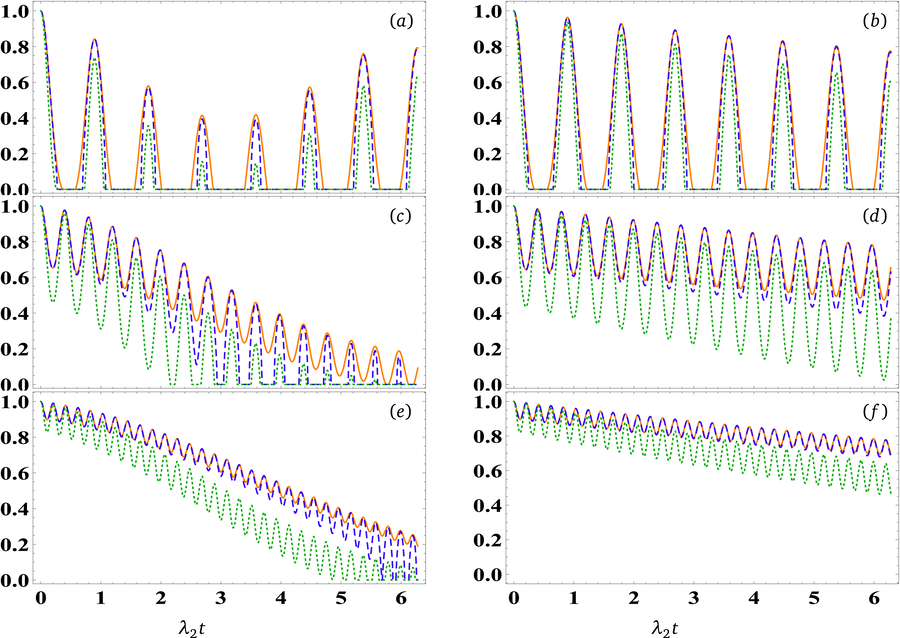
- The temporal evolution of quantum correlations
In the context of the second scenario, where
The impact of varying detuning parameter
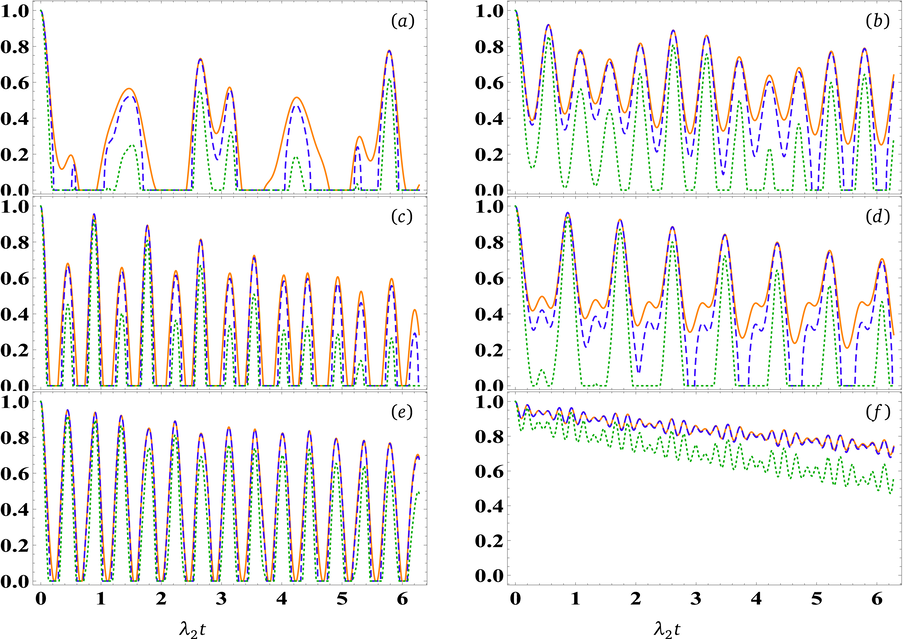
- The temporal evolution of quantum correlations
Fig. 4 exhibits the influence of increasing the number of photons (
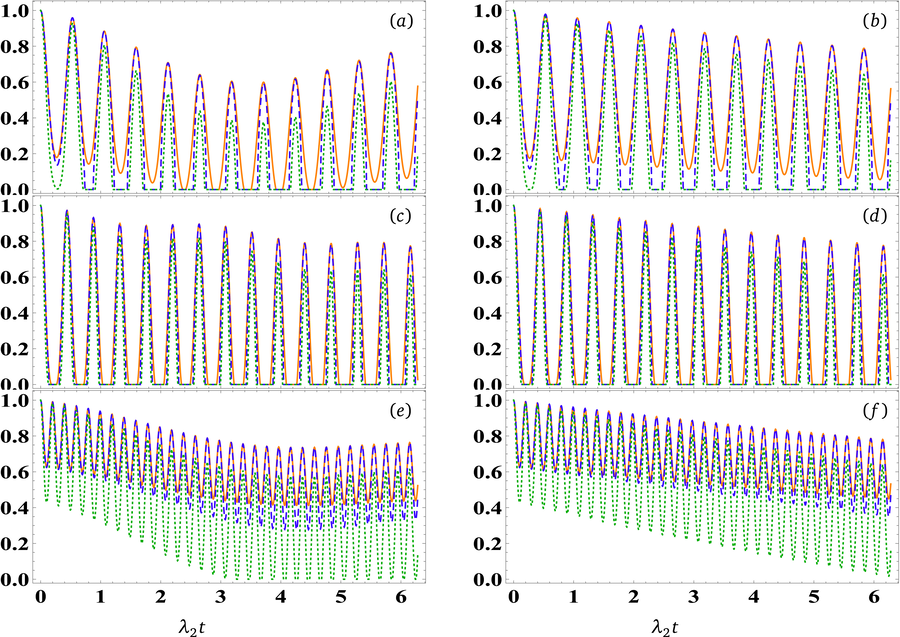
- The temporal evolution of quantum correlations
Fig. 5 depicts the impact of the dephasing environment, characterized by
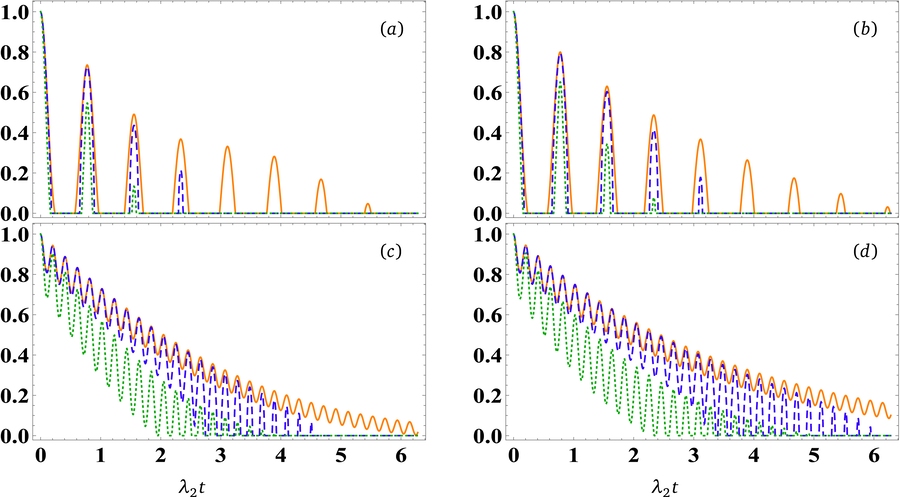
- The temporal evolution of quantum correlations
6 Conclusion
This paper has examined the teleportation process of a pair of entangled qubits traversing a channel composed of interacting atoms immersed in a quantum field, all within the confines of a dephasing environment. The primary focus of our investigation revolved around the comprehensive analysis of entanglement, steering, and non-locality exhibited by the teleported state, particularly concerning the channel parameters. The key factors under scrutiny encompassed the dipole coupling, detuning, photon number, and the influence exerted by the surrounding dephasing environment. Notably, our study has been grounded in the assumption that the channel atoms commence with a state of maximal entanglement, following two distinct scenarios, while the quantum field remains in a number state.
Our results showed that the initial state of the channel system has a clear effect on the state to be teleported and its associated quantum correlations. Furthermore, a noteworthy enhancement in quantum correlations has been observed with the escalation of dipole coupling. This amplification has been particularly evident in the transformation of the teleported state, transitioning from a de-entangled state to a partially entangled state. The minima of steering and non-locality have also experienced elevation in response to heightened coupling levels.
As we increased the detuning parameter, we observed the distortion of quantum correlations, accompanied by heightened oscillations. Notably, increasing the dipole coupling reconfigured these oscillations and mitigated the adverse effects resulting from detuning. Furthermore, the increase in the photon number amplified the oscillations, making the teleported state less reliant on the initial atomic state. Coupling this heightened photon count with the double coupling effect led to a marked enhancement in the maximum values of quantum correlations. Conversely, the interaction of our system with the dephasing environment diminished the strength of quantum correlations in the teleported state. However, the dipole coupling played a significant role in mitigating this interaction’s influence.
CRediT authorship contribution statement
Hanaa Abu-Zinadah: Writing – original draft, Methodology, Conceptualization. E.M. Khalil: Writing – review & editing, Writing – original draft, Software, Methodology, Investigation, Conceptualization.
Acknowledgments
This work was funded by the University of Jeddah, Jeddah, Saudi Arabia under grant No. (UJ-23-DR-220). Therefore, the authors thanks the University of Jeddah for its technical and financial support.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Detraction of decoherence that arises from the acceleration process. J. Opt. Soc. Am. B. 2023;40(3):585-593.
- [Google Scholar]
- Dense coding and quantum memory assisted entropic uncertainty relations in a two-qubit state influenced by dipole and symmetric cross interactions. Ann. Phys. (Berl.). 2022;534(9):2200204
- [Google Scholar]
- Noise-based damping of chaotic entanglement in pulsed driven two-qubit system. Ann. Phys. (Berlin) 20232300423
- [Google Scholar]
- Probing teleported quantum correlations in a two-qubit system inside a coherent field. Optik. 2024;296:171551
- [Google Scholar]
- Suppressing the information losses of accelerated qubit–qutrit system. Int. J. Quantum Inf.. 2019;17(04):1950032
- [Google Scholar]
- Improving the bidirectional steerability between two accelerated partners via filtering process. Modern Phys. Lett. A. 2022;37(22):2250143
- [Google Scholar]
- Non-classical correlations of accelerated observers interacting with a classical stochastic noise beyond the single mode approximation. Opt. Quantum Elect.. 2023;55(8):715.
- [Google Scholar]
- Quantum Fisher information of a teleported state in heisenberg XYZ chain with magnetic field and Kaplan–Shekhtman–Entin-Wohlman–Aharony interaction. IEEE Access. 2021;9:51325-51331.
- [Google Scholar]
- Generation, characterization, and manipulation of quantum correlations in electron beams. npj Quantum Inf.. 2021;7(1):42.
- [Google Scholar]
- Entanglement dynamics of two independent qubits in environments with and without memory. Phys. Rev. A. 2008;77:032342
- [Google Scholar]
- The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation. Springer Science & Business Media; 2013.
- Experimental observation of quantum correlations in four-wave mixing with a conical pump. Opt. Lett.. 2017;42(7):1201-1204.
- [Google Scholar]
- Proposed experiment to test local hidden variable theories. Phys. Rev. Lett.. 1970;24:549.
- [Google Scholar]
- Quantification of Einstein-Podolsky-Rosen steering for two-qubit states. Phys. Rev. A. 2016;93:020103
- [Google Scholar]
- Generation of non-classical correlated photon pairs via a ladder-type atomic configuration: Theory and experiment. Opt. Express. 2012;20(10):11433-11444.
- [Google Scholar]
- Constraint relation between steerability and concurrence for two-qubit states. Ann. Phys.. 2021;533(8):2100098
- [Google Scholar]
- Generation of quantum correlations for two qubits through a common reservoir. Phys. Scr.. 2012;2012(T147):014012
- [Google Scholar]
- Teleportation of quantum Fisher information under decoherence channels with memory. Laser Phys. Lett.. 2019;16(9):095203
- [Google Scholar]
- Optimal dense coding with mixed state entanglement. J. Phys. A: Math. Gen.. 2001;34(35):6907.
- [Google Scholar]
- Disentanglement, bell-nonlocality violation and teleportation capacity of the decaying tripartite states. Ann. Phys., NY. 2012;327(9):2332-2342.
- [Google Scholar]
- Thermal and phase decoherence effects on entanglement dynamics of the quantum spin systems. Physica B: Cond. Matt.. 2009;404(20):3499-3506.
- [Google Scholar]
- Robustness of a teleported state influenced by dipole interaction and magnetic field under intrinsic decoherence. Optik. 2022;267:169703
- [Google Scholar]
- Phonon-mediated generation of quantum correlations between quantum dot qubits. Sci. Rep.. 2016;6(1):23753.
- [Google Scholar]
- Temperature effects on quantum non-Markovianity via collision models. Phys. Rev. A. 2018;97(6):062104
- [Google Scholar]
- Dynamics of super quantum discord and optimal dense coding in quantum channels. J. Phys. A. 2018;51(34):345302
- [Google Scholar]
- Witnessing quantum correlations in two coupled quantum dots under intrinsic decoherence. Alex. Eng. J.. 2023;69:521-527.
- [Google Scholar]
- Thermal information and teleportation in two-qutrit Heisenberg XX chain model. Alex. Eng. J.. 2022;61(10):8335-8342.
- [Google Scholar]
- Two-qubit steerability, nonlocality, and average steered coherence under classical dephasing channels. Ann. Phys. (Berl.). 2023;535(4):2200523
- [Google Scholar]
- Geometric quantum computation and dynamical invariant operators. Phys. Rev. A. 2009;79(2):024304
- [Google Scholar]
- Dynamics of quantum and classical correlations of a two-atom system in thermal reservoirs. Chaos Solit. Fractals. 2013;57:117-122.
- [Google Scholar]
- Exploring quantum correlations of two-qubit heisenberg chain model influenced by magnetic dipole–dipole, magnetic field, and a symmetric cross interaction. Quantum Inf. Process.. 2023;22(6):229.
- [Google Scholar]







