Impurity effect on entanglement in an XY two-dimensional spin lattice

1 Introduction

Quantum entanglement is one of the main concepts in quantum theory with wide applications in modern physics (Peres, 1993). Entanglement is a nonlocal correlation between two (or more) quantum systems such that the description of their states has to be done with reference to each other even if they are spatially well separated. Quantifying entanglement and explaining its behavior may provide a clue for many questions of the static and dynamic properties of complex quantum systems (Kais, 2007). Particularly, entanglement is considered as the physical property responsible for the long-range quantum correlations accompanying a quantum phase transition in many body systems in the vicinity of zero temperature (Sondhi et al., 1997; Osborne and Nielsen, 2002; Zhang et al., 2009; Osenda et al., 2003; Huang et al., 2004). Entanglement plays a crucial role in particular fields such as quantum teleportation, cryptography and quantum computation. It provides the physical basis for manipulating the correlations among the different constituting spin entities in such systems (Nielsen and Chuang, 2000; Boumeester et al., 2000). Different physical systems have been considered as promising candidates for the underline technology for quantum information processing (Barenco et al., 1995; Vandersypen et al., 2001; Chuang et al., 1998; Jones et al., 1998; Cirac and Zoller, 1995; Turchette et al., 1995; Averin et al., 1997; Wei et al., 2010). The main task in each one of these systems is to specify certain quantum degree of freedom as the quit and find a controllable coupling mechanism to form an entanglement among these qubits to perform efficient quantum computing processes. Building an efficient network of such quantum system that is capable of performing efficient quantum computing algorithms comes next in the list of priorities. Therefore quantifying entanglement contained in the quantum states of multiparticle systems are in the focus of interest in the field of quantum information processing.

Studying quantum entanglement in two-dimensional systems face more obstacles in comparison of the one dimensional cases, particularly the rapid increase in the dimension of the Hilbert spaces which lead to much larger scale calculations relying mainly on the numerical methods. The existence of exact solutions has contributed enormously to the understanding of the entanglement for 1D systems (Lieb et al., 1961; Sachdev, 2001; Huang and Kais, 2005; Sadiek et al., 2010). Tuning the entanglement in a one dimensional XY spin chain system using impurities and anisotropy has been demonstrated (Osenda et al., 2003). In a recent work the entanglement in a 19-site two-dimensional transverse Ising model at zero temperature (Xu et al., 2010) was studied. The spin- $\frac{1}{2}$ particles are coupled through an exchange interaction J and subject to an external time-independent magnetic field h. It was demonstrated that for such a class of systems the entanglement can be tuned by varying the parameter λ = h/J and also by introducing impurities into the system. The system showed a quantum phase transition at a specific critical value of the parameter λ_c. In a very recent work we have investigated the time evolution of entanglement in a two dimensional triangular transverse Ising system in an external magnetic field. Different time dependent forms of the magnetic field were applied. The system has demonstrated different responses based on the type of applied field, where for a smoothly changing magnetic field the system entanglement follows that change in the field very closely (Xu et al., 2011).

In this paper, we consider the entanglement in a two-dimensional triangular spin system, where the nearest neighbor spins are coupled through an exchange interaction and subject to an external magnetic field, where the number of spins in the system is 7. We consider one of spins as an impurity spin with the coupling strength between the impurity spin and its neighbors different from that between the rest of the spins. We consider two different cases where the impurity spin is located one time at the border and one other time at the center of the lattice. We found that when the spin is located at a border site the entanglement between the impurity and its nearest neighbors increases monotonically with J′ reaching a saturation value which varies depending on the magnetic field strength h. The entanglement with the next nearest spins shows a critical behavior where it vanishes as J′ increases. The critical coupling value at which the entanglement vanishes increases as h increases. The entanglement between two spins excluding the impurity show that while the entanglement between two spins coupled to the impurity reach a saturation value as J′ increases, it vanishes for spins not coupled to the impurity. Examining the effect of a central impurity show that the entanglement between nearest neighbor and next nearest neighbor spins reaches an asymptotic value as J′ increases. It was demonstrated that the impurity can be used as a switch to control the entanglement between the different spins in the lattice. This paper is organized as follows. In the next section we present our model. In Section 3 we evaluate the entanglement of the system. In Section 4 we provide our results and discussion.

2 The two-dimensional XY spin model with single impurity

We consider a set of seven localized spin- $\frac{1}{2}$ particles in a two dimensional triangular lattice coupled through exchange interaction J and subject to an external time-dependent magnetic field of strength h(t) as sketched in Fig. 1. All the particles are identical except one of them which is considered as an impurity particle. The location of the impurity particle is chosen to be either at the center or at the boarder of the system. The Hamiltonian for such a system is given by

Close

Figure 1

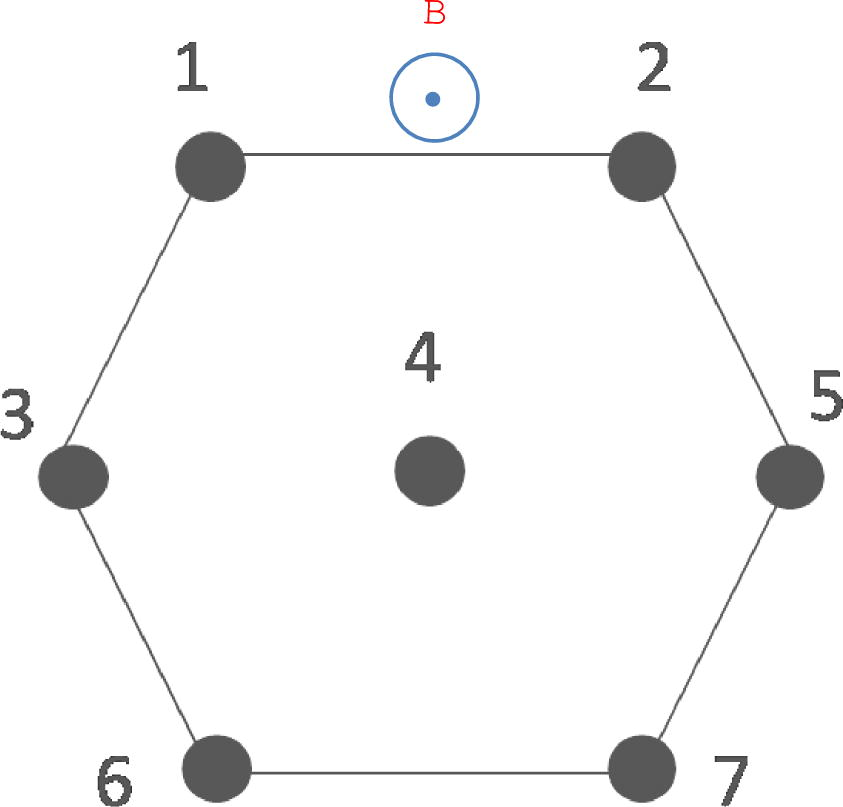
The two dimensional triangular spin lattice in presence of an external transverse magnetic field.

Export to PPT

3 Entanglement of formation

The entanglement between any two spins i and j can be obtained using the entanglement of formation approach, a well known measure to quantify entanglement (Wootters, 1998). All the information needed in this case is contained in the reduced density matrix ρ_i,j which can be obtained from the entire system density matrix by integrating out all the spins states except i and j. Wootters (1998) has shown that, for a pair of binary qubits, the concurrence C, which goes from 0 to 1, can be taken as a measure of entanglement. The concurrence between sites i and j is defined as

4 Results and discussion

We have investigated the dynamics of entanglement in a two-dimensional triangular XY spin lattice in an external transverse magnetic field. The spins are coupled to each other through nearest neighbor exchange interaction. We have studied nearest neighbor and next nearest neighbor Entanglement of the system under the effect of an impurity spin which is either located at one of the border sites or the central one. First we consider the effect of an impurity spin at the boarder site 1. We start by studying the entanglement between the impurity site and its nearest neighbors sites 2 and 4 represented by C₁₂ and C₁₄. In Fig. 2 we explore the concurrences C₁₂ and C₁₄ versus the exchange interaction J′ between the impurity and its nearest neighbors at different magnitudes of magnetic field strength. As can be noticed for small magnetic field (h = 0.25) C₁₂ and C₁₄ is zero for J′ = 0 and increases rapidly as J′ increases and reaches a saturation value for large J′. As the magnetic field increases to h = 0.5 as shown Fig. 2(b) the behavior is very much the same as in part (a) except that the transition is a little rough. For higher magnetic field h = 1 the concurrences C₁₂ and C₁₄ show a critical behavior where it increases, decreases and increases again at about J′ = 1 reaching almost the same saturation value of about 0.33. Interestingly for high magnetic field h = 2, shown in Fig. 2(c), the concurrences maintains a zero value until J′ ≈ 1.2. Therefore strong magnetic field aligns the spins in its direction and their total state is a product of their individual states and hence the entanglement is zero but as J′ exceeds the value of h the spins are aligned in different directions (x, y and z) then the entanglement increases rapidly as J′ increases reaching a saturation value that is about twice the ones in the previous cases (a), (b) and (c). For very high J′ ≈ 8 the concurrence suddenly decreases and saturates to about 0.32 which is the same as the asymptotic value of the previous cases. The final decrease in concurrence can be attributed to the fact that J′ ≫ h which forces the spins to align only in x and y directions not the z-direction and ends up in a situation similar to that of the cases in (a), (b) and (c). Next we consider the entanglement between the impurity spin and its next nearest neighbor spins at sites 5 and 7 represented by the concurrences C₁₅ and C₁₇ as shown in Fig. 3. It is interesting to notice that the behavior of the concurrence in this case is different from the nearest neighbor one, it does not reach an asymptotic finite value at large J′ but in contrary it vanishes for large J′. The critical value of J′ at which the concurrence vanishes varies depending on the value of the applied magnetic field, clearly as can be seen form Fig. 3(a), (b), (c) and (d) as the magnetic field increases the critical value increases. The concurrence shows a critical behavior where it starts from zero for zero J′ and reaches a maximum value and then decreases again until it vanishes. As we increase the magnetic field, the maximum value of the concurrence increases and the transition becomes sharper as can be seen. For high magnetic field, as shown in Fig. 3(d), the next nearest concurrence, as it was the case for the nearest concurrence, maintains a zero value until J′ ≈ 1.2 and then increases suddenly to its maximum value then decreases monotonically until it suddenly vanishes again at about J′ = 8.2. Fig. 3 show the impurity can be utilized as a switch to turn on and off the entanglement of the next nearest entanglement by varying its strength. In Fig. 4 we explore the nearest neighbor entanglement between two spins where none of them is the impurity spin at site 1, where the concurrences C₂₄ and C₂₅ are plotted versus J′. As one can see in Fig. 4(a), where h = 0.25, C₂₄ and C₂₅ behave differently, while both start from a finite value C₂₄, which is more affected by the impurity, decreases and then increases again when J′ > h. Monitoring higher values of J′ show that C₂₄ reaches a saturation value. On the other hand, C₂₅ increases monotonically reaching zero for high value of J′ ≈ 11. As can be concluded from Fig. 4(b), increasing the magnetic field to h = 0.5 does not change the behavior seen in Fig. 4(a) much, except that it decreases the initial values and shows some criticality at J′ ≈ h. Interestingly as h increases further, as shown in Fig. 4(c), C₂₄ starts from a finite value, increases a little bit and then sharply decreases reaching a zero value and then increases again. The concurrence C₂₅ starts at finite value, increases and then monotonically decreases to zero at higher value of J′. For high magnetic field h = 2, as shown Fig. 4(d), the concurrences maintain again a zero value until J′ is close to h, then C₂₄ increases abruptly decreasing monotonically and then sharply and finally increases again with a little value. The concurrence C₂₅ behaves in a completely opposite way to C₂₄ as can be seen in the figure. Studying the next nearest concurrences C₂₃, which is more affected by the impurity spin, and C₂₇, which is shown in Fig. 5 one can see that their behavior is very similar to that of Fig. 4 except that the magnitude of the concurrence is much lower than the previous case.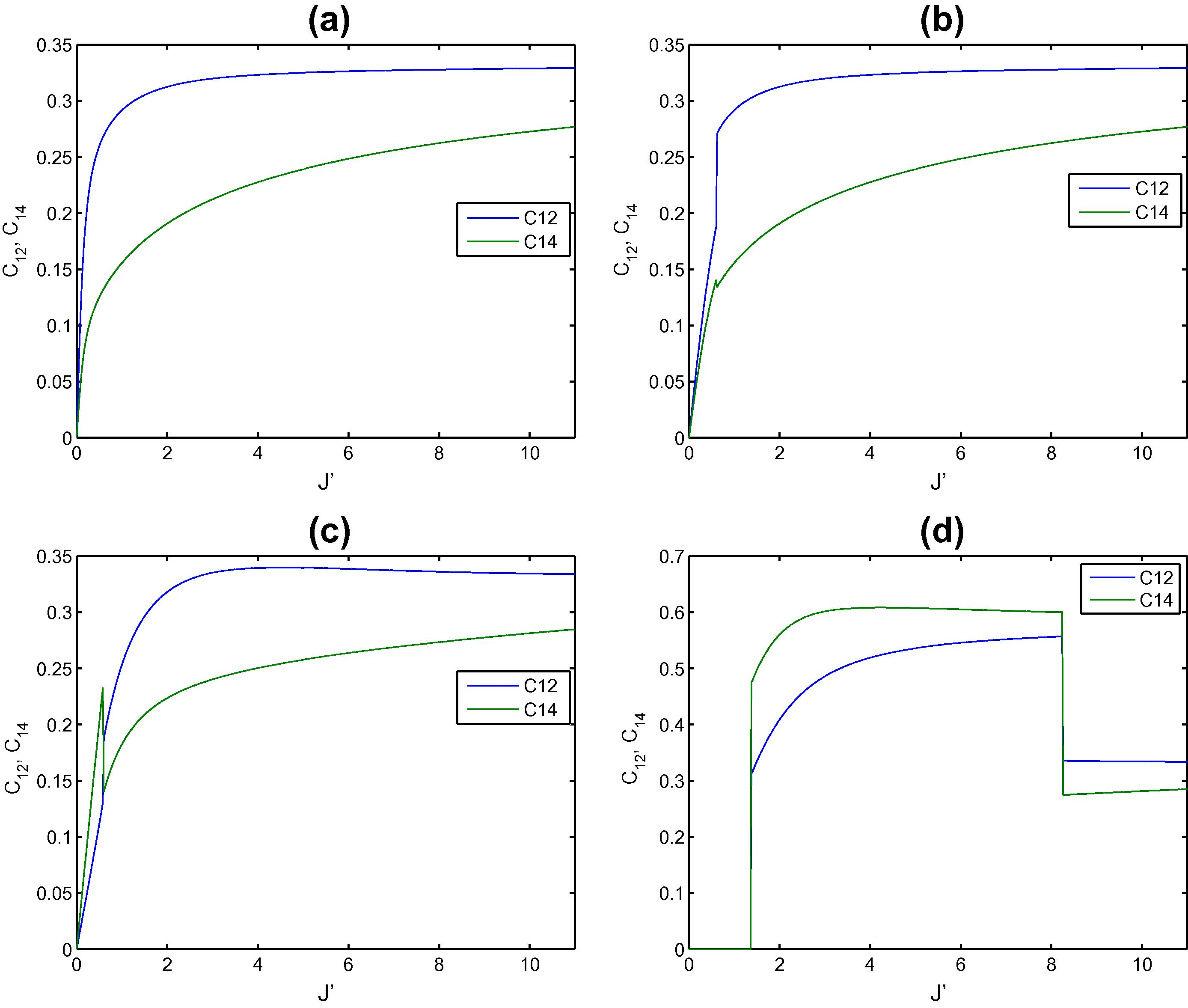

Close

Figure 2

The entanglements C₁₂ and C₁₄ versus the strength of the impurity at the border site 1 in the triangular two dimensional spin lattice at different applied magnetic field strength h equals: (a) 0.25, (b) 0.5, (c) 1 and (d) 2.

Export to PPT

Close

Figure 3

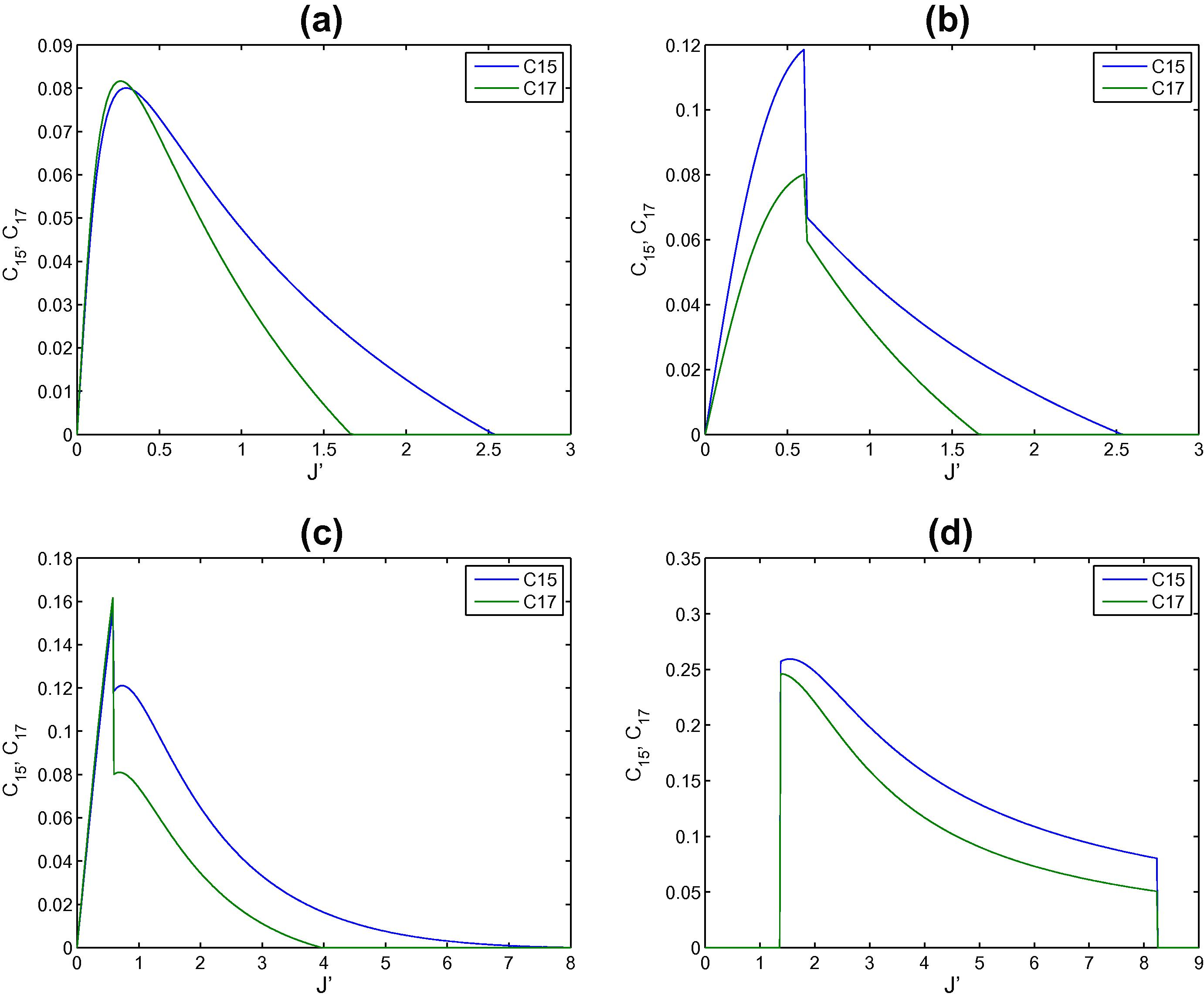
The entanglements C₁₅ and C₁₇ versus the strength of the impurity at the border site 1 in the triangular two dimensional spin lattice at different applied magnetic field strength h equals: (a) 0.25, (b) 0.5, (c) 1 and (d) 2.

Export to PPT

Close

Figure 4

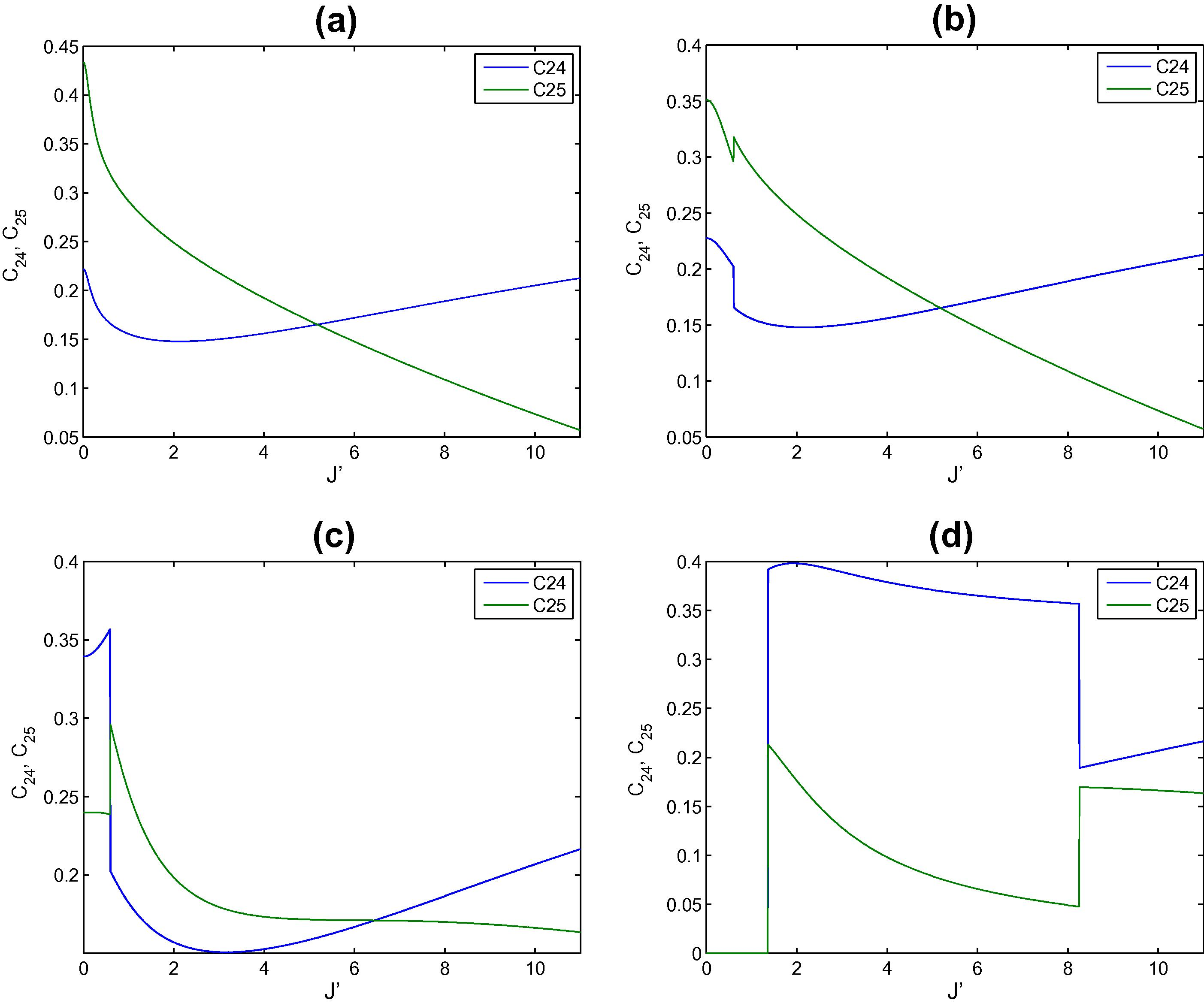
The entanglements C₂₄ and C₂₅ versus the strength of the impurity at the border site 1 in the triangular two dimensional spin lattice at different applied magnetic field strength h equals: (a) 0.25, (b) 0.5, (c) 1 and (d) 2.

Export to PPT

Close

Figure 5

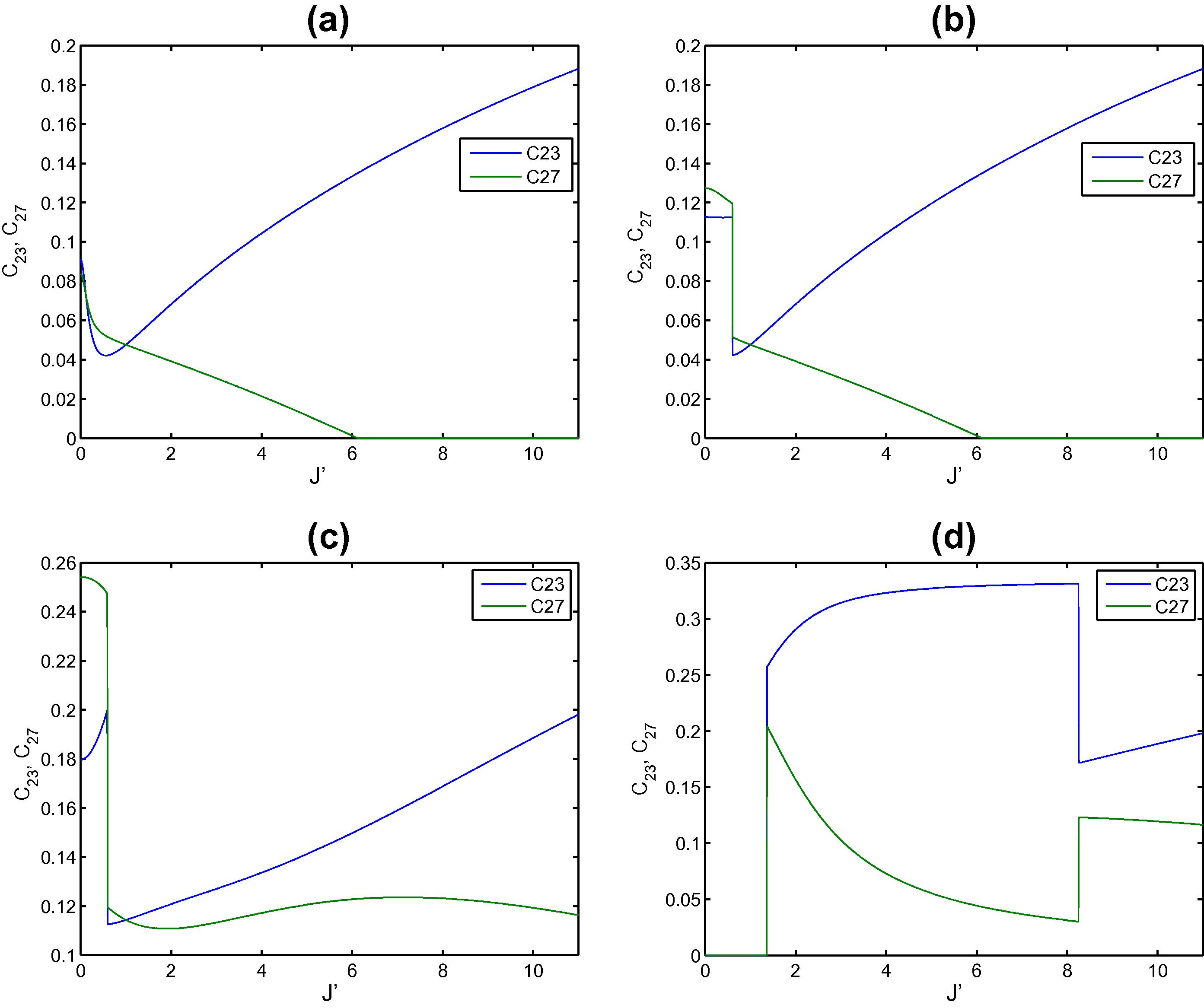
The entanglements C₂₃ and C₂₇ versus the strength of the impurity at the border site 1 in the triangular two dimensional spin lattice at different applied magnetic field strength h equals: (a) 0.25, (b) 0.5, (c) 1 and (d) 2.

Export to PPT

Now let us turn to the second case where we consider a central impurity spin, at site 4. In Fig. 6 we consider nearest neighbor concurrences C₁₂ and C₁₄ where the latter involves the impurity site 4. As can be noticed, in Fig. 6(a), C₁₂ starts at a finite value where h ≫ J′ and decreases monotonically until it reaches a saturation value for large J′ ≫ h where the spins are aligned in both x and y directions. On the other hand C₁₄ starts at zero as expected, since J′, but increases abruptly reaching a saturation value that is very close to that of C₁₂. As the magnetic field increases, as shown in Fig. 6(b), the behavior of C₁₂ and C₁₄ is still the same except of a rough behavior that takes place in both concurrences at J′ ≈ h where the concurrence increases and then decreases (decreases and then increases). As the magnetic field increases the rough behavior at J′ ≈ h increases as can be seen in Fig. 6(c). The effect of the impurity at site 4 clearly is more on C₁₄ than C₁₂ as expected. In Fig. 6(d) the effect of a high magnetic field is explored where both concurrences again maintain zero value as long as h ≫  J′ and then increases very sharply where C₁₂ reaches certain value and saturates within that value in a close to a Plateau form as J′ increases. On the other hand C₁₄ reaches a much higher value and continues in a plateau form for short change in J′ and then decays abruptly to a new plateau value that is close to the value of C₁₂. The behavior of the next nearest neighbor concurrence is tested in Fig. 7. It is interesting to notice that the behavior of the two concurrences C₁₅ and C₁₇ are very close but not exactly the same where all the four spins involved are neighbors to the impurity spin 4. For small magnetic field h = 0.25, as shown in Fig. 7(a), the concurrences keep a zero value until J′ ≈ h and then increases monotonically reaching a common asymptotic value for high J′. As the magnetic field increases, shown in Fig. 7(b), C₁₅ starts at a finite value, increases then decreases sharply showing a critical behavior at J′ ≈ h and then increases monotonically reaching the same saturation value as in Fig. 7(a). The concurrence C₁₇ behaves differently only at the small values of J′ where it differs from zero at J′ ≈ h, increases with a small value, increases again coinciding with C₁₅ afterward. For a magnetic field h = 1. The two concurrences behave very similar where they start at a finite value, decreases sharply at J′ ≈ h then increases, decreasing until it reaches a saturation value as shown in Fig. 7(c). High magnetic field effect is shown in Fig. 7(d) where again both concurrences maintain zero value until J′ ≈  1 then it increases sharply to a high maximum value, decreases again in step forms until it reaches a saturation value at high value of J′.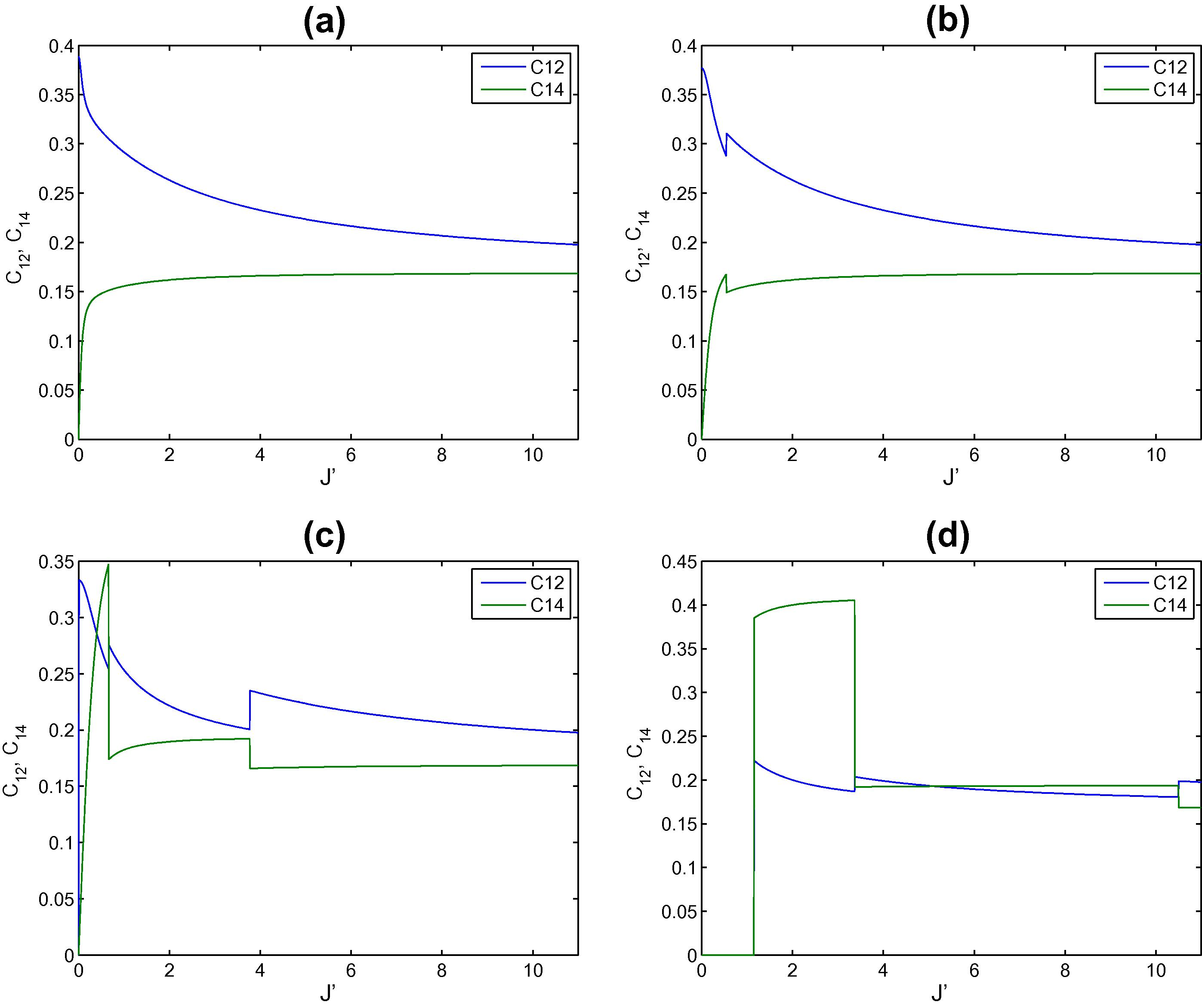

Close

Figure 6

The entanglements C₁₂ and C₁₄ versus the strength of the impurity at the central site 4 in the triangular two dimensional spin lattice at different applied magnetic field strength h equals: (a) 0.25, (b) 0.5, (c) 1 and (d) 2.

Export to PPT

Close

Figure 7

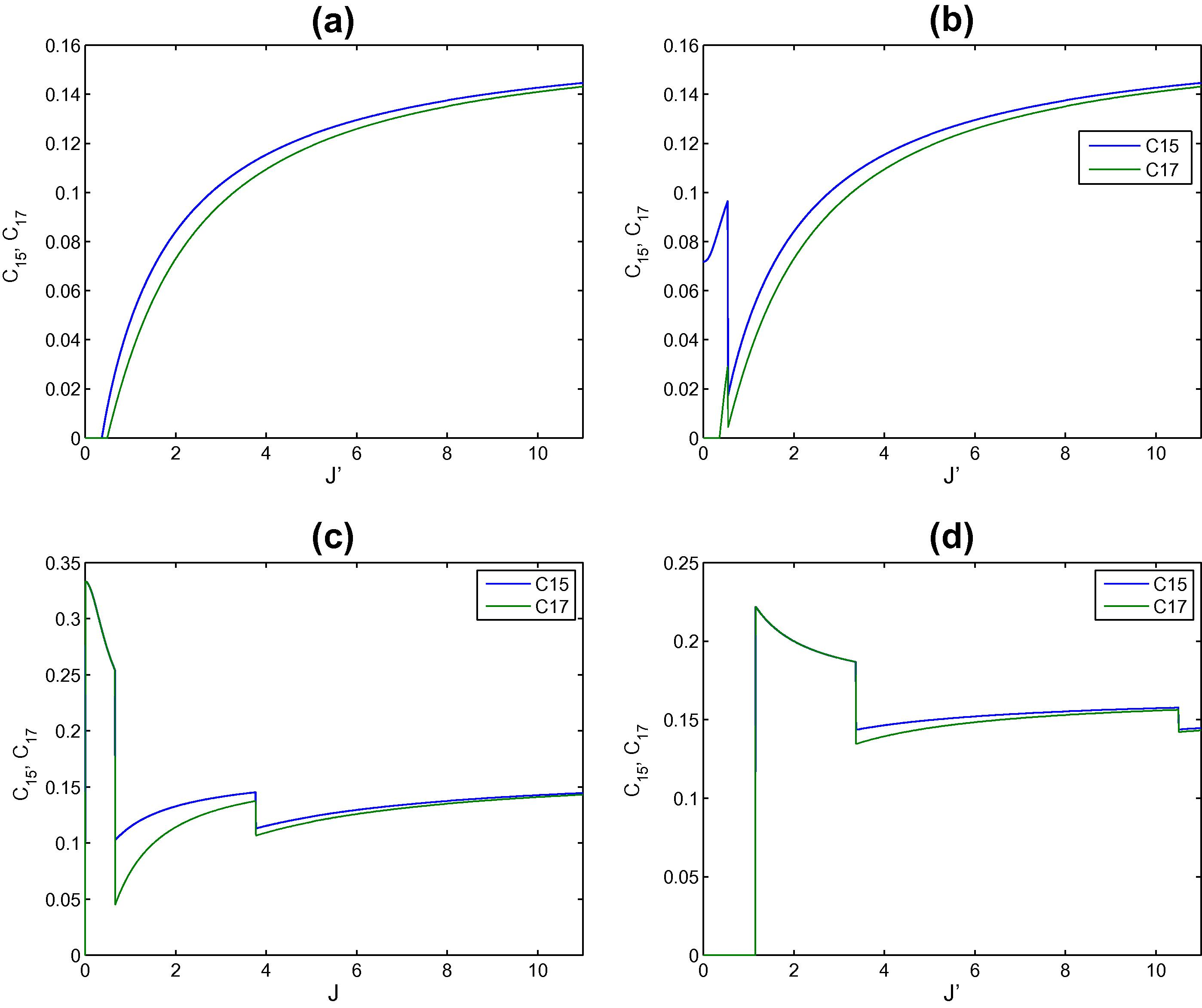
The entanglements C₁₅ and C₁₇ versus the strength of the impurity at the central site 4 in the triangular two dimensional spin lattice at different applied magnetic field strength h equals: (a) 0.25, (b) 0.5, (c) 1 and (d) 2.

Export to PPT

5 Conclusion

We investigated a two dimensional XY spin model consisting of a set of seven localized spin- $\frac{1}{2}$ particles in a two dimensional triangular lattice coupled through nearest neighbor exchange interaction in presence of an external magnetic field. We examined the effect of a single impurity spin coupled to its nearest neighbor through an exchange interaction J′ on the pairwise entanglement between the different spins in the lattice. Considering the spin located at a border site, the entanglement between the impurity and its nearest neighbors increases monotonically with J′ reaching a saturation value that depends on the magnetic field strength h. Studying the entanglement between the impurity spin and its next nearest spins shows a critical behavior as we change J′ where the entanglement increases and then decreases rapidly until it vanishes. The critical coupling value at which the entanglement vanishes depends significantly on the magnetic field strength and increases as h increases. Studying a different case for the entanglement where we focus on two spins none of them is the impurity, shows that the entanglement between two spins where each one of them is coupled to the impurity reach a saturation value as J′ increases. On the other hand for two spins where both of them are not coupled to the impurity, the entanglement vanishes as we increase J′. Turning to examining the effect of a central impurity located at site 4 show that the entanglement between nearest neighbor and next nearest neighbor spins reaches an asymptotic value as J′ increases. In all cases the entanglement shows dramatic change in the vicinity of the parameter values J′ ≈ h. Furthermore, we have shown that the impurity can be used as a switch to control the entanglement between the different spins in the lattice turning it on and off.