HAM solution of some initial value problems arising in heat radiation equations

Jafar Biazar; Behzad Ghanbari

doi:10.1016/j.jksus.2010.08.011

View/Download PDF

Buy Reprints

PDF

Translate this page into:

ORIGINAL ARTICLE

24 (

); 161-165

doi:

10.1016/j.jksus.2010.08.011

HAM solution of some initial value problems arising in heat radiation equations

Jafar Biazar^a, Behzad Ghanbari^a,b,*

a Department of Mathematics, Faculty of science Islamic Azad University, Rasht Branch, Iran

b Member of Young Researchers Club, Department of Mathematics, Faculty of Science Islamic Azad University, Rasht Branch, Iran

*Corresponding author at: Department of Nanotechnology, Kermanshah University of Technology, Kermanshah, Iran b.ghanbary@yahoo.com (Behzad Ghanbari)

Received: 2010-6-29, Accepted: 2010-8-17, Published: 2010-04-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 30 August 2010

Abstract

Mathematical modeling of many phenomena, especially in heat transfer, usually leads to a nonlinear equation. Traditional approaches for solving such equations are time consuming and difficult affairs tasks.

In this paper, based on the homotopy analysis method (HAM), a series solution for the problem of unsteady nonlinear convective–radiative equation is obtained.

In HAM, one would be able to control the convergence of approximation series and adjust its convergence region, conveniently. Ability and efficiency of proposed approach are tested via some cases of above mentioned problem.

It is found that homotopy analysis approach provides a greatly accelerated convergence series solution for problem.

Keywords

Homotopy analysis method

Heat transfer

Show Related Articles from PubMed

1 Introduction

Liao proposed the homotopy analysis method (HAM) in 1992, to get analytic approximations of highly nonlinear equations (Liao, 1992).

Unlike other existing methods, the HAM:

Provides us a simple way to ensure the convergence of solution series.
Provides great freedom to choose proper base functions.

These advantages point out the method as a powerful and flexible tool in mathematics and engineering, which can be readily distinguished from existing numerically and analytically methods.

This paper is arranged as follows; in Section 2 the basic idea of standard HAM and some its recent optimal modification are reviewed. In Section 3, the implementation of HAM on problem and some comparison discussions are presented. Finally, conclusions are drawn in Section 4.

2 Standard HAM and some its optimal modifications

Using the concept of homotopy, Liao (1992) introduced the early form of the homotopy analysis method (HAM) for a given nonlinear differential equation

(1)

N [u (x)] = 0,

(2)

(1 - p) L [U (x; p) - u_{0} (x)] = - pN [U (x; p)], p \in [0, 1] .

where

L

is an auxiliary linear operator and

u_{0} (x)

is an initial guess of the solution. It is evident that, at

p = 0

and

p = 1

, one has

U (x; 0) = u_{0} (x)

and

U (x; 1) = u (x)

, respectively.

In the view of HAM the solution of original equation is assumed to be as the power series in $p$ as

(3)

u (x) = u_{0} (x) + \sum_{i = 0}^{\infty} u_{i} (x) p^{i} .

As proved by Liao (2003), whereas (3) be convergent at

p = 1

, its limit must satisfy the original Eq. (1).

Liao introduced more artificial degrees of freedom by using the zeroth-order deformation equation in the following form (Liao, 1997a)

(4)

(1 - p) L [U (x; p) - u_{0} (x)] - c_{0} pN [U (x; p)] = 0, p \in [0, 1] .

Appling recently proposed “

m

th-order homotopy-derivative operator” (Liao, 2009)

D_{m} (ϕ) = {\frac{1}{m!} \frac{\partial^{m} ϕ}{\partial p^{m}}|}_{p = 0} .

to the both sides of (4), one reads

(5)

L [u_{m} (x) - χ_{m} u_{m - 1} (x)] = c_{0} R_{m - 1} (x),

where

R_{m - 1} (x) = D_{m - 1} (N [u (x; p)]) = {\frac{1}{(m - 1)!} \frac{\partial^{m - 1} N [u (x; p)]}{\partial p^{m - 1}}|}_{p = 0},

and

χ_{m} = \{\begin{matrix} 1, & m > 1, \\ 0, & m ⩽ 1 . \end{matrix}

In this way, the component solutions of

u_{m}, m ⩾ 1

, are not only dependent upon

x

but also the auxiliary parameter

c_{0}

As it is known, to find a proper convergence-control parameter $c_{0}$ , to get a convergent series solution or to get a faster convergent one, there is a classic way of plotting the so-called ‘‘ $c_{0}$ -curves” or ‘‘curves for convergence-control parameter”. For example, one can consider the convergence of $u^{'} (x)$ and $u^{″} (x)$ of a nonlinear differential equation $N [u (x)] = 0$ to find a region say $R_{h}$ so that, each $c_{0} \in R_{h}$ gives a convergent series solution of such kind of quantities. Such a region can be found, although approximately, by plotting the curves of these unknown quantities versus $c_{0}$ .

However, it is a pity that curves for convergence-control parameter (i.e. c₀-curves) give us only a graphically region and cannot tell us which value of gives the fastest convergent series. Recently in Mehmood et al. (2010), a misinterpreted usage of c₀-curves has reported. To find the optimal value for convergence-control parameter c₀, an optimal homotopy analysis approach has been presented in Liao (2010).

3 Appling method and comparison discussions

In this section some numerical experiments are provided to illustrate the validity of HAM approach described in Section 2.

We consider the problem of unsteady nonlinear convective–radiative equation, which in dimensionless form described as following initial value problem.

(6)

[1 + ɛ_{1} u (t)] \frac{du (t)}{dt} + u (t) + ɛ_{2} u^{4} (t) = 0, u (0) = 1 .

Recently, many authors have taken into consideration of different values of $ɛ_{1}, ɛ_{2}$ in (6) using different methods, some are discussed in Liao (1997b), Domairry and Nadim (2008), Ganji et al. (2007), Abbasbandy (2006, 2007), Marinca and Herişanu (2008) and Sajid and Hayat (2008).

Considering Eq. (6), we define

(7)

N (ϕ) = [1 + ɛ_{1} ϕ] \frac{d ϕ}{dt} + ϕ + ɛ_{2} ϕ^{4},

and

(8)

L (u) = u^{'} + u

as the auxiliary linear and nonlinear operators, respectively.

Subject to the initial condition (6) and linear operator (8), the temperature $u (t)$ can be expressed by the following set of base functions ${\exp (- kt) | k > 0},$ as the following series $u (t) = \sum_{k = 0}^{m} a_{m, k} \exp (- kt) .$

So, it is evident that initial guess should be as $θ_{0} (x) = e^{- t}$ .

We first construct the zeroth-order deformation equation defined by

(9)

(1 - p) L [u (t, p) - u_{0} (t)] = phN [u (t, p)] .

According to (5) and from initial condition (6), we have

(10)

L [u_{m} (t) - χ_{m} u_{m - 1} (t)] = {hR}_{m} (t) .

subject to initial conditions

(11)

u_{m} (0) = 0,

where

R_{m} (t) = u_{m}^{'} (x) + ɛ_{1} \sum_{i = 0}^{m} u_{i}^{'} (t) u_{m - i} (t) + u_{m} (t) + ɛ_{2} \sum_{i = 0}^{m - 1} (\sum_{j = 0}^{m - 1 - i} (\sum_{k = 0}^{m - 1 - i - j} u_{k} (t) u_{m - 1 - i - j - k} (t)) u_{j} (t)) u_{i} (t) .

The corresponding mth-order deformation equation reads $u_{m} (t) = u_{m}^{*} (t) + {Ce}^{- t} .$ where $u_{m}^{*} (t)$ is the particular solution of (10) and the constant $C$ are determined by the boundary conditions (11).

To obtain the valid values of $c_{0}$ , we have plotted the so-called $c_{0}$ -curve of 5th-order HAM approximation of $u^{″} (0)$ for different values of $ɛ_{2}$ in cases of $ɛ_{1} = 1$ , $ɛ_{1} = 2$ and $ɛ_{1} = 3$ in Figs. 1–3 , respectively.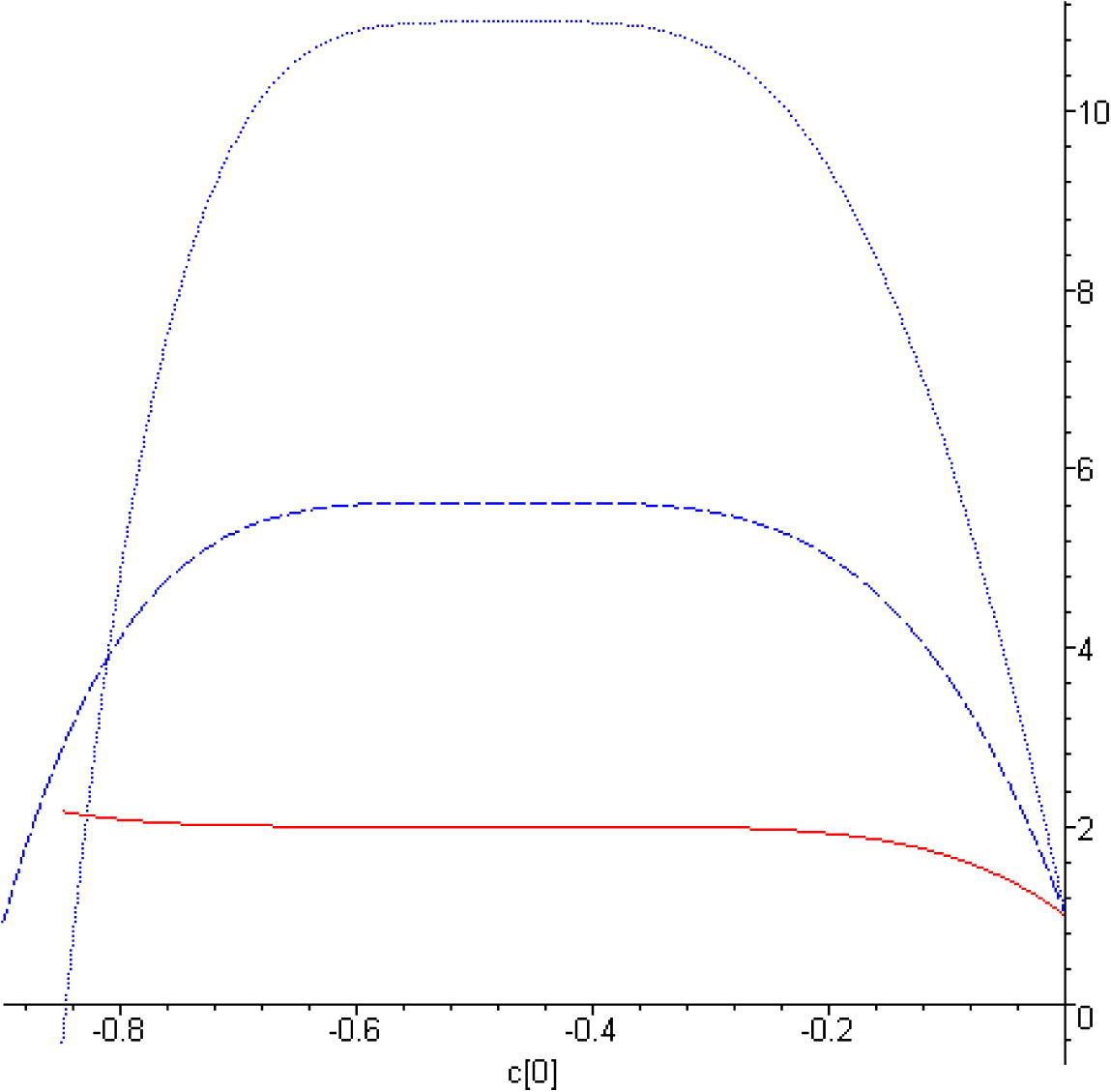

The c 0 -curves for 5th-order of HAM approximation of u ″ ( 0 ) , for ɛ 1 = 1 and different values of ɛ 2 . Solid line: ɛ 2 = 1 ; dashed line: ɛ 2 = 2 ; dotted line: ɛ 2 = 3 .

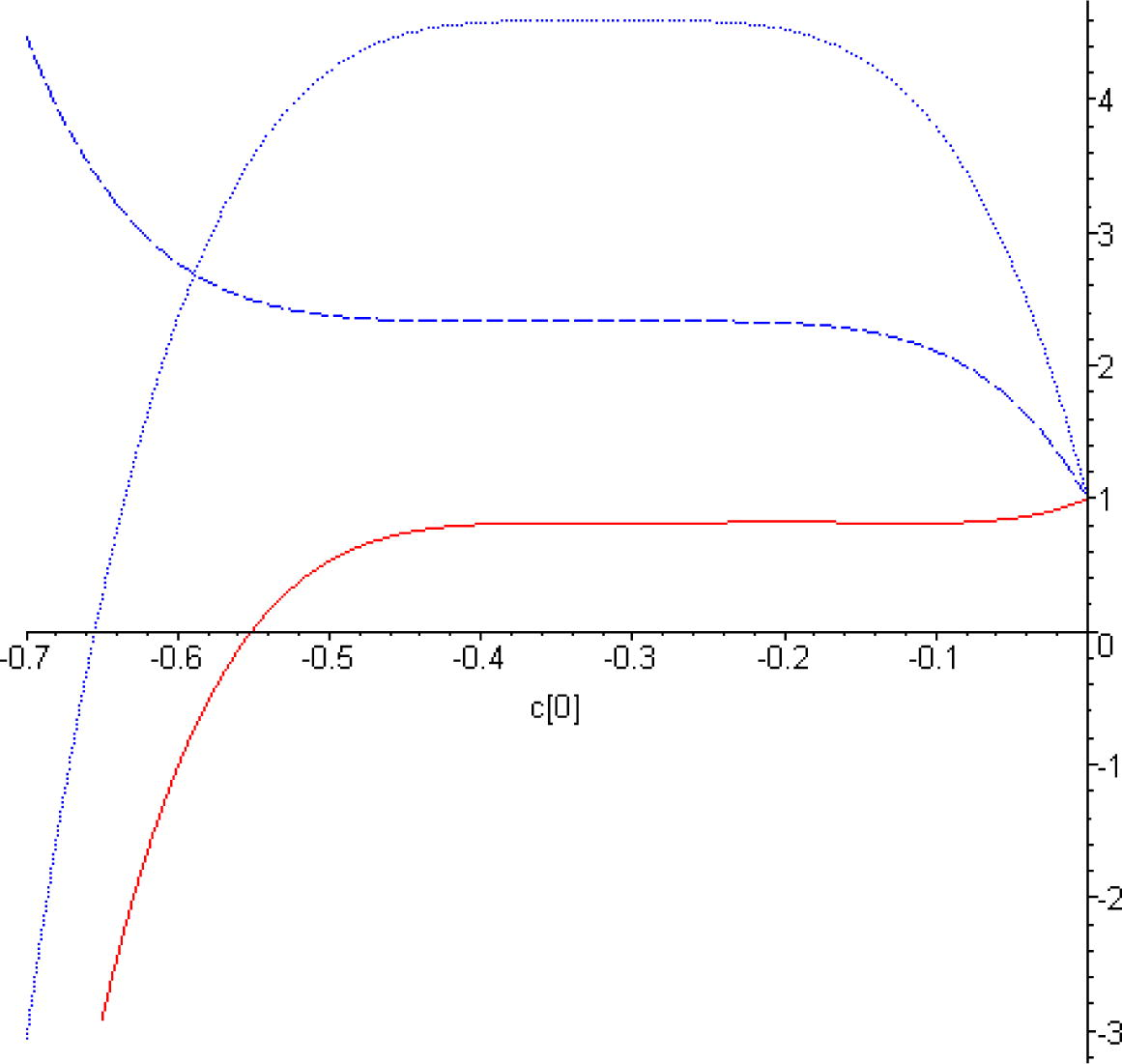
The c 0 -curves for 5th-order of HAM approximation of u ″ ( 0 ) , for ɛ 1 = 2 and different values of ɛ 2 . Solid line: ɛ 2 = 1 ; dashed line: ɛ 2 = 2 ; dotted line: ɛ 2 = 3 .

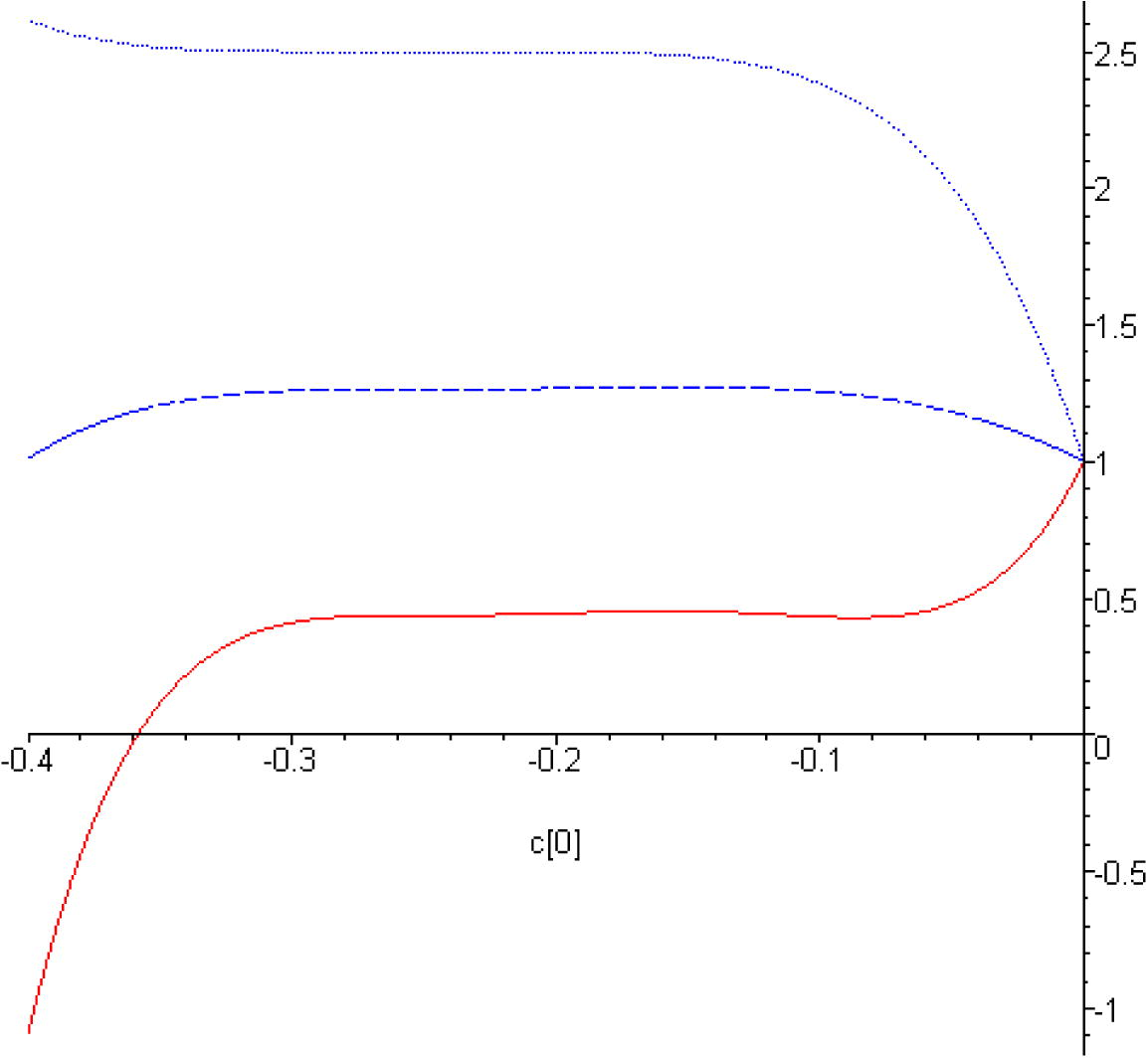
The c 0 -curves for 5th-order of HAM approximation of u ″ ( 0 ) , for ɛ 1 = 3 and different values of ɛ 2 . Solid line: ɛ 2 = 1 ; dashed line: ɛ 2 = 2 ; dotted line: ɛ 2 = 3 .

Comparisons are made between HAM and the homotopy perturbation method, HPM (HAM with $c_{0} = - 1$ ) and numerical results of the fourth order Runge–Kutta method, for some values of $ɛ_{1}, ɛ_{2}$ are plotted in Figs. 4–6 . In Tables 1–3 , results of comparisons between evaluated square residual error, similar to what was used in Niu and Wang (2010), as:

(12)

Δ_{m} = \int_{Ω} {(N [\sum_{i = 0}^{m} u_{i} (x)])}^{2} dx,

of different approaches are shown.

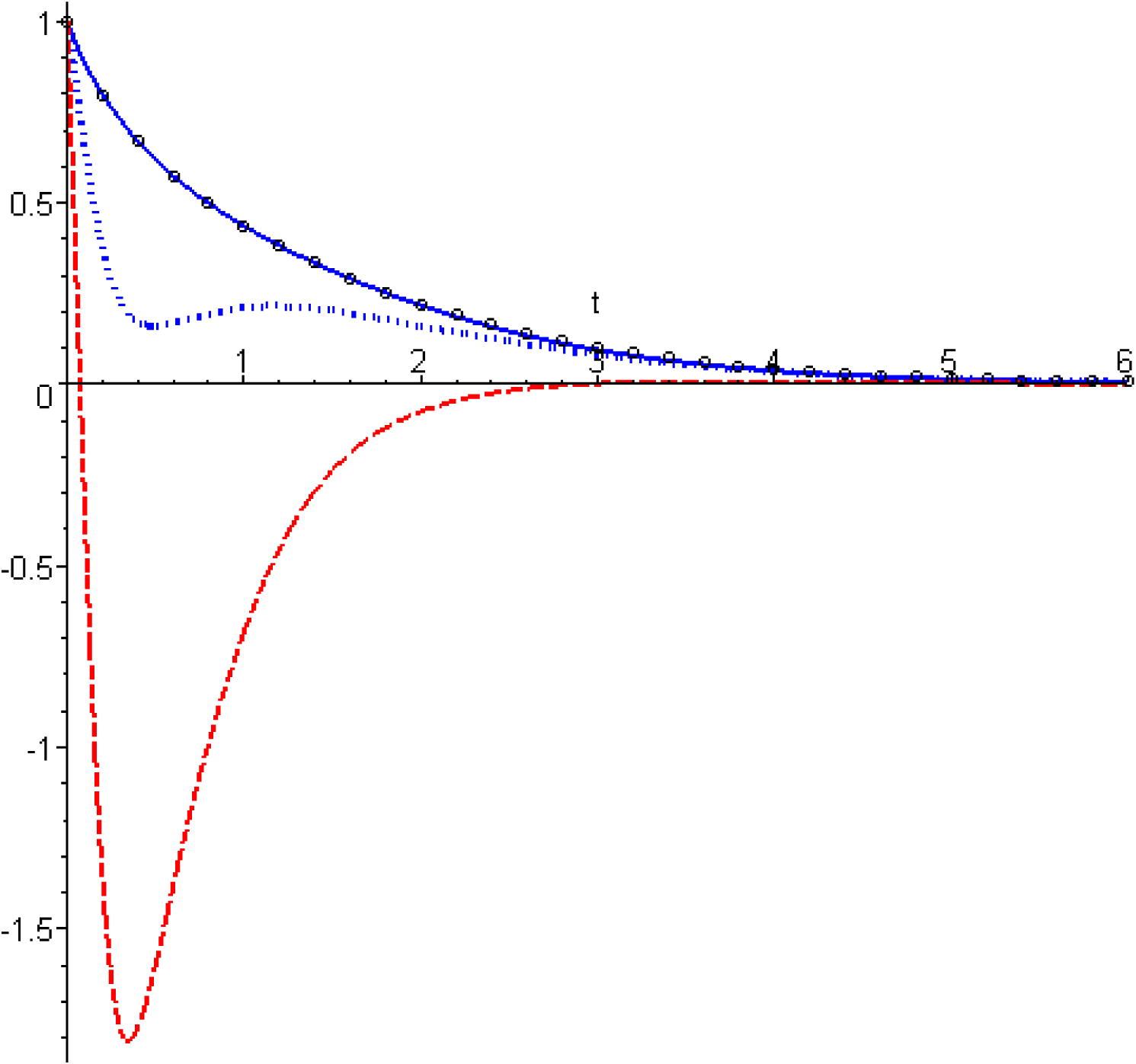
Comparison between the results obtained by the different method for ɛ 1 = 2 , ɛ 2 = 3 . Hollow symbols: numerical solution; solid line: present MHAM for h = - 1 / 3 ; dashed line: HPM; dotted line: HAM for h = - 0.8 .

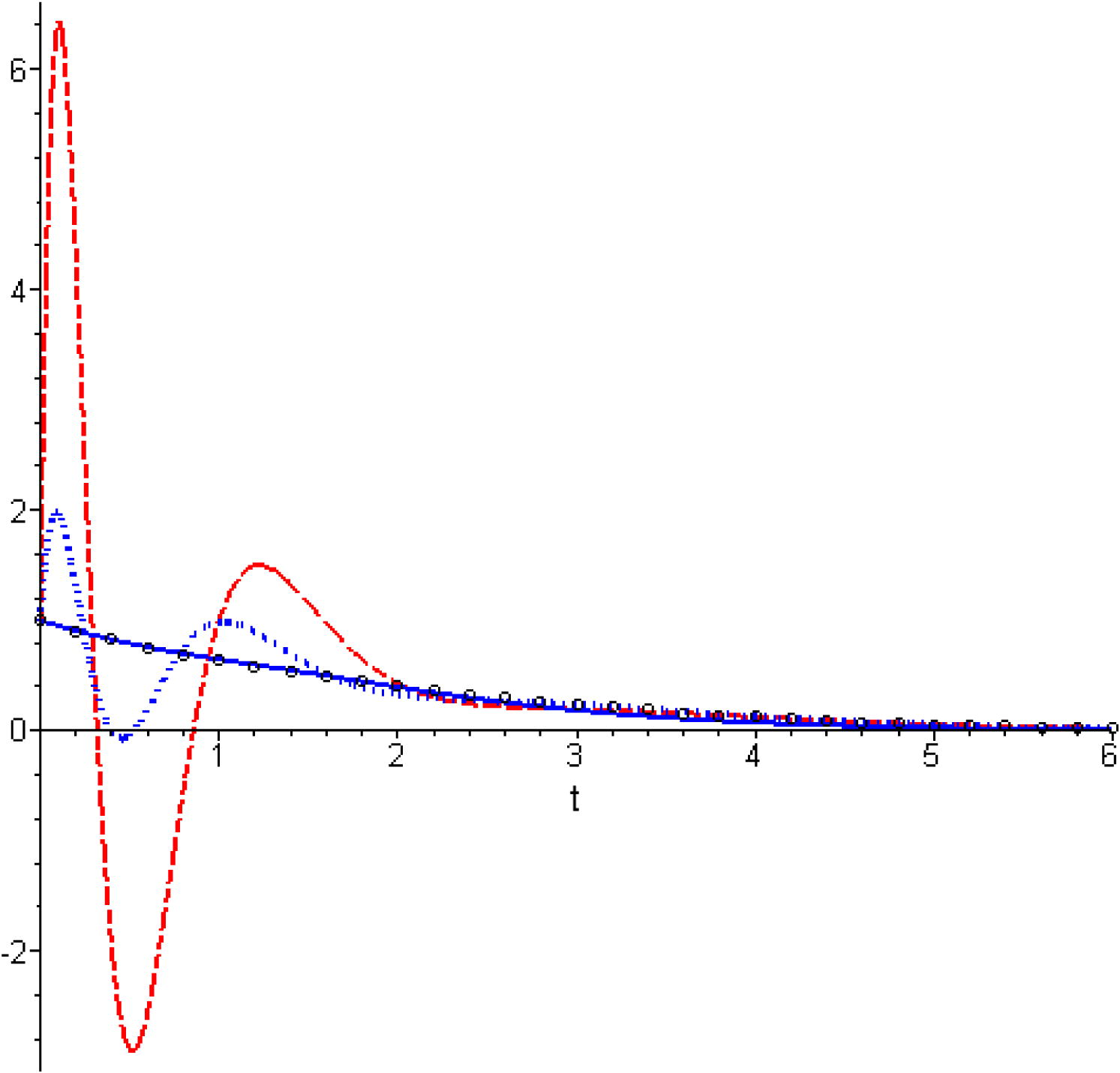
Comparison between the results obtained by the different method for ɛ 1 = 3 , ɛ 2 = 1 . Hollow symbols: numerical solution; solid line: present MHAM for h = - 1 / 4 ; dashed line: HPM; dotted line: HAM for h = - 0.8 .

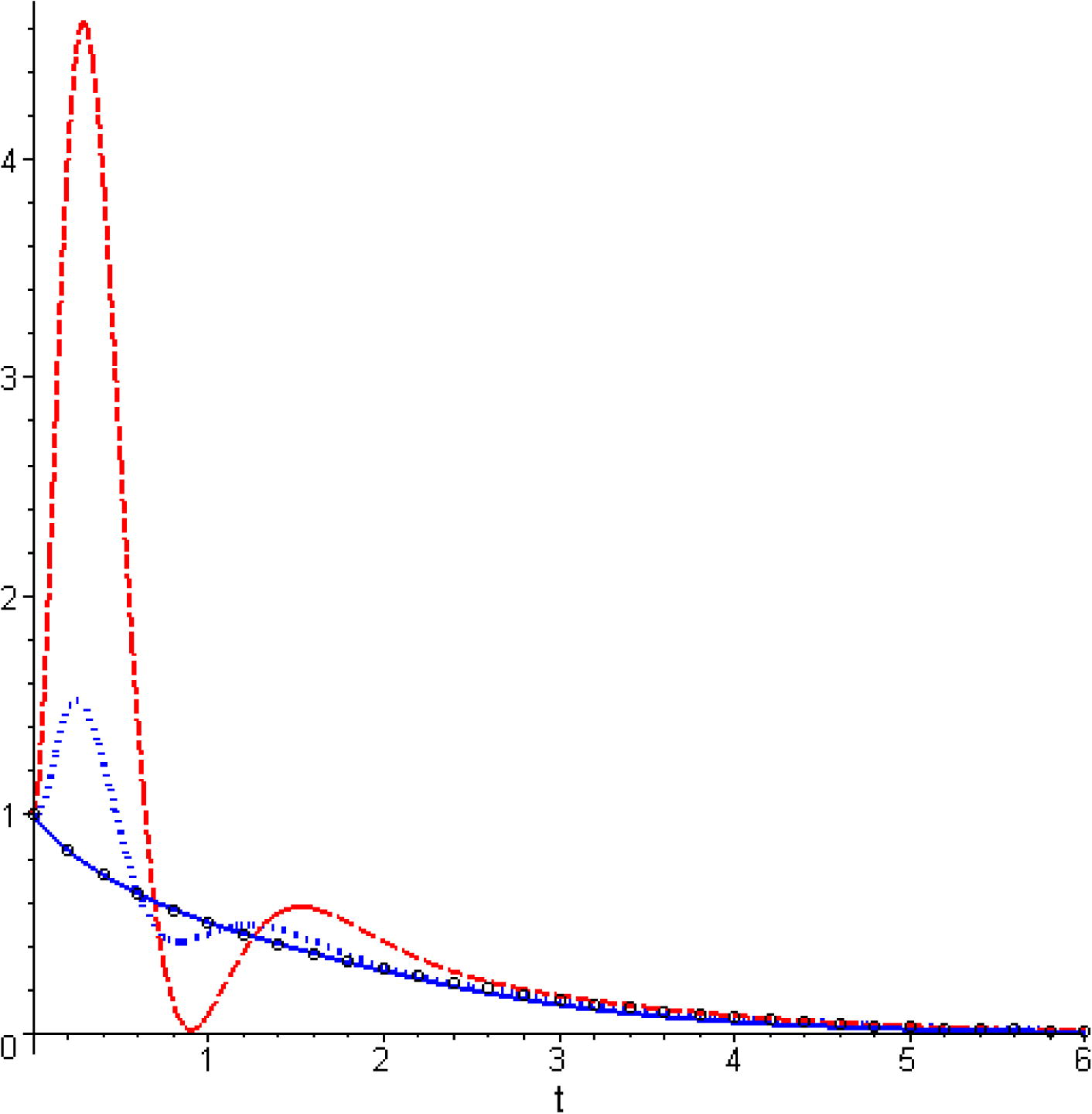
Comparison between the results obtained by the different method for ɛ 1 = 3 , ɛ 2 = 3 . Hollow symbols: numerical solution; solid line: present MHAM for h = - 1 / 4 ; dashed line: HPM; dotted line: HAM for h = - 0.8 .

Table 1 Comparisons of

Δ_{m}

of 5th-order solutions of different approaches for

ɛ_{1} = 1

	$ɛ_{2} = 1$	$ɛ_{2} = 2$	$ɛ_{2} = 3$
MHAM for $h = - 1 / 2$	0.00000645794	0.00000225316	0.00185417178
HAM for $h = - 0.8$ Abbasbandy (2007)	0.00001294614	0.06332372453	4.39671710926
HAM for $h = - 0.9$ Abbasbandy (2007)	0.00026131005	0.45943918392	270.979958125
HPM (HAM for $h = - 1$ )	0.00278084263	2.08587335265	358312.798216

Table 2 Comparisons of

Δ_{m}

of 5th-order solutions of different approaches for

ɛ_{1} = 2

	$ɛ_{2} = 1$	$ɛ_{2} = 2$	$ɛ_{2} = 3$
MHAM for $h = - 1 / 3$	0.0016937936	0.00043080927	0.00018897928
HAM for $h = - 0.8$ Abbasbandy (2007)	1.7740609725	0.29707799102	7.73726355555
HAM for $h = - 0.9$ Abbasbandy (2007)	13.500883632	2.52627773025	24.9031191524
HPM (HAM for $h = - 1$ )	86.150467589	18.0667149197	284.907280951

Table 3 Comparisons of

Δ_{m}

of 5th-order solutions of different approaches for

ɛ_{1} = 3

	$ɛ_{2} = 1$	$ɛ_{2} = 2$	$ɛ_{2} = 3$
MHAM for $h = - 1 / 4$	0.2251073087	0.007103244505	0.00301374746
HAM for $h = - 0.8$ Abbasbandy (2007)	741.25718288	527.1191196254	140.804634925
HAM for $h = - 0.9$ Abbasbandy (2007)	9333.2489875	15082.47186259	3983.73926254
HPM (HAM for $h = - 1$ )	329295.21567	14603605.62548	314587.045985

From Tables 1–3 , it seems that proposed approach gives better approximations than the compared approaches and its results are in good agreement with the exact solution.

Since the results of HPM can be obtained as a special case of HAM when $c_{0} = - 1$ , from Figs. 1–3 , it is evident that HPM losses its validity for relatively large values of $ɛ_{1}$ .

4 Concluding remarks

In this paper a initial value problem in heat transfer has been solved by means of homotopy analysis method are proposed. It is shown that HAM results are in a good agreement with numerical solution of problem. It was shown that homotopy analysis method provides a simple way to control and adjust the convergence regions of solution. It is also pointed out that HPM solutions are not converging in some cases of the understudied problem. Computations are performed by Maple11.

References

Abbasbandy S., . The application of homotopy analysis method to nonlinear equations arising in heat transfer. Phys. Lett. A. 2006;360:109-113.
[Google Scholar]
Abbasbandy S., . Homotopy analysis method for heat radiation equations. Int. Commun. Heat Mass Transf.. 2007;34:380-387.
[Google Scholar]
Domairry G., Nadim N., . Assessment of homotopy analysis method and homotopy perturbation method in non-linear heat transfer equation. Int. Commun. Heat Mass Transf.. 2008;35:93-102.
[Google Scholar]
Ganji D.D., Hosseini M.J., Shayegh J., . Some nonlinear heat transfer equations solved by three approximate methods. Int. Commun. Heat Mass Transf.. 2007;34:1003-1016.
[Google Scholar]
Liao, S.J., 1992. On the proposed homotopy analysis technique for nonlinear problems and its applications. Ph.D. dissertation, Shanghai Jio Tong University.
Liao S.J., . Numerically solving nonlinear problems by the homotopy analysis method. Comput. Mech.. 1997;20:530-540.
[Google Scholar]
Liao S.J., . General boundary element method for non-linear heat transfer problems governed by hyperbolic heat conduction equation. Comput. Mech.. 1997;20:397-406.
[Google Scholar]
Liao S.J., . Beyond Perturbation: Introduction to Homotopy Analysis Method. Boca Raton: Chapman & Hall/CRC Press; 2003.
Liao S., . Notes on the homotopy analysis method: some definitions and theorems. Commun. Nonlinear Sci. Numer. Simulat.. 2009;14:983-997.
[Google Scholar]
Liao S.J., . An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simulat.. 2010;15:2003-2016.
[Google Scholar]
Marinca V., Herişanu N., . Application of optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer. Int. Commun. Heat Mass Transf.. 2008;35:710-715.
[Google Scholar]
Mehmood, A., Munawar, S., Ali, A., 2010. Comments to: ‘‘Homotopy analysis method for solving the MHD flow over a non-linear stretching sheet (Commun. Nonlinear Sci. Numer. Simul. 14 (2009) 2653–2663)”. Commun. Nonlinear Sci. Numer. Simulat. (2010), doi:10.1016/j.cnsns.2009.12.039.
Niu Z., Wang C., . A one-step optimal homotopy analysis method for nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simulat.. 2010;15:2026-2036.
[Google Scholar]
Sajid, M., Hayat, T., 2008. Comparison of HAM and HPM solutions in heat radiation equations. Int. Commun. Heat Mass Transf. doi:10.1016/j.icheatmasstransfer.2008.08.010.