1 Introduction

The conduction of heat in solids has numerous applications in various branches of science and engineering (Holaman, 1984; Ozisik, 1993; Carslaw and Jaeger, 1959; Liukov, 1968; Mikhailov and Ozisik, 1984; Siegel and Howell, 1980; Monteiro et al., 2009). Solving the problem of transient heat diffusion in two-layer composite is mathematically difficult (Mulhholland and Cobble, 1972; Salt, 1983; Frankel et al., 1987). Because of its difficulty, these problems are mostly treated numerically with some exception where analytic solutions are presented. In the field of linear heat transfer, the transient heat diffusion equation is linearized by considering the thermal properties to be independent of temperature, furthermore, the boundary conditions are also assumed to be linear. This class of linear transient heat diffusion has been treated in detail (Holaman, 1984; Ozisik, 1993; Carslaw and Jaeger, 1959; Liukov, 1968; Mikhailov and Ozisik, 1984; Siegel and Howell, 1980) with exact, approximate, and purely numerical methods. However, when the thermophysical properties and/or the volumetric heat source become temperature dependent, the field equation becomes nonlinear. In addition, if the temperature level becomes high, radiation and/or change of phase may occur, and, as a result, the boundary conditions become nonlinear (Davies, 1988). The problems of heat diffusion with nonlinear boundary conditions appear in combustion systems (Carslaw and Jaeger, 1959; Liukov, 1968), wherein the pre-ignition heating, the particle entering a furnace and traveling toward a flame front receives heat uniformly by thermal radiation from the furnace walls and losses heat uniformly by convection to the surrounding gases.

This work presents an analysis of transient heat diffusion in the two-region composite medium which simplifies the mathematical analysis of the problem and produces a governing equation with some auxiliary conditions. However, these problems were presented in (Abdel-Hamid and Frankel, 1991; Helal, 2003; Abd-El-Malek and Helal, 2006). The paper extends this work for solving nonlinear heat problems in spherical domains. In this work, one layer is lumped by assuming a uniform temperature all over at any given instance and treating the nonlinear term in the boundary condition as a source to obtain the associated linear homogeneous problem. However, the temperature is allowed to vary with time.

The validity of the proposed formulation is examined by comparing the temperature distribution in the first layer obtained from the approximation with the temperature distribution in the same layer obtained from the exact analytic solution. In order to quantify or find the limiting criterion where stop working of the approximation occurs, the two formulations are compared for different values of Biot number and different thermal characteristics ratio.

The advantage of using the integral transform techniques is that it provides a systematic and straight-forward approach to the solution of a certain class of heat equations (Monteiro et al., 2009; Cotta and Mikhailov, 1993; Cotta, 1994; Serfaty and Cotta, 1990; Naveira et al., 2007). The method is particularly suitable for the solution of both homogeneous and nonhomogeneous boundary value problems of heat conduction. The proposed method (Abdel-Hamid and Frankel, 1991; Helal, 2003; Abd-El-Malek and Helal, 2006) will be extended to solve the heat diffusion problem in a composite spherical finite region subject to nonlinear boundary conditions due to radiation exchange at the interface according to the fourth power law. The proposed method provides a straightforward methodology for heat equation problems subject to nonlinear boundary conditions and gives an algorithm that is more efficient and simpler than the other classical schemes, so the proposed method becomes applicable to solve a wider variety of nonlinear problems over the other methods. However, it is more transparent and requires less effort to arrive at the final results.

The utilities of the given method are summarized in the following sentence; this method presents an analysis of transient heat diffusion in the two-region composite medium which simplifies the mathematical analysis of the problem and produces a governing equation with some auxiliary conditions. The proposed method reduces the two-layer problem to a one-region problem with a new set of boundary conditions which compensates the effect of the outer layer. Solving the problem of transient heat diffusion subject to nonlinear boundary conditions due to radiation exchange at the interface according to the fourth power law. Treating the nonlinear term in the boundary condition as a source is employed to obtain the associated homogeneous problem. Then the problem can be solved by any conventional method.

2 Mathematical formulation

A two-layer sphere contains an inner region 0 ⩽ r ⩽ R_in and an outer region R_in ⩽ r ⩽ R_out which are in perfect thermal contact, k₁ and k₂ are the thermal conductivities. The outer surface transfers heat to a convecting medium maintained at T_∞ and having a heat transfer coefficient h_∞. Heat transfer from the surface takes place by radiation to the enclosure. Fig. 1 illustrates a small area of solid sphere with emissivity ɛ and exchanges energy by radiation with the enclosure at temperature T_r. The transient heat conduction equation in the ith layer of the composite may be written as (Ozisik, 1993):

Close

Figure 1

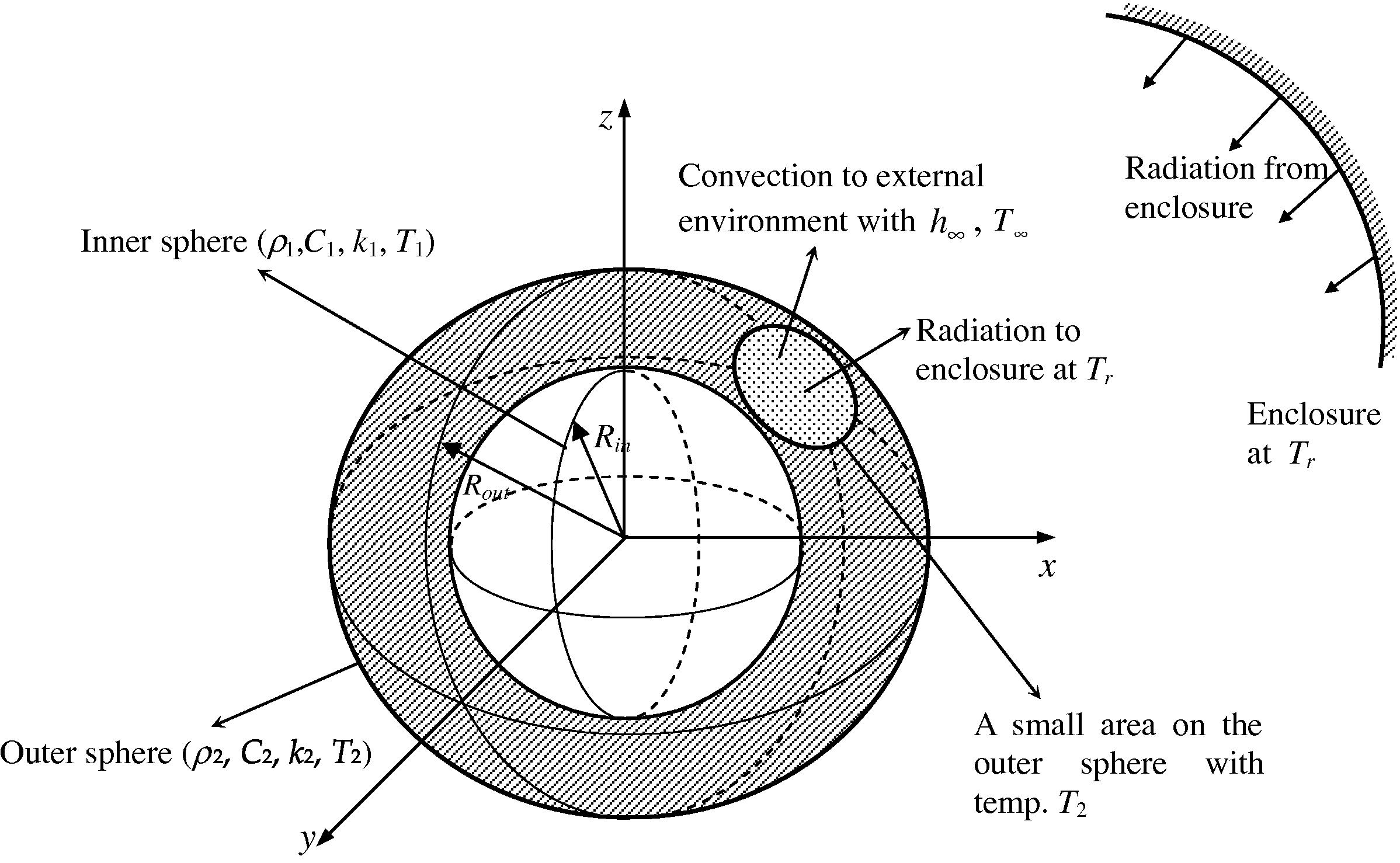
The exchanges of convection and radiation between a small area of solid sphere with the enclosure.

Export to PPT

3 Nondimensionalization

For convenience, we recast the above system of the governing equations and auxiliary conditions into a dimensionless form. Redefining the variables as follows $$\begin{array}{cc}\hfill & \chi =\frac{r}{R_{\mathit{out}}}\text{,}\tau =\frac{{\alpha }_{2}t}{R_{\mathit{out}}^2}\text{,}{\vartheta }_i(\chi \text{,}\tau )=\frac{T_i(r\text{,}t)}{T_0}\text{,}\xi =\frac{R_{\mathit{in}}}{R_{\mathit{out}}}\text{,}{\kappa }_i=\frac{k_i}{k_2}\hfill \\ \hfill & {\gamma }_i=\frac{{\alpha }_i}{{\alpha }_2}\text{,}{\beta }_{\mathit{out}}=\frac{h_{\infty }{R}_{\mathit{out}}}{k_2}\text{,}\mathrm{\Omega }=\frac{\sigma \varepsilon R_{\mathit{out}}{T}_0^3}{k_2}\text{,}{\vartheta }_r=\frac{T_r}{T_0}\text{,}{\vartheta }_{\infty }=\frac{T_{\infty }}{T_0}\hfill \\ \hfill & f(\chi \text{,}\tau \text{,}{\vartheta }_2)={\beta }_{\mathit{out}}{\vartheta }_{\infty }-\mathrm{\Omega }\left({\vartheta }_2^4(\chi \text{,}\tau )-{\vartheta }_r^4\right)\hfill \end{array}$$

Introducing these new (dimensionless) variables into the governing equations and the auxiliary to obtain the problem in the more concise form:

4 The alternative method

The first approach, a new formulation based on the work in (Abdel-Hamid and Frankel, 1991; Helal, 2003) is presented. The problem was formulated by lumping the inner layer and treating it as thin film. The inner layer of the composite sphere is lumped by assuming a uniform temperature throughout. The temperature, however, is allowed to vary with time. This assumption reduces the two-layer problem to a one-region problem with a new set of boundary conditions which compensates the effects of the second layer. Theses boundary conditions will be derived if we assume a radially averaged value of the temperature such that the quantity of heat due to the averaged temperature is equal to the quantity of heat into the inner sphere at any given instance. The equation of the temperature throughout the inner sphere is

The second approach is introduced here by solving the problem (4.7)–(4.10) discussed above by treating the nonlinearity term in the boundary condition (4.9) as a source in the differential Eq. (4.7). The nonlinear term must appear only at χ = 1, and hence we make use of the Dirac-delta function to represent the function f(χ, τ, ϑ₂) as a source at χ = 1. Also, the time dependent term in the first boundary condition (4.8) causes difficulties that arise in traditional finite integral transform technique. Treating this term as a source, the problem can be made easier to solve. The Dirac-delta function represents the term $\frac{1}{3}\xi \frac{{\kappa }_1}{{\gamma }_1}\frac{\partial {\vartheta }_2(\chi \text{,}\tau )}{\partial \tau }$ as a source at χ = ξ. The other condition is unchanged; therefore, we may consider the following equivalent problem:

5 Problem solution

The finite integral transform method is applied to determine the temperature distribution Θ₂(χ, τ). In the finite integral technique, the integral transform pair needed for the solution of a given problem is developed by considering representation of an arbitrary function in terms of the eigenfunctions corresponding to the given eigenvalue problem. Obtaining the required eigenvalue problem may be accomplished by considering the homogeneous part of the nonhomogeneous field equation and then employing separation of variables to obtain the following eigenvalue problem (Holaman, 1984; Ozisik, 1993; Carslaw and Jaeger, 1959; Liukov, 1968):

The appropriate integral transform pair can now be defined as

Integral transform:

Operating on Eq. (4.15) with ${\int }_{\xi }^1{\psi }_n(\xi )d\xi$ , we obtain:

Following the standard transformation procedures (Monteiro et al., 2009; Cotta and Mikhailov, 1993; Cotta, 1994; Serfaty and Cotta, 1990; Naveira et al., 2007) and with the aid of Eqs. (5.10) and (5.11), Eq. (5.9) reduces to the following first order nonhomogeneous ordinary differential equation:

For j = 0, 1, 2, … , we have

Consider, for n = 1, 2, …, m, that

Assume

6 Comparison between original and alternative formulations

A comparison between the solutions of the original formulation obtained from a numerical solution developed using an explicit finite difference method (Ozisik, 1993 pp. 436–498) and the alternative formulation obtained by solving the outer sphere after lumping the inner sphere as discussed in the previous section. To determine the parameters needed for a valid comparison, all the dimensionless variables which appeared in both solutions were examined. By inspection of these parameters, it is easy to conclude that the Biot number of the outer sphere (β_out), thickness ratio (ξ), thermal conductivity ratio (κ_i), the thermal diffusivity (γ_i) and the nonlinearity term Ω are the dimensionless parameters required for a valid comparison. The effect of each parameter is examined by allowing one parameter at a time to vary, while keeping the remaining parameters fixed. The study is conducted for a wide range of values of each parameter, however, only representative results are displayed in Figs. 3–11. In all figures, solid lines denote the results from the exact formulation (two-region composite) and dotted lines represent the results from the alternative formulation (lumped).

The effect of the thermal diffusivity γ₁ results in little deviation between the original and alternative formulations as shown in Figs. 2 and 3 when ξ, β_out, Ω and κ₁ are kept at fixed values. The difference in dimensionless temperature predicted from the two solution methods is within (0.1–0.5%).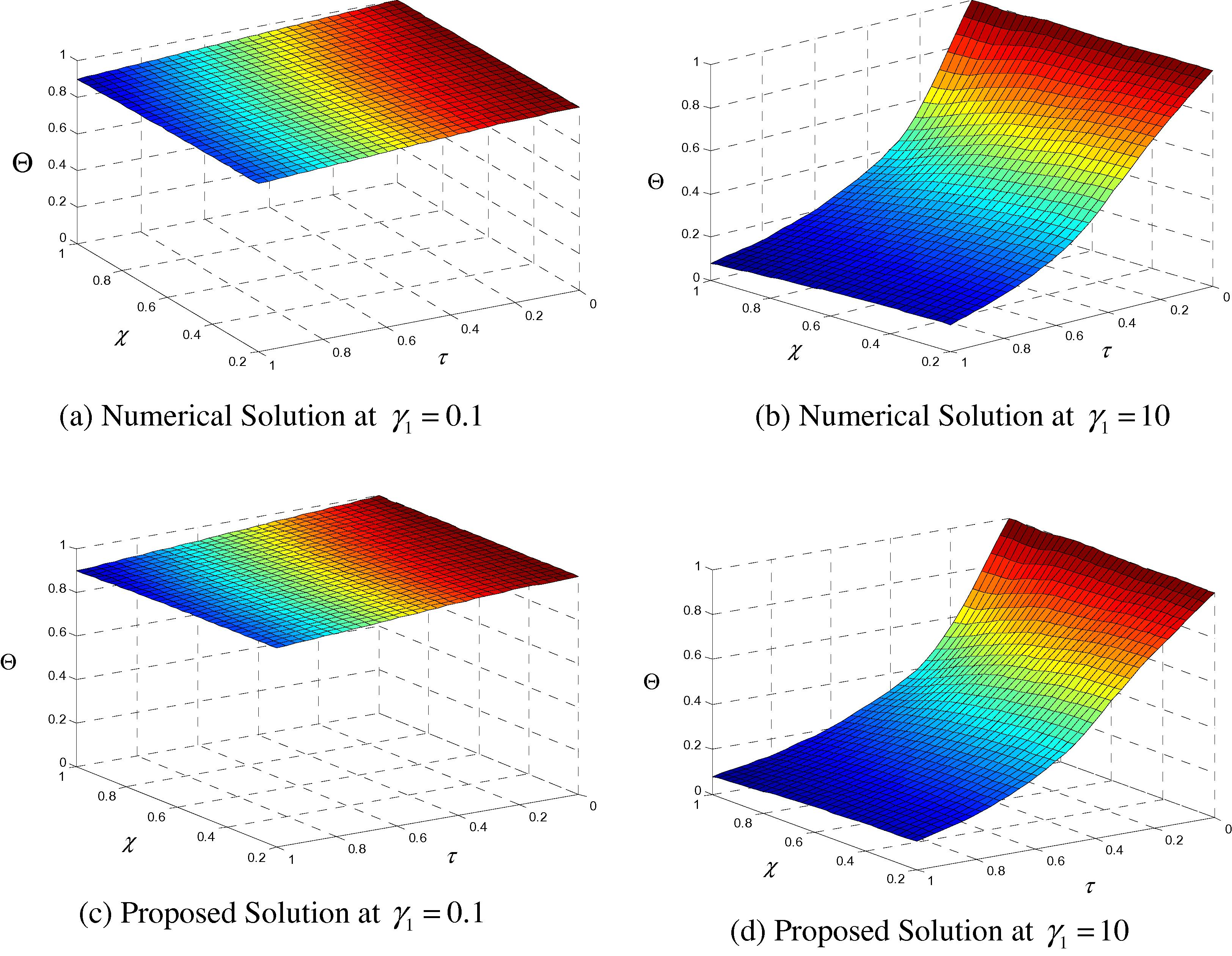

Close

Figure 2

Dimensionless temperature as a function of the radius variation for different thermal diffusivity ratio values and for (β  = 1, Ω = 0, κ₁ = 10 and ξ = 0.2).

Export to PPT

Close

Figure 3

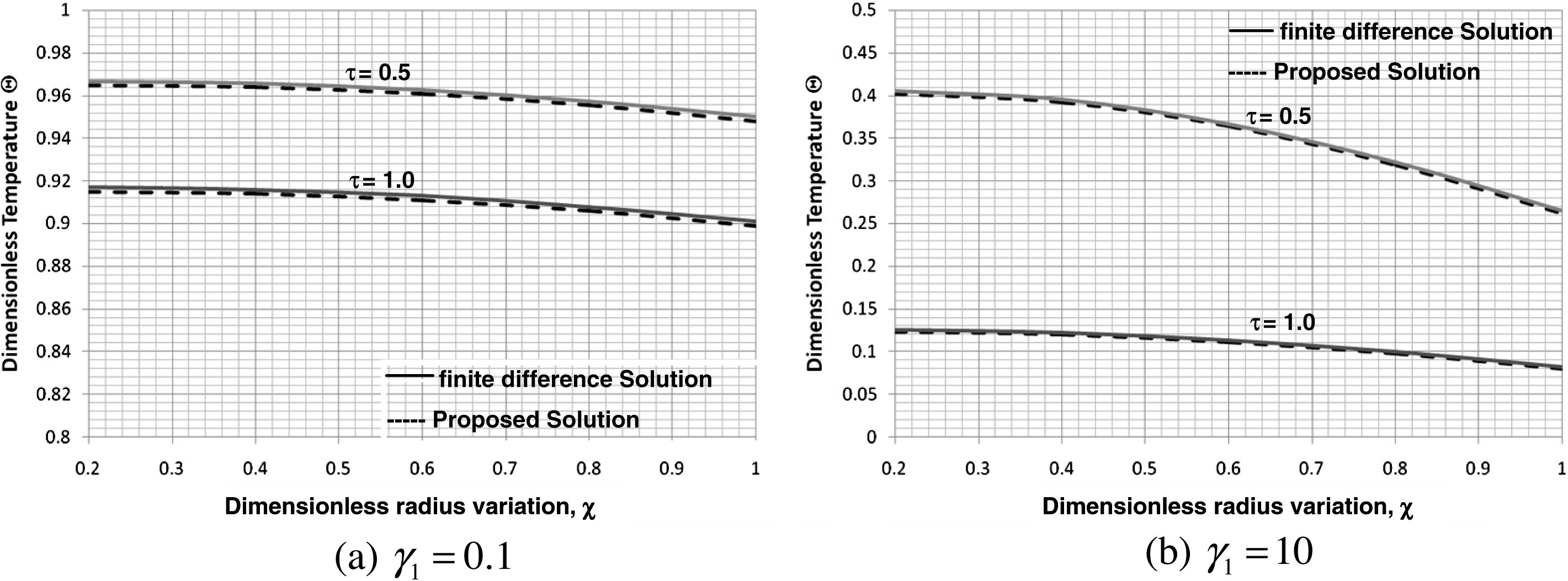
Effect of thermal diffusivity ratio on the accuracy of the proposed solution (β = 1, Ω = 0, κ₁ = 10 and ξ = 0.2).

Export to PPT

The effect of the thermal conductivity ratio κ₁ on the temperature distribution from both the original and alternative formulations is displayed in Figs. 4 and 5. The difference between the original and alternative formulations decreases as κ₂ increases. A maximum difference of about 14% at κ₂ = 0.5 decreases to 0.02% at κ₂ = 10.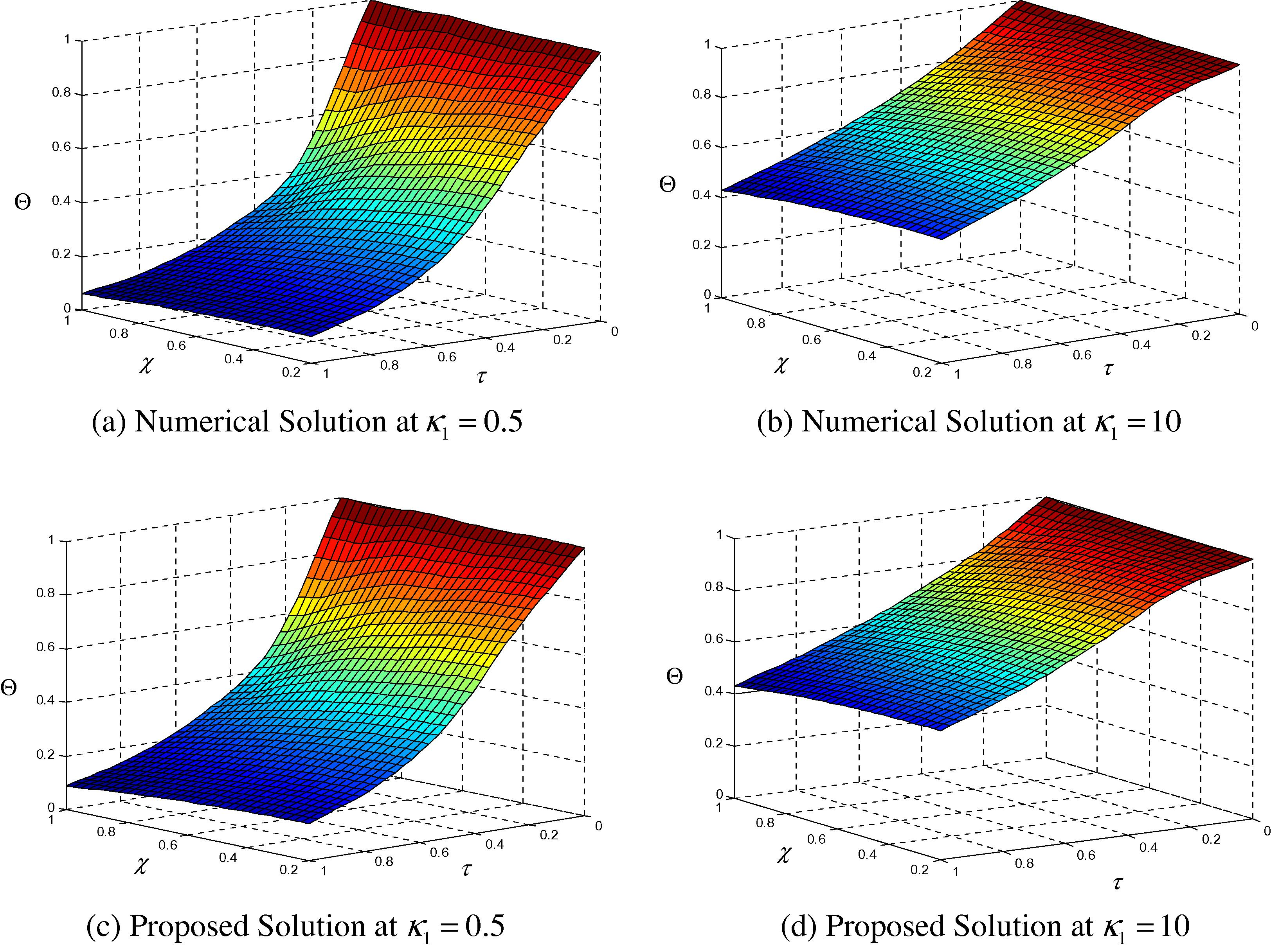

Close

Figure 4

Dimensionless temperature as a function of the radius variation for different thermal conductivity ratio values and for (β  = 1, Ω = 0, γ₁ = 1 and ξ = 0.2).

Export to PPT

Close

Figure 5

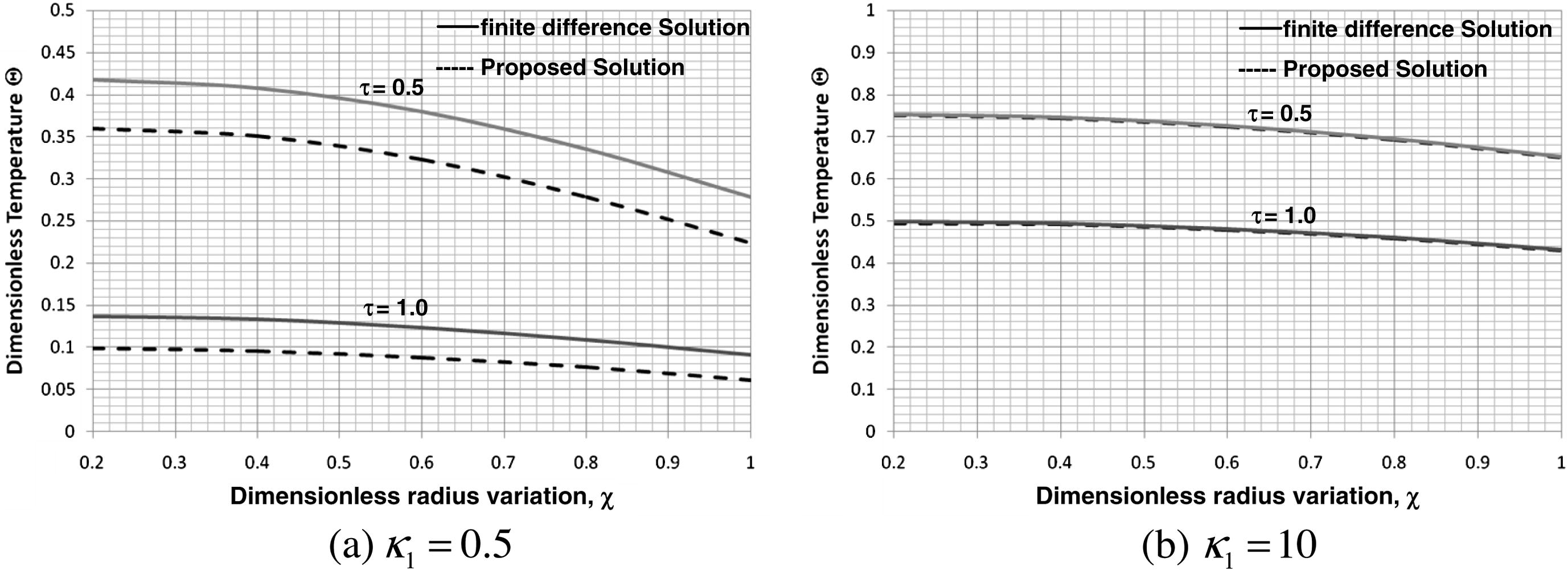
Effect of thermal conductivity ratio on the accuracy of the proposed solution (β = 1, Ω = 0, γ₁ = 1 and ξ = 0.2).

Export to PPT

Figs. 6 and 7 display the effect of thickness ratio ξ on the two formulations. Results show that the difference between the original and alternative formulations increases as ξ increases. A maximum difference of about 5% is calculated when ξ = 0.6.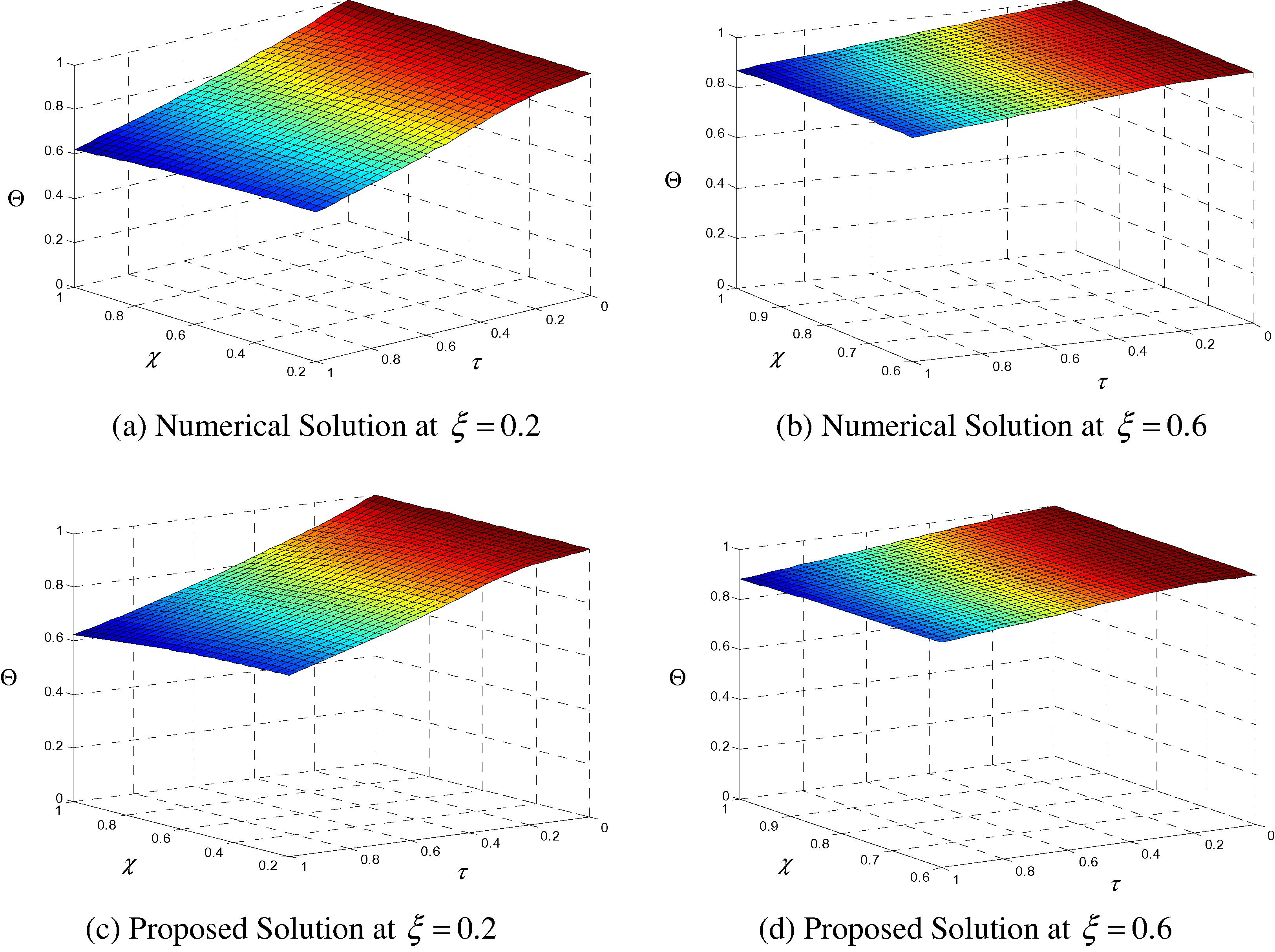

Close

Figure 6

Dimensionless temperature as a function of the radius variation for different radius variation ratio values and for (β = 1, Ω = 0, γ₁ = 0.5, and κ₁ = 10).

Export to PPT

Close

Figure 7

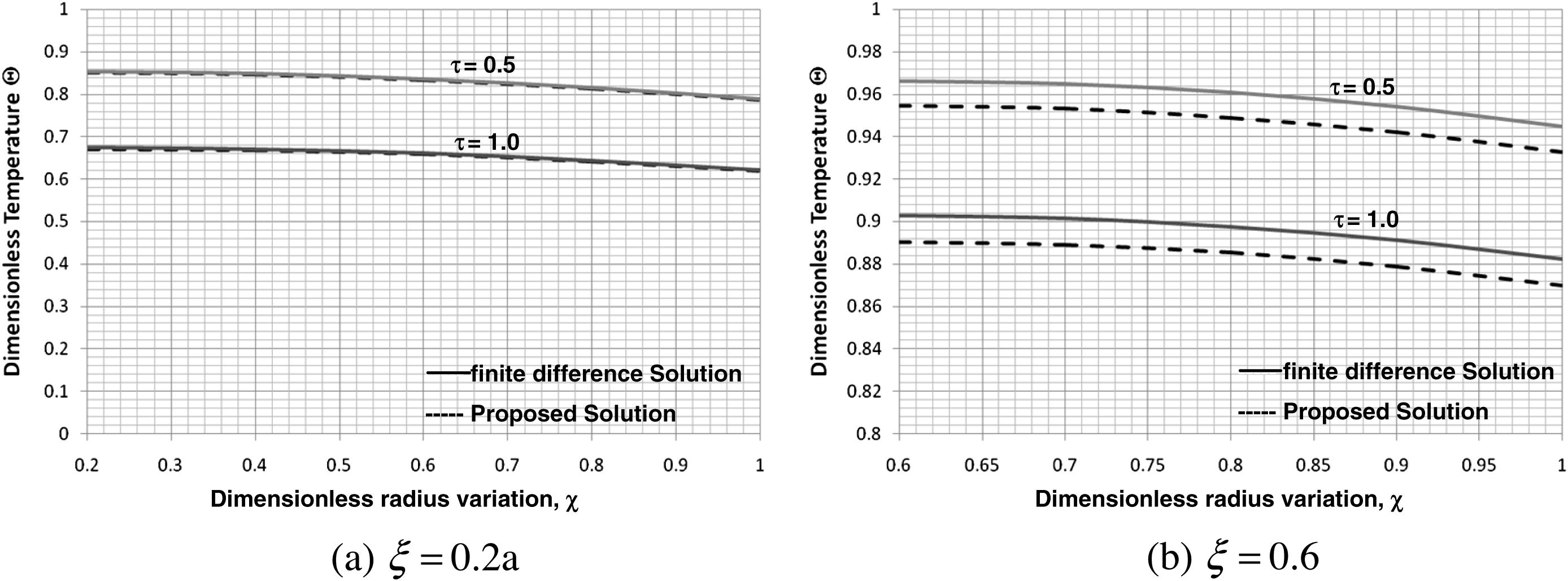
Effect of radius variation ratio on the accuracy of the proposed solution (β = 1, Ω = 0, γ₁ = 0.5, and κ₁ = 10).

Export to PPT

Figs. 8 and 9 display the effect of Biot number β_in on the two formulations. The difference between the original and alternative formulations is also increased as β_out increases. A maximum difference of 4% occurs when β_out = 10.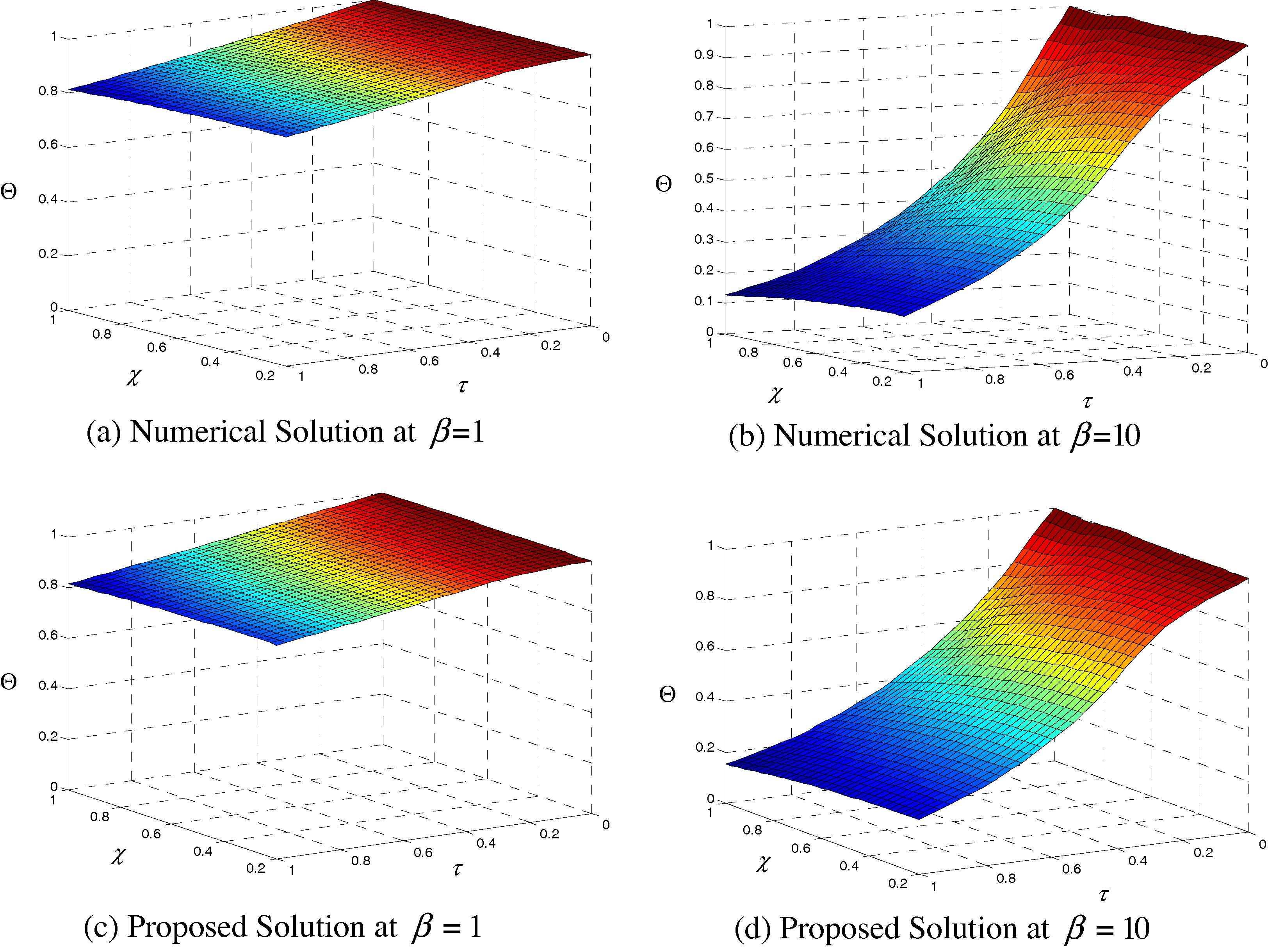

Close

Figure 8

Dimensionless temperature as a function of the radius variation for different values of Biot number and for (Ω = 0, γ₁ = 0.1, κ₁ = 5 and ξ = 0.2).

Export to PPT

Close

Figure 9

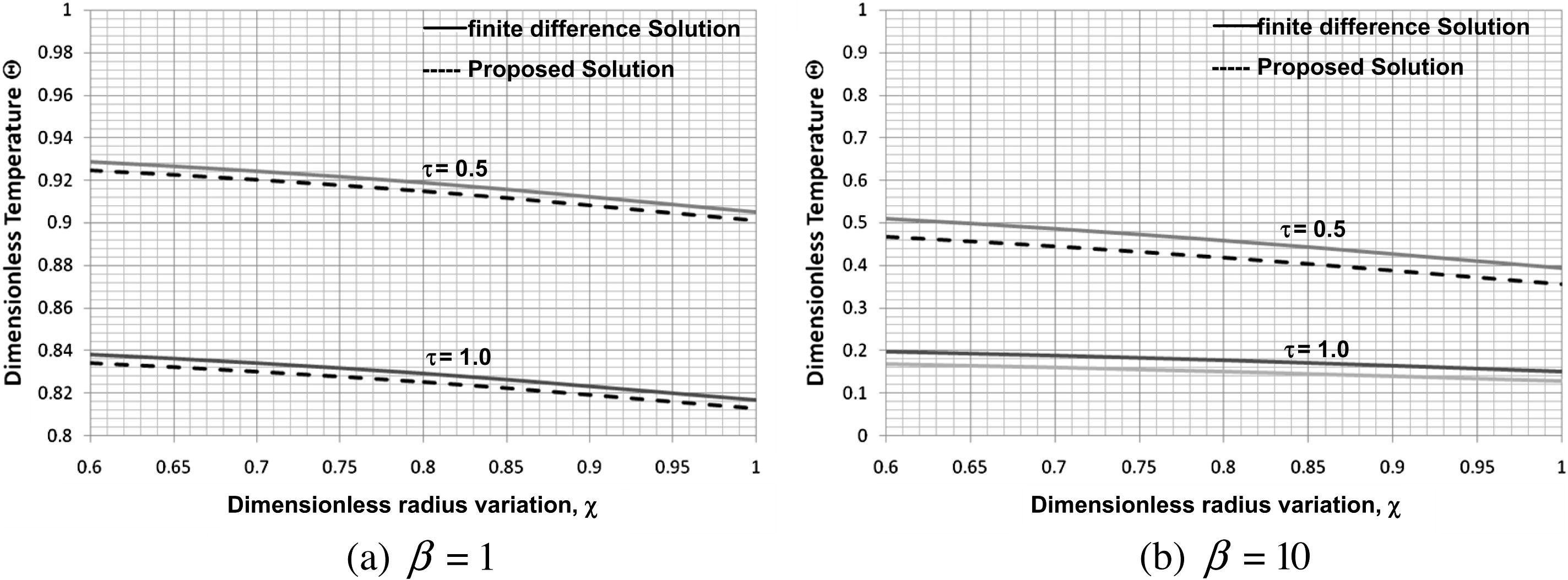
Effect of Biot number on the accuracy of the proposed solution (Ω = 0, γ₁ = 0.1, κ₁ = 5 and ξ = 0.2).

Export to PPT

The effect of stronger nonlinearity Ω is considered by taking Ω = 2 as in Figs. 10 and 11. A difference within (0.1% to 0.4%) between the two solutions was noticed.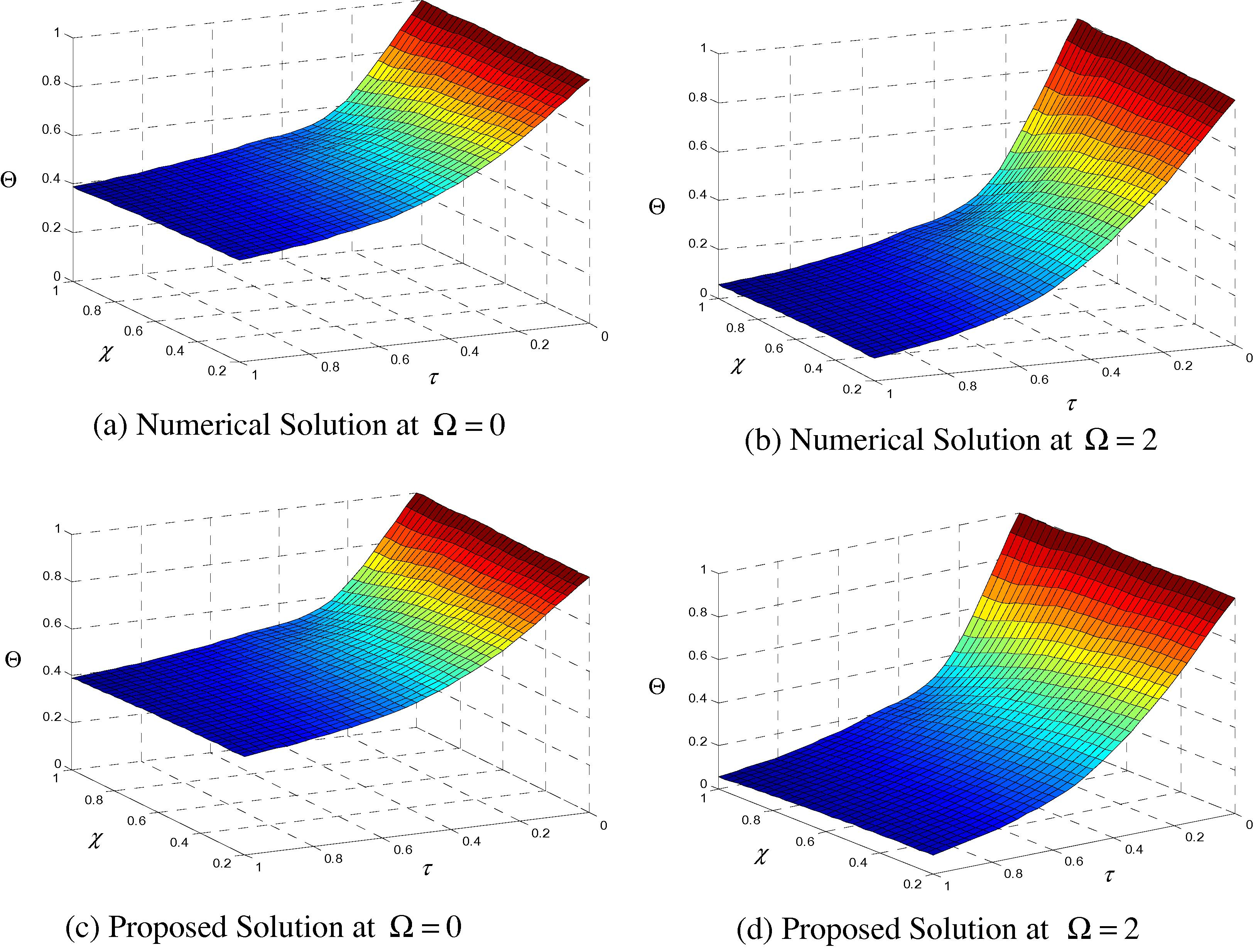

Close

Figure 10

Dimensionless temperature as a function of the radius variation at the existence of nonlinear term Ω and for (β  = 0.1, γ₁ = 1, κ₁ = 1 and ξ = 0.2).

Export to PPT

Close

Figure 11

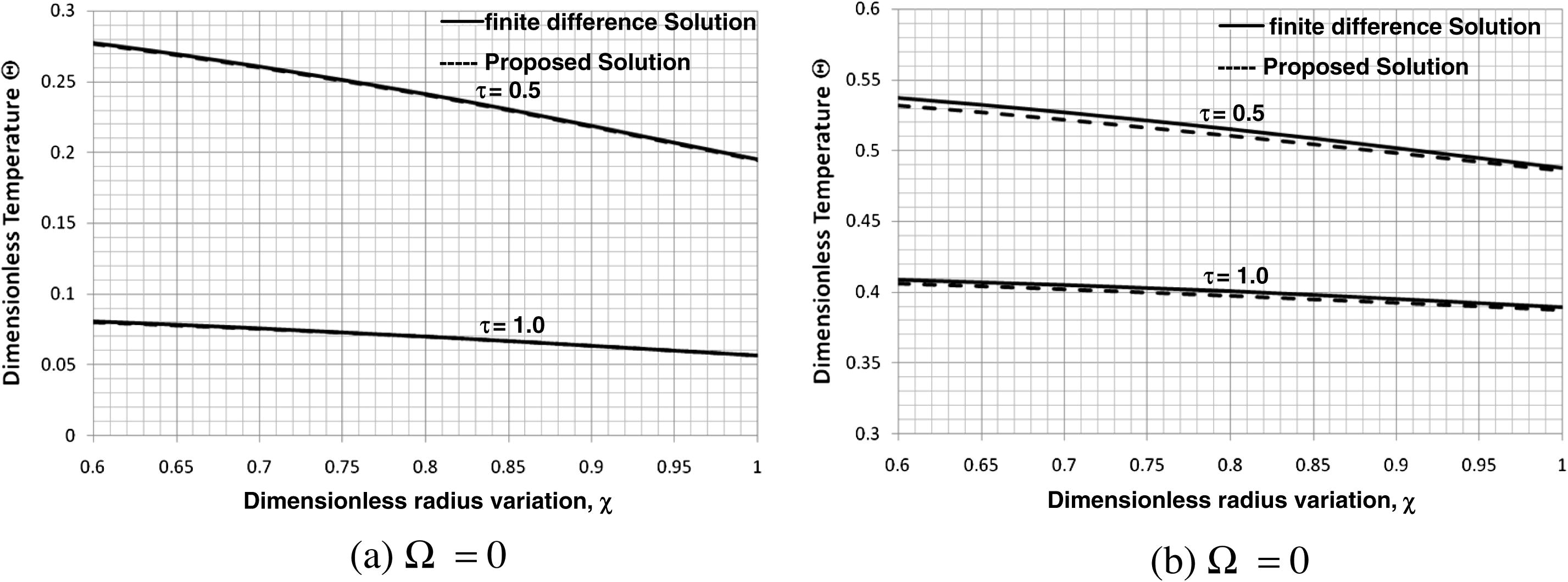
Effect of the nonlinear term Ω on the accuracy of the proposed solution (β = 0.1, γ₁ = 1, κ₁ = 1 and ξ = 0.2).

Export to PPT

By the aid of the all cases studied, we can find that an acceptable factor is always achieved for using the lumped layer approximation. An acceptable approximation occurs when:

7 Conclusion

New formulation for the transient heat conduction problem in a two-layer composite sphere subject to a nonlinear boundary condition due to coupled convection–radiation heat exchange was considered. The problem was formulated by lumping the inner layer and treating it as thin film. The validity of the alternative formulation was examined by comparing the temperature distribution obtained from the alternative formulation to that obtained from the original formulation. The obtained results from the proposed approach are consistent with the results that were obtained from the explicit finite difference method. It was found from the numerical results that the thermal diffusivity ratio, has little effect on the approximation. Results show that the difference between the solutions of original and alternative formulations increases as thickness ratio increases. The difference between the solutions of original and alternative formulations also increases as the Biot number increases. The effect of stronger nonlinearity Ω is considered by taking Ω = 2. A difference within (0.1–0.4%) between the two solutions was noticed. It was also shown that a reasonable approximation can be achieved if the Biot number of the inner layer multiplying by the nonlinear term is less than (0.1).