Fully developed MHD natural convection flow in a vertical annular microchannel: An exact solution

Basant K. Jha; Babatunde Aina; Sani Isa

doi:10.1016/j.jksus.2014.12.002

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

27 (

); 253-259

doi:

10.1016/j.jksus.2014.12.002

Fully developed MHD natural convection flow in a vertical annular microchannel: An exact solution

Basant K. Jha, Babatunde Aina^*, Sani Isa

Department of Mathematics, Ahmadu Bello University, Zaria, Nigeria

*Corresponding author. Tel.: +234 8063178775 ainavicdydx@gmail.com (Babatunde Aina),

Received: 2014-9-30, Accepted: 2014-12-2, Published: 2014-07-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 9 December 2014

Peer review under responsibility of King Saud University.

Abstract

An exact solution of steady fully developed natural convection flow of viscous, incompressible, electrically conducting fluid in a vertical annular micro-channel with the effect of transverse magnetic field in the presence of velocity slip and temperature jump at the annular micro-channel surfaces is obtained. Exact solution is expressed in terms of modified Bessel function of the first and second kind. The solution obtained is graphically represented and the effects of radius ratio (η), Hartmann number (M), rarefaction parameter (β_vKn), and fluid–wall interaction parameter (F) on the flow are investigated. During the course of numerical computations, it is found that an increase in Hartmann number leads to a decrease in the fluid velocity, volume flow rate and skin friction. Furthermore, it is found that an increase in curvature radius ratio leads to an increase in the volume flow rate.

Keywords

Annular micro-channel

Natural convection

Hartmann number

Velocity slip and temperature jump

Show Related Articles from PubMed

Nomenclature

B₀: constant magnetic flux density
C_ρ₀: specific heat at constant pressure
F: fluid–wall interaction parameter, β_t/β_ν
g: gravitational acceleration
k₁: radius of the inner cylinder
k₂: radius of the outer cylinder
Kn: Knudsen number, $λ / w$
M: Hartmann number
q: volume flow rate
Q: dimensionless volume flow rate
Pr: Prandtl number
r: dimensional radial coordinate
R: dimensionless radial coordinate
$\hat{R}$: specific gas constant
T: temperature of fluid
T₀: reference temperature
T₁: temperature at outer surface of the inner cylinder
u: axial velocity
U: dimensionless axial velocity
w: dimensional gap between the cylinders
σ_t, σ_v: thermal and tangential momentum accommodation coefficients, respectively

α: thermal diffusivity
β₀: coefficient of thermal expansion
β_t, β_v: dimensionless variables
γ: ratio of specific heats
μ₀: dynamic viscosity
θ: dimensionless temperature
ρ₀: density
ν: fluid kinematic viscosity (μ₀/ρ₀)
η: ratio of radii (k₁/k₂)
$λ$: molecular mean free path
k₀: thermal conductivity
σ: electrical conductivity of the fluid
τ: skin-friction

1 Introduction

Recently, a growing interest in micro-channel fluid mechanics and heat transfer has emerged because of possible cooling applications in space systems, manufacturing and material processing operations, and in high-power-density chips in supercomputers and other electronics (Al-Nimr and Khadrawi, 2004) . As this area continues to grow, it becomes increasingly important to understand the mechanisms and fundamental differences involved with fluid mechanics and heat transfer mechanisms in macro-channel and micro-channel.

A series of investigations have been conducted recently in the field of micro geometry flow. However, to cite a few works in this direction, Chen and Weng (2005) analytically studied the fully developed natural convection in open-ended vertical parallel plate micro-channel with asymmetric wall temperature distribution in which the effect of rarefaction and fluid wall interaction was shown to increase the volume flow rate and decrease the heat transfer. This result is further extended by taking into account suction/injection on the micro-channel walls by Jha et al. (2014). They concluded that skin frictions as well as the rate of heat transfer are strongly dependent on suction/injection parameter. In another work, Weng and Chen (2009) studied the impact of wall surface curvature on steady fully developed natural convection flow in an open-ended vertical micro-annulus with an asymmetric heating of the annulus surface. Recently, Jha et al. (in press) further extended the work of Weng and Chen (2009) by taking into account suction/injection on a vertical annular micro-channel. They discovered that skin-friction decreases at the outer surface of the inner porous cylinder with an increase of fluid–wall interaction parameter in the case of injection at the outer surface of the inner porous cylinder and simultaneous suction at inner surface of the outer porous cylinder while the result is just reverse at the inner surface of outer porous cylinder. In a related article, Avci and Aydin (2009) studied the fully developed mixed convective heat transfer of a Newtonian fluid in a vertical micro-annulus between two concentric micro-tubes. Recently, Jha and Aina (2014) further extended the work of Avci and Aydin (2009) to the case when the vertical micro-annulus formed by two concentric micro-tubes is porous, i.e. where there is suction or injection through the annulus surfaces.

On the other hand, the MHD phenomenon has received considerable attention during the last two decades due to its importance from the energy generation point of view, and one may envisage MHD generators for power generation. MHD pumps are already in use in chemical energy technology for pumping electrically conducting fluids at some of the atomic energy centres. Besides these applications, when the fluid is electrically conducting, the free convection flow is appreciably influenced by an imposed magnetic field. Therefore, to refer to few works in this direction, Sheikholeslamia et al. (2014a) investigated the magnetic field effect on nanofluid flow and heat transfer in a semi-annulus enclosure via control volume based finite element method. Khan and Ellahi (2008) observed the effects of magnetic field and porous medium on some unidirectional flows of a second grade fluid. Farhad et al. (2012) examines the slip effect on hydromagnetic rotating flow of viscous fluid through a porous space. In another work, Ali et al. (2012) investigated the effects of slip condition on the unsteady magnetohydrodynamics (MHD) flow of incompressible viscoelastic fluids in a porous channel under the influence of transverse magnetic field and Hall current with heat and mass transfer. An analysis to investigate the combined effects of heat and mass transfer on free convection unsteady magnetohydrodynamics (MHD) flow of the viscous fluid embedded in a porous medium is presented by Ali et al. (2013a)

Some recent works related to the present investigation are found in the literature (Ali et al., 2013b, 2014; Sheikholeslamia et al., 2014b; Sheikholeslami et al., 2012a,b; Ashorynejad et al., 2013 ). In Ali et al. (2013b), Farhad et al. presented an exact analysis of combined effects of radiation and chemical reaction on the magnetohydrodynamics (MHD) free convection flow of an electrically conducting incompressible viscous fluid over an inclined plate embedded in a porous medium. Ali et al. (2014) studied the unsteady free convection flow of a second grade fluid past an isothermal vertical plate oscillating in its plane with constant viscosity. Also, Sheikholeslamia et al. (2014b) studied the magnetohydrodynamic effect on natural convection heat transfer of Cu–water nanofluid in an enclosure with a hot elliptic cylinder. Sheikholeslami et al. (2012a) numerically examined the natural convection of nanofluids in a concentric annulus between a cold outer square cylinder and a heated inner circular. Flow and heat transfer of a nanofluid over a stretching cylinder in the presence of magnetic field has been investigated by Ashorynejad et al. (2013). Recently, Sheikholeslami et al. (2012b) presented the numerical solution for natural convection of nanofluids in a cold outer circular enclosure containing a hot inner sinusoidal cylinder. Sheikholeslamia et al. (2013) carried out a numerical investigation on natural convection nanofluid flow in a half annulus enclosure with one wall under constant heat flux in the presence of a magnetic field.

However, to the best knowledge of the authors, no studies have been carried out on the fully developed MHD natural convection flow in a vertical annular micro-channel. This prompts the present work.

2 Mathematical analysis

The flow considered is a fully developed steady natural convection flow of viscous, incompressible, electrically conducting fluid in vertical annular micro-channel under the effect of transverse magnetic field as presented in Fig. 1. The X-axis is parallel to the gravitational acceleration g but in the opposite direction while the r-axis is in the radial direction. The radius of the inner and outer cylinder walls are k₁ and k₂ respectively. A magnetic field of uniform strength B₀ is assumed to be applied in the direction perpendicular to the direction of flow. It is assumed that the magnetic Reynolds number is very small, which corresponds to negligibly induced magnetic field compared to the externally applied one (Sarris et al., 2006; Jha and Apere, 2013; Crammer and Pai, 1973; Pai, 1962 ). The outer surface of the inner cylinder is heated to a temperature (T₁) greater than that of the surrounding fluid having temperature (T₀) and the inner surface of the outer cylinder is maintained at temperature (T₀). Due to this temperature difference, natural convection occurs in the vertical annular micro-channel. Since the flow is fully developed and cylinders are of infinite length, the flow depends only on radial coordinate (r). In the recent past, Weng and Chen (2009) analysed the drag reduction and heat transfer enhancement of viscous incompressible fluid in vertical micro-annulus. Following Weng and Chen and considering the viscous incompressible electrically conducting fluid in the presence of a transverse magnetic field to the flow direction, the mathematical model for the present physical situation under Boussinesq’s approximation in dimensional form is

(1)

\frac{ν}{r} \frac{d}{dr} (r \frac{du}{dr}) + g β_{0} (T - T_{0}) - \frac{σ B_{0}^{2} u}{ρ_{0}} = 0,

(2)

\frac{1}{r} \frac{d}{dr} (r \frac{dT}{dr}) = 0 .

The boundary conditions for the velocity and temperature field in the presence of velocity slip and temperature jump are (Weng and Chen, 2009; Avci and Aydin, 2009):

(3)

u (r = k_{1}) = \frac{2 - σ_{v}}{σ_{v}} λ {\frac{du}{dr}|}_{r = k_{1}},

(4)

u (r = k_{2}) = - \frac{2 - σ_{v}}{σ_{v}} λ {\frac{du}{dr}|}_{r = k_{2}},

(5)

T (r = k_{1}) = T_{1} + \frac{2 - σ_{t}}{σ_{t}} \frac{2 γ}{γ + 1} \frac{λ}{\Pr} {\frac{dT}{dr}|}_{r = k_{1}},

(6)

T (r = k_{2}) = T_{0} - \frac{2 - σ_{t}}{σ_{t}} \frac{2 γ}{γ + 1} \frac{λ}{\Pr} {\frac{dT}{dr}|}_{r = k_{2}} .

By introducing the following non-dimensional quantities

(7)

R = \frac{r - k_{1}}{w}, w = k_{2} - k_{1}, U = \frac{u}{u_{c}}, θ = \frac{T - T_{0}}{T_{1} - T_{0}}, u_{c} = \frac{ρ_{0} g β_{0} (T_{1} - T_{0}) w^{2}}{μ_{0}}, \Pr = \frac{C_{ρ_{0}} μ_{0}}{k_{0}}, Kn = \frac{λ}{w}, F = \frac{β_{t}}{β_{ν}}, η = \frac{k_{1}}{k_{2}}, β_{ν} = \frac{2 - σ_{ν}}{σ_{ν}}, β_{t} = \frac{2 - σ_{t}}{σ_{t}} \frac{2 γ}{γ + 1} \frac{1}{\Pr}, λ = \frac{\sqrt{π \hat{R} T_{0} / 2 μ_{0}}}{ρ_{0}}, M^{2} = \frac{σ B_{0}^{2} w^{2}}{ρ_{0} ν},

Using Eq. (7) in Eqs. (1)–(6), the mathematical model representing the present physical situation in dimensionless form in the presence of velocity slip and temperature jump on annular microchannel surfaces is:

(8)

\frac{1}{[η + (1 - η) R]} \frac{d}{dR} [[η + (1 - η) R] \frac{dU}{dR}] - M^{2} U + θ = 0,

(9)

\frac{1}{[η + (1 - η) R]} \frac{d}{dR} [[η + (1 - η) R] \frac{d θ}{dR}] = 0 .

The boundary conditions which describe velocity slip and temperature jump conditions at the fluid–wall interface in dimensionless form are (Weng and Chen, 2009)

(10)

U (0) = β_{v} Kn {\frac{dU}{dR}|}_{R = 0}, U (1) = - β_{v} Kn {\frac{dU}{dR}|}_{R = 1},

(11)

θ (0) = 1 + β_{v} KnF {\frac{d θ}{dR}|}_{R = 0}, θ (1) = - β_{v} KnF {\frac{d θ}{dR}|}_{R = 1} .

The physical quantities used in the above equations are defined in the nomenclature.

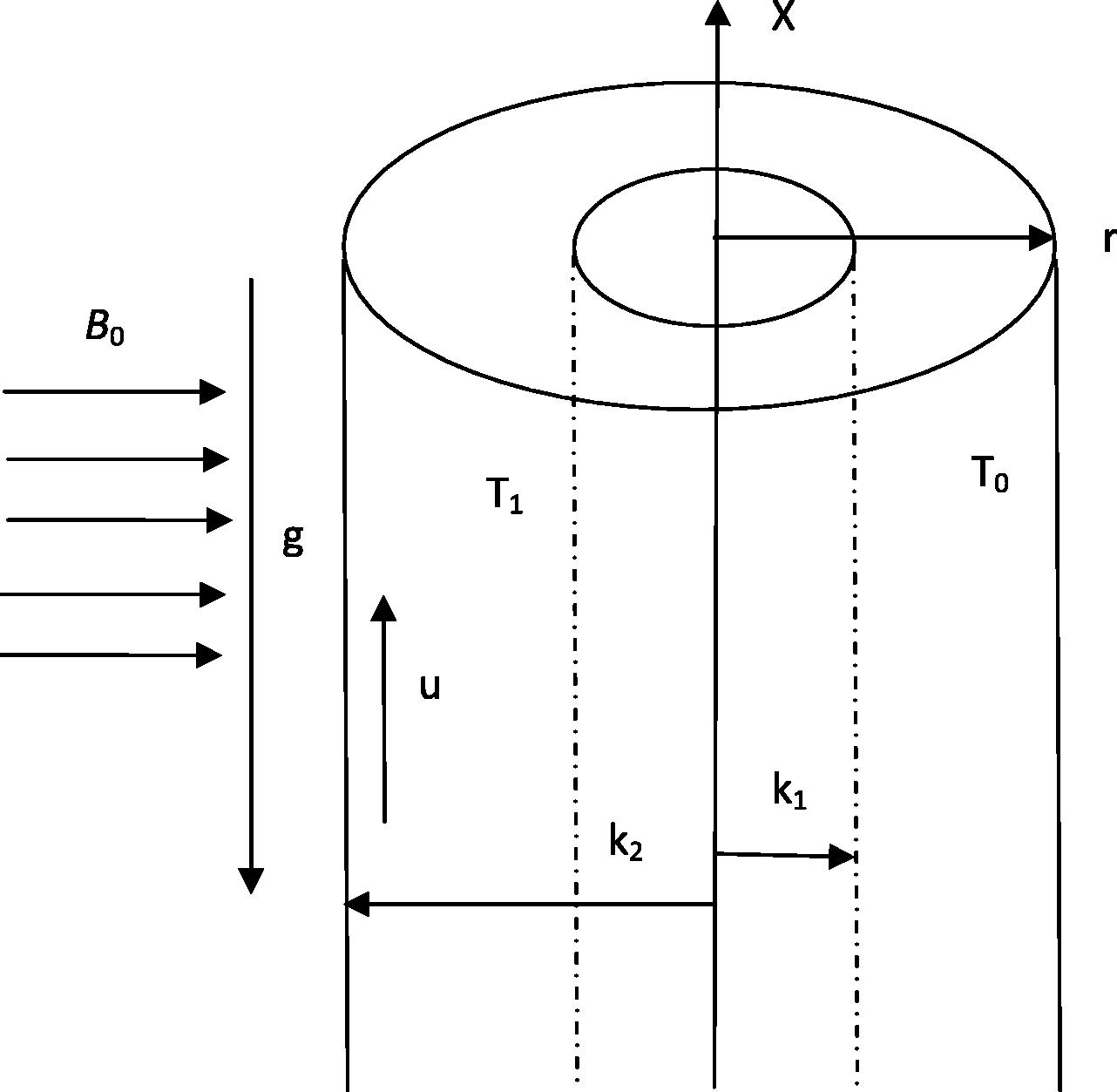
Flow configuration and coordinate system.

By using the transformation Z = η + (1 − η)R, the Eqs. (8)–(11) can be written as:

(12)

\frac{1}{Z} \frac{d}{dZ} [Z \frac{dU}{dZ}] - \frac{M^{2} U}{{(1 - η)}^{2}} + \frac{θ}{{(1 - η)}^{2}} = 0,

(13)

\frac{1}{Z} \frac{d}{dZ} [Z \frac{d θ}{dZ}] = 0 .

Subject to the boundary conditions

(14)

U (η) = β_{ν} Kn (1 - η) {\frac{dU}{dZ}|}_{Z = η}, U (1) = - β_{ν} Kn (1 - η) {\frac{dU}{dZ}|}_{Z = 1},

(15)

θ (η) = 1 + β_{ν} KnF (1 - η) {\frac{d θ}{dZ}|}_{Z = η}, θ (1) = - β_{ν} KnF (1 - η) {\frac{d θ}{dZ}|}_{Z = 1} .

Integrating equation (13) and applying the boundary conditions (15) gives:

(16)

θ (Z) = A_{0} + A_{1} In (Z),

where:

(17)

A_{1} = \frac{1}{In (η) - β_{ν} KnF (1 - η) (1 + \frac{1}{η})}, A_{0} = - β_{ν} KnF (1 - η) A_{1} .

The general solution of Eq. (12) after substitution equation (16) in Eq. (12) is obtained by rearranging the homogeneous part to take the general form of the Bessel equation (Arpaci, 1966). The particular solution of Eq. (12) is sought by assuming an appropriate form (according to the forcing function i.e., the right hand side of Eq. (12))).The exact solution of Eq. (12) under the appropriate velocity slip condition defined in Eq. (13) is:

(18)

U (Z) = C_{1} I_{0} (ZE) + C_{2} K_{0} (ZE) + \frac{1}{M^{2}} [A_{0} + A_{1} In (Z)] .

Two important parameters for convective micro-flow are the volume flow rate, and skin-friction. The dimensionless volume flow rate is:

(19)

Q = \frac{q}{2 π w^{2} u_{c}} = \frac{1}{{(1 - η)}^{2}} \int_{η}^{1} ZU (Z) dZ .

Substituting equation (18) into Eq. (19), one obtains

(20)

Q = \frac{1}{{(1 - η)}^{2}} [\frac{C_{1} I_{1} (E) - C_{2} K_{1} (E)}{E} + \frac{η (C_{2} K_{1} (E η) - C_{1} I_{1} (E η))}{E} + {(1 - η)}^{2} \{\frac{A_{0}}{2 M^{2}} - \frac{A_{1}}{4 M^{2}}\} - \frac{A_{1}}{2 M^{2}} η^{2} In (η)] .

The skin-frictions (τ) at the cylinder walls are obtained by differentiating the velocity as follows:

(21)

τ_{0} = {\frac{dU}{dR}|}_{R = 0} = (1 - η) {\frac{dU}{dZ}|}_{Z = η},

(22)

τ_{0} = [\{C_{1} I_{1} (η E) - C_{2} K_{1} (η E)\} E + \frac{A_{1}}{M^{2} η}] (1 - η),

(23)

τ_{1} = {\frac{dU}{dR}|}_{R = 1} = (1 - η) {\frac{dU}{dZ}|}_{Z = 1},

(24)

τ_{1} = [\{C_{1} I_{1} (E) - C_{2} K_{1} (E) E\} + \frac{A_{1}}{M^{2}}] (1 - η),

where C₁, C₂, E, E₁, …, E₆ are all constants given in the Appendix A.

3 Results and discussion

Numerical values of the velocity, volume flow rate, and skin friction are computed and the graphs are presented in Figs. 2–10 so that the influences of radius ratio (η), Hartmann number (M), rarefaction parameter (β_vKn), and fluid–wall interaction parameter (F) can be easily seen at a glance. The present parametric study has been performed in the continuum and slip flow regimes $(Kn ⩽ 0.1)$ . Also, for air and various surfaces, the values of β_v and β_t range from near 1 to 1.667 and from near 1.64 to more than 10, respectively. So, this study has been performed over the reasonable ranges of $0 ⩽ β_{v} Kn ⩽ 0.1$ and $0 ⩽ F ⩽ 10$ . The selected reference values of β_vKn, and F for the present analysis are 0.05 and 1.64 respectively as given in Weng and Chen (2009).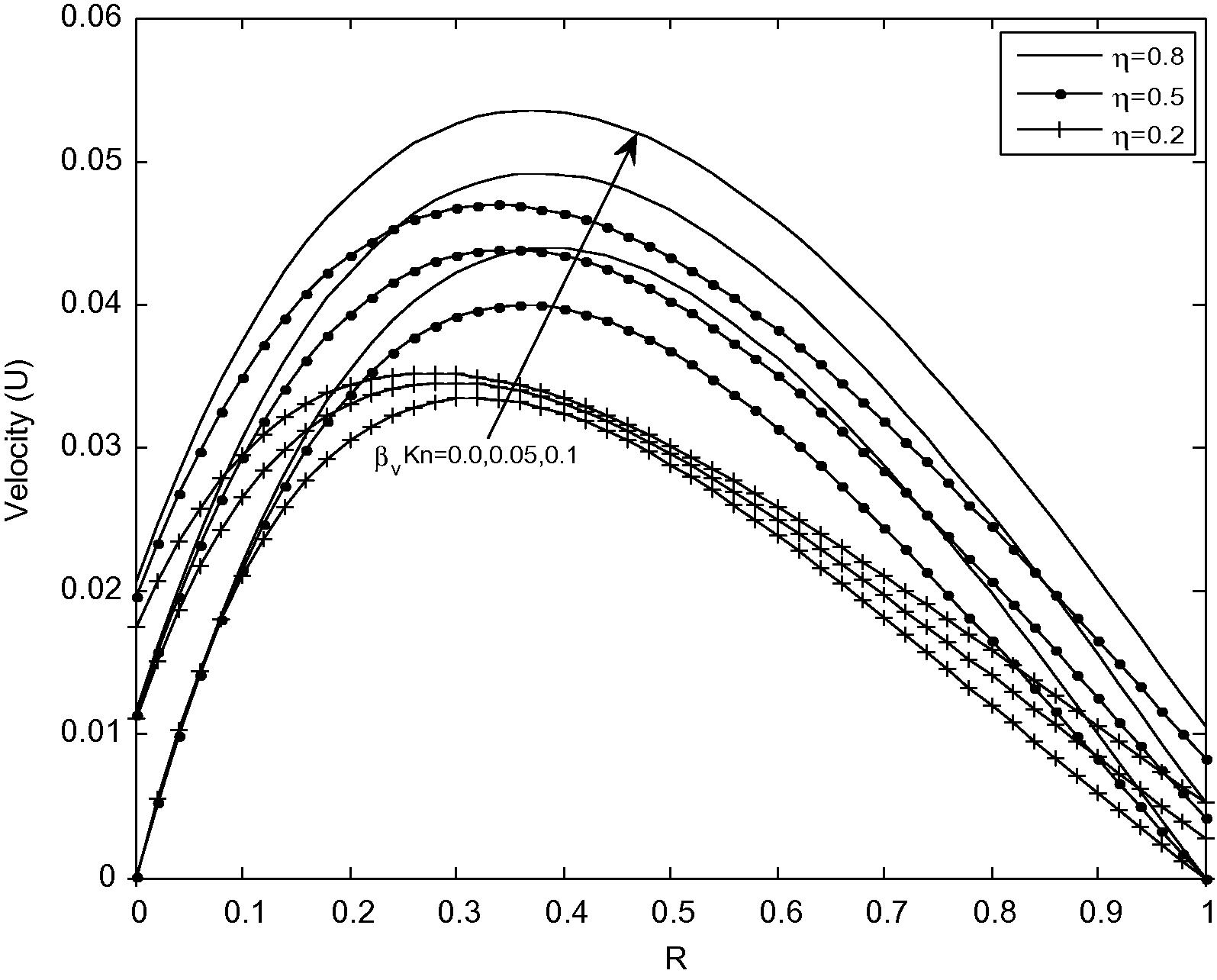

Velocity distribution for different values of βvKn with F = 1.64 and M = 2.0.

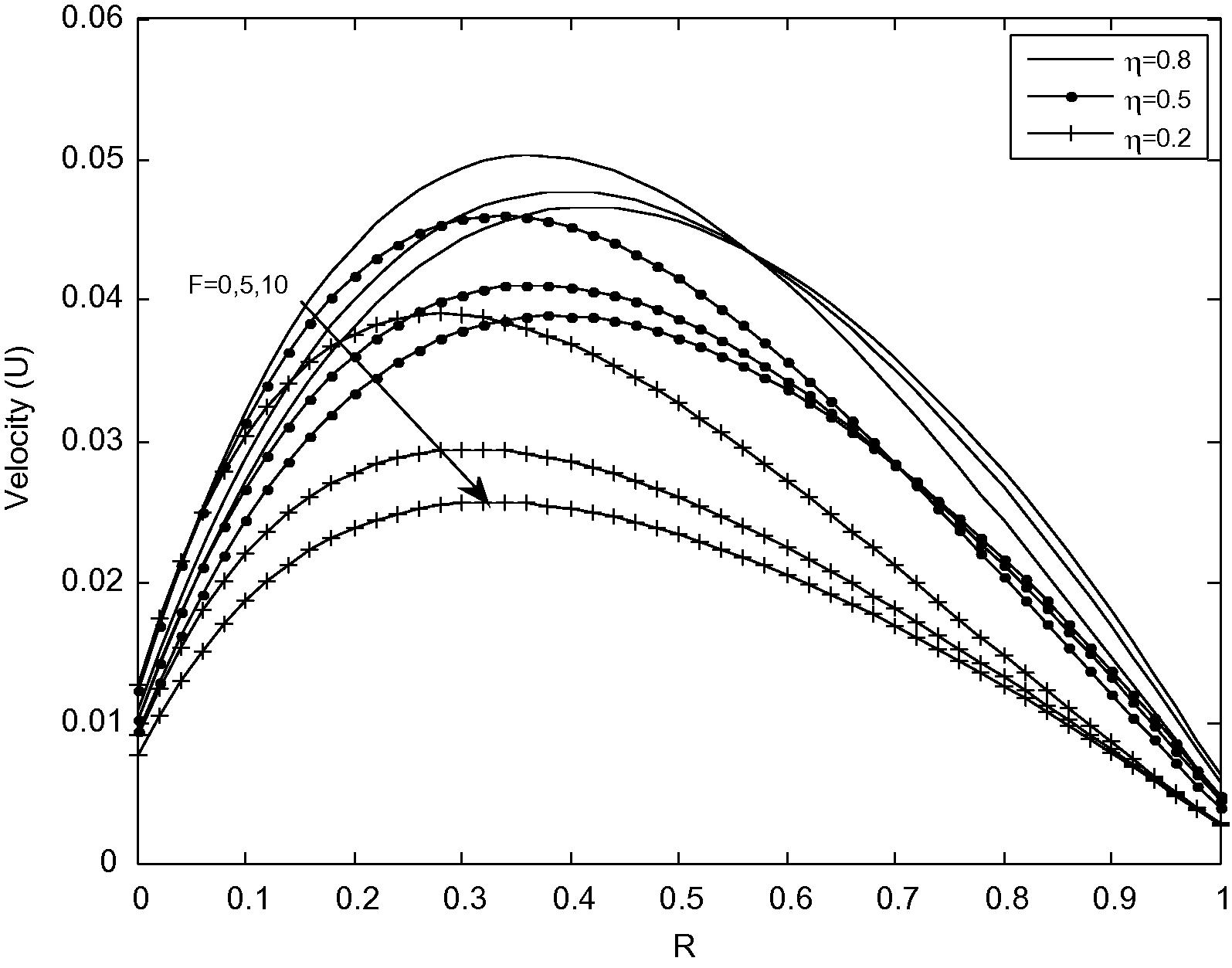
Velocity distribution for different values of F with βvKn = 0.05 and M = 2.0.

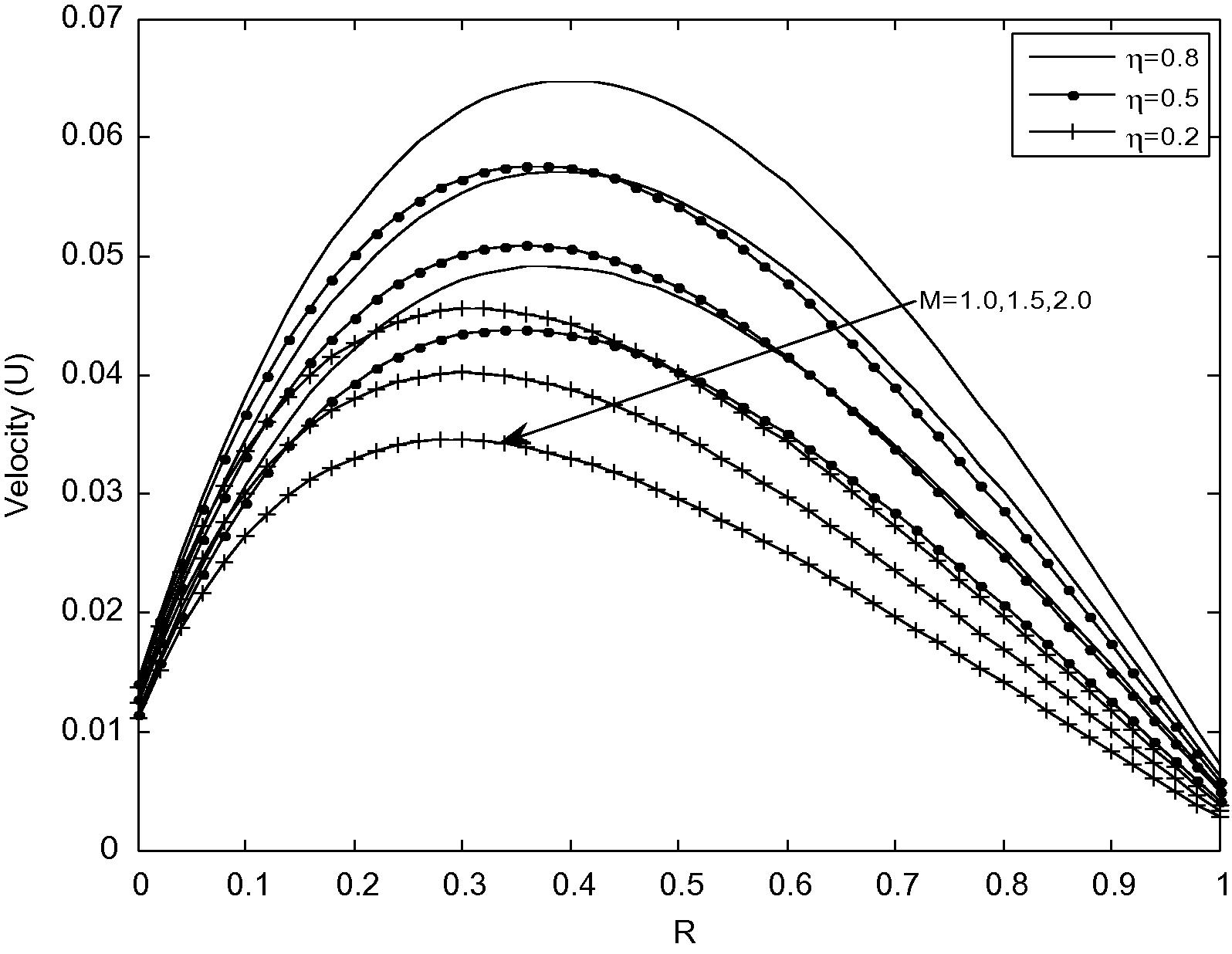
Velocity distribution for different values of M with βvKn = 0.05 and F = 1.64.

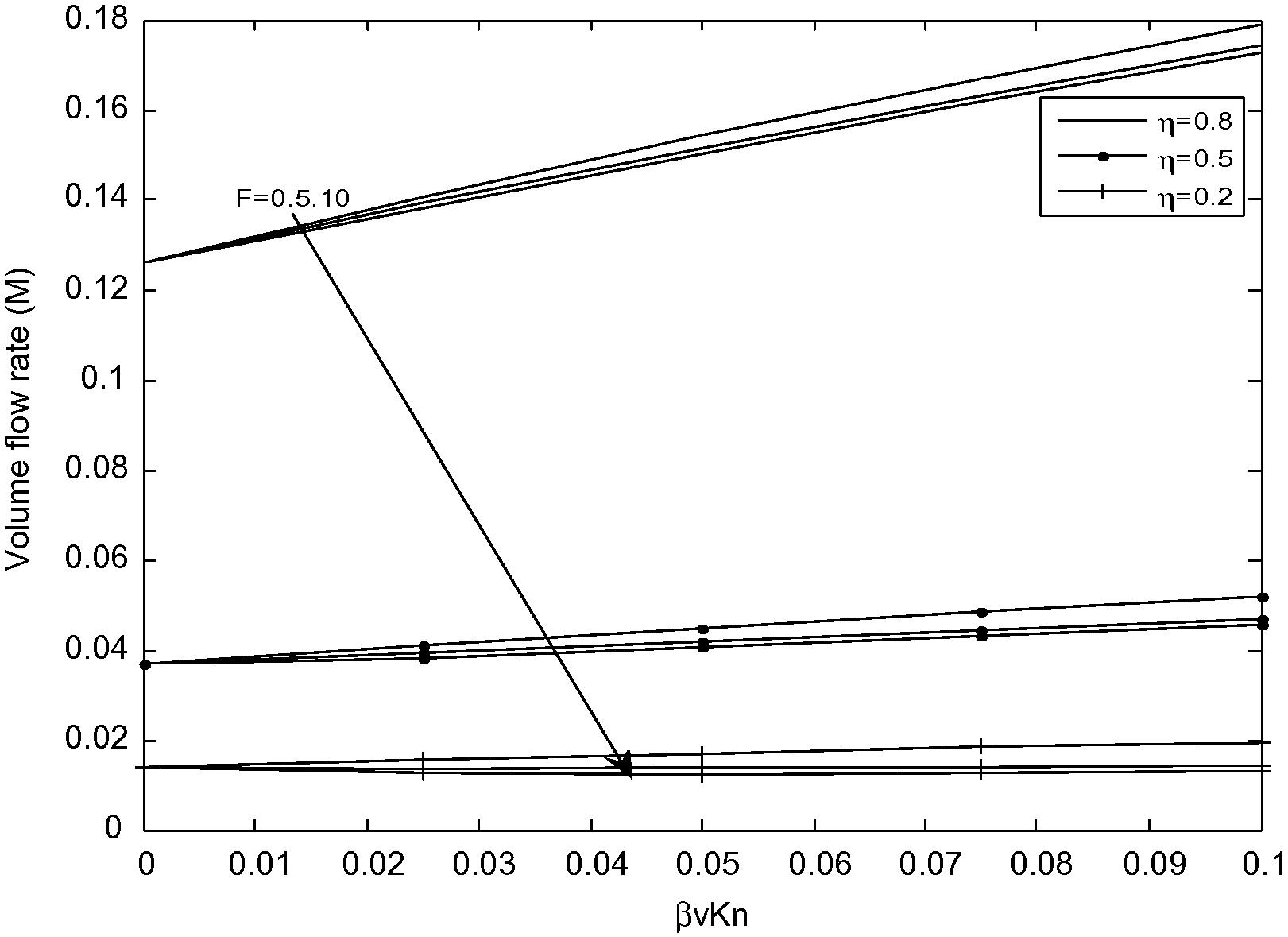
Volume flow rate versus βvKn for different values of F with M = 2.0.

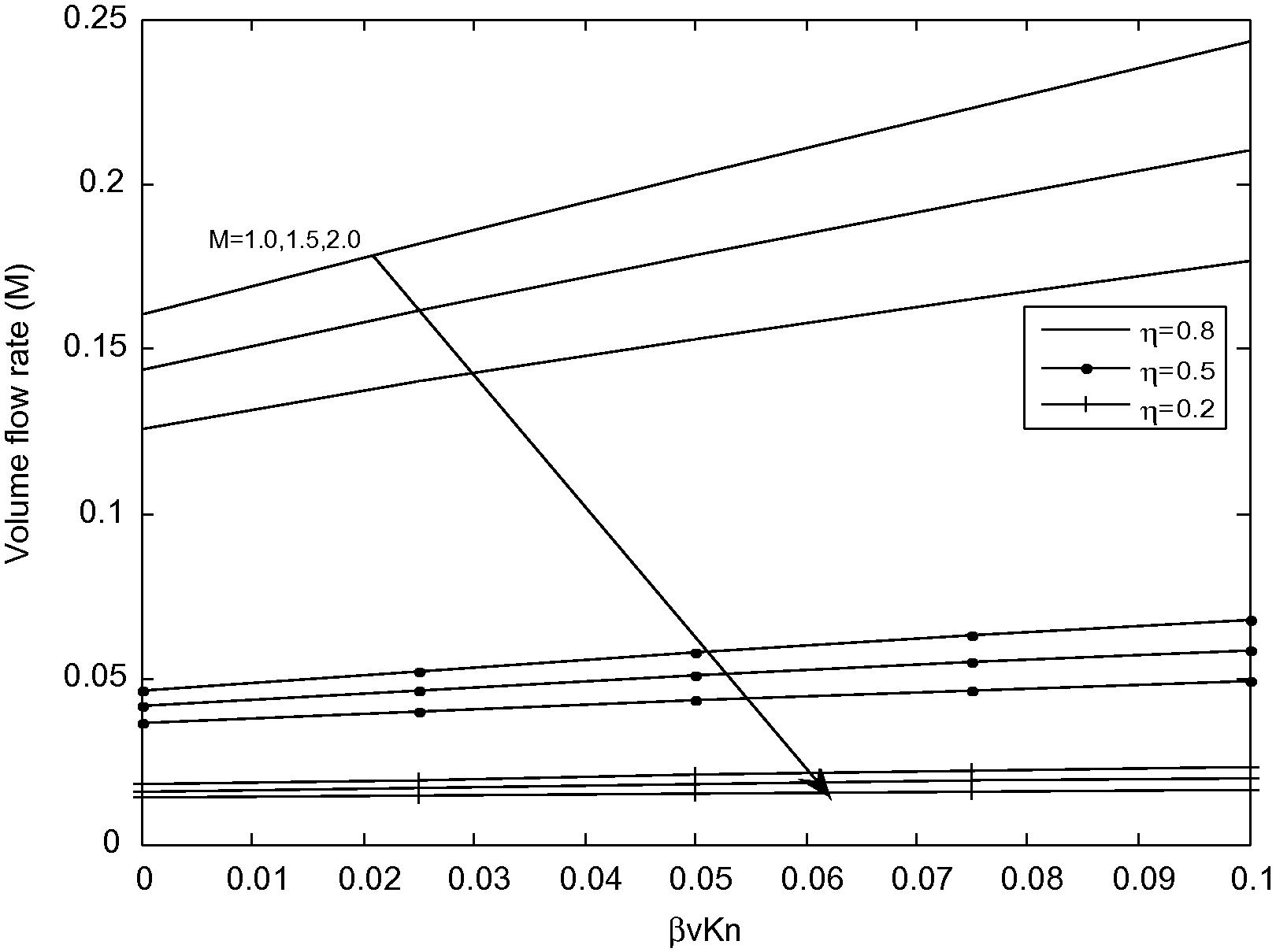
Volume flow rate versus βvKn for different values of M with F = 1.64.

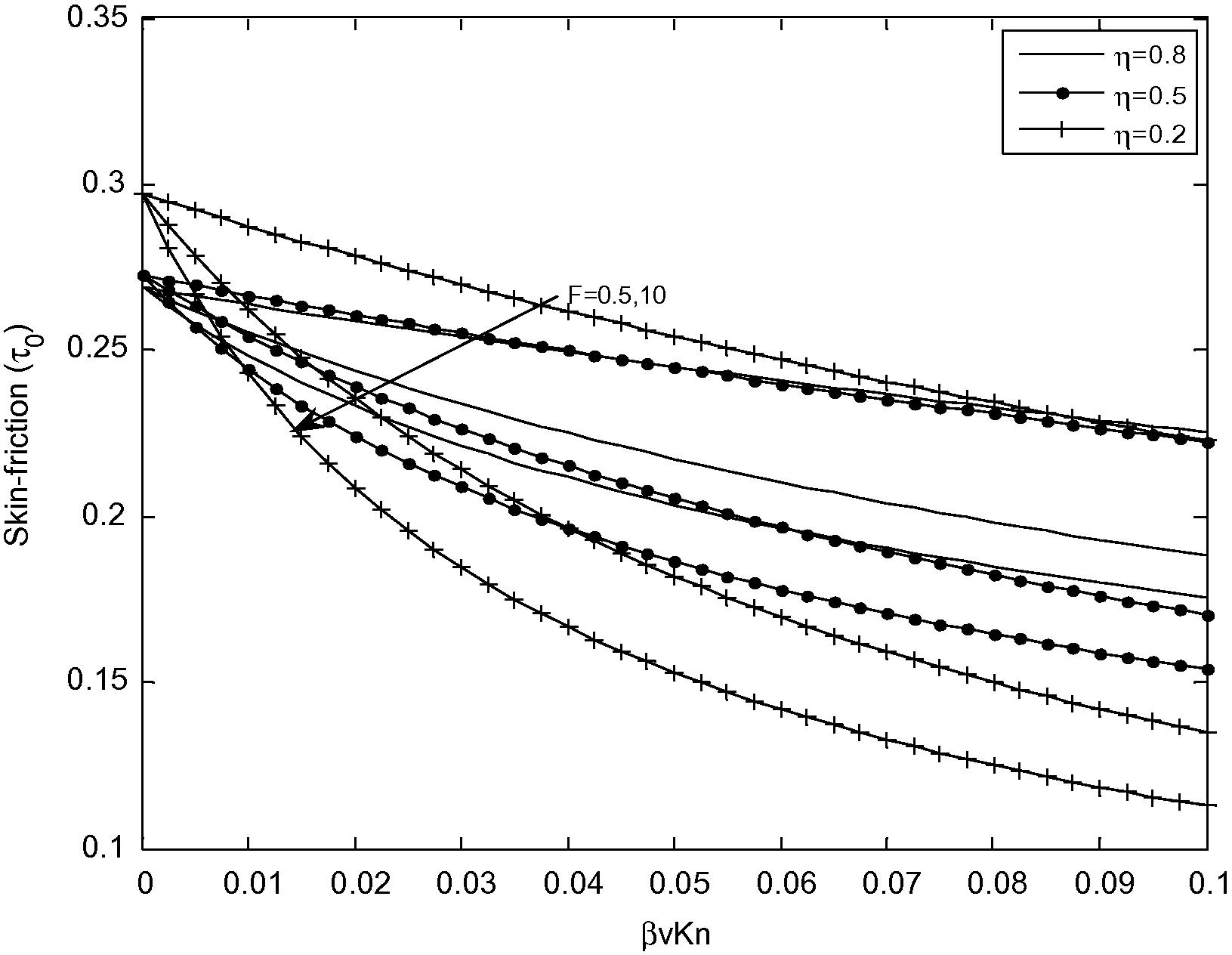
Variation of skin friction for different values of F at (R = 0).

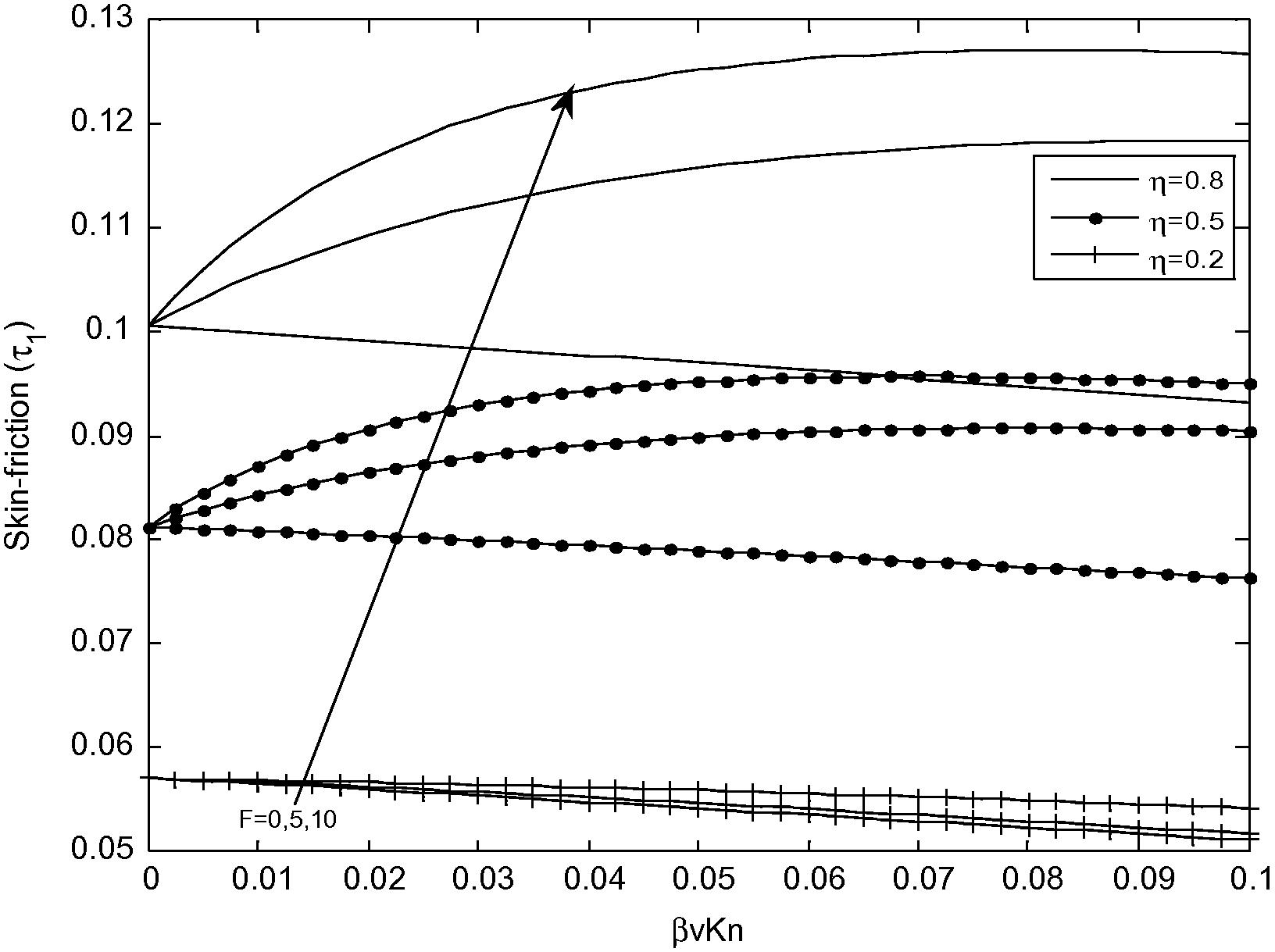
Variation of skin friction for different values of F at (R = 1).

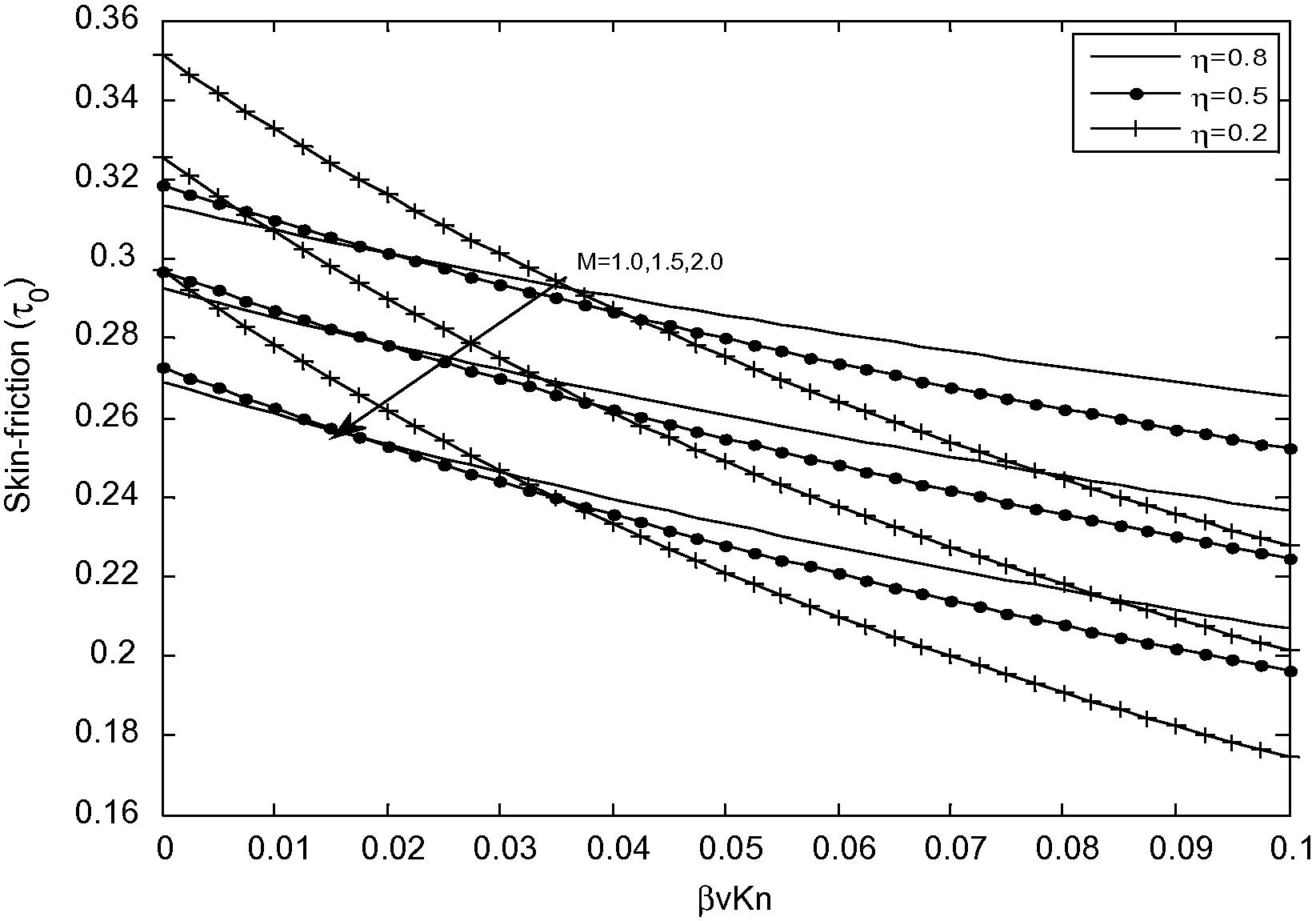
Variation of skin friction for different values of M at (R = 0).

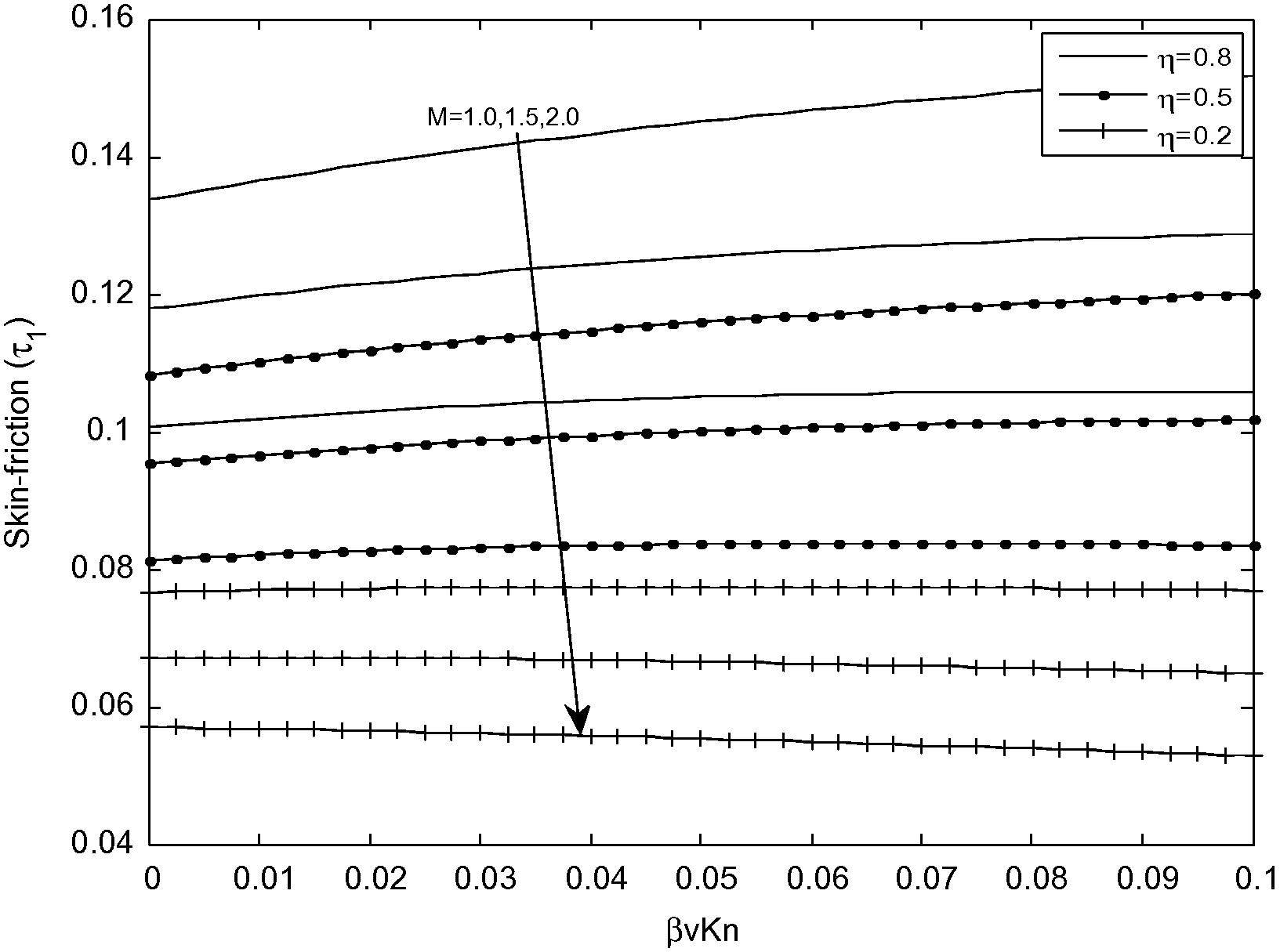
Variation of skin friction for different values of M at (R = 1).

The present work extends the work of Weng and Chen (2009) by considering the influence of externally applied transverse magnetic field on a steady fully developed natural convection flow of viscous, incompressible, electrically conducting fluid in a vertical annular micro-channel. The values of Hartmann number (M) are taken over the range of $1 ⩽ M ⩽ 2$ with a reference value of M = 2.

The expression for the temperature in Eq. (10), the effect of the rarefaction parameter (β_vKn), and fluid–wall interaction parameter (F) on the temperature profile and rate of heat transfer which is expressed as the Nusselt number are exactly the same as those given by Weng and Chen (2009).

Fig. 2 shows the velocity distribution for different values of rarefaction parameter (β_vKn) with fixed values of M = 2.0 and F = 1.64. It is observed that, as rarefaction parameter (β_vKn) increases, the velocity slip at the cylindrical surfaces increases which reduces the retarding effect of boundaries. This yields an observable increase in the fluid velocity near both boundaries. This is due to the fact that, as (β_vKn) increases, the temperature jump increases and this reduces the amount of heat transfer from the cylindrical surfaces to the fluid (Weng and Chen, 2009). This reduction in heat transfer reduces the buoyancy effect, which derives the flow and hence reduces the fluid velocity far from the outer surface of inner cylinder (near the inner surface of outer cylinder). The reduction in velocity due to the reduction in heat transfer is offset by the increase in velocity due to the reduction in the frictional retarding forces near the cylindrical surfaces. Furthermore, the slip induced by rarefaction effect increases as radius ratio (η) increases.

Fig. 3 shows the velocity distribution for different values of fluid–wall interaction parameter (F) with fixed values of β_vKn = 0.05 and M = 2.0. It is evident from Fig. 3 that, the increase in fluid–wall interaction parameter (F) leads to the decrease in fluid velocity and increase in slip velocity near the outer surface of the inner cylinder while the reverse trend is observed at the inner surface of the outer cylinder. In addition, the slip induced by fluid–wall interaction parameter (F) increases as the radius ratio (η) decreases while, the impact of fluid–wall interaction parameter (F) on the slip is more visible for smaller radius ratio (η).

Fig. 4 depicts the velocity distribution for different values of the Hartmann number (M) with fixed values of β_vKn = 0.05 and F = 1.64. It is observed that as the Hartmann number (M) increases, there is a decrease in the fluid velocity and an increase in slip velocity. It is also observed that there is higher slip at the inner surface of outer cylinder compared to the outer surface of the inner cylinder. In addition, for the fixed Hartmann number (M), as radius ratio (η) increases there is an increase in the slip. Further, it is seen that the particular case of Eq. (18) corresponding M → 0 reduces to the one in Weng and Chen (2009).

Fig. 5 shows the variation of volume flow rate (Q) against the rarefaction parameter (β_vKn) for different values of fluid–wall interaction (F). It is interesting to note that the volume flow rate (Q) is a decreasing function of fluid–wall interaction (F). Furthermore, it is found that an increase in radius ratio (η) and rarefaction parameter (β_vKn) leads to an increase in the volume flow rate.

Fig. 6 reveals the volume flow rate (Q) plotted against the rarefaction parameter (β_vKn) for different values of Hartmann number (M). It is observed from Fig. 6 that, the volume flow rate (Q) decreases as Hartmann number (M) increases. Also, it is interesting to note that an increase in the rarefaction parameter (β_vKn) leads to an increase in the volume flow rate.

Fig. 7 depicts the variation of skin-friction at the outer surface of the inner cylinder (R = 0). It is clear from Fig. 7 that, the skin - friction decreases with the increase of fluid–wall interaction parameter (F) and rarefaction parameter (β_vKn). It is interesting to note that the impact of these parameters is significant for a small value of radius ratio (η).

Fig. 8 shows a variation of skin-friction at the inner surface of the outer cylinder (R = 1). It is obvious from Fig. 8 that increases in radius ratio (η) and rarefaction parameter (β_vKn) lead to the increase in the skin-friction at the inner surface of the outer cylinder.

Figs. 9 and 10 presents a variation of skin-friction at the outer surface of the inner cylinder (R = 0) and the inner surface of outer cylinder (R = 1), respectively for different values of the Hartmann number (M). It is observed from these figures that, skin friction decreases as the Hartmann number (M) increases.

4 Conclusions

This study considered the fully developed steady natural convection flow of a viscous, incompressible, electrically conducting fluid in vertical annular micro-channel under the effect of a transverse magnetic field. The influence of the radius ratio (η), Hartmann number (M), rarefaction parameter (β_vKn), and fluid–wall interaction (F) on the fluid velocity, volume flow rate and skin-friction is analysed. This study exactly agrees with the finding of Weng and Chen (2009) in the absence of a magnetic field and further concludes as follows:

It is found that as the Hartmann number (M) increases, there is a decrease in the fluid velocity and an increase in slip velocity.
The slip induced by rarefaction effect and the Hartmann number increases as the radius ratio (η) increases while the slip induced by fluid–wall interaction parameter (F) increases as the radius ratio (η) decreases.
The increase in radius ratio (η) and rarefaction parameter (β_vKn) leads to an increase in the volume flow rate.
The increase in the Hartmann number (M) leads to a decrease in the volume flow rate.
Finally, the skin friction decreases as the Hartmann number (M) increases.

References

Ali Farhad, Khan Ilyas, Samiulhaq, Mustapha Norzieha, Shafie Sharidan, . Unsteady magnetohydrodynamic oscillatory flow of viscoelastic fluids in a porous channel with heat and mass transfer. J. Phys. Soc. Jpn.. 2012;81:064402.
[Google Scholar]
Ali Farhad, Khan Ilyas, Shafie Sharidan, Musthapa Norzieha, . Heat and mass transfer with free convection MHD flow past a vertical plate embedded in a porous medium. Math. Prob. Eng.. 2013;2013 (Special Issue Mathematical Modeling of Heat and Mass Transfer in Energy Science and Engineering (MMTP) http://dx.doi.org/10.1155/2013/346281
[Google Scholar]
Ali Farhad, Khan Ilyas, Samiulhaq, Shafie Sharidan, . Conjugate effects of heat and mass transfer on MHD free convection flow over an inclined plate embedded in a porous medium. PLoS ONE. 2013;8(6):e65223.
[Google Scholar]
Ali Farhad, Khan Ilyas, Shafie Sharidan, . Closed form solutions for unsteady free convection flow of a second grade fluid over an oscillating vertical plate. PLoS ONE. 2014;9(2):e85099.
[Google Scholar]
Al-Nimr M.A., Khadrawi A.F., . Thermal behavior of a stagnant gas confined in a horizontal microchannel as described by the dual-phase-lag heat conduction model. Int. J. Thermophys.. 2004;25(6):1953-1964.
[Google Scholar]
Arpaci V.S., . Conduction Heat Transfer. Reading, MA: AddisonWesley; 1966. pp. 135–136
Ashorynejad H.R., Sheikholeslami, Pop I., Ganji D.D., . Nanofluid flow and heat transfer due to a stretching cylinder in the presence of magnetic field. Heat Mass Transfer. 2013;49:427-436.
[Google Scholar]
Avci M., Aydin O., . Mixed convection in a vertical microannulus between two concentric Microtubes. ASME J. Heat Transfer. 2009;131:014502-014504.
[Google Scholar]
Chen C.K., Weng H.C., . Natural convection in a vertical microchannel. J. Heat Transfer. 2005;127:1053-1056.
[Google Scholar]
Crammer K.R., Pai S., . Magnetohydrodynamics for Engineers and Applied Physicist. New York: McGraw Hill Book Company; 1973.
Farhad A., Norzieha M., SSharidan S., Khan I., Samiuthaq, . On hydromagnetic rotating flow in a porous medium with slip condition and hall current. Int. J. Phys. Sci.. 2012;7(10):1540-1548.
[Google Scholar]
Jha B.K., Aina Babatunde, . Mathematical modelling and exact solution of steady fully developed mixed convection flow in a vertical micro-porous-annulus. J. Afrika Matematika 2014
[CrossRef] [Google Scholar]
Jha B.K., Apere C.A., . Time-dependent MHD Couette flow in a porous annulus. Commun. Nonlinear Sci. Numer. Simul.. 2013;18:1959-1969.
[Google Scholar]
Jha B.K., Aina B., Joseph S.B., . Natural convection flow in a vertical micro-channel with suction/injection. J. Process Mech. Eng.. 2014;228(3):171-180.
[Google Scholar]
Jha, B.K., Aina, Babatunde, Shehu, A.M., in press. Combined effects of suction/injection and wall surface curvature on natural convection flow in a vertical micro-porous-annulus. J. Thermophys. Aerodyn., in press.
Khan I., Ellahi R., . Some unsteady MHD flows of a second grade fluid through porous medium. J. Porous Media. 2008;11(4):389-400. (ISI Indexed, I.F 0.684)
[Google Scholar]
Pai S., . Magnetohydrodynamics and Plasma Dynamics. Berlin: Springer; 1962.
Sarris I.E., Zikos G.K., Grecos A.P., Vlachos N.S., . On the limits of validity of the low magnetic Reynolds number approximation in MHD natural convection heat transfer. Numer. Heat Transfer: Part B – Fundam.. 2006;50:157-180.
[Google Scholar]
Sheikholeslami M., Gorji-Bandpay M., Ganji D.D., . Magnetic field effects on natural convection around a horizontal circular cylinder inside a square enclosure filled with nanofluid. Int. Commun. Heat Mass Transfer. 2012;39:978-986.
[Google Scholar]
Sheikholeslami M., Gorji-Bandpy M., Ganji D.D., Soleimani Soheil, Seyyedi S.M., . Natural convection of nanofluids in an enclosure between a circular and a sinusoidal cylinder in the presence of magnetic field. Int. Commun. Heat Mass Transfer. 2012;39:1435-1443.
[Google Scholar]
Sheikholeslamia M., Gorji-Bandpy M., Ganji D.D., Soleiman Soheil, . Effect of a magnetic field on natural convection in an inclined half-annulus enclosure filled with Cu–water nanofluid using CVFEM. Adv. Powder Technol.. 2013;24:980-991.
[Google Scholar]
Sheikholeslamia M., Gorji-Bandpy M., Ganji D.D., Rana P., Soleimani Soheil, . Magnetohydrodynamic free convection of Al2O3–water nanofluid considering thermophoresis and Brownian motion effects. Comput. Fluid. 2014;94:147-160.
[Google Scholar]
Sheikholeslamia M., Gorji Bandpy M., Ellahi R., Hassan Mohsan, Soleimani Soheil, . Effects of MHD on Cu–water nanofluid flow and heat transfer by means of CVFEM. J. Magn. Magn. Mater.. 2014;349:188-200.
[Google Scholar]
Weng H.C., Chen C.K., . Drag reduction and heat transfer enhancement over a heated wall of a vertical annular microchannel. Int. J. Heat Mass Transfer. 2009;52:1075-1079.
[Google Scholar]

Appendix A

Constants used in the present work. $C_{1} = \frac{[E_{6} E_{2} - E_{3} E_{5}]}{[E_{2} E_{4} - E_{1} E_{5}]}, C_{2} = \frac{[E_{1} E_{6} - E_{3} E_{4}]}{[E_{1} E_{5} - E_{2} E_{4}]}, E = \frac{M}{(1 - η)},$ $E_{1} = [I_{0} (E η) - (β_{ν} Kn (1 - η) E) I_{1} (η E)], E_{2} = [K_{0} (E η) + (β_{ν} Kn (1 - η) E) K_{1} (η E)],$ $E_{3} = \frac{A_{1}}{M^{2} η} β_{ν} Kn (1 - η) - \frac{1}{M^{2}} [A_{0} + A_{1} In (η)] E_{4} = [I_{0} (E) + β_{ν} Kn (1 - η) {EI}_{1} (E)],$ $E_{5} = [K_{0} (E) - β_{ν} Kn (1 - η) {EK}_{1} (E)], E_{6} = - [\frac{A_{0}}{M^{2}} + \frac{β_{ν} Kn (1 - η) A_{1}}{M^{2}}]$

Introduction

Mathematical analysis

Results and discussion

Conclusions

Fulltext Views
5

PDF downloads
9

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Ali Farhad, Khan Ilyas, Samiulhaq, Mustapha Norzieha, Shafie Sharidan, . Unsteady magnetohydrodynamic oscillatory flow of viscoelastic fluids in a porous channel with heat and mass transfer. J. Phys. Soc. Jpn.. 2012;81:064402.
[Google Scholar]

[2] Ali Farhad, Khan Ilyas, Shafie Sharidan, Musthapa Norzieha, . Heat and mass transfer with free convection MHD flow past a vertical plate embedded in a porous medium. Math. Prob. Eng.. 2013;2013 (Special Issue Mathematical Modeling of Heat and Mass Transfer in Energy Science and Engineering (MMTP) http://dx.doi.org/10.1155/2013/346281
[Google Scholar]

[3] Ali Farhad, Khan Ilyas, Samiulhaq, Shafie Sharidan, . Conjugate effects of heat and mass transfer on MHD free convection flow over an inclined plate embedded in a porous medium. PLoS ONE. 2013;8(6):e65223.
[Google Scholar]

[4] Ali Farhad, Khan Ilyas, Shafie Sharidan, . Closed form solutions for unsteady free convection flow of a second grade fluid over an oscillating vertical plate. PLoS ONE. 2014;9(2):e85099.
[Google Scholar]

[5] Al-Nimr M.A., Khadrawi A.F., . Thermal behavior of a stagnant gas confined in a horizontal microchannel as described by the dual-phase-lag heat conduction model. Int. J. Thermophys.. 2004;25(6):1953-1964.
[Google Scholar]

[6] Arpaci V.S., . Conduction Heat Transfer. Reading, MA: AddisonWesley; 1966. pp. 135–136

[7] Ashorynejad H.R., Sheikholeslami, Pop I., Ganji D.D., . Nanofluid flow and heat transfer due to a stretching cylinder in the presence of magnetic field. Heat Mass Transfer. 2013;49:427-436.
[Google Scholar]

[8] Avci M., Aydin O., . Mixed convection in a vertical microannulus between two concentric Microtubes. ASME J. Heat Transfer. 2009;131:014502-014504.
[Google Scholar]

[9] Chen C.K., Weng H.C., . Natural convection in a vertical microchannel. J. Heat Transfer. 2005;127:1053-1056.
[Google Scholar]

[10] Crammer K.R., Pai S., . Magnetohydrodynamics for Engineers and Applied Physicist. New York: McGraw Hill Book Company; 1973.

[11] Farhad A., Norzieha M., SSharidan S., Khan I., Samiuthaq, . On hydromagnetic rotating flow in a porous medium with slip condition and hall current. Int. J. Phys. Sci.. 2012;7(10):1540-1548.
[Google Scholar]

[12] Jha B.K., Aina Babatunde, . Mathematical modelling and exact solution of steady fully developed mixed convection flow in a vertical micro-porous-annulus. J. Afrika Matematika 2014
[CrossRef] [Google Scholar]

[13] Jha B.K., Apere C.A., . Time-dependent MHD Couette flow in a porous annulus. Commun. Nonlinear Sci. Numer. Simul.. 2013;18:1959-1969.
[Google Scholar]

[14] Jha B.K., Aina B., Joseph S.B., . Natural convection flow in a vertical micro-channel with suction/injection. J. Process Mech. Eng.. 2014;228(3):171-180.
[Google Scholar]

[15] Jha, B.K., Aina, Babatunde, Shehu, A.M., in press. Combined effects of suction/injection and wall surface curvature on natural convection flow in a vertical micro-porous-annulus. J. Thermophys. Aerodyn., in press.

[16] Khan I., Ellahi R., . Some unsteady MHD flows of a second grade fluid through porous medium. J. Porous Media. 2008;11(4):389-400. (ISI Indexed, I.F 0.684)
[Google Scholar]

[17] Pai S., . Magnetohydrodynamics and Plasma Dynamics. Berlin: Springer; 1962.

[18] Sarris I.E., Zikos G.K., Grecos A.P., Vlachos N.S., . On the limits of validity of the low magnetic Reynolds number approximation in MHD natural convection heat transfer. Numer. Heat Transfer: Part B – Fundam.. 2006;50:157-180.
[Google Scholar]

[19] Sheikholeslami M., Gorji-Bandpay M., Ganji D.D., . Magnetic field effects on natural convection around a horizontal circular cylinder inside a square enclosure filled with nanofluid. Int. Commun. Heat Mass Transfer. 2012;39:978-986.
[Google Scholar]

[20] Sheikholeslami M., Gorji-Bandpy M., Ganji D.D., Soleimani Soheil, Seyyedi S.M., . Natural convection of nanofluids in an enclosure between a circular and a sinusoidal cylinder in the presence of magnetic field. Int. Commun. Heat Mass Transfer. 2012;39:1435-1443.
[Google Scholar]

[21] Sheikholeslamia M., Gorji-Bandpy M., Ganji D.D., Soleiman Soheil, . Effect of a magnetic field on natural convection in an inclined half-annulus enclosure filled with Cu–water nanofluid using CVFEM. Adv. Powder Technol.. 2013;24:980-991.
[Google Scholar]

[22] Sheikholeslamia M., Gorji-Bandpy M., Ganji D.D., Rana P., Soleimani Soheil, . Magnetohydrodynamic free convection of Al2O3–water nanofluid considering thermophoresis and Brownian motion effects. Comput. Fluid. 2014;94:147-160.
[Google Scholar]

[23] Sheikholeslamia M., Gorji Bandpy M., Ellahi R., Hassan Mohsan, Soleimani Soheil, . Effects of MHD on Cu–water nanofluid flow and heat transfer by means of CVFEM. J. Magn. Magn. Mater.. 2014;349:188-200.
[Google Scholar]

[24] Weng H.C., Chen C.K., . Drag reduction and heat transfer enhancement over a heated wall of a vertical annular microchannel. Int. J. Heat Mass Transfer. 2009;52:1075-1079.
[Google Scholar]

Fully developed MHD natural convection flow in a vertical annular microchannel: An exact solution

Abstract

Keywords

Annular micro-channel

Natural convection

Hartmann number

Velocity slip and temperature jump

Nomenclature

Greek letters

1 Introduction

2 Mathematical analysis

3 Results and discussion

4 Conclusions

References

Appendix A