Translate this page into:
Fluid flow and radiative nonlinear heat transfer over a stretching sheet
*Tel.: +34 963877523 rcortell@fis.upv.es (R. Cortell)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Available online 24 August 2013

Abstract
In the present paper, we endeavor to perform a numerical analysis in connection with the boundary layer flow induced in a quiescent fluid by a continuous sheet stretching with velocity uw (x) ∼x1/3 with heat transfer. The effects of thermal radiation using the nonlinear Rosseland approximation are investigated. We search for similarity solutions and reduce the problem to a couple of ordinary differential equations containing three dimensionless parameters: the radiation parameter NR, the temperature ratio parameter θw and the Prandtl number Pr. The computational results for velocity, temperature and heat transfer characteristics are presented in both graphical and tabular forms.
Keywords
Laminar boundary layer
Nonlinearly stretching surfaces
Thermal radiation
Nonlinear Rosseland approximation
Nomenclature
- cP
-
Specific heat of the fluid at constant pressure J kg−1 K−1
-
Derivative with respect to η
- f
-
Dimensionless stream function
- k∗
-
Rosseland mean absorption coefficient m−1
- k
-
Fluid thermal conductivity W m−1 K−1
- L
-
Characteristic length m
- NR
-
Radiation parameter
- Pr
-
Prandtl number
- qr
-
Component of radiative heat flux in y direction W m−2
- T
-
temperature K
- u, v
-
Velocity components along x and y directions, respectively m s−1
- x, y
-
Cartesian coordinates along the plate and normal to it, respectively. m
Greek symbols
- α
-
Thermal diffusivity m2 s−1
- η
-
Dimensionless similarity variable
- θ
-
Dimensionless temperature
- μ
-
Absolute viscosity kg m−1 s−1
- υ
-
Kinematic viscosity m2 s−1
- ρ
-
Density kg m−3
- σ∗
-
Stefan-Boltzmann constant W m−2 K−4
Subscripts
- w, ∞
-
Conditions at the surface and within the free stream, respectively
Superscript
- prime
-
Derivative with respect to η
1 Introduction
In contrast to the well-known Blasius flow problem (see, for instance, Cortell, 2005), and ref. therein) which involves laminar viscous boundary layer fluid flow above a fixed flat plate, the flow of a viscoelastic fluid over a rigid plate moving steadily in an otherwise quiescent fluid is sometimes referred to as Sakiadis flow (see Sakiadis, 1961) after the pioneering work of that researcher. Ahmad and Al-Barakati (2009) obtained an approximate analytical solution of the Blasius problem. Sakiadis flow’s studies were recently dealt by Sadeghy et al. (2005) in their work on boundary layer of an upper-convected Maxwell fluid flow where the role played by fluid′s elasticity in the flow characteristics was analyzed.
When the difference between the sheet and the ambient temperature is large the thermal radiation effects become important, and also at high operating temperature the presence of thermal radiation alters the thermal boundary layer structure and the rate of heat transfer also results altered. In such industrial processes knowledge of radiative heat transfer becomes relevant. Abo-Eldahab and Azzam Gamal El-Din (2005) gave examples like nuclear power plants, gas turbines, satellites, etc. Viskanta and Grosh (1962) studied boundary layer flow in thermal radiation absorbing and emitting media by using the Rosseland approximation (Rosseland, 1931). Numerical results for hydro-magnetic mixed convection flow over a permeable non-isothermal wedge were reported by Prasad et al. (2013). Hossain et al. (1999) studied thermal radiation’s effects using the Rosseland diffusion approximation on natural convection flow of an optically thick viscous incompressible flow past a uniformly heated vertical porous surface with constant suction, and further, Hossain et al. (2001) analyzed the effect of variable viscosity on this type of flow. On the other hand, Raptis and Perdikis (1998) used a linearized form of the aforesaid Rosseland approximation in view to analyze the steady flow of a visco-elastic fluid past an unmoving surface. These simplifications permit an easier analysis, and many investigations (see, for instance, Cortell, 2008a,2011a; Abdul Hakeem et al., 2013) have been carried out in the recent past that deal with thermal studies by applying the cited linearized form, which is derived by assuming sufficiently small temperature differences within the flow that may assure to express T4 as a linear function of temperature. Studies about motion and mass transfer with chemically reactive species in a porous space were recently undertaken by Cortell (2007a, 2007b). Moreover, treatments to the radiative heating for flows generated by linear/nonlinear stretching sheets enclosing magneto-hydrodynamics, non-Newtonian fluids, porous media, etc. constitute analytical or numerical attempts which have been made in the recent past (Arpaci, 1968; Cortell 2008b, 2011b, 2012a, 2012b; Turkyilmazoglu, 2011; Misra and Sinha, 2013). The problem of steady micropolar fluid flow past a stretching surface has been devised by many authors (see, for instance, Ishak, 2010; Hsiao, 2010) and even, very recently, unsteady fluid flow with (Hsiao, 2012) or without (Bachok et al., 2011) thermal radiation effects has also been analyzed.
One of the objectives of the present paper is to extend the investigation of Cortell (2008c) to analyze the Sakiadis flow generated by a sheet stretched with a velocity which is assumed to be proportional to the x1/3quantity, x being the distance from the slit. We also assume appropriate boundary conditions for the energy equation that may assure the existence of similarity solutions (i.e., constant temperature at the surface) when radiative nonlinear heat transfer is studied. Very recently, Rahman and Eltayeb (2013), Pantokratoras and Fang (2013) used the Rosseland diffusion approximation in studying radiative nonlinear heat transfer in different geometries. Unlike the linearized Rosseland approximation which is derived by assuming sufficiently small temperature differences between the plate and the ambient fluid, when use is made of the nonlinear Rosseland diffusion approximation one can obtain results for both small and large differences between Tw (constant surface temperature) and T∞ (the constant ambient fluid temperature). It is also known that the inclusion of nonlinear radiative effects in the energy equation had led to a highly nonlinearity in the governing equations (see El-Hakim and Rashad, 2007).
The fluid is at rest and the motion is created by the surface whose velocity varies nonlinearly with the distance x from a fixed point and the sheet is held at a temperature higher than the temperature T∞ of the ambient fluid. For the stated problem and to our knowledge, the presented data on thermal analysis have not been considered before.
This paper aims to find similarity numerical solutions for problem above-mentioned. In Section 2 we shall examine the analysis of the flow and its mechanical characteristics. Heat transfer of a viscous fluid over a nonlinear stretching sheet in the presence of thermal radiation will be analyzed in Sections 3–4 by means of the nonlinear Rosseland diffusion approximation. The paper ends with its conclusions in Section 5.
2 Flow analysis
Let us consider the flow of an incompressible viscous fluid past a flat sheet coinciding with the plane y = 0, the flow being confined to y > 0. Two equal and opposite forces are applied along the x-axis so that the wall is stretched keeping the origin fixed. The fluid is assumed to be a gray, absorbing-emitting but non-scattering medium. Use is made of usual notation and then we can express the basic equations describing the conservation of mass and momentum in the boundary layer as
The mass and momentum Eqs. (1) and (2) must be solved subject to the boundary conditions
Now we introduce the following non-dimensional variables.
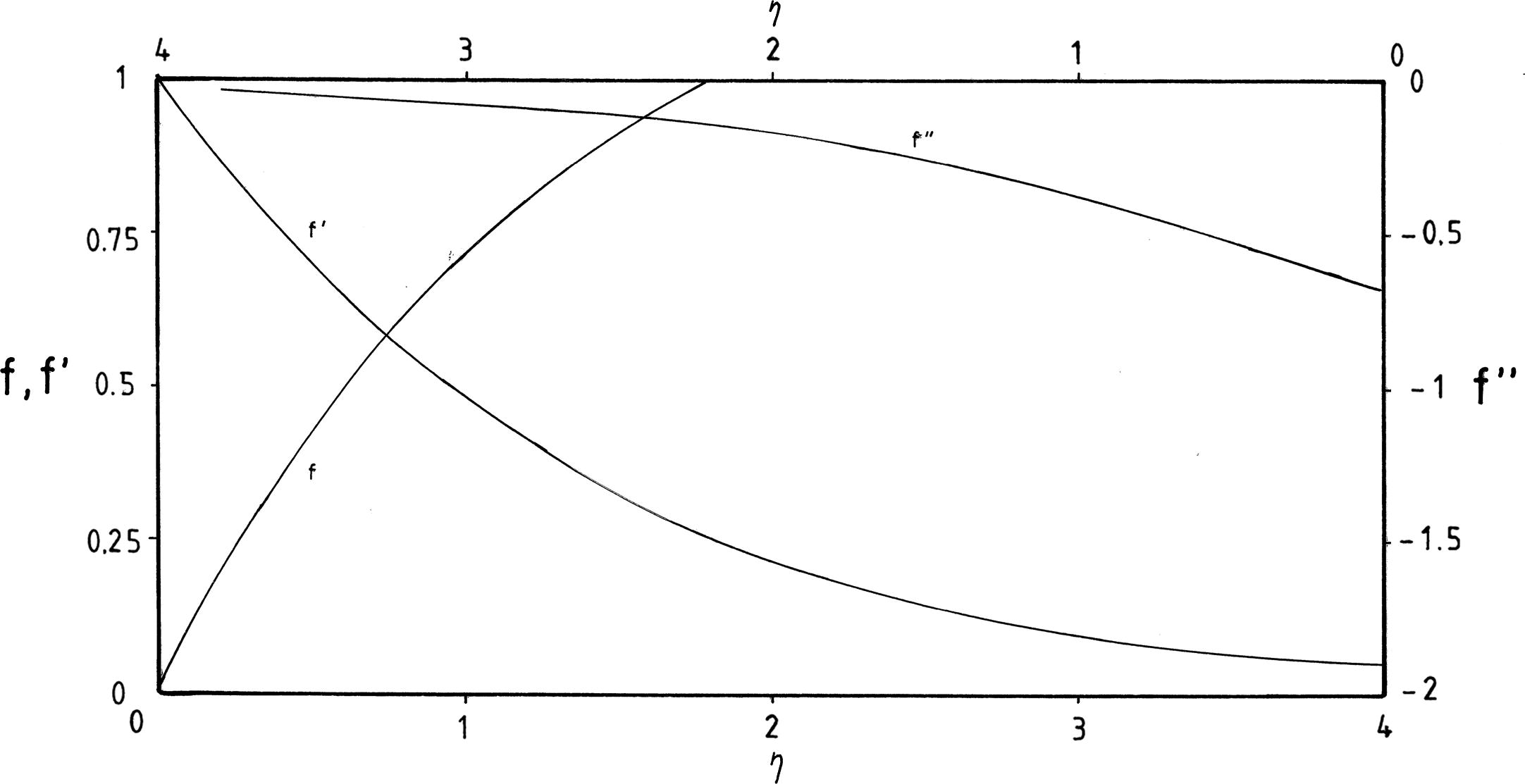
Plot of the functions f, f′ and f′′ for problem (5 and 6)
3 Heat transfer analysis
By using usual boundary layer approximations, the equation of the energy for temperature T in the presence of thermal radiation is given by
Using the Rosseland approximation for radiation (Rosseland, 1931), the radiative heat flux is simplified as
At this stage, it is necessary to note that for a boundary layer flow over a horizontal flat plate (see Pantokratoras and Fang, 2013), from Eq. (8) we get
The boundary conditions are
By defining the non dimensional temperature θ(η) as
Taking into account the above we get
The boundary conditions for θ(η) can now be expressed as
4 Results and discussion
Without a break, we begin now the development of the procedure for completing the numerical solution for θ(η). There is no any analytical solution for the momentum transfer problem and, accordingly, one had to use numerical techniques. It is clear that f′′(0) = −0.677647 (Cortell, 2008c) in that problem. Hence, the present numerical analysis extends the most recent thermal study of Cortell, 2008c to the case of nonlinear Rosseland approximation for thermal radiation, and with its use we will obtain numerical values of θ′(0) (i.e., temperature-gradient at the wall) in order to show the influences of the dimensionless parameters Pr, θw and NR onto the heat transfer characteristics and temperature distributions. Since the flow problem is uncoupled from the thermal problem, changes in the values of Pr, θw and NR will not affect the fluid velocity. For this reason, both the function f and its derivatives are identical in the complete problem (flow and heat transfer). In view of the above discussions, use will be made of f′′(0) = −0.677647 (Cortell, 2008c) and, with this result, we shall solve numerically the momentum and heat transfer problems. The best approximate for solving Eqs. (5), (6), (15–16) that can be used is the Runge-Kutta fourth order numerical method with shooting procedure (see White, 1991). Many other results are obtained throughout this work, and hence a selected set of results is presented graphically in Figs. 2–4 in order to analyze the distinct physical aspects of the problem. The effects of Prandtl number Pr on temperature profiles are depicted in Fig. 2 at
From this figure one can immediately observe that the thermal boundary layer thicknesses decrease drastically with an increase in Pr and, as a consequence, an increase (in absolute sense) in the wall temperature gradient occurs. Low Prandtl number Pr indicates fluids with large thermal conductivity and this produces thicker thermal boundary layer structures than that for high Pr number.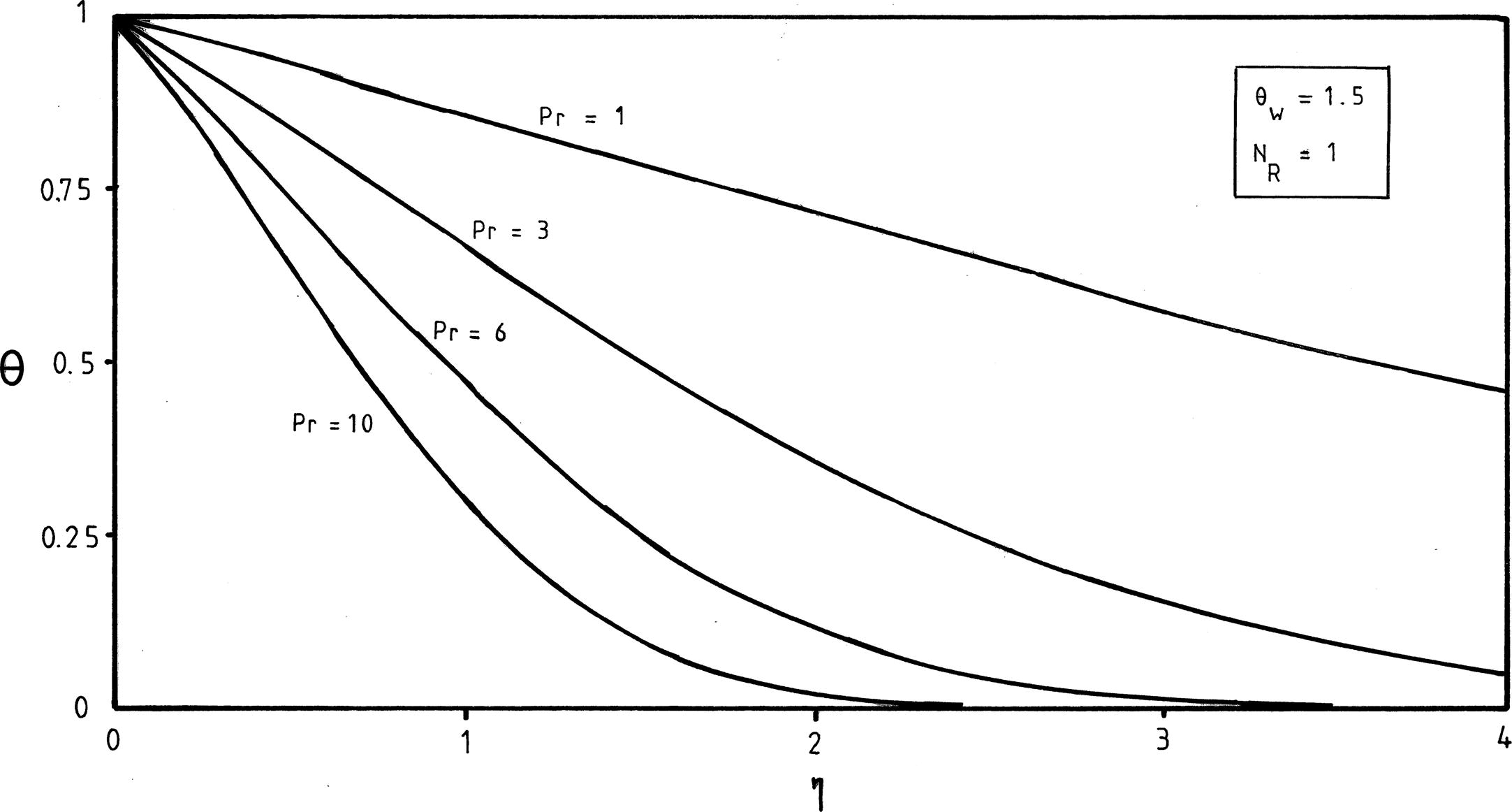
Effects of Prandtl number Pr on temperature profiles at
.
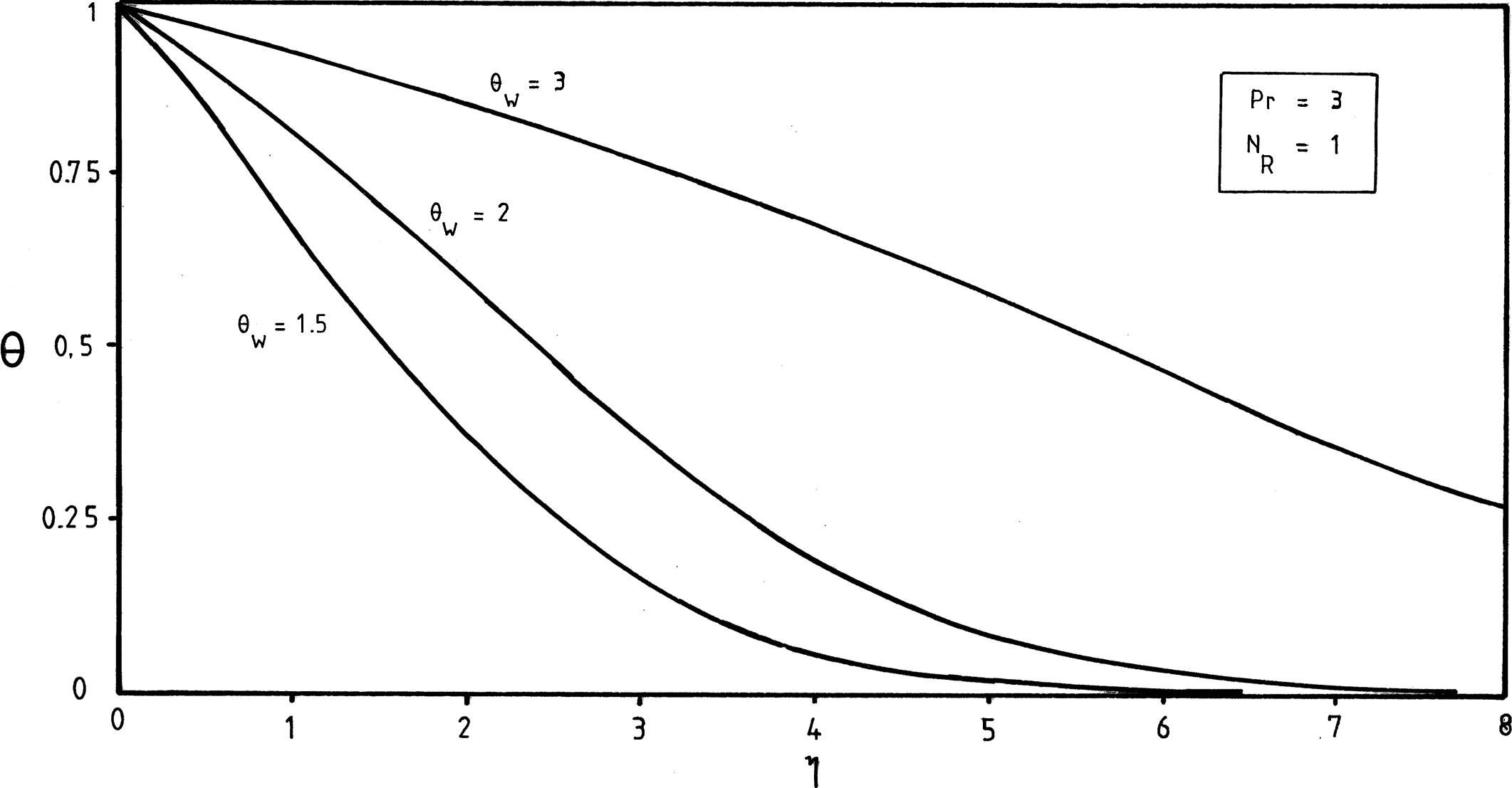
Effects of the temperature ratio parameter θw on temperature profiles at
.
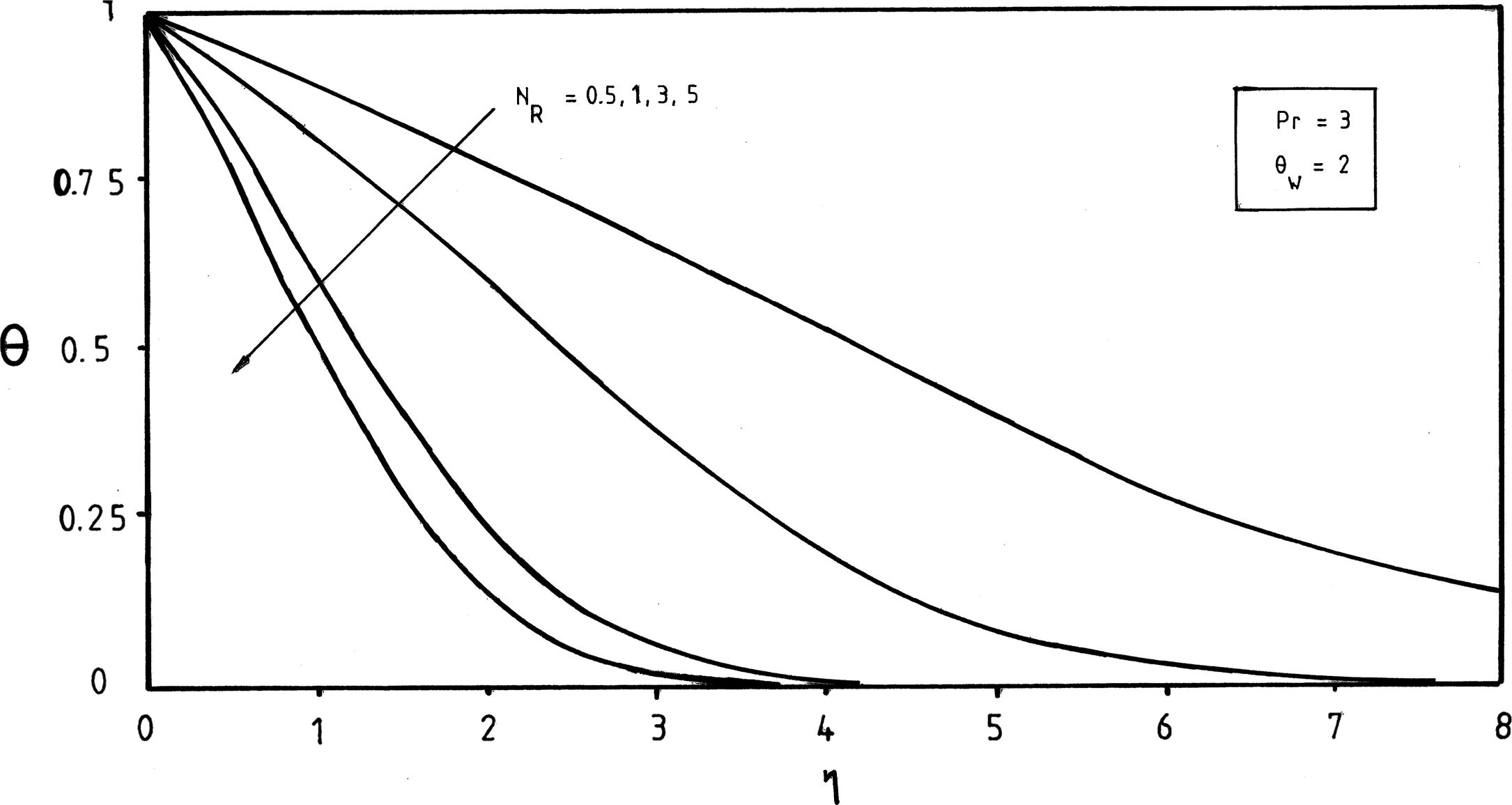
Effects of the thermal radiation parameter NR on temperature profiles at
.
Fig. 3 illustrates the effect of temperature ratio parameter θw on θ(η) curves. It should be noticed that increasing the temperature ratio parameter θw increases the thermal state of the fluid, resulting in increases in temperature profiles. However, as the thermal radiation parameter NR increases, it is observed from Fig. 4 that the temperature profiles decrease and then the thermal boundary layer thicknesses shrink.
As was already pointed out by Rahman and Eltayeb (2013) when use is made of the nonlinear Rosseland approximation to take into account thermal radiatiońs effect a point of inflection appeared on temperature profiles. In this paper, making use of our numerical approach, we find out the full set of η∞ (i.e., the extent of our integration domain), θ(η), and θ′(η) results, and for each studied case, we will be able to give the location of the aforesaid point onto temperature distributions.
In Table 1 we display some numerical results of θ(η) and θ′(η) when
. The computed values displayed in Table 1 indicate that the point of inflection for the θ(η) curve is located at η = 0.84 when |θ′(η)| reaches its maximum value in the interval [0, η∞]. For each set of fixed values of the three dimensionless parameters entering the problem, it is clear that an only missed value at η = 0 is guessed in our numerical approach, that is, the temperature-gradient at the wall θ′(0). The suitable guess value is chosen and the integration for heat transfer problem, Eqs. (15), (16), is carried out as an initial value problem by the Runge-Kutta shooting method of fourth order. For each numerical solution θ(η) the value of θ′(0) is iteratively estimated under the simultaneous assumptions
(see Table 1 in which temperature and temperature gradient profiles tend to zero at infinity simultaneously in an asymptotical fashion). Due to the fact no heat fluxes should exist outside the thermal boundary layer we need here to adopt the extra boundary condition
, and in this manner we circumvent possible unphysical behaviors of the solution. The latter was already established in the literature for related problems (see Van Gorder and Vajravelu, 2010). Also, in accord with Van Gorder and Vajravelu (2010), we also adopted the extra boundary condition
in Cortell (2008c) with a view to obtain f′′(0) = −0.677647 numerically; however, the aforementioned numerical treatment has been used in our studies since early 1990s (see, for example, Cortell, 1994). On the other hand, during the last years, numerous comparisons between our own numerical data and results obtained by means of several numerical procedures were presented in the open literature (note, for instance, the recently published numerical data by Rohni et al. (2012)). In Rohni et al. (2012) a completion for the shrinking sheet case but without thermal radiation effects of the Cortell’s paper (Cortell, 2012a) was carried out. Regarding existence and uniqueness of the solution, which we do not analyze in this short communication, boundary conditions (Van Gorder, 2010) and even additional terms in the energy equation (i.e., dissipative term) (Turkyilmazoglu and Pop, 2013) play an important role in these types of nonlinear boundary value problems.
η
θ(η)
−
0
1
0.304279
0.2
0.93773
0.317966
0.4
0.87303
0.328431
0.6
0.80659
0.335256
0.8
0.73919
0.338071
0.82
0.73243
0.338119
0.84
0.72567
0.338125
0.86
0.71891
0.338087
1
0.67165
0.336591
3
0.15644
0.145608
5
0.01999
0.021663
10
0.00015
0.000086
Finally, the values of the wall temperature gradient [−θ′(0)] as a function of all the parameters of the thermal boundary layer treated in this work have been tabulated in Table 2. It is apparent from this table that the effect of Prandtl number Pr on [−θ′(0)] is such that the |θ′(0)| value increases sharply with an increase in Pr and hence produces an increase in the heat transfer rate. As can be expected, the heat transfer rate |θ′(0)| also increases as NR increases with all other parameter fixed, that is, an increase in the radiation parameter NR will produce a decrease in the thermal boundary layer thickness, associated with the reduction in the temperature profiles. However, an augment in θw yields an augment in θ(η) and the rate of heat transfer tends to zero as the temperature ratio parameter θw increases (see Table 2).
Pr
θw
NR
−θ′(0)
0.677647 Cortell (2008c)
1
1.5
1
0.131636
3
0.304279
6
0.478746
10
0.652147
3
1.5
1
0.304279
2
0.169978
3
0.064057
3
2
0.5
0.100474
1
0.169978
3
0.335764
5
0.434466
5 Conclusions
The thermal radiation effects on flow influenced by a nonlinearly stretching sheet were studied numerically. The radiative heat flux term in the energy equation is introduced by means of the nonlinear Rosseland diffusion approximation. The effects of various physical parameters like Pr, θw and NR on heat transfer phenomena have been studied. It should also be concluded that in contrast to the linear Rosseland diffusion approximation, when use is made of the nonlinear one, the problem is also governed by the newly temperature ratio parameter θw. Similarity solutions for the case of stretching materials which have a wide variety of technical and environmental applications were found for all the aforementioned dimensionless physical parameters. The results presented indicate quite clearly that θw, which is an indicator of the small/large temperature difference between the surface and the ambient fluid, has a relevant effect on heat transfer characteristics and temperature distributions within the flow region generated by an isothermal sheet stretched in a non-linear fashion. From the above numerical research, the following conclusions may be drawn:
-
An increasing Prandtl number Pr causes diminution in the thickness of the thermal boundary layer.
-
For fixed Pr and NR, the rate of heat transfer (0)| extinguishes as the temperature ratio parameter θw increases.
-
From a qualitative point of view, the temperature ratio parameter θw and the thermal radiation parameter NR have the opposite effect, that is, temperature increases with increasing θw, whereas NR does the reverse.
Acknowledgement
The valuable comments and suggestions from the reviewers are greatly acknowledged.
References
- Abdul Hakeem, K., Ganesh, N. V., Ganga, B., 2013. Effect of heat radiation in a Walteŕs liquid B fluid over a stretching sheet with non-uniform heat source/sink and elastic deformation. Journal of King Saud University Engineering. in press, doi.: 10.1016/j.jksues.2013.05.006.
- An approximate analytic solution of the Blasius problem. Communications in Nonlinear Science and. Numerical Simulation. 2009;14:1021-1024.
- [Google Scholar]
- Thermal radiation effects on MHD flow past a semi-infinite inclined plate in the presence of mass diffusion. Heat and Mass Transfer. 2005;41:1056-1065.
- [Google Scholar]
- Effect of thermal radiation on the laminar free convection from a heated vertical plate. International Journal of Heat and Mass Transfer. 1968;11:871-881.
- [Google Scholar]
- Flow and heat transfer over a unsteady stretching sheet in a micropolar fluid. Meccanica. 2011;46:935-942.
- [Google Scholar]
- Application of the fourth-order Runge-Kutta method for the solution of high-order general initial value problems. Computers and Structures. 1993;49:897-900.
- [Google Scholar]
- Similarity solutions for flow and heat transfer of a viscoelastic fluid over a stretching sheet. International Journal of Non-Linear Mechanics. 1994;29:155-161.
- [Google Scholar]
- Numerical solutions of the classical Blasius flat-plate problem. Applied Mathematics and Computation. 2005;170:706-710.
- [Google Scholar]
- MHD flow and mass transfer of an electrically conducting fluid of second grade in a porous medium over a stretching sheet with chemically reactive species. Chemical Engineering and Processing: Process Intensification. 2007;46(8):721-728.
- [Google Scholar]
- Toward an understanding of the motion and mass transfer with chemically reactive species for two classes of viscoelastic fluid over a porous stretching sheet. Chemical Engineering and Processing: Process Intensification. 2007;46(10):982-989.
- [Google Scholar]
- A numerical tackling on Sakiadis flow with thermal radiation. Chinese Physics Letters. 2008;25:1340-1342.
- [Google Scholar]
- Effects of viscous dissipation and radiation on the thermal boundary layer over a nonlinearly stretching sheet. Physics Letters A. 2008;372(5):631-636.
- [Google Scholar]
- Similarity solutions for flow and heat transfer of a quiescent fluid over a nonlinearly stretching surface. Journal of Materials Processing Technology. 2008;203:176-183.
- [Google Scholar]
- Heat and fluid flow due to non-linearly stretching surfaces. Applied Mathematics and Computation. 2011;217:7564-7572.
- [Google Scholar]
- Suction, viscous dissipation and thermal radiation effects on the flow and heat transfer of a power-law fluid past an infinite porous plate. Chemical Engineering Research and Design. 2011;89(1):85-93.
- [Google Scholar]
- Combined effect of viscous dissipation and thermal radiation on fluid flows over a non-linearly stretched permeable wall. Meccanica. 2012;47(3):769-781.
- [Google Scholar]
- Heat transfer in a fluid through a porous medium over a permeable stretching surface with thermal radiation and variable thermal conductivity. Canadian Journal of Chemical Engineering. 2012;90(5):1347-1355.
- [Google Scholar]
- Effect of radiation on non-Darcy free convection from a vertical cylinder embedded in a fluid-saturated porous medium with a temperature-dependent viscosity. Journal of Porous Media. 2007;10(2):209-218.
- [Google Scholar]
- Effect of radiation on free convection from a porous vertical plate. International Journal of Heat and Mass Transfer. 1999;42:181-191.
- [Google Scholar]
- The effect of radiation on free convection flow of fluid with variable viscosity from a porous vertical plate. International Journal of Thermal Sciences. 2001;40:115-124.
- [Google Scholar]
- Heat and mass transfer for micropolar flow with radiation effect past a nonlinearly stretching sheet. Heat and mass transfer. 2010;46:413-419.
- [Google Scholar]
- Multimedia feature for unsteady fluid flow over a non-uniform heat source stretching sheet with magnetic radiation physical effects. Applied Mathematics and Information Sciences. 2012;6(1S):59S-65S.
- [Google Scholar]
- Thermal boundary layer flow over a stretching sheet in a micropolar fluid with radiation effect. Meccanica. 2010;45(2010):367-373.
- [Google Scholar]
- J. C. Misra. J. C., Sinha, A., 2013. Effect of thermal radiation on MHD flow of blood and heat transfer in a permeable capillary in stretching motion. Heat and Mass Transfer, in press, doi.: 10.1007/s00231-012-1107-6.
- Pantokratoras, A., Fang, T., 2013. Sakiadis flow with nonlinear Rosseland thermal radiation. Physica Scripta 87, 015703 (5pp).
- Prasad, K. V., Datti, P. S., Vajravelu, K., 2013. MHD mixed convection flow over a permeable non-isothermal wedge. Journal of King Saud University Science. 25, 313–324.
- Radiative heat transfer in a hydromagnetic nanofluid past a non-linear stretching surface with convective boundary condition. Meccanica. 2013;48:601-615.
- [Google Scholar]
- Viscoelastic flow by the presence of radiation. Zeits. Angew. Mathematik und Mechanik. 1998;78(4):277-279.
- [Google Scholar]
- Note on Cortelĺs non-linearly stretching permeable sheet. International Journal of Heat and Mass Transfer. 2012;55:5846-5852.
- [Google Scholar]
- Astrophysik und Atom-Theoretische Grundlagen. Berlin: Springer Verlag; 1931. pp. 41–44
- Sakiadis flow of an upper-convected Maxwell fluid. International Journal of Non-Linear Mechanics. 2005;40:1220-1228.
- [Google Scholar]
- Boundary-layer behaviour on continuous solid surfaces. American Institute of Chemical Engineers. 1961;7:26-28.
- [Google Scholar]
- Thermal radiation effects on the time-dependent MHD permeable flow having variable viscosity. International Journal of Thermal Sciences. 2011;50:88-96.
- [Google Scholar]
- Exact analytical solutions for the flow and heat transfer near the stagnation point on a stretching/shrinking sheet in a Jeffrey fluid. International Journal of Heat and Mass Transfer. 2013;57:82-88.
- [Google Scholar]
- A general class of coupled nonlinear differential equations arising in self-similar solutions of convective heat transfer problems. Applied Mathematics and Computation. 2010;217:460-465.
- [Google Scholar]
- High-order nonlinear boundary value problems admitting multiple exact solutions with application to the fluid flow over a sheet. Applied Mathematics and Computation. 2010;216:2177-2182.
- [Google Scholar]
- Heat transfer by simultaneous conduction and radiation in an absorbing medium. Journal of Heat Transfer. 1962;84:63-72.
- [Google Scholar]
- Viscous Fluid Flow. New York: McGraw-Hill; 1991.







