Facile Growth, Physical Characterization, and Dielectric Response of As-Grown NiO Nanostructures

3.1.1 Rietveld refinement based on powder X-ray diffraction analysis

The presence of intense and sharp diffraction peaks and the absence of diffraction halo in the recorded XRD pattern (Fig. 1(a)) indicate the presence of crystalline phase only and the lack of any amorphous or crystalline-amorphous phase formation, respectively (Abdullah et al., 2014). The obtained and reported (JCPDS: 04-0835) d-values are almost similar, which confirms the cubic system of unit crystal structures.

Close

Fig. 1

(a) Powder X-ray Diffraction pattern along with Rietveld refinement of the as-grown nanostructured NiO. The solid black circles and the red line are the observed (I_obs) and calculated (I_cal.) NiO X-ray diffraction patterns respectively, the bottom black line is the difference between them (I_obs-I_cal) and the vertical lines (l) indicate the NiO reflection lines, (b-c) low to high magnification FESEM images, (d) corresponding EDS-spectrum (e) Lattice resolved HRTEM image, and (f) the SAED pattern along the [1 1 0] zone axis of as-grown well-crystallized NiO nanostructures.

Export to PPT

Rietveld refinement (Rietveld, 1969) of the x-ray diffraction pattern is known to be an excellent method to extract the structural parameters. In this method the difference between the observed and the calculated intensities of the diffraction pattern is minimized in order to obtain the weighted residual factor $R_{\mathit{wp}}=\sqrt{\left\{\frac{{\sum }_i{w}_i{(I_{\mathit{obs}}-I_{\mathit{calc}})}^2}{{\sum }_i{w}_i{(I_{\mathit{obs}})}^2}\right\}}$ , the expected residual factor $R_{\mathit{exp}}=\sqrt{\left\{\frac{N-P}{{\sum }_i{w}_i{(I_{\mathit{obs}})}^2}\right\}}$ , the R pattern $R_p=\left\{\frac{{\sum }_i(I_{\mathit{obs}}-I_{\mathit{calc}})}{{\sum }_i{I}_{\mathit{obs}}}\right\}$ as well as the goodness of fit $\mathit{GOF}=\frac{R_{\mathit{wp}}}{R_{\mathit{exp}}}$ , where ‘I_obs’ and ‘I_calc’ are the observed and the calculated intensities of the diffraction pattern. ‘w_i’ is a weighting factor defined as w_i = 1/I_obs at the ith step in the diffraction pattern. ‘N’ is the number of experimental observations, and ‘P’ is the number of refined parameters. (McCusker et al., 1999). A NiO cubic system with space group (Fm-3 m (2 5 5)) was used in the refinement, where Ni and O atoms were assigned to specific positions of (4a)(0,0,0) and (4b)(0.5,05,0.5) respectively. A very good Rietveld fit was obtained as shown in Fig. 1(a). Moreover, the fitting parameters (R values) of the final fit are summarized in Table 1, indicating the validity of the fit. The refined lattice parameter a = 4.1770(2) Å.

A separate refinement was performed to extract the crystallite size and the micro-strain of NiO nanocrystals. To achieve this, a Si standard material was used to evaluate the instrumental broadening (Van-Berkum, 1994), and then subtract it off. Table 1 summarizes the derived structural parameters obtained from the Rietveld refinement of the NiO pattern. The derived average crystallite size is 25.66 nm. Whereas, the average micro-strain is found to be 0.340.

3.1.2 Morphological, elemental, and structural analysis using FESEM, and HRTEM

The FESEM images (Fig. 1(b–c)) show the general morphologies of the as-grown NiO nanostructures. Large numbers of the sphere like shapes can be seen in the low magnification image (Fig. 1(b)). These spheres like shapes exhibit the agglomerated nanostructures of NiO. The average diameter of these spherical-shaped arrays is around 6 μm. Furthermore, the high-magnification FESEM image (Fig. 1(c)) clearly shows the unbroken network of interconnected nanostructures within the spherical shape. Most of these nanostructures depict the sheet-like structures. Typically, the average thickness of these nanosheets is around 50 nm. The EDS spectrum (Fig. 1(d)) of as-grown NiO nanostructures shows the peaks of nickel and oxygen only, and thus indicates the absence of impurity. The elemental composition of Ni and O are in stoichiometric proportion and is in agreement with previous studies (Dıaz et al., 2017).

Furthermore, the crystal structures of as-grown nanostructures were characterized by HRTEM. Fig. 1(e) shows the lattice resolved HRTEM image of NiO nanocrystal corresponding to (1 1 1) crystal plane with a d-spacing of 0.24 nm. Fig. 1(f) represents the corresponding selected area electron diffraction (SAED) patterns along the [1 1 0] axis. The SAED pattern illustrates the perfect rectangular diffraction spots. Which indicates the single crystalline nature of NiO nanocrystals. Dots in SAED pattern correspond to the (1 1 1), (0 0 2), and (2 2 0) planes.

3.1.3 Optical analysis using UV–VIS spectrophotometer

The optical absorption spectrum (Fig. 2(a)) of the as-grown NiO nanostructures demonstrates the common tendency of optical absorption. Fig. 2(a) shows the lower cut off wavelength around 295 nm. Tauc’s relation (1) (Abdullah et al., 2013) was used to evaluate the optical band gap (E_g)

Close

Fig. 2

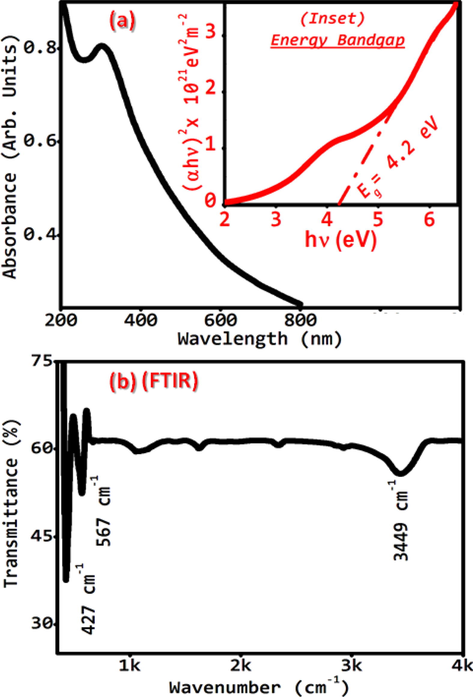
Typical (a) UV–VIS absorbance spectrum, (Inset Fig. 2(a)) direct band gap evaluation, and (b) FT-IR spectra of as-grown NiO nanostructures.

Export to PPT

where ‘α’ is the absorption coefficient. ‘A’ is a constant. And ‘n = ½’ for the direct band gap. The direct ‘E_g’ (=4.2 eV) was evaluated by extrapolating the straight line to the energy axis (Inset of Fig. 2(a)). The calculated and reported values (Table 2) are in good agreement (Jian et al., 2012). Earlier reported value of the direct band gap in the corresponding NiO thin film is in the range 2.10 eV − 3.90 eV (Ezema et al, 2008; Marek et al, 2011; Srivastava et al, 2008) whereas, for NiO single crystal it is reported to be equal to 3.87 eV (Dong-Kang et al., 2007). Table 2 shows the highest energy band gap for nanostructures compared to the thin film and single crystal. The variation in energy band gap is due to the possible optical quantum confinement effect. (Abdullah et al., 2015; Zong et al., 2013).

3.1.4 Spectroscopic analysis using FTIR

The FTIR spectra (Fig. 2(b)) shows the three sharp bands at 427, 567, and 3449 cm⁻¹. The first two bands are attributed to Ni–O stretching-vibration (Dharamraj et al., 2006) whereas, the peak found at 3449 cm⁻¹ corresponds to –OH stretching-vibration (Ikram-ul-Haq, 2010). The band at 3449 cm⁻¹ shows that the specimen has physically absorbed the water molecule during the pellet preparation. The weak serrated peaks in the range 1000–2500 cm⁻¹ demonstrate the presence of O—C⚌O and C—O stretching vibration. This shows that the material absorbed a negligible amount of H₂O and CO₂ (Hongxia et al., 2009).

3.2.1 Evaluation of dielectric constant (ε)

The response graph (Fig. 3(a) solid blackline) of the frequency dependent dielectric constant (ε) shows that the value of ‘ε’ is lower at higher frequencies. This indicates the presence of all four kinds of dielectric polarization in the low frequency range. Due to this, we found the higher values of ‘ε’ (Abdullah et al., 2011). Simultaneously, Fig. 3(a) (solid blackline) shows a fast decrease in the value of ‘ε’ in the low-frequency region. Such a radical fall is mainly due to the fast decrease in interfacial space charge polarization (Abdullah et al., 2014). Thus, it is found that the space charge polarization is responsible for this dielectric behaviour. The mechanism of the observed trend of ‘ε’ can also be understood more clearly on the basis of a conduction relaxation process, which is related to the charge hopping motion occurring inside the matrix. In the lower frequency region, the randomly oriented motion of the charges generates a higher value of stretching effect inside the matrix. The higher value of the stretching effects amplifies the relaxation time, which in turn increases the hopping length of the charges, and thus produces the higher values of dielectric constant. As the strength of the applied electric field increases with frequency, the electron hoping concentration decreases. Due to this, the value of ‘ε’ in the higher frequency region decreases (Abdullah et al., 2018). The fig (Fig. 3(a) solid blackline) shows that the evaluated values of dielectric constants (9–20) are almost regular in the broad range of frequency (1 MHz − 30 MHz). Therefore, this material can be used in devices to get a steady value of ‘ε’ in this broad frequency range. The value of ‘ε’ for nanostructure was found to increase compared to their bulk counterpart. As, for example, let us consider the frequency of 100 KHz. At this specific frequency, the value of ‘ε’ reported for single crystals and thin films is 11.2 (Rao and Samakula, 1965) and ∼30 (Makhlouf, 2008), respectively while in the present work, it is 42. This distinct higher value of ε is possibly due to the difference in the exposed surface areas of nanosize NiO and bulk size NiO. Furthermore, the dielectric materials of higher values are useful for microelectronic devices such as memory devices, high K-gate dielectrics, etc. (Yu-Jen Hsiao et al., 2007).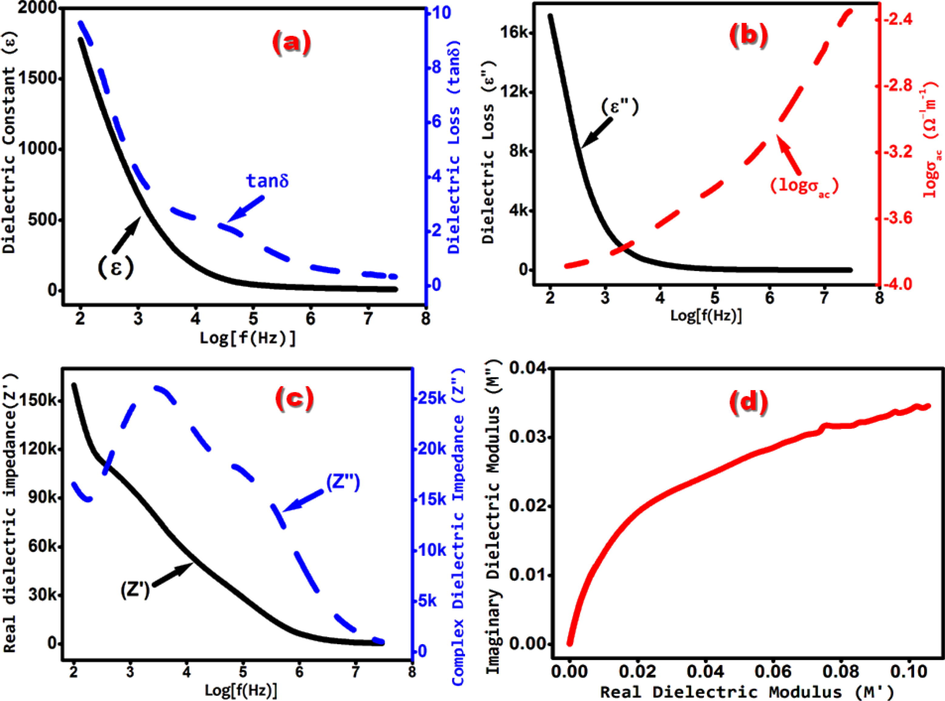

Close

Fig. 3

(a) solid blackline shows dielectric constant ‘ε’, and the dashed blueline shows dielectric loss tangent ‘tanδ’ (b) solid blackline shows dielectric loss (ε′′), and the dashed redline shows ac conductivity ‘σ_ac’, (c) solid blackline shows the real dielectric impedance (Z′), and the dashed blueline shows the complex dielectric impedance (Z′′) (d) shows the Cole – Cole plot of real part of the dielectric modulus (M') verses imaginary part of the dielectric modulus (M“) of as-grown NiO nanostructures.

Export to PPT

3.2.2 Evaluation of dielectric loss tangent (tanδ), and dielectric loss $({\epsilon }^{″})$

The observed behavior of frequency-dependent dielectric loss tangent ‘tanδ’ (Fig. 3(a) dashed blueline) is more or less analogous to the behavior obtained for ‘ε’ (Fig. 3(a) solid blackline). Some small variations are possible due to the relaxation effects occurring because of impurities etc. around the sensitive transition region (Bhatt et al., 2007). On an average, the value of ‘tanδ’ (Fig. 3(b) dashed blueline) is low (9.57–0.32) in the entire frequency region, whereas, it is shallow (0.69–0.32) in the high-frequency range (1 MHz–30 MHz) and is more or less regular. Smaller ‘tanδ’ advocates the enhanced optical quality of the material with minor defects, which is one of the important required parameters for the fabrication of nonlinear optical devices (Abdullah et al., 2011). A strong resistance non-linearity, and third harmonic generation have been explored in NiO thin films (Lee et al., 2008) and giant non-linear absorption in NiO single crystal was also found (Shablaev and Pisarev, 2003). Therefore, the NiO in nano size could be a potential material in non-linear optical devices.

Fig. 3(b) solid blackline, shows the frequency dependence of dielectric loss ( ${\mathit{\epsilon }}^{\mathbf{″}}$ ) for NiO nanostructures. The response graph demonstrates the radical fall in the value of ${\mathit{\epsilon }}^{\mathbf{″}}$ in the low frequency region, whereas it is almost constant and low in the high frequency region. At low frequency, the higher value of ${\mathit{\epsilon }}^{\mathbf{″}}$ is due to space charge polarization, whereas, at the high frequency, lower value of ${\mathit{\epsilon }}^{\mathbf{″}}$ is possibly because of the movement of the free charges. The absence of peaks in ${\mathit{\epsilon }}^{\mathbf{″}}$ (Fig. 3(b) solid blackline) is because of the fact that there is only one straight line in the high frequency region of the graph of ε (Fig. 3(a) solid blackline), which revealed the occurrence of hopping transport mechanism and confirms the non-Deby type dielectric relaxation. (Gaurav et al., 2015; Sharma et al., 2016; Gerhardt, 1994).

3.2.3 Analysis of electrical conductivity

Dashed redline in Fig. 3, shows the characteristic graph of ‘σ_ac’. The graph was drawn using Eq. (2) (Vasudevan et al., 2011)

The figure (dashed redline in Fig. 3) shows almost the frequency independent conductivity in the low-frequency region. Whereas, in the mid and high-frequency range, it shows dependent conductivity. A possible consistent response of conductivity in the low-frequency range corresponds to the dc conductivity. While a relative increase of conductivity in the remaining higher frequency range follows the frequency power law (Jonscher, 1977) as given beow in eq. (4)

This shows that dc conductivity occurs for n → 0, and for ω → 0 limits. Thus we found that the slope of the plotted graph tends to zero in case of dc conductivity. The occurrence of the dc conductivity is because of the loss factor, which has been explained by Jonscher as (Jonscher, 1977)

The mechanism of polarization can be explained in terms of discontinuous hopping of electrons or ions, or jumping of dipoles (Jonscher, 1977). As per jump relaxation model (JRM) (Funke, 1993), the successful hop of charges occurs in the low-frequency range. Whereas unsuccessful hops of ions are attributed to the mid and high-frequency range. The successful hop contributes the long-range translational motion of charges. Which is responsible for the leakage of dc current. The unsuccessful hop of ions contributes the short-range translation movement of ions. The occurrence of unsuccessful hop increases with frequency, which in turn produces the localized or reorientation hopping in the high-frequency region. Thus, it has been found that the successful jump of ions is responsible for the dc conductivity and the unsuccessful hopping is accountable for the ac current.

3.2.4 Impedance and modulus spectroscopy

The solid blackline in Fig. 3(c) shows the variation of real dielectric impedance (Z') with frequency. From the figure, one can find that the values of Z’ decrease as the frequency increase and reached to minimum constant values at higher-frequencies. This tendency of the graph is due to the increase in ac conductivity (σ_ac) with increasing frequency which further confirms the inverse proportional between them. The response graph of Z' in the low-frequency range is accredited to space charge polarization. In the high-frequency range, nearly a shallow constant value of Z′ is due to the inefficient space charge polarization against high-frequency fields. (Jethva and Joshi, 2018; Plocharski et al., 1988; Ganguly et al., 2011).

The dashed blueline in Fig. 3(c) shows the variation of complex dielectric impedance (Z^′′) with frequency. From the figure, it has been found that the variation of Z^′′ with frequencies exhibit a peak in the low frequency range, and then after that, the value of Z^′′ decreases monotonically with increasing frequency in the mid and high frequency region. The appearance of the peak in the low-frequency region indicates the grain boundary relaxation mechanism in the sample (Jethva and Joshi, 2018). The presence of only one peak specifies the presence of a single dielectric relaxation process (Belal and Akhter, 2015). The full-width at half-maximum (FWHM) of a peak reveals the type of relaxation occurring within the dielectric material. For Debye type dielectric relaxation, FWHM of the peak should be less than 1.14 decades (Jethva and Joshi, 2018). But, the calculated value of FWHM of the peak (dashed blueline in Fig. 3(c)) is 1.2 decades, which confirms the presence of non-Debye type relaxation behaviour of the material. The maximum of the peaks (f_max) gives the value of relaxation frequency (Ebru and Ayse, 2012) which is equal to 2000 Hz (dashed blueline in Fig. 3(c)). By knowing the value of ‘f_max’ the value of relaxation-time (τ) can be obtained by using the relation 2πf_maxτ = 1, (Belal and Akhter, 2015) which is found to be equal to 80 microseconds.

The dielectric response of NiO nanoparticles can also be described using the Cole-Cole plot of the real part of the dielectric modulus (M') versus the imaginary part of the dielectric modulus (M“). If the plotted graph represents a semicircle with their center on the x-axis (i.e., on M′′ line), then it indicates a Debye type relaxation in the compound. Otherwise, the curve other than a semicircle confirms the existence of non-Debye type relaxation (Reenu et al., 2015). Fig. 3(d) shows the cole-cole plot of the real (M′) versus imaginary (M′′) part of the dielectric modulus of NiO nanoparticles. The Fig. 3(d) shows a single circular arc in the complex modulus plane. The center of this arc lies below the M′ axis. This confirms the formation of a single phase compound and non-Debye type dielectric relaxation. (Piyush et al., 2012; Shweta et al., 2016).