Exp-function method for traveling wave solutions of modified Zakharov–Kuznetsov equation

Syed Tauseef Mohyud-Din; Muhammad Aslam Noor; Khalida Inayat Noor

doi:10.1016/j.jksus.2010.04.015

View/Download PDF

Buy Reprints

PDF

Translate this page into:

ORIGINAL ARTICLE

22 (

); 213-216

doi:

10.1016/j.jksus.2010.04.015

Exp-function method for traveling wave solutions of modified Zakharov–Kuznetsov equation

Syed Tauseef Mohyud-Din^a,*, Muhammad Aslam Noor^b,c, Khalida Inayat Noor^b

a HITEC University, Taxila Cantt, Pakistan

b Department of Mathematics, COMSATS Institute of Information Technology, Islamabad, Pakistan

c Department of Mathematics, King Saud University, Saudi Arabia

*Corresponding author. Tel.: +92 333 5151290 syedtauseefs@hotmail.com (Syed Tauseef Mohyud-Din),

Received: 2010-4-20, Accepted: 2010-4-29, Published: 2010-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Abstract

In this paper, we apply the exp-function method to construct generalized solitary and periodic solutions of modified Zakharov–Kuznetsov equation which play a very important role in mathematical physics and engineering sciences. The suggested algorithm is quite efficient and is practically well suited for use in these problems. Numerical results clearly indicate the reliability and efficiency of the proposed exp-function method.

Keywords

Exp-function method

Zakharov–Kuznetsov equation

Nonlinear evolution equations

Show Related Articles from PubMed

1 Introduction

This paper is devoted to the study of a nonlinear evolution equation which is called the Zakharov–Kuznetsov (ZK) equation and is of the form

(1)

u_{t} + u^{2} u_{x} + u_{xxx} + u_{xyy} = 0 .

The ZK equation arises in number of scientific models including fluid mechanics, astrophysics, solid state physics, plasma physics, chemical kinematics, chemical chemistry, optical fiber and geochemistry, see (Mohyud-Din et al., 2008; Tascan et al., 2008; Wazwaz, 2008 ) and the references therein. The basic motivation of this paper is to extend the application of a very reliable and efficient technique which is called the exp-function method for traveling wave solutions of modified Zakharov–Kuznetsov (ZK) equation. The proposed method was developed by He and Wu (He and Wu, 2006) to seek the solitary, periodic and compacton like solutions of nonlinear differential equations; see (Abdou et al., 2007; El-Wakil et al., 2007; He and Wu, 2006; He and Abdou, 2007; Mohyud-Din et al., 2009, 2010, 2008; Noor et al., 2008a,b; Tascan et al., 2008; Wazwaz, 2008; Wu and He, in press, 2007; Yusufoglu, 2008; Zhou, 2007; Zhou et al., 2008; Zhang, 2007; Zhu, 2007a,b ) and the references therein.

2 Exp-function method

We consider the general nonlinear PDE of the type

(2)

P (u, u_{t}, u_{x}, u_{y}, u_{tt}, u_{xx}, u_{yy}, u_{xt}, u_{xy}, u_{ty} \dots) = 0 .

Using a transformation

(3)

η = kx + ω y + ρ t, or η = α x + β y + ρ t,

where

k, ω, α, β

and

ρ

are constants, we can rewrite Eq. (3) in the following nonlinear ODE;

(4)

Q (u, u^{'}, u^{″}, u^{‴}, \dots) = 0 .

According to exp-function method, which was developed by He and Wu (2006), we assume that the wave solution can be expressed in the following form:

(5)

u (η) = \frac{\sum_{n = - d}^{c} a_{n} \exp [n η]}{\sum_{m = - q}^{p} b_{m} \exp [m η]},

where

p, q, c

and d are positive integers which are known to be further determined,

a_{n}

and

b_{m}

are unknown constants. We can rewrite Eq. (6) in the following equivalent form:

(6)

u (η) = \frac{a_{c} \exp [c η] + \dots + a_{- d} \exp [- d η]}{b_{p} \exp [p η] + \dots + b_{- q} \exp [- q η]} .

This equivalent formulation plays an important and fundamental part for finding the analytic solution of problems. To determine the value of c and p, we balance the linear term of highest order of Eq. (4) with the highest order nonlinear term. Similarly, to determine the value of d and q, we balance the linear term of lowest order of Eq. (4) with lowest order nonlinear term (Abdou et al., 2007; El-Wakil et al., 2007; He and Wu, 2006; He and Abdou, 2007; Mohyud-Din et al., 2009, 2010, 2008; Noor et al., 2008a,b; Tascan et al., 2008; Wazwaz, 2008; Wu and He, in press, 2007; Yusufoglu, 2008; Zhou, 2007; Zhou et al., 2008; Zhang, 2007; Zhu, 2007a,b ).

3 Solution procedure

Consider the modified Zakharov–Kuznetsov (ZK) Eq. (1) $u_{t} + u^{2} u_{x} + u_{xxx} + u_{xyy} = 0 .$

Introducing a transformation as $η = α x + β y + ρ t$ , we can covert Eq. (1) into an ODE as

(7)

ρ u^{'} + α u^{2} u^{'} + (α^{3} + α β^{2}) u^{‴} = 0 .

The solution of the Eq. (7) can be expressed as follows:

(6)

u (η) = \frac{a_{c} \exp [c η] + \dots + a_{- d} \exp [- d η]}{b_{p} \exp [p η] + \dots + b_{- q} \exp [- q η]} .

To determine the value of c and p, we balance the linear term of highest order of Eq. (7) with the highest order nonlinear term

(8)

u^{‴} = \frac{c_{1} \exp [(7 p + c) η] + \dots}{c_{2} \exp [8 p η] + \dots}

and

(9)

u^{2} u^{'} = \frac{c_{3} \exp [(p + 3 c) η] + \dots}{c_{4} \exp [4 p η] + \dots} = \frac{c_{3} \exp [(5 p + 3 c) η] + \dots}{c_{4} \exp + [8 p η] \dots},

where

c_{i}

are determined coefficients only for simplicity; balancing the highest order of exp-function in (8) and (9), we have

(10)

7 p + c = 5 p + 3 c,

which in turn gives

(11)

p = c .

To determine the value of d and q, we balance the linear term of lowest order of Eq. (7) with the lowest order nonlinear term

(12)

u^{‴} = \frac{\dots + d_{1} \exp [(- d - 7 q) η]}{\dots + d_{2} \exp [- 8 q η]}

and

(13)

u^{'} u^{″} = \frac{\dots + d_{3} \exp [(- q - 3 d) η]}{\dots + d_{4} \exp [- 4 q η]} = \frac{\dots + d_{3} \exp [(- 3 d - 5 q) η]}{\dots + d_{4} \exp [- 8 q η]},

where

d_{i}

are determined coefficients only for simplicity. Now, balancing the lowest order of exp-function in (12) and (13), we have

(14)

- 7 q - d = - 5 q - 3 d,

which in turn gives

(15)

q = d .

Case 3.1.1

We can freely choose the values of c and d, but we will illustrate that the final solution does not strongly depend upon the choice of values of c and d. For simplicity, we set $p = c = 1$ and $q = d = 1$ , then the trial solution, Eq. (6) reduces to

(16)

u (η) = \frac{a_{1} \exp [η] + a_{0} + a_{- 1} \exp [- η]}{b_{1} \exp [η] + a_{0} + b_{- 1} \exp [- η]} .

Substituting Eq. (16) into (7), we have

(17)

\frac{1}{A} [c_{3} \exp (3 η) + c_{2} \exp (2 η) + c_{1} \exp (η) + c_{0} + c_{- 1} \exp (- η) + c_{- 2} \exp (- 2 η) + c_{- 3} \exp (- 3 η)] = 0,

where

A = (b_{1} \exp (η) + b_{0} + b_{- 1} \exp (- η))^{4}

c_{i} (i = - 3, \dots, 0, \dots, 3)

are constants obtained by Maple 11.

Equating the coefficients of $\exp (n η)$ to be zero, we obtain

(18)

{c_{- 3} = 0, c_{- 2} = 0, c_{- 1} = 0, c_{0} = 0, c_{1} = 0, c_{2} = 0, c_{3} = 0} .

Solution of (18) will yield

(19)

a_{- 1} = 0, b_{0} = b_{0}, b_{1} = b_{1}, b_{- 1} = \frac{1}{24} \frac{a_{0}^{2}}{b_{1} (β^{2} + α^{2})}, a_{1} = 0, ρ = - α β^{2} - α^{3}, a_{0} = a_{0} .

We, therefore, obtained the following generalized solitary solution $u (x, y, t)$ of Eq. (1)

(20)

u (x, y, t) = \frac{a_{0}}{b_{1} e^{(α x + β y + ρ t)} + \frac{1}{24} \frac{a_{0}^{2}}{b_{1} (β^{2} + α^{2})} e^{(- α x - β y - ρ t)}},

where

ρ = - α β^{2} - α^{3},

and

a_{0}, b_{1}, α

and

β

are real numbers (see Fig. 3.1).

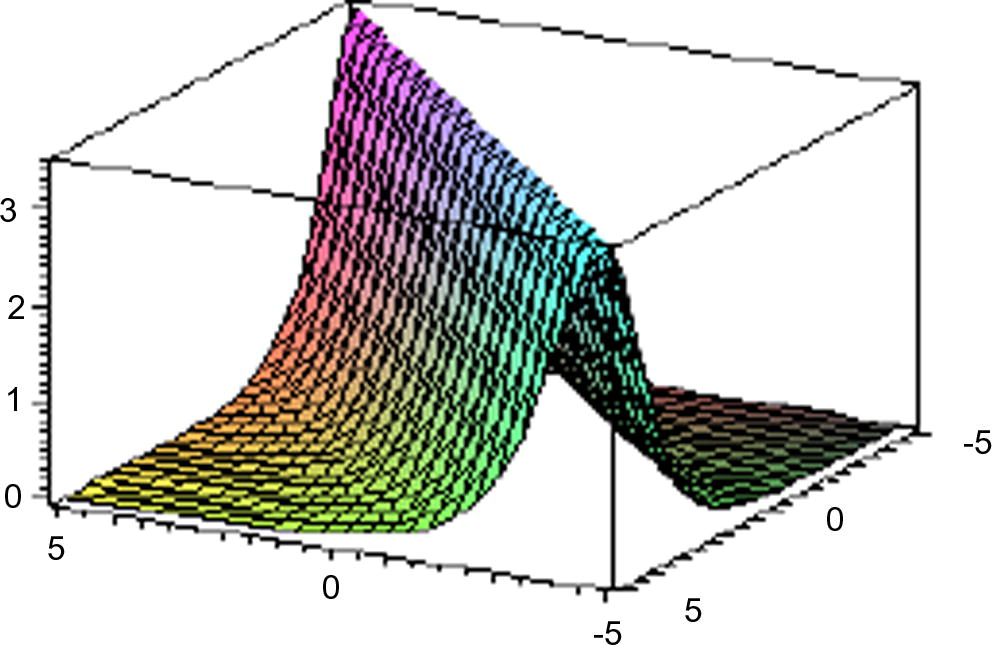
Depicts soliton solutions of Eq. (1), when a 0 = b 1 = β = α = 1 .

In case $α$ and $β$ are imaginary numbers, the obtained soliton solution can be converted into periodic solution or compact-like solution. Therefore, we write $α = i ω$ and $β = i θ$ , respectively. Consequently, Eq. (20) becomes $u (x, y, t) = \frac{a_{0}}{b_{1} e^{(i ω x + i θ y + ρ t)} - \frac{a_{0}^{2}}{24 b_{1} (ω^{2} + θ^{2})} e^{(- i ω x - i θ y - ρ t)}},$ where $ρ = i (ω θ^{2} + ω^{3})$ , and $a_{0}, b_{1}, θ$ and $ω$ are real numbers, consequently

(21)

u (x, y, t) = \frac{[\begin{matrix} \cos (ω x + θ y + t ω θ^{2} + t ω^{3}) [576 b_{1}^{2} θ^{2} + 576 b_{1}^{2} ω^{2} - 24 a_{0}^{2}] \\ + i \sin (ω x + θ y + t ω θ^{2} + t ω^{3}) [- 576 b_{1}^{2} θ^{2} - 576 b_{1}^{2} ω^{2} - b_{1} a_{0} (θ^{2} + ω^{2})] \end{matrix}]}{[\begin{matrix} \cos (ω x + θ y + t ω θ^{2} + t ω^{3})^{2} [- 96 b_{1}^{2} a_{0}^{2} (θ^{2} + ω^{2})] + 576 b_{1}^{4} (θ^{4} + ω^{4}) \\ + 1152 b_{1}^{4} θ^{2} ω^{2} + 48 b_{1}^{2} a_{0}^{2} (θ^{2} + ω^{2}) + a_{0}^{4} \end{matrix}]} .

For periodic or compact-like solutions, the imaginary part in Eq. (21) must be zero, hence

(22)

u (x, y, t) = \frac{\cos (ω x + θ y + t ω θ^{2} + t ω^{3}) [576 b_{1}^{2} θ^{2} + 576 b_{1}^{2} ω^{2} - 24 a_{0}^{2}]}{[\begin{matrix} \cos (ω x + θ y + t ω θ^{2} + t ω^{3})^{2} [- 96 b_{1}^{2} a_{0}^{2} (θ^{2} + ω^{2})] + 576 b_{1}^{4} (θ^{4} + ω^{4}) \\ + 1152 b_{1}^{4} θ^{2} ω^{2} + 48 b_{1}^{2} a_{0}^{2} (θ^{2} + ω^{2}) + a_{0}^{4} \end{matrix}]},

which is periodic solution of Eq. (1) (see Fig. 3.2).

Case 3.1.2

If $p = c = 2,$ and $q = d = 2$ , then Eq. (6) reduces to

(23)

u (η) = \frac{a_{2} \exp [2 η] + a_{1} \exp [η] + a_{0} + a_{- 1} \exp [- η] + a_{- 2} \exp [- 2 η]}{b_{2} \exp [2 η] + + b_{1} \exp [η] + b_{0} + b_{- 1} \exp [- η] + b_{- 2} \exp [- 2 η]} .

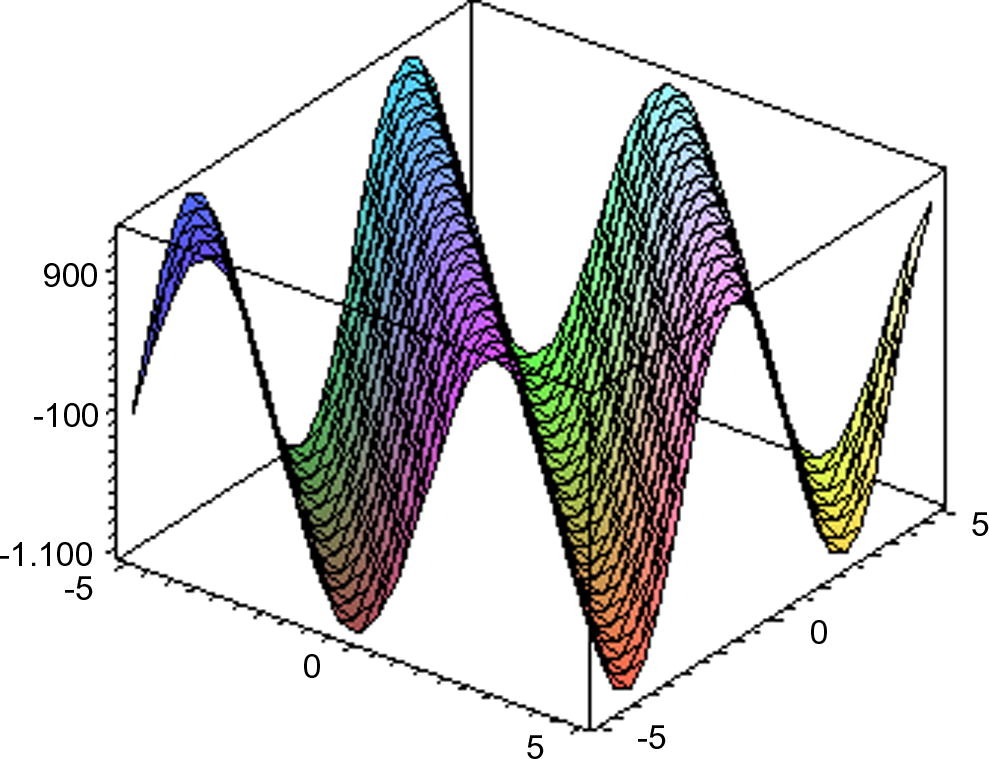
Depicts periodic solutions of Eq. (1), when a 0 = b 1 = θ = ω = 1 .

Setting $b_{1} = b_{- 1} = 0$ , the trial-function (23) is simplified as follows: $u (η) = \frac{a_{2} \exp [2 η] + a_{1} \exp [η] + a_{0} + a_{- 1} \exp [- η] + a_{- 2} \exp [- 2 η]}{b_{2} \exp [2 η] + b_{0} + b_{- 2} \exp [- 2 η]} .$

Proceeding as before, we obtain

(24)

a_{- 1} = 0, a_{2} = 0, b_{2} = \frac{1}{96} \frac{a_{0}^{2}}{b_{- 2} (β^{2} + α^{2})}, b_{0} = 0, a_{- 2} = 0, a_{1} = 0, b_{- 2} = b_{- 2}, ρ = - 4 (β^{2} + α^{2}) α, a_{0} = a_{0} .

Hence we get the generalized solitary wave solution $u (x, y, t)$ of Eq. (1) as follows:

(25)

u (x, y, t) = \frac{a_{0}}{\frac{1}{96} \frac{a_{0}^{2}}{b_{- 2} (β^{2} + α^{2})} e^{2 (α x + β y + ρ t)} + b_{- 2} e^{- 2 (α x + β y + ρ t)}},

where

ρ = - 4 (β^{2} + α^{2})

and

a_{0}, b_{- 2}, α

and

β

are real numbers (see Fig. 3.3).

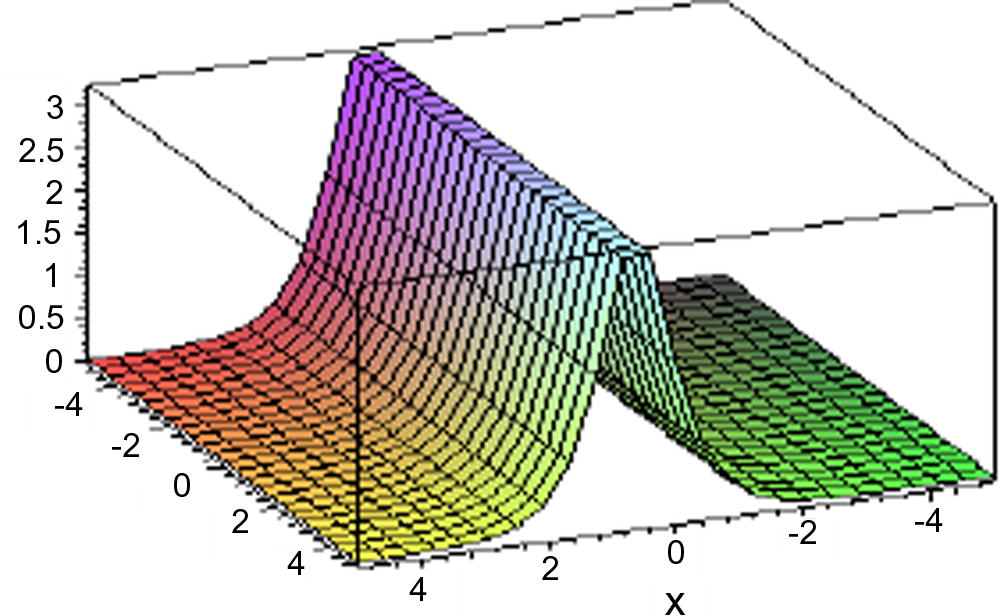
Depicts soliton solutions of Eq. (1) in Case 3.1.2, when a 0 = b - 2 = α = β = ρ = 1 .

4 Conclusion

In this paper, we applied the exp-function method to obtain the generalized solitary and periodic solutions of the modified Zakharov–Kuznetsov equation. It is concluded that exp-function method is a very effective and powerful mathematical tool for finding solitary and periodic solutions of the nonlinear partial differential equations.

References

Abdou M.A., Soliman A.A., Basyony S.T., . New application of exp-function method for improved Boussinesq equation. Phys. Lett. A. 2007;369:469-475.
[Google Scholar]
El-Wakil S.A., Madkour M.A., Abdou M.A., . Application of exp-function method for nonlinear evolution equations with variable co-efficient. Phys. Lett. A. 2007;369:62-69.
[Google Scholar]
He J.H., Abdou M.A., . New periodic solutions for nonlinear evolution equation using exp-method. Chaos Solitons & Fractals 2007:1421-1429.
[Google Scholar]
He J.H., Wu X.H., . Exp-function method for nonlinear wave equations. Chaos Solitons & Fractals. 2006;30(3):700-708.
[Google Scholar]
Mohyud-Din S.T., Noor M.A., Waheed A., . Exp-function method for generalized travelling solutions of good Boussinesq equations. J. Appl. Math. Comput. Springer. 2008;29:81-94.
[CrossRef] [Google Scholar]
Mohyud-Din, S.T., Noor, M.A., Noor, K.I., 2009. Some relatively new techniques for nonlinear problems. Math. Probl. Eng., Article ID 234849, 25pp. doi:10.1155/2009/234849.
Mohyud-Din S.T., Noor M.A., Waheed A., . Exp-function method for generalized travelling solutions of Calogero–Degasperis–Fokas equation. Z. Naturforsch. A. 2010;65a:78-84. (IF = 0.691)
[Google Scholar]
Noor M.A., Mohyud-Din S.T., Waheed A., . Exp-function method for solving Kuramoto–Sivashinsky and Boussinesq equations. J. Appl. Math. Comput. 2008
[CrossRef] [Google Scholar]
Noor M.A., Mohyud-Din S.T., Waheed A., . Exp-function method for generalized travelling solutions of master partial differential equations. Acta Applicandac. Math. 2008
[CrossRef] [Google Scholar]
Tascan F., Bekir A., Kopran M., . Traveling wave solutions of nonlinear evolution equation by using the first-integral method. Commun. Nonlin. Sci. Num. Sim. 2008
[CrossRef] [Google Scholar]
Wazwaz A.M., . The extended tanh method for Zakharov–Kuznetsov equation (ZK), the modified ZK equation and its generalized forms. Commun. Nonlin. Sci. Num. Sim.. 2008;13:1039.
[Google Scholar]
Wu X.H., He J.H., . Solitary solutions, periodic solutions and compacton like solutions using the exp-function method. Comput. Math. Appl.. 2007;54:966-986.
[Google Scholar]
Wu, X.H., He, J.H., in press. Exp-function method and its applications to nonlinear equations. Chaos Solitons & Fractals.
Yusufoglu E., . New solitonary solutions for the MBBN equations using exp-function method. Phys. Lett. A. 2008;372:442-446.
[Google Scholar]
Zhang S., . Application of exp-function method to high-dimensional nonlinear evolution equation. Chaos Solitons & Fractals. 2007;365:448-455.
[Google Scholar]
Zhou S.D., . Exp-function method for the Hybrid–Lattice system. Int. J. Nonlin. Sci. Num. Sim.. 2007;8(3):461-464.
[Google Scholar]
Zhou X.W., Wen Y.X., He J.H., . Exp-function method to solve the nonlinear dispersive k(m, n) equations. Int. J. Nonlin. Sci. Num. Sim.. 2008;9(3):301-306.
[Google Scholar]
Zhu S.D., . Exp-function method for the Hybrid–Lattice system. Int. J. Nonlin. Sci. Num. Sim.. 2007;8:461-464.
[Google Scholar]
Zhu S.D., . Exp-function method for the discrete mKdV lattice. Int. J. Nonlin. Sci. Num. Sim.. 2007;8:465-468.
[Google Scholar]

Introduction

Exp-function method

Solution procedure

Conclusion

Fulltext Views
18

PDF downloads
11

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abdou M.A., Soliman A.A., Basyony S.T., . New application of exp-function method for improved Boussinesq equation. Phys. Lett. A. 2007;369:469-475.
[Google Scholar]

[2] El-Wakil S.A., Madkour M.A., Abdou M.A., . Application of exp-function method for nonlinear evolution equations with variable co-efficient. Phys. Lett. A. 2007;369:62-69.
[Google Scholar]

[3] He J.H., Abdou M.A., . New periodic solutions for nonlinear evolution equation using exp-method. Chaos Solitons & Fractals 2007:1421-1429.
[Google Scholar]

[4] He J.H., Wu X.H., . Exp-function method for nonlinear wave equations. Chaos Solitons & Fractals. 2006;30(3):700-708.
[Google Scholar]

[5] Mohyud-Din S.T., Noor M.A., Waheed A., . Exp-function method for generalized travelling solutions of good Boussinesq equations. J. Appl. Math. Comput. Springer. 2008;29:81-94.
[CrossRef] [Google Scholar]

[6] Mohyud-Din, S.T., Noor, M.A., Noor, K.I., 2009. Some relatively new techniques for nonlinear problems. Math. Probl. Eng., Article ID 234849, 25pp. doi:10.1155/2009/234849.

[7] Mohyud-Din S.T., Noor M.A., Waheed A., . Exp-function method for generalized travelling solutions of Calogero–Degasperis–Fokas equation. Z. Naturforsch. A. 2010;65a:78-84. (IF = 0.691)
[Google Scholar]

[8] Noor M.A., Mohyud-Din S.T., Waheed A., . Exp-function method for solving Kuramoto–Sivashinsky and Boussinesq equations. J. Appl. Math. Comput. 2008
[CrossRef] [Google Scholar]

[9] Noor M.A., Mohyud-Din S.T., Waheed A., . Exp-function method for generalized travelling solutions of master partial differential equations. Acta Applicandac. Math. 2008
[CrossRef] [Google Scholar]

[10] Tascan F., Bekir A., Kopran M., . Traveling wave solutions of nonlinear evolution equation by using the first-integral method. Commun. Nonlin. Sci. Num. Sim. 2008
[CrossRef] [Google Scholar]

[11] Wazwaz A.M., . The extended tanh method for Zakharov–Kuznetsov equation (ZK), the modified ZK equation and its generalized forms. Commun. Nonlin. Sci. Num. Sim.. 2008;13:1039.
[Google Scholar]

[12] Wu X.H., He J.H., . Solitary solutions, periodic solutions and compacton like solutions using the exp-function method. Comput. Math. Appl.. 2007;54:966-986.
[Google Scholar]

[13] Wu, X.H., He, J.H., in press. Exp-function method and its applications to nonlinear equations. Chaos Solitons & Fractals.

[14] Yusufoglu E., . New solitonary solutions for the MBBN equations using exp-function method. Phys. Lett. A. 2008;372:442-446.
[Google Scholar]

[15] Zhang S., . Application of exp-function method to high-dimensional nonlinear evolution equation. Chaos Solitons & Fractals. 2007;365:448-455.
[Google Scholar]

[16] Zhou S.D., . Exp-function method for the Hybrid–Lattice system. Int. J. Nonlin. Sci. Num. Sim.. 2007;8(3):461-464.
[Google Scholar]

[17] Zhou X.W., Wen Y.X., He J.H., . Exp-function method to solve the nonlinear dispersive k(m, n) equations. Int. J. Nonlin. Sci. Num. Sim.. 2008;9(3):301-306.
[Google Scholar]

[18] Zhu S.D., . Exp-function method for the Hybrid–Lattice system. Int. J. Nonlin. Sci. Num. Sim.. 2007;8:461-464.
[Google Scholar]

[19] Zhu S.D., . Exp-function method for the discrete mKdV lattice. Int. J. Nonlin. Sci. Num. Sim.. 2007;8:465-468.
[Google Scholar]