Exact traveling wave solutions for nonlinear elastic rod equation

M.M. Kabir

doi:10.1016/j.jksus.2017.08.010

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

31 (

); 390-397

doi:

10.1016/j.jksus.2017.08.010

Exact traveling wave solutions for nonlinear elastic rod equation

M.M. Kabir^¹

Frank H. Dotterweich College of Engineering, Texas A&M University-Kingsville, TX, United States

Received: 2017-7-25, Accepted: 2017-8-21, Published: 2017-07-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Abstract

An analytical study on a nonlinear elastic rod equation is conducted in this paper. The modified Kudryashov method, the (G′/G)-expansion method, and the Exp-function method are employed to extract exact solutions for the equation. As a result, a range of exact traveling wave solutions is obtained, including: solitary wave solutions, trigonometric and hyperbolic function solutions. Some particular cases of the general solutions derived from each of the proposed techniques are compared and verified together. Finally, merits and drawbacks of these methods are comprehensively discussed.

Keywords

Nonlinear elastic rod equation

Modified Kudryashov method

(G′/G)-expansion method

Exp-function method

Solitary wave solutions

Periodic, Pluses and Minuses

Show Related Articles from PubMed

1 Introduction

“The most incomprehensible thing about the world is that it is at all comprehensible” (Albert Einstein), but the question coming up is how we can fully appreciate incomprehensible issues? Nonlinear sciences provide clues for this context.

The world surrounding us is intrinsically nonlinear. In this regards, nonlinear partial differential equations (NPDEs) are of a substantial significance to describing complicated physical phenomena; for instance, nonlinear wave propagation can arise in the scopes of elasticity theory, fluid dynamics, plasma physics, and nonlinear optics. Both the procedures applied for and the solutions derived from equations of nonlinear wave propagation differ remarkably from those seen in the linear wave equations. Of several types of nonlinear wave propagation, solitons or solitary waves are best-known. In this way, there is an intense inclination towards the explicit solitary wave solutions. The investigation of analytical, exact solutions for NPDEs has become quite notable due to the recently great advances gained in the computational techniques. In the numerical approaches, stability and convergence should specifically be considered and have still remained a serious challenge in order to avoid inappropriate or divergent outcomes (Abdi Aghdam and Kabir, 2010; Borhanifar et al., 2011; Kabir and Demirocak, 2017 ). However, in the recent decade, several efficient analytical and semi-analytical approaches were established and developed remarkably for solving NPDEs, consisting mainly of the homotopy analysis method (HAM) (Abbasbandy, 2010; Rashidi and Shahmohamadi, 2009), bilinear differential operator extension method (Lu and Ma, 2016; Lu et al., 2016a, 2016b, 2016c; Gao et al., 2016 ), Darboux transformation method (Lu and Lin, 2016), Madelung fluid description approach (Lu et al., 2016d), variational methods (Hashemi Kachapi et al., 2009; Helal and Seadawy, 2009; Seadawy, 2015a ), the extended direct algebraic method (Seadawy and El-Rashidy, 2013; Seadawy, 2014, 2015b, 2016a, 2016b, 2017 ), the tanh method (Wazwaz, 2005), the differential transform method (DTM) (Biazar and Eslami, 2011), the Exp-function method (He and Wu, 2006; Borhanifar et al., 2009; Borhanifar and Kabir, 2009; Kabir and Khajeh, 2009; Kabir, 2011a; Kabir and Abdi Aghdam, 2012 ), the (G′/G)-expansion method (Wang et al., 2008; Kabir, 2011a; Kabir et al., 2011a; Kabir and Bagherzadeh, 2011; Kabir and Abdi Aghdam, 2012 ), and many others. Notwithstanding the rapidly burgeoning emergence of analytical methods, it is important to point out that most of these methods yield equivalent exact solutions to each other. Furthermore, there are some cautions and considerations to be observed in applying such approaches. In this regard, Kudryashov has admonished research community to avoid a number of common errors as well as misleading, redundant solutions have taken place when applying these recent analytical methods (Kudryashov, 2009, 2012; Kudryashov and Loginova, 2009; Kudryashov and Soukharev, 2009 ).

The aim of the present study is to investigate exact traveling wave solutions for the nonlinear elastic rod equation by applying the modified Kudryashov method, (G′/G)-expansion, and Exp-function methods. More importantly, we aimed this equation to make prominent comparisons among the mathematical approaches presented in the paper. Besides, to our knowledge, a few studies have been undertaken to date in order to find exact traveling wave solutions of this equation through analytical techniques. Abdou (2009) implemented the extended mapping method to find some of the periodic and solitary solutions of nonlinear elastic rod equation. For the first time, Zhuang and Zhang (1986) extracted the following nonlinear partial differential equation showing the longitudinal oscillation in an elastic rod coupled with lateral inertia (Li and Zhang, 2008):

(1.1)

\frac{\partial^{2} u}{\partial t^{2}} - c_{0}^{2} [1 + {na}_{n} {(\frac{\partial u}{\partial x})}^{n - 1}] \frac{\partial^{2} u}{\partial x^{2}} - (\frac{υ^{2} J_{p}}{s}) \frac{\partial^{4} u}{\partial t^{2} \partial x^{2}} = 0,

where

s, J_{p}

and

c_{0}^{2} = \frac{E}{ρ}, υ, ρ,

and E are the rod’s cross-sectional area, polar moment of inertia, the square velocity of linear longitudinal waves, Poisson’s ratio, the rod density, and Young’s modulus, respectively. n and

a_{n}

also are an integer and the constant of rod materials. In the hard nonlinear substances (e.g. polymers and rubbers)

a_{n} > 0

, while for the soft nonlinear ones (e.g. most of the metals)

a_{n} < 0

(Zhuang and Zhang, 1986).

Nonlinear dynamics of slender elastic rods and beams under external forces and torques as well as parametric excitations remains interesting to the engineering and applied mathematics research communities. Analysis of nonlinear dynamics of elastic rod equation poses important applications in accelerating space crafts and missiles, turbo-machinery parts operating at high speeds, manipulator arms of robots, Micro-Electro-Mechanical Systems (MEMS), bridge elements (e.g. cables and towers), and other structural components.

2 A brief review on the proposed methods

2.1

2.1 The modified Kudryashov method

The classic version of the method was introduced by Kudryashov (1988), then it was modified for the first time by Kabir et al. (2011b) and applied to higher-order nonlinear differential equations as well as the nonlinear transient heat conduction equations in one- and two-dimensional spaces with nonlinearity of n (Kabir, 2011b).

As a brief review of the method, a general NPDE is first considered in the following form

(2.1)

P (u, u_{t}, u_{x}, u_{xx}, u_{tt}, u_{tx}, \dots) = 0 .

where P accounts for a nonlinear function of the given variables or a function that can be mitigated to a polynomial through employing some suitable transformations.

Introducing a wave variable $η$ described as

(2.2)

u = u (η), η = kx - ct

Eq. (2.1) reduces to the following ordinary differential equation (ODE)

(2.3)

P (u, - {cu}^{'}, {ku}^{″}, k^{2} u^{″}, c^{2} u^{″}, - {kcu}^{″}, \dots) = 0 .

where

c

and

k

are two constants which will be determined later. Now, we should seek a rational function type of solution for the given PDE, in terms of

\exp (η),

in the form of:

(2.4)

u (η) = \sum_{k = 0}^{m} \frac{a_{k}}{{[1 + \exp (η)]}^{k}}

in which

a_{0}, a_{1}, \dots, a_{m}

are constants that will be specified from the solution of Eq. (2.3).

The next step is the calculation of value m in the above formula. The m value can be specified using the pole order of general solutions for Eq. (2.3). Substituting $u (η) = η^{- m}$ , where m > 0 into all the terms of Eq. (2.3), then comparing those terms which have the smallest powers we will obtain the value of m to expand the Eq. (2.4) (Kudryashov, 2012).

Differentiating (2.4) with respect to $η$ , inserting the outcome into Eq. (2.3), and equating the coefficients of the same powers of $e^{η}$ with zero, we can achieve an algebraic system. The rational function solutions of Eq. (2.1) are then found by determining $a_{0}, a_{1}, \dots, a_{m}$ from the system.

2.2

2.2 The Exp-function method

Follow the steps described above before Eq. (2.4). Afterwards, it is assumed that the travelling wave solution of Eq. (2.3) is expressed as

(2.5)

u (η) = \frac{\sum_{n = - e}^{f} a_{n} \exp (n η)}{\sum_{m = - g}^{h} b_{m} \exp (m η)} = \frac{a_{e} \exp (e η) + \dots + a_{- f} \exp (- f η)}{b_{g} \exp (g η) + \dots + b_{- h} \exp (- h η)},

where

e, f, g

h

are positive integers that can be selected arbitrarily;

a_{n}

and

b_{m}

are also unknown constants which will be specified later.

2.3

2.3 The (G′/G)-expansion method

Based on the (G′/G)-expansion method, the solution of Eq. (2.3) is assumed to be a polynomial in the $(\frac{G^{'}}{G})$ terms:

(2.6)

U (η) = \sum_{i = 1}^{m} α_{i} {(\frac{G^{'}}{G})}^{i} + α_{0}, α_{m} \neq 0

in which

α_{0}

, and

α_{i}

, for

i = 1, 2, \dots, m

stand for constants that will be determined further, and

G (η)

can satisfy the following second-order linear ordinary differential equation:

(2.7)

\frac{d^{2} G (η)}{d η^{2}} + λ \frac{dG (η)}{d η} + μ G (η) = 0

where

λ

and μ account for arbitrary constants. Regarding the general solution of Eq. (2.7), we have

(2.8)

\frac{G^{'} (η)}{G (η)} = \{\begin{matrix} \frac{\sqrt{λ^{2} - 4 μ}}{2} (\frac{C_{1} \sinh (\frac{\sqrt{λ^{2} - 4 μ}}{2} η) + C_{2} \cosh (\frac{\sqrt{λ^{2} - 4 μ}}{2} η)}{C_{1} \cosh (\frac{\sqrt{λ^{2} - 4 μ}}{2} η) + C_{2} \sinh (\frac{\sqrt{λ^{2} - 4 μ}}{2} η)}) - \frac{λ}{2}, λ^{2} - 4 μ > 0, \\ \frac{\sqrt{4 μ - λ^{2}}}{2} (\frac{- C_{1} \sin (\frac{\sqrt{4 μ - λ^{2}}}{2} η) + C_{2} \cos (\frac{\sqrt{4 μ - λ^{2}}}{2} η)}{C_{1} \cos (\frac{\sqrt{4 μ - λ^{2}}}{2} η) + C_{2} \sin (\frac{\sqrt{4 μ - λ^{2}}}{2} η)}) - \frac{λ}{2}, λ^{2} - 4 μ < 0, \end{matrix}

and it follows from (2.6) and (2.7) that

(2.9)

\begin{matrix} U^{'} = - \sum_{i = 1}^{m} i α_{i} [{(\frac{G^{'}}{G})}^{i + 1} + λ {(\frac{G^{'}}{G})}^{i} + μ {(\frac{G^{'}}{G})}^{i - 1}], \\ U^{″} = \sum_{i = 1}^{m} i α_{i} [\begin{matrix} (i + 1) {(\frac{G^{'}}{G})}^{i + 2} + λ (2 i + 1) {(\frac{G^{'}}{G})}^{i + 1} + i (λ^{2} + 2 μ) {(\frac{G^{'}}{G})}^{i} \\ + μ λ (2 i - 1) {(\frac{G^{'}}{G})}^{i - 1} + μ^{2} (i - 1) {(\frac{G^{'}}{G})}^{i - 2} \end{matrix}] \end{matrix}

The prime in the above expressions indicates the derivative with respect to $η$ .

To explicitly reach u, the following four stages are implemented:

Stage 1. Ascertain the integer m through inserting Eq. (2.6) coupled with Eq. (2.7) into Eq. (2.3), and then setting a balance between the highest-order nonlinear term(s) and the highest-order partial derivative.

Stage 2. Substitute Eq. (2.6) with the magnitude of m specified in Stage 1, along with Eq. (2.7) into Eq. (2.3) and gather all the terms having the same order $(\frac{G^{'}}{G})$ ; the left side of Eq. (2.3) is transformed to a polynomial in $(\frac{G^{'}}{G})$ . Then equate each coefficient of the polynomial with zero in order to extract an algebraic system with $k, c, α_{0}$ and $α_{i}$ , for $i = 1, 2, \dots, m$ .

Stage 3. Solving the algebraic system derived in Stage 2 to find $k, c, α_{0}$ and $α_{i}$ , for $i = 1, 2, \dots, m$ , using the Maple.

Stage 4. Use the results gained from the above stages to extract a set of fundamental solutions $u (η)$ of Eq. (2.3) as a function of $(\frac{G^{'}}{G})$ ; given that the solutions of Eq. (2.7) are well-known, we can achieve exact solutions of Eq. (2.1).

3 Application of the methods to the nonlinear elastic rod equation

3.1

3.1 Application of the modified Kudryashov method

To seek traveling wave solutions of Eq. (1.1), we take advantage of the wave variable $η$ defined as Eq. (2.2), then Eq. (1.1) reduces to the following ODE:

(3.1)

(c^{2} - c_{0}^{2} k^{2}) u^{″} - {na}_{n} c_{0}^{2} k^{n + 1} {(u^{″})}^{n - 1} u^{″} - (\frac{υ^{2} J_{p}}{s}) k^{2} c^{2} ϕ^{⁗} = 0,

where c is the wave speed, and ′ is the derivative with respect to

η

. Taking

ϕ (η) = u {(η)}^{'}

, integrating the resulting equation once, and then choosing the integration constant as zero leads to

(3.2)

(c^{2} - c_{0}^{2} k^{2}) ϕ - a_{n} c_{0}^{2} k^{n + 1} ϕ^{n} - (\frac{υ^{2} J_{p}}{s}) k^{2} c^{2} ϕ^{″} = 0,

Denote that $α = \frac{υ^{2} J_{p}}{s}, β = c_{0}^{2}$ and $γ = a_{n} c_{0}^{2}$ . Then, for $n = 2$ we obtain

(3.3)

- k^{2} c^{2} α ϕ^{″} + (c^{2} - β k^{2}) ϕ - γ k^{3} ϕ^{2} = 0,

In the next stage, as previously described in the Section 2.1, substituting $ϕ (η) = η^{- m}$ into all the terms of the above equation and then comparing terms, we obtain m = 2 to extend Eq. (2.4), which yields:

(3.4)

ϕ (η) = a_{0} + \frac{a_{1}}{1 + \exp (η)} + \frac{a_{2}}{{(1 + \exp (η))}^{2}},

in which

a_{0}, a_{1}, a_{2}

are unknown constants that will be determined from the solution of (3.3). Differentiating (3.4) with respect to

η

, inserting the result into Eq. (3.3), and setting the coefficients of the same power of

e^{η}

equal to zero, we obtain a set of algebraic equations. With the aid of Maple 18, the solutions of the algebraic system are below found:

Case 1.

(3.5)

c = \pm k \sqrt{\frac{β}{1 - α k^{2}}}, a_{0} = 0, a_{1} = \frac{6 α β k}{γ (1 - α k^{2})}, a_{2} = - \frac{6 α β k}{γ (1 - α k^{2})}

Inserting Eq. (3.5) into (3.4) and simplifying the result, the solitary wave solution of Eq. (3.3) is achieved in the following form:

(3.6)

ϕ_{1} = \frac{6 α β k}{γ (1 - α k^{2})} [\frac{e^{η}}{{(1 + e^{η})}^{2}}],

where

η = k (x \pm \sqrt{\frac{β}{1 - α k^{2}}} t)

and k is a free parameter which may be computed by the relevant initial and boundary conditions.

Using the transformation

(3.7)

\begin{matrix} \exp (η) = \cosh η + \sinh η, \\ \exp (- η) = \cosh η - \sinh η \end{matrix}

then Eq. (3.6) can be easily converted to

(3.8)

ϕ = \frac{3 α β k}{2 γ (1 - α k^{2})} \sec h^{2} (\frac{η}{2}),

The exact solution obtained above is shown at described parameters in Fig. 1.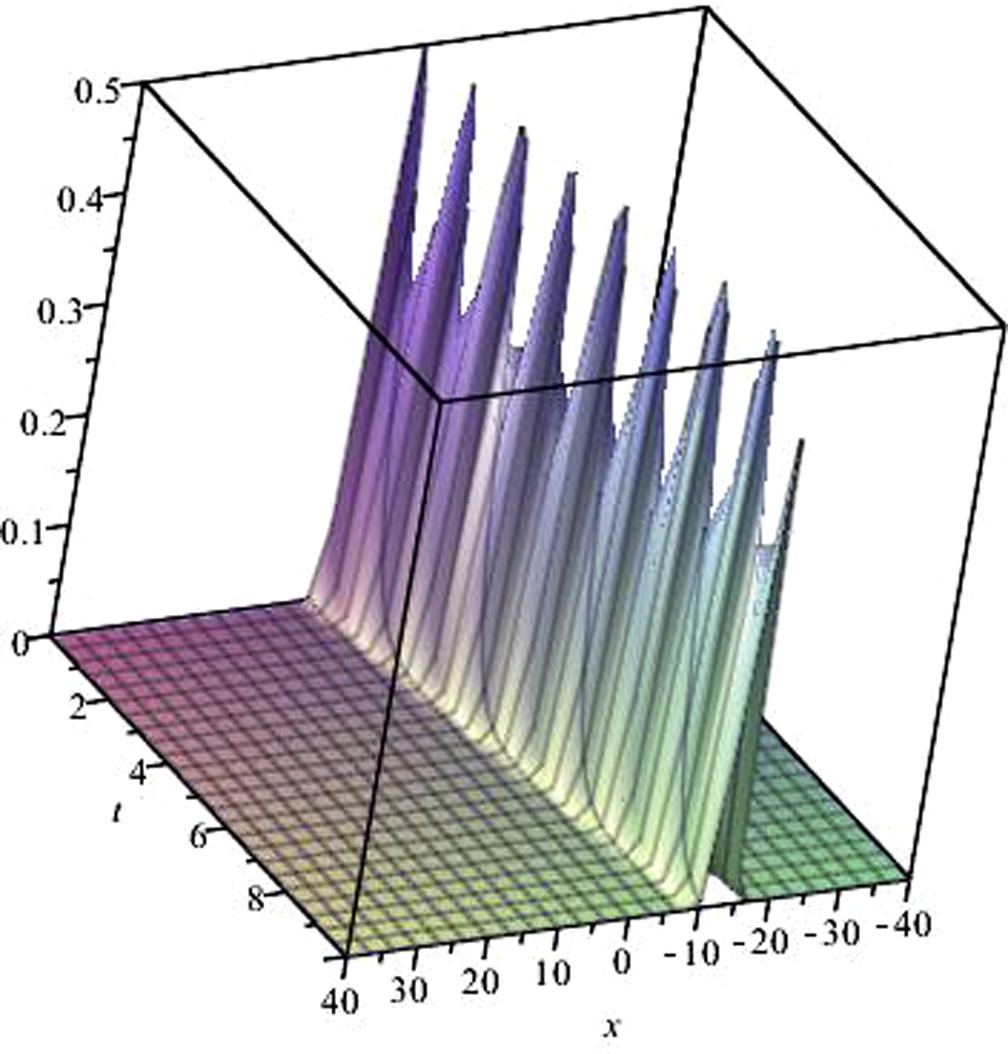

Exact hyperbolic-type solutions (3.8) and (3.28) at k = 2 , α = 0.1 , β = 1 , γ = 1 . .

In case k is an imaginary number, the above obtained solitary solution may be transformed to periodic solution. We therefore write $k = iK$ where K is a real number.

With the aid of the following transformation:

(3.9)

\begin{matrix} η = i ξ ξ = K (x \pm \sqrt{\frac{β}{1 + α K^{2}}} t) \\ \exp (η) = \cos (ξ) + i \sin (ξ), \\ \exp (- η) = \cos (ξ) - i \sin (ξ) . \end{matrix}

and substituting Eq. (3.9) into Eq. (3.8) yields

(3.10)

ϕ = (\frac{3 α β K}{2 γ (1 + α K^{2})}) i \sec^{2} (\frac{ξ}{2})

Case 2.

(3.11)

c = \pm k \sqrt{\frac{β}{1 + α k^{2}}}, a_{0} = - \frac{α β k}{γ (1 + α k^{2})}, a_{1} = \frac{4 α β k}{γ (1 + α k^{2})}, a_{2} = - \frac{4 α β k}{γ (1 + α k^{2})}

Inserting Eq. (3.11) into (3.4), we attain another solitary wave solution as follows:

(3.12)

ϕ_{2} = - \frac{α β k}{γ (1 + α k^{2})} [\frac{e^{2 η} - 4 e^{η} + 1}{{(1 + e^{η})}^{2}}],

where

η = k (x \pm \sqrt{\frac{β}{1 + α k^{2}}} t)

Using the transformation (3.7), we are able to achieve the hyperbolic form of the solution:

(3.13)

ϕ = - (\frac{α β k}{γ (1 + α k^{2})}) [1 - \frac{3}{2} \sec h^{2} (\frac{η}{2})],

The exact solution gained above is shown at described parameters in Fig. 2.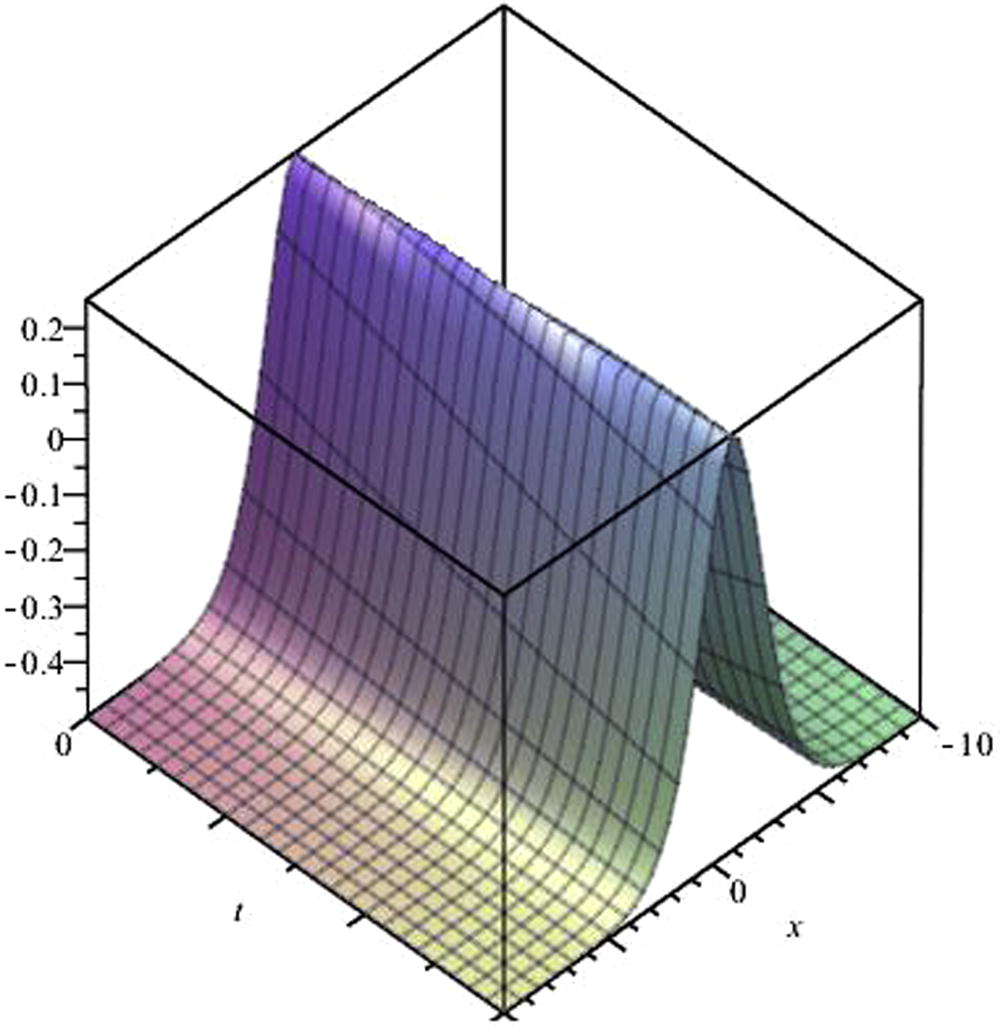

Exact hyperbolic-form solutions (3.13) and (3.37) at k = 1 , α = 1000 , β = 100 , γ = 200 . .

When k is an imaginary number, the obtained solitary solution can be converted into periodic solution. Following the same manipulation demonstrated in the prior case, we find this particular solution:

(3.14)

ϕ = - (\frac{α β K}{γ (1 - α K^{2})}) i [1 - \frac{3}{2} \sec^{2} (\frac{ζ}{2})],

in which

ξ = K (x \mp \sqrt{\frac{β}{1 - α K^{2}}} t)

3.2

3.2 Application of the Exp-function method

Now, we seek to solve the Eq. (3.3) by applying Exp-function method. To specify values of $e$ and $g$ cited in the Section (2.2), we need to set a balance between the highest order nonlinear term $ϕ^{2}$ and the linear term of the highest order $ϕ^{″}$ in Eq. (3.3) as follows:

(3.15)

ϕ^{″} = \frac{c_{1} \exp [(3 g + e) η] + \dots}{c_{2} \exp (4 g η) + \dots},

(3.16)

ϕ^{2} = \frac{c_{3} \exp (2 e η) + \dots}{c_{4} \exp (2 g η) + \dots} \times \frac{\exp (2 g η)}{\exp (2 g η)} = \frac{c_{3} \exp ((2 e + 2 g) η) + \dots}{c_{4} \exp (4 g η) + \dots},

where

c_{i}

stand for the determined coefficients used for simplicity. Making a balance between the highest orders of the Exp functions in Eqs. (3.15) and (3.16) results in

(3.17)

3 g + e = 2 e + 2 g,

which leads to

(3.18)

e = g .

Likewise, to determine the values of $f$ and $h$ , we write

(3.19)

ϕ^{″} = \frac{\dots + d_{1} \exp [(- (3 h + f) η]}{\dots + d_{2} \exp (- 4 h η)},

(3.20)

ϕ^{3} = \frac{\dots + d_{3} \exp (- 2 f η)}{\dots + d_{4} \exp (- 2 h η)} \times \frac{\exp (- 2 h η)}{\exp (- 2 h η)} = \frac{\dots + d_{3} \exp (- 2 (f + h) η)}{\dots + d_{4} \exp (- 4 h η)},

where

d_{i}

stand for the determined coefficients. Making a balance between the lowest orders of the Exp functions in Eqs. (3.19) and (3.20) results in

(3.21)

3 h + f = 2 (f + h),

and then

(3.22)

f = h .

We can arbitrarily select the values of

f

and

e

. For simplicity, the values

e = g = 1

and

f = h = 1

are set which reduce Eq. (2.4) to

(3.23)

ϕ (η) = \frac{a_{1} \exp (η) + a_{0} + a_{- 1} \exp (- η)}{\exp (η) + b_{0} + b_{- 1} \exp (- η)},

Substituting Eq. (3.23) into Eq. (3.3) then using Maple, we reach

(3.24)

\frac{1}{A} [c_{3} \exp (3 η) + c_{2} \exp (2 η) + c_{1} \exp (η) + c_{0} + c_{- 1} \exp (- η) + c_{- 2} \exp (- 2 η) + c_{- 3} \exp (- 3 η)] = 0,

in which

(3.25)

A = {[\exp (η) + b_{0} + b_{- 1} \exp (- η)]}^{3},

and the

c_{n}

are coefficients of

\exp (n η)

. Vanishing the coefficients for all the powers of

\exp (n η)

leads to an algebraic system for

a_{0}, b_{0}, a_{1}, a_{- 1}, b_{- 1}, k

and c. Solving this algebraic system using Maple 18, we achieve the following:

Case 1.

(3.26)

c = \pm k \sqrt{\frac{β}{1 - α k^{2}}}, a_{1} = 0, a_{- 1} = 0, b_{0} = b_{0}, a_{0} = - \frac{3 α β {kb}_{0}}{(α k^{2} - 1) γ}, b_{- 1} = \frac{b_{0}^{2}}{4}

Substituting Eq. (3.26) into (3.23), we can obtain the generalized solitary wave solution of Eq. (3.3):

(3.27)

ϕ (η) = \frac{\frac{3 α β {kb}_{0}}{(1 - α k^{2}) γ}}{e^{η} + b_{0} + \frac{b_{0}^{2}}{4} e^{- η}},

where

η = k (x \mp \sqrt{\frac{β}{1 - α k^{2}}} t)

and

b_{0}

accounts for an arbitrary parameter that is specified using initial and boundary conditions.

If we set $b_{0} = 2$ and apply the transformation (3.7), then Eq. (3.27) can be simply converted to

(3.28)

ϕ = \frac{3 α β k}{2 γ (1 - α k^{2})} \sec h^{2} (\frac{η}{2}),

Similarly, if we set $b_{0} = - 2$ in the general solution (3.27), we obtain

(3.29)

ϕ = - \frac{3 α β k}{2 γ (1 - α k^{2})} \csc h^{2} (\frac{η}{2}),

Comparing our results together, Eq. (3.28) with the exact solution (3.8) derived by the modified Kudryashov method, it can vividly be observed that both are exactly the same.

In case k is assumed to be an imaginary number, the above obtained solitary solutions are transformed into periodic solutions, we set $k = iK$ where K is a real number.

Substituting the transformation (3.9) into Eq. (3.27) yields

(3.30)

ϕ (ξ) = \frac{(\frac{3 α β b_{0} K}{γ (1 + α K^{2})}) i}{[(1 + \frac{b_{0}^{2}}{4}) \cos (ξ) + b_{0} + (1 - \frac{b_{0}^{2}}{4}) i \sin (ξ)]},

If we look for a periodic or a compact-like solution, the imaginary part in the denominator of Eq. (3.30) must be eliminated, that requires

(3.31)

1 - \frac{b_{0}^{2}}{4} = 0,

from Eq. (3.31) we obtain

(3.32)

b_{0} = \pm 2,

Substituting $b_{0} = 2$ into Eq. (3.30) results

(3.33)

ϕ = (\frac{3 α β K}{2 γ (1 + α K^{2})}) i \sec^{2} (\frac{ξ}{2}),

and similarly inserting

b_{0} = - 2

into Eq. (3.30) leads to

(3.34)

ϕ = (\frac{3 α β K}{2 γ (1 + α K^{2})}) i \csc^{2} (\frac{ξ}{2}) .

Validating our results together, Eq. (3.33) with the periodic solution (3.10) obtained by the modified Kudryashov method, it can obviously be seen that both are exactly the same.

Case 2.

(3.35)

c = \pm k \sqrt{\frac{β}{1 + α k^{2}}}, b_{0} = b_{0}, b_{- 1} = \frac{b_{0}^{2}}{4}, a_{0} = \frac{2 α β {kb}_{0}}{(1 + α k^{2}) γ}, a_{- 1} = - \frac{α β {kb}_{0}^{2}}{4 γ (1 + α k^{2})}, a_{1} = - \frac{α β k}{(1 + α k^{2}) γ}

Inserting Eq. (3.35) into (3.23), one admits to the solitary wave solution as follows:

(3.36)

ϕ (η) = \frac{- \frac{α β k}{(1 + α k^{2}) γ} e^{η} + \frac{2 α β {kb}_{0}}{(1 + α k^{2}) γ} - \frac{α β {kb}_{0}^{2}}{4 γ (1 + α k^{2})} e^{- η}}{e^{η} + b_{0} + \frac{b_{0}^{2}}{4} e^{- η}} = - (\frac{α β k}{(1 + α k^{2}) γ}) [1 - \frac{3 b_{0}}{e^{η} + b_{0} + \frac{b_{0}^{2}}{4} e^{- η}}],

where

η = k (x \pm \sqrt{\frac{β}{1 + α k^{2}}} t)

and

b_{0}

is an arbitrary constant which may be determined through initial and boundary conditions.

If we take $b_{0} = 2$ and use the transformation (3.7), then Eq. (3.36) can be easily converted to

(3.37)

ϕ = - (\frac{α β k}{γ (1 + α k^{2})}) [1 - \frac{3}{2} \sec h^{2} (\frac{η}{2})],

and similarly replacing

b_{0} = - 2

into Eq. (3.36) leads to

(3.38)

ϕ = - (\frac{α β k}{γ (1 + α k^{2})}) [1 + \frac{3}{2} \csc h^{2} (\frac{η}{2})],

Comparing our results together, Eq. (3.37) with the hyperbolic-type solution (3.13) obtained by the modified Kudryashov method, it can vividly be seen that both are exactly the same.

If k is assumed to be an imaginary number, the solitary wave solutions already obtained will be transformed to the periodic solutions. Adopting the same procedure as represented in the prior case, we find:

(3.39)

ϕ (ξ) = - (\frac{α β K}{γ (1 - α K^{2})}) i [1 - \frac{3 b_{0}}{((1 + \frac{b_{0}^{2}}{4}) \cos (ξ) + b_{0} + (1 - \frac{b_{0}^{2}}{4}) i \sin (ξ))}],

where

η = i ξ, ξ = K (x \pm \sqrt{\frac{β}{1 - α K^{2}}} t)

If we look for periodic-type or compaction-like solutions, the imaginary part of denominator in Eq. (3.39) have to be set zero. To satisfy this aim, we set $b_{0} = 2$ , which results

(3.40)

ϕ = - (\frac{α β K}{γ (1 - α K^{2})}) i [1 - \frac{3}{2} \sec^{2} (\frac{ζ}{2})],

and inserting

b_{0} = - 2

into Eq. (3.39), yields

(3.41)

ϕ = - (\frac{α β K}{γ (1 - α K^{2})}) i [1 - \frac{3}{2} \csc^{2} (\frac{ζ}{2})] .

Finally, to validate our results together, Eq. (3.40) with the periodic solution (3.14) extracted through the modified Kudryashov method, it can obviously be seen that both are exactly the same.

3.3

3.3 Application of the (G′/G)-expansion method

According to Step 1 mentioned in Section 2.3, a homogeneous balance between the terms $ϕ^{″}$ and $ϕ^{2}$ in Eq. (3.3) leads to

(3.42)

m + 2 = 2 m,

and then

(3.43)

m = 2 .

Assume the solutions of (3.3) is expressed in the following polynomial form:

(3.44)

ϕ (η) = α_{0} + α_{1} (\frac{G^{'}}{G}) + α_{2} {(\frac{G^{'}}{G})}^{2}, α_{1}, α_{2} \neq 0,

in which

α_{0}

α_{1}

and

α_{2}

are unknown constants which will be determined further.Inserting Eq. (3.44) coupled with Eq. (2.7) into Eq. (3.3), and then gathering the terms with the same (G′/G) powers, the left side of Eq. (3.3) is transformed to a polynomial in the terms of (G′/G). Vanishing each of the coefficients results in an algebraic system for

α_{0}

α_{1},

α_{2}

, k, c,

λ

and

μ

. Getting assistance from Maple 18 to solve this algebraic system of equations, we have:

Case 1.

(3.45)

c = \pm k \sqrt{\frac{β}{1 - α k^{2} (λ^{2} - 4 μ)}}, α_{0} = - \frac{6 α β k μ}{γ [1 - α k^{2} (λ^{2} - 4 μ)]}, α_{1} = - \frac{6 α β k λ}{γ [1 - α k^{2} (λ^{2} - 4 μ)]}, α_{2} = - \frac{6 α β k}{γ [1 - α k^{2} (λ^{2} - 4 μ)]},

where

k, λ

and

μ

are arbitrary constants.

Case 1.A. $λ^{2} - 4 μ > 0$

Using Eq. (3.45), the expression (3.44) turns into

(3.46)

ϕ (η) = - \frac{6 α β k}{γ [1 - α k^{2} (λ^{2} - 4 μ)]} [μ + λ (\frac{G^{'}}{G}) + {(\frac{G^{'}}{G})}^{2}],

Inserting the general solution of (2.8) into Eq. (3.46), we gain the following generalized traveling wave solution:

(3.47)

ϕ = - \frac{3 α β k (λ^{2} - 4 μ)}{2 γ [1 - α k^{2} (λ^{2} - 4 μ)]} [{(\frac{C_{1} \sinh (ξ) + C_{2} \cosh (ξ)}{C_{1} \cosh (ξ) + C_{2} \sinh (ξ)})}^{2} - 1],

where

ξ = \frac{\sqrt{λ^{2} - 4 μ}}{2} η = \frac{\sqrt{λ^{2} - 4 μ}}{2} . k (x \pm \sqrt{\frac{β}{1 - α k^{2} (λ^{2} - 4 μ)}} t)

Now, to show some particular cases of the above general solution, we take $C_{1} = 0$ ; then (3.47) yields

(3.48)

ϕ = - \frac{3 α β k (λ^{2} - 4 μ)}{2 γ [1 - α k^{2} (λ^{2} - 4 μ)]} [\coth^{2} (ζ) - 1] = - \frac{3 α β k (λ^{2} - 4 μ)}{2 γ [1 - α k^{2} (λ^{2} - 4 μ)]} \csc h^{2} (ζ),

and, when

C_{2} = 0

, the general solution (3.47) becomes

(3.49)

ϕ = - \frac{3 α β k (λ^{2} - 4 μ)}{2 γ [1 - α k^{2} (λ^{2} - 4 μ)]} [\tanh^{2} (ζ) - 1] = \frac{3 α β k (λ^{2} - 4 μ)}{2 γ [1 - α k^{2} (λ^{2} - 4 μ)]} \sec h^{2} (ζ),

We note that, if we set $λ^{2} - 4 μ = 1$ in the above solutions (3.49) and (3.48) obtained by (G′/G)-expansion method, we can recover the same hyperbolic-type solutions (3.8), (3.28), and (3.29), respectively, obtained already by the modified Kudryashov method and the Exp-function method.

Case 1.B. $λ^{2} - 4 μ < 0$

Following the same procedure as shown in the Case 1.A; inserting Eq. (3.45) into Eq. (3.44), and then substituting the general solution of (2.8) into the obtained result, we can easily obtain the generalized solitary wave solutions as

(3.50)

ϕ = - \frac{3 α β k (4 μ - λ^{2})}{2 γ [1 + α k^{2} (4 μ - λ^{2})]} [{(\frac{- C_{1} \sin (ξ) + C_{2} \cos (ξ)}{C_{1} \cos (ξ) + C_{2} \sin (ξ)})}^{2} + 1],

where

ξ = \frac{\sqrt{4 μ - λ^{2}}}{2} η = \frac{\sqrt{4 μ - λ^{2}}}{2} . k (x \mp \sqrt{\frac{β}{1 + α k^{2} (4 μ - λ^{2})}} t)

Likewise, to extract some particular cases of the above solution, we set $C_{1} = 0$ , then (3.50) leads to

(3.51)

ϕ = - \frac{3 α β k (4 μ - λ^{2})}{2 γ [1 + α k^{2} (4 μ - λ^{2})]} [\cot^{2} (ζ) + 1] = - \frac{3 α β k (4 μ - λ^{2})}{2 γ [1 + α k^{2} (4 μ - λ^{2})]} \csc^{2} (ζ),

and, when

C_{2} = 0

, the exact solution (3.50) will be

(3.52)

ϕ = - \frac{3 α β k (4 μ - λ^{2})}{2 γ [1 + α k^{2} (4 μ - λ^{2})]} [\tan^{2} (ζ) + 1] = - \frac{3 α β k (4 μ - λ^{2})}{2 γ [1 + α k^{2} (4 μ - λ^{2})]} \sec^{2} (ζ) .

Comparing our results together, if we put $λ^{2} - 4 μ = - 1$ in the solutions (3.52) and (3.51) extracted from the (G′/G)-expansion method, those can be simply converted to the same periodic solutions (3.10), (3.33), and (3.34), respectively, obtained previously by the Exp-function and modified Kudryashov methods.

Case 2.

(3.53)

c = \pm k \sqrt{\frac{β}{1 + α k^{2} (λ^{2} - 4 μ)}}, α_{0} = - \frac{α β k (2 μ + λ^{2})}{γ [1 + α k^{2} (λ^{2} - 4 μ)]}, α_{1} = - \frac{6 α β k λ}{γ [1 + α k^{2} (λ^{2} - 4 μ)]}, α_{2} = - \frac{6 α β k}{γ [1 + α k^{2} (λ^{2} - 4 μ)]},

where

k, λ

and

μ

are arbitrary constants.

Case 2.A. $λ^{2} - 4 μ > 0 .$

By the similar procedure as explained in the cases 1.A and 1.B, we can finally find the following exact solutions:

(3.54)

ϕ = - \frac{3 α β k (λ^{2} - 4 μ)}{2 γ [1 + α k^{2} (λ^{2} - 4 μ)]} [{(\frac{C_{1} \sinh (ξ) + C_{2} \cosh (ξ)}{C_{1} \cosh (ξ) + C_{2} \sinh (ξ)})}^{2} - \frac{1}{3}],

where

ξ = \frac{\sqrt{λ^{2} - 4 μ}}{2} η = \frac{\sqrt{λ^{2} - 4 μ}}{2} . k (x \mp \sqrt{\frac{β}{1 + α k^{2} (λ^{2} - 4 μ)}} t)

In particular, if we take $C_{1} = 0$ in the above general solution; then (3.54) leads to

(3.55)

ϕ = - \frac{3 α β k (λ^{2} - 4 μ)}{2 γ [1 + α k^{2} (λ^{2} - 4 μ)]} [\coth^{2} (ζ) - \frac{1}{3}] = - \frac{α β k (λ^{2} - 4 μ)}{γ [1 + α k^{2} (λ^{2} - 4 μ)]} [\frac{3}{2} \csc h^{2} (ζ) + 1],

and, when

C_{2} = 0

, the exact solution (3.54) becomes

(3.56)

ϕ = - \frac{3 α β k (λ^{2} - 4 μ)}{2 γ [1 + α k^{2} (λ^{2} - 4 μ)]} [\tanh^{2} (ζ) - \frac{1}{3}] = - \frac{α β k (λ^{2} - 4 μ)}{γ [1 + α k^{2} (λ^{2} - 4 μ)]} [- \frac{3}{2} \sec h^{2} (ζ) + 1]

We note that, if we set $λ^{2} - 4 μ = 1$ in the above solutions (3.56) and (3.55), we can reach the same hyperbolic-form solutions (3.13), (3.37), and (3.38), respectively, derived already through the modified Kudryashov and Exp-function methods.

Case 2.B. $λ^{2} - 4 μ < 0 .$

Following the same procedure as represented in the previous cases, we have

(3.57)

ϕ = - \frac{3 α β k (4 μ - λ^{2})}{2 γ [1 - α k^{2} (4 μ - λ^{2})]} [{(\frac{- C_{1} \sin (ξ) + C_{2} \cos (ξ)}{C_{1} \cos (ξ) + C_{2} \sin (ξ)})}^{2} + \frac{1}{3}],

where

ξ = \frac{\sqrt{4 μ - λ^{2}}}{2} η = \frac{\sqrt{4 μ - λ^{2}}}{2} . k (x \mp \sqrt{\frac{β}{1 - α k^{2} (4 μ - λ^{2})}} t)

Likewise, to show some particular cases of the above solution, we choose $C_{1} = 0$ ; then (3.57) results in

(3.58)

ϕ = - \frac{3 α β k (4 μ - λ^{2})}{2 γ [1 - α k^{2} (4 μ - λ^{2})]} [\cot^{2} (ζ) + \frac{1}{3}],

and, when

C_{2} = 0

, the exact solution (3.57) is converted to

(3.59)

ϕ = - \frac{3 α β k (4 μ - λ^{2})}{2 γ [1 - α k^{2} (4 μ - λ^{2})]} [\tan^{2} (ζ) + \frac{1}{3}] .

Validating our results, if we set $λ^{2} - 4 μ = - 1$ in the solutions (3.59) and (3.58) gained via (G′/G)-expansion method, those can simply be transformed to the same periodic solutions (3.14), (3.40), and (3.41), respectively, obtained previously by the modified Kudryashov and Exp-function methods.
Remark 1. In addition to comparing and validating the exact solutions together, extracted through the proposed approaches, we have verified and double-checked all the solutions obtained in the present study through inserting them into the original equation using Maple 18.
Remark 2. It is important to note that unlike the modified Kudryashov method, each of the (G′/G)-expansion and Exp-function methods applied to the target equation contributed to other two sets of solutions appearing as a constant after careful simplifications. Such redundant and misleading sets of solutions may set the stage for making mistakes in introducing NEW exact solutions to the research community.

4 Discussions & conclusions

The exact traveling wave solutions of the nonlinear elastic rod equation were extracted using three analytical approaches which have attracted a considerable amount of attention in recent years. As the implication of the study, despite the fact that all the methods applied to the target equation led to the same exact solutions, the modified Kudryashov method showed more straightforward and faster solution procedure as compared to the other two methods which got involved with considerably larger-volume computations. Furthermore, both the (G′/G)-expansion and Exp-function methods set the stage for obtaining a broad spectrum of misleading solutions leading to redundant and constant ones after simplification, while the modified Kudryashov method does not produce such solutions. This merit is also well-predictable with regard to the function form of solution considered originally for the modified Kudryashov method. On the other hand, given the more complicated function form introduced in the Exp-function method in comparison with the modified Kudryashov method, the former does not enable us to reach exact solutions for higher-order NPDEs, since a large system of algebraic equations coupled with the abundant parameters is not directly solved by the current mathematical tools in the market, consisting of: Maple, Mathematica, etc. This issue had already been investigated by Kabir et al. (2011b) to find the exact solutions of the KS (Kuramoto–Sivashinsky) and the sSK (seventh-order Sawada–Kotera) equations, as well as in another study (Kudryashov, 2012) for solving another seventh-order nonlinear differential equation.

On the down side, there are two drawbacks in association with the modified Kudryashov method. First, even though the method enables us to extract all the one-periodic and solitary wave solutions, it doesn’t permit us to investigate two-periodic solutions. Hence, we need to employ more complex methods which have been developed in the other recent studies (Demina and Kudryashov, 2010, 2011; Kudryashov et al., 2011 ). The latter is that the method does not provide the opportunity of finding all the possible solutions once there are two or more expansion bunches of the Laurent series in the general solution. Nevertheless, it is noted that majority of the other methods are also unable to obtain these solutions. In such cases, we need to refer to more complicated methods (Demina and Kudryashov, 2010, 2011; Kudryashov et al., 2011 ).

References

Abbasbandy S., . Homotopy analysis method for the Kawahara equation. Nonlinear Anal. Real World Appl.. 2010;11(1):307-312.
[Google Scholar]
Abdi Aghdam E., Kabir M.M., . Validation of a blowby model using experimental results in motoring condition with the change of compression ratio and engine speed. Exp. Therm. Fluid Sci.. 2010;34:197-209.
[Google Scholar]
Abdou M.A., . Exact travelling wave solutions in a nonlinear elastic rod equation. Int. J. Nonlinear Sci.. 2009;7(2):167-173.
[Google Scholar]
Biazar J., Eslami M., . Differential transform method for nonlinear fractional gas dynamics equation. Int. J. Phys. Sci.. 2011;6(5):1203-1206.
[Google Scholar]
Borhanifar A., Kabir M.M., . New periodic and soliton solutions by application of Exp-function method for nonlinear evolution equations. J. Comp. Appl. Math.. 2009;229:158-167.
[Google Scholar]
Borhanifar A., Kabir M.M., Vahdat M., . New periodic and soliton wave solutions for the generalized Zakharov system and (2+1)-dimensional Nizhnik–Novikov–Veselov system. Chaos Solit. Fract.. 2009;42:1646-1654.
[Google Scholar]
Borhanifar A., Kabir M.M., Hossein Pour.A., . A Numerical Method for Solution of the Heat Equation with Nonlocal Nonlinear Condition. World Appl. Sci. J.. 2011;13:2405-2409.
[Google Scholar]
Demina M.V., Kudryashov N.A., . From Laurent series to exact meromorphic solutions: the Kawahara equation. Phys. Lett. A. 2010;374:4023-4029.
[Google Scholar]
Demina M.V., Kudryashov N.A., . Explicit expressions for meromorphic solutions of autonomous nonlinear ordinary differential equations. Commun. Nonlinear Sci. Num. Simul.. 2011;16:1127-1134.
[Google Scholar]
Gao L.N., Zhou X.Y., Zi Y.Y., Yu J., Lu X., . Resonant behavior of multiple wave solutions to a Hirota bilinear equation. Comp. Math. Appl.. 2016;72:1225-1229.
[Google Scholar]
Hashemi Kachapi S.H.A., Ganji D.D., Davodi A.G., Varedi S.M., . Periodic solution for strongly nonlinear vibration systems by He’s variational iteration method. Math. Meth. Appl. Sci.. 2009;32(18):2339-2349.
[Google Scholar]
He J.H., Wu X.H., . Exp-function method for nonlinear wave equations. Chaos Solit. Fract.. 2006;30(3):700-708.
[Google Scholar]
Helal M.A., Seadawy A.R., . Variational method for the derivative nonlinear Schrödinger equation with computational applications. Phys. Scr.. 2009;80:035004.
[Google Scholar]
Kabir M.M., Khajeh A., . New explicit solutions for the Vakhnenko and a generalized form of the nonlinear heat conduction equations via Exp-function method. Int. J. Nonlinear Sci. Num. Simul.. 2009;10(10):1307-1318.
[Google Scholar]
Kabir M.M., . Analytic solutions for generalized forms of the nonlinear heat conduction equation. Nonlinear Anal. Real World Appl.. 2011;12:2681-2691.
[Google Scholar]
Kabir M.M., . Modified Kudryashov method for generalized forms of the nonlinear heat conduction equation. Int. J. Phys. Sci.. 2011;6(25):6061-6064.
[Google Scholar]
Kabir M.M., Bagherzadeh R., . Application of (G′/G)-expansion method to nonlinear variants of the (2+1)-dimensional Camassa-Holm-KP equation. Middle-east J. Sci. Res.. 2011;9(5):602-610.
[Google Scholar]
Kabir M.M., Borhanifar A., Abazari R., . Application of (G′/G)-expansion method to Regularized Long Wave (RLW) equation. Comp. Math. Appl.. 2011;61(8):2044-2047.
[Google Scholar]
Kabir M.M., Khajeh A., Abdi Aghdam E., Koma A., . Modified Kudryashov method for finding exact solitary wave solutions of higher-order nonlinear equations. Math. Meth. Appl. Sci.. 2011;34:213-219.
[Google Scholar]
Kabir M.M., Abdi Aghdam E., . Analytic solutions for a nonlinear Schrödinger-type system. Nonlinear Sci. Lett. A. 2012;3:78-94.
[Google Scholar]
Kabir M.M., Demirocak D.E., . Degradation mechanisms in Li‐ion batteries: a state‐of‐the‐art review. Int. J. Energy Res. 2017 In press
[CrossRef] [Google Scholar]
Kudryashov N.A., . Exact soliton solutions of the generalized evolution equation of wave dynamics. J. Appl. Math. Mech.. 1988;52(3):360-365.
[Google Scholar]
Kudryashov N.A., . Seven common errors in finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Num. Simul.. 2009;14:3507-3529.
[Google Scholar]
Kudryashov N.A., Loginova N.B., . Be careful with the Exp-function method. Commun. Nonlinear Sci. Num. Simul.. 2009;14(5):1881-1891.
[Google Scholar]
Kudryashov N.A., Soukharev M.B., . Popular ansatz methods and solitary wave solutions of the Kuramoto-Sivashinsky equation. Reg. Chao. Dyn.. 2009;14(3):407-419.
[Google Scholar]
Kudryashov N.A., Sinelshchikov D.I., Demina M.V., . Exact solutions of the generalized Bretherton equation. Phys. Lett. A. 2011;375:1074-1079.
[Google Scholar]
Kudryashov N.A., . On one of methods for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Num. Simul.. 2012;17(6):2248-2253.
[Google Scholar]
Li J., Zhang Y., . Exact travelling wave solutions in a nonlinear elastic rod equation. Appl. Math. Comp.. 2008;202(2):504-510.
[Google Scholar]
Lu X., Lin F., . Soliton excitations and shape-changing collisions in alpha helical proteins with interspine coupling at higher order. Comm. Non. Sci. Num. Simul.. 2016;32:241-261.
[Google Scholar]
Lu X., Ma W.X., . Study of lump dynamics based on a dimensionally reduced Hirota bilinear equation. Nonlinear Dyn.. 2016;85:1217-1222.
[Google Scholar]
Lu X., Ma W.X., Chen S.T., Khalique C.M., . A note on rational solutions to a Hirota-Satsuma-like equation. Appl. Math. Lett.. 2016;58:13-18.
[Google Scholar]
Lu X., Ma W.X., Zhou Y., Khalique C.M., . Rational solutions to an extended Kadomtsev-Petviashvili-like equation with symbolic computation. Comp. Math. Appl.. 2016;71:1560-1567.
[Google Scholar]
Lu X., Chen S.T., Ma W.X., . Constructing lump solutions to a generalized Kadomtsev–Petviashvili–Boussinesq equation. Nonlinear Dyn.. 2016;86:523-534.
[Google Scholar]
Lu X., Ma W.X., Yu J., Khalique C.M., . Solitary waves with the Madelung fluid description: a generalized derivative nonlinear Schrödinger equation. Comm. Non. Sci. Num. Simul.. 2016;31:40-46.
[Google Scholar]
Rashidi M.M., Shahmohamadi H., . Analytical solution of three-dimensional Navier-Stokes equations for the flow near an infinite rotating disk. Comm. Non. Sci. Num. Simul.. 2009;14(7):2999-3006.
[Google Scholar]
Seadawy A.R., El-Rashidy K., . Traveling wave solutions for some coupled nonlinear evolution equations. Math. Comp. Model.. 2013;57:1371-1379.
[Google Scholar]
Seadawy A.R., . Stability analysis for Zakharov-Kuznetsov equation of weakly nonlinear ion-acoustic waves in a plasma. Comp. Math. Appl.. 2014;67:172-180.
[Google Scholar]
Seadawy A.R., . Approximation solutions of derivative nonlinear Schrodinger equation with computational applications by variational method. Eur. Phys. J. Plus.. 2015;130:182.
[Google Scholar]
Seadawy A.R., . Fractional solitary wave solutions of the nonlinear higher-order extended KdV equation in a stratified shear flow: Part I. Comp. Math. Appl.. 2015;70:345-352.
[Google Scholar]
Seadawy A.R., . Three-dimensional nonlinear modified Zakharov-Kuznetsov equation of ion-acoustic waves in a magnetized plasma. Comp. Math. Appl.. 2016;71:201-212.
[Google Scholar]
Seadawy A.R., . Stability analysis solutions for nonlinear three-dimensional modified Korteweg–de Vries–Zakharov–Kuznetsov equation in a magnetized electron–positron plasma. Phys. A. 2016;455:44-51.
[Google Scholar]
Seadawy A.R., . Ion acoustic solitary wave solutions of two-dimensional nonlinear Kadomtsev–Petviashvili–Burgers equation in quantum plasma. Math. Meth. Appl. Sci.. 2017;40:1598-1607.
[Google Scholar]
Wang M., Li X., Zhang J., . The (G′/G)-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A. 2008;372:417-423.
[Google Scholar]
Wazwaz A.M., . The tanh method and the sine–cosine method for solving the KP-MEW equation. Int. J. Comput. Math.. 2005;82(2):235-246.
[Google Scholar]
Zhuang W., Zhang G.T., . The propagation of solitary waves in a nonlinear elastic rod. Appl. Math. Mech.. 1986;7:615-626.
[Google Scholar]

Introduction

A brief review on the proposed methods

The modified Kudryashov method
The Exp-function method
The (G′/G)-expansion method

Application of the methods to the nonlinear elastic rod equation

Application of the modified Kudryashov method
Application of the Exp-function method
Application of the (G′/G)-expansion method

Discussions & conclusions

Fulltext Views
5

PDF downloads
0

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abbasbandy S., . Homotopy analysis method for the Kawahara equation. Nonlinear Anal. Real World Appl.. 2010;11(1):307-312.
[Google Scholar]

[2] Abdi Aghdam E., Kabir M.M., . Validation of a blowby model using experimental results in motoring condition with the change of compression ratio and engine speed. Exp. Therm. Fluid Sci.. 2010;34:197-209.
[Google Scholar]

[3] Abdou M.A., . Exact travelling wave solutions in a nonlinear elastic rod equation. Int. J. Nonlinear Sci.. 2009;7(2):167-173.
[Google Scholar]

[4] Biazar J., Eslami M., . Differential transform method for nonlinear fractional gas dynamics equation. Int. J. Phys. Sci.. 2011;6(5):1203-1206.
[Google Scholar]

[5] Borhanifar A., Kabir M.M., . New periodic and soliton solutions by application of Exp-function method for nonlinear evolution equations. J. Comp. Appl. Math.. 2009;229:158-167.
[Google Scholar]

[6] Borhanifar A., Kabir M.M., Vahdat M., . New periodic and soliton wave solutions for the generalized Zakharov system and (2+1)-dimensional Nizhnik–Novikov–Veselov system. Chaos Solit. Fract.. 2009;42:1646-1654.
[Google Scholar]

[7] Borhanifar A., Kabir M.M., Hossein Pour.A., . A Numerical Method for Solution of the Heat Equation with Nonlocal Nonlinear Condition. World Appl. Sci. J.. 2011;13:2405-2409.
[Google Scholar]

[8] Demina M.V., Kudryashov N.A., . From Laurent series to exact meromorphic solutions: the Kawahara equation. Phys. Lett. A. 2010;374:4023-4029.
[Google Scholar]

[9] Demina M.V., Kudryashov N.A., . Explicit expressions for meromorphic solutions of autonomous nonlinear ordinary differential equations. Commun. Nonlinear Sci. Num. Simul.. 2011;16:1127-1134.
[Google Scholar]

[10] Gao L.N., Zhou X.Y., Zi Y.Y., Yu J., Lu X., . Resonant behavior of multiple wave solutions to a Hirota bilinear equation. Comp. Math. Appl.. 2016;72:1225-1229.
[Google Scholar]

[11] Hashemi Kachapi S.H.A., Ganji D.D., Davodi A.G., Varedi S.M., . Periodic solution for strongly nonlinear vibration systems by He’s variational iteration method. Math. Meth. Appl. Sci.. 2009;32(18):2339-2349.
[Google Scholar]

[12] He J.H., Wu X.H., . Exp-function method for nonlinear wave equations. Chaos Solit. Fract.. 2006;30(3):700-708.
[Google Scholar]

[13] Helal M.A., Seadawy A.R., . Variational method for the derivative nonlinear Schrödinger equation with computational applications. Phys. Scr.. 2009;80:035004.
[Google Scholar]

[14] Kabir M.M., Khajeh A., . New explicit solutions for the Vakhnenko and a generalized form of the nonlinear heat conduction equations via Exp-function method. Int. J. Nonlinear Sci. Num. Simul.. 2009;10(10):1307-1318.
[Google Scholar]

[15] Kabir M.M., . Analytic solutions for generalized forms of the nonlinear heat conduction equation. Nonlinear Anal. Real World Appl.. 2011;12:2681-2691.
[Google Scholar]

[16] Kabir M.M., . Modified Kudryashov method for generalized forms of the nonlinear heat conduction equation. Int. J. Phys. Sci.. 2011;6(25):6061-6064.
[Google Scholar]

[17] Kabir M.M., Bagherzadeh R., . Application of (G′/G)-expansion method to nonlinear variants of the (2+1)-dimensional Camassa-Holm-KP equation. Middle-east J. Sci. Res.. 2011;9(5):602-610.
[Google Scholar]

[18] Kabir M.M., Borhanifar A., Abazari R., . Application of (G′/G)-expansion method to Regularized Long Wave (RLW) equation. Comp. Math. Appl.. 2011;61(8):2044-2047.
[Google Scholar]

[19] Kabir M.M., Khajeh A., Abdi Aghdam E., Koma A., . Modified Kudryashov method for finding exact solitary wave solutions of higher-order nonlinear equations. Math. Meth. Appl. Sci.. 2011;34:213-219.
[Google Scholar]

[20] Kabir M.M., Abdi Aghdam E., . Analytic solutions for a nonlinear Schrödinger-type system. Nonlinear Sci. Lett. A. 2012;3:78-94.
[Google Scholar]

[21] Kabir M.M., Demirocak D.E., . Degradation mechanisms in Li‐ion batteries: a state‐of‐the‐art review. Int. J. Energy Res. 2017 In press
[CrossRef] [Google Scholar]

[22] Kudryashov N.A., . Exact soliton solutions of the generalized evolution equation of wave dynamics. J. Appl. Math. Mech.. 1988;52(3):360-365.
[Google Scholar]

[23] Kudryashov N.A., . Seven common errors in finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Num. Simul.. 2009;14:3507-3529.
[Google Scholar]

[24] Kudryashov N.A., Loginova N.B., . Be careful with the Exp-function method. Commun. Nonlinear Sci. Num. Simul.. 2009;14(5):1881-1891.
[Google Scholar]

[25] Kudryashov N.A., Soukharev M.B., . Popular ansatz methods and solitary wave solutions of the Kuramoto-Sivashinsky equation. Reg. Chao. Dyn.. 2009;14(3):407-419.
[Google Scholar]

[26] Kudryashov N.A., Sinelshchikov D.I., Demina M.V., . Exact solutions of the generalized Bretherton equation. Phys. Lett. A. 2011;375:1074-1079.
[Google Scholar]

[27] Kudryashov N.A., . On one of methods for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Num. Simul.. 2012;17(6):2248-2253.
[Google Scholar]

[28] Li J., Zhang Y., . Exact travelling wave solutions in a nonlinear elastic rod equation. Appl. Math. Comp.. 2008;202(2):504-510.
[Google Scholar]

[29] Lu X., Lin F., . Soliton excitations and shape-changing collisions in alpha helical proteins with interspine coupling at higher order. Comm. Non. Sci. Num. Simul.. 2016;32:241-261.
[Google Scholar]

[30] Lu X., Ma W.X., . Study of lump dynamics based on a dimensionally reduced Hirota bilinear equation. Nonlinear Dyn.. 2016;85:1217-1222.
[Google Scholar]

[31] Lu X., Ma W.X., Chen S.T., Khalique C.M., . A note on rational solutions to a Hirota-Satsuma-like equation. Appl. Math. Lett.. 2016;58:13-18.
[Google Scholar]

[32] Lu X., Ma W.X., Zhou Y., Khalique C.M., . Rational solutions to an extended Kadomtsev-Petviashvili-like equation with symbolic computation. Comp. Math. Appl.. 2016;71:1560-1567.
[Google Scholar]

[33] Lu X., Chen S.T., Ma W.X., . Constructing lump solutions to a generalized Kadomtsev–Petviashvili–Boussinesq equation. Nonlinear Dyn.. 2016;86:523-534.
[Google Scholar]

[34] Lu X., Ma W.X., Yu J., Khalique C.M., . Solitary waves with the Madelung fluid description: a generalized derivative nonlinear Schrödinger equation. Comm. Non. Sci. Num. Simul.. 2016;31:40-46.
[Google Scholar]

[35] Rashidi M.M., Shahmohamadi H., . Analytical solution of three-dimensional Navier-Stokes equations for the flow near an infinite rotating disk. Comm. Non. Sci. Num. Simul.. 2009;14(7):2999-3006.
[Google Scholar]

[36] Seadawy A.R., El-Rashidy K., . Traveling wave solutions for some coupled nonlinear evolution equations. Math. Comp. Model.. 2013;57:1371-1379.
[Google Scholar]

[37] Seadawy A.R., . Stability analysis for Zakharov-Kuznetsov equation of weakly nonlinear ion-acoustic waves in a plasma. Comp. Math. Appl.. 2014;67:172-180.
[Google Scholar]

[38] Seadawy A.R., . Approximation solutions of derivative nonlinear Schrodinger equation with computational applications by variational method. Eur. Phys. J. Plus.. 2015;130:182.
[Google Scholar]

[39] Seadawy A.R., . Fractional solitary wave solutions of the nonlinear higher-order extended KdV equation in a stratified shear flow: Part I. Comp. Math. Appl.. 2015;70:345-352.
[Google Scholar]

[40] Seadawy A.R., . Three-dimensional nonlinear modified Zakharov-Kuznetsov equation of ion-acoustic waves in a magnetized plasma. Comp. Math. Appl.. 2016;71:201-212.
[Google Scholar]

[41] Seadawy A.R., . Stability analysis solutions for nonlinear three-dimensional modified Korteweg–de Vries–Zakharov–Kuznetsov equation in a magnetized electron–positron plasma. Phys. A. 2016;455:44-51.
[Google Scholar]

[42] Seadawy A.R., . Ion acoustic solitary wave solutions of two-dimensional nonlinear Kadomtsev–Petviashvili–Burgers equation in quantum plasma. Math. Meth. Appl. Sci.. 2017;40:1598-1607.
[Google Scholar]

[43] Wang M., Li X., Zhang J., . The (G′/G)-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A. 2008;372:417-423.
[Google Scholar]

[44] Wazwaz A.M., . The tanh method and the sine–cosine method for solving the KP-MEW equation. Int. J. Comput. Math.. 2005;82(2):235-246.
[Google Scholar]

[45] Zhuang W., Zhang G.T., . The propagation of solitary waves in a nonlinear elastic rod. Appl. Math. Mech.. 1986;7:615-626.
[Google Scholar]