Exact solution of Helmholtz equation for the case of non-paraxial Gaussian beams

1 Introduction

The full 3-dimensional spatial Helmholtz equation provides solutions that describe the propagation of waves over space (e.g., electromagnetic waves) under proper boundary conditions; it should be presented in a spherical coordinate system R, θ, φ as given below (Sommerfeld, 1949; Serway, 2004):

Besides, in spherical coordinate system (Kamke, 1971): $$\mathrm{\Delta }A=\frac{{\partial }^{2}A}{\partial R^2}+\frac{2}{R}\frac{\partial A}{\partial R}+\frac{1}{R^2{\sin }^2\theta }\frac{{\partial }^{2}A}{\partial {\phi }^2}+\frac{1}{R^2}\frac{{\partial }^{2}A}{\partial {\theta }^2}+\frac{1}{R^2}\cot \theta \frac{\partial A}{\partial \theta }\text{.}$$

Special solutions to this equation have generated continuing interest in the optical physics community since the discovery of unusual non-diffracting waves such as Bessel and Airy beams (Alonso and Bandres, 2014a, 2014b, 2012).

Let us search for solutions of Eq. (1.1) in a classical form of Gaussian beams (Yi-Qing, 2013; Tagirdzhanov et al., 2011; Chen et al., 2002), which could be presented in Cartesian coordinate system as given below (Svelto, 2010): $$A=a·\frac{w_0}{w(z)}\exp \left[-\frac{x^2+y^2}{w^2(z)}-\mathit{ikz}-\mathit{ik}\frac{x^2+y^2}{2r(z)}+i\zeta (z)\right]$$ - where w(z), r(z), ζ(z) – are the real functions, describing appropriate parameters of a beam; w(z) is the beam waist size, r(z) is a wavefront radius of curvature and ζ (z) is the Gouy’s phase shift properly (Svelto, 2010).

The classical form of Gaussian beams above could be also represented as given below $$\exp \left[i\left(\zeta (z)-\mathit{kz}+i·\ln w(z)+\left(\frac{i}{w^2(z)}-\frac{k}{2R(z)}\right)·(x^2+y^2)\right)\right]=\exp \left[i\left(p(z)+\frac{x^2+y^2}{2q(z)}\right)\right]$$ - where p(z) is the complex phase-shift of the waves during their propagation along the z axis; q(z) is the proper complex parameter of a beam, which is determining Gaussian profile of a wave in the transverse plane at position z.

Besides, let us also note that at the left part of the expression above we express the term (1/w(z)) in a form for Gaussian beams, as exp (i² ln w(z)) = exp (−ln w(z)).

The right part of the expression above could be transformed in a spherical coordinate system to the form given below:

The solution (*) is additionally assumed to be independent of the azimuthal co-ordinate to observe it under well-known paraxial approximation (Svelto, 2010) also.

Then having substituted the expression (*) into Eq. (1.1), we should obtain (θ ≠ 0):

2 Exact solutions

Let us re-designate appropriate term in (*) as given below: $$f(R\text{,}\theta )=p(R\text{,}\theta )+\frac{R^2·{\sin }^2\theta }{2q(R\text{,}\theta )}\text{.}$$

In such a case, Eq. (1.2) could be transformed as shown below (θ ≠ 0):

But we should especially note that during the process of obtaining a solution (for example, if we are simply assuming a special eikonal solution (Svelto, 2010; Milonni and Eberly, 2010) to the Helmholtz equation), some of main features of the solution could be reduced; so, such a solution need not have any relation to Gaussian form (*).

Besides, one of the obvious solutions of PDE-equations (2.1):

Let us assume as given below:

3 Presentation of exact solution

Under assumption (**), Eq. (2.2) could be represented as shown below:

Besides, Eq. (2.3) could be presented as given below (C = 0):

Indeed, let us assume (k ≠ 0, R ≠ 0): $$\begin{array}{c}{y}_1=u_1+\frac{i}{R}\text{,}{y}_1^{\prime }(R)=-i·y_1^2-\frac{2}{R}{y}_1+i·k^2\hfill \\ \Rightarrow u_1^{\prime }(R)=-i·u_1^2+i·k^2\Rightarrow \int \frac{{\mathit{du}}_1}{k^2-u_1^2}=i·R\hfill \\ \Rightarrow \left\{\begin{array}{c}{u}_1=k·\tanh (i·k·R)\text{,}|i·\tan (k·R)|<1\text{,}\hfill \\ u_1=k·\coth (i·k·R)\text{,}|i·\tan (k·R)|>1\text{,}\hfill \end{array}\right.\hfill \end{array}$$ - then, we obtain:

Taking into consideration the expression (**) for the solution as well as (3.2)–(3.4), let us finally present a new type of non-paraxial solution, which is proved to satisfy the Helmholtz equation (1.1), as shown below: $$\left\{\begin{array}{c}A=a·\left(\int \csc \theta d\theta \right)·\frac{\cosh (i·k·R)}{R}\text{,}|k·R|<\pi /4\text{,}\hfill \\ A=a·\left(\int \csc \theta d\theta \right)·\frac{\sinh (i·k·R)}{R}\text{,}|k·R|>\pi /4\text{,}\hfill \end{array}\right.$$ - or

4 Discussions and conclusion

A new type of exact solutions of the full 3 dimensional spatial Helmholtz equation for the case of non-paraxial Gaussian beams is presented here.

We consider an appropriate representation of the solution for Gaussian beams in a spherical coordinate system by substituting it to the full 3 dimensional spatial Helmholtz equation.

Analyzing the structure of the final equation, we obtain that governing equations for the components of our solution are represented by the proper Riccati equations of complex value, which has no analytical solution in general case. We should note that a modern method exists for obtaining the numerical solution of Riccati equations with a good approximation (Bender and Orszag, 1999).

But we find one of the possible exact solutions (3.5) which is proved to satisfy the Helmholtz equation (1.1) for beams (*).

Indeed, since the functions g(R) = (sin(k·R))/(k·R) or g(R) = (cos(k·R))/(k·R) in (3.5) are itself an exact solution of the full Helmholtz equation (1.1) Sommerfeld, 1949; Serway, 2004, the formula for the Laplacian in spherical coordinates gives for A = h(θ)·g(R), h(θ) = ln(tg(θ/2)): $$\frac{1}{R^2}\frac{{\partial }^{2}A}{\partial {\theta }^2}+\frac{1}{R^2}\cot \theta \frac{\partial A}{\partial \theta }=0\to \frac{d\left(\frac{1}{\sin \theta }\right)}{d\theta }+\cot \theta ·\left(\frac{1}{\sin \theta }\right)=0\text{,}$$ - which is obviously valid for the range of parameter θ ∈ (0, π).

As for the appropriate example of paraxial approximation for such a non-paraxial exact solution (3.5) of the full Helmholtz equation (1.1), it could be easily obtained in the case θ → +0 (see the expression (3.5) above).

Let us express the real part of solution (3.5) in Cartesian co-ordinates X, Y, Z as given below (|k·R| < π/4, r(X, Y) ≪ Z):

$$\begin{array}{c}A=(k·a)·\ln \left(\tan \left(\frac{\theta }{2}\right)\right)·\frac{\cos (k·R)}{k·R}=\\ =\frac{(k·a)}{2}·\ln \left(\frac{\sqrt{{\left(r\right(X\text{,}Y\left)\right)}^2+Z^2}-Z}{\sqrt{{\left(r\right(X\text{,}Y\left)\right)}^2+Z^2}+Z}\right)·\frac{\cos (k·\sqrt{{\left(r\right(X\text{,}Y\left)\right)}^2+Z^2})}{k·\sqrt{{\left(r\right(X\text{,}Y\left)\right)}^2+Z^2}}\cong (k·a)·\ln \left(\frac{r\left(X\text{,}Y\right)}{2Z}\right)·\frac{\cos (k·Z)}{k·Z}\end{array}$$ As we know, a spherical-wave solution g(R) = (cos(k·R))/(k·R) could be schematically imagined in the Cartesian co-ordinate system as given below (Sommerfeld, 1949; Serway, 2004):

- where each of spherical waves is assumed to be a concentric sphere evenly enlarging from a fixed point (a source of waves), see Figs. 1 and 2.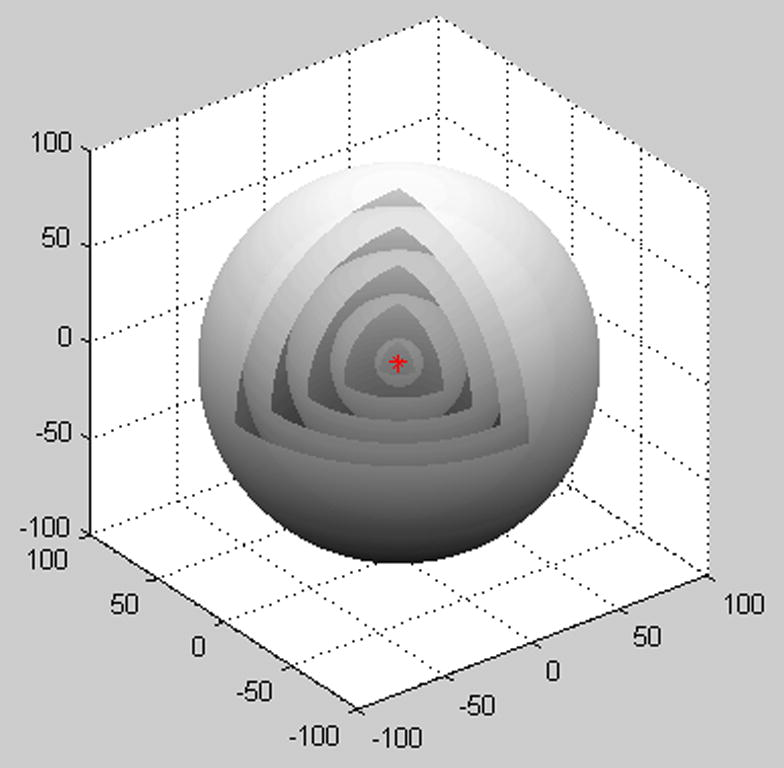

Close

Figure 1

A schematic plot of a spherical-wave type of the solutions.

Export to PPT

Close

Figure 2

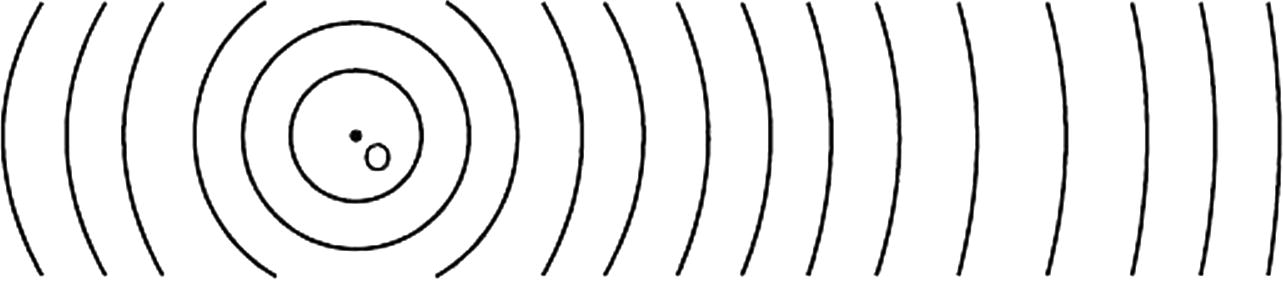
A schematic plot of the plane spherical-wave solutions.

Export to PPT

The solution (3.5) differs from the spherical-waves on a factor ln(tan(θ/2)), but the total energy of a beam should not exceed the total energy of the appropriate spherical-waves solution of Helmholtz equation. The energy of the beam is, of course, essentially the absolute magnitude of the solution spherically integrated over space.

So, we should restrict the range of parameter θ ∈ (0, π) to the range of θ ∈ [θ₀, θ₁] {where θ₀ = 2·arctan(1/e) ≅ 0,2244 π, e = 2.71828…, θ₁ = 2·arctan(e) ≅ 0,7756 π} for the reason that inequality: |lntan(θ/2)| < |tan(θ/2)| ⩽ 1 should be valid for all meanings of function ln(tan(θ/2)) in that range of θ, especially if |k·R| > π/4.

So, these unusual beams with limited amplitude A could be compared to the spherical-waves solution (which is much more closer to each other than other exotic beams) only at the range of parameter θ ∈ [∼40,4°, ∼139,6°].

As for the appropriate examples of paraxial approximation r(X,Y) = √(X² + Y²) ≪ Z, expressed by Eq. (4.1) in Cartesian co-ordinates X, Y, Z, see Fig. 3 and 4.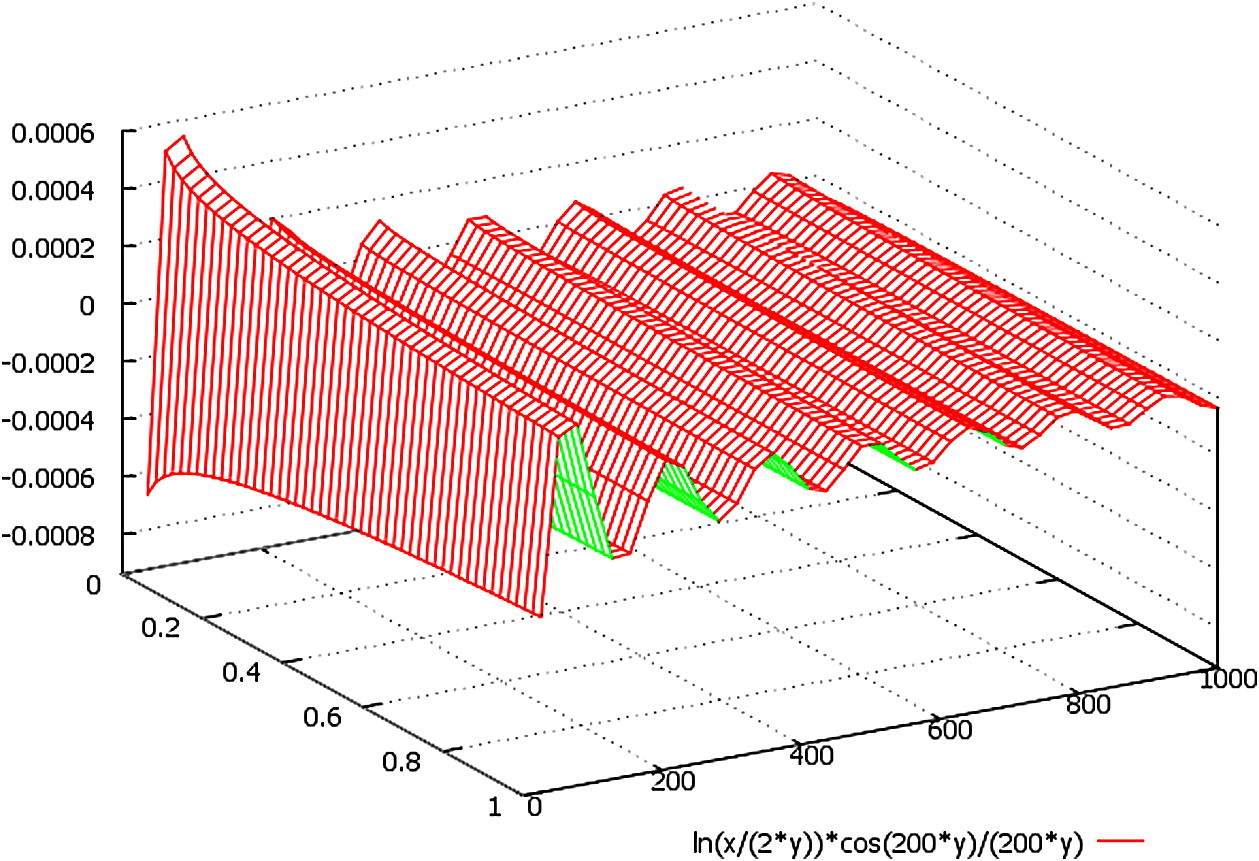

Close

Figure 3

A schematic plot of the function ln(x/2y)*(cos(k·y)/(k·y)), here we designate: x = r(X,Y) = √(X² + Y²) ∈ (0, 1), y = Z ∈ (0, 1000).

Export to PPT

Close

Figure 4

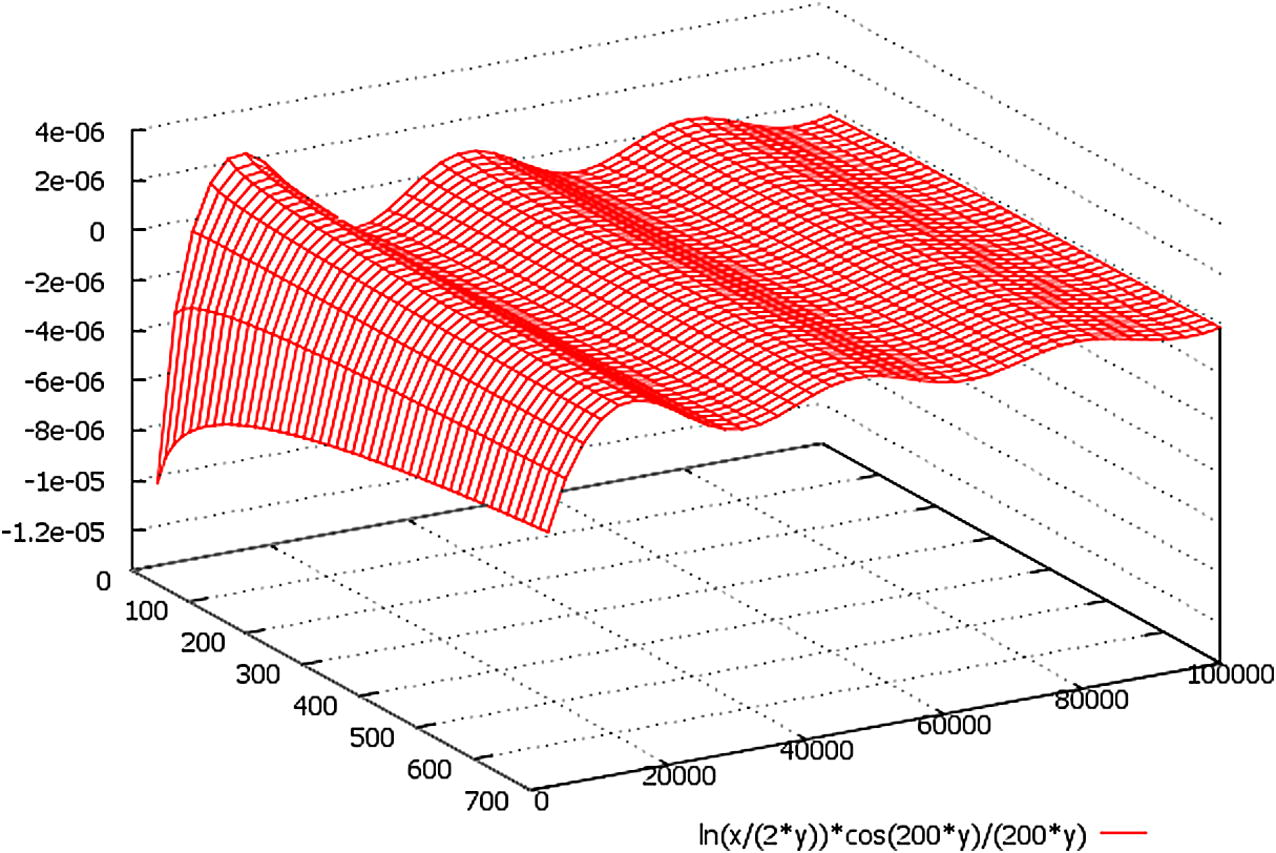
A schematic plot of the function ln(x/2y)*(cos(k·y)/(k·y)), here we designate: x = r(X,Y) = √(X² + Y²) ∈ (0, 700), y = Z ∈ (0, 100,000).

Export to PPT

Let us also schematically imagine the spherical-wave solution to compare it with the solution above: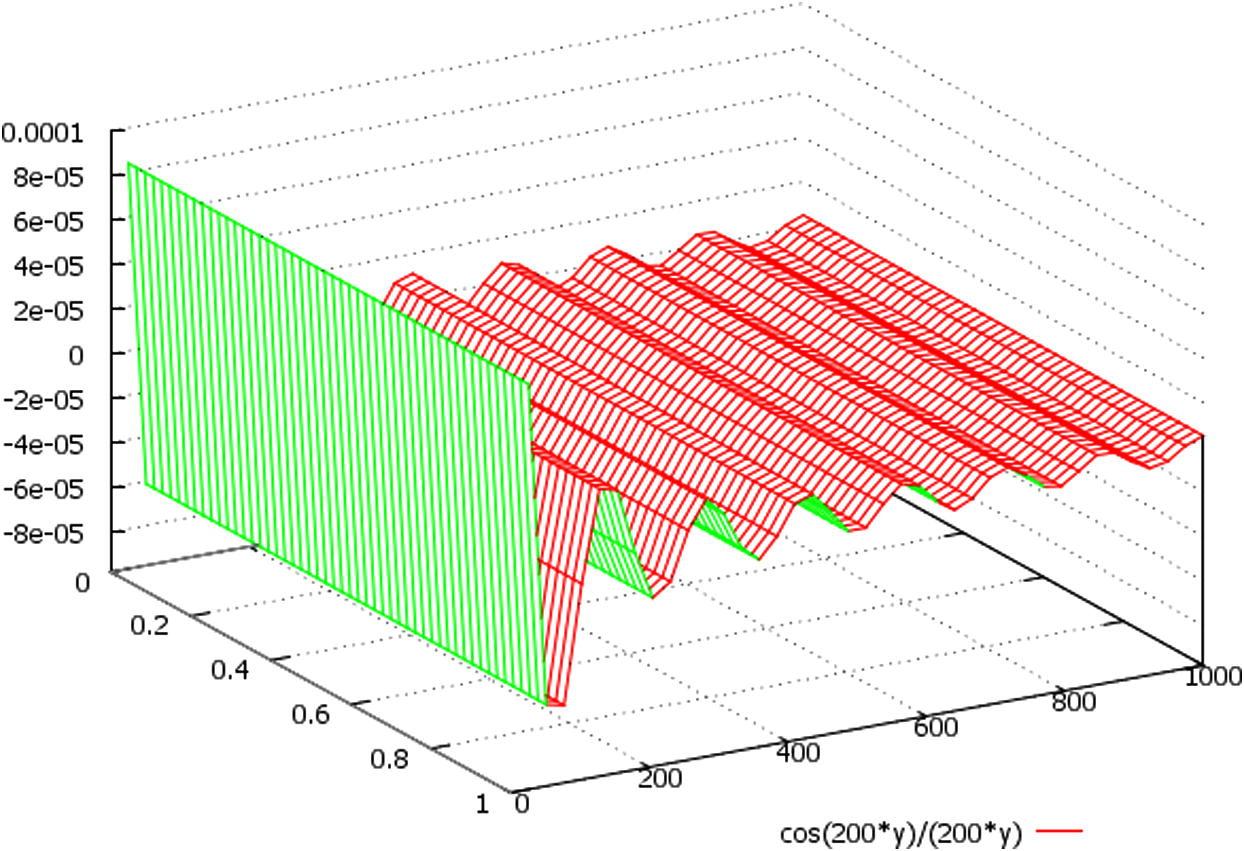

Close

Figure 5

A schematic plot of the function (cos(k·y)/(k·y)), here we designate: y = Z ∈ (0, 1000).

Export to PPT

Close

Figure 6

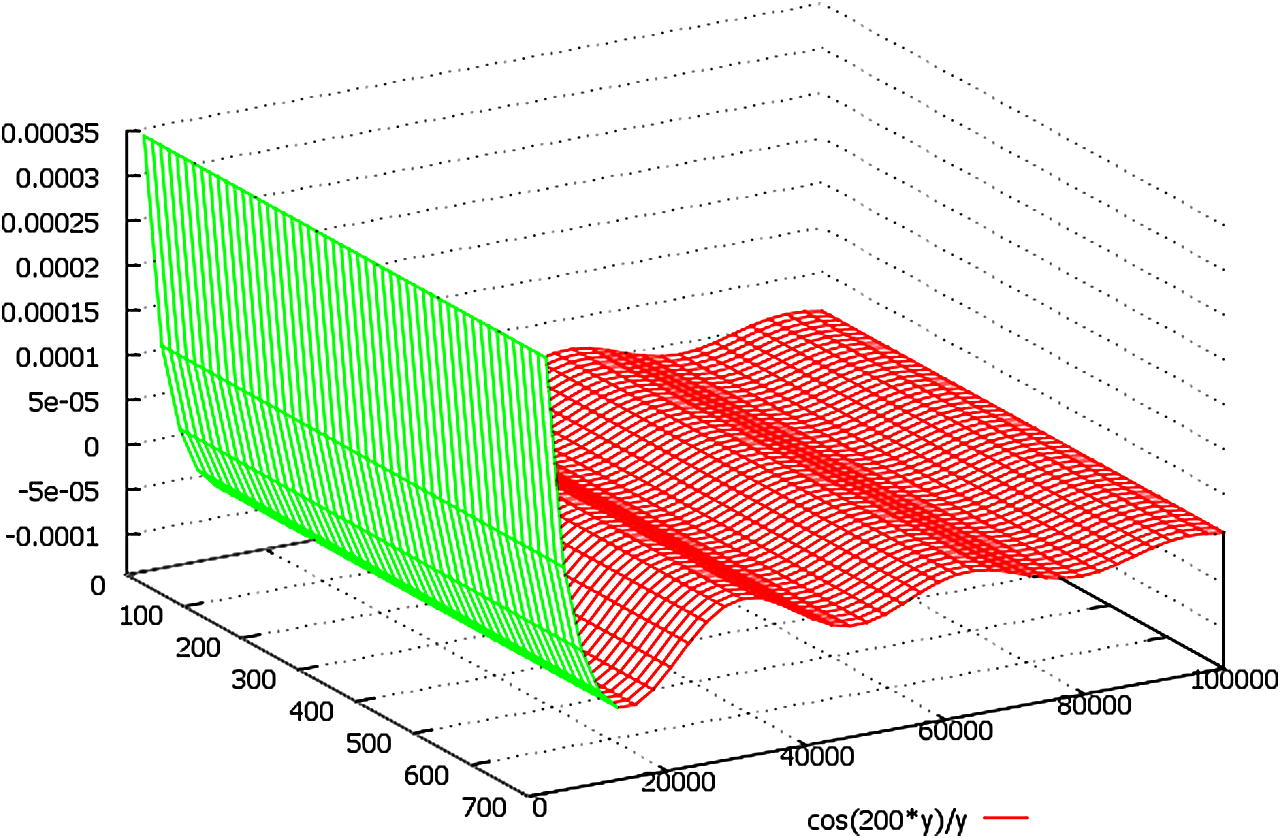
A schematic plot of the function (cos(k·y)/k·y), here we designate: y = Z ∈ (0, 100,000).

Export to PPT

Also, let us note that these unusual beams could be comparing to the Bessel beam solutions (Milonni and Eberly, 2010) at all the ranges of parameter θ ∈ (0, π). To obtain the energy of the beam, we should spherically integrate the absolute magnitude of the solution over space, so such a calculations should produce the infinite energy of a beam due to the structure of the solution: A = (a·k)·ln(tan(θ/2))·(cos(k·R))/(k·R). As for the point of clarifying the physical content of the derived solution, Fig. 3–6 could present a wave travelling on the ocean surface, for a example.

Such a solution is supposed to be linearly enhancing their radius R during propagation in R-direction, but it is modulated by the function ln(tan(θ/2)) so that the total amplitude A = (a·k)·ln(tan(θ/2))·(cos(k·R))/(k·R).

Jumping of a phase-function of a solution (*) in a form (3.5) for an amplitude A being equal to zero at the meaning of parameter θ = π/2, could be associated with the existing of an optical vortex (Svelto, 2010) at this point. Optical vortex (also known as a screw dislocation or phase singularity) is a zero of an optical field, a point of zero intensity. Research into the properties of vortices has thrived since a comprehensive paper (Nye and Berry, 1974), described the basic properties of “dislocations in wave trains”.