Exact solitary wave and numerical solutions for geophysical KdV equation

1 Introduction

Research on partial differential equations (PDEs) and relevant topics have been widely increased recently. It has become an active topic in several spheres of engineering, physical and mathematical sciences, particularly, in mechanical engineering, fluid mechanics, traveling waves, plasma physics, fibers, nonlinear optics, signal processing, control theory, and others. Exact and numerical solutions play an essential role in investigating these phenomena. Over the previous decades, several powerful approaches have been successfully invoked to extract the analytic solutions of nonlinear equations (NLEEs) for instance the homogeneous balance technique (Wang et al., 1996), the improved $\exp (-F(x))$ -expansion method (Chen et al., 2019), the improved Kudryashov approach (Kumar et al., 2018), the first integral technique (Bekir and Unsal, 2012), the Adomian decomposition strategy (Adomain, 1994; Wazwaz, 2002), etc. Soliton solutions may form different types of shapes e.g. S-shaped soliton, kink wave, bell shape, lump wave, M-shaped soliton, peakons, cuspons and some others (Rao et al., 2019; Abdullah and Wang, 2019; Liu and Zhang, 2018; Alharbi and Almatrafi, 2020; Alam and Tunç, 2020; Alharbi and Almatrafi, 2020; Alharbi and Almatrafi, 2020; Özkan et al., 2020; El-Shiekh and Gaballah, 2020; Khater et al., 2020; Almatrafi et al., 2020; Alharbi et al., 2020; Alharbi et al., 2020; Akbar et al., 2021; Akinyemi et al., 2021; Zafar et al., 2022; Nisar et al., 2021; Houwe et al., 2022; Martínez et al., 2021).

Korteweg-de Vries (KdV) like equations are widely used to describe a massive number of applications in several branches of nonlinear science and engineering. Historically, KdV problem was found by Korteweg and De Vries in 1895 (Korteweg et al., 1895). Then, researchers have introduced many modifications for this equation. For example, Johnson (2002) described a specific approach to find the Camassa-Holm problem in the context of water waves and presented the connection with the KdV equation. In Wazzan (2009), Wazzan successfully applied a modified tanh-coth approach to extract new solutions for the KdV and Korteweg-de Vries-Burgers’ problems. Moreover, Kudryashov (2009) analyzed some exact solutions of KdV and KdV-Burgers problems. The Hirota’s bilinear technique was used in Wazwaz (2010) to investigate the solutions of the perturbed KdV equation. Triki et al. (2017) applied auxiliary equation approach to extract some soliton-like solutions for a second order wave equation of KdV. The derivation of the gKdV equation was achieved in Geyer and Quirchmayr (2017) using techniques from asymptotic analysis. Some explicit traveling wave solutions for the gKdV equation were presented in Geyer and Quirchmayr (2017) using Jacobi elliptic functions. In Ak et al. (2020), the Coriolis effect on oceanic flows was deeply investigated via the gKdV equation. The propagation of some solitary solutions was produced in Ak et al. (2020). Moreover, the authors implemented the finite element approach to construct numerical simulations for the gKdV equation. The homotopy perturbation technique was used in Karunakar and Chakraverty (2019) to deal with the gKdV equation and develop some analytic solutions. Furthermore, Rizvi et al. (2020) used the Hirota bilinear method to show some lump soliton solutions for gKdV equation.

In this work, we discuss a novel and reputed PDE known as geophysical Korteweg-de Vries equation (Geyer and Quirchmayr, 2017) which is given by

The outline of this work is explained in this paragraph. Section 2 presents a summary for the improved $\exp (-F(\eta ))$ -expansion technique. In Section 3, we analyze some new solutions for the gKdV problem. In Section 4, we discuss the numerical solution of the relevant equation while Section 5 presents the finite difference, the stability and the accuracy of the numerical approximation. Moreover, Section 6 is added to highlight the outcomes accomplished in this study. Ultimately, Section 7 concludes this article.

2 Methodology

This part is devoted to introduce the improved $\exp (-F(\eta ))$ -expansion approach, as given in Chen et al. (2019). Assume that

The constants $\beta ,r_0,r_1,r_2$ and $a_i$ $(i=1,2,\dots ,N+1)$ are obtained later. In order to calculate the value of N, we apply the homogeneous balance. we use some Jacobi elliptic function solutions presented in Chen et al. (2019) for Eq. (5). Next, we plug Eqs. (5) and (6) into Eq. (4) and equate the coefficients of $\exp (-F(\xi ))$ to zero to end up with an algebraic system solved by using Mathematica or Maple. The values of the above-mentioned constants are contained in the solutions of this system. Substituting the values of these constants into Eq. (5) yields the exact solutions.

3 Exact solutions

This section explores the solitary wave solutions of the considered problem. Using Eq. (3), we can express Eq. (1) by

We now balance terms to have $N=2$ . Hence, from Eq. (5), we have

Next, we substitute Eq. (8) into Eq. (7) to end up with algebraic equations whose solutions are given by $$\begin{array}{cc}\hfill a_0=& \frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right),\hfill \\ \hfill a_1=& 0,\hfill \\ \hfill a_2=& -\frac{4{\beta }^2{r}_0}{3},\hfill \\ \hfill \delta =& \frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)\text{.}\hfill \end{array}$$

Now, when $m⟶1$ , we can obviously develop several exact solutions given as follows. If $r_0=1,r_1=-1-m^2$ and $r_2=m^2$ . Then, the exact traveling wave solution is given by $${\psi }_1=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\coth }^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=1-m^2,r_1=-1+2m^2$ and $r_2=-m^2$ . Then, the exact traveling wave solutions are given by $${\psi }_2=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\mathit{sech}}^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=m^2,r_1=-1-m^2$ and $r_2=1$ . Then, the exact traveling wave solutions are given by $${\psi }_3=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\tanh }^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=-m^2,r_1=2m^2-1$ and $r_2=-1-m^2$ . Then, the exact traveling wave solutions are given by $${\psi }_4=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\cosh }^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=1,r_1=2-m^2$ and $r_2=-1-m^2$ . Then, the exact traveling wave solutions are given by $${\psi }_5=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\sinh }^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=1-m^2,r_1=2-m^2$ and $r_2=1$ . Then, the exact traveling wave solutions are given by $${\psi }_6=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\mathit{csch}}^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

Now, when $m⟶0$ , we can clearly obtain several exact solutions given as follows. If $r_0=1,r_1=-1-m^2$ and $r_2=m^2$ . Then, the exact traveling wave solution is given by $${\psi }_1=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\csc }^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=1-m^2,r_1=-1+2m^2$ and $r_2=-m^2$ . Then, the exact traveling wave solutions are given by $${\psi }_2=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\cos }^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=m^2,r_1=-1-m^2$ and $r_2=1$ . Then, the exact traveling wave solutions are given by $${\psi }_3=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\sin }^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=-m^2,r_1=2m^2-1$ and $r_2=-1-m^2$ . Then, the exact traveling wave solutions are given by $${\psi }_4=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\sec }^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=1,r_1=2-m^2$ and $r_2=-1-m^2$ . Then, the exact traveling wave solutions are given by $${\psi }_5=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\tan }^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

If $r_0=1-m^2,r_1=2-m^2$ and $r_2=1$ . Then, the exact traveling wave solutions are given by $${\psi }_6=\frac{4}{9}{\beta }^2\left(-r_1\pm \sqrt{r_1^2-3r_0{r}_2}\right)-\frac{4{\beta }^2{r}_0}{3}{\mathit{cot}}^2\left(\beta \left(x-\frac{1}{3}\left(-3\mu \pm 2{\beta }^2\sqrt{r_1^2-3r_0{r}_2}\right)t\right)\right)\text{.}$$

4 Numerical solution

We now investigate the numerical solution of Eq. (7) by implementing the nonlinear shooting method. We only take an initial value at $x_0$ and then we choose an initial guess for the first derivative at $x_0$ . It is worth known that we use MATLAB sub-routine ODE15s (Shampine and Reichelt, 1994) and modify the parameter until the second boundary condition is satisfied. Moreover, we use the solution obtained by shooting method as an initial condition for the adaptive moving mesh approach which is straightforwardly employed to obtain the numerical solution of the proposed problem. Eq. (7) can be written as

It is notable that Eq. (9) is discretized by utilizing the finite difference notations on a fixed mesh resulting in a nonlinear equations system. We solve the resulting system using MATLAB sub-routine FSOLVE (Shampine and Reichelt, 1994) which applies the Quasi-Newton method.

5 Finite difference semi-discretization scheme

In this section, we construct a semi-discretization scheme by executing the adaptive moving mesh process with a finite difference for the numerical solutions of the gKdV equation. This method applies a transformation coordinate from a computational domain $[0,1]$ , to a physical one $[a,b]$ . That is $$x=x(\eta ,t):[0,1]\to [a,b],t\in [0,T_e],$$ where $\eta \in [0,1]$ is a computational coordinate and $T_e$ is a fixed time. Thus, the solution $\psi$ is now dependent on a moving mesh coordinate $x(\eta ,t)$ . The moving mesh coordinate associated with $\psi$ is given by $$\left\{\begin{array}{c}{x}_i(\eta )=x_i({\eta }_i,t),i=0,1,2,\dots ,N_x,\hfill \\ x_0=a,x_{N_x}=b,\hfill \\ x_i({\eta }_i,0)=i\frac{b-a}{N_x},\hfill \end{array}\right.$$ where a and b represent the boundaries of the domain. A computational coordinate is represented as $$\left\{\begin{array}{c}{\eta }_i=i\frac{1}{N_x},i=0,1,2,\dots ,N_x,\hfill \\ {\eta }_0=0,{\eta }_{N_x}=1\text{.}\hfill \end{array}\right.$$

By applying the chain rule, Eq. (1) is given by

In order to establish a new equidistributing mesh, we require to solve the most common moving mesh partial differential equation (MMPDE) given by

1. We compute the mesh density function ${\rho }^n$ at $t=t^n$ using $x^n$ and ${\psi }^n$ .

2. We discretize the moving mesh PDE (MMPDE) in a computational coordinate using the central finite differences. Then, we integrate the resulting system over $[t^n,t^{n+1}]$ to obtain a new equidistributing mesh coordinate $x^{n+1}$ . The computation is done by using the function ${\rho }^n$ . Observe that the solution ${\psi }^n$ is not developed during this computation.

3. Linear interpolation is used to match the new mesh $x^{n+1}$ with the previous solution ${\psi }^n$ .

4. The physical PDE (Eq. (10)) is discretized in the new mesh. Then, we integrate the resulting system using an ODE MATLAB solver to obtain the solution ${\psi }^{n+1}$ . Here, we use ODE15i. ODE15i solver is a MATLAB solver based on the backward-differentiation formulas (BDFs) of the highest order up to 5. This solver is intended to be utilized with fully implicit differential equations (DEs) and differential–algebraic equations (DAEs). In this estimate, we use $${\dot{x}}_i=\frac{x_i^{n+1}-x_i^n}{h_t}\text{.}$$

5. Repeat these steps starting from the first step.

In this study, the central finite differences method is invoked to fully discretize the derivatives of the MMPDE6.

Systems (12) and (13) lead to a tridiagonal coefficient matrices which consist of three diagonals and the remaining entries are zeros. Therefore, we use the Crout factorization method to reduce the number of operations and obtain the results at a higher speed. The advantage of this method is to avoid finding the inverse of the coefficient matrices and only uses the backward substitution. Here, we use MATLAB to obtain the numerical results.

6 Results

We now highlight the significant results achieved in this work. The improved $\exp (-F(\eta ))$ -expansion approach is successfully executed to extract various hyperbolic and trigonometric exact solutions for Eq. (1). Some solitary wave solutions are plotted in Figures 1, 2 and when $\beta =\delta =1$ and $N=400$ . The shooting approach is effectively applied to solve the proposed problem. The obtained solution is used as an initial condition for the adaptive moving mesh technique which is implemented to construct the numerical results of Eq. (1). In Fig. 3, we plot the exact solitary traveling wave solution, the solution of the shooting method, and the solution of the boundary value problem method. As can be observed in this figure, the solutions are compatible and move together. This strongly indicates that the used method are reliable, valid, and effective.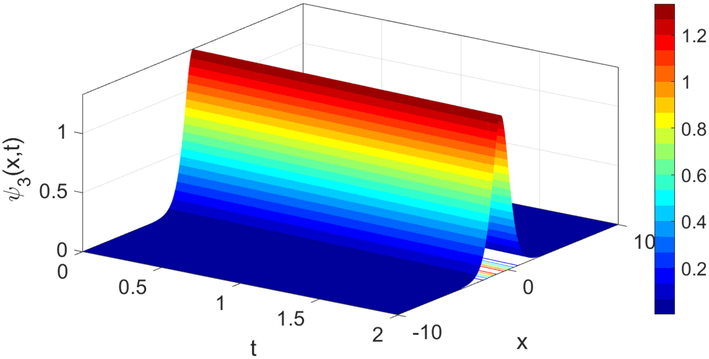

Close

Fig. 1

A 3D surface sketching a single wave for the analytic solution ${\psi }_3(x,t)$ under the values $\beta =1,\delta =1$ , and $N=400$ .

Export to PPT

Close

Fig. 2

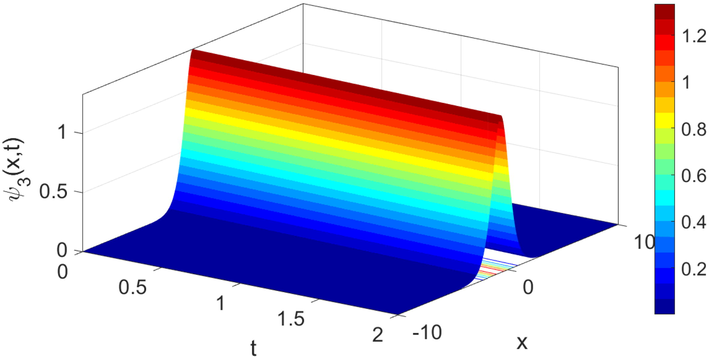
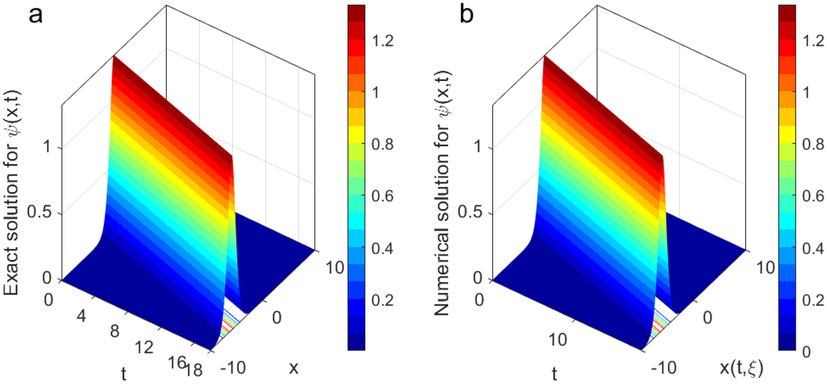
The solitary wave solution of ${\psi }_3(x,t)$ when $\beta =1,\delta =1$ , and $N=400$ .

Export to PPT

Close

Fig. 3

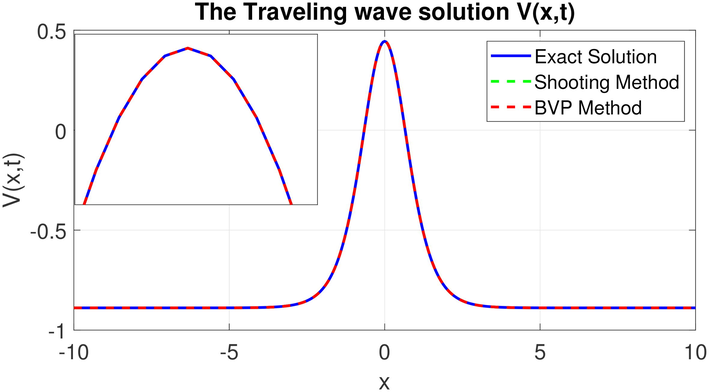
The exact solution of $V(x,t)$ obtained by employing the improved $\exp (-F(\eta ))$ -expansion technique, the solution obtained by shooting method and the numerical solution are compatible together. This figure is plotted under the values $\beta =1,\delta =1,N=400$ .

Export to PPT

Moreover, we specifically invoke Taylor series expansion to analyze the accuracy of the scheme. The accuracy is found from the second order. However, the accuracy of the proposed numerical approach is nearly from the third order, as can be seen in the slope of Fig. 7 which is roughly equal to $2.953$ . Therefore, the accuracy of the adaptive approach is much better than the accuracy of the second order. Furthermore, the Von Neumann analysis is well used to prove that the numerical scheme is unconditionally stable. In Fig. 4, we draw the time evolution for the exact and numerical results for $-10<x<8$ . Fig. 4(a) indicates that the constructed exact traveling solutions agree with the numerical solutions where $\beta =1,\delta =1$ , and $N=400$ . Various times are considered in this figure. In Fig. 4(b), we describe the time evolution of the used mesh $x=x(\eta ,t)$ .

Close

Fig. 7

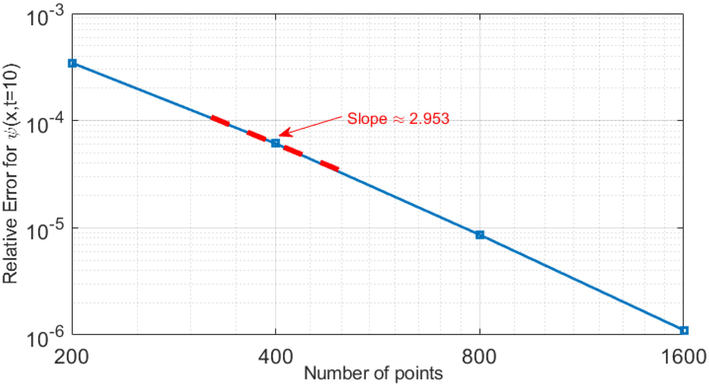
Relative error for $\psi (x,t)$ which is found by the numerical method against the grid of points $N_x$ with $\beta =1,\delta =1,t=10$ .

Export to PPT

Close

Fig. 4

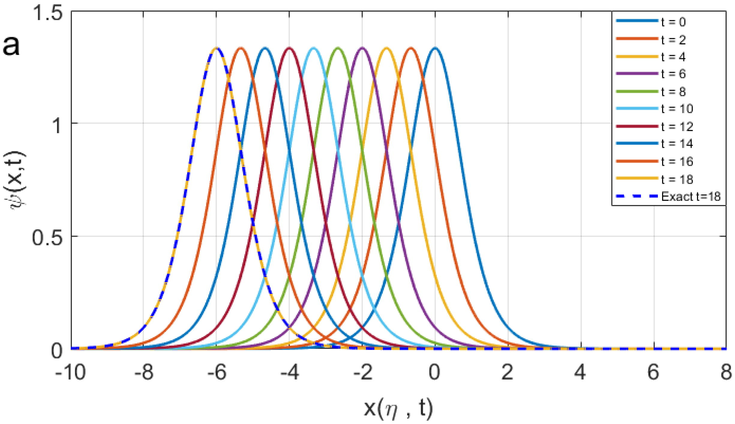
Time development for the analytic and numerical solutions for $-10<x<8$ . It shows an appropriate match between the exact and numerical solutions for various times. We use the values $\beta =1,\delta =1,N=400,t=0:0.5:2$ , and $t=2$ to sketch these figures.

Export to PPT

Fig. 5(a, b) show 3D plots for the obtained exact solitary traveling wave solutions and numerical solutions from $t=0\to 3$ . Then, we increase time to be from $t=0\to 18$ , as can be seen in Fig. 6(a, b). As can be easily observed from these figures, the exact solutions have nearly the same behaviors of the numerical solutions. In addition, the effectiveness of the used methods is clearly shown in Table 1 and Fig. 7. In this table, we demonstrate $L_2$ error and CPU time consumed to reach $t=5$ using the adaptive technique. We start with $N=200$ points and found that $L_2$ error is virtually approaching $3.51\times {10}^{-4}$ which is normally acceptable. The error decreases sharply when we increase the number of the points. Nevertheless, the CPU time increases somewhat when the number of the points is increased. For instance, when $N=1600,L_2$ error arrives at $1.11\times {10}^{-6}$ during $1.14\times {10}^{+2}$ minutes. The slight increment in the CPU time is for the reason that the used functions are computed with the process. Further, Fig. 7 presents that the relative error for $\psi (x,t=10)$ dramatically drops for large values of the points. The error rapidly declines because the adaptive process supplies the places with high error by adequate and sufficient points. Consequently, the adaptive technique is more computationally powerful and applicable in solving nonlinear partial differential equations.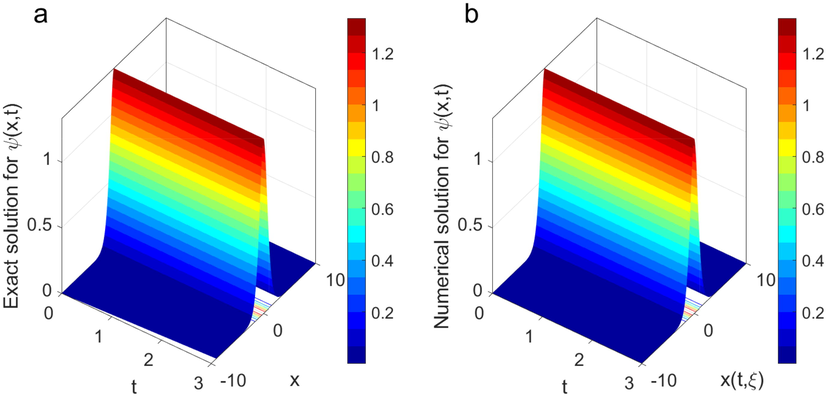

Close

Fig. 5

The exact traveling wave solution is shown in (a) while the numerical solution is presented in (b). The solutions are plotted under the values $\beta =1,\delta =1,N=400,t=0:0.5:2,t=0\to 3$ .

Export to PPT

Close

Fig. 6

A single traveling wave solution is depicted in (a) for the exact solution while (b) demonstrates one traveling wave for the numerical solution. The solutions are illustrated under the values $\beta =1,\delta =1,N=400,t=0:0.5:2,t=0\to 18$ .

Export to PPT

7 Conclusions

This paper has implemented the improved $\exp (-F(\eta ))$ -expansion method on the gKdV equation to extract new forms of solitary wave solutions. The obtained solutions have been presented as hyperbolic and trigonometric functions. The shooting method has been used to construct the solution of the gKdV problem. Then, we used this solution as an initial condition for the adaptive moving mesh technique which has been successfully used to obtain the numerical solution of the proposed problem. The validation of the constructed solutions has been well achieved by making a comprehensive comparison between the analytic and numerical outcomes. The solutions have nearly the same behavior. The accuracy of the adaptive method is much better and is from the third order. The numerical scheme is found unconditional stable. Moreover, a large number of points reduces the relative error. The used techniques are computationally efficient to be employed on other nonlinear partial differential problems.