Translate this page into:
Evaluation of the influence of toll systems on energy consumption and CO2 emissions: A case study of a Spanish highway
*Corresponding author. Tel.: +34 650015474 pjperez@caminos.upm.es (P.J. Pérez-Martínez)
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 30 December 2010
Abstract
This paper studies the energy consumption and subsequent CO2 emissions of road highway transportation under three toll systems in Spain for four categories of vehicles: cars, vans, buses and articulated trucks. The influence of toll systems is tested for a section of AP-41 highway between Toledo and Madrid. One system is free flow, other is traditional stop and go and the last toll system operates with an electronic toll collection (ETC) technology. Energy consumption and CO2 emissions were found to be closely related to vehicle mass, wind exposure, engine efficiency and acceleration rate. These parameters affect, directly or indirectly, the external forces which determine the energy consumption. Reducing the magnitude of these forces through an appropriate toll management is an important way of improving the energy performance of vehicles. The type of toll system used can have a major influence on the energy efficiency of highway transportation and therefore it is necessary to consider free flow.
Keywords
Energy efficiency
Toll management systems
Highway transportation
Spain
1 Introduction
This paper presents a study of the energy consumption of road vehicle transportation on highways based on a mechanical model. The influence of the different toll systems on energy consumption and subsequent CO2 emissions has been analyzed related to the parameters of the vehicle and traffic conditions, depending and not depending on transport services. A mechanical model was chosen to estimate the energy demand and subsequent CO2 emissions to overcome external forces for a given trip under different toll systems. This type of mechanical model has been widely used in transport research (Burgess and Choi, 2003; Lai and Barkan, 2005; Lutsey and Sperling, 2005; Zachariadis and Samaras, 2001) and includes rolling resistance, aerodynamic drag resistance, air entrance resistance, inertial and gravitational losses.
The mechanical model of energy demand has been applied to a case study of a section of AP-41 toll highway between Toledo (82,291 inhabitants) and Madrid (3,255,944 inhabitants), central Spain. This highway communicates the two cities, 52.3 km apart, and there is a small quantity of daily traffic between the two cities, 2768 vehicles/day (mainly commuters but also transit traffic to Madrid). The route constitutes and alternative road to the non-toll highway A-4, which connects southern Spain with the city capital Madrid (Fig. 1, left). The route is flat and fast without significant curves and speed restrictions and the toll, to which the estimations on energy consumption and CO2 emissions are associated, is situated in the kilometer point 14.3. The annual wind direction is N/NNE–SW/SSW, same as the general direction of highway AP-41 (Fig. 1, right). The mechanical model has been applied to calculate the energy demand in three scenarios of toll, including free-flow, traditional toll and electronic toll collection (ETC). From these three scenarios, a comparison among different toll systems is made to evaluate the effects of them, and a sensitivity study of the parameters in the model is also performed. Finally, an estimation of the potential energy and CO2 emissions savings is done for the Spanish toll network.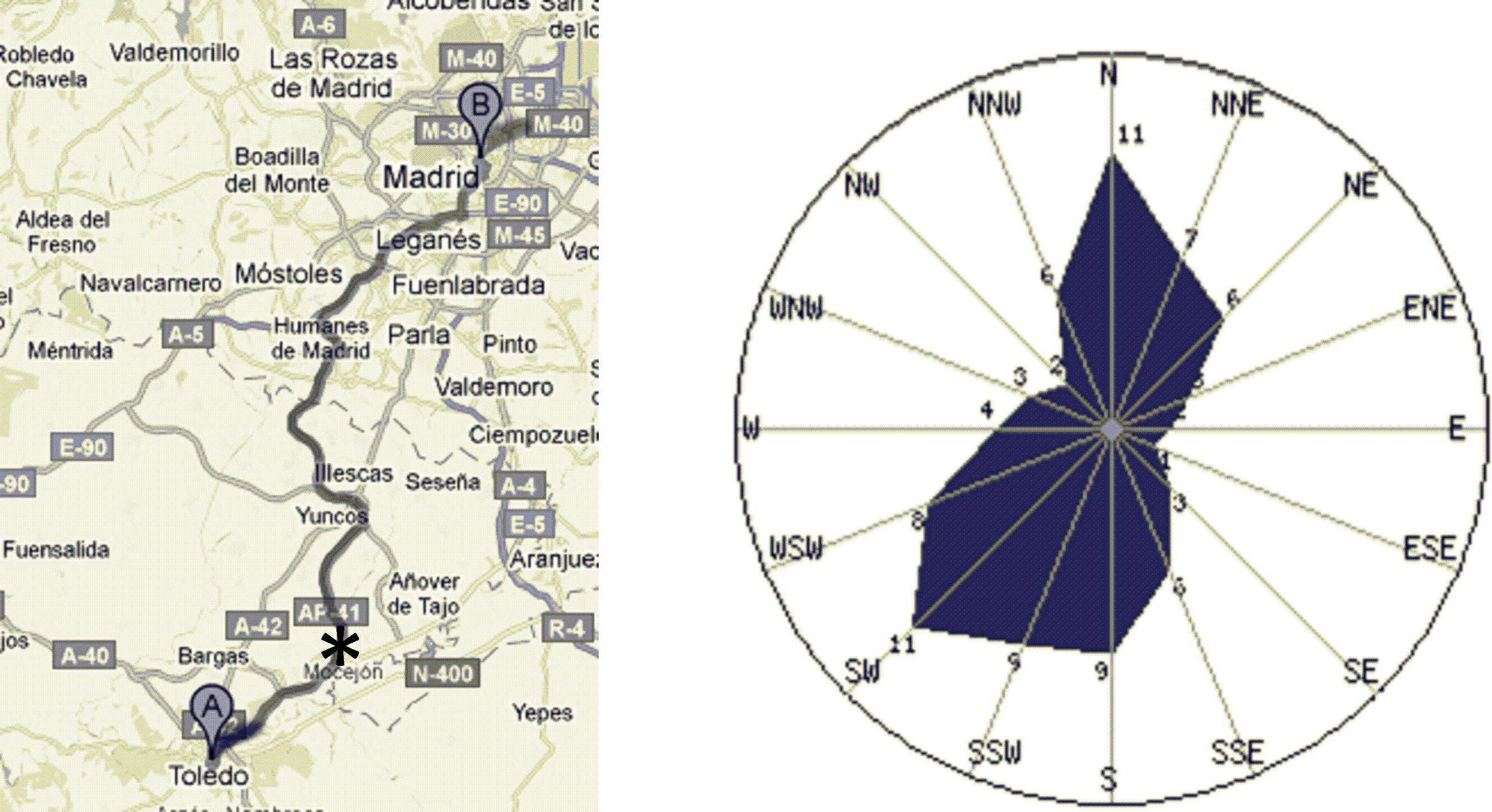
left: Map of highway AP-41 (∗situation of the toll, kilometer point 14.3). Right: Annual wind distribution of Madrid (2008).
2 Methodology and assumptions of estimates
2.1 Mechanical model for calculating the energy consumption
Energy consumption rates from “top-down” models are normally based on transportation demand and depend on several factors at a national scale: occupation rate, speed and journey length. These rates measure the current energy efficiencies given actual occupation rates at a national level. Comparing energy consumption between modes based on these rates may lead to serious errors when the circumstances are not comparable, and makes it difficult to obtain valid conclusions at a local scale. The use of energy consumption “bottom-up” mechanical model improves the quality of the assessments, and enables evaluation of the energy consumption impacts of new policy measures regarding infrastructure and modal shift, and permits the differential reasons to be identified. The mechanical model is important for enabling a better understanding of – and thus an improvement in – energy consumption. Energy consumption calculations derived with this mechanical model can be used as reference levels for adjusting public subsidies in order to encourage energy efficiency. Tests are required to ensure a better calibration of the model. The mechanical model used in this paper to estimate the energy consumption of a vehicle type i (passenger cars, vans, coaches, articulated trucks) and motor technology j (mostly gasoline and diesel) can be expressed, in mega-joules per vehicle-kilometer (MJ/veh-km), as follows:
In the equation above, the energy consumption Ui,j consists of five groups of external forces:
2.2 Assumptions, vehicle configurations and toll scenarios
In order to apply Eq. (1) properly, energy consumption parameters were assumed, as shown in Table 1. In this paper, no cornering forces or gravitational losses are considered based on the assumption that most toll stations are located in straight sections of highways without slope. No wind was taken into consideration based on the hypothesis that the dominant wind exposures, northeast and northwest, are coincident with the axis of the AP-41 highway and the balance between the positive and negative wind exposures is null (Fig. 1).
Parameter
Units
Value
Source/assumptions
Rolling resistance coefficient
Cr
–
0.01
Lutsey and Sperling (2005)
Vehicle massa
m
kg
2100–40,000
Volvo (2010), Mercedes-Benz (2010), Volkswagen (2010)
Gravitational constant
g
m/s2
9.81
Road gradient
θ
rad
0
No slope
Air density
ρ
kg/m3
1225
Frontal areab
Af
m2
2.52–8.67
Volvo, (20100, Mercedes-Benz (2010), Volkswagen (2010)
Drag resistance coefficient
Cd
–
0.35
Lutsey and Sperling (2005)
Relative vehicle velocityc
vr
m/s
0–27.8
Taking into account the wind
Vehicle velocityc
vv
m/s
0–27.8
No effective wind
Mass correction factor for rotational inertia acceleration
Ci
–
1.05
Burgess and Choi (2003)
Rate of deceleration/accelerationc
a
m/s2
0–2.5
Path radius from centre of gravity
R
m
999,999
No cornering forces
Total cornering stiffness
Cav
kN/rad
999,999
No cornering forces
Distance application forcec
d
m
0–192.2
Engine efficiency
ηmotor
–
0.27–0.40
Ang-Olson and Schroeer (2002), Orasch and Wirl (1997) Ruzzenenti and Basosi (2009) Saricks et al. (2003)
Wind exposure
ev
–
1.0
No effective wind
Using the equation of energy consumption, we can estimate the amount of energy units consumed per vehicle kilometer travelled (MJ/veh-km) by different vehicle categories, fuel sources and toll scenarios. According to different studies, the engine efficiency is 0.27 for gasoline engines and 0.4 for Otto diesel ones (Table 1). In this paper, vehicles are generally classified into four categories: passenger cars, vans, tourist coaches and articulated trucks. Each vehicle category has individual average vehicle mass (m, kg) and frontal area (Af, m2). The configurations of researched vehicles are shown in Table 1.
The aim of this paper is to compare the influence of toll systems applied on highways, on vehicle energy consumption and CO2 emissions. To reach this objective, different case scenarios related to different toll systems are set. For all the scenarios, the area of modeling includes a 316–347 m road section and the tolling station is located roughly in the middle. Table 2 shows the assumptions for each scenario. In case B, a 3-min-pause at the toll was assumed, for people to pay fees and communicate with the toll staff. As in case C, because of the adopting of Electronic toll collection (ETC) technology, commuters just have to slow down their cars to a certain speed (8.3 m/s) for tolling instead of completely stop the vehicle. The section total length differs between scenarios because of different deceleration and acceleration distances. These distances are bigger in case scenario B than in scenario C; in the later case, the vehicle does not stop totally at the toll station. We can consider the distance of case scenario A equal to the distance of scenario B. However and according to model equation (1), the length of road section does not influence the results on energy consumption rates expressed in mega-joules per vehicle kilometer. Effective distances travelled are both in the numerator and denominator of model equation (1). In scenarios B and C, acceleration and deceleration energy consumption, before and after passing by the toll station, are taken into account. In all scenarios we consider no traffic congestion.
Scenario/toll system
Driving condition
Case A
Free flow: vehicles pass toll without stop
Constant velocity: 27.8 m/s
Distance travelled: 346.5 m
dec
acc
Units
Case B
Traditional toll: vehicles pass toll with a 3 min stop.a There are three steps of the procedure: deceleration (dec) – stop – acceleration (acc)
dec/acc
2.0
2.5
m/s2
Initial velocity vi
27.8
0.0
m/s
Final velocity vf
0.0
27.8
m/s
Distance travelled
192.2
154.3
m
Case C
Electronic toll collection (ETC): vehicles slows down to pass the toll system, without stop. There are two steps of the procedure: deceleration (dec) – acceleration (acc)
dec/acc
2.0
2.5
m/s2
Initial velocity vi
27.8
8.3
m/s
Final velocity vf
8.3
27.8
m/s
Distance travelled
175.5
140.4
m
2.3 CO2 emissions and traffic measurements
The CO2 emissions are estimated from the energy consumption through the carbon emission factor (CEF). According to ADEME (2007), the grams of CO2 emitted per mega-joule of energy (g CO2/MJ) are 81 and 86 for diesel and gasoline fuels, respectively. Therefore, the carbon emission of a vehicle type i (passenger cars, vans, coaches, articulated trucks) and motor technology j (gasoline and diesel) can be expressed, in grams of CO2 equivalent per vehicle-kilometer (g CO2/veh-km), as follows:
In this paper, we applied the energy and CO2 emissions model to a road section on the highway AP-41 from Toledo to Madrid (Spain) including a toll station (located at kilometer point 14.3). The section length (L) depends on the case scenario considered (Table 2). The length is 0.347 and 0.316 km, for case scenarios B and C, respectively, including the toll station roughly in the middle and connected highways on both ways. The monthly average daily traffic (MADT) of the four categories of vehicles considered at this point is given by the Spanish Road Traffic Survey (SRTS) from the Spanish Ministry of Public Works (2009a) (Table 3). The SRTS provides a comprehensive measure of the distance travelled by vehicles. Source: Spanish Road Traffic Survey, Ministry of Public Works (2009a).
Year/month
MADT (vehicles/day)
Cars
Vans
Buses
Trucks
2008 January
2005
568
170
95
February
2206
624
187
103
March
2120
598
179
93
April
2174
624
218
103
May
2064
589
206
86
June
2062
611
275
106
July
1759
573
429
102
August
1157
409
409
69
September
1837
543
244
90
October
2040
575
172
88
November
1995
562
169
84
December
1901
540
189
71
2009 January
1624
456
136
63
February
1880
530
159
81
March
1797
506
152
75
By multiplying the MADT by the CO2 emissions per vehicle-km and the section length, the daily CO2 emissions on highway AP-41 can be obtained at this section. Consequently, based on CO2 emissions, the comparison among different scenarios is made. The daily carbon emissions of a vehicle type i and motor technology j were computed using the following expression:
3 Results
3.1 Scenario analysis
The results of CO2 emissions per vehicle kilometer by vehicle and fuel categories for all three scenarios are shown in Fig. 2. Note that in case B, a 3-min-pause at the toll is included, during which the vehicles continue to burn fuel and emit CO2. For diesel and gasoline engines, the emission rate of CO2 is 0.05 and 0.06 kg/min (Fuzzi et al., 2006). As a result, the pause step in case B contributes with 0.15 kg (0.17 kg) to the total CO2 emissions.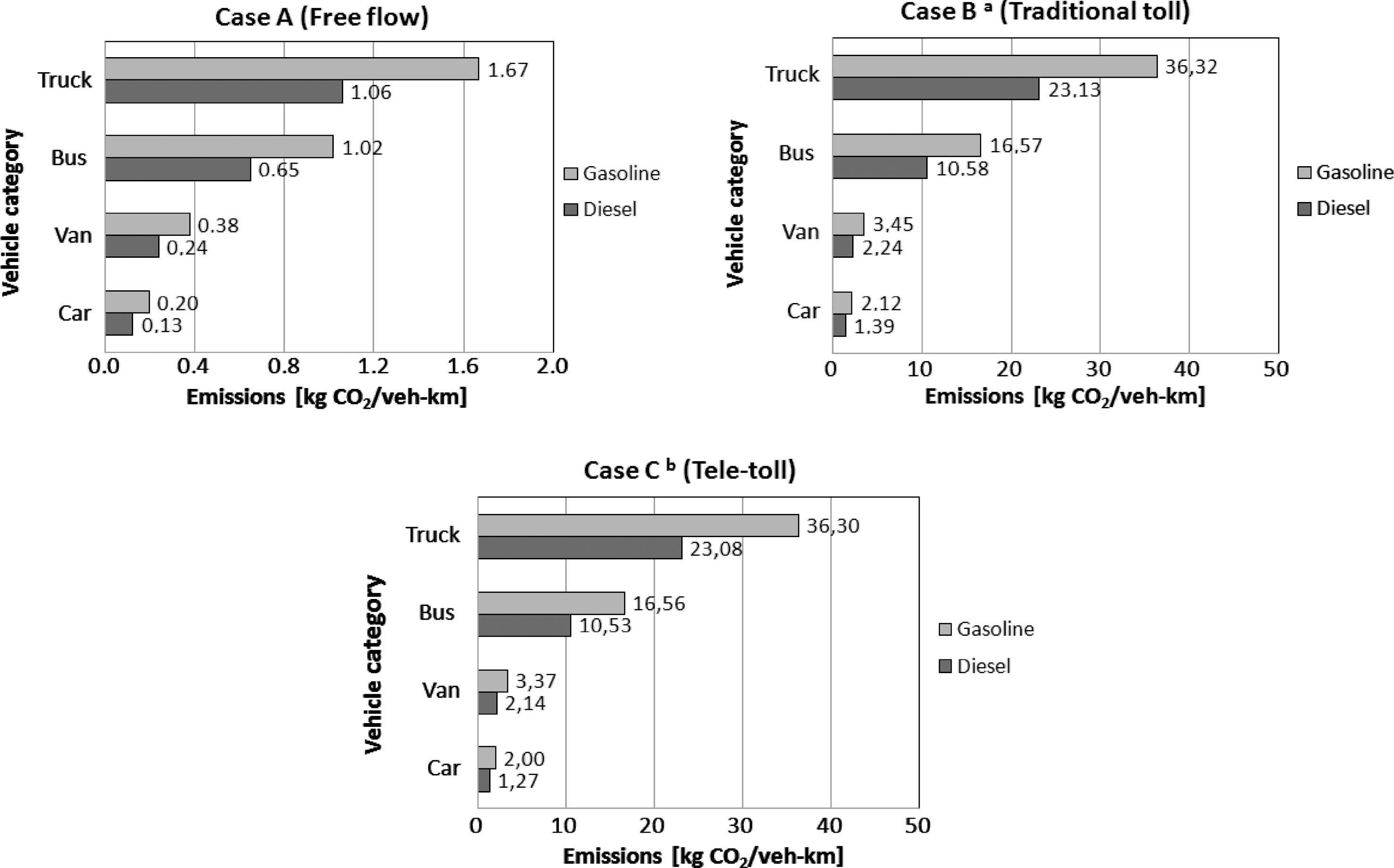
CO2 emissions per veh-km by vehicle type and engine category and case scenarios: free flow, traditional toll and tele-toll. Note: aCase B consists of three steps of vehicle movement: deceleration, stop and acceleration. Data shown in the graph are the summary of fuel consumptions of all three steps. bCase C consists of two steps of vehicle movement: deceleration and acceleration. Data shown in the graph are the summary of fuel consumptions of both two steps.
For each scenario, the comparison among different vehicles is illustrated in Fig. 2. It is evident that the vehicle mass affects CO2 emissions significantly, since heavy vehicles like articulated trucks emit 8.4 times as that of passenger cars. Besides, there are major differences between case A and case B (case B counts up to 20 times of case A), whereas case B and case C are similar. So far, there are no big advantages of using ETC toll system instead of traditional one in terms of energy consumption and CO2 emissions. In addition, the type of engine fuel (gasoline or diesel) can also influence CO2 emissions significantly, especially in articulated trucks and buses. For this reason in Spain there are only diesel trucks and buses.
Fig. 3 shows the emission share of different movement steps, namely the deceleration, stop and acceleration steps in case scenario B, and deceleration and acceleration steps in case scenario C. The main emission shares go together with the acceleration step (note the value of the labels of Fig. 3 around 90%). Also in case B, the share of the stop step decreases with the vehicle mass because it seems that heavy vehicles consume much more energy with the deceleration and acceleration steps that light vehicles, while the consumption during stop step is relatively constant.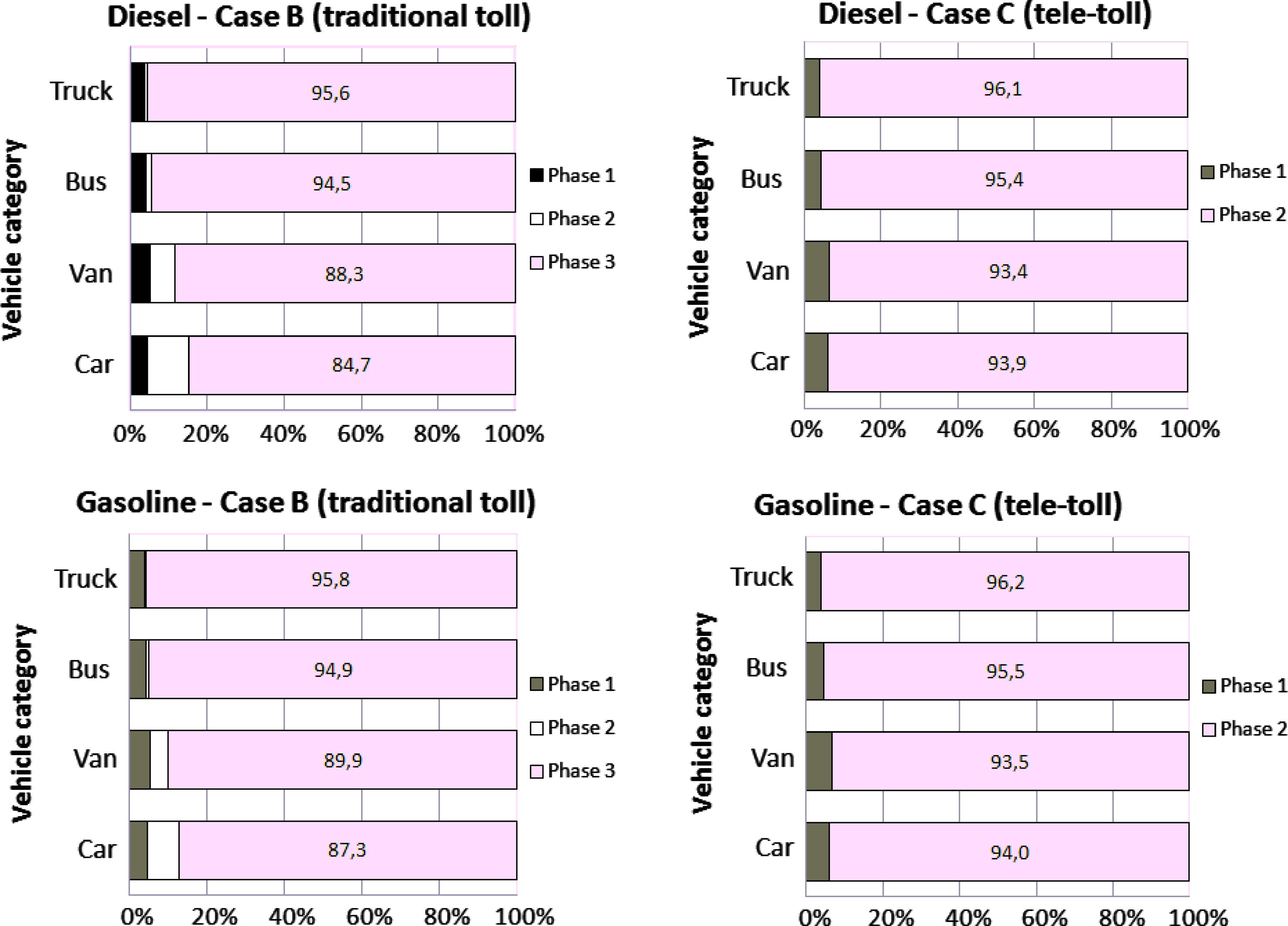
Emission percentage of each movement steps in case B and case C.
3.2 Total emission on road section of highway AP-41
By multiplying the monthly average daily traffic of vehicles (MADT) by the corresponding CO2 emission rates (Fig. 2) and the length of the section (constant equal to 0.347 km), the CO2 emissions on the road section of highway AP-41 are calculated. In the estimation of the emissions, we consider that buses and trucks use only diesel fuel. Diesel vans and cars represent, respectively, 68% and 64% of the total light vehicle traffic in Spain, according with the interurban national traffic measurements and records of fuel purchases (Perez-Martinez and Monzón, 2010). Consequently, the MADT was weighted up according to these shares and applied the respective fuel emission rates. Fig. 4 shows the amount of emissions released per day for each case scenario and vehicle category. The figure shows year-through significant differences of CO2 emissions among the three case scenarios and vehicle categories during the period January (2008) to March (2009). It is evident that either case B or case C produces much more CO2 emissions than case A in any type of vehicles, but the variation between case B and case C is much smaller, especially regarding heavy vehicles. The technology of ETC does not seem to reduce the CO2 emissions significantly, but more to shorten the time for drivers to pass the toll area. Free flow is beneficial for reducing CO2 emissions, but ETC seems of no help in this aspect.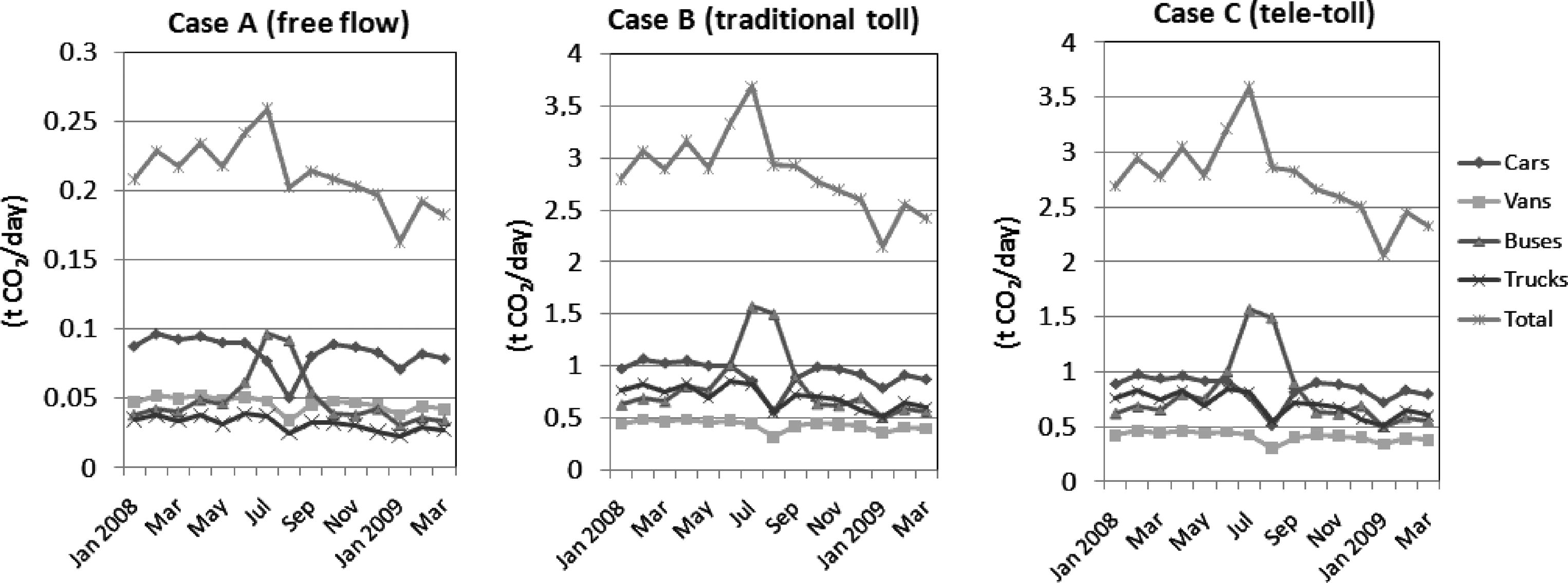
CO2 emissions per day on road section of AP-41: comparison among case scenarios and vehicle categories, January 2008–March 2009.
Across the year, passenger cars have a bigger responsibility for emitting CO2, in spite of their low CO2 emission rate per kilometer. All vehicles, except buses, present lower daily emissions during summer time; whereas buses have the highest CO2 emissions during summer time. Throughout the analyzed period, the total emissions of the vehicles present a downward trend due to the negative growth of the daily traffic between Toledo and Madrid. From May to July, more CO2 is produced due to the peak season of tourism. CO2 emissions in 2008 were estimated to be 80.1, 1087.7 and 1049.3 tones under cases A, B and C, respectively. Throughout the year, cases B and C emit more than 13 times of the emission under free flow. Based on the data in case B, the difference between A and B is 93% while the difference between B and C only accounts to 4%, which further weakened the importance of ETC technologies in highways.
4 Sensitivity analyses
The energy consumption rates and consequent CO2 emission rates presented in this study correspond to a special case study, and may therefore be different in other cases. The most relevant contribution of this work is not the results per se, but rather the equation used to calculate them. This equation makes it possible to estimate the sensitivity of energy consumption to different factors and underlying parameters (i.e. vehicle real mass, vehicle frontal section) to explain the differences between categories of vehicles and case scenarios. The study of sensitivity of parameters in the mechanical equation is to find out which factor is the most influential to the energy consumption, as well as to the CO2 emissions. These parameters determine the market niches and sources of improvement in energy consumption (Perez-Martinez and Sorba, 2010). Sensitivity analyses were performed to passenger gasoline cars under the scenario case B, traditional toll system, using the parameters set in Table 4. After performing sensitivity analysis of the energy consumption estimates, it is concluded that the parameters included in Table 4 are the most representative parameters, within the whole set of parameters in the energy consumption equation (1), and their break-even values significantly affect the final outcome. Finally, Table 5 shows the respective influence of each group o external forces (coming from Eq. (2)) on total energy consumption and subsequent CO2 emissions. Inertial acceleration forces constitute the most of energy consumption. In the estimation, we consider no cornering and gravitational forces due to the location of the toll station.
Parameter
Symbol
Unit measure
Valuea
Rolling resistance coefficient
Cr
–
0.01
Vehicle mass
m
kg
2100
Gravitational constant
g
m/s2
9.81
Angle ascent/descent with respect to the ground level
θ
rad
0
Density air
ρ
kg/m3
1225
Frontal area
Af
m2
2.52
Drag resistance coefficient
Cd
–
0.35
Relative vehicle velocity
vr
m/s
13.89
Mass correction factor for rotational inertia acceleration
Ci
–
1.05
Rate of acceleration
a
m/s2
2.5
Vehicle velocity
vv
m/s
13.89
Path radius from centre of gravity
R
m
109
Total cornering stiffness
Cav
kN/rad
109
Engine efficiency
ηmotor
–
0.27
Wind exposure factor
ev
–
1
Parameter
Symbol
Unit measure
Value
Rolling resistance
Ur
MJ/veh-km
0.21
Cornering forces at the tires
Uc
MJ/veh-km
0
Aerodynamics drag resistance
Ua
MJ/veh-km
0.11
Inertial acceleration forces
Ui
MJ/veh-km
5.51
Gravitational losses
Ug
MJ/veh-km
0
Energy consumption (total)
U
MJ/veh-km
21.57
CO2 emission
C
kg CO2/veh-km
1.85
4.1 Road slope, wind exposure factor and parameters depending on service type
This paper shows that energy consumption is most sensitive to slope (Fig. 5). Increasing road slope by 10%, the energy demand increased significantly from 21.56 to 29.18 MJ/veh-km (35%, Fig. 5), as vehicles consume more energy on unfavorable slopes during the acceleration phase under the case study B. While it is critical to vehicle fuel consumption and CO2 emissions, the slope of road seems unlikely to change. Topography, construction and economy have to be considered in building a highway, which sometimes make the chosen of steep slope inevitable. However, tolls are located in segments of highways with small slopes and curves.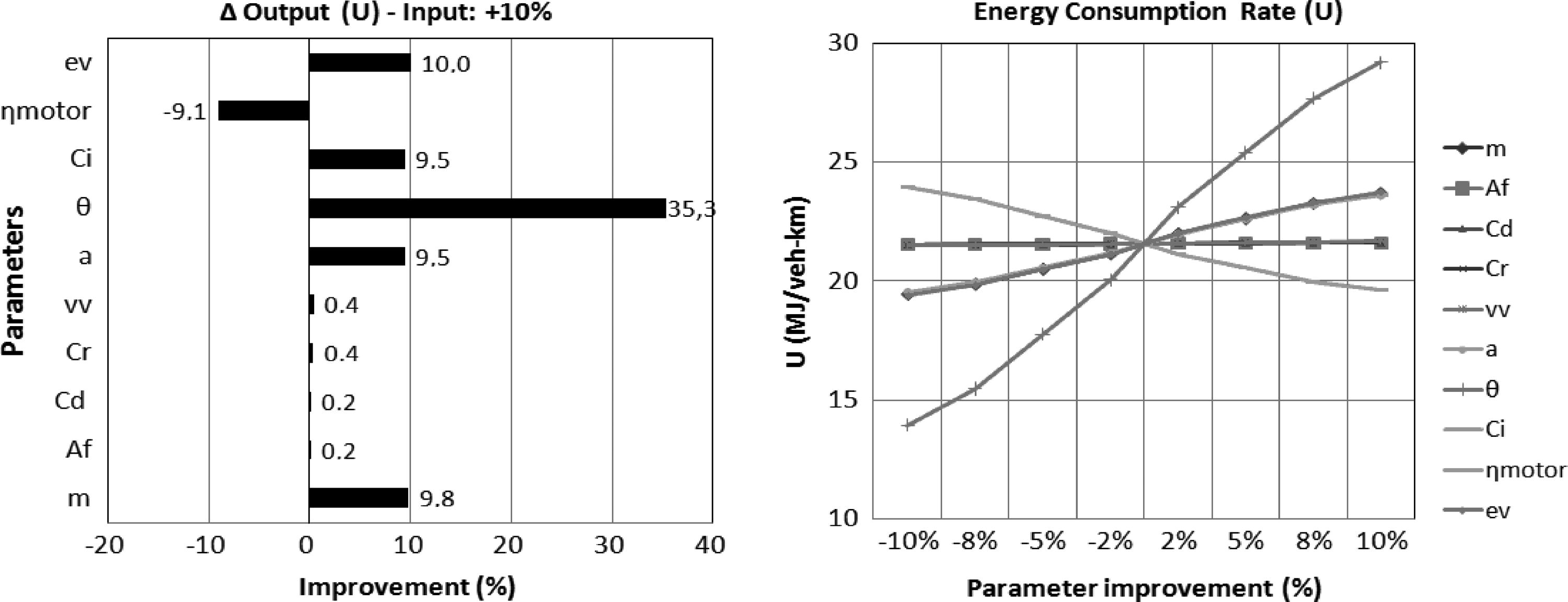
Sensitivity analyses: energy consumption and CO2 emissions of gasoline cars upon parameter changes and under case B scenario. Note: Case B consists of three steps of vehicle movement: deceleration, stop and acceleration.
Wind exposure factor (ev) is the second most influential parameter concerning vehicle energy consumption (Fig. 5). A 10% reduction in ev can decrease total energy demand by 10%. While in the scenarios of this paper the ev is set to 1.0 to ignore its effect, it is influential either positively or negatively to the energy consumption in many practical situations. If the wind is from the backside of vehicles, the ev parameter is below 1.0 to consider wind push during cruising. In contrast, vehicles suffer from wind resistance when driving toward the wind direction. Fig. 1 shows the annual wind distribution of Madrid and map of highway AP-41. From the figure, it is obvious that either driving from Madrid to Toledo or reversely, wind effect is considerable, since the annual wind direction is N/NNE–SW/SSW, same as the general direction of highway AP-41.
Mass correction factor for rotational inertia acceleration (Ci) and acceleration rate (a) contribute to the inertial resistance (Ui) when vehicle is accelerating. In the scenarios discussed in this paper, namely case B and case C, vehicles are assumed to decelerate (to 0 or to a low speed) and then accelerate. Therefore, the fuel consumed by rotational inertia acceleration is remarkable. A 10% reduction in Ci and a can decrease total energy demand by 9.5%.
The average vehicle speed (vv) is not as detrimental factor as ev and a even though to the square effect on the aerodynamic drag and the kinetic energy losses. The sensitivity analyses in this paper show that a 10% reduction in the average vehicle speed can decrease total energy demand by only 0.3%. In this case, kinetic energy losses are more dependent on parameters such as, vehicle acceleration a, engine size and vehicle mass (m). Other factors involved in this case study include traffic conditions at the toll station, the number of stops during the phase 2, driver behavior, braking coefficient and highway profile (i.e. presence or absence of slope at the station). This range of factors, some of them depending directly on service type, makes it difficult to model fuel efficiency on a per-vehicle basis due to the great amount of variables involved in the calculations. In this study we consider acceleration–deceleration rates according to the gear used and for all vehicle types (Table 2). In general, reducing the number of stops can decrease inertial acceleration losses. In this regard, case study B (traditional toll) makes more stops than alternative toll systems (free flow and ETC), and consume more energy due to inertial losses.
4.2 Parameters not depending on service type
Vehicle mass (m) is one of the most significant parameters affecting the energy demand of a vehicle, since energy demand is directly proportional to rolling resistance (Ur), inertial acceleration resistance (Ui) and gravitational losses (Ug), and indirectly proportional to cornering resistance (Uc) according to Eq. (1). Therefore, reducing the vehicle real mass is one of the most effective ways of decreasing the energy demand of passenger land transport modes. By reducing mass by 10%, using lighter construction components, the vehicle energy consumption would decrease by 9.8%, as shown in Fig. 5. Despite the importance of mass on energy consumption, cars have actually been increasing in mass in the last few years due to several factors such as improved safety, pollution control devices and additional auxiliary services (i.e. air conditioning, electronic windows and mirrors, etc.) (Van den Brink and Van Wee, 2001; Van Wee et al., 2005). In the future, the ways of producing new materials with high strength to mass ratio can be useful for reducing vehicle weight.
Apart from the deceleration and acceleration processes, other parameters show sensitivity to energy consumption in a constant speed cruising. Losses due to rolling resistance are proportional to the friction coefficient of the tires (Cr). A 10% reduction in rolling resistance coefficient could reduce energy demand by 0.4%. Similarly, the main factors affecting aerodynamic losses are the aerodynamic drag resistance (Cd) and the vehicle frontal area (Af). A 10% reduction in drag resistance coefficient and frontal area could reduce energy demand by 0.2%. The frontal area of the vehicle is bigger in collective transport modes than in private cars and measures the space available inside the car (Table 1). The frontal area has increased in recent years, especially in private cars, due to consumer demand for greater comfort (Van den Brink and Van Wee, 2001; Advenier et al., 2002). Conversely, the aerodynamic drag resistance coefficient has decreased in all systems due to better design parameters, and this has a major influence on energy consumption, particularly in windy conditions.
4.3 Engine efficiency
In Fig. 5, engine efficiency (ηmotor) is the only parameter inverse-proportional to the energy consumption. This is because the improvement of engine efficiency would actually cut down energy wasted, thus decreases the total energy demand. According to heat engine theory, modern gasoline engine has an average efficiency of about 30%, because most of the energy produced is consumed by friction, mechanical sound and turbulence. In the scenarios set in this paper, the ηmotor is even lower; since at slow speed the efficiency is lower than average, due to a larger percentage of the available heat being absorbed by the metal parts of the engine, instead of being used to perform useful work. In this sensitivity analyses, if the ηmotor is improved by 10%, the energy consumption could be reduced by 11%. However, the raise of engine efficiency has been a problem to engineers for years, which is depending on varied factors such as compression ratio, oxygen, fuel quality and manufacturing level. Future improvement could be aiming on new engine technologies and better fuels (Kaul and Edinger, 2004; Niedzballa and Schmitt, 2001).
The final result of Fig. 5 is a combination of total “tank to wheel” energy and associated CO2 emissions. We must add to these values the energy losses and emissions that occur between the primary sources and the vehicle (“well to tank”). In the case of gasoline oil in Spain these losses are significant and are around 19%. The calculation of energy losses and emissions before reaching the vehicle for different fuel used in transport and in the local circumstances of Spain can be seen in López Martínez et al. (2008).
4.4 Uncertainty of estimates
The traffic measurements and the energy consumption and emission rates calculated using model from Eq. (4) are subject to uncertainties mainly because of traffic measuring errors, speed distribution, fleet composition and road gradient. Kühlwein and Friedrich (2005) performed a detailed error analysis to quantify the margins of error of the traffic-related input parameters on the total energy consumption and CO2 emissions in a German highway. These authors estimated that total traffic flow data are subject to a variation coefficient (VC) of less than 1% for automatic counting results and their effects on the energy consumption and CO2 emission rates were quantified to be less than 1.2%. Similarly, the effects of speed distribution, fleet composition and road gradient were quantified to range from 0.2% to 5%. Total error of the energy consumption and CO2 emission rates can be estimated from the quantified uncertainties of the traffic-related model input parameters from the sum of effects of the individual single errors on the total emission. In our case study, automatic counting of traffic flows on a highway segment with no slope, the mean total error could be in the range of 7.5–10%, mainly due to fleet composition and simplification of model to only four types of vehicles (cars, vans, buses and trucks).
5 Estimation of the potential energy savings and CO2 emissions in the Spanish toll network
Fig. 6 shows the evolution of the traffic in the toll highways in Spain during the period 1990–2008 (Ministry of Public Works, 2009b). The traffic demand has increased from 9466 million veh-km in 1990 to 23,793 million veh-km in 2008. The increase in traffic demand is due to the enlargement of the toll road network that has been developed during this period. The Spanish interurban toll network has increased from 1895 km in 1990 to 2928 km in 2008 including all types of concessions and ownerships (Regional Authorities and State Highways). Road transport in toll highways has experienced higher growth during the period 1996–2002, due to the new registered motor vehicles and increasing average annual daily traffic (AADT). The AADT has increased from 13,685 vehicles/day in 1990 to 22,263 vehicles/day (19,258 light vehicles and 3005 heavy vehicles) in 2008, at an annual rate of 3.5%. In 2008, toll highway transport represented 9.5% of veh-km of the total interurban road transport in Spain, registering an annual growth of 8.4%.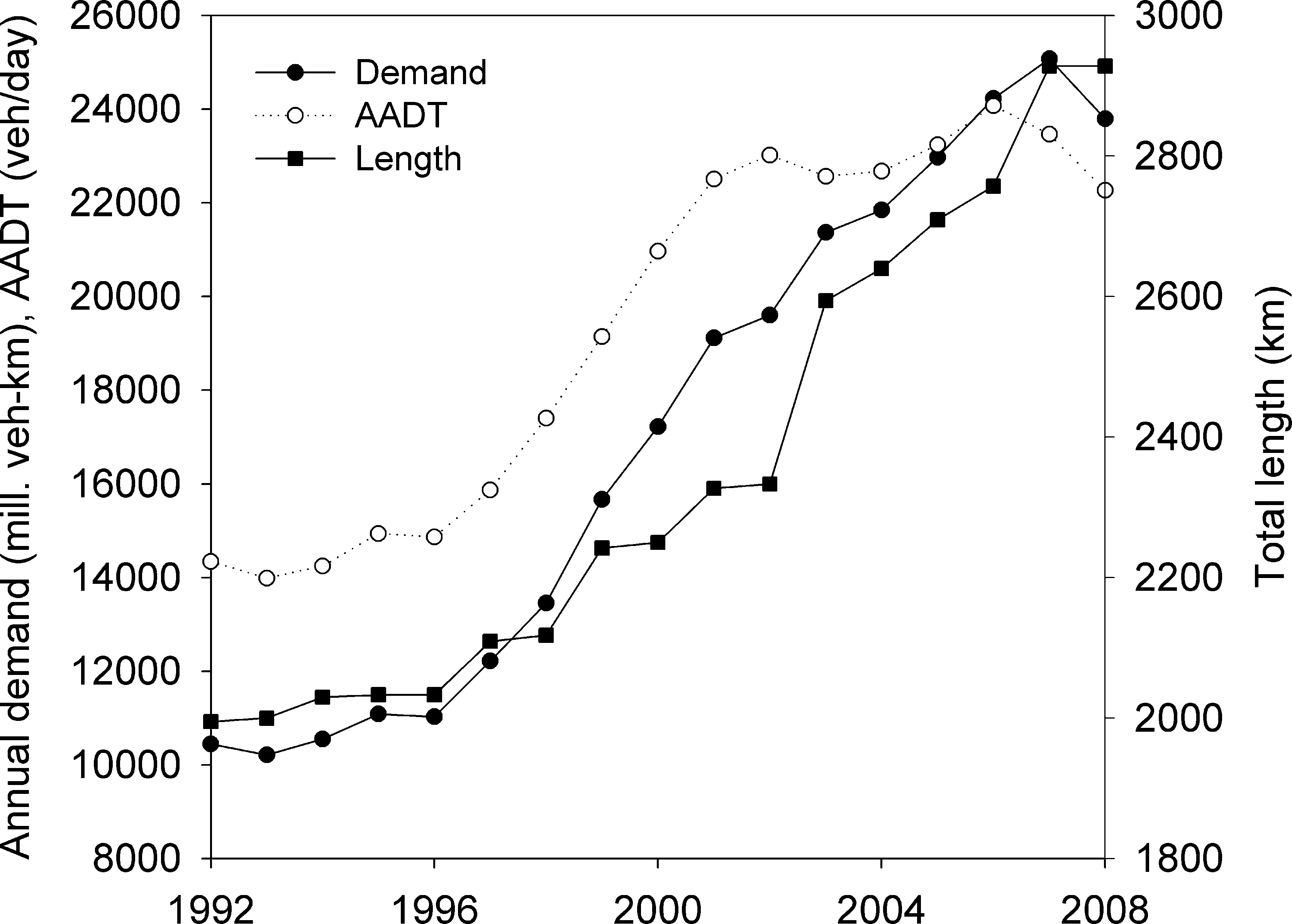
Trends in the traffic of toll highways and tunnels in Spain. Source: Transport and Postal Services, Ministry of Public Works (2009b).
To estimate the potential energy savings and consequent CO2 emissions in the Spanish toll network from changing the traditional toll system (scenario B) to free-flow (scenario A), we consider the annual savings of the case study of this paper. In 2008, 1007.7 tones of CO2 (difference of the case scenario B emissions, 1087.8 tones of CO2 and A, 80.1 tones of CO2) could have been saved by changing the toll system. Knowing that the annual traffic of AP-41 at the toll station, 0.36 million veh-km, we divide the annual potential CO2 savings by the annual traffic, giving an emission saving rate of 2809.4 g CO2/veh-km.
In 2008, the Spanish toll network has 8.13 million veh/year. Considering the length of the network, 2928 km, and a separation of 30 km between toll stations, we have around 100 stations in the network. Assuming an average length of the toll stations of 350 m, we calculate the annual traffic demand in the toll stations, 284.4 million veh-km (1.2% total traffic of the toll network), by multiplying the vehicles per day by the length and the number of the stations. Finally, using the former emission saving rate to the Spanish toll network, we can estimate the amount of CO2 emissions potential savings and energy consumption. In 2008, around 0.8 million of tones of CO2 equivalent (representing 1.1% of total interurban road transport emissions and energy consumption), 11,530 terajoules (TJ), could have been saved by changing the management of tolls. This value represents a significant amount considering that toll road transport constitutes a small share of the total interurban road transport in Spain (around 10%) and traffic at toll stations constitutes only 1.2% of the total vehicles kilometer travelled in the toll network.
The importance of the right management of toll stations in the overall energy consumption and CO2 emissions is due to big differences in the energy consumption and emissions rates of the different toll scenarios. The factor of 10 that we got from the results is a good estimate of the toll system management effect on energy consumption and associated CO2 emissions. This factor explains why the effects calculated on this short portion of highways (350 m) are very high (more than 1000% CO2 as difference between scenario A and B-C).
6 Conclusions and research needs
The energy consumption and CO2 emissions of a toll station on highway AP-41 in Spain have been modeled and the parameter sensitivity study has been performed. In the study, different vehicle categories and toll scenarios have been assumed. Results in scenarios show that parameters such as gradient of the road, wind exposure, vehicle mass, mass correction factor for rotational inertia acceleration, acceleration and engine efficiency have a major impact on energy consumption. Notably, the road slope around the toll station, 150 m of road section on both sides, is critical since it has a great influence on the acceleration of vehicles. A good correlation was found between energy consumption and vehicle mass for heavy vehicles, and especially for trucks. A combination of light vehicles, with low rolling and drag coefficients, constant speed profiles and no stops, leads to lower energy consumption and CO2 emissions per vehicle kilometer.
In the comparison among different toll scenarios settings, the advantage of ETC (which enables vehicles to speed down for tolling instead of completely stop) was found quite small in contrast with the great difference between free-flow system and traditional toll system. The energy consumption as well as CO2 emissions in a free-flow scenario is only 7.4% of that in traditional scenario, while an adoption of ETC only reduces 4% of CO2 emissions from the traditional ones. The weakest link between CO2 emissions, vehicle type and toll management system was found for diesel cars in free flow services (0.13 kg CO2 equiv./veh-km). Conversely, the strongest link between CO2 emissions, vehicle type and toll system was found for trucks in both traditional toll (36.32 kg CO2 equiv./veh-km) and tele-toll systems (36.30 kg CO2 equiv./veh-km).
In this case study, around 1000 tons of CO2 could have been saved annually by changing the toll system, from traditional toll to free flow, giving an emission saving rate of 2809 g CO2/veh-km. Using this emission saving rate, we can roughly estimate the potential savings in the Spanish toll network (0.8 million of tones, 11,539 TJ). However, the emission saving rate depends on toll service type, fleet composition and other variables related to driving conditions, making it difficult to model fuel and emissions savings on a per-vehicle basis. Consequently, the saving value presented in this paper is subject to uncertainty and must be considered as a relative estimation. Further development of the comparison of the energy consumption and CO2 emissions of vehicles per travelled kilometer would require a discussion of capacities and actual use of the energy consumption and CO2 emissions model. The energy consumption and CO2 emissions models presented in this study are for use in any form of analysis for the purpose of reaching decisions about journeys, highway transport infrastructure or modal choice preferences.
The use of an energy consumption mechanical model enables evaluation of the energy consumption impacts of new policy measures regarding road infrastructure and modal tolling, and permits the differential reasons to be identified. The model is important for enabling a better understanding of, and thus an improvement in, energy consumption and subsequent CO2 emissions. Energy consumption and CO2 estimations derived with this model can be used as reference levels for adjusting different toll systems in order to encourage energy and environmental efficiencies. Further tests are required to ensure better calibration of the model based on energy empirical data under different toll service types and fleet composition.
From the main results of the study, we cannot assume that detailed mechanical engineering models are better suited to policy analysis and forecasting. The proposed methodology, broken down into the modes and toll management systems currently in use, is valid for current vehicle and toll technologies, although it has limitations in forecasting and analyzing any new vehicles and toll systems that may be developed. At a more detailed level, demographics, working hours, etc., could have stronger impacts in the future than the efficiency differential between vehicles and toll management systems. In this case, the differential efficiencies between vehicles and toll systems determine only part of energy conservation due to the rebound effect, which is particularly relevant in transport. The crucial question from the perspective of energy policy – namely, how to move from one mode to another and from one toll system to another – lies beyond the scope of this paper.
Acknowledgements
The authors are grateful to the financial support provided by CENIT/OASIS Project of the Ministry of Science and Technology, Government of Spain, Madrid to undertake this work. The contribution of anonymous reviewers is gratefully acknowledged.
References
- ADEME, 2007. Bilan Carbone Enterprises et Collectivités – Guide des facteurs d’émissions Version 5.0. Calcul des facteurs d’émissions et sources bibliographiques utilisées. <http://www.ww2.ademe.fr/>.
- Energy consumption and CO2 emissions of road transportation: comparative analysis of technologies and fuels. Energy and Environment. 2002;13(4–5):631-646.
- [Google Scholar]
- Energy efficiency strategies for freight trucking. Potential impact on fuel use and greenhouse gas emissions. Transportation Research Record. 2002;1815:11-18.
- [Google Scholar]
- A parametric study of the energy demands of car transportation: a case study of two competing commuter routes in the UK. Transportation Research Part D. 2003;8:21-36.
- [Google Scholar]
- Fuzzi, F., Cocco, I., Bassoli, N., Grassi, A., 2006. L’inquinamento alle code dei caselli autostradali. Università di Bologna.
- Efficiency versus cost of alternative fuels from renewable resources: outlining decision parameters. Energy Policy. 2004;32(7):929-935.
- [Google Scholar]
- Traffic measurements and high-performance modelling of motorway emission rates. Atmospheric Environment. 2005;39:5722-5736.
- [Google Scholar]
- Options for improving the energy efficiency of intermodal freight trains. Transportation Research Record. 2005;1916:47-55.
- [Google Scholar]
- López Martínez, J.M., Sánchez Alejo, J., Gómez, A., Fernández, A., 2008. Flujos del petróleo y del gas natural para el transporte. Monografías EnerTrans/8. Fundación Española Ferrocarriles, Madrid.
- Energy efficiency, fuel economy, and policy implications. Transportation Research Record. 2005;1941:8-17.
- [Google Scholar]
- Ministry of Public Works, 2009a. Spanish Road Traffic Survey. Madrid.
- Ministry of Public Works, 2009b. Transport and Postal Services. Madrid.
- Comparison of the specific energy demand of aeroplanes and other vehicle systems. Aircraft Design. 2001;4(4):163-178.
- [Google Scholar]
- Technological efficiency and the demand for energy (road transport) Energy Policy. 1997;25:1129-1136.
- [Google Scholar]
- Perez-Martinez, P.J., Monzón, A., 2010. Transport Energy Use and Emission Trends in Spain.
- Energy consumption of passenger land transport modes. Energy and Environment. 2010;21(6):577-600.
- [Google Scholar]
- Evaluation of the energy efficiency evolution in the European road freight transport sector. Energy Policy. 2009;37:4079-4085.
- [Google Scholar]
- Fuel consumption of heavy duty trucks: potential effect of future technologies for improving energy efficiency and emissions. Transportation Research Record. 2003;1842:9-19.
- [Google Scholar]
- Why has car-fleet specific fuel consumption not shown any decrease since 1990? Quantitative analysis of the Dutch passenger car-fleet specific fuel consumption. Transportation Research Part D. 2001;6:75-93.
- [Google Scholar]
- Comparing energy use and environmental performance of land transport modes. Transport Reviews. 2005;25(1):3-24.
- [Google Scholar]
- Validation of road transport statistics through energy efficiency calculations. Energy. 2001;26:467-491.
- [Google Scholar]
Web references
- <http://www.volvo.com/trucks/italy-market/it-it/trucks/Volvo-FH/productPage_FH.htm> (Articulated Trucks).







