Evaluation of the dosimetric characteristics of 6 MV flattened and unflattened photon beam

2.1 Monte Carlo simulations

The EGSnrc-based user codes BEAMnrc (Rogers et al., 2001) and DOSXYZnrc (Walters et al., 2005) have been used to perform the simulation of 6 MV with and without flattening filter photon beams.

BEAMnrc user code was used to model the linac’s head and to simulate the photon beams. The phase space files, that were located at Z = 100 cm from the target, were generated.

Variance reduction techniques were applied: as the photon and electron cut-off energies were set to 10 keV (PCUT) and 711 keV (ECUT), respectively. Electron range rejection was set to 1 MeV (ESAVE). The threshold for secondary particle production was set to ECUT for charged particles and PCUT for photons. Directional bremsstrahlung splitting (DBS) was used with a splitting number of 100, SSD = 100, field size = 10 and Russian roulette turned off. EGSnrc parameters were set as default. For all simulations 6 × 10⁶ histories were run.

Secondly, the dose distributions were calculated by DOSXYZ user code in a homogenous water phantom, placed at 100 cm from the target, of 40 × 40 × 40 cm³. Non-uniform voxels have been defined. In this step a phase space file which is generated by BEAMnrc user code, and fixed at the isocentre level, will be used as a source of particles in DOSXYZ.

EGSnrc parameters were set as default. Electron range rejection was set to 1 MeV (ESAVE). A 4 × 10⁸ histories were used for each simulation.

Other beam characteristics such as mean energy, energy spectra, distribution angular and others, were obtained when phase space files were analyzed by BEAMDP (Ma and Rogers, 2004) user code.

2.2 Monte Carlo validation

Before studying the dosimetric properties of both flattened and unflattened photon beams, the optimum parameters of the incident electron must be selected, such as mean energy and beam width. For this purpose, the dose distribution (percentage depth dose (PDD) and beam profile) was calculated and compared to the experimental data, using gamma index criteria. The simulations were carried out for square field sizes of 3 × 3, 10 × 10 and 20 × 20 cm² in a homogenous water phantom of 40 × 40 × 40 cm³, which were recommended from the manufacturer, placed at SSD = 100 cm.

2.3 Dosimetric proprieties calculations

After selecting the optimum electron parameters, the characteristics of with and without flattening filter photon beams such as PDDs, beam profile and energy spectra were investigated.

2.4 Surface dose and build-up

Surface dose or skin dose is the dose calculated at the skin or the entrance of the phantom. It is still clinically important thank to the knowledge of the build-up effect which can facilitate the preservation of skin sparing or the delivery of an adequate dose to superficial target volumes (Wang et al., 2012). In our previous study for 12 MV photon beams (Maged Mohammed et al., 2015), we found that the surface dose and build-up region doses are affected by field size, energy and SSD. In this present work, the surface dose of 6MV FF and FFF configurations was evaluated for 3 × 3, 6 × 6, 15 × 15, 10 × 10 and 20 × 20 cm² open field sizes.

2.5 PDDs, d_max and dose rate

The PDDs curves for FF and FFF beams were calculated in the central axis of a homogenous water phantom. The depth of maximum dose ranges from 0 to 5 cm for orthovoltage X-ray to 25 MV photon beams (Pichandi et al., 2014). It depends on the energy and field size. The dose rate ratio of flattened and unflattened beams is calculated at a depth of 10 cm.

2.6 Beam profiles and out-of-field

Lateral beam profiles of both FF and FFF beams of different field sizes were evaluated at a depth of 10 cm. Beam profiles were normalized to the dose at central axis. The difference of out-of-field doses was calculated at 3 cm from the field edge.

3.1 MC validation

To validate the MC model, the PDDs and lateral profile curves which were calculated in a homogenous water phantom were compared with experimental data that were provided by the manufacturer. PDDs curves were normalized to maximum dose and beam profile to the dose on the central axis at 10 cm depth. The Fig. 1 shows the comparisons of dose distribution calculated and measured. For selecting the mean energy, the group with energy from 5.5 to 6.5 MeV with step of 0.1 MeV was tested on all field sizes and the beam width set to 0.2 mm.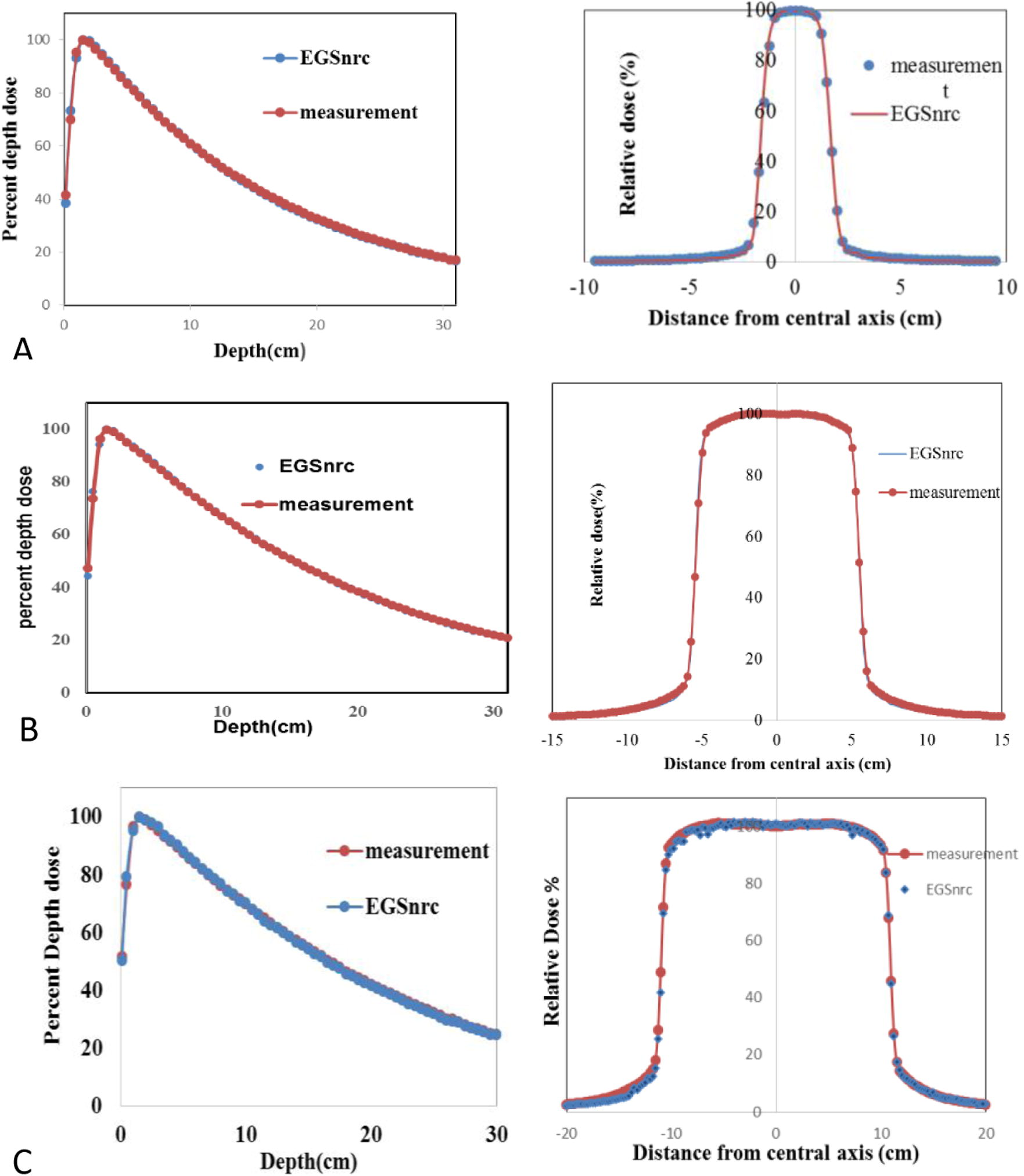

Close

Figure 1

A comparison of measured and calculated PDDs and beam profile curves of the 6 MV photon beam for: (A) 3 × 3, (B) 10 × 10 and (C) 20 × 20 cm² field sizes.

Export to PPT

After selecting the optimal mean energy value, a full width half mean (FWHM) of the electron incident from 0.1 to 3 mm with step of 0.1 mm was tested.

About 60 simulations were carried out for tuning the electrons incidents parameters, in each simulation our results were compared with experimental data using gamma index criteria. The statistical uncertainty in each simulation was less than 0.4% and it was less than 1% in out-off field dose. Depending on the Gamma index analysis, a match between measurement and simulation was found for an incident electron beam with a mean energy of 5.7 MeV and a focal spot size was 1.6 mm (FWHM). The agreement between MC calculations and measurements was within 1.5% for depth dose curves and within 2% for beam profiles. The results of the present work were compatible with the study of Hrbacek et al. (2011), Mesbahi et al. (2006) and Wiant et al. (2013).

3.2 Dose rate

The data presented in Fig.2 shows the central – axis depth absorbed-dose distribution per primary particles of both configurations of FFF and FF beams in a homogenous water phantom for 3 × 3, 6 × 6, 15 × 15, 10 × 10 and 20 × 20 cm² field sizes. The dose rate of FFF was found to be 2.46 times higher than that for the flattened beams. This value was obtained on the central axis dose at a depth 10 cm and SSD = 100 cm. The present study reports a difference less than 0.15 compared with the findings of Mesbahi (2007) and Vassiliev et al. (2006), the difference owing to the filter material. Studies have reported that the dose rate increases on the central axis by more than a factor of 2 compared to irradiation with the FF beams (Titt et al., 2006). The results reported in the present paper seem convergent with the findings of Titt et al. (2006) for a 6 MV photon beam. The increase in dose rate in FFF configuration due to the flattening filter eliminates a large part of the primary photons from the beam center, especially close to the central axis, and a greater number of primary photons will be attenuated. The increase in dose rate is one of the advantages of removing the flattening filter, this feature may offer an improvement in the treatment of cancer or this can lead to reduction in the irradiation time per treatment fraction (Titt et al., 2006). Reducing the delivery time will benefit some motion control techniques, such as breath-hold and mostly for treatment of small field sizes (Xiao et al., 2015). The higher dose rates improve treatment delivery efficiency and there are no radiobiological correction factors that need to be considered when using unflattened beams (Georg et al., 2011). Previous studies report usefulness of FFF beams compared with FF beams but caution is needed for accurate measurements and better planning to protect the cells health.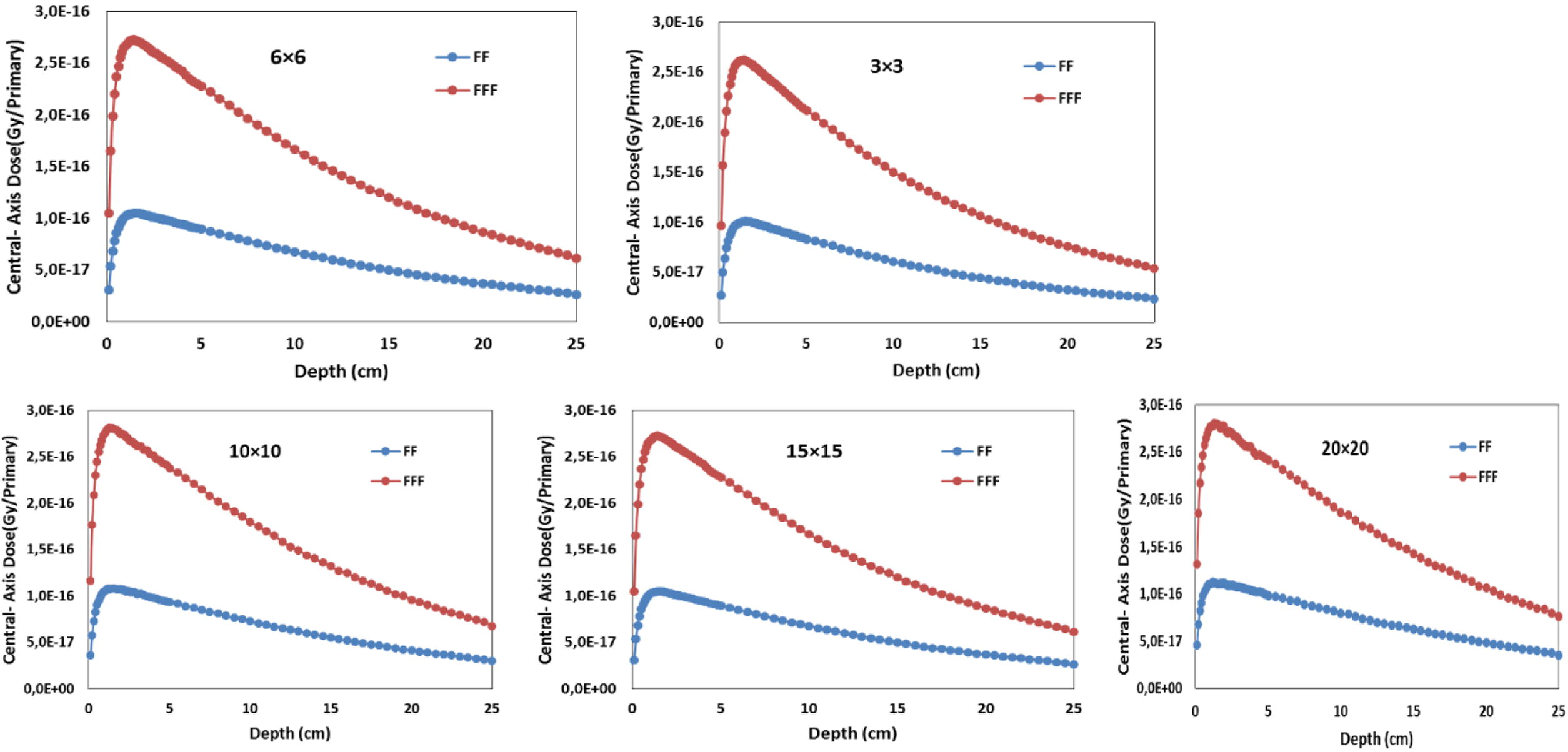

Close

Figure 2

Comparisons of the central axis depth dose per primary particles of FF and FFF beams for 3 × 3, 6 × 6, 15 × 15, 10 × 10 and 20 × 20 cm² field sizes.

Export to PPT

3.3 PDDs at the central axis

The percentage depth dose curves, of both configurations FF and FFF were calculated on the central axis of a homogenous water phantom placed at 100 cm from the source. The Fig. 3 illustrates the simulation results obtained for open field sizes from 3 × 3 to 20 × 20 cm². It can be seen that after the maximum dose, unflattening beams have a steep downward movement with depth compared to flattened beams. Due to the softness energy spectrum, we found that a large part of FFF beams energy was deposited to a build-up region compared to the depth more than d_max. Through Fig. 3, it can be seen that the spacing between two curves increases with field size. This effect quantified by using the ratio of the dose in 20 cm to 10 cm depth (D₂₀/D₁₀). This ratio is summarized in Table 1 and, it was consistent with that reported by Kragl et al. (2009) in this work, we found that the unflattened beam energy of 10 × 10 cm² field size (%dd at 10 cm) decreased from 67.4% to 63.7%. Vassiliev et al. (2006) found that PDD of unflattened 6 MV beams was corresponding to standard 4 MV beams.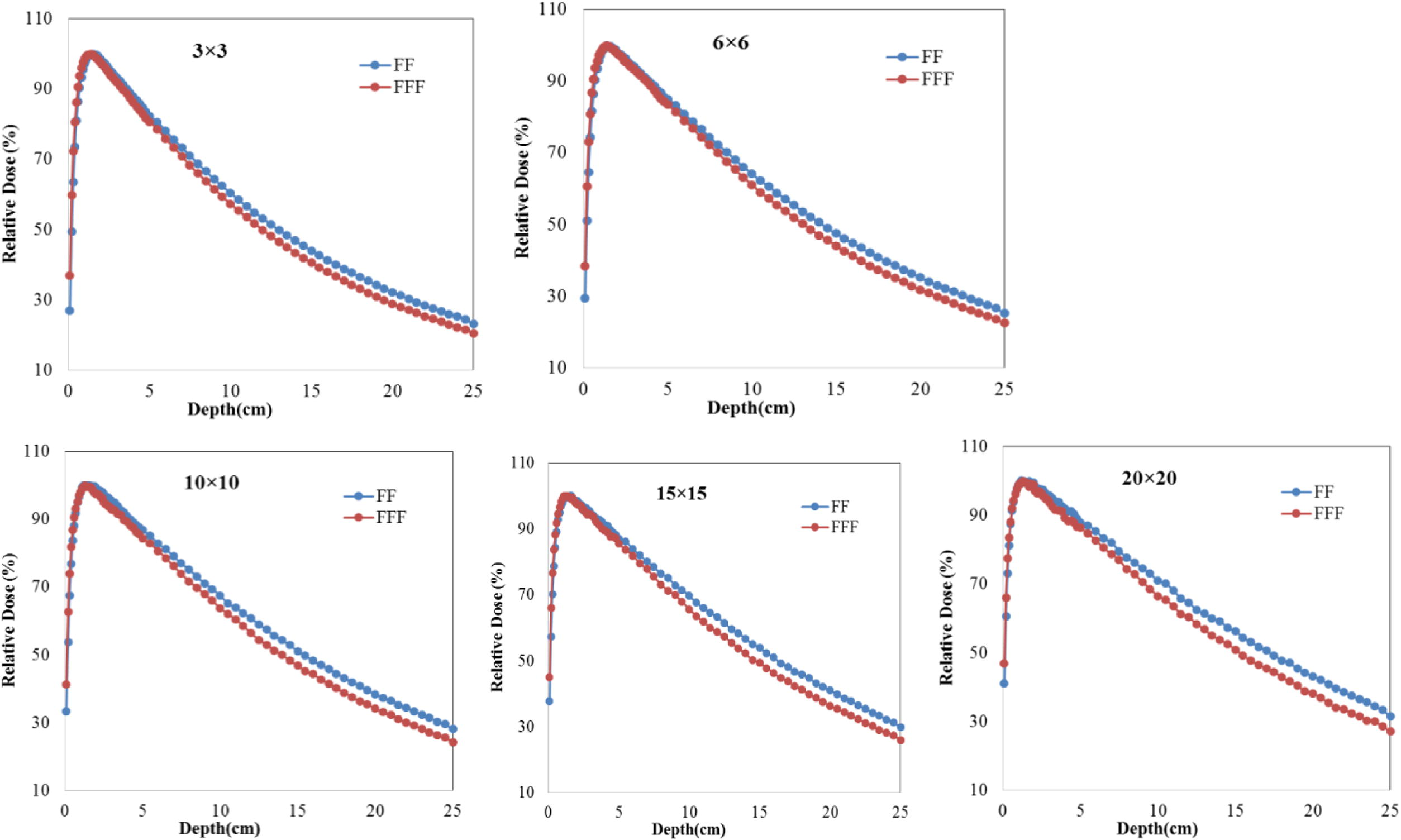

Close

Figure 3

Percentage depth doses of the unflattened and flattened photon beams by measurements and Monte Carlo simulations in water phantom for 3 × 3, 6 × 6, 15 × 15, 10 × 10 and 20 × 20 cm² field sizes.

Export to PPT

Analyzing the phase space files of both FF and FFF beams shows that the number of electrons in FFF phase space was more than twice of FF one. The replacement of the air column, under the jaws to the phantom surface, by helium leads to the reduction of the electron contamination due to many of the electrons created when the radiation interacts with the air molecules. In FFF simulation case, the same number of electrons was recorded compared to standard flattened beams when the simulations were carried out with helium molecules.

3.4 Surface dose and build-up region

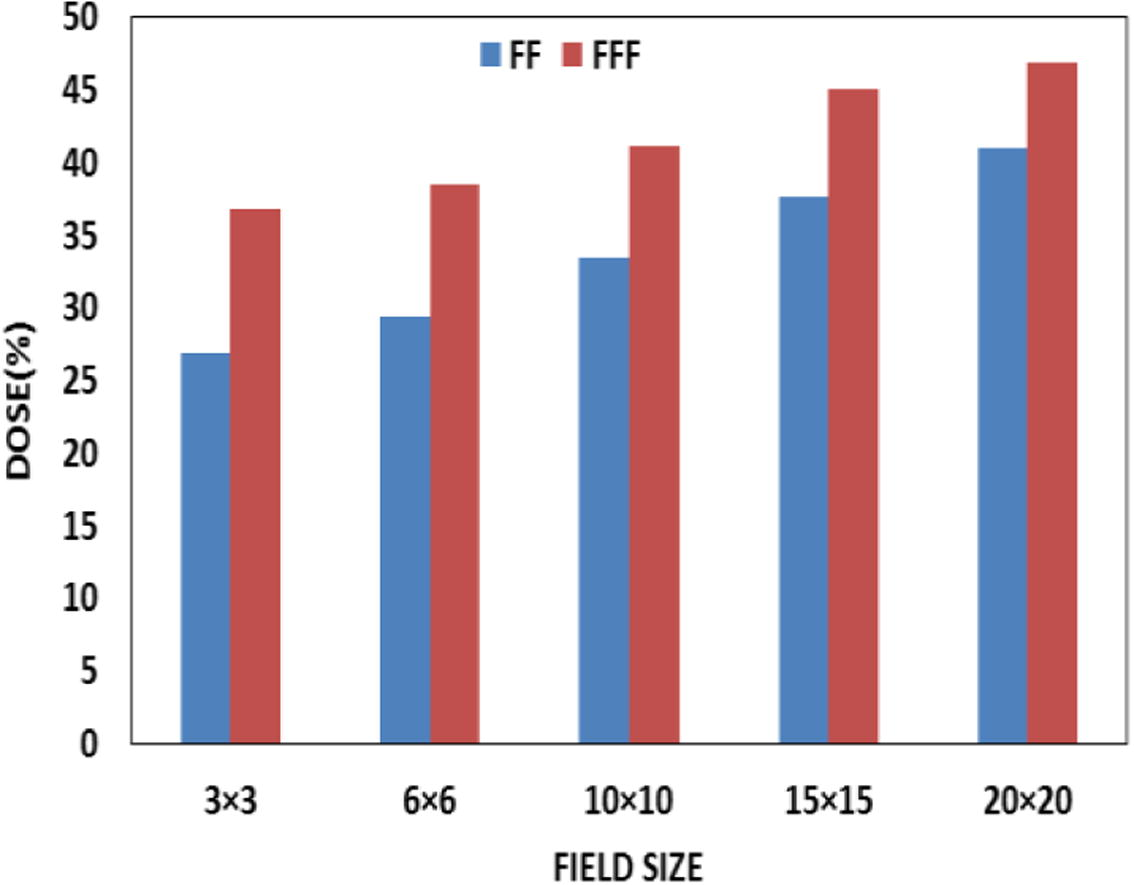
The surface dose and build-up region of FF and FFF photon beams were evaluated for 3 × 3 to 20 × 20 cm² square field sizes. The surface dose value of any field size is defined as the dose calculated at the first millimeter (1 mm) of a homogeneous water phantom divided by the dose at D_max for the corresponding field. Simulation results summarized in Table 2 show that the surface dose increased linearly with field size for both FF and FFF photon beams. The surface dose values of FFF beams were higher than that of the FF for all field sizes, due to the increasing of incident contaminant charged particles and low energy photons in FFF beams (Mesbahi, 2007; Titt et al., 2006; Vassiliev et al., 2006; Wang et al., 2012). The difference between them is clear in the Fig. 4. The surface dose ratios of FFF and FF beams decrease with field size due to an increasing of scattering radiation from the filter with field size. The results reported in the present paper seem convergent with the findings of Vassiliev et al. (2006) and Yarahmadi et al. (2013), with a slight disparity (about 0.04) because they calculated it at 3 mm (present work at 1 mm). Using helium molecules decreased the ratio from 1.233 to 1.13 for 10 × 10 cm² field size, and there is a decrease in build-up region doses, as seen in Fig. 5. The build-up region dose (depth, from 0 to d_max) for FFF configuration is larger than that of FF configuration for open field sizes from 3 × 3 to 20 × 20 cm². Our results are consistent with that obtained in the previous study of Wang et al. (2012). They concluded that, the difference is not substantial and can be clinically insignificant. Sigamani et al. (2016) and Wang et al. (2012) reported that the dose delivered to surface dose and build-up region is useful for implementations of IMRT, SRS, and SBRT techniques. Using helium particles play an efficient role by increasing the efficiency and quality of unflattened beams and the patients would benefit considerably from the reduction in surface dose.

Close

Figure 4

Surface doses comparisons of 6MV FF and FFF photon beam calculated at 1 mm within the water phantom.

Export to PPT

Close

Figure 5

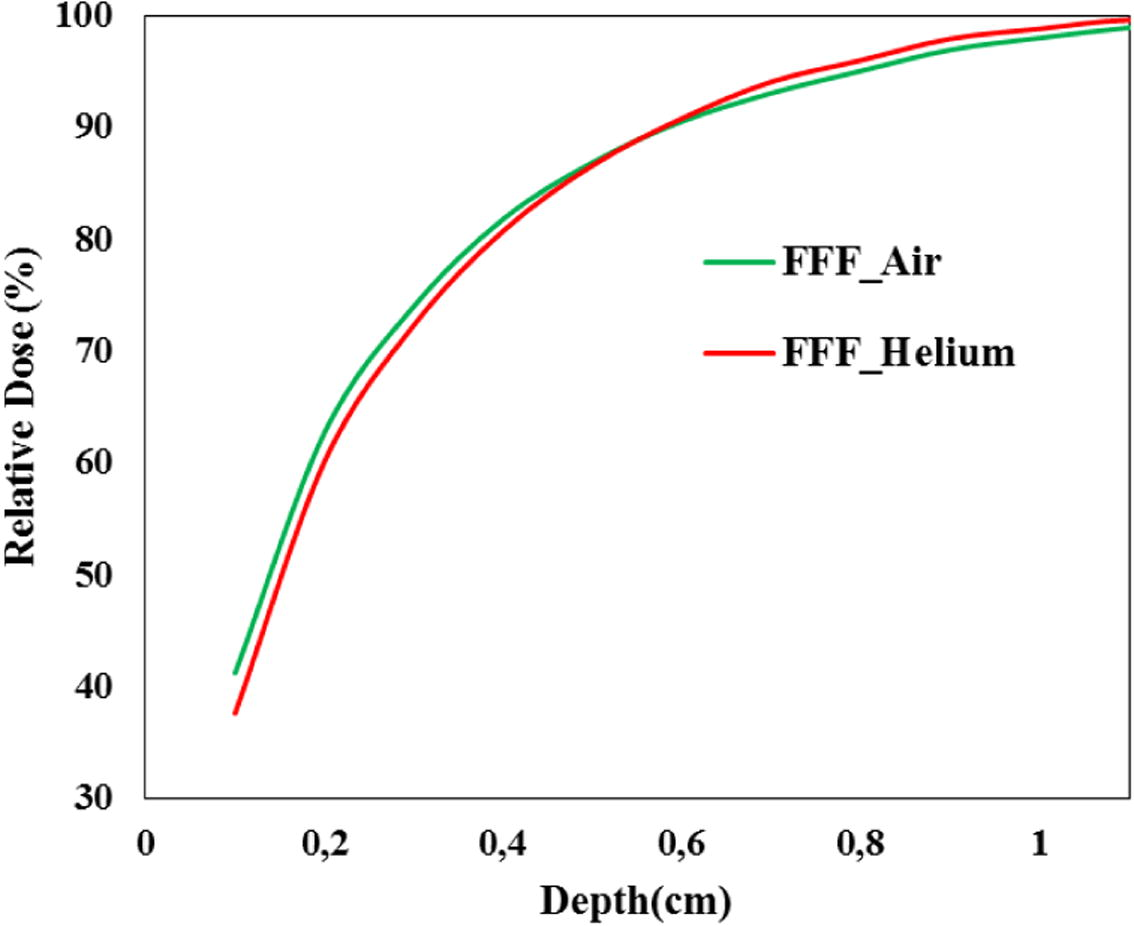
Build-up doses of 6MV unflattened beam for both air and Helium molecules.

Export to PPT

3.5 Beam profiles

Fig. 6 shows the lateral profiles dose, of both FF and FFF beams for the open field size from 3 × 3 to 20 × 20 cm², that is calculated at a depth of 10 cm. From Fig. 6, we can see clearly the lack of flatness feature in FFF beams that have their maximum dose on the central axis and decrease gradually toward the field edge. This shape becomes more pronounced with increasing of field size and beam energy (Hrbacek et al., 2011). This behavior is quantified by calculating the ratio of maximum and minimum dose on the central axis (within 80% of the field size), and summarizes in Table 3. We can see that for a field up to 3 × 3 cm² this ratio increases with field size, Table 3.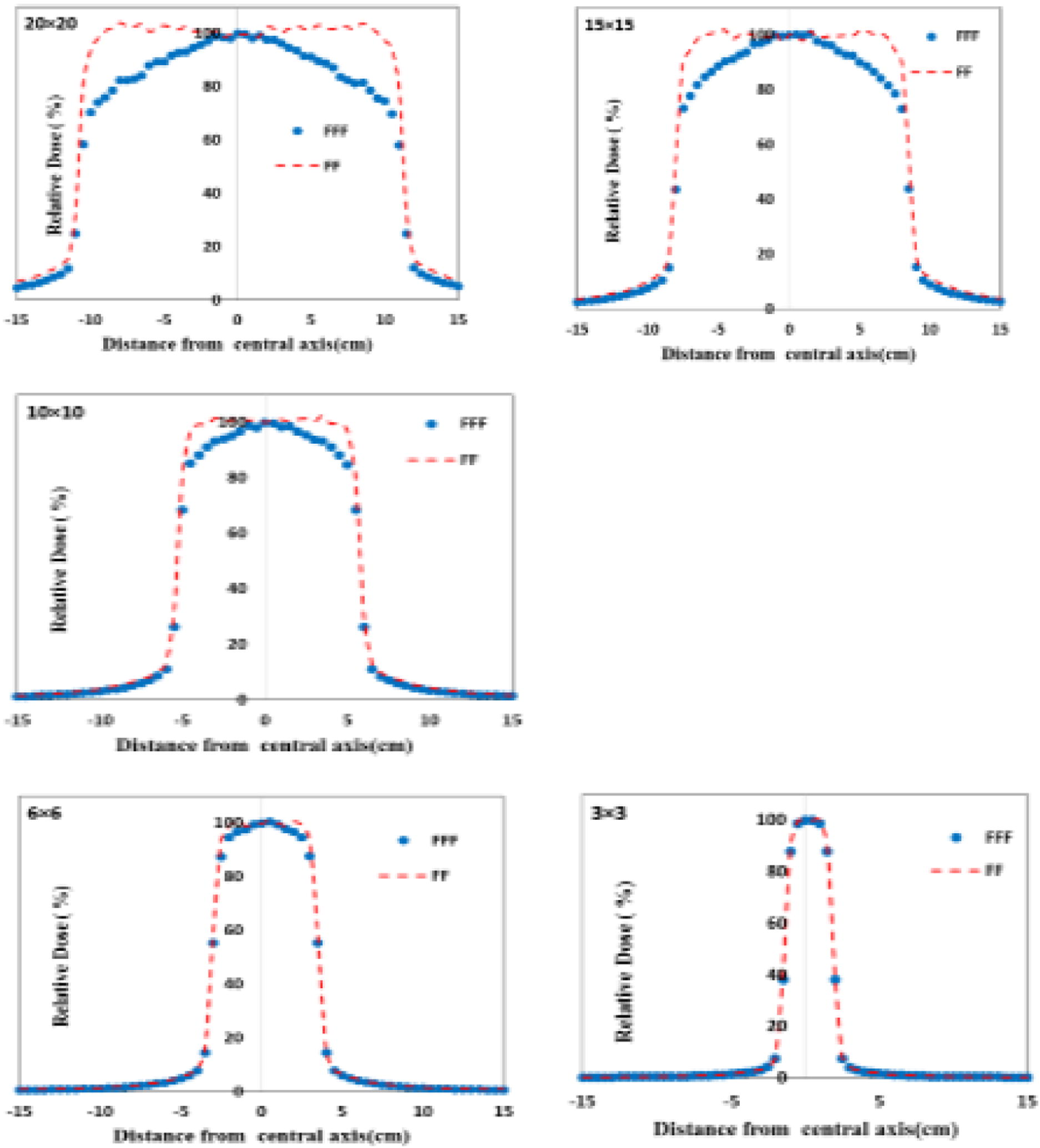

Close

Figure 6

Comparison of beam profiles of FF and FFF 6 MV photon beams for different field sizes.

Export to PPT

The obtained results show that removing the filter leads to the reduction of the penumbra dose. We found that the average ratios of FF and FFF in the penumbra region were obtained from 1.04 to 1.33 for 3 × 3 to 20 × 20 cm² field sizes, respectively. At the same time, smaller penumbra width was produced due to the softer beam spectrum of FFF and missing scatter from the flattening filter (Pönisch et al., 2006).

Out-of-field doses of flattened and non-flattened beams were assessed for square filed sizes from 3 × 3 to 20 × 20 cm², in beam profiles which were calculated at a depth of 10 cm. From the Figs. 6 and 7, it is clear that the removal of the filter produces lower dose outside treatment field due to the reduction of leakage radiation and head scatter (Georg et al., 2011), the difference between FFF and FF doses in outside the field (at 3.5 cm from the treatment field border) were 40%, 35%, 31%, 20% and 15% for 20 × 20, 15 × 15, 10 × 10,6 × 6 and 3 × 3 cm² field sizes, respectively. The difference is more accentuated with large field size, Fig. 7, because of more collimator scatter with flattened beams. In clinical situations, the dose outside the cancer will be influenced by many parameters such as size, location, and shape of the target as well as degree of modulation and delivery technique used (intensity-modulated radiotherapy or volumetric modulated arc therapy) and their interplay with beam characteristics. In a previous study of Diallo et al. (2009) reported that 49% of the secondary cancer occurs at the field edge. Based on the results of this work, the best possible dose reduction outside the field was achieved with FFF beams. This reduces the damage on healthy tissues close the target.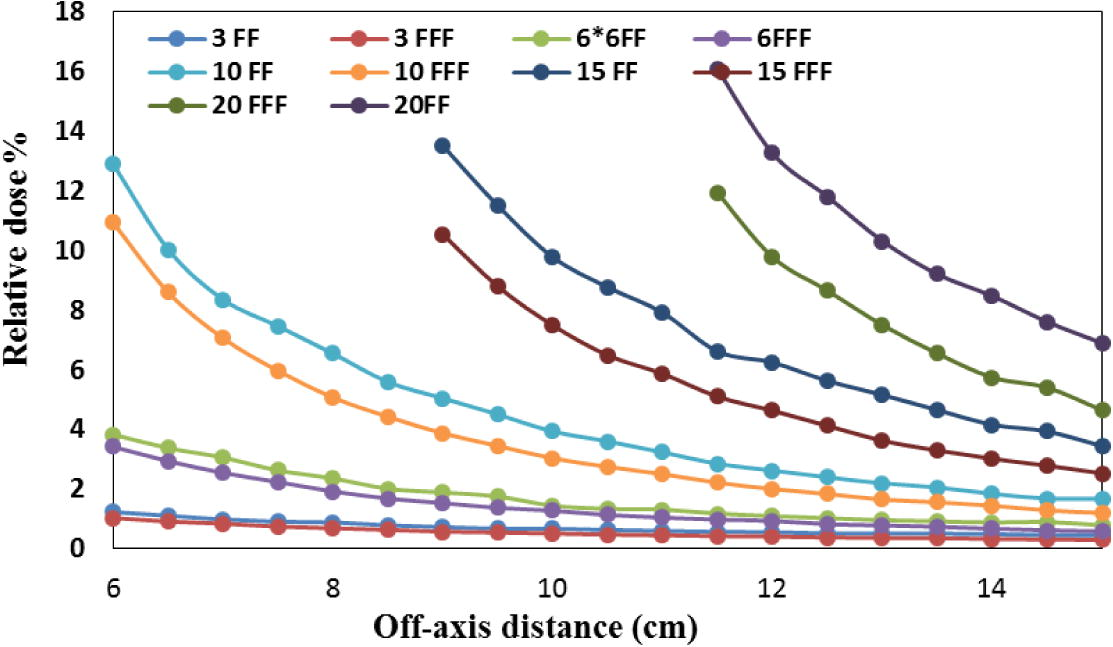

Close

Figure 7

Comparison of out-of-field dose of FF and FFF 6 MV photon beams for different field sizes.

Export to PPT

3.6 Total scatter factor (Sc,p)

It’s the ratio of the dose at a reference depth in a water phantom for a given field size to the dose at the corresponding point and depth in a phantom for the reference field size (10 × 10 cm²) for FF and FFF beams (Smathers, 2003).

Sc values of FF and FFF photon beams were calculated at depth of 10 cm for different field sizes. The results obtained are presented in Table 4. The previous study of (Georg et al., 2011; Hrbacek et al., 2011; Pichandi et al., 2014; Vassiliev et al., 2006) has consistent results, and reported that the flattening filter is one of the components which contribute to the dispersion of the number of particles. So, the removal of filter reduces the dose outside the region of interest, and the organs besides the cancer arebetter protected.

3.7 Photon energy spectra

Photon energy spectra of each field size were evaluated by analyzing the phase space files which were placed at the water phantom surface (Z = 100 cm) using BEAMDP user code. The photon energy spectra of two configurations FF and FFF beams are shown in Fig. 8. By looking to the Fig. 8, it’s clear that the photon energy spectra of FFF beams are higher than FF beams for all field sizes. This is due to the beam attenuation in standard case (FF beams). On the other hand, as it is clear in the Table 5, the differential ratio for FFF to FF beams decreases with a field size, it decreases from 3.76 to 2.19 for 3 × 3 to 20 × 20 cm² field size, respectively, due to the fixed form of the flattening filter (FF). The results presented in Fig. 4 are compared to the study of Mesbahi (2007), and we noted that there are slightly different due to the results of present paper are calculated in a circle of radius 10 cm at the phantom surface and his calculations were performed over the irradiated field size.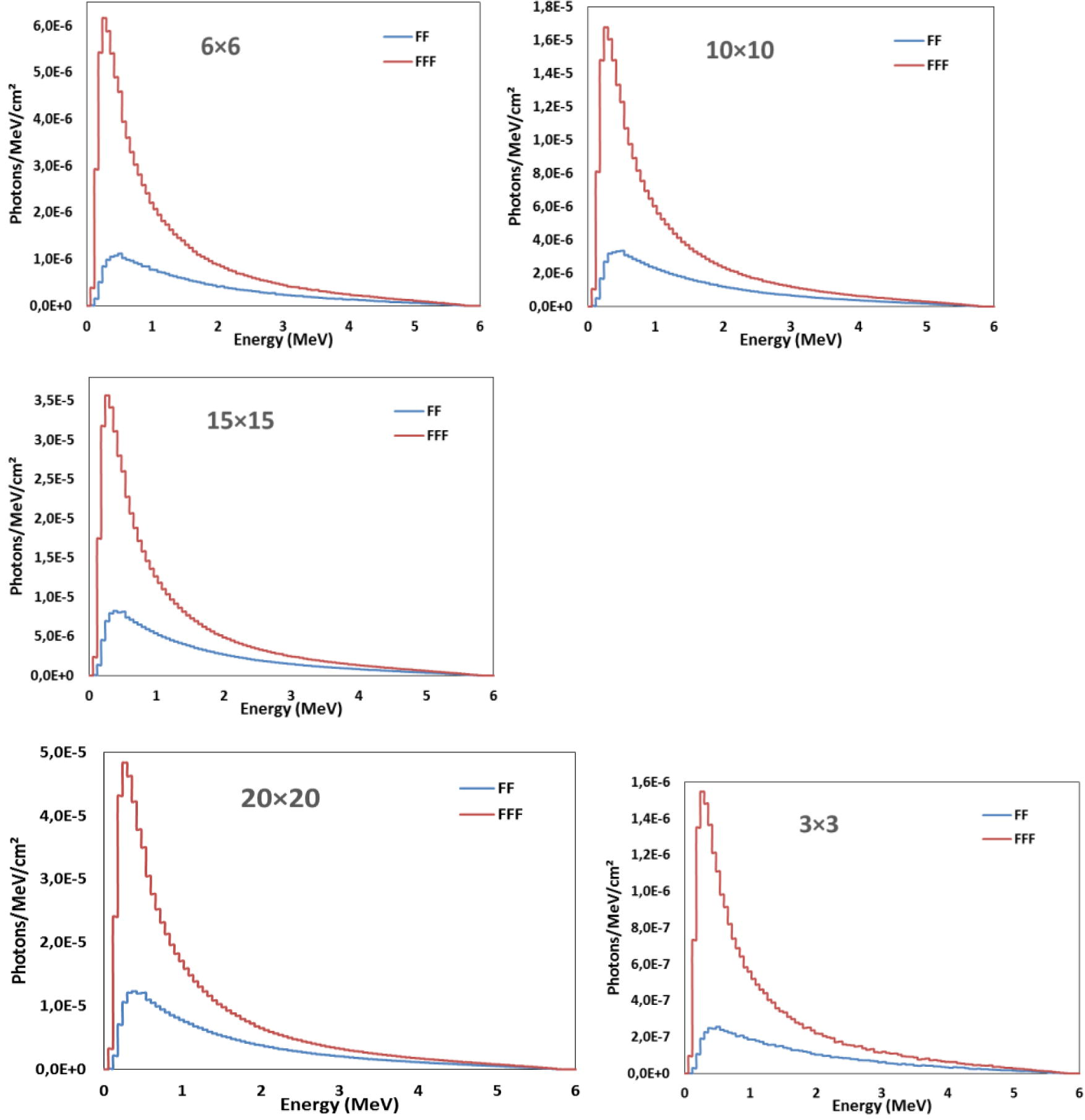

Close

Figure 8

Comparison of photon beams spectrum of FF and FFF 6 MV photon beams for different field sizes.

Export to PPT