1 Introduction

Nuclear research reactors are mainly used to provide a neutron source for various applications. These have a wide variety of different types of reactor that are not used for power generation. In comparison with power generation reactors, research reactors are smaller and simpler with far less fuel and fission products’ build-up. Their power ratings are designated in megawatts in a range from zero up to 200 MWt (IAEA, 2016). Around the world, 224 research reactors are operating for producing medical radiopharmaceuticals, research, education, training, material structure studies, neutron radiography and therapy, silicon doping, and neutron activation analysis (IAEA, 2009a, 2014, 2015).

Radioactive waste generation from nuclear reactors during operation is unavoidable. The types and amounts of operational waste generated depend on the reactor type, operational schedule, and main applications (IAEA, 2009b). The waste management plan is critical to ensure the protection of workers, the public, and the environment. It should consider proper classification of the waste, segregation of the waste types and stream, and a detailed inventory of the amount and type of the waste, treatment, conditioning, storage, safe handling, transport, and final deposition (IAEA, 2007, 2009b, 2009c).

For final deposition, near surface disposal repository (NSDR), which are an option for permanent storage of radioactive waste, have been developed by many countries such as Canada and Finland for low and intermediate radioactive waste (LILW) generated from nuclear reactors (IAEA, 2004; Vieno and Nordman, 1998). LILWs have a small fraction of total activity produced in the world but represent 90% of the total volume of radioactive waste. Thus, it should be managed properly to minimize the risk associated with the radioactive waste (Aguiar and Damaso, 2010).

The safety assessment for NSDR should address the following key components: specification of the assessment context, description of the waste disposal system, development and justification of scenarios, the formulation and implementation of models, and analysis of results and building of confidence (IAEA, 2004). The safety of NSDR is determined by the physical and chemical properties of the waste, and the host environment. In the past, multiple barriers models were considered as collections of independent individual barriers that worked in sequence (Nair and Krishnamoorthy, 1999). Currently, all these models have simultaneously integrated dependent barriers (IAEA, 2002). In this study, a mathematical model was adopted to estimate the activity release from NSDR for a hypothetical open pool light-water research reactor (OP-LWR) in Saudi Arabia.

2 Methods

The first NSDR in Saudi Arabia is proposed to be in a remote and unpopulated area in the Riyadh region, which is the central region in the country. This region has a low chance of precipitation and a very low risk of earthquakes and volcanos, and is mainly bounded by the Phanerozoic sedimentary rocks (The Saudi Geological Survey, 2017). The hypothetical NSDR for nuclear waste from OP-LWR contains six cement barriers, as shown in Fig. 1. These barriers are: upper cover (0.50 m high), lower cover (0.40 m high), radioactive waste (3 m high, 10 m long, and 5 m width), side covers (0.70 m thick), end cover (0.60 m high), and biosphere (20 m thick).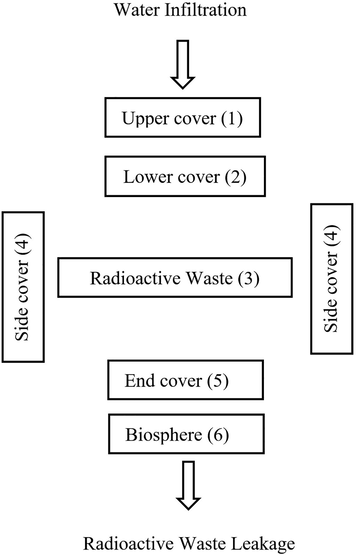

Close

Fig. 1

The barriers for the hypothetical near surface disposal repository.

Export to PPT

We assume that all compartments in this model work in a parallel alignment and that a model collapse will happen when barrier (1) and (2) and (3) and [(4) or (5)], and (6) collapse. Barrier (1) and (2) are covers against water (rain) infiltration, while barriers (3), (4), and (5) are covers against radioactive waste leakage. Barriers (3) contains all the radioactive waste from the hypothetical OP-LWR. The waste may drain through the end or side covers and flows through the biosphere.

The collapse time of each barrier is assumed a random variable with a particular probability density function. To express the collapse time of each barrier, exponential distribution was used. As seen in Fig. 2, we adapted the Markov model since our model has passive parallel barriers and correlational relation between its compartments. Markov method has been used in previous studies (Aguiar and Damaso, 2010, 2011) to model a randomly changing systems and estimate the activity release rate.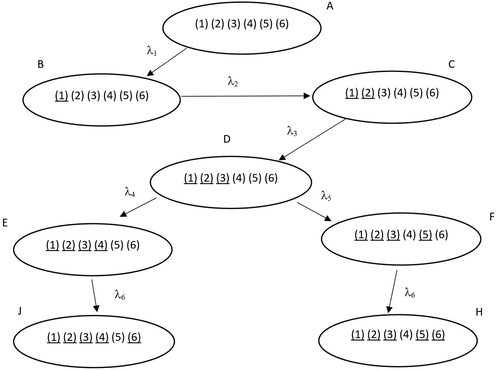

Close

Fig. 2

Transition illustration of the Markov method for the hypothetical model. The underline indicates a barrier collapse.

Export to PPT

The most common radionuclides released as waste from the OP-LWR reactor are: Co-60, Ni-59, Sr-90, Tc-99, I-129, Cs-135, Cs-137, Pu-238, Pu-239, Pu-240, Pu-241, and Am-241 (Breysse and Gerard, 1997; de Kageneck and Pinel, 1998). In this study, some long-lived radionuclides (half-life more than 200,000 years) were chosen to further assess the performance of this depository.

Porosity (σ), which is the ratio of the volume of pores to the volume of bulk rock, is variable that fluctuates with time. Specific mass ( $\rho$ ), which is the mass of a given substance per unit volume, depends of the fluctuation of the porosity. Similarly, hydraulic conductivity (ε), which is a term that describes the ease with which a fluid can move through pore spaces, mainly relies on porosity and specific mass. In this study, the following presumptions for variables change with time will be adopted: (1) porosity of 0.13 and specific mass of 2.8 g/cm³ will designate the physical properties of cement at time zero (Vieno and Nordman, 1998); (2) after 500 years, porosity will increase to 0.45; (3) the values of hydraulic conductivity will be dependent on the porosity, as seen in Eq. (1) (Vieno and Nordman, 1998); and (4) the values of distribution coefficients (D_c) for both cement and biosphere (ICRP, 2012) are given in Table 1 and will change over time, as shown in Table 2.

The distribution coefficient provided is defined as the ratio of solute concentration in the solid material (cement/rock) to the solute concentration in the surrounding water.

Also, Table 1 contains half-life and hypothetical radionuclide inventory after repository closure. However, actual inventory can be implemented in this model for more accurate estimation.

Given that the performance history of cement is quite short compared to the long time periods considered for the performance of NSDR, there is some uncertainty in predicting the long-term integrity of cement. To address this uncertainty, the estimated time required for radionuclides to transit each compartment in the model will be added to 100 years (ICRP, 2012). Under the assumption that the force of the water column above the upper cover is negligible, the speed of water that infiltrates the upper cover is equal to the hydraulic conductivity. The equations that better address the change of hydraulic conductivity, porosity, and specific mass with time are respectively:

The retardation factor (R_F) for each radionuclide in the inventory is estimated by:

To estimate the speed of water (v_w), Darcy’s equation for the flow of a fluid through a porous medium was adopted. The speed of radionuclide (v_r) is basically the speed of water divided by the retardation factor:

The mean passage time was estimated by dividing each barrier thickness by the speed of water for barriers [(1) and (2)] and speed of radionuclide for barriers [(3), (4), (5), and (6)]. Therefore, the mean time to collapse (MTTC) of each cover is equal to the water mean passage time for barrier (1) and (2) or radionuclide transit time for barrier (3), (4), (5), and (6).

After establishing the equations for water/radionuclide speed, mean passage time, and MTTC, the activity release due to the collapse of this hypothetical repository will be estimated using Bateman’s equation (Cho et al., 1992), which describes the abundances and activities in a decay chain as a function of time, based on the decay rates and initial abundances. The activity release is the product of probability density function (PDF) and the activity (Aguiar and Damaso, 2010, 2011).

Where,

$\overline{A}\left(t\right)$ is activity release per year (Bq/y),

$\beta \left(t\right)$ is probability density function ( ${\mathrm{y}}^{-1}$ ),

A(t) is activity at a given time (Bq),

${\mathrm{A}}_0$ is initial activity (Bq),

$\alpha$ is decay constant ( ${\mathrm{y}}^{-1}$ ), $${\eta }_A\left(t\right)={-\lambda }_1{\lambda }_2{\lambda }_3{e}^{-{\lambda }_{6}t}{\tau }_1{\tau }_2{\tau }_3{\tau }_5{\tau }_6{\tau }_8{\left({\tau }_{10}\right)}^2$$ $${\eta }_B\left(t\right)={+\lambda }_1{\lambda }_2{\lambda }_3{\lambda }_6{e}^{-\left({\lambda }_4+{\lambda }_5\right)t}{\tau }_1{\tau }_2{\tau }_4{\tau }_5{\tau }_7{\tau }_9{\tau }_{10}$$ $${\eta }_C\left(t\right)={-\lambda }_1{\lambda }_2{\lambda }_6{e}^{-{\lambda }_{3}t}{\tau }_1{\tau }_3{\tau }_4{\tau }_6{\tau }_7{\left({\tau }_{10}\right)}^2{\tau }_{11}$$ $${\eta }_D\left(t\right)={+\lambda }_1{\lambda }_3{\lambda }_6{e}^{-{\lambda }_{2}t}{\tau }_2{\tau }_3{\tau }_4{\tau }_8{\tau }_9{\left({\tau }_{10}\right)}^2{\tau }_{11}$$ $${\eta }_E\left(t\right)={-\lambda }_2{\lambda }_3{\lambda }_6{e}^{-{\lambda }_{1}t}{\tau }_5{\tau }_6{\tau }_7{\tau }_8{\tau }_9{\left({\tau }_{10}\right)}^2{\tau }_{11},$$ $${\tau }_1={\lambda }_1-{\lambda }_2,{\tau }_2={\lambda }_1-{\lambda }_3,{\tau }_3={\lambda }_1-{\lambda }_4-{\lambda }_5,{\tau }_4={\lambda }_1-{\lambda }_6,{\tau }_5={\lambda }_2-{\lambda }_3,$$ $${\tau }_6={\lambda }_2-{\lambda }_4-{\lambda }_5,{\tau }_7={\lambda }_2-{\lambda }_6,{\tau }_8={\lambda }_3-{\lambda }_4-{\lambda }_5,{\tau }_9={\lambda }_3-{\lambda }_6,{\tau }_{10}={\lambda }_4+{\lambda }_5,$$

${\tau }_{11}={\lambda }_4+{\lambda }_5-{\lambda }_6$ , and

${\lambda }_1$ , ${\lambda }_2$ , ${\lambda }_3$ , ${\lambda }_4$ , ${\lambda }_5$ , ${\lambda }_6$ are collapse rates for barriers (1), (2), (3), (4), (5), and (6) respectively.

Mathematical calculations were performed using Mathcad (version 15; PTC, Mathsoft; Massachusetts, USA).

3 Results

The retardation factors (R_F) for each radionuclide were calculated in both cement and biosphere using Eq. (5) and the results are listed in Table 3. The MTTC for each barrier is listed in Table 4.

Equation (7) was used to estimate the activity release rate in the biosphere for each radionuclide, and the results are illustrated by radionuclide in Figs. 3, 4, and 5.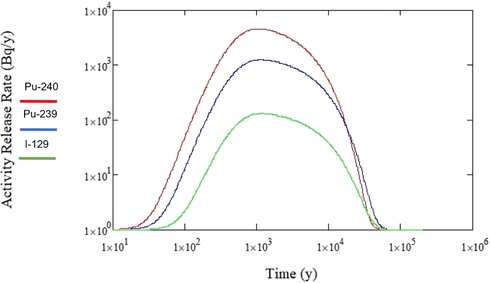

Close

Fig. 3

Activity release rate in the biosphere for Pu-240, Pu-239, and I-129.

Export to PPT

Close

Fig. 4

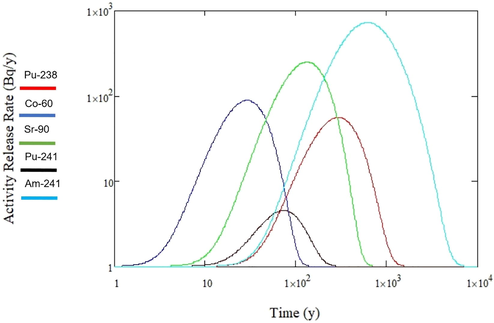
Activity release rate in the biosphere for Pu-238, Co-60, Sr-90, Pu-241, and Am-241.

Export to PPT

Close

Fig. 5

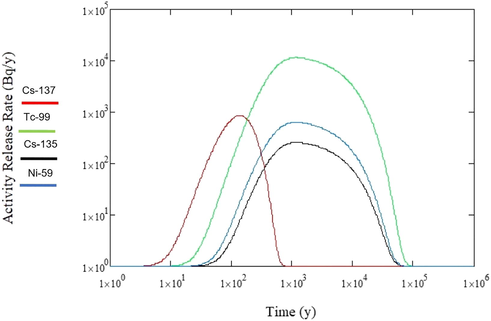
Activity release rate in the biosphere for Cs-137, Tc-99, Cs-135, and Ni-59.

Export to PPT

4 Discussion

The results show there is a direct proportionality between distribution coefficient, retardation factor, and the MTTC. MTTC in cement is higher for nickel because it has the highest value of distribution and retardation coefficient among all other radionuclides.

The results from the calculated retardation factor (R_F) for each radionuclide in the inventory (Eq. (5)) shows that nickel, cobalt, and plutonium have the highest R_F values and are expected to move the slowest through the model compared to other radionuclides. Similarly, technetium, iodine, and strontium have the lowest R_F values and are expected to move the fastest through the biosphere compared to other radionuclides. As a result, technetium, iodine, and strontium are predicted to accumulate faster in the biosphere, whereas nickel, cobalt, and plutonium are predicted to accumulate slower in the biosphere.

However, these tendencies are somewhat changed: a radionuclide with a longer half-life needs more mass to produce a particular amount of activity compared to a shorter half-life radionuclide. Also, a long half-life radionuclide needs a longer time to reach its highest cumulative activity in the biosphere, despite its speed through the model and biosphere.

These results show that Co-60, which has the shortest half-life among all the radionuclides in the inventory, reached its highest cumulative activity of 88 Bq in the shortest time (29 years). Likewise, the other radionuclides with a moderately short half-life, such as Pu-241, Sr-90, Cs-137, and Pu-238, reach their respective highest cumulative activity of 4.5, 250, 858, and 56 Bq in 73, 130, 140, 290 years respectively. Moreover, radionuclides with a long half-live, such as Am-241, Pu-240, Pu-239, I-129, Tc-99, Ni-59, and Cs-135, reached their respective highest cumulative activity of $7.2\times {10}^2$ , $4.5\times {10}^3$ , $1.2\times {10}^3$ , $1.3\times {10}^2$ , $1.1\times {10}^4$ , $6.3\times {10}^2$ , and $2.5\times {10}^2$ Bq in $6\times {10}^2$ , $1.1\times {10}^3$ , $1.2\times {10}^3$ , $1.2\times {10}^3$ , $1.2\times {10}^3$ , $1.1\times {10}^3$ , and $1\times {10}^3$ years respectively.

In general, the deduction in cumulative activity in the biosphere is due to radionuclide decay. Thus, the cumulative activities of long half-life radionuclides are continued over long periods of time. For long half-life radionuclides, the values for highest cumulative activity in the biosphere are the largest portions of initial activity enclosed in the repository. Of note, the results of this study are specific to this particular disposal facility site.

5 Conclusion

A mathematical model was used to estimate the activity release from near surface disposal repository for a hypothetical open pool light-water research reactor (OP-LWR) in Riyadh, Saudi Arabia. For this model, the hydraulic conductivity, specific mass, and porosity of the cement and the local geosphere were considered, as well as the expected radioactive waste inventory produced by OP-LWR. The results show that there is a direct proportionality between distribution coefficient, retardation factor, and the MTTC. Also, they reveal that nickel has the highest MTTC among all the other radionuclides in the proposed model. The highest cumulative activity release in the biosphere was found to be $1.1\times {10}^4$ Bq for Tc-99 after 1300 years. The impact of the radiological behavior of each selected radionuclide enabled finding the effect on the repository performance.

Funding

None.