Embedding (3 + 1)-dimensional diffusion, telegraph, and Burgers’ equations into fractal 2D and 3D spaces: An analytical study

Marwan Alquran; Imad Jaradat; Ruwa Abdel-Muhsen

doi:10.1016/j.jksus.2018.05.024

View/Download PDF

Embedding (3 + 1)-dimensional diffusion, telegraph, and Burgers’ equations into fractal 2D and 3D spaces: An analytical study

Marwan Alquran, Imad Jaradat^⁎, Ruwa Abdel-Muhsen

Department of Mathematics & Statistics, Jordan University of Science and Technology P.O. Box 3030, Irbid 22110, Jordan

⁎Corresponding author. iajaradat@just.edu.jo (Imad Jaradat),

Received: 2018-5-1, Accepted: 2018-5-21, Published: 2018-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

Fractional derivatives can be utilized as a promising tool for characterizing systems with embedded memory or describing viscoelasticity of advanced materials. Motivated by the significance of fractional derivatives, we provide assorted of analytical representations for the solution of higher-dimensional fractional differential equations that involve multi-memory indices. Then, an iterative parallel scheme of the power series method with underlying these representations is applied to extract fractal closed-form and supportive approximate solutions for several multi-memory models. Some of the obtained closed-form solutions are given in terms of the generalized exponential and hyperbolic functions which might be more suitable for representing nonlinear physical behaviors.

Keywords

26A33

41A58

35R11

35C10

Fractional derivatives

Fractional differential equations

Series solutions

1 Introduction

The significance of fractional derivatives has been heightened in the last two decades due to its potential applications in many fields of applied sciences. It has been shown in many studies that the fractional derivatives can be utilized in describing memory phenomena (Rossikhin and Shitikova, 2009; Du et al., 2013). Besides that, it has been shown that the spectrum of relaxation modes of a viscoelastic material can be stretched or compressed when the fractional derivative order varies from zero to one (Wharmby and Bagley, 2013). Further, it has been proven that in a particular case of a linearly time-varying non-Newtonian viscosity, the fluid’s response has the same power-law as the linear viscoelasticity that is characterized by the fractional derivative (called a springpot) (Pandey and Holm, 2016). More physical and engineering phenomena that have been successfully modeled and interpreted by fractional derivatives can be found in Koeller (1984), Magin (2006), Mainardi (2008), Hilfer (2000), Nigmatullin (2009), Coussot et al. (2009), Butera and Paola (2014), Mainardi and Paradisi (2001), Alquran et al. (2015), Bhrawy et al. (2016), Le et al. (2016), Kumar et al. (2016), Alquran and Jaradat (2018), Gómez-Aguilar et al. (2016a).

Various forms of fractional derivatives have been suggested in the literature, all of which converge to the integer-order derivative as the fractional-order derivative approach an integer value. Recently, new forms of fractional derivatives based on the exponential law (Caputo and Fabrizio, 2015) and on the Mittag–Leffler function (Atangana and Baleanu, 2016) have been proposed. Some noteworthy works in this matter can be found in Mirza and Vieru (2017), Koca and Atangana (2016), Gómez-Aguilar (2017a,b), Morales-Delgado et al. (2017), Coronel-Escamilla et al. (2017), Gómez-Aguilar et al. (2016b,c).

In our present study, we consider $(3 + 1)$ -dimensional fractional differential equations (FDEs) that are endowed with multi-fractional derivatives on several variable-coordinates to study and simulate the multi-memory effects. Expressly, we are interested in the equations of the forms

(1.1)

F (u (\overline{x}, t), D_{t}^{α} [u (\overline{x}, t)], D_{x}^{β} [u (\overline{x}, t)], u_{y} (\overline{x}, t), u_{z} (\overline{x}, t), \dots) = 0

and

(1.2)

G (u (\overline{x}, t), D_{t}^{α} [u (\overline{x}, t)], D_{x}^{β} [u (\overline{x}, t)], D_{y}^{γ} [u (\overline{x}, t)], u_{z} (\overline{x}, t), \dots) = 0,

where

\overline{x}

denotes the space-variables

(x, y, z)

and

α, β, γ \in (0, 1)

are the fractional derivative orders in Caputo sense, which is defined for the case of

α

(1.3)

D_{t}^{α} [u (\overline{x}, t)] = \frac{\partial^{α} u (\overline{x}, t)}{\partial t^{α}} = \frac{1}{Γ (1 - α)} \int_{0}^{t} \frac{\partial u (\overline{x}, κ)}{\partial κ} \frac{d κ}{{(t - κ)}^{α}} .

In Caputo sense as well as in most fractional derivative definitions, we have

(1.4)

D_{t}^{α} [t^{a}] = \frac{Γ (a + 1)}{Γ (a - α + 1)} t^{a - α}

for

a > 0

and this will direct us to employ an appropriate form of the power series expansion as a reliable suggested solution for (1.1) and (1.2).

2 Solution representations in fractal 2D and 3D spaces

In this section, we propose two different solution expansions of (3 + 1)-dimensional FDEs that are embedded into fractal 2D and 3D spaces respectively. Consequently, fractional versions of Taylor’s formula regarding these forms are also given. We should point out here that similar expansions are utilized to solve FDEs in lower dimensions (Jaradat et al., 2018a,b,c,d ).

Definition 2.1

An $(α, β) -$ fractional power series with variable coefficients is an infinite series of the form

(2.1)

\sum_{\binom{i + j = 0}{i, j \in N_{0}}}^{\infty} f_{ij} (y, z) t^{i α} x^{j β} = \underset{i + j = 0}{\underset{︸}{f_{00} (y, z)}} + \underset{i + j = 1}{\underset{︸}{f_{10} (y, z) t^{α} + f_{01} (y, z) x^{β}}} + \dots + \underset{i + j = n}{\underset{︸}{\sum_{k = 0}^{n} f_{n - k, k} (y, z) t^{(n - k) α} x^{k β}}} + \dots .

The next result provides a formula for the mixed-higher fractional derivatives of the functions that can be represented in the form of (2.1). The proof is followed by the linearity of Caputo operator and using the 2D mathematical induction. In fact, the proof of the Lemma is similar to the proof of Jaradat et al. (2018b, Lemma 2.2).

Lemma 2.2

Let $u (\overline{x}, t)$ has a FPS representation as (2.1) for $(\overline{x}, t) \in [0, R_{x}) \times I \times J \times [0, R_{t})$ . If $D_{t}^{r α} D_{x}^{s β} [u (\overline{x}, t)] \in C ((0, R_{x}) \times I \times J \times (0, R_{t}))$ for r,s $\in N_{0}$ , then

(2.2)

D_{t}^{r α} D_{x}^{s β} [u (\overline{x}, t)] = \sum_{i + j = 0}^{\infty} f_{i + r, j + s} (y, z) \frac{Γ ((i + r) α + 1) Γ ((j + s) β + 1)}{Γ (i α + 1) Γ (j β + 1)} t^{i α} x^{j β} .

Remark 1

By letting $(x, t) = (0, 0)$ in (2.2), we have the following fractional version of Taylor’s formula that is associated to (2.1)

(2.3)

u (\overline{x}, t) = \sum_{i + j = 0}^{\infty} \frac{D_{t}^{r α} D_{x}^{s β} [u (\overline{x}, t)] ∣_{(x, t) = (0, 0)}}{Γ (i α + 1) Γ (j β + 1)} t^{i α} x^{j β} .

Definition 2.3

An $(α, β, γ) -$ fractional power series with variable coefficients is an infinite series of the form

(2.4)

\sum_{\binom{i + j + k = 0}{i, j, k \in N_{0}}}^{\infty} f_{ijk} (z) t^{i α} x^{j β} y^{k γ} = \underset{i + j + k = 0}{\underset{︸}{f_{000} (z)}} + \underset{i + j + k = 1}{\underset{︸}{f_{100} (z) t^{α} + f_{010} (z) x^{β} + f_{001} (z) y^{γ}}} + \dots + \underset{i + j + k = n}{\underset{︸}{\sum_{r = 0}^{n} \sum_{s = 0}^{r} f_{n - r, r - s, s} (z) t^{(n - r) α} x^{(r - s) β} y^{s γ}}} + \dots .

Using again the linearity of the Caputo operator, one can show inductively the following.

Lemma 2.4

Let $u (\overline{x}, t)$ has a FPS representation as (2.4) for $(\overline{x}, t) \in [0, R_{x}) \times [0, R_{y}) \times I \times [0, R_{t})$ . If $D_{t}^{r α} D_{x}^{s β} D_{y}^{m γ} [u (\overline{x}, t)] \in C ((0, R_{x}) \times (0, R_{y}) \times I \times (0, R_{t}))$ for r,s,m $\in N_{0}$ , then

(2.5)

D_{t}^{r α} D_{x}^{s β} D_{y}^{m γ} [u (\overline{x}, t)] = \sum_{i + j + k = 0}^{\infty} f_{i + r, j + s, k + m} (z) \frac{Γ ((i + r) α + 1) Γ ((j + s) β + 1) Γ ((k + m) γ + 1)}{Γ (i α + 1) Γ (j β + 1) Γ (k γ + 1)} t^{i α} x^{j β} y^{k γ} .

Remark 2

Similarly, by letting $(x, y, t) = (0, 0, 0)$ in (2.5), we have the following fractional version of Taylor’s formula that is associated to (2.4)

(2.6)

u (\overline{x}, t) = \sum_{i + j + k = 0}^{\infty} \frac{D_{t}^{r α} D_{x}^{s β} D_{y}^{k γ} [u (\overline{x}, t)] ∣_{(x, y, t) = (0, 0, 0)}}{Γ (i α + 1) Γ (j β + 1) Γ (k γ + 1)} t^{i α} x^{j β} y^{k γ} .

3 Applications

Herein, we consider the (3 + 1)-dimensional diffusion, telegraph, and Burgers’ equations that are embedded into fractal 2D and 3D spaces and provide their solutions analytically in fractal closed-forms. The solutions are obtained by using a parallel scheme to the power series method with underlying the expansions (2.1) and (2.4) respectively.

3.1

3.1 (3 + 1)-D diffusion, telegraph, and Burgers’ equations in fractal 2D space

Example 3.1

Consider the following $(3 + 1)$ -D diffusion equation in fractal 2D space:

(3.1)

\frac{\partial^{α} u (\overline{x}, t)}{\partial t^{α}} = \frac{\partial^{2 β} u (\overline{x}, t)}{\partial x^{2 β}} + \frac{\partial^{2} u (\overline{x}, t)}{\partial y^{2}} + \frac{\partial^{2} u (\overline{x}, t)}{\partial z^{2}},

subject to the initial condition

(3.2)

u (\overline{x}, 0) = (1 - y) e^{z} E_{β} (x^{β}),

where

(3.3)

E_{β} (x^{β}) = \sum_{j = 0}^{\infty} \frac{x^{j β}}{Γ (j β + 1)}

is the one-parameter Mittag–Leffler function. We seek a solution to (3.1),(3.2) in the form of (2.1). Substituting all the related formulas (2.2) into (3.1) and (3.2) and equating the coefficients of like terms from both sides, will give the following difference-differential equation for all

i, j ⩾ 0

(3.4)

\frac{Γ ((i + 1) α + 1)}{Γ (i α + 1)} f_{i + 1, j} (y, z) - \frac{Γ ((j + 2) β + 1)}{Γ (j β + 1)} f_{i, j + 2} (y, z) - \frac{\partial^{2} f_{ij} (y, z)}{\partial y^{2}} - \frac{\partial^{2} f_{ij} (y, z)}{\partial z^{2}} = 0,

subject to the initial condition

(3.5)

f_{0 j} (y, z) = \frac{(1 - y) e^{z}}{Γ (j β + 1)} .

Solving (3.4) and (3.5) successively yields the following series coefficients

(3.6)

f_{ij} (y, z) = \frac{2^{i} (1 - y) e^{z}}{Γ (i α + 1) Γ (j β + 1)} .

Therefore, the exact solution of (3.1) and (3.2) is given by

(3.7)

\begin{matrix} u (\overline{x}, t) & = \sum_{i + j = 0}^{\infty} \frac{2^{i} (1 - y) e^{z}}{Γ (i α + 1) Γ (j β + 1)} t^{i α} x^{j β} \\ = (1 - y) e^{z} (\sum_{j = 0}^{\infty} \frac{x^{j β}}{Γ (j β + 1)}) (\sum_{i = 0}^{\infty} \frac{2^{i} t^{i α}}{Γ (i α + 1)}) \\ = (1 - y) e^{z} E_{β} (x^{β}) E_{α} (2 t^{α}) . \end{matrix}

We point out here that for the time-fractional version of (3.1) and (3.2) (i.e.,

β = 1

), we have the solution

u (\overline{x}, t) = (1 - y) e^{x + z} E_{α} (2 t^{α})

which is identical to the solution obtained by using the reduced differential transform method (RDTM) (Singh and Srivastava, 2015) and the modified homotopy perturbation method (MHPM) (Kumar et al., 2015). Moreover, if

α = β = 1

, we get the exact solution

u (\overline{x}, t) = (1 - y) e^{x + z + 2 t}

for the

(3 + 1)

-D diffusion integer-version equation.

Example 3.2

Consider the following $(3 + 1)$ -D telegraph equation in fractal 2D space:

(3.8)

\frac{\partial^{2 α} u (\overline{x}, t)}{\partial t^{2 α}} + 2 \frac{\partial^{α} u (\overline{x}, t)}{\partial t^{α}} + u (\overline{x}, t) = \frac{\partial^{2 β} u (\overline{x}, t)}{\partial x^{2 β}} + \frac{\partial^{2} u (\overline{x}, t)}{\partial y^{2}} + \frac{\partial^{2} u (\overline{x}, t)}{\partial z^{2}},

subject to the initial conditions

(3.9)

\begin{matrix} u (\overline{x}, 0) & = \sinh_{β} (x^{β}) \sinh (y) \sinh (z), \\ \frac{\partial^{α} u (\overline{x}, 0)}{\partial t^{α}} & = - \sinh_{β} (x^{β}) \sinh (y) \sinh (z), \end{matrix}

where

(3.10)

\sinh_{β} (x^{β}) = \sum_{j = 0}^{\infty} \frac{x^{(2 j + 1) β}}{Γ ((2 j + 1) β + 1)} .

Again, by substituting all the associated formulas (2.2) into (3.8), (3.9) and gathering of like powers of variables, we have the following difference-differential equation for all

i, j ⩾ 0

(3.11)

\frac{Γ ((i + 2) α + 1)}{Γ (i α + 1)} f_{i + 2, j} (y, z) + \frac{Γ ((i + 1) α + 1)}{Γ (i α + 1)} f_{i + 1, j} (y, z) + f_{i, j} (y, z) - \frac{Γ ((j + 2) β + 1)}{Γ (j β + 1)} f_{i, j + 2} (y, z) - \frac{\partial^{2} f_{i, j} (y, z)}{\partial y^{2}} - \frac{\partial^{2} f_{i, j} (y, z)}{\partial z^{2}} = 0,

subject to the initial conditions

(3.12)

\begin{matrix} f_{0 j} (y, z) & = \frac{\sinh (y) \sinh (z)}{Γ (j β + 1)}, \\ f_{1 j} (y, z) & = \frac{- \sinh (y) \sinh (z)}{Γ (α + 1) Γ (j β + 1)} . \end{matrix}

Solving (3.11) and (3.12) successively yields the following series coefficients

(3.13)

f_{i, 2 j + 1} (y, z) = \frac{{(- 1)}^{i} ({(1 + \sqrt{3})}^{i} + {(1 - \sqrt{3})}^{i})}{2 Γ (i α + 1) Γ ((2 j + 1) β + 1)} \sinh (y) \sinh (z) .

Thus, the exact solution of (3.8) and (3.9) is given by

(3.14)

\begin{matrix} u (\overline{x}, t) & = \sum_{i + j = 0}^{\infty} \frac{{(- 1)}^{i} ({(1 + \sqrt{3})}^{i} + {(1 - \sqrt{3})}^{i}) \sinh (y) \sinh (z)}{2 Γ (i α + 1) Γ ((2 j + 1) β + 1)} t^{i α} x^{(2 j + 1) β} \\ = \frac{1}{2} \sinh (y) \sinh (z) (\sum_{j = 0}^{\infty} \frac{x^{(2 j + 1) β}}{Γ ((2 j + 1) β + 1)}) (\sum_{i = 0}^{\infty} \frac{{(- 1)}^{i} ({(1 + \sqrt{3})}^{i} + {(1 - \sqrt{3})}^{i})}{Γ (i α + 1)} t^{i α}) \\ = \frac{1}{2} \sinh (y) \sinh (z) \sinh_{β} (x^{β}) E_{α} (- (1 + \sqrt{3}) t^{α}) E_{α} (- (1 - \sqrt{3}) t^{α}) . \end{matrix}

In particular, when

α = β = 1

, we have the exact solution

u (\overline{x}, t) = \sinh (x) \sinh (y) \sinh (z) \cosh (\sqrt{3} t) e^{- t}

for the

(3 + 1)

-D telegraph integer-version equation (Srivastava et al., 2017).

Example 3.3

Consider the following nonlinear $(3 + 1)$ -D Burgers’ equation in fractal 2D space:

(3.15)

\frac{\partial^{α} u (\overline{x}, t)}{\partial t^{α}} = \frac{\partial^{2 β} u (\overline{x}, t)}{\partial x^{2 β}} + \frac{\partial^{2} u (\overline{x}, t)}{\partial y^{2}} + \frac{\partial^{2} u (\overline{x}, t)}{\partial z^{2}} + u (\overline{x}, t) \frac{\partial^{β} u (\overline{x}, t)}{\partial x^{β}},

subject to the nonhomogeneous initial condition

(3.16)

u (\overline{x}, 0) = x^{β} + y + z .

Applying the initial condition into the ansatz (2.1), we get

f_{00} (y, z) = y + z, f_{01} (y, z) = 1

, and

f_{0 j} (y, z) = 0

for

j ⩾ 2

. Upon plugging all the relevant quantities (2.2) into (3.15) and solving the resulting difference-differential equations successively, we get

(3.17)

\begin{matrix} f_{i 0} (y, z) = (y + z) f_{i, 1} (y, z), & i ⩾ 0 \\ f_{ij} (y, z) = 0, & otherwise, \end{matrix}

where the coefficients

f_{i 1} (y, z)

are recursively given by

(3.18)

\begin{matrix} f_{11} (y, z) & = \frac{Γ (β + 1)}{Γ (α + 1)} \\ f_{i 1} (y, z) & = \frac{Γ ((i - 1) α + 1) Γ (β + 1)}{Γ (i α + 1)} \sum_{m = 1}^{k} 2 f_{m - 1, 1} (y, z) f_{i - m, 1} (y, z); i = 2 k \\ f_{i 1} (y, z) & = \frac{Γ ((i - 1) α + 1) Γ (β + 1)}{Γ (i α + 1)} (f_{k, 1}^{2} (y, z) + \sum_{m = 1}^{k} 2 f_{m - 1, 1} (y, z) f_{i - m, 1} (y, z)); i = 2 k + 1 . \end{matrix}

Therefore, the

n -

th approximate solution of (3.15) and (3.16) is given by

(3.19)

\begin{matrix} u_{n} (\overline{x}, t) & = \sum_{i + j = 0}^{n} f_{ij} (y, z) t^{i α} x^{j β} \\ = \sum_{i = 0}^{n} f_{i 0} (y, z) t^{i α} + \sum_{i = 0}^{n} f_{i 1} (y, z) t^{i α} x^{β} \\ = (x^{β} + y + z) \sum_{i = 0}^{n} f_{i 1} (y, z) t^{i α} . \end{matrix}

We remark here that

f_{i 1} (y, z) = 1

when

α = β = 1

. Therefore, the exact solution of the

(3 + 1)

-D Burgers’ integer-version equation is

(3.20)

u (\overline{x}, t) = \lim_{n \to \infty} u_{n} (\overline{x}, t) = (x + y + z) \sum_{i = 0}^{\infty} t^{i} = \frac{x + y + z}{1 - t},

as long as

t \in [0, 1)

3.2

3.2 (3 + 1)-D diffusion, telegraph, and Burgers’ equations in fractal 3D space

Example 3.4

Consider the following $(3 + 1)$ -D diffusion equation in fractal 3D space:

(3.21)

\frac{\partial^{α} u (\overline{x}, t)}{\partial t^{α}} = \frac{\partial^{2 β} u (\overline{x}, t)}{\partial x^{2 β}} + \frac{\partial^{2 γ} u (\overline{x}, t)}{\partial y^{2 γ}} + \frac{\partial^{2} u (\overline{x}, t)}{\partial z^{2}},

with initial condition

(3.22)

u (\overline{x}, 0) = (1 - y^{γ}) e^{z} E_{β} (x^{β}) .

We seek a solution to (3.21) and (3.22) in the form of (2.4). Substituting all the related formulas (2.5) into (3.21) and (3.22) and equating the coefficients of like terms from both sides, will give the following difference-differential equation for all

i, j ⩾ 0

(3.23)

\frac{Γ ((i + 1) α + 1)}{Γ (i α + 1)} f_{i + 1, j, k} (z) - \frac{Γ ((j + 2) β + 1)}{Γ (j β + 1)} f_{i, j + 2, k} (z) - \frac{Γ ((k + 2) γ + 1)}{Γ (k γ + 1)} f_{i, j, k + 2} (z) - \frac{\partial^{2} f_{ij} (y, z)}{\partial z^{2}} = 0,

subject to the initial conditions

(3.24)

\begin{matrix} f_{0 j 0} (z) & = \frac{e^{z}}{Γ (j β + 1)}, \\ f_{0 j 1} (z) & = \frac{- e^{z}}{Γ (j β + 1)}, \\ f_{0 jk} (z) & = 0 for k ⩾ 2 . \end{matrix}

Solving (3.23) and (3.24) successively yields that

f_{ij 1} (z) = - f_{ij 0} (z)

for

i, j ⩾ 0

and

f_{ijk} (z) = 0

otherwise, where

(3.25)

f_{ij 0} (z) = \frac{2^{i} e^{z}}{Γ (i α + 1) Γ (j β + 1)} .

Therefore, the exact solution of (3.21) and (3.22) is given by

(3.26)

\begin{matrix} u (\overline{x}, t) & = \sum_{i + j = 0}^{\infty} f_{ij 0} (z) t^{i α} x^{j β} - \sum_{i + j = 0}^{\infty} f_{ij 0} (z) t^{i α} x^{j β} y^{γ} \\ = (1 - y^{γ}) \sum_{i + j = 0}^{\infty} \frac{2^{i} e^{z}}{Γ (i α + 1) Γ (j β + 1)} t^{i α} x^{j β} \\ = (1 - y^{γ}) e^{z} (\sum_{j = 0}^{\infty} \frac{x^{j β}}{Γ (j β + 1)}) (\sum_{i = 0}^{\infty} \frac{2^{i} t^{i α}}{Γ (i α + 1)}) \\ = (1 - y^{γ}) e^{z} E_{β} (x^{β}) E_{α} (2 t^{α}) . \end{matrix}

In particular, when

γ = 1

, we have the same solution obtained in Example 3.1.

Fig. 1 represents the level curves behaviour of the 10th-approximate solution (3.26) labeled by the parameters $α, β$ , and $γ$ respectively. Apparently, the level curve when $α = β = γ = 1$ coincide with the level curve of the exact solution for the integer-order diffusion equation. This reveals the generality of these fractional models. Moreover, it is evident that the level curves are sequentially connected, as the fractional derivative parameters increase, to reach the exact solution of the corresponding integer-order case. To some extent, this behaviour indicates for an inherited memory.

Example 3.5

Consider the following $(3 + 1)$ -D telegraph equation in fractal 3D space:

(3.27)

\frac{\partial^{2 α} u (\overline{x}, t)}{\partial t^{2 α}} + 2 \frac{\partial^{α} u (\overline{x}, t)}{\partial t^{α}} + u (\overline{x}, t) = \frac{\partial^{2 β} u (\overline{x}, t)}{\partial x^{2 β}} + \frac{\partial^{2 γ} u (\overline{x}, t)}{\partial y^{2 γ}} + \frac{\partial^{2} u (\overline{x}, t)}{\partial z^{2}},

subject to the initial conditions

(3.28)

\begin{matrix} u (\overline{x}, 0) & = \sinh_{β} (x^{β}) \sinh_{γ} (y^{γ}) \sinh (z), \\ \frac{\partial^{α} u (\overline{x}, 0)}{\partial t^{α}} & = - \sinh_{β} (x^{β}) \sinh_{γ} (y^{γ}) \sinh (z) . \end{matrix}

Substituting all the associated formulas (2.5) into (3.27),(3.28) and gathering of like powers of indeterminate, we have the following difference-differential equation for all

i, j ⩾ 0

(3.29)

\begin{matrix} \frac{Γ ((i + 2) α + 1)}{Γ (i α + 1)} f_{i + 2, j, k} (z) + \frac{Γ ((i + 1) α + 1)}{Γ (i α + 1)} f_{i + 1, j, k} (z) + f_{i, j, k} (z) - \frac{Γ ((j + 2) β + 1)}{Γ (j β + 1)} f_{i, j + 2, k} (z) \\ - \frac{Γ ((k + 2) γ + 1)}{Γ (k γ + 1)} f_{i, j, k + 2} (z) - \frac{d^{2} f_{i, j, k} (z)}{{dz}^{2}} = 0, \end{matrix}

with initial conditions

(3.30)

\begin{matrix} f_{0, 2 j + 1, 2 k + 1} (z) & = \frac{\sinh (z)}{Γ ((2 j + 1) β + 1) Γ ((2 k + 1) γ + 1)}, \\ f_{1, 2 j + 1, 2 k + 1} (z) & = - \frac{\sinh (z)}{Γ (α + 1) Γ ((2 j + 1) β + 1) Γ ((2 k + 1) γ + 1)} . \end{matrix}

Thus, the exact solution of (3.27) and (3.28) is given by

(3.31)

\begin{matrix} u (\overline{x}, t) & = \sum_{i + j + k = 0}^{\infty} \frac{{(- 1)}^{i} ({(1 + \sqrt{3})}^{i} + {(1 - \sqrt{3})}^{i}) \sinh (z)}{2 Γ (i α + 1) Γ ((2 j + 1) β + 1) Γ ((2 k + 1) γ + 1)} t^{i α} x^{(2 j + 1) β} y^{(2 k + 1) γ} \\ = \frac{1}{2} \sinh (z) (\sum_{j = 0}^{\infty} \frac{x^{(2 j + 1) β}}{Γ ((2 j + 1) β + 1)}) (\sum_{k = 0}^{\infty} \frac{y^{(2 k + 1) γ}}{Γ ((2 k + 1) γ + 1)}) (\sum_{i = 0}^{\infty} \frac{{(- 1)}^{i} ({(1 + \sqrt{3})}^{i} + {(1 - \sqrt{3})}^{i}) t^{i α}}{Γ (i α + 1)}) \\ = \frac{1}{2} \sinh (z) \sinh_{β} (x^{β}) \sinh_{γ} (y^{γ}) E_{α} (- (1 + \sqrt{3}) t^{α}) E_{α} (- (1 - \sqrt{3}) t^{α}) . \end{matrix}

In particular, if

γ = 1

, we have the same solution obtained in Example 3.2.

Example 3.6

Finally, we consider the nonlinear $(3 + 1)$ -D Burgers’ equation in fractal 3D space:

(3.32)

\frac{\partial^{α} u (\overline{x}, t)}{\partial t^{α}} = \frac{\partial^{2 β} u (\overline{x}, t)}{\partial x^{2 β}} + \frac{\partial^{2 γ} u (\overline{x}, t)}{\partial y^{2 γ}} + \frac{\partial^{2} u (\overline{x}, t)}{\partial z^{2}} + u (\overline{x}, t) \frac{\partial^{β} u (\overline{x}, t)}{\partial x^{β}},

subject to the nonhomogeneous initial condition

(3.33)

u (\overline{x}, 0) = x^{β} + y^{γ} + z .

Applying the initial condition into the ansatz (2.4) leads to

f_{000} (z) = z, f_{010} (z) = 1, f_{001} (z) = 1

, and

f_{0 jk} (z) = 0

for

j, k ⩾ 2

. Upon substituting all the related quantities (2.5) into (3.32) and solving the resulting difference-differential equations successively, we obtain

(3.34)

\begin{matrix} f_{i 00} (z) & = {zf}_{i 10} (z) = {zf}_{i 01} (z), i ⩾ 0 \\ f_{ijk} (z) & = 0, otherwise, \end{matrix}

where the coefficients

f_{i 10} (z)

are recursively given by

(3.35)

\begin{matrix} f_{110} (z) & = \frac{Γ (β + 1)}{Γ (α + 1)} \\ f_{i 10} (z) & = \frac{Γ ((i - 1) α + 1) Γ (β + 1)}{Γ (i α + 1)} \sum_{m = 1}^{k} 2 f_{m - 1, 1, 0} (z) f_{i - m, 1, 0} (z); i = 2 k \\ f_{i 10} (z) & = \frac{Γ ((i - 1) α + 1) Γ (β + 1)}{Γ (i α + 1)} (f_{k, 1, 0}^{2} (z) + \sum_{m = 1}^{k} 2 f_{m - 1, 1, 0} (z) f_{i - m, 1, 0} (z)); i = 2 k + 1 . \end{matrix}

Therefore, the

n -

th approximate solution of (3.32) and (3.33) in fractal 3D space is

(3.36)

\begin{matrix} u_{n} (\overline{x}, t) & = \sum_{i + j + k = 0}^{n} f_{ijk} (y) t^{i α} x^{j β} y^{k γ} \\ = \sum_{i = 0}^{n} f_{i 00} (z) t^{i α} + \sum_{i = 0}^{n} f_{i 10} (z) t^{i α} x^{β} + \sum_{i = 0}^{n} f_{i 01} (z) t^{i α} y^{γ} \\ = z \sum_{i = 0}^{n} f_{i 10} (z) t^{i α} + x^{β} \sum_{i = 0}^{n} f_{i 10} (z) t^{i α} + y^{γ} \sum_{i = 0}^{n} f_{i 10} (z) t^{i α} \\ = (x^{β} + y^{γ} + z) \sum_{i = 0}^{n} f_{i 10} (z) t^{i α} . \end{matrix}

Again, for

γ = 1

, we have the same solution obtained in Example 3.3. Remarkably, when

α = β = γ = 1

, we have

f_{i 10} (z) = 1

and hence the exact solution for the

(3 + 1)

-D Burgers’ integer-version equation is

(3.37)

u (\overline{x}, t) = \lim_{n \to \infty} u_{n} (\overline{x}, t) = (y + z + x) \sum_{i = 0}^{\infty} t^{i} = \frac{x + y + z}{1 - t},

provided that

t \in [0, 1)

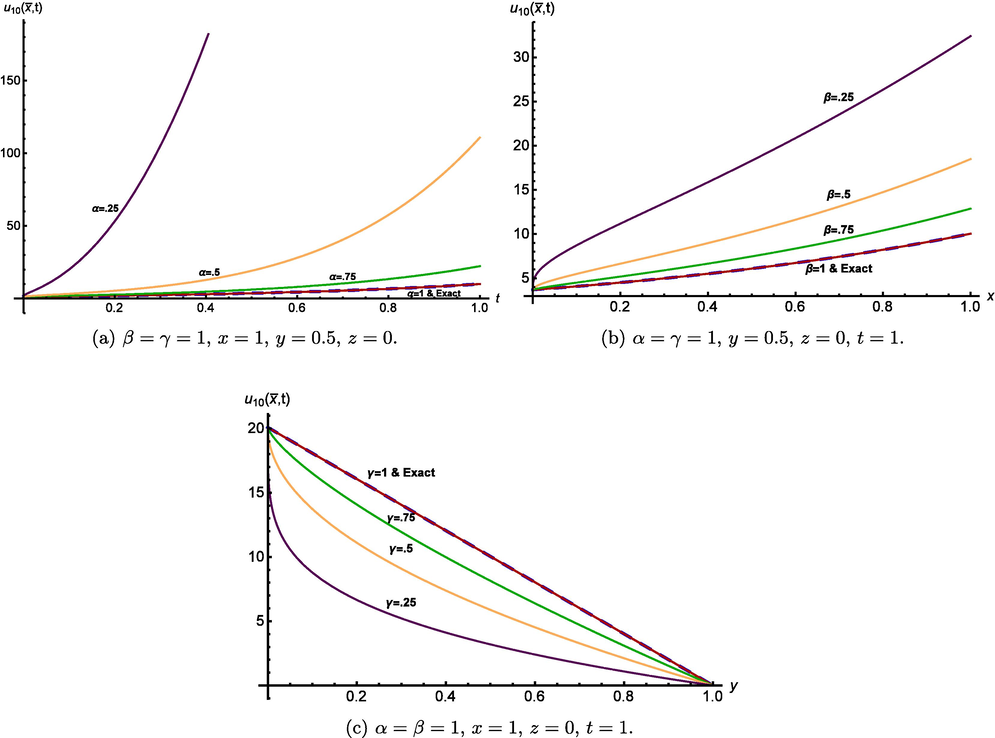
Level curves of the 10th-approximate solution (3.26).

4 Conclusion

In this work, we have presented two distinct series solution forms, namely (2.1) and (2.4), for $(3 + 1)$ -D partial differential equations that embedded into fractal 2D and 3D spaces respectively. The associated power series scheme is then employed to furnish a fractal closed-form solution for $(α, β) -$ and $(α, β, γ) -$ diffusion, telegraph, and Burgers’ equations. The obtained results exhibit the validity of our proposed solution forms without employing any fractional complex transformation, linearization, or perturbation. This exposes the potential of the proposed method and the propagation of fractional differential equations. Analogously, we can extend these solution forms to be customized into fractal 4D space as

(4.1)

\sum_{i + j + k + m = 0}^{\infty} c_{ijkm} t^{i α} x^{j β} y^{k γ} z^{m δ}

where

i, j, k, m \in N_{0}

and

α, β, γ, δ \in (0, 1]

are the fractional derivative parameters.

As future work, we intend to consider more physical models in fractal spaces that are related to optics (Aslan et al., 2017a,b; Inc et al., 2016, 2017a,b; Al Qurashi et al., 2017a,b,c; Tchier et al., 2016; Kilic and Inc, 2017; Aslan and Inc, 2017 ), where the unknown functions are of a complex-valued type. We believe that conducting similar schemes to study such hybrid models will be an important direction in optics.

Conflicts of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

Alquran M., Jaradat I., . A novel scheme for solving Caputo time-fractional nonlinear equations: theory and application. Nonlinear Dyn.. 2018;91(4):2389-2395.
[CrossRef] [Google Scholar]
Alquran M., Al-Khaled K., Tridip S., Chattopadhyay J., . Revisited Fisher’s equation in a new outlook: a fractional derivative approach. Physica A. 2015;438:81-93.
[CrossRef] [Google Scholar]
Al Qurashi M.M., Ates E., Inc M., . Optical solitons in multiple-core couplers with the nearest neighbors linear coupling. Optik. 2017;142:343-353.
[CrossRef] [Google Scholar]
Al Qurashi M.M., Yusuf A., Aliyu A.I., Inc M., . Optical and other solitons for the fourth-order dispersive nonlinear Schrödinger equation with dual-power law nonlinearity. Superlattice Microst.. 2017;105:183-197.
[CrossRef] [Google Scholar]
Al Qurashi M.M., Baleanu D., Inc M., . Optical solitons of transmission equation of ultra-short optical pulse in parabolic law media with the aid of Bäcklund transformation. Optik. 2017;140:114-122.
[CrossRef] [Google Scholar]
Aslan E.C., Inc M., . Soliton solutions of NLSE with quadratic-cubic nonlinearity and stability analysis. Wave Random Complex. 2017;27(4):594-601.
[CrossRef] [Google Scholar]
Aslan E.C., Inc M., Baleanu D., . Optical solitons and stability analysis of the NLSE with anti-cubic nonlinearity. Superlattice Microst.. 2017;109:784-793.
[CrossRef] [Google Scholar]
Aslan E.C., Tchier F., Inc M., . On optical solitons of the Schrödinger-Hirota equation with power law nonlinearity in optical fibers. Superlattice Microst.. 2017;105:48-55.
[CrossRef] [Google Scholar]
Atangana A., Baleanu D., . New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model. Therm. Sci.. 2016;20(2):763-769.
[CrossRef] [Google Scholar]
Bhrawy A.H., Alzaidy J.F., Abdelkawy M.A., Biswas A., . Jacobi spectral collocation approximation for multi-dimensional time-fractional Schrödinger equations. Nonlinear Dyn.. 2016;84(3):1553-1567.
[CrossRef] [Google Scholar]
Butera S., Paola M.D., . A physically based connection between fractional calculus and fractal geometry. Ann. Phys.. 2014;350:146-158.
[CrossRef] [Google Scholar]
Caputo M., Fabrizio M., . A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl.. 2015;1(2):73-85.
[Google Scholar]
Coronel-Escamilla A., Gómez-Aguilar J.F., Baleanu D., Córdova-Fraga T., Escobar-Jiménez R.F., Olivares-Peregrino V.H., Qurashi M.M., . Bateman-Feshbach Tikochinsky and Caldirola-Kanai oscillators with new fractional differentiation. Entropy. 2017;19(2):55.
[CrossRef] [Google Scholar]
Coussot C., Kalyanam S., Yapp R., Insana M., . Fractional derivative models for ultrasonic characterization of polymer and breast tissue viscoelasticity. IEEE Trans. Ultrason. Ferroelectr., Freq. Control. 2009;56(4):715-725.
[CrossRef] [Google Scholar]
Du M., Wang Z., Hu H., . Measuring memory with the order of fractional derivative. Sci. Rep.. 2013;3 3431-01-03
[CrossRef] [Google Scholar]
Gómez-Aguilar J.F., . Irving-Mullineux oscillator via fractional derivatives with Mittag-Leffler kernel. Chaos Solitons Fract.. 2017;95:179-186.
[CrossRef] [Google Scholar]
Gómez-Aguilar J.F., . Chaos in a nonlinear Bloch system with Atangana-Baleanu fractional derivatives. Numer. Methods Partial Differ. Equ.. 2017;1–23
[CrossRef] [Google Scholar]
Gómez-Aguilar J.F., Córdova-Fraga T., Tórres-Jiménez J., Escobar-Jiménez R.F., Olivares-Peregrino V.H., Guerrero-Ramírez G.V., . Nonlocal transport processes and the fractional Cattaneo-Vernotte equation. Math. Probl. Eng.. 2016;2016 ID: 7845874
[CrossRef] [Google Scholar]
Gómez-Aguilar J.F., Torres L., Ypéz-Martnez H., Baleanu D., Reyes J.M., Sosa I.O., . Fractional Liénard type model of a pipeline within the fractional derivative without singular kernel. Adv. Differ. Equ.. 2016;2016:173.
[CrossRef] [Google Scholar]
Gómez-Aguilar J.F., López-López M.G., Alvarado-Martínez V.M., Reyes-Reyes J., Adam-Medina M., . Modeling diffusive transport with a fractional derivative without singular kernel. Phys. A. 2016;447:467-481.
[CrossRef] [Google Scholar]
Hilfer R., . Fractional Calculus, Applications in Physics. Singapore: World Scientific; 2000.
Inc M., Ates E., Tchier F., . Optical solitons of the coupled nonlinear Schrödinger’s equation with spatiotemporal dispersion. Nonlinear Dyn.. 2016;85(2):1319-1329.
[CrossRef] [Google Scholar]
Inc M., Aliyu A.I., Yusuf A., . Solitons and conservation laws to the resonance nonlinear Schrödinger’s equation with both spatio-temporal and inter-modal dispersions. Optik. 2017;142:509-522.
[CrossRef] [Google Scholar]
Inc M., Aliyu A.I., Yusuf A., Baleanu D., . Optical solitons and modulation instability analysis of an integrable model of $(2 + 1) -$ Dimensional Heisenberg ferromagnetic spin chain equation. Superlattice Microst.. 2017;112:628-638.
[CrossRef] [Google Scholar]
Jaradat I., Alquran M., Al-Khaled K., . An analytical study of physical models with inherited temporal and spatial memory. Eur. Phys. J. Plus. 2018;133:162.
[CrossRef] [Google Scholar]
Jaradat I., Alquran M., Abdel-Muhsen R., . An analytical framework of 2D diffusion, wave-like, telegraph, and Burgers’ models with twofold Caputo derivatives ordering. Nonlinear Dyn. 2018
[CrossRef] [Google Scholar]
Jaradat I., Alquran M., Al-Dolat M., . Analytic solution of homogeneous time-invariant fractional IVP. Adv. Differ. Equ.. 2018;2018:143.
[CrossRef] [Google Scholar]
Jaradat I., Al-Dolat M., Al-Zoubi K., Alquran M., . Theory and applications of a more general form for fractional power series expansion. Chaos Solitons Fract.. 2018;108:107-110.
[CrossRef] [Google Scholar]
Kilic B., Inc M., . Optical solitons for the Schrödinger-Hirota equation with power law nonlinearity by the Bäcklund transformation. Optik. 2017;138:64-67.
[CrossRef] [Google Scholar]
Koca I., Atangana A., . Solutions of cattaneo-hristov model of elastic heat diffusion with caputo-fabrizio and atangana-baleanu fractional derivatives. Therm. Sci.. 2016;21(6):2299-2305.
[CrossRef] [Google Scholar]
Koeller R.C., . Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech.. 1984;51(2):299-307.
[CrossRef] [Google Scholar]
Kumar D., Singh J., Kumar S., . Numerical computation of fractional multi-dimensional diffusion equations by using a modified homotopy perturbation method. J. Asso. Arab. Univ. Basic Appl. Sci.. 2015;17:20-26.
[CrossRef] [Google Scholar]
Kumar S., Kumar A., Baleanu D., . Two analytical methods for time-fractional nonlinear coupled Boussinesq–Burger’s equations arise in propagation of shallow water waves. Nonlinear Dyn.. 2016;85(2):699-715.
[CrossRef] [Google Scholar]
Le K.N., McLean W., Mustapha K., . Numerical solution of the time-fractional Fokker-Planck equation with general forcing. SIAM J. Numer. Anal.. 2016;54(3):1763-1784.
[CrossRef] [Google Scholar]
Magin R.L., . Fractional Calculus in Bioengineering. Connecticut: Begell Houuse Publishers; 2006.
Mainardi F., . Fractional Calculus and Waves in Linear Viscoelasticity. London: Imperial College Press; 2008.
Mainardi F., Paradisi P., . Fractional diffusive waves. J. Comp. Acous.. 2001;9(4):1417-1436.
[CrossRef] [Google Scholar]
Mirza I.A., Vieru D., . Fundamental solutions to advection-diffusion equation with time-fractional Caputo-Fabrizio derivative. Comput. Math. Appl.. 2017;73:1-10.
[CrossRef] [Google Scholar]
Morales-Delgado V.F., Gómez-Aguilar J.F., Taneco-Hernandez M.A., . Analytical solutions for the motion of a charged particle in electric and magnetic fields via non-singular fractional derivatives. Eur. Phys. J. Plus. 2017;132:527.
[CrossRef] [Google Scholar]
Nigmatullin R.R., . To the theoretical explanation of the universal response. Phys. Stat. Solidi B. 2009;123(2):739-745.
[CrossRef] [Google Scholar]
Pandey V., Holm S., . Linking the fractional derivative and the Lomnitz creep law to non-Newtonian time-varying viscosity. Phys. Rev. E. 2016;94(3):;1. 032606-01-06
[CrossRef] [Google Scholar]
Rossikhin A., Shitikova M.V., . Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. Appl. Mech. Rev.. 2009;63(1) 1010801-01-51
[CrossRef] [Google Scholar]
Singh B.K., Srivastava V.K., . Approximate series solution of multi-dimensional, time fractional-order (heat-like) diffusion equations using FRDTM. R. Soc. Open Sci.. 2015;2(4) 140511-01-13
[CrossRef] [Google Scholar]
Srivastava V.K., Awasthi M.K., Chaurasia R.K., . Reduced differential transform method to solve two and three dimensional second order hyperbolic telegraphic equations. J. King Saud Univ. Eng. Sci.. 2017;29(2):166-171.
[CrossRef] [Google Scholar]
Tchier F., Aslan E.C., Inc M., . Optical solitons in parabolic law medium: Jacobi elliptic function solution. Nonlinear Dyn.. 2016;85(4):2577-2582.
[CrossRef] [Google Scholar]
Wharmby A.W., Bagley R.L., . Generalization of a theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol.. 2013;57(5):1429-1440.
[CrossRef] [Google Scholar]

Introduction

Solution representations in fractal 2D and 3D spaces

Applications

(3 + 1)-D diffusion, telegraph, and Burgers’ equations in fractal 2D space
(3 + 1)-D diffusion, telegraph, and Burgers’ equations in fractal 3D space

Conclusion

Conflicts of interest

Fulltext Views
22

PDF downloads
10

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Alquran M., Jaradat I., . A novel scheme for solving Caputo time-fractional nonlinear equations: theory and application. Nonlinear Dyn.. 2018;91(4):2389-2395.
[CrossRef] [Google Scholar]

[2] Alquran M., Al-Khaled K., Tridip S., Chattopadhyay J., . Revisited Fisher’s equation in a new outlook: a fractional derivative approach. Physica A. 2015;438:81-93.
[CrossRef] [Google Scholar]

[3] Al Qurashi M.M., Ates E., Inc M., . Optical solitons in multiple-core couplers with the nearest neighbors linear coupling. Optik. 2017;142:343-353.
[CrossRef] [Google Scholar]

[4] Al Qurashi M.M., Yusuf A., Aliyu A.I., Inc M., . Optical and other solitons for the fourth-order dispersive nonlinear Schrödinger equation with dual-power law nonlinearity. Superlattice Microst.. 2017;105:183-197.
[CrossRef] [Google Scholar]

[5] Al Qurashi M.M., Baleanu D., Inc M., . Optical solitons of transmission equation of ultra-short optical pulse in parabolic law media with the aid of Bäcklund transformation. Optik. 2017;140:114-122.
[CrossRef] [Google Scholar]

[6] Aslan E.C., Inc M., . Soliton solutions of NLSE with quadratic-cubic nonlinearity and stability analysis. Wave Random Complex. 2017;27(4):594-601.
[CrossRef] [Google Scholar]

[7] Aslan E.C., Inc M., Baleanu D., . Optical solitons and stability analysis of the NLSE with anti-cubic nonlinearity. Superlattice Microst.. 2017;109:784-793.
[CrossRef] [Google Scholar]

[8] Aslan E.C., Tchier F., Inc M., . On optical solitons of the Schrödinger-Hirota equation with power law nonlinearity in optical fibers. Superlattice Microst.. 2017;105:48-55.
[CrossRef] [Google Scholar]

[9] Atangana A., Baleanu D., . New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model. Therm. Sci.. 2016;20(2):763-769.
[CrossRef] [Google Scholar]

[10] Bhrawy A.H., Alzaidy J.F., Abdelkawy M.A., Biswas A., . Jacobi spectral collocation approximation for multi-dimensional time-fractional Schrödinger equations. Nonlinear Dyn.. 2016;84(3):1553-1567.
[CrossRef] [Google Scholar]

[11] Butera S., Paola M.D., . A physically based connection between fractional calculus and fractal geometry. Ann. Phys.. 2014;350:146-158.
[CrossRef] [Google Scholar]

[12] Caputo M., Fabrizio M., . A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl.. 2015;1(2):73-85.
[Google Scholar]

[13] Coronel-Escamilla A., Gómez-Aguilar J.F., Baleanu D., Córdova-Fraga T., Escobar-Jiménez R.F., Olivares-Peregrino V.H., Qurashi M.M., . Bateman-Feshbach Tikochinsky and Caldirola-Kanai oscillators with new fractional differentiation. Entropy. 2017;19(2):55.
[CrossRef] [Google Scholar]

[14] Coussot C., Kalyanam S., Yapp R., Insana M., . Fractional derivative models for ultrasonic characterization of polymer and breast tissue viscoelasticity. IEEE Trans. Ultrason. Ferroelectr., Freq. Control. 2009;56(4):715-725.
[CrossRef] [Google Scholar]

[15] Du M., Wang Z., Hu H., . Measuring memory with the order of fractional derivative. Sci. Rep.. 2013;3 3431-01-03
[CrossRef] [Google Scholar]

[16] Gómez-Aguilar J.F., . Irving-Mullineux oscillator via fractional derivatives with Mittag-Leffler kernel. Chaos Solitons Fract.. 2017;95:179-186.
[CrossRef] [Google Scholar]

[17] Gómez-Aguilar J.F., . Chaos in a nonlinear Bloch system with Atangana-Baleanu fractional derivatives. Numer. Methods Partial Differ. Equ.. 2017;1–23
[CrossRef] [Google Scholar]

[18] Gómez-Aguilar J.F., Córdova-Fraga T., Tórres-Jiménez J., Escobar-Jiménez R.F., Olivares-Peregrino V.H., Guerrero-Ramírez G.V., . Nonlocal transport processes and the fractional Cattaneo-Vernotte equation. Math. Probl. Eng.. 2016;2016 ID: 7845874
[CrossRef] [Google Scholar]

[19] Gómez-Aguilar J.F., Torres L., Ypéz-Martnez H., Baleanu D., Reyes J.M., Sosa I.O., . Fractional Liénard type model of a pipeline within the fractional derivative without singular kernel. Adv. Differ. Equ.. 2016;2016:173.
[CrossRef] [Google Scholar]

[20] Gómez-Aguilar J.F., López-López M.G., Alvarado-Martínez V.M., Reyes-Reyes J., Adam-Medina M., . Modeling diffusive transport with a fractional derivative without singular kernel. Phys. A. 2016;447:467-481.
[CrossRef] [Google Scholar]

[21] Hilfer R., . Fractional Calculus, Applications in Physics. Singapore: World Scientific; 2000.

[22] Inc M., Ates E., Tchier F., . Optical solitons of the coupled nonlinear Schrödinger’s equation with spatiotemporal dispersion. Nonlinear Dyn.. 2016;85(2):1319-1329.
[CrossRef] [Google Scholar]

[23] Inc M., Aliyu A.I., Yusuf A., . Solitons and conservation laws to the resonance nonlinear Schrödinger’s equation with both spatio-temporal and inter-modal dispersions. Optik. 2017;142:509-522.
[CrossRef] [Google Scholar]

[24] Inc M., Aliyu A.I., Yusuf A., Baleanu D., . Optical solitons and modulation instability analysis of an integrable model of $(2 + 1) -$ Dimensional Heisenberg ferromagnetic spin chain equation. Superlattice Microst.. 2017;112:628-638.
[CrossRef] [Google Scholar]

[25] Jaradat I., Alquran M., Al-Khaled K., . An analytical study of physical models with inherited temporal and spatial memory. Eur. Phys. J. Plus. 2018;133:162.
[CrossRef] [Google Scholar]

[26] Jaradat I., Alquran M., Abdel-Muhsen R., . An analytical framework of 2D diffusion, wave-like, telegraph, and Burgers’ models with twofold Caputo derivatives ordering. Nonlinear Dyn. 2018
[CrossRef] [Google Scholar]

[27] Jaradat I., Alquran M., Al-Dolat M., . Analytic solution of homogeneous time-invariant fractional IVP. Adv. Differ. Equ.. 2018;2018:143.
[CrossRef] [Google Scholar]

[28] Jaradat I., Al-Dolat M., Al-Zoubi K., Alquran M., . Theory and applications of a more general form for fractional power series expansion. Chaos Solitons Fract.. 2018;108:107-110.
[CrossRef] [Google Scholar]

[29] Kilic B., Inc M., . Optical solitons for the Schrödinger-Hirota equation with power law nonlinearity by the Bäcklund transformation. Optik. 2017;138:64-67.
[CrossRef] [Google Scholar]

[30] Koca I., Atangana A., . Solutions of cattaneo-hristov model of elastic heat diffusion with caputo-fabrizio and atangana-baleanu fractional derivatives. Therm. Sci.. 2016;21(6):2299-2305.
[CrossRef] [Google Scholar]

[31] Koeller R.C., . Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech.. 1984;51(2):299-307.
[CrossRef] [Google Scholar]

[32] Kumar D., Singh J., Kumar S., . Numerical computation of fractional multi-dimensional diffusion equations by using a modified homotopy perturbation method. J. Asso. Arab. Univ. Basic Appl. Sci.. 2015;17:20-26.
[CrossRef] [Google Scholar]

[33] Kumar S., Kumar A., Baleanu D., . Two analytical methods for time-fractional nonlinear coupled Boussinesq–Burger’s equations arise in propagation of shallow water waves. Nonlinear Dyn.. 2016;85(2):699-715.
[CrossRef] [Google Scholar]

[34] Le K.N., McLean W., Mustapha K., . Numerical solution of the time-fractional Fokker-Planck equation with general forcing. SIAM J. Numer. Anal.. 2016;54(3):1763-1784.
[CrossRef] [Google Scholar]

[35] Magin R.L., . Fractional Calculus in Bioengineering. Connecticut: Begell Houuse Publishers; 2006.

[36] Mainardi F., . Fractional Calculus and Waves in Linear Viscoelasticity. London: Imperial College Press; 2008.

[37] Mainardi F., Paradisi P., . Fractional diffusive waves. J. Comp. Acous.. 2001;9(4):1417-1436.
[CrossRef] [Google Scholar]

[38] Mirza I.A., Vieru D., . Fundamental solutions to advection-diffusion equation with time-fractional Caputo-Fabrizio derivative. Comput. Math. Appl.. 2017;73:1-10.
[CrossRef] [Google Scholar]

[39] Morales-Delgado V.F., Gómez-Aguilar J.F., Taneco-Hernandez M.A., . Analytical solutions for the motion of a charged particle in electric and magnetic fields via non-singular fractional derivatives. Eur. Phys. J. Plus. 2017;132:527.
[CrossRef] [Google Scholar]

[40] Nigmatullin R.R., . To the theoretical explanation of the universal response. Phys. Stat. Solidi B. 2009;123(2):739-745.
[CrossRef] [Google Scholar]

[41] Pandey V., Holm S., . Linking the fractional derivative and the Lomnitz creep law to non-Newtonian time-varying viscosity. Phys. Rev. E. 2016;94(3):;1. 032606-01-06
[CrossRef] [Google Scholar]

[42] Rossikhin A., Shitikova M.V., . Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. Appl. Mech. Rev.. 2009;63(1) 1010801-01-51
[CrossRef] [Google Scholar]

[43] Singh B.K., Srivastava V.K., . Approximate series solution of multi-dimensional, time fractional-order (heat-like) diffusion equations using FRDTM. R. Soc. Open Sci.. 2015;2(4) 140511-01-13
[CrossRef] [Google Scholar]

[44] Srivastava V.K., Awasthi M.K., Chaurasia R.K., . Reduced differential transform method to solve two and three dimensional second order hyperbolic telegraphic equations. J. King Saud Univ. Eng. Sci.. 2017;29(2):166-171.
[CrossRef] [Google Scholar]

[45] Tchier F., Aslan E.C., Inc M., . Optical solitons in parabolic law medium: Jacobi elliptic function solution. Nonlinear Dyn.. 2016;85(4):2577-2582.
[CrossRef] [Google Scholar]

[46] Wharmby A.W., Bagley R.L., . Generalization of a theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol.. 2013;57(5):1429-1440.
[CrossRef] [Google Scholar]

Embedding (3 + 1)-dimensional diffusion, telegraph, and Burgers’ equations into fractal 2D and 3D spaces: An analytical study

Abstract

Keywords

26A33

41A58

35R11

35C10

Fractional derivatives

Fractional differential equations

Series solutions

1 Introduction

2 Solution representations in fractal 2D and 3D spaces

3 Applications

3.1 (3 + 1)-D diffusion, telegraph, and Burgers’ equations in fractal 2D space

3.2 (3 + 1)-D diffusion, telegraph, and Burgers’ equations in fractal 3D space

4 Conclusion

Conflicts of interest

References

Suggested read for related articles:

Embedding (3 + 1)-dimensional diffusion, telegraph, and Burgers’ equations into fractal 2D and 3D spaces: An analytical study

3.1 (3 + 1)-D diffusion, telegraph, and Burgers’ equations in fractal 2D space

3.2 (3 + 1)-D diffusion, telegraph, and Burgers’ equations in fractal 3D space