Translate this page into:
Effects on magnetic field in squeezing flow of a Casson fluid between parallel plates
⁎Corresponding author. syedtauseefs@hotmail.com (Syed Tauseef Mohyud-Din)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Squeezing flow of an electrically conducting Casson fluid has been taken into account. The laws of conservations under the similarity transformation suggested by Wang (1976) have been used to extract a highly nonlinear ordinary differential equation governing the magneto hydrodynamic (MHD) flow. Resulting equation has been solved analytically by using the variation of parameters method (VPM). A RK-4 numerical solution has also been sought to examine the validity of analytical results. Both the solutions are found to be in an excellent agreement. Convergence of the solution is also discussed. Flow behavior under the modifying involved physical parameters is also discussed and explained in detail with the graphical aid. It is observed that magnetic field can be used as a control phenomenon in many flows as it normalizes the flow behavior. Also, squeeze number plays an important role in these types of problems and an increase in squeeze number increases the velocity profile.
Keywords
Squeezing flows
Variation of parameters method (VPM)
Magneto hydrodynamic (MHD)
Parallel plates
Casson fluid
1 Introduction
Many mechanical equipment work under the principle of moving pistons where two plates exhibit the squeezing movement normal to their own surfaces. Electric motors, engines and hydraulic lifters also have this clutching flow in some of their parts. Due to this practical significance squeezing flow between parallel plates has become one of the most active research fields in fluid mechanics. Its biological applications are also of equal importance. Flow inside syringes and nasogastric tubes is also a kind of squeezing flows.
Foundational work regarding squeezing flows can be named to Stefan (1874) who presented basic formulation of these types of flows under lubrication assumption. After him numbers of scientist have shown their interests toward squeezing flows and have carried out many scientific studies to understand these flows. Some of selected contributions are mentioned in forthcoming lines.
1986 Reynolds (1886) investigated the squeezing flow between elliptic plates. Archibald (1956) considered the same problem for rectangular plates. After that several attempts have been made by different researchers to understand squeezing flows in a better way (Grimm, 1976; Wolfe, 1965; Kuzma, 1968; Tichy and Winer, 1970; Jackson, 1962).
Earlier studies on squeezing flows were based on Reynolds equation whose insufficiency for some cases has been shown by Jackson (1962) and Usha and Sridharan (1996). Due to efforts of Birkhoff (1960), Yang (1958) and Wang and Watson (1979) more flexible and useful similarity transforms are now available. These similarity transforms reduce the Navier–Stokes equation into a fourth order nonlinear ordinary differential equation and have further been used in some other investigations as well (Wang, 1976; Laun et al., 1999; Hamdan and Baron, 1992; Nhan, 2000; Rashidi et al., 2008).
Flow of electrically conducting non-Newtonian fluid is a very important phenomenon as in most of the practical situations we have to deal with the flow of conducting fluid which exhibits different behaviors under the influence of magnetic forces. In these cases magneto hydro dynamic (MHD) aspect of the flow is also needed to be considered. Homotopy perturbation solution for Two-dimensional MHD squeezing flow between parallel plates has been determined by Siddiqui et al. (2008). Domairry and Aziz (2009) investigated the same problem for the flow between parallel disks. Recently, Mustafa et al. (2012) examined heat and mass transfer for squeezing flow between parallel plates using the homotopy analysis method (HAM).
In most of realistic models the fluids involved are not simple Newtonian. Complex rheological properties of non-Newtonian fluids cannot be captured by a single model. Different mathematical models have been used to study different types of non-Newtonian fluids. One of such models is known as Casson fluid model. (Mrill et al., 1965; McDonald, 1974) showed that it is the most compatible formulation to simulate blood type fluid flows. It is clear from the literature survey that the squeezing flow of a Casson fluid between the plates moving normal to their own surface is yet to be inspected.
Due to the inherent nonlinearity of the equations governing the fluid flow exact solutions are very rare. Even where they are available immense simplification assumptions have been imposed. Those overly imposed suppositions may not be used for more realistic flows. However to deal with this hurdle many analytical approximation techniques have been developed which are commonly used nowadays (Abbasbandy, 2007a; Abbasbandy, 2007b; Abdou and Soliman, 2005; Noor and Mohyud-Din, 2007; Asadullah et al., 2013; Khan et al., 2012; Ahmed et al., 2014). Variation of parameters method (VPM) is one of these recently developed analytical techniques that have been used to solve different problems (Khan et al., 2014; Noor et al., 2008; Mohyud-Din et al., 2009; Khan et al., 2014a; Khan et al., 2014b; Khan et al., 2014c; Zaidi et al., 2013).
A literature survey reveals that no attempt has ever been made to study the MHD squeezing flow of a Casson fluid. So, in this paper we have presented a comprehensive study for this problem. VPM has been applied to study the nonlinear ordinary differential equation. A numerical solution to the problem has also been sought by using the Runge Kutta order 4 method. Comparison between both the solutions shows that the results obtained by VPM are in excellent agreement with the numerical results.
2 Governing equations
We consider an incompressible flow of a Casson fluid between two parallel plates separated by a distance
, where l is the initial gap between the plates (at a time
). Additionally
corresponds to a squeezing motion of both the plates until they touch each other at
, for
the plates bear a receding motion and dilate as described in Fig. a. Rheological equation for Casson fluid is defined as under (Nadeem et al., 2012; Nadeem et al., 2013; Nadeem et al., 2014a; Nadeem et al., 2014b; Nadeem et al., 2014c; Ahmed et al., 2013; Casson, 1959; Akber and Khan, 2015; Akbar et al., 2014; Nakamura and Sawada, 1987; Nakamura and Sawada, 1988)
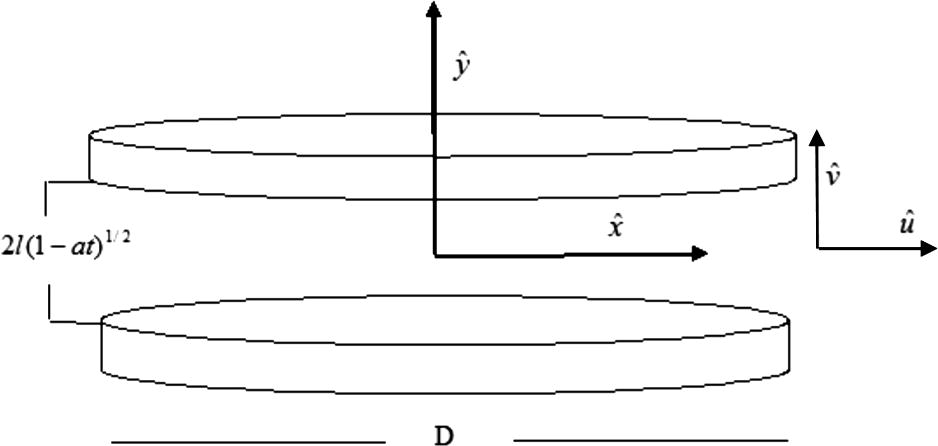
Schematic diagram for the flow problem.
A constant magnetic field of strength is imposed perpendicular and relatively fixed to the walls. We are also applying the following assumptions on the flow model:
-
The effects of induced magnetic and electric fields produced due to the flow of electrically conducting fluid are negligible.
-
No external electric field is present.
Under aforementioned constraints the conservation equations for the flow are:
Supporting conditions for the problem are as follows
We can simplify the above system of equations by eliminating the pressure terms from Eqs. (2) and (3) and using Eq. (1). After cross differentiation and introducing vorticity ω we get
Transform introduced by Wang (1976) for a two-dimensional flow is sated as
Substituting Eqs. (7)–(9) in Eq. (5) using (6), we obtain a nonlinear ordinary differential equation describing the Casson fluid flow as
Here, squeeze number S describes the movement of the plates (S > 0 corresponds to the plates moving apart, while S < 0 corresponds to collapsing movement of the plates). It is pertinent to mention here that for M = 0 and γ → ∞, our study reduces to the one obtained by Wang (1976).
Skin friction coefficient is defined as
In terms of Eqs. (7)–(9), we have
3 Solution procedure
Using the standard procedure for VPM (Noor et al., 2008; Mohyud-Din et al., 2009; Khan et al., 2014a; Khan et al., 2014b; Khan et al., 2014c; Zaidi et al., 2013), we can write Eq. (10) as
Here,
and
are the constants obtained by taking the highest order linear term of the Eq. (10) and integrating it 4 times to get the final form of the scheme. Using the boundary conditions given in Eq. (11), the above equation can be written as
First few terms of the solution are given as
4 Results and discussions
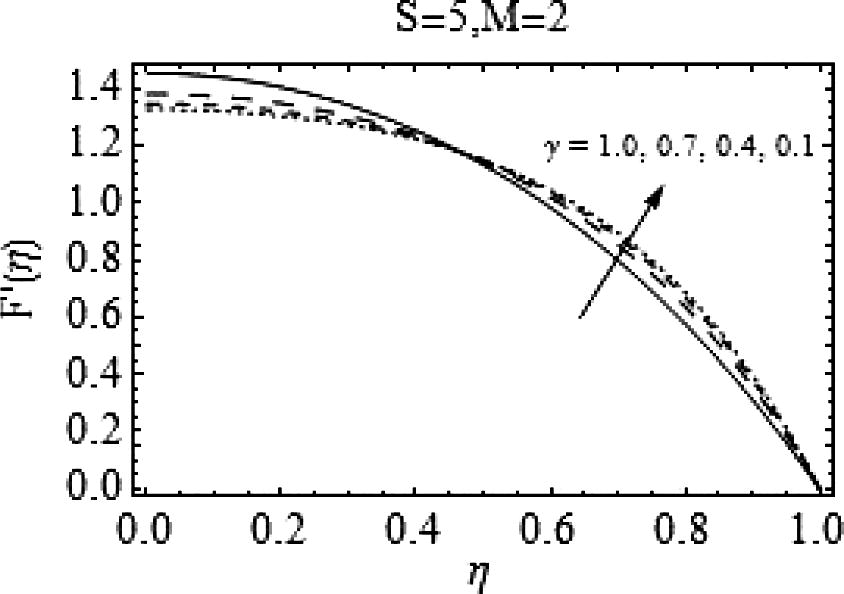
In this section the influences of squeeze number S, Casson fluid parameter γ and the magnetic number M on the axial (F(η))and radial (F′|(η)) velocities are characterized. Figs. 1–16 are displayed for the said purpose. First eight figures are for the case when the plates are moving apart (S > 0). Fig. 1 depicts the effects of increasing values of squeeze number Son the axial velocity F(η). It is clear, increasing S results in a decreased axial velocity. Effects of rising S on radial velocity are shown in Fig. 2. For increasing S, a decrease in F′(η) is observed when
. However, there is an increase in F′(η) for
. Fig. 3 illustrates the behavior of Casson fluid parameter γ on F(η). Increase in γ decelerates the axial flow. Effects of growing γ on radial velocity are shown in Fig. 4. Increasing γ decreases F′(η) for
and a rise in F′(η) is observed for
.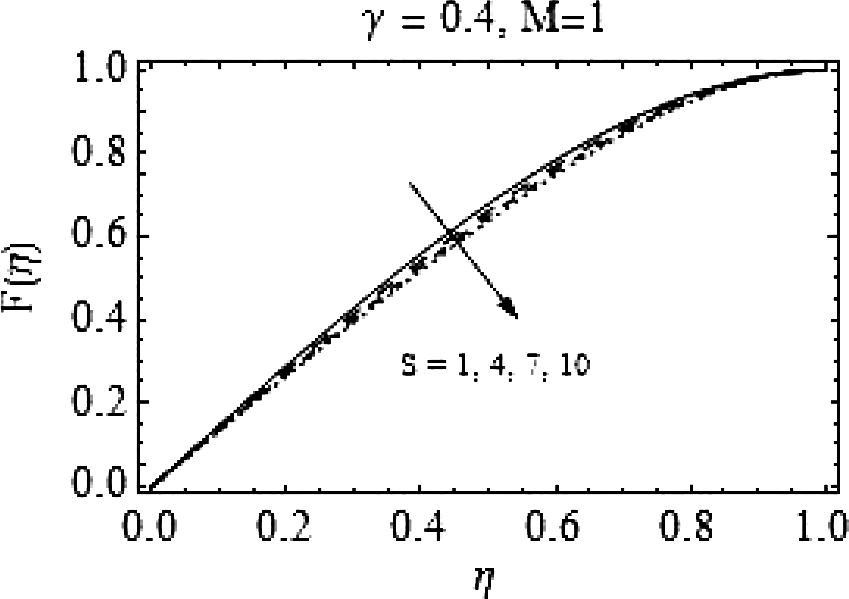
Effects of positive values of S on
.
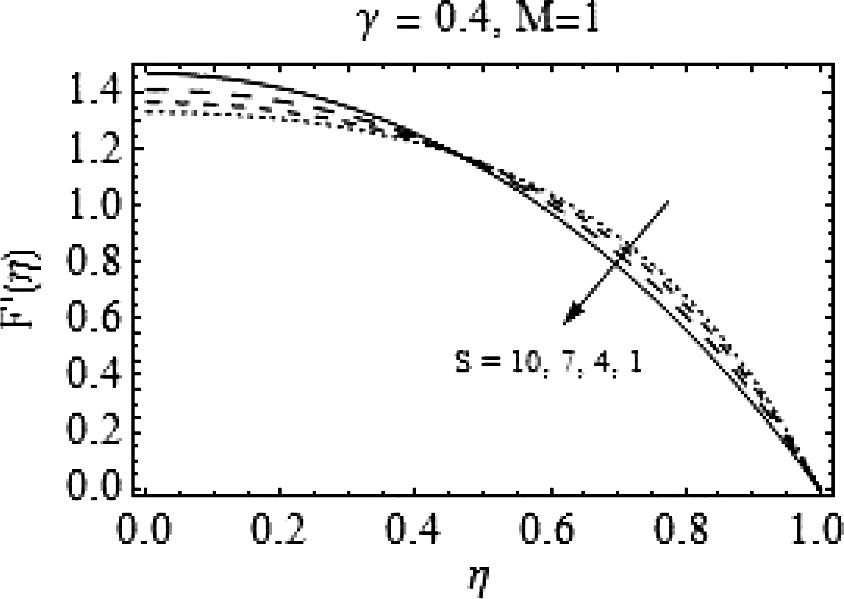
Effects of positive values of S on
.
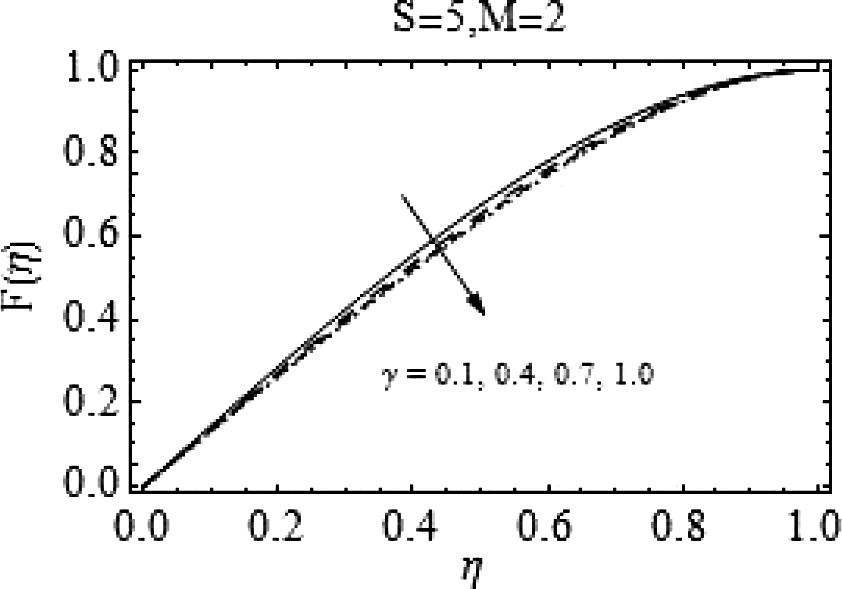
Effects of
on
.
Effects of
on
.
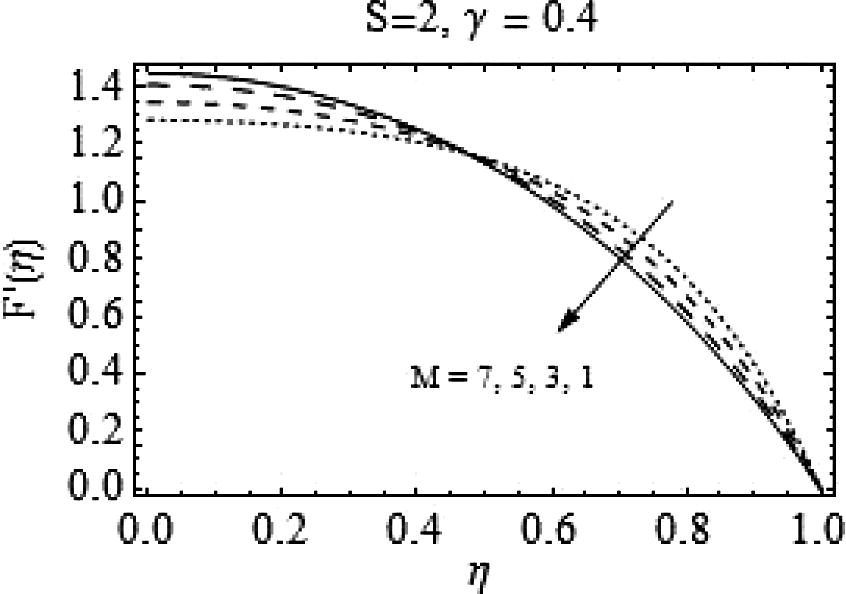
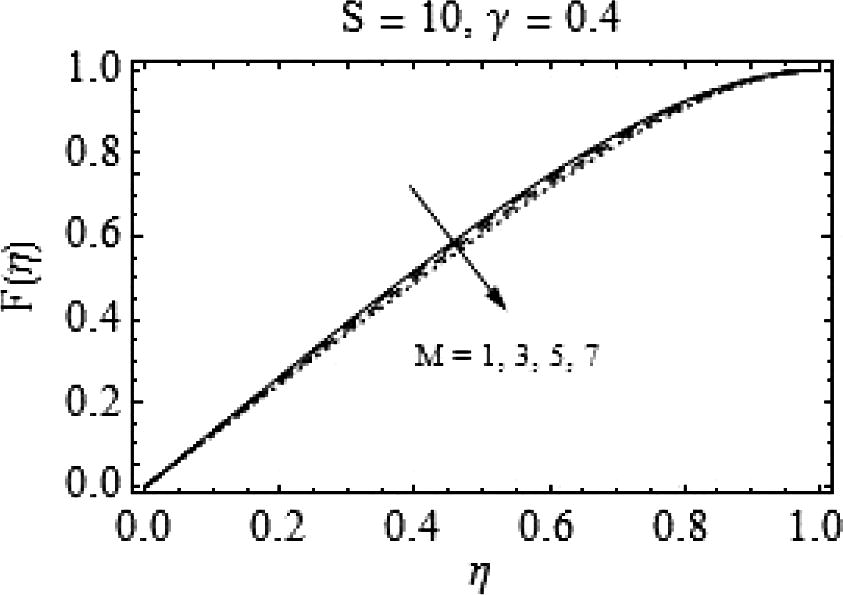
In Figs. 5–8, the consequences of varying magnetic number M on F(η) and F′(η) are portrayed. It can be observed from Fig. 5 that for increasing M, there is a decrease in F(η) for slightly lower values of squeeze number S; while for
, the increase in M provides a velocity profile similar to the case of increasing S. That is, increasing the magnitude of magnetic field fallouts in a uniform decrease in the velocity. Figs. 7 and 8 are drawn to analyze the effects of magnetic field for slightly higher values of squeeze number S. The behavior of axial and radial velocities remains almost similar to lower S.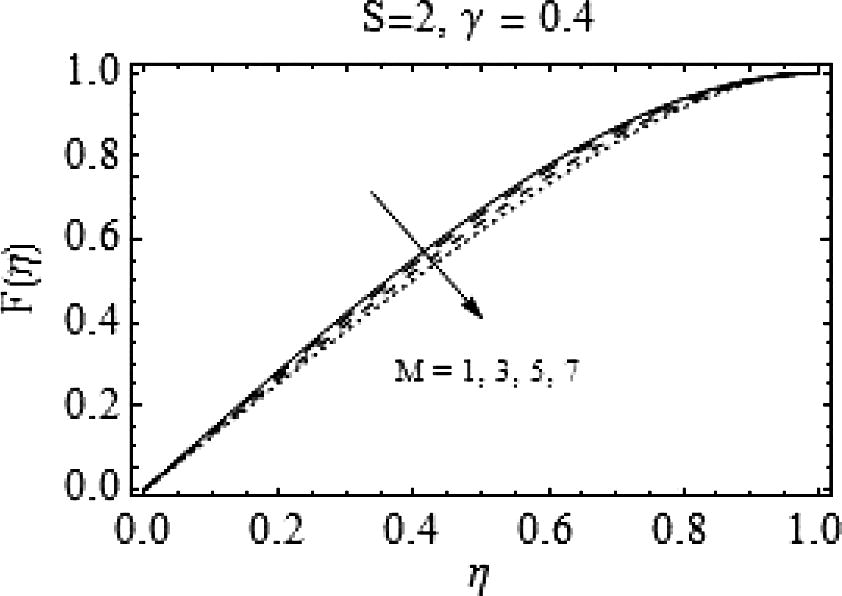
Effects of Mon
.
Effects of Mon
.
Effects of Mon
.
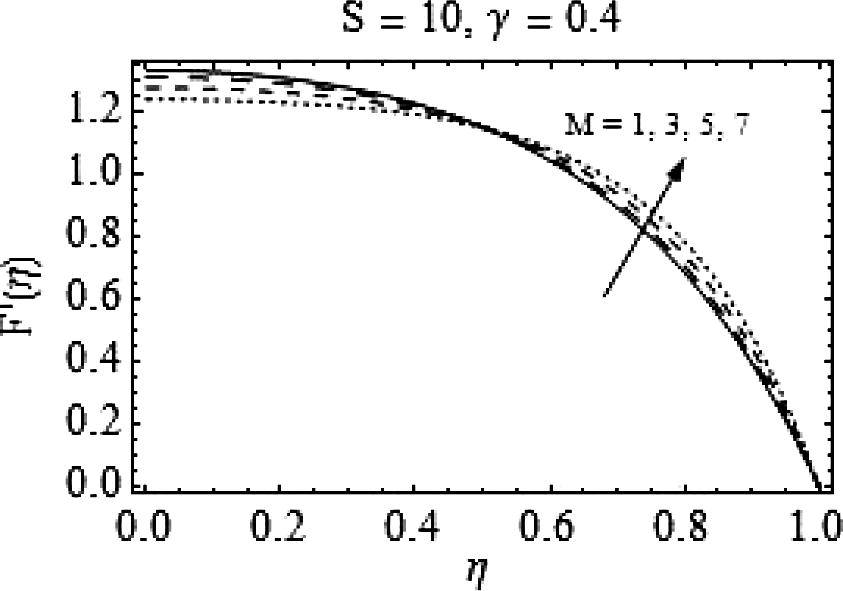
Effects of Mon
.
Figs. 9–16 are presented to study the effects of physical parameters for dilating plates (S < 0). In Fig. 9, considerable axial acceleration is observed for falling S. Fig. 10 demonstrates the effects of decreasing squeeze number on radial velocity. It is clear that F′(η) increases with squeeze rate for
. A sudden change in F′(η) is observed when
, i.e. for decreasing values of squeeze number there is a rapid decrease in radial velocity of the fluid. Figs. 11 and 12 show the effects of Casson fluid parameter on axial and radial velocities respectively. Almost an identical behavior is observed for Casson fluid parameter γand the squeeze number S when plates are coming together.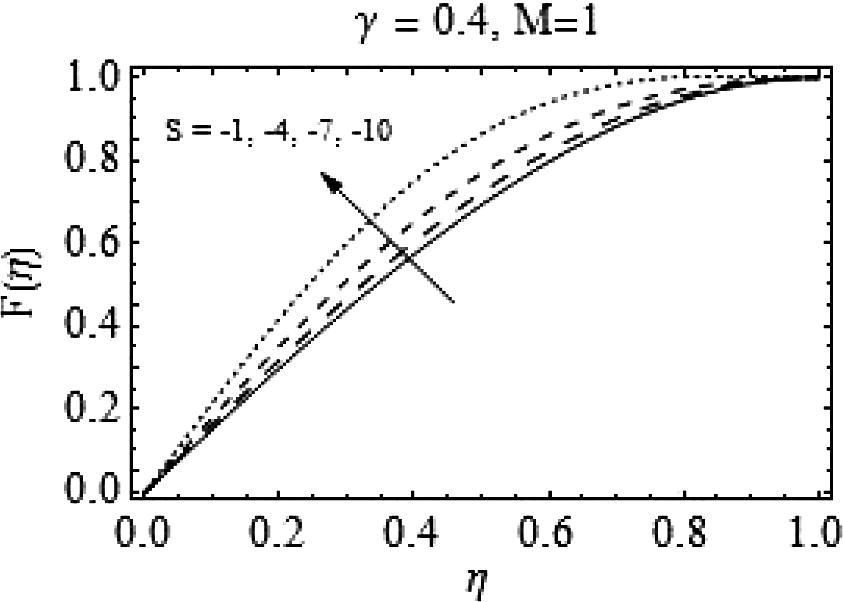
Effects of negative values of S on
.
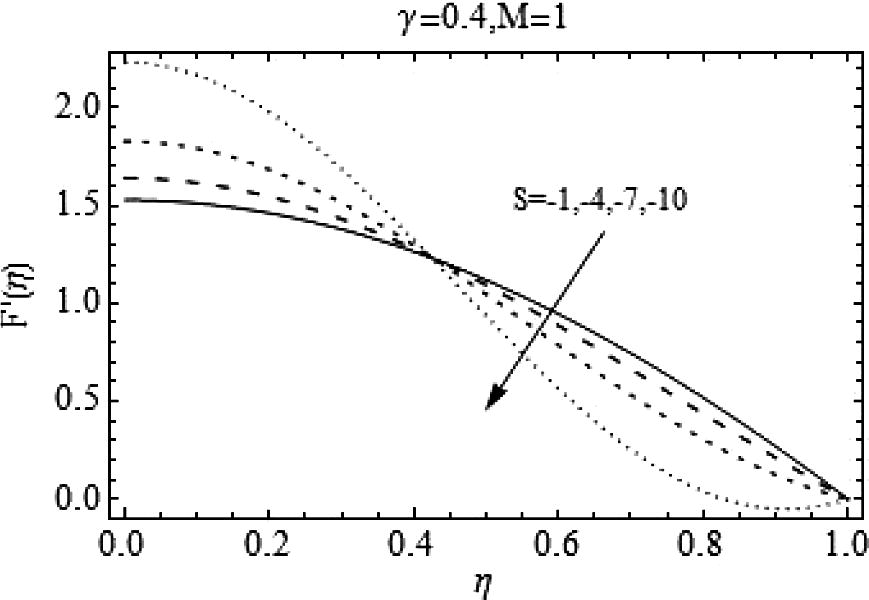
Effects of negative values of S on
.
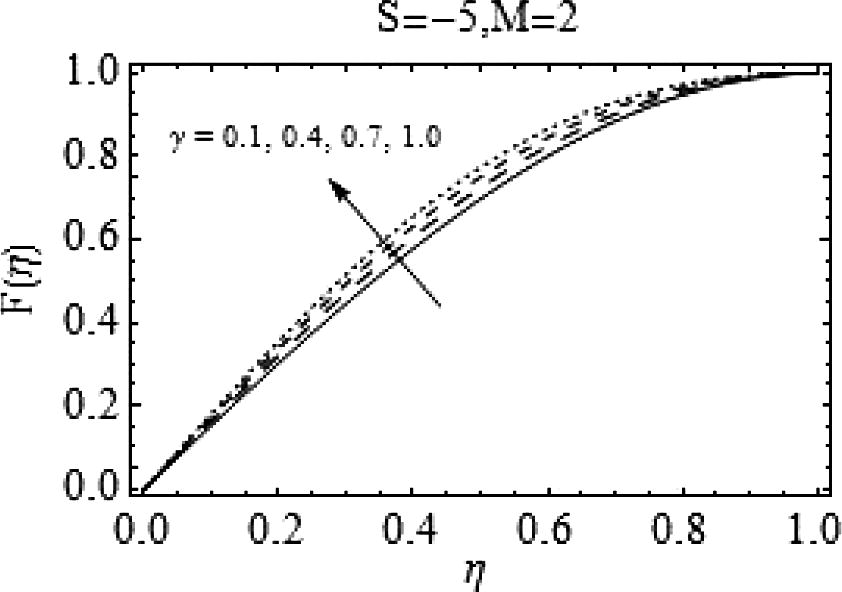
Effects of
on
.
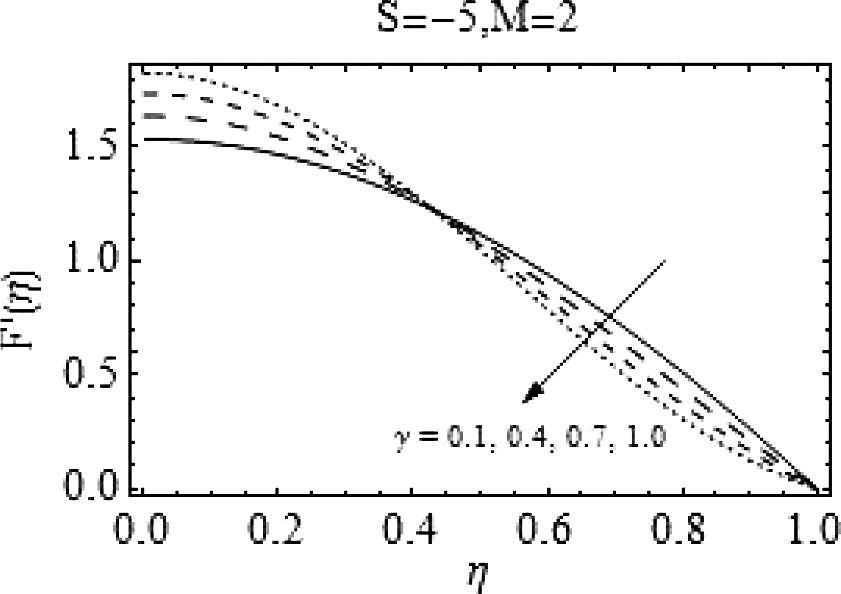
Effects of
on
.
Figs. 13–16 present behavior of the flow when plates are coming together (S < 0) and the magnetic number is varying. In Fig. 13, the effects of increasing magnetic number on F(η) are displayed and a decrease in F(η) is observed for slightly higher values of S. Fig. 14 gives us a graphical demonstration of F′(η) for growing magnetic number. It shows F′(η) decreases for
however for
it behaves otherwise, i.e. for increasing values of magnetic number, there is a rapid increase in radial velocity of the fluid. A similar type of behavior is observed for increasing magnetic number when S = -10 with more prominent effects. Similarly, in Fig. 16, a quite rapid change can be observed for increasing values of magnetic number. Also, with a decrease in squeeze number the backflow may emerge and a strong magnetic field is required to enhance the flow as shown in Fig. 16.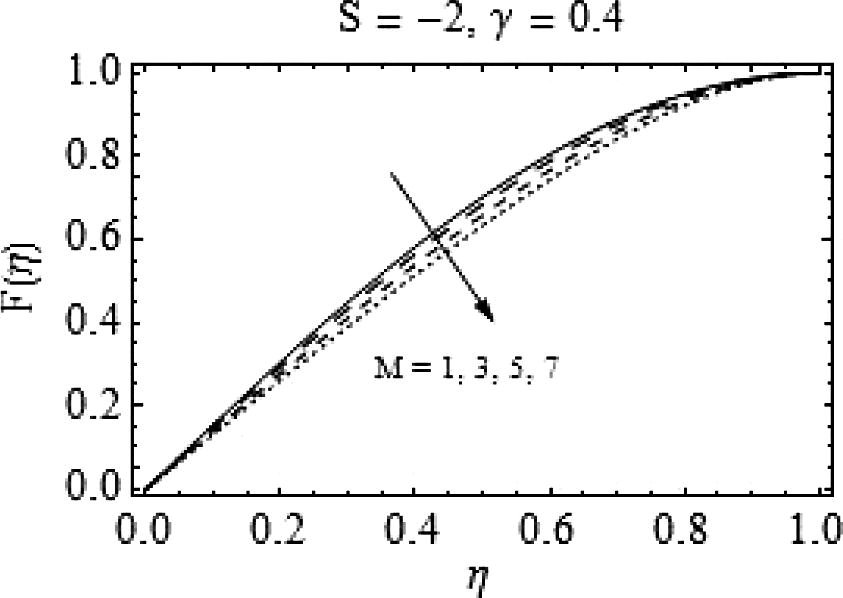
Effects of M on
.
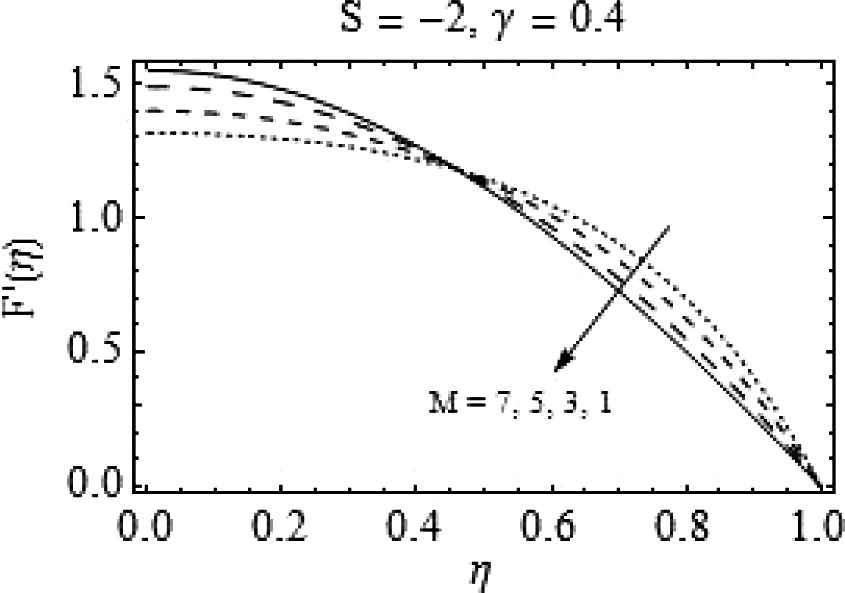
Effects of M on
.
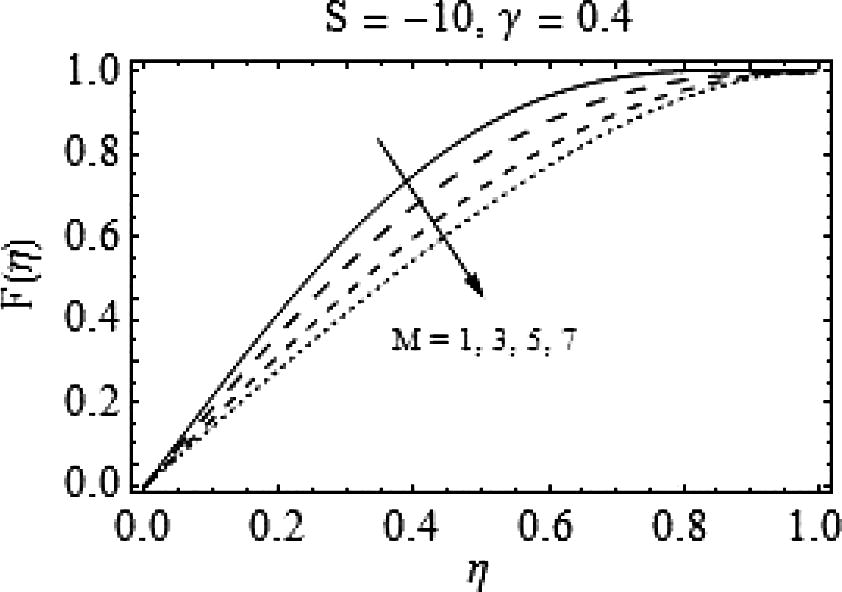
Effects of M on
.
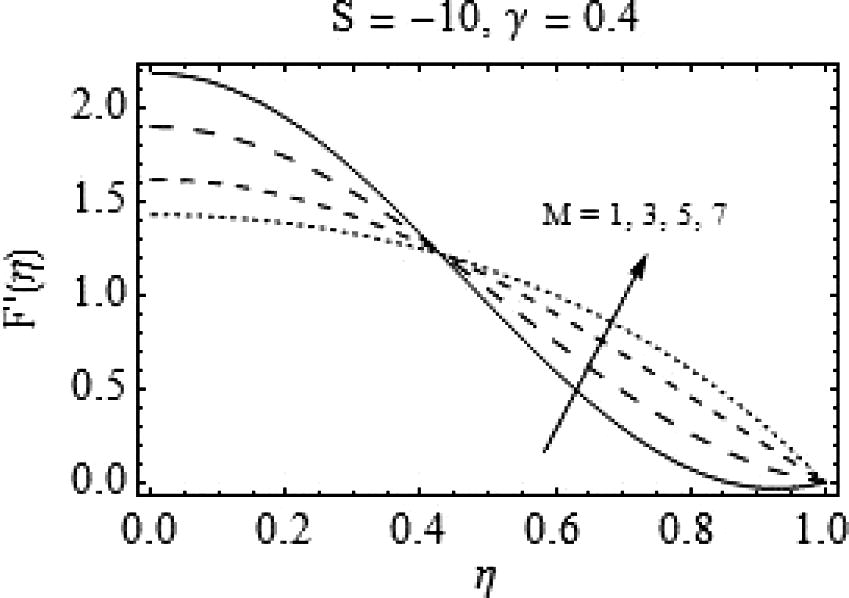
Effects of M on
.
It is important to check the convergence of the series solution obtained in Eq. (15). For this purpose, the numerical values of unknown constants A2 and A4 are computed in Tables 1. It is pertinent to mention that VPM converges only after6 approximations. Obtained analytical results are also compared with the ones acquired by using the RK-4 method and an excellent agreement is found.
Order of Approximations
S = 5
S = −5
1
1.378126
−1.526101
1.797777
−6.800000
2
1.351366
−1.331071
1.730490
−6.059060
3
1.347469
−1.308010
1.733885
−6.092031
4
1.347157
−1.306332
1.733850
−6.091734
5
1.347136
−1.306259
1.733850
−6.091732
6
1.347136
−1.306257
1.733850
−6.091732
8
1.347136
−1.306257
1.733850
−6.091732
10
1.347136
−1.306257
1.733850
−6.091732
Numerical (RK-4)
1.347136
−1.306257
1.733850
−6.091732
A comparison between the analytical and numerical solutions is shown in Table 2 for the axial and radial velocities. It can clearly be seen that the solutions agree very well. Table 3 compares the present results with some already existing solutions in the literature and again an excellent agreement is observed.
η
S = 5
S = −5
F(η)
F′(η)
F(η)
F′(η)
VPM
Numerical
VPM
Numerical
VPM
Numerical
VPM
Numerical
0
0
0
1.359393
1.359393
0
0
1.677216
1.677216
0.1
0.139081
0.139081
1.348452
1.348452
0.166839
0.166839
1.650804
1.650804
0.2
0.276358
0.276358
1.357517
1.357517
0.328444
0.328444
1.572994
1.572994
0.3
0.409918
0.409918
1.310148
1.310148
0.479861
0.479861
1.447971
1.447971
0.4
0.537628
0.537628
1.239953
1.239953
0.616685
0.616685
1.282424
1.282424
0.5
0.657014
0.657014
1.142869
1.142869
0.735286
0.735286
1.085120
1.085120
0.6
0.765125
0.765125
1.013414
1.013414
0.832992
0.832992
0.866366
0.866366
0.7
0.858383
0.858383
0.844480
0.844480
0.908218
0.908218
0.637365
0.637365
0.8
0.932408
0.932408
0.627096
0.627096
0.960506
0.960506
0.409532
0.409532
0.9
0.981819
0.981819
0.350136
0.350136
0.990529
0.990529
0.193804
0.193804
1.0
1
0
0
0
1
1
0
0
S↓
Present results(HPM)
Present results(RK-4)
Wang (1976)
−0.9780
−2.1915
−2.1915
−2.235
−0.4977
−2.6193
−2.6193
−2.6272
−0.09998
−2.9277
−2.9277
−2.9279
0
−3.000
−3.000
−3.000
0.09403
−3.0663
−3.0663
−3.0665
0.4341
−3.2943
−3.2943
−3.2969
1.1224
−3.708
−3.708
−3.714
Table 4 presents the numerical values of skin friction coefficient. It can be seen that for all increasing parameters an increase in the magnitude of skin friction coefficient is obtained.
S
γ
M
−5.0
0.4
1.0
−6.298708
−3.0
−8.320727
−1.0
−9.970376
1.0
−11.376240
3.0
−12.610669
5.0
−13.718095
−3.0
0.1
−30.991005
0.3
−10.873387
0.5
−6.771549
3.0
0.1
−35.260196
0.3
−15.149577
0.5
−11.078736
−3.0
0.4
2
−13.101572
4
−14.908219
6
−17.501183
3.0
0.4
2
−9.038196
4
−11.531983
6
−14.819321
5 Conclusions
MHD squeezing flow of a non-Newtonian namely Casson fluid is presented between parallel plates. Governing equations are reduced to a single ordinary differential equation using a similarity transform. Two cases are considered, i.e. one when plates are moving apart and other when plates are coming closer. VPM is used to solve the equations governing the flow. Effects of emerging parameters on flow are demonstrated graphically and a comprehensive discussion is provided. A numerical solution is also obtained using RK-4 method to compare the results obtained by VPM and an excellent agreement is found among the solutions. It can be concluded from the graphs that a strong magnetic field can be used to enhance the flow when plates are coming together and squeeze number increases the velocity profile for both the cases, i.e., when plates are coming closer and when plates are going apart.
References
- A new application of He’s variational iteration method for quadratic Riccati differential equation by using A domian’s polynomials. J. Comput. Appl. Math.. 2007;207:59-63.
- [Google Scholar]
- Numerical solutions of nonlinear Klein-Gordon equation by variational iteration method. Int. J. Numer. Meth. Energy. 2007;70:876-881.
- [Google Scholar]
- Variational iteration method for solving Burger’s and coupled Burger’s equations. J. Comput. Appl. Math.. 2005;181:245-251.
- [Google Scholar]
- Magneto hydrodynamic (MHD) squeezing flow of a Casson fluid between parallel disks. Int. J. Phys. Sci.. 2013;8(36):1788-1799.
- [Google Scholar]
- MHD flow of an incompressible fluid through porous medium between dilating and squeezing permeable walls. J. Porous Media. 2014;17(10):861-867.
- [Google Scholar]
- Peristaltic impulsion of MHD biviscosity fluid in a lopsided channel: closed form solution. Eur. Phys. J. Plus. 2014;129:123.
- [Google Scholar]
- Load capacity and time relations for squeeze films. J. Lubr. Technol.. 1956;78:A231-A245.
- [Google Scholar]
- MHD flow of a Jeffery fluid in converging and diverging channels. Int. J. Modern Math. Sci.. 2013;6:92-106.
- [Google Scholar]
- Hydrodynamics, a Study in Logic, Fact and Similitude (Revised ed.). Princeton University Press; 1960. 137
- A flow equation for pigment-oil suspension of the printing ink-type.Rheology of Disperse Systems. London: Pergamon; 1959. 84–104
- Approximate analysis of MHD squeeze flow between two parallel disks with suction or injection by homotopy perturbation method. Math. Prob. Eng. 2009 603916
- [Google Scholar]
- Squeezing flows of Newtonian liquid films: an analysis include the fluid inertia. Appl. Sci. Res.. 1976;32(2):149-166.
- [Google Scholar]
- Heat transfer analysis on the magnetohydrodynamic flow of a non-Newtonian fluid in the presence of thermal radiation: An analytic solution, Zeitschrift für Naturforschung A. A J. Phys. Sci.. 2012;67(3–4):147-152.
- [Google Scholar]
- Unsteady Squeezing flow of Casson fluid between parallel plates. World J. Model. Simul.. 2014;10(4):308-319.
- [Google Scholar]
- On unsteady two-dimensional and axisymmetric squeezing flow between parallel plates. Alexandria Eng. J.. 2014;53:463-468.
- [Google Scholar]
- Thermo-diffusion effects on MHD stagnation point flow towards a stretching sheet in a nanofluid. Propul. Power Res.. 2014;3(3):151-158.
- [Google Scholar]
- Analytical solutions for squeeze flow with partial wall slip. J. Non-Newtonian Fluid Mech.. 1999;81:1-15.
- [Google Scholar]
- Blood Flows in Arteries (second ed.). London: Arnold; 1974.
- Variation of parameter method for solving sixth-order boundary value problems. Commun. Korean Math. Soc.. 2009;24:605-615.
- [Google Scholar]
- Pressure flow relations of human blood hollow fibers at low flow rates. J. Appl. Physiol.. 1965;20:954-967.
- [Google Scholar]
- On heat and mass transfer in the unsteady squeezing flow between parallel plates. Meccanica. 2012;47:1581-1589.
- [Google Scholar]
- MHD flow of a Casson fluid over an exponentially shrinking sheet. Scientia Iranica. 2012;19:1150-1553.
- [Google Scholar]
- MHD three dimensional flow of Casson fluid past a porous linearly Stretching sheet. Alexandria Eng. J.. 2013;52:577-582.
- [Google Scholar]
- Optimized analytical solution for oblique flow of a Casson-nano fluid with convective boundary conditions. Int. J. Thermal Sci.. 2014;78:90-100.
- [Google Scholar]
- MHD three dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Trans. Nanotechnol.. 2014;13:109-115.
- [Google Scholar]
- Oblique stagnation point flow of a Casson-Nano fluid towards a stretching surface with heat transfer. J. Comput. Theor. Nanosci.. 2014;11:1422-1432.
- [Google Scholar]
- Numerical study on the laminar pulsatile flow of slurries. J. Non-Newtonian Fluid Mech.. 1987;22:191-206.
- [Google Scholar]
- Numerical study on the flow of a Non-Newtonian fluid through an axisymmetric stenosis. J. Biomech. Eng.. 1988;110:137-143.
- [Google Scholar]
- Squeeze flow of a viscoelastic solid. J. Non-Newtonian Fluid Mech.. 2000;95:343-362.
- [Google Scholar]
- Variational iteration technique for solving higher order boundary value problems. Appl. Math. Comp.. 2007;189:1929-1942.
- [Google Scholar]
- Variation of parameters method for solving fifth-order boundary value problems. Appl. Math. Inf. Sci. 2008;2:135-141.
- [Google Scholar]
- Analytic approximate solutions for unsteady two-dimensional and axisymmetric squeezing flows between parallel plates. Math. Prob. Eng. 2008:1-13.
- [Google Scholar]
- On the theory of lubrication and its application to Mr Beauchamp Tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. Royal Soc. London. 1886;177:157-234.
- [Google Scholar]
- Heat transfer analysis of bi-viscous ciliary motion fluid. Int. J. Biomath.. 2015;8(2):13.
- [CrossRef] [Google Scholar]
- Unsteady squeezing flow of a viscous MHD fluid between parallel plates, a solution using the homotopy perturbation method. Math. Model. Anal.. 2008;13:565-576.
- [Google Scholar]
- Versuch¨ Uber die scheinbare adhesion”, Sitzungsberichte der Akademie der Wissenschaften in Wien. Mathematik-Naturwissen. 1874;69:713-721.
- [Google Scholar]
- Inertial considerations in parallel circular squeeze film bearings. J. Lubr. Technol.. 1970;92:588-592.
- [Google Scholar]
- Arbitrary squeezing of a viscous fluid between elliptic plates. Fluid Dyn. Res.. 1996;18:35-51.
- [Google Scholar]
- Squeezing of a viscous fluid between elliptic plates. Appl. Sci. Res.. 1979;35:195-207.
- [Google Scholar]
- Unsteady laminar boundary layers in an incompressible stagnation flow. J. Appl. Math. Trans. ASME. 1958;80:421-427.
- [Google Scholar]
- Variation of parameters method for thin film flow of a third grade fluid down an inclined plane. Italian J. Pure Appl. Math.. 2013;31:161-168.
- [Google Scholar]







