Translate this page into:
Effects of slip condition and Newtonian heating on MHD flow of Casson fluid over a nonlinearly stretching sheet saturated in a porous medium
⁎Corresponding author. Tel.: +60 137731773. sharidan@utm.my (Sharidan Shafie),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The effect of slip condition on MHD free convective flow of non-Newtonian fluid over a nonlinearly stretching sheet saturated in porous medium with Newtonian heating is analyzed. The governing nonlinear coupled partial differential equations with auxiliary conditions are transformed into the system of coupled ordinary differential equations via similarity transformations and then solved numerically using Keller-box method. The results for skin friction coefficient and the reduced Nusselt number are obtained and compared with previous results in the literature and are found to be in excellent agreement. Results show that the slip parameter reduces the velocity of Casson fluid and enhances the shear stress. It is also observed that slip effect is more pronounced on temperature profile in comparison with velocity profile. It is also seen that velocity and dimensionless temperature are increasing functions of Newtonian heating parameter. Further, temperature gradient is an increasing function of thermal buoyancy parameter and Newtonian heating parameter whereas a decreasing function of porosity parameter and nonlinear stretching sheet parameter.
Keywords
MHD
Casson fluid
Porous medium
Slip flow
Free convection
Newtonian heating
1 Introduction
The study of non-Newtonian fluids has gained considerable attention in the last few years because of its widespread applications in engineering and industry. Several fluids exist including drilling mud, polymer solutions, paints, ketchup and shampoo and so on, which do not obey Newton’s law of viscosity which shows the nonlinear relationship between stress and rate of strain of these fluids. The complex nature of non-Newtonian fluids presents a challenge to engineers, physicists and mathematicians. Several models have been proposed for the study of non-Newtonian fluids in the literature. It is also claimed that no single model exists which exhibits all properties of non-Newtonian fluids. The Maxwell model, which is efficient to predict stress relaxation, is considered as simplest viscoelastic model among them. The most common model used in existing literature is power law model which has tendency to demonstrate both shear thinning and shear thickening behavior of non-Newtonian fluids. There is another non-Newtonian fluid known as Casson fluid (Das and Batra, 1993) which exhibits yield stress. If the applied shear stress is less than yield stress then behavior of fluid is like solid, whereas it starts moving, if applied shear stress is greater than yield stress. Some common examples of Casson fluid are jelly, blood, honey, tomato sauce, concentration juices etc. In literature, the Casson model is regarded as one of the best rheological model for the analysis of boundary layer flows (Dash et al., 1996; Butt et al., 2013; Nadeem et al., 2014a; Animasaun et al., 2015).
The problems of non-Newtonian fluids over stretching surfaces have several industrial applications, and have attracted the attention of many researchers during the last few decades. The flow caused by stretching sheet whose velocity is linearly proportional to a fixed origin was first investigated by Crane (1970). Later on, several researchers have extended this work by considering different effects, see for example, (Gupta and Gupta, 1997; Gorla and Sidawi, 1997; Sharidan et al., 2006; Khan and Pop, 2010; Bhattacharyya, 2013; Tufail et al., 2014), and the references therein. Most of the studies mentioned in these references are focused on linearly stretching sheet. However, the velocity of stretching sheet is not required to be linear (Gupta and Gupta, 1997). Keeping this in mind Kumaran and Ramanaiah (1996) successfully studied the boundary layer flow over a stretching sheet where quadratic velocity of sheet is considered. Nadeem et al. (2012) and Sharada and Shankar (2012) studied boundary layer flow of Casson fluid over exponentially stretching sheet. Motivated by this, Vajravelu (2001) and Vajravelu and Cannon (2006) considered the nonlinear velocity of stretching sheet in the study of boundary layer flow. They observed that large values of nonlinearly stretching parameter have no significant effects on velocity of fluid. Cortell (2007) investigated heat transfer effects on incompressible boundary layer flow over nonlinearly stretching sheet numerically. Mukhopadhyay (2013a) discussed heat transfer flow of Casson fluid over nonlinearly stretching sheet. The numerical solutions are carried out by shooting method. She concluded that skin friction and temperature gradient are increasing functions of Casson fluid parameter. Recently, Mustafa and Khan (2015) investigated magnetic field effects on Casson nanofluid over nonlinearly stretching sheet.
In recent years, MHD boundary layer flows through porous medium has gained attention of many researchers. It is because that in electrically conducting fluid flows; applied magnetic field influenced heat generation/absorption and in result controlled the desired characteristics of final product. Several researchers have considered the stretching sheet problems embedded in porous medium under the influence of magnetic field for various types of non-Newtonian fluids. Cortell (2006) analyzed MHD flow of second grade fluid flow over stretching sheet embedded in porous medium with chemical reaction. The two dimensional boundary layers flow through porous medium over vertical stretching sheet under the influence of magnetic field is discussed by Hayat et al. (2010). The steady state electrically conducting flow of Casson fluid over a stretching sheet in a porous medium is reported by Shawky (2012). In the subsequent year, Nadeem et al. (2013) explored three dimensional electrically conducting boundary layer flow of Casson fluid over stretching sheet saturated in a porous medium. Jat et al. (2014) analyzed MHD boundary layer flow of viscous fluid past nonlinearly stretching sheet embedded in porous medium. They observed that velocity decreases with increasing porosity parameter which results in increasing the magnitude of skin friction coefficient. An interesting study on stagnation point flow on porous shrinking sheet under the influence of magnetic field has been carried out by Akbar et al. (2014a,b). Recently, Khalid et al. (2015) investigated the effects of magnetic field on free convection flow of Casson fluid over oscillating plate embedded in porous medium.
On the other hand, slip condition has significant applications in various industries and is very efficient in manufacturing process. It is a common belief that heat transfer can be increased by adding velocity slip at the boundary. Beavers and Joseph (1967) were the first who used partial slip to the fluid past permeable wall. The addition of velocity slip at wall also plays a vital role for flow in micro devices (Gad-el-hak, 1999). For this reason, researchers have paid considerable attention to include the slip condition at wall rather than no slip condition. Hayat et al. (2008, 2011) investigated the slip effects on boundary layer flow over non-permeable and permeable stretching sheet, respectively. Mukhopadhyay (2013b) studied the effects of slip on viscous fluid over nonlinearly stretching sheet. The problem is solved numerically and it is found that shear stress is an increasing function of slip parameter. Poornima et al. (2014) considered the velocity slip at wall for Casson fluid over a porous stretching surface. They found that slip parameter decreases fluid velocity and enhances shear stress at the wall. The mechanism of slip condition on stagnation point flow of Casson fluid has been reported by Hayat et al. (2015a). Very recently, Nadeem et al. (2015) explored the combined effects of partial slip and magnetic field on stagnation point flow of Casson fluid over stretching surface. They concluded that slip parameter reduces the velocity of fluid in the boundary region.
Recently, many researchers have paid attention to Newtonian heating instead of constant surface temperature because in many physical situations constant temperature assumption at surface fails to work. Newtonian heating is defined as the process in which internal resistance is negligible as compared to surface resistance. The applications of Newtonian heating include heat exchanger, conjugate heat transfer around fins, petroleum industry, solar radiation etc. Merkin (1994) was the first who studied four types of temperature distributions at wall and Newtonian heating was one among the others. Salleh et al. (2010) investigated heat transfer effects on boundary layer flow over stretching sheet with Newtonian heating. Motivated by this, Haq et al. (2014) and Nadeem et al. (2014b) explored two and three dimensional boundary layer flow of Casson nanofluid over stretching sheet under the influence of magnetic field and convective boundary condition, respectively. They concluded that convective heat parameter enhances temperature of the fluid. The steady incompressible flow of power law nanofluid past stretching sheet with Newtonian heating was studied by Hayat et al. (2015b).
From the above discussion, it is very much clear that Newtonian heating effects on Casson fluid over nonlinearly stretching sheet embedded in porous medium has not been reported yet. In the present study an attempt is made to investigate combined effects of slip condition and Newtonian heating on MHD free convectional flow of Casson fluid over a nonlinearly stretching sheet in saturated porous medium. The governing coupled nonlinear partial differential equations are converted to nonlinear coupled ordinary differential equations using suitable transformations. The system of equations is solved numerically by using Keller box method (Cebeci and Bradshaw, 1984). Numerical calculations are carried out for physical parameters up to desired level of accuracy. The results for shear stress and temperature gradient at wall are also calculated carefully as applications of both are very important in engineering and industry. It is hoped that findings from the present study will be useful in many technological and manufacturing processes.
2 Mathematical formulation
Consider steady two dimensional and incompressible free convectional flow of Casson fluid over a nonlinearly stretching sheet saturated in a porous medium under the influence of magnetic field. Further, the slip and Newtonian heating effects are also taken into account. The sheet is stretched in a nonlinear way along the x-axis with the velocity of uw(x) = cxn and y-direction is taken for fluid flow with the origin fixed (see Fig. 1). Here c is constant and
is the nonlinear stretching sheet parameter, n = 1 represents the linear sheet case and n ≠ 1 is for nonlinear case. A non-uniform transverse magnetic field of strength B0 is applied normal to the sheet. The ambient fluid temperature is denoted by T∞. The induced magnetic field is neglected due to the small magnetic Reynolds number. Under these assumptions the rheological equation for incompressible flow of Casson fluid is given by (see Bhattacharyya, 2013; Sharada and Shankar, 2015).
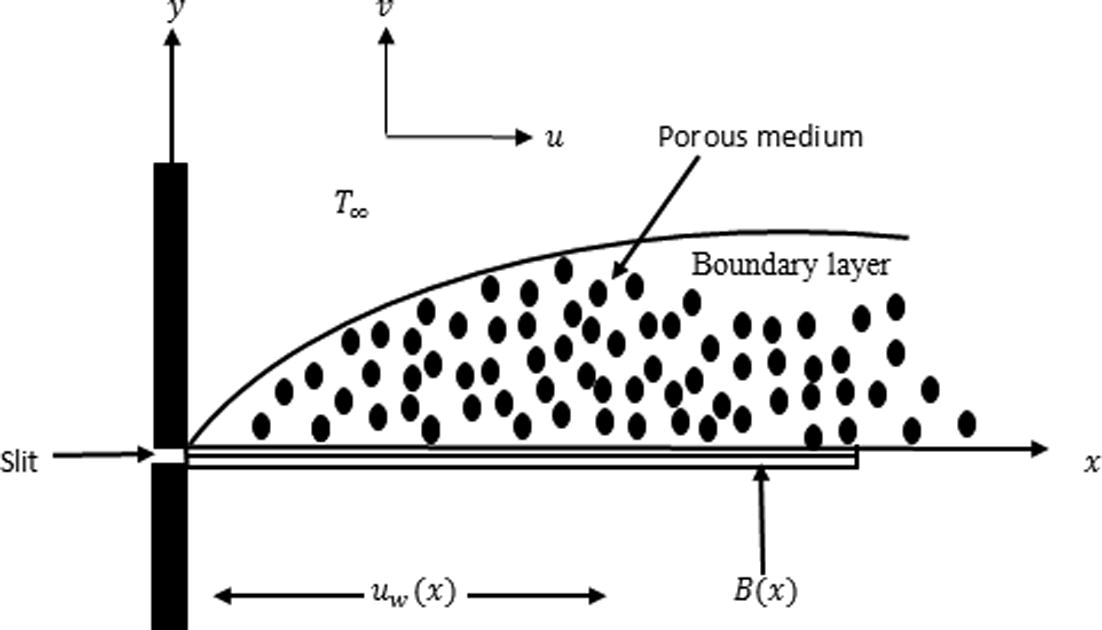
Sketch of physical problem and coordinate system.
Here, π = eijeij and eij is the -th component of the deformation rate, π is the product of the component of deformation rate with itself, πc is a critical value of this product based on the non-Newtonian model, μB is the plastic dynamic viscosity of the non-Newtonian fluid, and py is the yield stress of the fluid.
The governing equations of continuity, momentum and energy are given by
In the above equations u and υ denote the velocity component in x- and y-directions respectively, ρ is the fluid density, ν is kinematic viscosity, β is the Casson fluid parameter, σ is the electrically conductivity of the fluid, is the magnetic field with constant magnetic strength B0, is the porosity, k is the permeability of porous medium, g is the gravitational acceleration, βT is the volumetric coefficient of thermal expansion, T is the fluid temperature, α is the thermal diffusivity of the Casson fluid.
The corresponding boundary conditions for the problem can be written as follows:
Here denotes velocity of slip factor depends on x and represents the heat transfer parameter for Newtonian heating.
We introduce the following similarity transformations:
The above expression also satisfies the continuity Eq. (1). From Eqs. (2)–(7), one arrives at the following non-dimensional systems:
The corresponding transformed boundary conditions are:
The parameters with physical interest are the skin friction coefficient Cfx and Nusselt number Nux and are defined as follows
Using Eq. (6) in Eq. (13), we get the following non-dimensional skin friction coefficient and local Nusselt number
3 Numerical scheme
The nonlinear ordinary differential equations shown in Eqs. (11) and (12) subject to boundary conditions (13) and (14) are solved numerically using implicit finite difference scheme known as the Keller box method. This method is unconditionally stable and more accurate for parabolic problems. It is also found that this method is very suitable in solving large number of nonlinear coupled equations. This method is described in details in the book of Cebeci and Bradshaw (1984). The following four steps are involved while working with this method.
-
The nonlinear governing equations are reduced to first order system.
-
The resulting first order system is reduced to a set of algebraic equations with the help of central difference scheme.
-
Newton’s method is employed to linearize the obtained algebraic equations and then arrange in matrix form.
-
Finally, block-elimination method is used to solve the linear system of equations.
In this study a step size Δη = 0.01 is used and iterations are repeated until the convergence criteria 10−4 satisfied.
4 Results and discussion
The non-linear system of equations given in Eqs. (8) and (9) has been computed numerically using an implicit finite difference scheme, namely Keller box method. The step size of Δη = 0.01 is used in this study. Further, an algorithm developed in MATLAB software to generate numerical results for the given boundary value problem.
In order to analyze the behavior of velocity and temperature profiles of the physical problem, numerical calculations are carried out for various values of Casson fluid parameter β, magnetic parameter M, nonlinear stretching parameter n, porosity parameter K, thermal buoyancy parameter
, Prandtl number Pr, slip parameter δ and Newtonian heating parameter γ. The results for skin friction and local Nusselt number are compared with the previous published results, and are shown in Tables 1–3. It is observed that the obtained results are in good agreement with the published results.
n
Cortell (2007)
Present
0.0
0.627547
0.6276
0.2
0.766758
0.7668
0.5
0.889477
0.8896
1
1.0
1.0
3
1.148588
1.1486
10
1.234875
1.2349
100
1.276768
1.2768
−θ′(0)
Pr = 1
Pr = 5
n
Cortell (2007)
Present results
Cortell (2007)
Present results
0.2
0.610262
0.6102
1.607175
1.6076
0.5
0.595277
0.5949
1.586744
1.5868
1.5
0.574537
0.5747
1.557463
1.5576
3.0
0.564472
0.5647
1.542337
1.5430
1.0
0.554960
0.5549
1.528573
1.5286
Pr
Wang (1989)
Gorla and Sidawi (1994)
Khan and Pop (2010)
Present results
0.70
0.4539
0.5349
0.4539
0.4544
2.0
0.9114
0.9114
0.9113
0.9113
7.0
1.8954
1.8905
1.8954
1.8953
20.0
3.3539
3.3539
3.3539
3.3538
70.0
6.4622
6.4622
6.4621
6.4638
Tables 1 and 2 present the values of skin friction coefficient and reduced Nusselt number for different values of n and Pr, respectively. The present results are compared with the results of Cortell (2007). It is also observed from Table 1 that magnitude of skin friction coefficient increases with the increase in n whereas reduced Nusselt number decreases with the increase in n and increases with increase in Pr (see Table 2). Table 3 shows the comparison of the present results for reduced Nusselt number with various values of Pr with the results of Wang (1989), Gorla and Sidawi (1994) and Khan and Pop (2010). It is found that the rate of heat transfer coefficient increases as Pr increases.
Table 4 demonstrates the numerical results of wall shear stress and rate of heat transfer of the present study for various values of parameters involved.
β
n
M
K
λ
Pr
δ
γ
−θ′(0)
0.2
0.6
0.4
0.6
0.5
0.72
0.2
0.4
−2.9090
0.1602
0.8
−1.7792
0.1427
5
−1.2884
0.1283
0.2
1
−3.0587
0.1590
5
−3.4292
0.1563
0.2
0.6
1
−3.6272
0.1527
1.5
−4.4963
0.1439
0.2
0.6
0.4
1
−3.2695
0.1564
2
−4.0388
0.1485
0.2
0.6
0.4
0.6
1.5
−2.6916
0.1619
3
−2.3736
0.1644
0.2
0.6
0.4
0.6
0.5
1
−2.9233
0.1973
5
−2.9724
0.4733
0.2
0.6
0.4
0.6
0.5
0.72
0.8
−2.1741
0.1423
1.5
−1.0535
0.1068
0.2
0.6
0.4
0.6
0.5
0.72
0.2
1
−2.8270
0.2815
10
−2.6721
0.5157
Figs. 2–8 are plotted to study dimensionless velocity profile for various effects of β, n, M, K,
, δ and γ. It is observed from Fig. 2 that velocity decreases with the increase in β in the absence and presence of M. Physically, with increase in β the fluid become more viscous and in result the fluid velocity reduces. Also, the momentum boundary layer thickness decreases as β increases. Further, as β → ∞ the present phenomenon reduces to Newtonian fluid. Fig. 3 demonstrates the influence of n on velocity profile. Also n = 0 represents the flat plate case, n = 1 represent linear stretching sheet case and n ≠ 1 presents the nonlinear stretching sheet case. It is found that increasing values of n decreases the velocity in the boundary layer. The effect of M is illustrated in Fig. 4. It is seen that fluid velocity reduces as M increases, as expected. It is due to the fact that drag force, also known as Lorentz force is produced when magnetic field is applied to the fluid. This force has the tendency to slow down the velocity of fluid in the boundary layer. The decreasing pattern of velocity field clearly shows that transverse magnetic field opposes the transport phenomenon. Fig. 5 demonstrates the variation of K on velocity profile. It is found that increasing values of K reduces the fluid velocity in the boundary layer. Physically, the permeability increases resistance of the porous medium which tends to reduce the fluid velocity. On the other hand, velocity of fluid enhances with the increase in
(Fig. 6). The explanation for this phenomenon is that thermal buoyancy parameter is defined as the ratio of buoyancy to viscous forces in the boundary-layer, therefore an increase in its values reduces the viscosity of the fluid and in result increases the flow velocity. Fig. 7 shows the variation of δ on velocity profile in the absence and presence of M. It is found that velocity is a decreasing function of δ. The reduction in momentum boundary layer thickness is also observed. It is because the momentum provided by stretching sheet is partly transmitted to the Casson fluid under the velocity-slip boundary condition. The opposite nature of velocity is noticed for the effect of γ as shown in Fig. 8.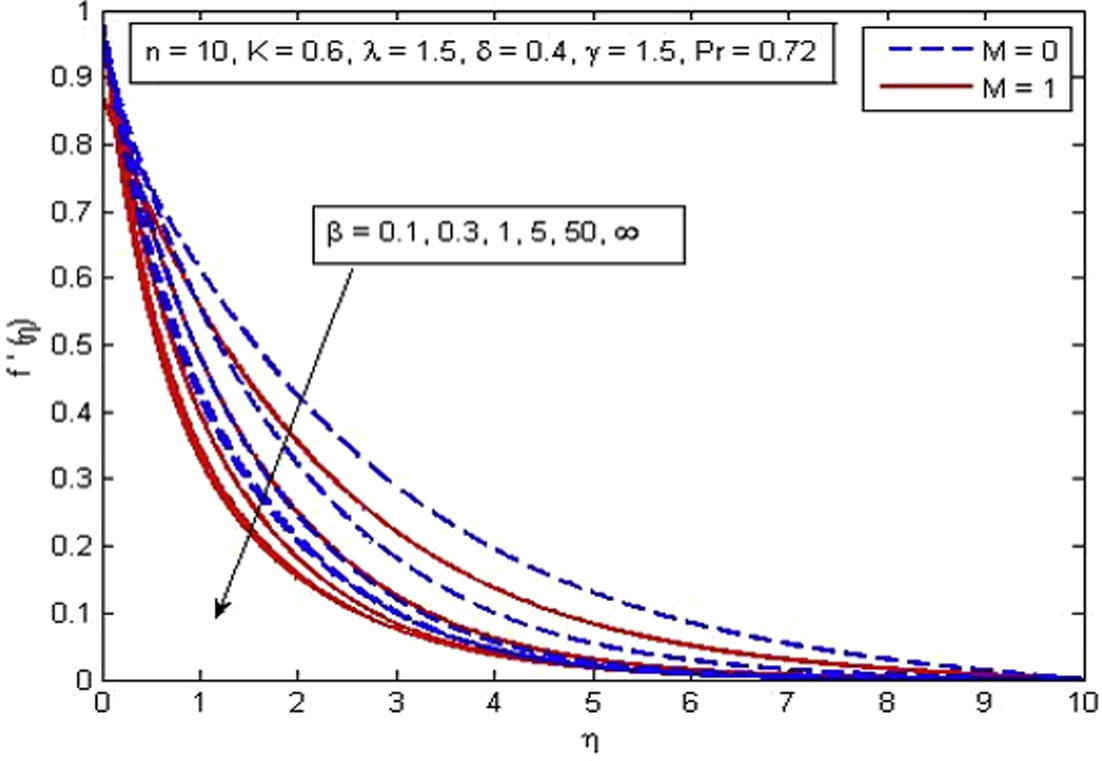
Effect of β on velocity for two different values of M.
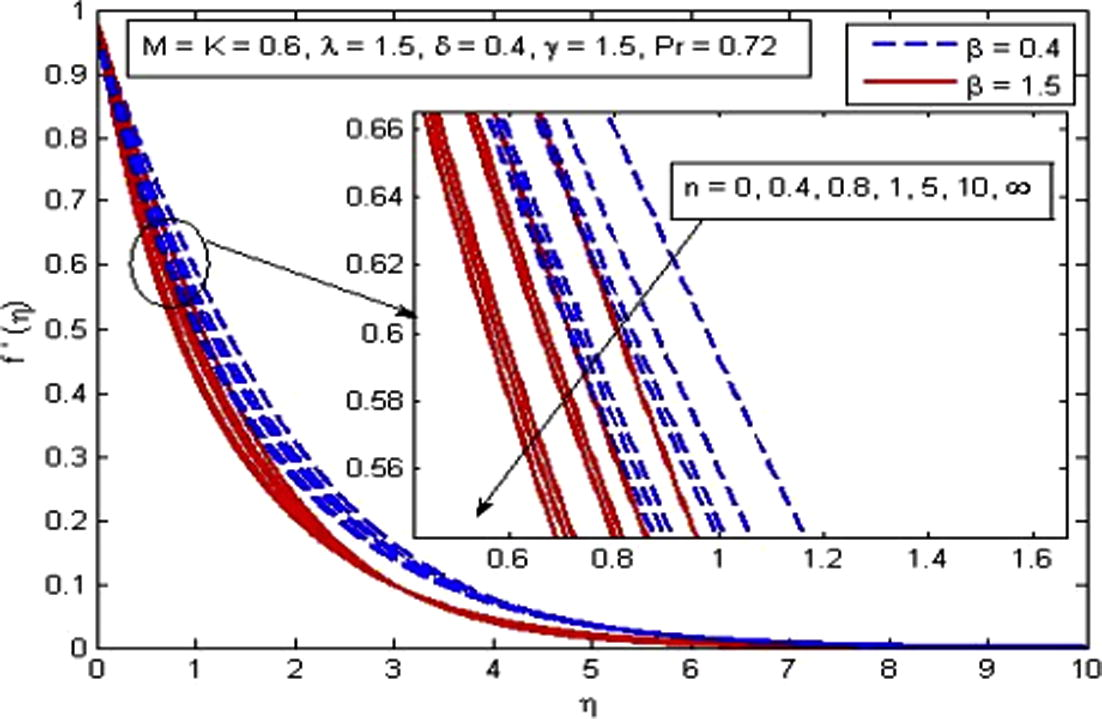
Effect of n on velocity for two different values of β.
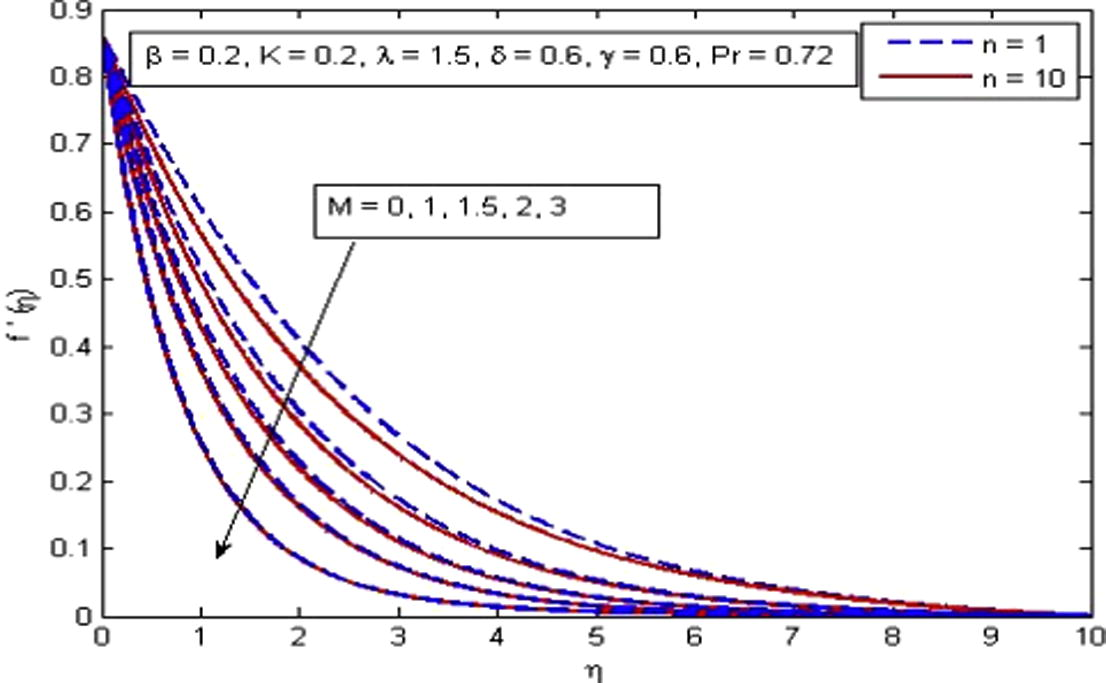
Effect of M on velocity for
.
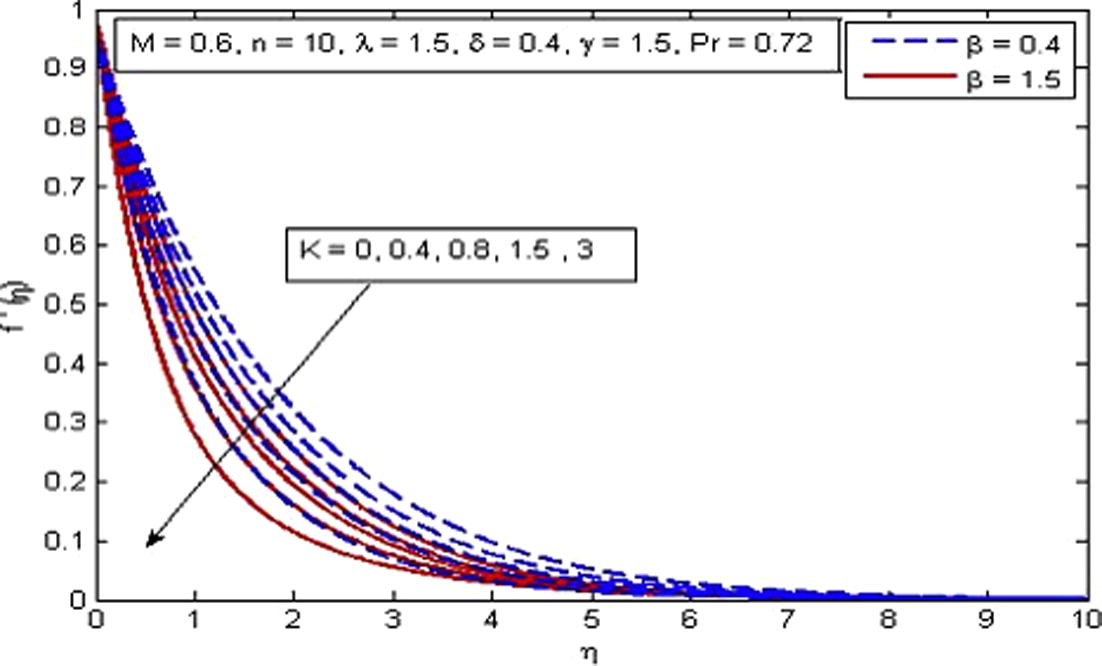
Effect of K on velocity for two different values of β.
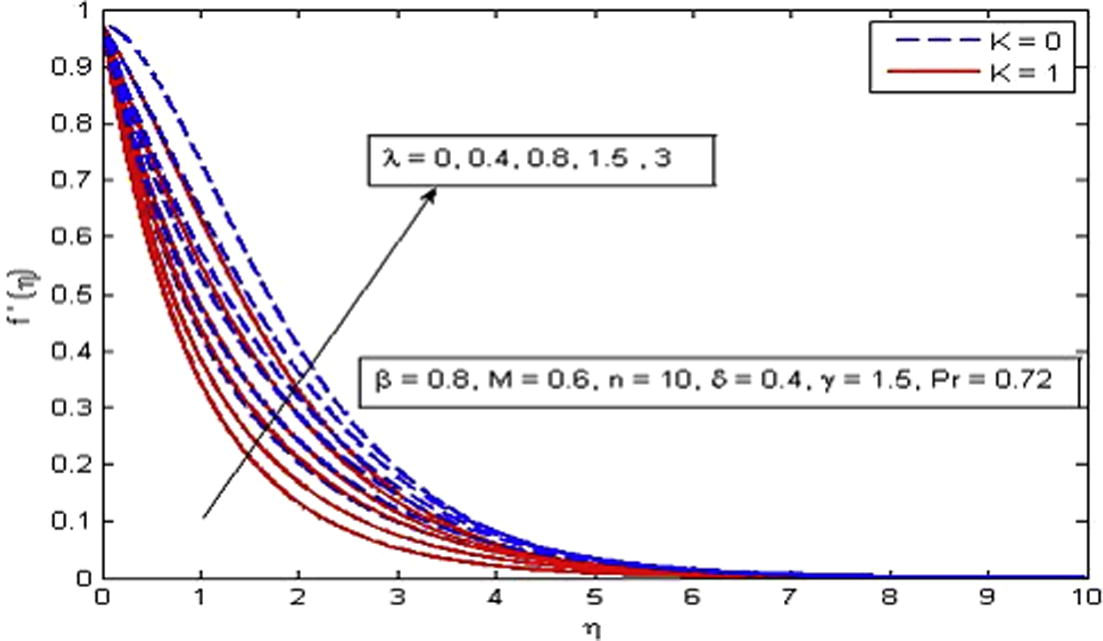
Effect of
on velocity for two different values of K.
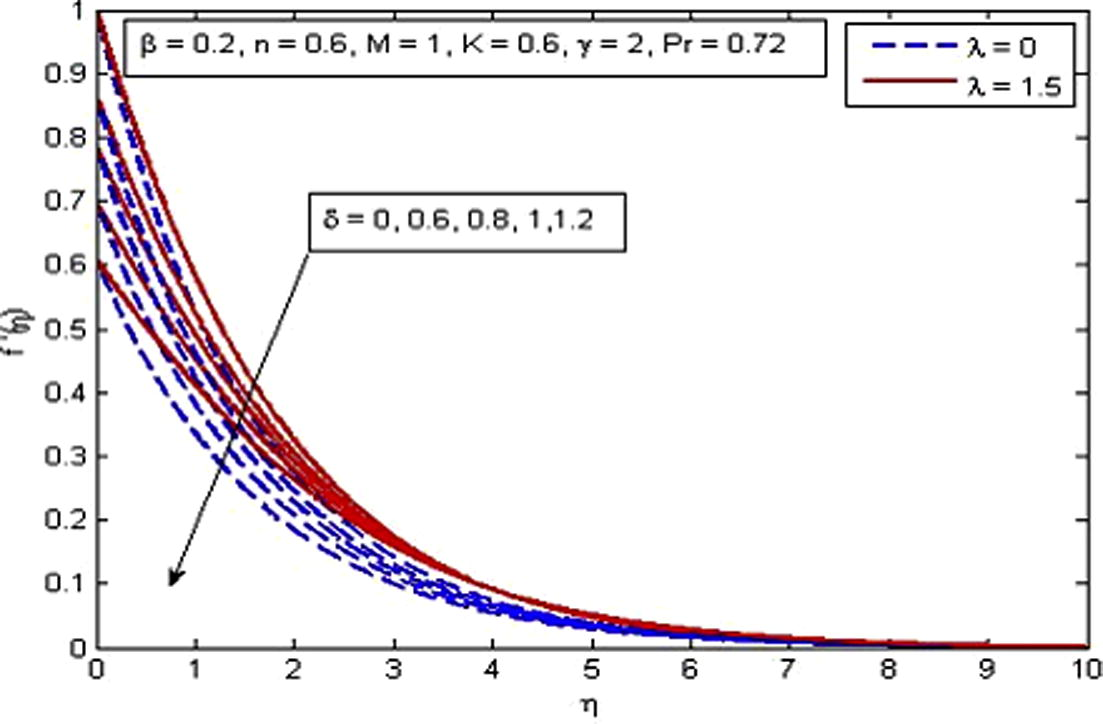
Effect of δ on velocity for two different values of
.
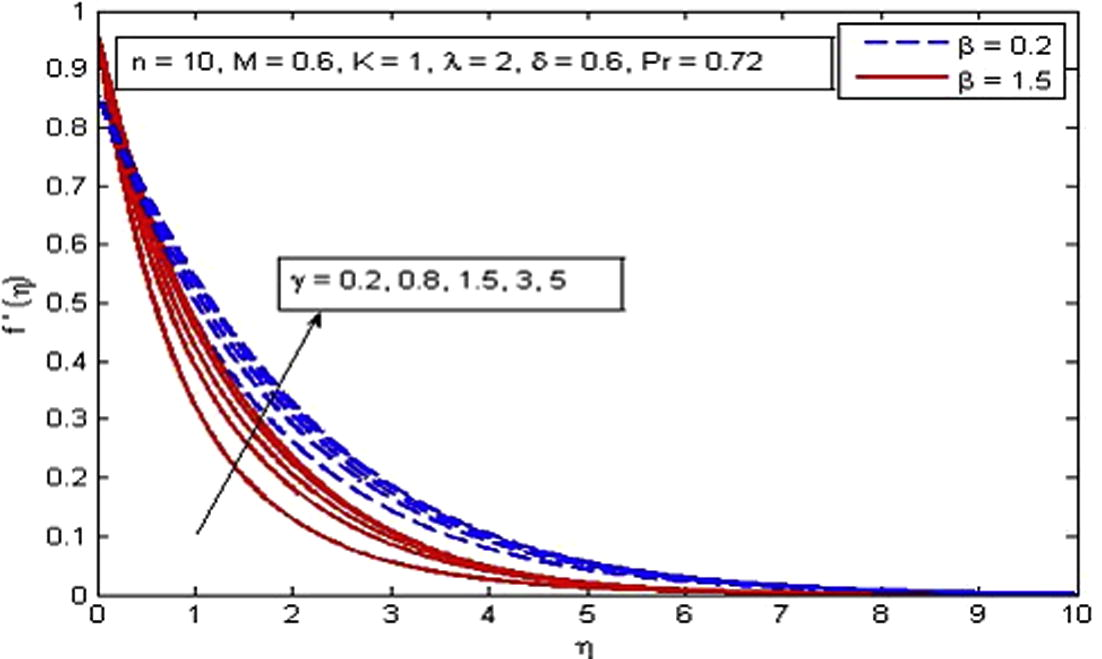
Effect of γ on velocity for two different values of β.
Figs. 9–16 are depicted to analyze various effects of β, n, M, K,
, Pr, δ and γ on temperature profiles, respectively. From Fig. 9, it is noted that the dimensionless temperature increases with the increase in β. Also K = 0 corresponds to non-porous medium and K ≠ 0 corresponds to porous medium. Further, a rapid increase in temperature is seen for increasing values of β in porous medium as compared to non-porous medium. An opposite trend is observed for dimensionless temperature for increasing values of n (see Fig. 10). The variation of M on dimensionless temperature is plotted in Fig. 11. It is noticed that increasing M causes an increase in dimensionless temperature and thermal boundary layer thickness. A similar behavior of fluid temperature is observed for the effect of K (see Fig. 12), but the increase in temperature for M is more pronounced as compared to K. Fig. 13 illustrates the effect of
on dimensionless temperature. It is to be mentioned that K = 0 represents non-porous medium and K ≠ 0 corresponds to porous medium case. It is noticed that temperature reduces as
increases. It is very well agreed with the fact that buoyancy force increases the fluid velocity which in turn causes the temperature of the fluid to decrease. It is also observed that temperature increases more rapidly in porous medium as compared to non-porous medium. The increase in thermal boundary layer thickness is also noted. Fig. 14 shows the behavior of temperature profile for increasing values of Pr. As expected, the increasing values of Pr decreases the fluid temperature as well as thermal boundary layer thickness. It is also observed that higher values of Pr decrease the fluid temperature significantly and boundary layer squeezed closer to the wall. The explanation of this phenomenon is that the Prandtl number is define as the ratio of momentum diffusion to thermal diffusion, therefore increasing Pr leads to a decrease in thermal diffusion and results in thinning boundary layer. An opposite trend is noticed for the variation of δ on dimensionless temperature profile (see Fig. 15). The variation of γ on dimensionless temperature is plotted in Fig. 16. It is evident that temperature is an increasing function of γ. As γ → ∞, the Newtonian heating condition becomes prescribed wall temperature case. It is also noticed that fluid temperature tends to zero at γ = 0.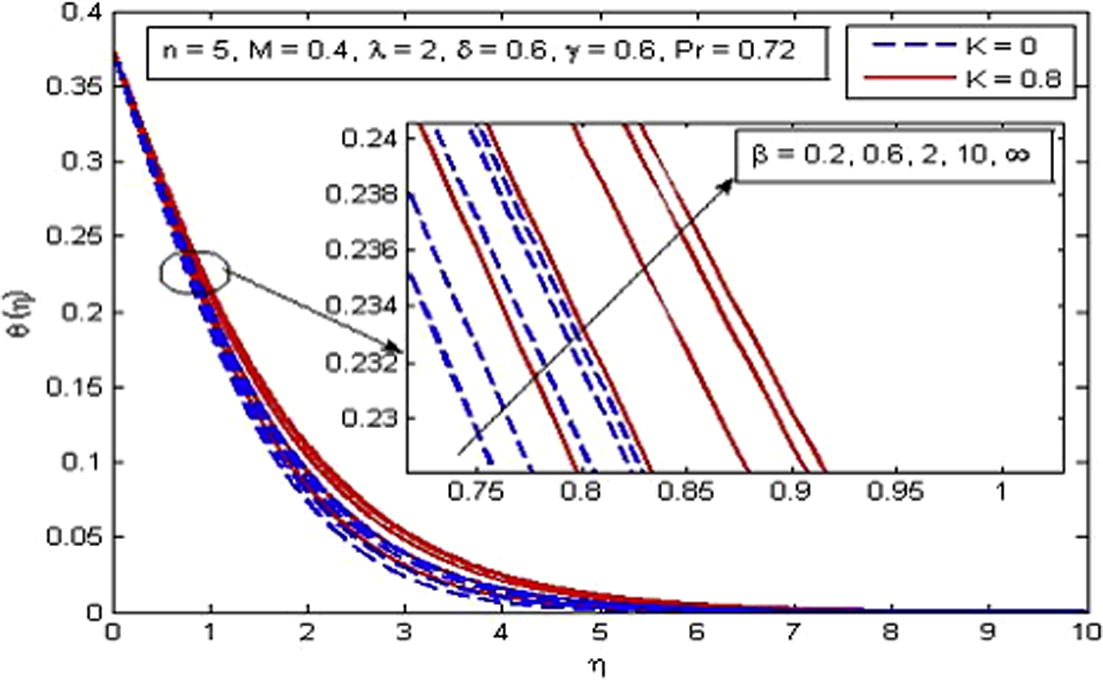
Effect of β on temperature for two different values of K.
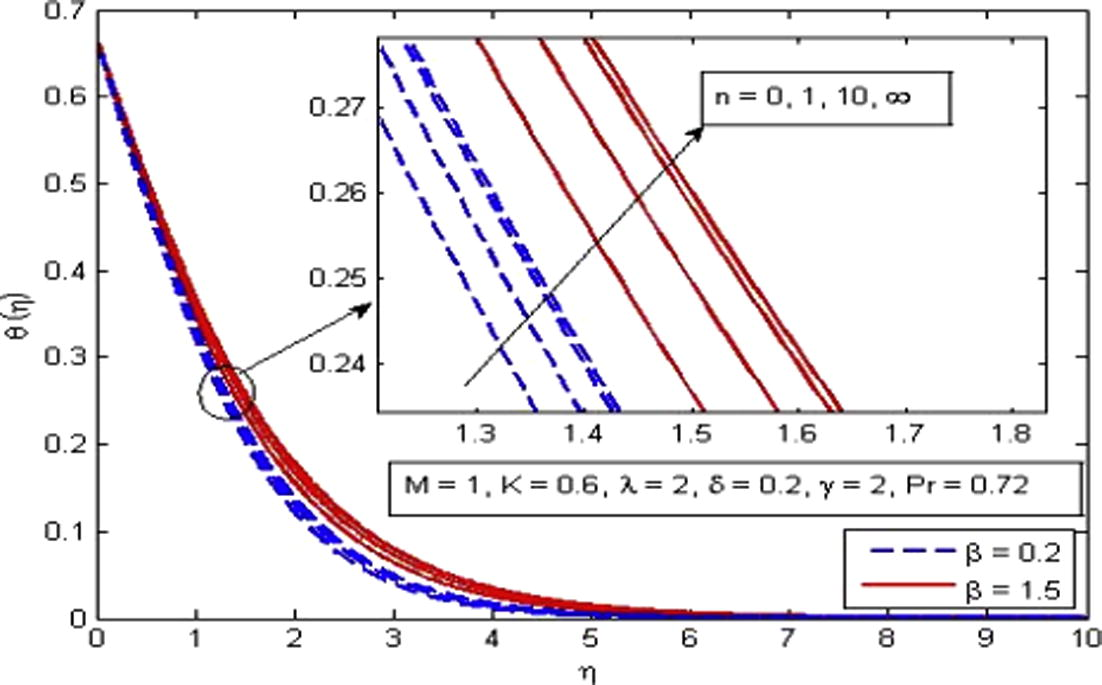
Effect of n on temperature for two different values of β.
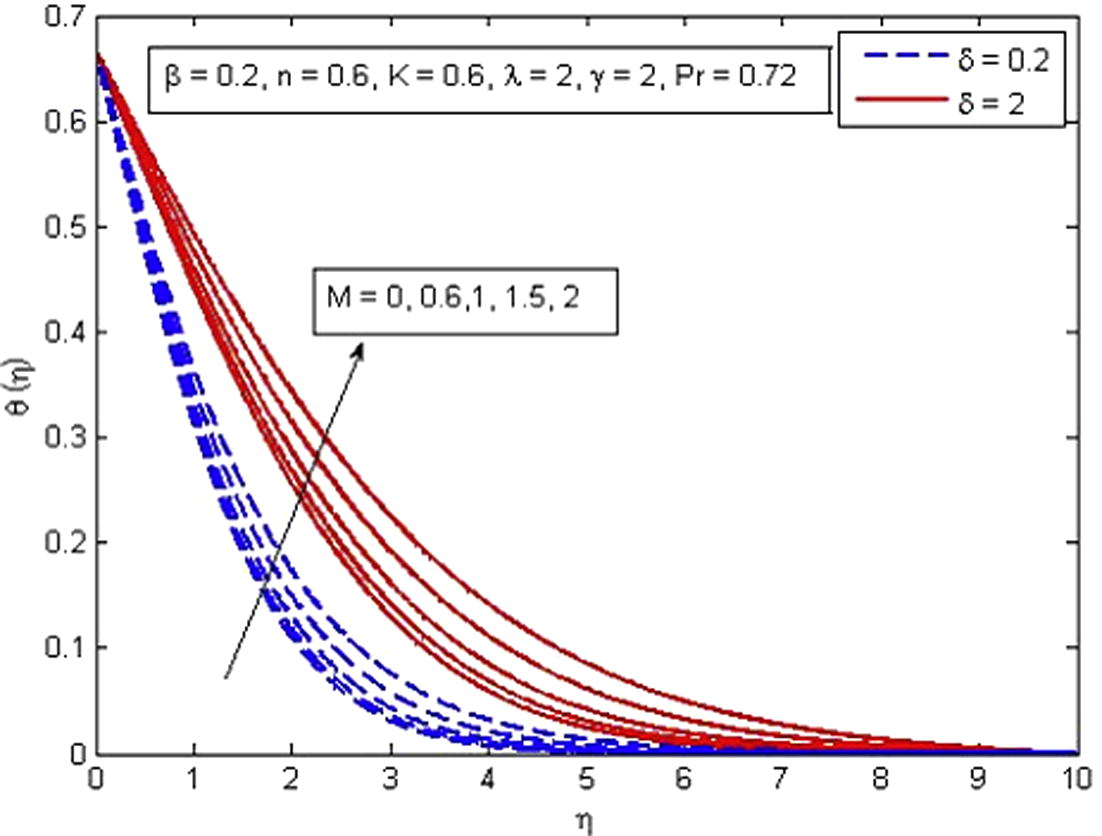
Effect of M on temperature for two different values of δ.
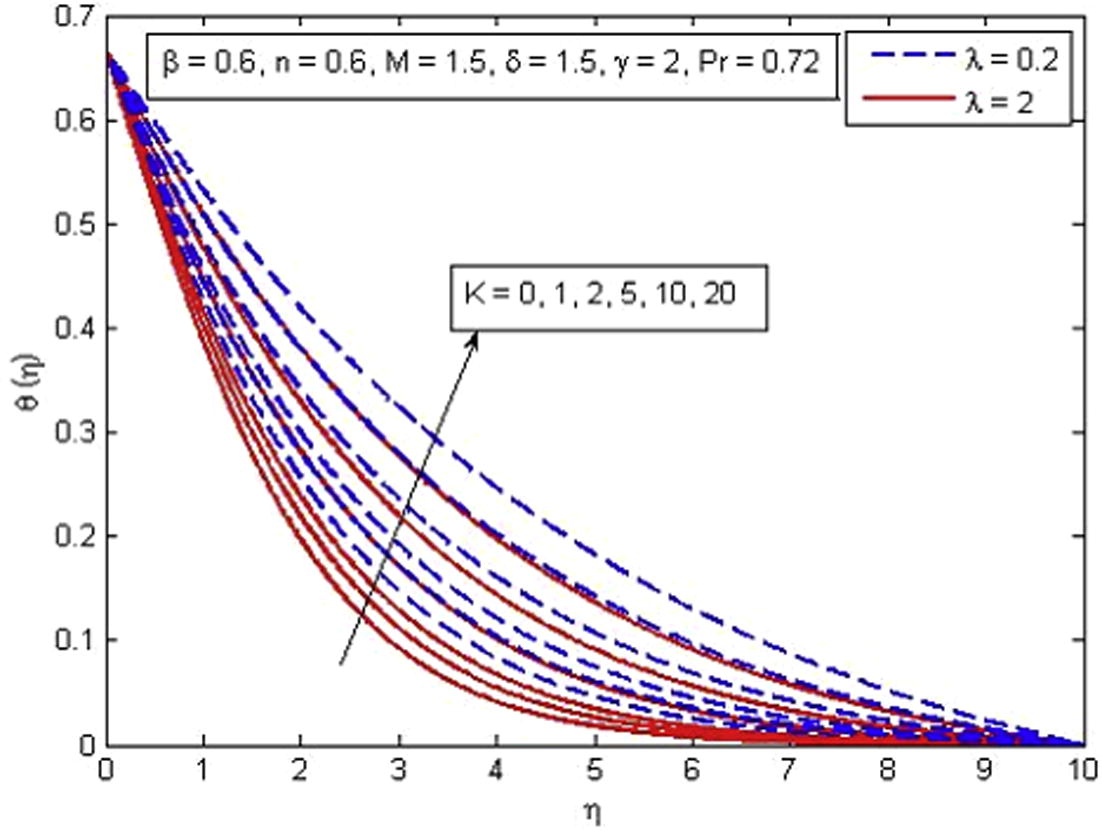
Effect of K on temperature for two different values of
.
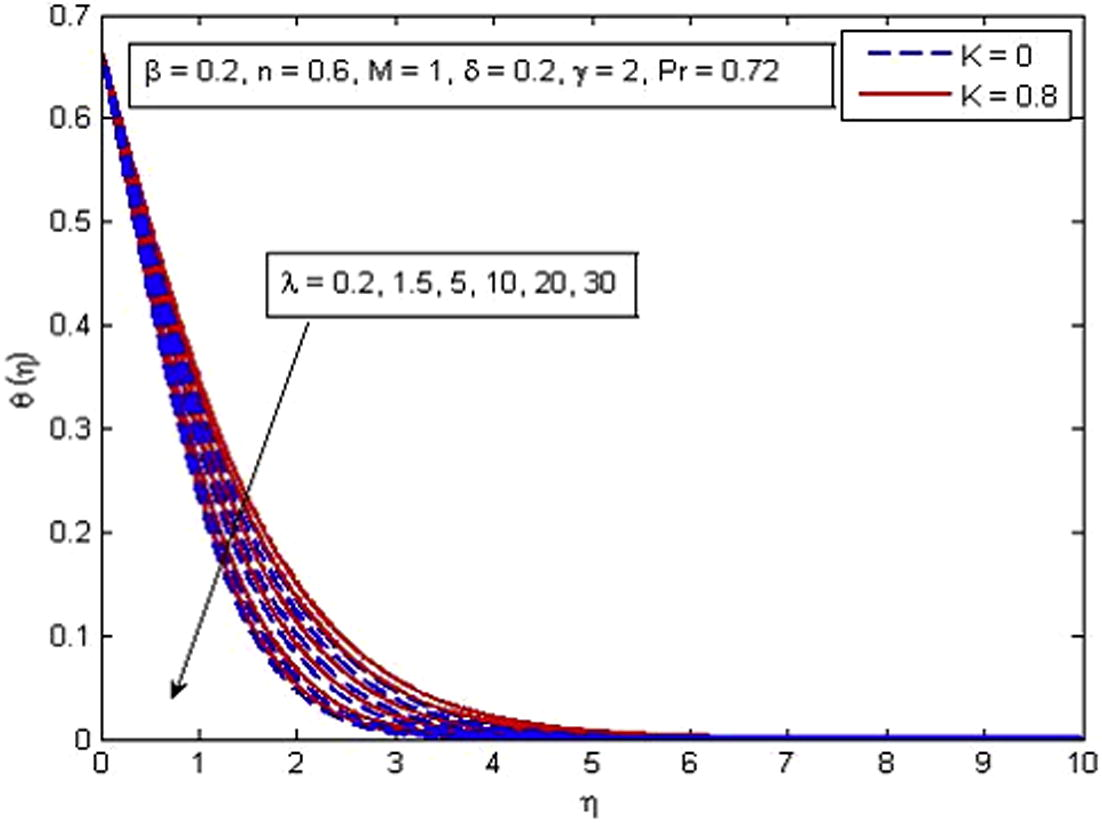
Effect of
on temperature for two different values of K.
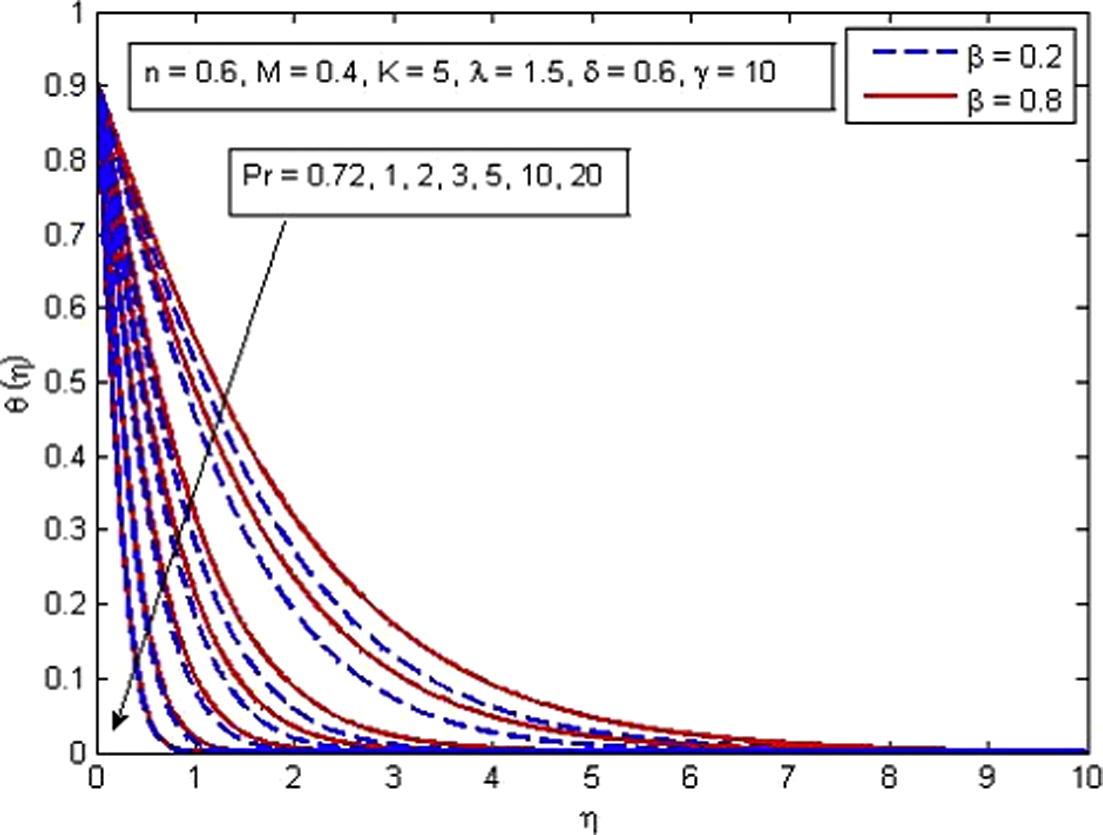
Effect of Pr on temperature for two different values of β.
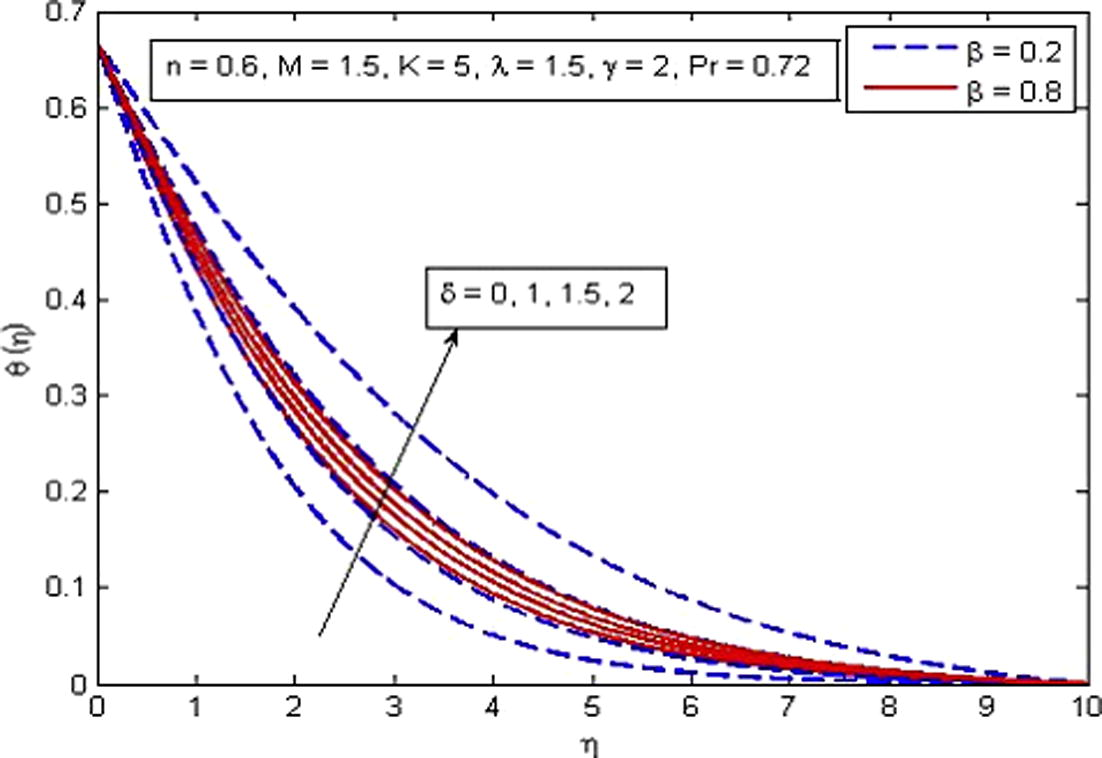
Effect of δ on temperature for two different values of β.
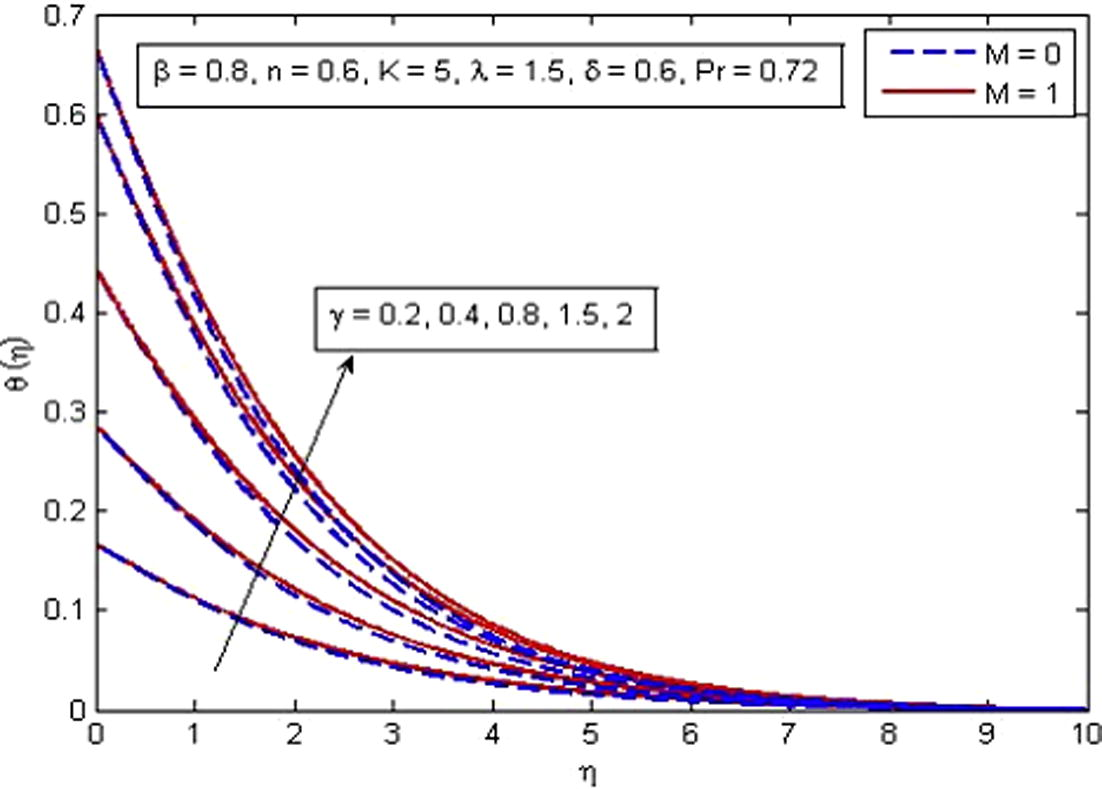
Effect of γ on temperature for two different values of M.
In order to analyze local skin friction coefficient and reduced Nusselt number for various parameters, Figs. 17–21 are depicted. From Fig. 17, it is noticed that skin friction coefficient reduces with an increase in K whereas increases as β and
increase. The negative values of skin friction coefficient show that the surface exhibits a drag force on the fluid and positive implies the lift force. Fig. 18 illustrates the variation of skin friction coefficient for various values of n, δ and M. It is found that increasing values of δ enhance shear stress. Physically, it happens because with the increase in δ, the fluid velocity decreases and as a result shear stress increases at wall. When slip phenomenon occurs, the stretching sheet exerts a force that can be transferred to the fluid partially. On the other hand, skin friction coefficient decreases with the increase in n and M. Fig. 19 demonstrates the variation of temperature gradient for different values of K, γ and β. It is noticed that the rate of heat transfer reduces with the increase in K whereas enhances significantly with the increase in γ and β. It is also observed that larger values of γ (γ → ∞) contribute less toward the temperature gradient. Further, β → ∞ reduces the present phenomenon to Newtonian fluid. Finally, Fig. 20 exhibits the variation of reduced Nusselt number for different values of
, Pr and n. It is found that rate of heat transfer is higher for higher values of
and Pr whereas decreases with the increase in n. Here
represents no convection and
corresponds to favorable pressure gradient case. Physically
indicates that heat is transferred from the surface of stretching sheet to the ambient fluid. In other words, we can say that free convection parameter can be used effectively for the fast cooling of the sheet. Fig. 21 reveals the effects of δ, γ and K on rate of heat transfer. It is noticed that the rate of heat transfer is higher for increasing values of γ whereas the rate of heat transfer falls as δ and K increase.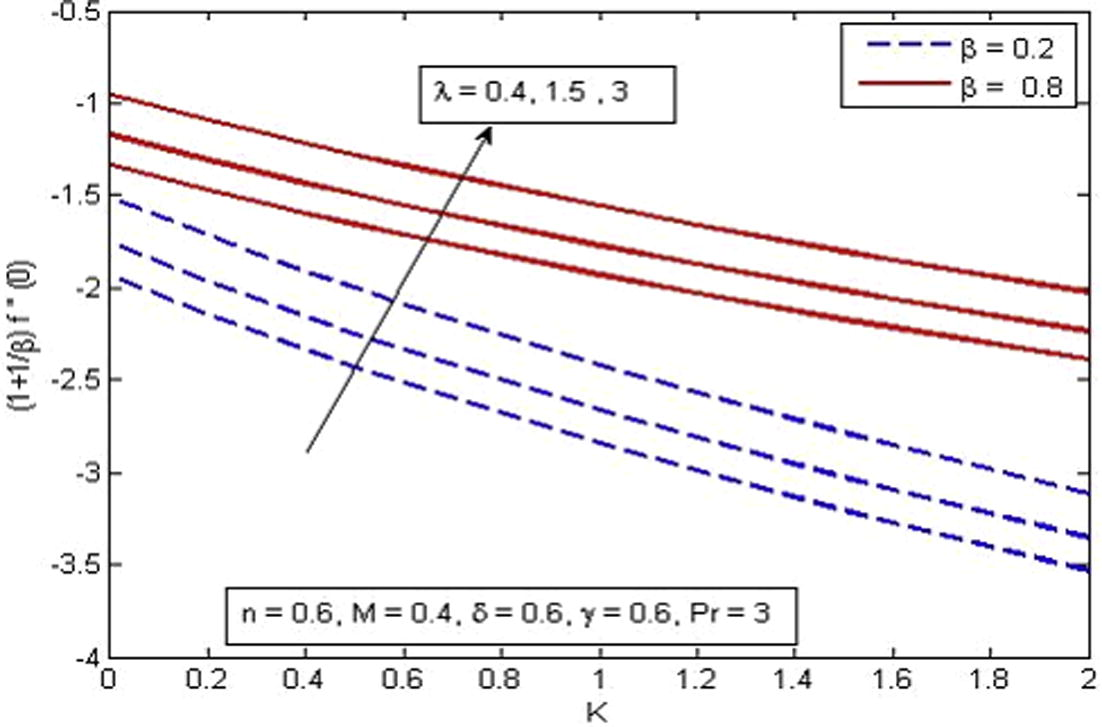
Variation of skin friction coefficient for various β,
and K.
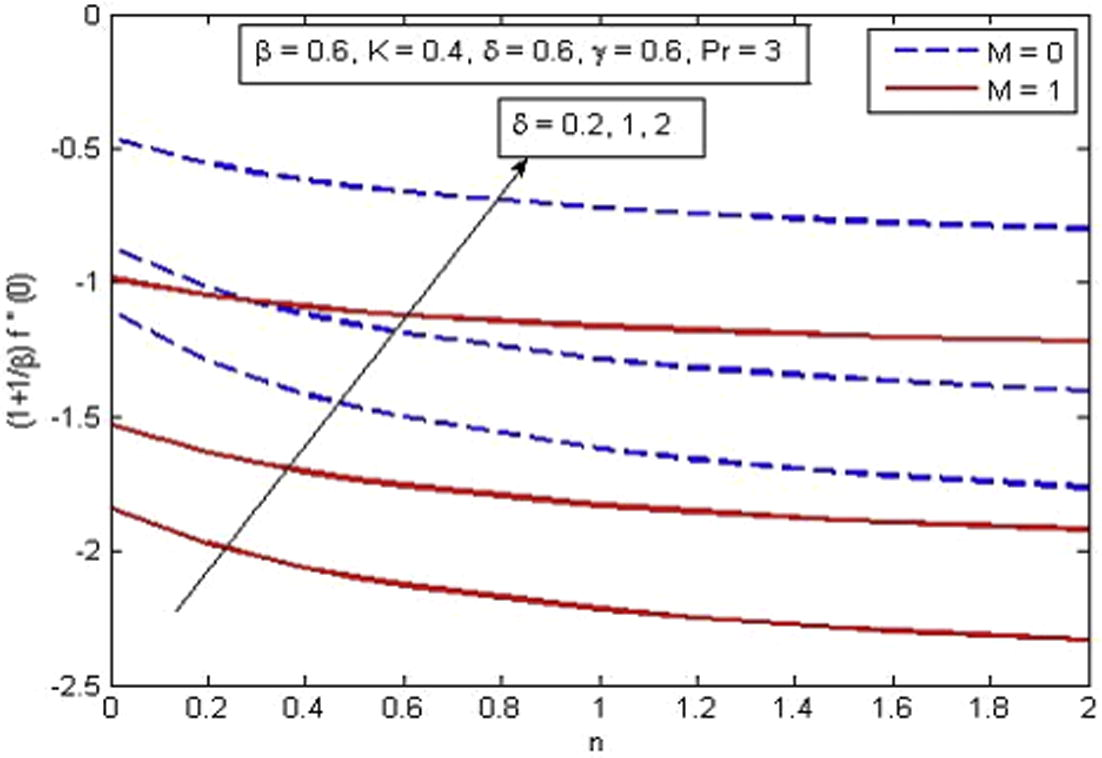
Variation of skin friction coefficient for various δ, n and M.
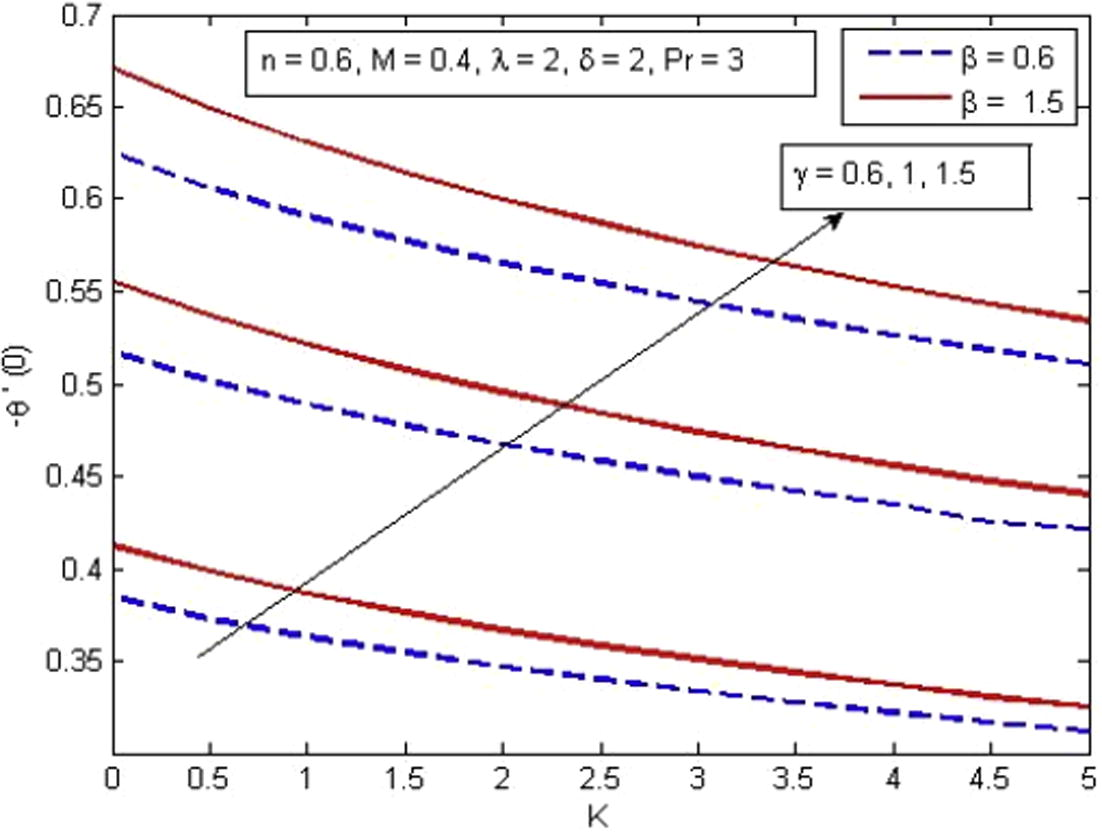
Variation of reduced Nusselt number for various γ, Pr, γ and β.
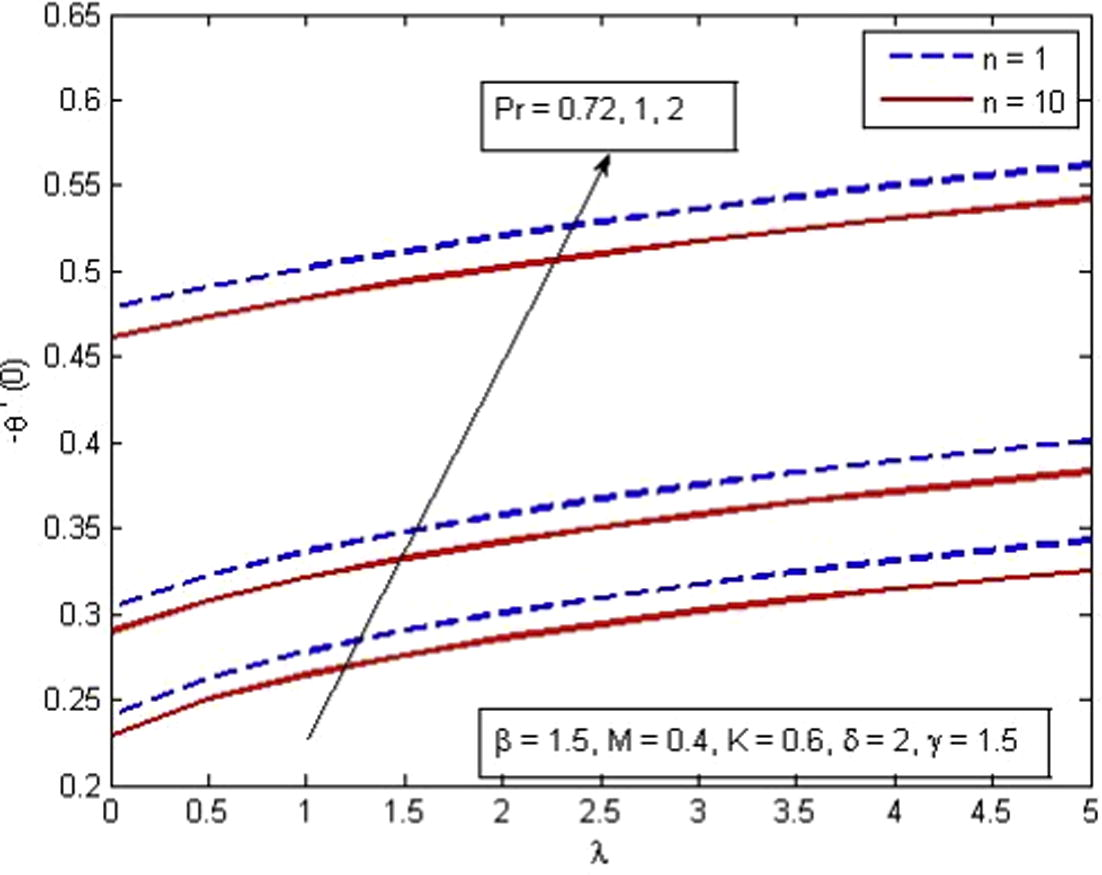
Variation of reduced Nusselt number for various
, Pr and n.
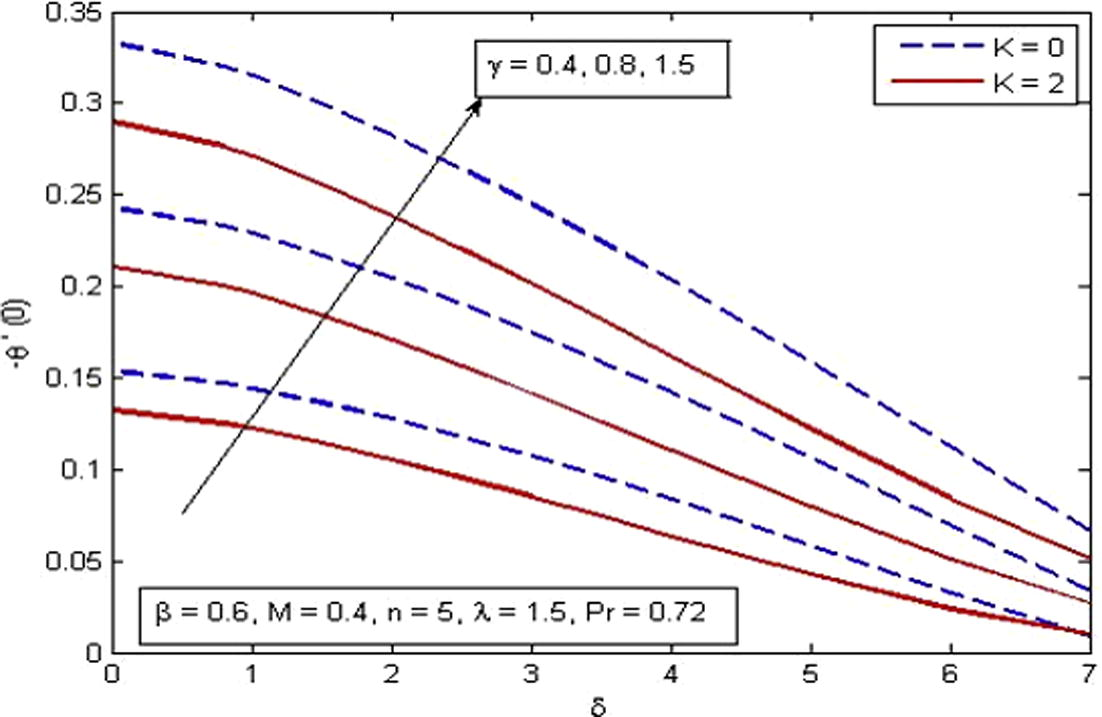
Variation of reduced Nusselt number for various δ, γ and K.
5 Conclusions
The present study investigates the numerical solution of MHD free convection flow of Casson fluid over nonlinearly stretching sheet in the presence of velocity slip and Newtonian heating. The non-linear governing partial differential equations are transformed using suitable transformations and solved numerically by finite difference scheme. Physically, the effect of Casson parameter β, magnetic parameter M, nonlinear stretching sheet parameter n, porosity parameter n, thermal buoyancy parameter , Prandtl number Pr, slip parameter δ and Newtonian heating parameter γ is studied in detail and the results are discussed graphically. The main findings of this study can be summarized as follows:
-
Velocity decreases with the increase in β, n, M, K and δ.
-
Velocity increases as and γ increase.
-
Temperature increases with the increase in β, n, M, K, δ and γ.
-
Temperature decreases with the increase in and Pr.
-
Local skin friction increases with the increase in β, and δ.
-
Local skin friction coefficient decreases with the increase in n, M and K.
-
Reduced Nusselt number increases with the increase in β, , Pr and γ.
-
Reduced Nusselt number decrease with the increase in n and K.
Acknowledgements
The authors would like to acknowledge Ministry of Higher Education (MOHE) and Research Management Centre Universiti Teknologi Malaysia (UTM) for the financial support through vote numbers 4F713, 4F538 and 06H67 for this research.
References
- MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: dual solutions. Ain Shams Eng. J.. 2014;5:1233-1239.
- [Google Scholar]
- Dual solutions in MHD stagnation-point flow of Prandtl fluid impinging on shrinking sheet. Appl. Math. Mech.. 2014;35:813-820.
- [Google Scholar]
- Casson fluid flow with variable thermo-physical property along exponentially stretching sheet with suction and exponentially decaying internal heat generation using the homotopy analysis method. J. Nigerian Math. Soc. 2015
- [CrossRef] [Google Scholar]
- Boundary conditions at a naturally permeable wall. J. Fluid Mech.. 1967;30:197-207.
- [Google Scholar]
- MHD stagnation-point flow of Casson fluid and heat transfer over a stretching sheet with thermal radiation. J. Thermodyn. 2013
- [CrossRef] [Google Scholar]
- Study of Flow and Heat Transfer on a Stretching Surface in a Rotating Casson Fluid. Proc. Natl. Acad. Sci., India Sect. A Phys. Sci.. 2013;85:421-426.
- [Google Scholar]
- Physical and computational aspects of convective heat transfer (first ed.). New York: Springer Verlag; 1984.
- MHD flow and mass transfer of an electrically conducting fluid of second grade in a porous medium over a stretching sheet with chemically reactive species. Int. J. Heat Mass Transf.. 2006;49:1851-1856.
- [Google Scholar]
- Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl. Math. Comput.. 2007;184:864-873.
- [Google Scholar]
- Secondary flow of a Casson fluid in a slightly curved tube. Int. J. Nonlinear Mech.. 1993;28:567-577.
- [Google Scholar]
- Casson fluid flow over a pipe filled with a homogeneous porous medium. Int. J. Eng. Sci.. 1996;34:1145-1156.
- [Google Scholar]
- The fluid mechanics of microdevices-the freeman scholar lecture. J. Fluids Eng.. 1999;121:5-33.
- [Google Scholar]
- Free convection on a vertical stretching surface with suction and blowing. Appl. Sci. Res.. 1994;52:247-257.
- [Google Scholar]
- Heat and mass transfer on stretching sheet with suction or blowing. Can. J. Chem. Eng.. 1997;55:744-746.
- [Google Scholar]
- Convective heat transfer and MHD effects on Casson nanofluid flow over a shrinking sheet. Cent. Eur. J. Phys.. 2014;129:862-871.
- [Google Scholar]
- Slip flow and heat transfer of a second grade fluid past a stretching sheet through a porous space. Int. J. Heat Mass Transf.. 2008;51:4528-4534.
- [Google Scholar]
- Effects of radiation and magnetic field on the mixed convection stagnation-point flow over a vertical stretching sheet in a porous medium. Int. J. Heat Mass Transf.. 2010;53:466-474.
- [Google Scholar]
- MHD flow and heat transfer over permeable stretching sheet with slip conditions. Int J. Numer. Methods Fluids. 2011;66:963-975.
- [Google Scholar]
- Thermally stratified stagnation point flow of Casson fluid with slip conditions. Int. J. Numer. Methods Heat Fluid Flow. 2015;25:724-748.
- [Google Scholar]
- Flow of power-law nanofluid over a stretching surface with Newtonian heating. J. Appl. Fluid Mech.. 2015;8:273-280.
- [Google Scholar]
- MHD heat and mass transfer for viscous flow over nonlinearly stretching sheet in a porous medium. Therm. Energy Power Eng.. 2014;3:191-197.
- [Google Scholar]
- Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng. Sci. Technol. Int. J.. 2015;80:1-9.
- [Google Scholar]
- Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf.. 2010;53:2477-2483.
- [Google Scholar]
- Natural convection boundary-layer flow on a vertical surface with Newtonian heating. Int. J. Heat Fluid Flow. 1994;15:392-398.
- [Google Scholar]
- Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin. Phys. B. 2013;22
- [CrossRef] [Google Scholar]
- Analysis of boundary layer flow over a porous nonlinearly stretching sheet with partial slip at the boundary. Alexandria Eng. J.. 2013;52:563-569.
- [Google Scholar]
- Model for flow of Casson nanofluid past a nonlinearly stretching sheet considering magnetic field effects. AIP Adv.. 2015;5
- [CrossRef] [Google Scholar]
- MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci. Iranica. 2012;19:1550-1553.
- [Google Scholar]
- MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alexandria Eng. J.. 2013;52:577-582.
- [Google Scholar]
- Oblique stagnation point flow of a Casson nano fluid towards a stretching surface with heat transfer. J. Comp. Theor. Nanosci.. 2014;11:1422-1432.
- [Google Scholar]
- MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Trans. Nanotechnol.. 2014;13:1326-1332.
- [Google Scholar]
- Combined effects of magnetic field and partial slip on obliquely striking rheological fluid over a stretching surface. J. Magn. Magn. Mater.. 2015;378:457-462.
- [Google Scholar]
- Slip flow of casson rheological fluid under variable thermal conductivity with radiation effects. Heat Transf. Res.. 2014;44:718-737.
- [Google Scholar]
- Boundary layer flow and heat transfer over a stretching sheet with Newtonian heating. J. Taiwan Inst. Chem. Eng.. 2010;41:651-655.
- [Google Scholar]
- MHD mixed convection flow of a casson fluid over an exponentially stretching surface with the effects of soret, dufour, thermal radiation and chemical reaction. World J. Mech.. 2015;5:165-177.
- [Google Scholar]
- Similarity solutions for the unsteady boundary layer flow and heat transfer due to a stretching sheet. Int. J. Appl. Mech. Eng.. 2006;11:647-654.
- [Google Scholar]
- Magnetohydrodynamic Casson fluid flow with heat and mass transfer through a porous medium over a stretching sheet. J. Porous Media. 2012;15:393-401.
- [Google Scholar]
- Heat source/sink effects on non-Newtonian MHD fluid flow and heat transfer over a permeable stretching surface: lie group analysis. Indian J. Phys.. 2014;88:75-82.
- [Google Scholar]
- Viscous flow over a nonlinearly stretching sheet. Appl. Math. Comput.. 2001;124:281-288.
- [Google Scholar]
- Fluid flow over a nonlinearly stretching sheet. Appl. Math. Comput.. 2006;181:609-618.
- [Google Scholar]
- Free convection on a vertical stretching surface. J. Appl. Math. Mech. (ZAMM). 1989;69:418-420.
- [Google Scholar]







