Translate this page into:
Dynamic penalty function approach for ramp metering with equity constraints
*Tel.: +60 3 41079802; fax: +60 3 41079803 khoohl@utar.edu.my (Hooi Ling Khoo)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
This study proposes a non-linear programming optimization model that could simultaneously consider the ramp metering efficiency and equity issue. Equity indexes are defined to capture the degree of equity of the ramp metering, which are formulated as constraints in the model. Dynamic penalty method is adopted to deal with the constraints since they are soft in nature in which solutions with small violations could be acceptable. A modified cell transmission model (MCTM) is chosen to simulate the traffic flow propagation in the network where the objective function value is derived from it. The results of the case study show that the proposed methodology could give better solutions compared to initial solutions. However, the equity indexes obtained are low. It is anticipated that the results for equity indexes can be improved if the penalty coefficients could be fine tuned properly.
Keywords
Ramp metering
Dynamic penalty function
Genetic algorithm
Dynamic stochastic user equilibrium
Cell transmission model
1 Introduction
Ramp metering is a cost-benefit strategy which is implemented to mitigate traffic congestion due to merging of on-ramps vehicles on expressways. By systematically regulating the entrance of vehicles at the on-ramps, ramp metering increases expressways’ throughput, reduces total system travel time and enhances traffic safety (Papageorgiou and Kotsialos, 2002). There are many studies carried out since the past decades to improve and enhance the efficiency of the ramp metering strategy, for example, Yang and Yagar (1994), Papageorgiou et al. (1990), and Zhang et al. (1996). In these studies, algorithm designs and analyses of the optimal ramp metering rate are the main focuses in order to minimize the total travel time of the system. Some other studies, such as Jacobson et al. (1989), Papageorgiou et al. (1991), Hellinga and Van-Aerde (1995), and Chu et al. (2004) tend to focus on the operational algorithm of the ramp metering.
Nevertheless, none of the above studies address the ramp metering equity issue. There are two types of the ramp metering equity, namely temporal and spatial equity (Levinson and Zhang, 2006). Temporal equity measures the difference of travel time, delay or speed among drivers who travel on the same route but arrive at the on-ramp at different times. Spatial equity measures these differences among drivers who arrive at different on-ramps at the same time. A perfect equitable metering is the one with no difference among drivers, whenever and wherever they access to the expressways through the on-ramps. The equity issue is important as Levinson and Zhang (2004) showed that current ramp metering algorithm provokes an inequity issue in Twin Cities, in which long trip drivers are favored compared to short trip drivers. Such inequity issue has adversely affected the public acceptance of the application and handicapped the widespread adoption of ramp metering.
There are some studies addressing the ramp metering equity issue. Benmohamed and Meerkov (1994) proposed a dynamic traffic control architecture that considers the local measurements for the benefit of individual expressway’s segment. Papageorgiou and Kotsialos (2001) defined an equity constraint that could keep the queuing length at the on-ramp within a desired threshold. The constraint is associated into the objective function by defining a static penalty term. Kotsialos and Papageorgiou (2004) imposed a maximum queue requirement to the optimization model in order to distribute evenly the burden of queuing among the on-ramps in the system. Zhang and Levinson (2005) proposed a framework that weighs the on-ramps waiting time nonlinearly in their transformed objective function in order to give more priority to ramps’ users. Yin et al. (2004) proposed a concave transformation function to capture the equity issue. It could be observed that there are limitations in the existing studies. They are either ad hoc in nature or require some transformation relationship (which might not exist in practice) in capturing the equity issue. Meng and Khoo (2010) defined an equity index to measure the degree of spatial equity of the ramp metering system. They proposed a multiobjective optimization model incorporating with the dynamic traffic flow model to simultaneously consider the efficiency and equity issue. This can overcome some of the difficulties encountered by the previous studies.
This study aims to formulate an optimization model that can consider ramp metering equity and efficiency issue simultaneously. An equity index which takes the ratio of the minimum to the maximum average travel delay incurred by on-ramp members in a group is defined to express the equity issue of ramp metering. A non-linear optimization model that aims to optimize the efficiency of the ramp metering, expressed by minimizing the total travel time of the expressway–arterial1 system is developed. Instead of formulating the equity indexes as objectives of the model (Meng and Khoo, 2010), this study shows that they could be formulated as constraints of the optimization model. Dynamic penalty is adopted to transform the equity constraints to the objective function in solving the optimization model. Genetic algorithms (GA) are employed as the solution method for the optimization model. The modified cell transmission model (MCTM) (Meng and Khoo, 2010) is adopted as the dynamic traffic flow model to simulate the traffic flow propagation on the expressway–arterial system in which the total travel time of the system is derived.
Dynamic penalty is suitable to be adopted in solving the constrained optimization model developed in the study. This is because the ramp metering equity constraint defined by the equity index is soft in nature. Practically, a perfect equity could not be achieved. One could, however, accept the solutions with small constraint violations. Dynamic penalty is appropriate in such cases as it could allow the search algorithm to include infeasible solutions into the search procedure. In addition, this could prevent GA from being trapped in the local minima. Long stagnation periods at each of minima may lead to serious difficulties in achieving satisfactory exploration efficiency of GA. Dynamic penalty has advantages over the static penalty as it could adjust the penalty value according to the degree of constraint violation for each solution. Accordingly, solutions with small constraint violation will have higher probability to stay through the iterations compared to other infeasible solutions. For more information of dynamic penalty, readers could refer to Richardson et al. (1989), Smith and Coit (1995), Gen and Cheng (1996), Tessema and Yen (2006), and Paszkowicz (2009). Penalty function approach has been applied in a few transportation studies that deal with equity. For instance, some of the notable studies are: Meng et al. (2001), Yang and Zhang (2002), Kalashnikov et al. (2008), and Sumalee et al. (2009). Nevertheless, the proposed adoption of dynamic penalty in solving the ramp metering equity issue in the study is a novel attempt in the transportation study.
2 The dynamic traffic flow model: modified cell transmission model (MCTM)
The cell transmission model (CTM) is developed by Daganzo (1994, 1995). It is an approximate method solving the hydrodynamic traffic flow model. The model assumes the fundamental relationship of traffic flow to follow piecewise linear functions. The links of the CTM network are divided into three types, namely ordinary links, merging links, and diverging links. The maximum connection for a link is three. In the case of a network with some nodes whose degree is greater than three, Daganzo (1995) demonstrated that the cell-based network can be constructed by shortening the time interval. The vehicle flow among the cells within the time horizon is calculated by two procedures. The first procedure calculates the flow of the vehicle on a link from the current time interval to the next time interval. The second procedure updates the vehicle volume of the cell according to the flow conservation equations. Daganzo (1994, 1995) did not explain in detail how to deal with the traffic flow stream at the on-ramps merging points. Meng and Khoo (2010) proposed sets of modified rules to the first procedure in order to incorporate the FIFO rules to govern the merging process. A rule of thumb is to find out the minimum waiting time of the merging traffic stream. Streams of traffic that have waiting time more than the minimum is allowed to have the priority to flow. If they have equal waiting time, only parts of them are allowed to flow. No vehicle is allowed to merge if their waiting time is lesser than the minimum waiting time. The full derivation of the model is not shown herein in view of the length limitation. Interested readers could refer to Meng and Khoo (2010).
3 Problem formulation
Let the expressway–arterial system be represented by a directed graph G = (N, A), where N is the set of nodes denoting heads and tails of on-ramps or off-ramps, A is the set of directed arcs denoting the on-ramps, the off-ramps, the expressway stretches, and the arterial roads, connecting two consecutive points meeting an on-ramp or an off-ramp, namely A ⊂ N × N. More specifically, let set , where , , Aoff, AE, and Aart, are the sets of metered on-ramps, un-metered on-ramps, off-ramps, expressway stretches, and arterial segments. Note that any two of these five subsets are disjoint. Let R and S denote the sets of origins and destinations, respectively, and R, S ⊆ N. Let also Krs denote the set of all routes from an origin r ɛ R to a destination s ɛ S, namely OD pair rs and r ≠ s. Assume that the demand for an OD pair rs at time t is denoted by qrs(t) and is loaded at the origin node r. The traffic will travel to the destinations via Krs routes. At each node, the stream of traffic chooses to move to the next node according to a pre-determined route of the best route in terms of travel time. The traffic is allowed to enter the expressway through any on-ramp and to leave the expressway using any off-ramp between the origin–destination. Alternatively, traffic may choose to use arterial roads to travel. An interested time period is discretized into T equal time intervals of length Δt, namely, [0, Δt, 2Δt, 3Δt, … , (T − 1)Δt]. Without loss of generality, it is assumed that Δt = 1 for easy of exposition.
3.1 The non-linear programming model
The objective of the ramp metering problem is to find the optimal ramp metering rate that can improve the efficiency of the ramp metering by minimizing the total travel time of the expressway–arterial system. Nonetheless, an acceptable ramp metering rate solution should be the one that could address the ramp metering equity issue as well. Accordingly, the equity index defined to capture the ramp metering equity is formulated as the constraint of the optimization model.
3.1.1 Decision variables, objective function, and constraints
The entrance flow of the traffic is controlled by the on-ramp meters, which is defined by the metering rates. The metering rate is allowed to vary after multiple consecutive time intervals, but not at every time interval, in order to ensure stability of traffic flow in the expressway–arterial network system. As such, the discretized time horizon is partitioned into N disjoint ramp metering periods, where N is a positive integer, named by (Δl−1, Δl], l = 0, 1, 2, … , N, in which Δ0 = 0 and ΔN = (T − 1)Δ. Let Za(t) be the metering rate from clock tick t to clock tick t + 1, where t ∈ [0, 1, 2, … , T − 1], for on-ramp
, and Z is a dynamic ramp metering rate solution, denoted by a row vector of all on-ramp time-dependent metering rates, namely:
To consider the efficiency of the ramp metering, the objective function of the optimization model is to minimize the total travel time of the expressway–arterial network system. Essentially, the total travel time is defined as the summation of the travel time spent by drivers on all used routes for all OD pairs during the time period. It is expressed as follows:
3.1.2 Equity index as a constraint
In order to capture the spatial equity, i.e. to ensure fair distribution of the delay encountered by drivers at the on-ramps, an equity index could be derived. To facilitate this, the average travel delay encountered by drivers at the on-ramp is derived from the MCTM. The delay is computed as the extra time a vehicle spends in waiting or queuing in the system. Accordingly, if a vehicle could not proceed to the next cell at current time interval, it will encounter extra one time interval delay. The average travel delay of vehicles incurred at an on-ramp over the time horizon is computed as:
By grouping the on-ramps, the equity index is defined for the on-ramp group by the ratio of the minimum and maximum average travel delay incurred by the on-ramp members in the group, expressed as:
3.2 The ramp metering optimization model with penalty function
Thus, the optimization model for ramp metering operation is presented as:
Eq. (10) indicates that the perfect equity condition which takes after Eq. (7). Nevertheless, in many of the cases, the perfect equity is difficult to achieve. As such, Eq. (10) should be a soft constraint rather than a hard constraint. Solutions with some violation to this constraint could be acceptable if there is no other better solution found. Hence, the implementation of the dynamic penalty function is appropriate in such situation. The adoption of the dynamic penalty function allows the algorithm to improve the solution in the feasible and infeasible solution space. Eq. (9) indicates the ramp metering rate function at time t for ramp a. The function Za(t) in Eq. (9) is identical to Eq. (2) which indicates the traffic responsive type of ramp metering scheme adopted in regulating the entry of vehicles.
The constrained optimization model shown in Eqs. (8)–(10) can be transformed to an unconstrained one by letting the new objective function as:
The performance of the genetic algorithms depends critically on the value of the penalty coefficient (Richardson et al., 1989). Adopting too high a value may restrict the search region too quickly that traps at the local optimal. However, if setting a too low value, the algorithm might spend too much effort in searching within the infeasible solution space. It is also worth noting that the value of αgen is also affected by the input parameters, μ and γ, which might need calibration to determine their values.
4 Solution method
The non-linear optimization model could be solved by using the meta-heuristics method. In this study, MCTM is embedded in the genetic algorithms in order to find the optimal solution. A dynamic ramp metering rate solution, Z, is encoded into a binary string, of which a specified portion represents a metering rate for a particular on-ramp at time t. More specifically, the metering ratio, for the period-dependent ramp metering rate schemes shown in Eq. (2) is encoded as the binary strings. The strings then are decoded to find the corresponding dynamic ramp metering rate solution by means of Eq. (2). This is then embedded into MCTM to compute the corresponding actual route travel time.
The step-by-step procedure is shown as follows:
-
Step 0. (Initialization of penalty parameters’ value). Set the values of μ and γ. Set gen = 1.
-
Step 1. (Computation of the value for αgen). Compute the value of αgen according to Eq. (12).
-
Step 2. (Initialization). Randomly generate a population of B strings.
-
Step 3. (Decoding). For each string, decode the string to get the dynamic time dependent ramp metering rate for the on-ramps of the expressway–arterial network, Z.
-
Step 4. (Call MCTM). Decode each string b in the population and run the MCTM to get the total travel time according to Eq. (4).
-
Step 5. (Fitness function calculation). Compute the value of objective function defined by Eq. (11) for each string. Note that for each infeasible string, a penalty value is imposed on it.
-
Step 6. (Generation of a new population). Repeat the following four sub-steps until the new population is completed.
-
○
Step 6.1. (Selection). According to the objective functions value evaluated in Step 3, use the rank selection method to choose two parent strings from the population.
-
○
Step 6.2. (Crossover). With a crossover probability, denoted by pc, crossover the parents to form a new offspring according to the one point crossover method. If no crossover is performed, offspring is the exact copy of the parents.
-
○
Step 6.3. (Mutation). With a mutation probability, denoted by pm, mutate new offspring at selected position in string.
-
-
Step 7. If all the strings in the population have been decoded, go to Step 8. Otherwise, go to Step 3.
-
Step 8. (Stopping criterion). If a stopping criterion is fulfilled, terminate the algorithm. Otherwise, set gen = gen + 1, and go to Step 1.
The stopping criterion of the algorithm is that it must have at least three consecutive generations with the objective functions’ value differing by less than 10%.
5 An illustrative case study
5.1 Network and algorithm setting
An illustrative expressway–arterial network system shown in Fig. 1 is used to test the applicability of the proposed methodology. It is a hypothetical network based on the I210W expressway–ramp network in Pasadena, CA (Munoz et al., 2004). It is 22-km long and consisted of 21 on-ramps and 18 off-ramps. From the figure, it is observed that the expressway mainline is connected to the arterial roads through the on-ramps and off-ramps. The arterial roads serve as alternative roads to the expressway–ramp system. The origins and destinations nodes are labeled in the figure. In addition, dummy links are created to load the demand from these origins into the network. The origin cells serve as the big parking lots that store all the vehicles that will be loaded into the network system. The vehicles are loaded into the network through dummy links/cells. The on-ramps are divided into groups to facilitate the definition of equity index. Each of the groups consists of three vicinities on-ramps, in which a total of seven groups are defined for the network.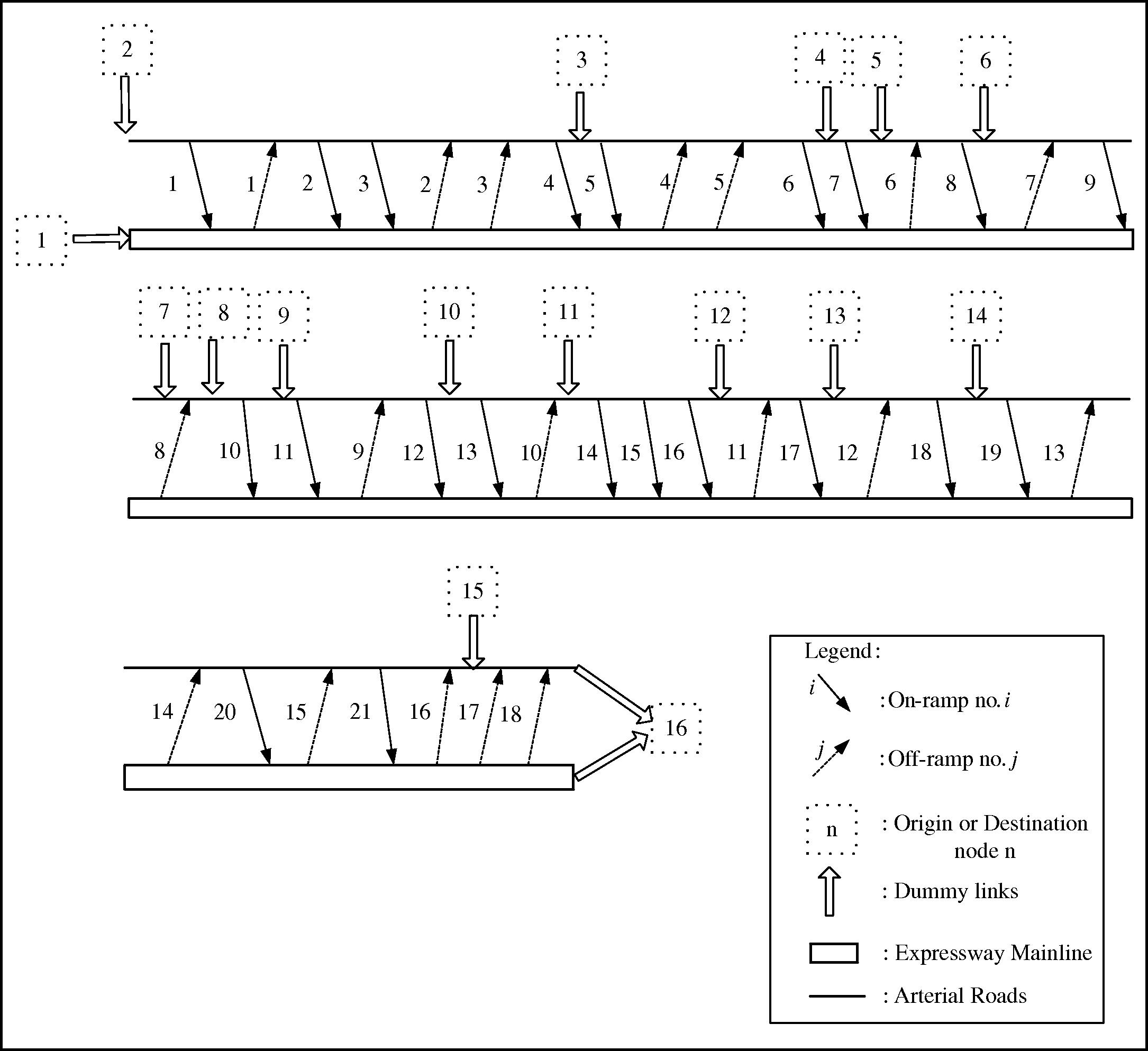
The hypothetical expressway–arterial network system.
The input parameters for the MCTM are such as follows – the free flow speed for expressway mainline section, ramps, and arterial roads are 100, 60, and 60 km/h, respectively. The backward shock wave speed is 28 km/h, and the jam densities are 17 veh/km/lane for the expressways, ramps, and arterial roads. The size of a cell on the expressway mainline segments, ramps, and arterial roads are 0.28, 0.17, and 0.17 km, respectively. The time interval, δ, also termed as a time step, is 10 s, and the time dependent ramp metering period is 5 min. The capacity of the expressway is set to be 2200 veh/h/lane while the arterial roads’ capacity is 2000 veh/h/lane. The ramp capacity is 2000 veh/h for one-lane ramp with speed of 60 km/h and 2400 veh/h for two-lane ramp. This is obtained by referring to the Highway Capacity Manual (HCM, 2000). Assume that there are 30 pairs of origin–destination (OD) trips in the network system with assumed demand value. These OD pairs and their demand are presented in Table 1. The departure time of the drivers is fixed and is carried out during the first 10 time step of the assignment period. The simulation is run until all the vehicles arrived at the destinations, which takes about 40 min of the simulation time.
OD pair
Origin node
Destination node
Total demand
OD pair
Origin node
Destination node
Total demand
1
1
16
750
16
7
16
150
2
2
16
500
17
8
16
200
3
3
16
200
18
8
15
150
4
6
16
200
19
8
10
200
5
11
16
155
20
12
16
150
6
14
16
195
21
12
14
200
7
4
15
200
22
12
15
150
8
4
13
150
23
12
15
200
9
4
9
200
24
12
13
150
10
4
16
150
25
3
10
200
11
5
16
200
26
3
9
150
12
5
12
150
27
6
15
200
13
5
15
200
28
6
10
150
14
7
12
150
29
11
9
200
15
7
15
200
30
11
10
150
For the genetic algorithms setting, each ramp metering ratio in Eq. (2), , is encoded by a 7-bit binary chromosome. With a total of 21 on-ramps, the length of a chromosome is 147 genes in the GA embedding with the MCTM. In addition, the population size is 50, the crossover probability is 0.7 and the mutation probability is 0.03. The μ and γ in Eq. (12) are set as 1 and 0.05, respectively.
5.2 Results
Fig. 2 shows the results obtained for the case study. The algorithm has gone through six outer loop iterations while the number of inner loop completed is different for each generation. The algorithm is terminated when there are continuously three generations with the objective function value differing by less than 10%. From the figure, it is observed that after the first outer loop, the inner loop converges at the objective function value of 3000 veh-h. It is thus believed that this is the local optimum of the solution. However, with dynamic penalty function, the algorithm can escape from the local optimum. As the penalty value increases with the number of generations, the algorithm will start a new search at the search space with higher objective function value. This could be observed from loops 3, 4, and 5 of Fig. 2. The best objective function obtained is 2717 veh-h. The equity index obtained for each of the ramp groups are 0.07, 0.13, 0.08, 0.49, 0.04, 0.06, and 1, respectively. The average equity index obtained is 0.27. The equity index value is low except for the last group in which a perfect equity is obtained. The corresponding ramp metering rate obtained is presented in Fig. 3. Despite the low equity index value, the results show that the proposed methodology is viable in searching for the best ramp metering rate solution by considering the equity issue. It is expected that the value setting of μ and γ of Eq. (12) has certain effect on the low equity index value obtained. With the value chosen, the fitness function is linearly related to the objective function according to Eq. (11). As such, the penalty value imposed on the violated solutions is not efficient enough to direct the algorithm to search in a highly feasible space. In the future study, calibration of the penalty coefficients is necessary besides investigating the impact of these values on the solution.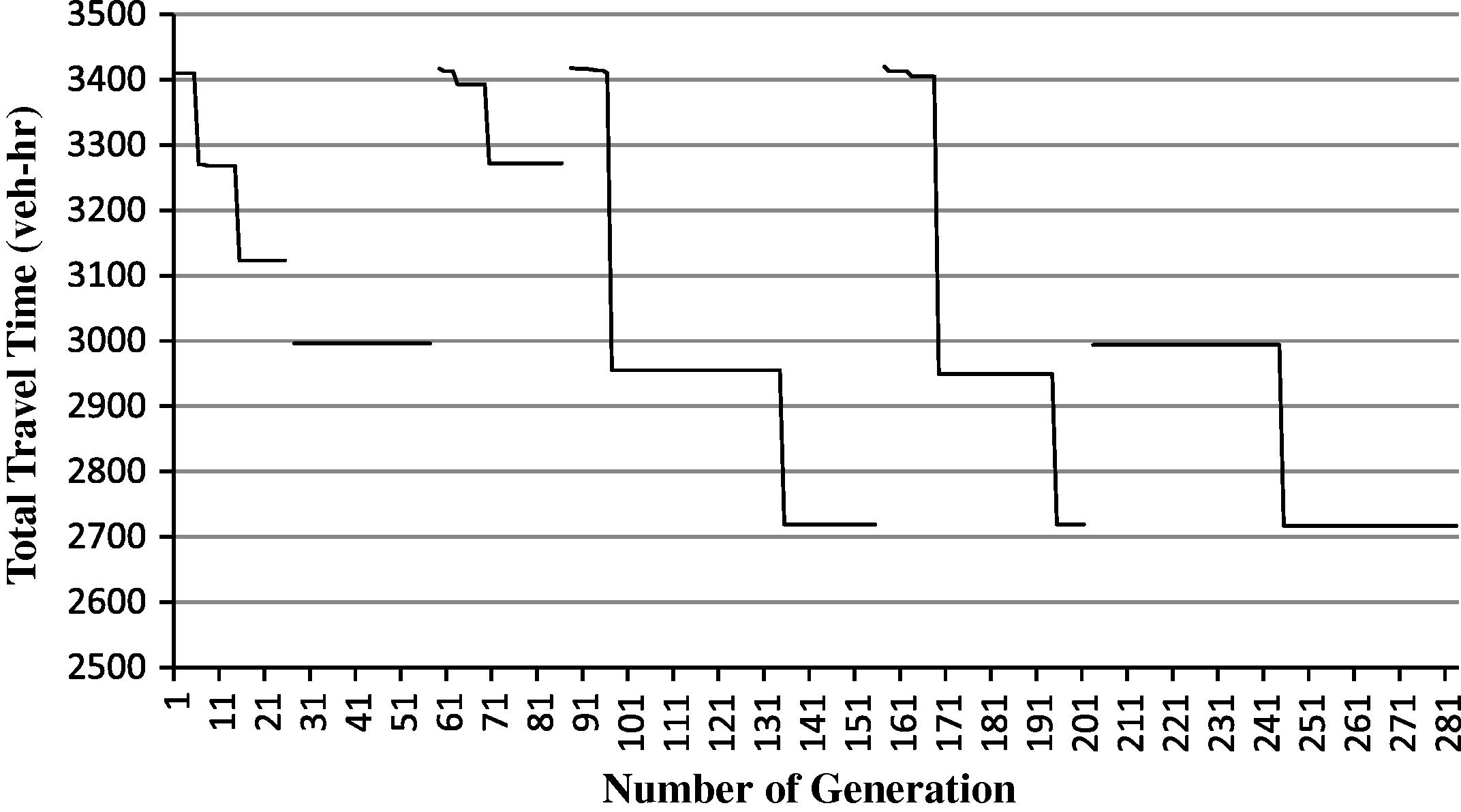
The convergence trend of the GA with dynamic penalty function.
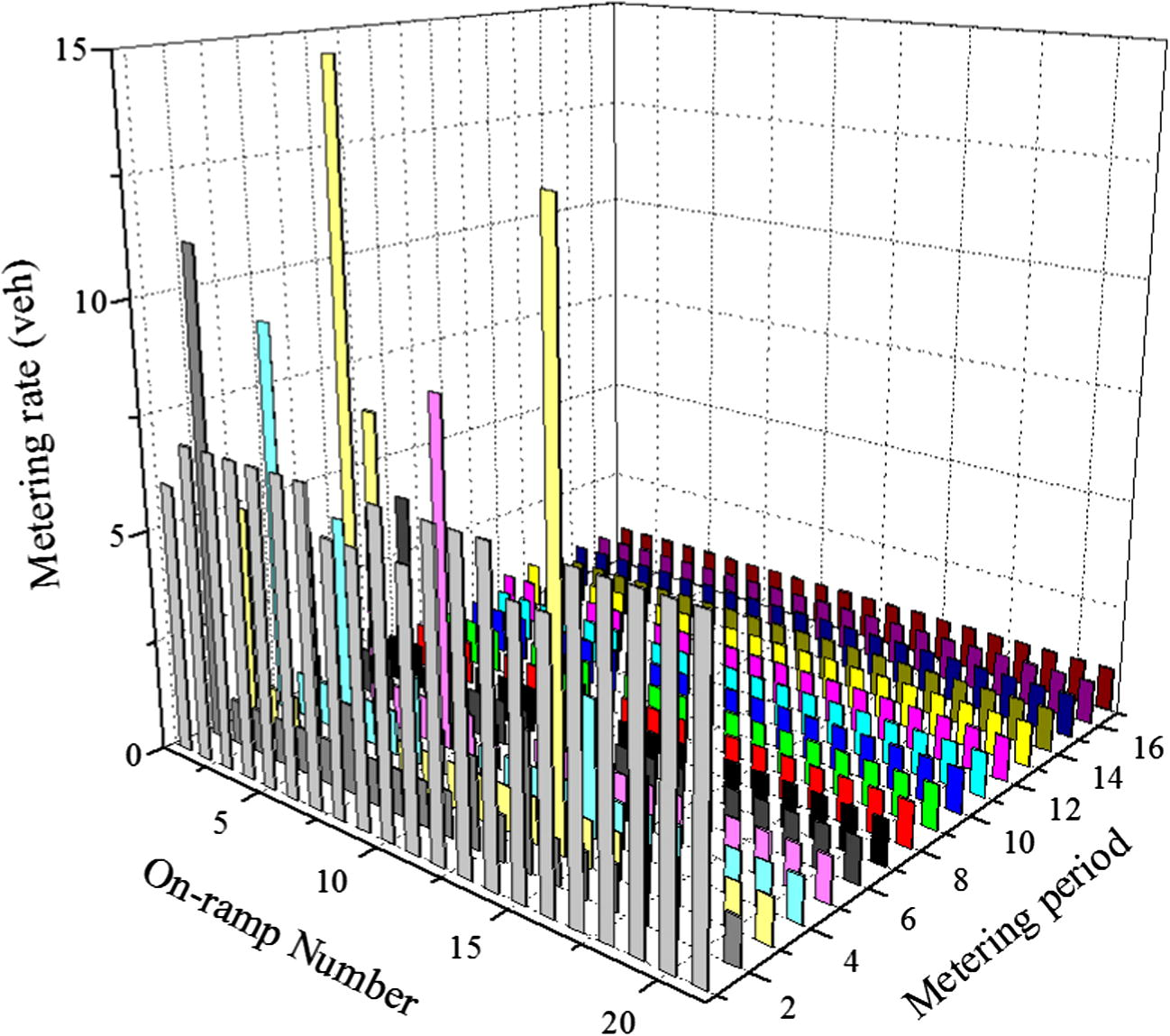
Metering rate solutions.
6 Conclusions
This paper addresses the ramp metering equity issue. Equity indexes are defined to quantify the degree of equity achieved. They are formulated as the constraints of the non-linear optimization model which is then solved by the dynamic penalty method. The advantage of adopting the dynamic penalty method is that it allows the heuristic algorithm to search in the infeasible spaces in order to avoid the local optimum. Besides, the equity constraints in this study are soft constraints in which the perfect equity could not be achieved in practical. By applying the dynamic penalty method, it could search in the infeasible space in order to find a better solution. The case study tested shows that the proposed methodology could give a better solution compared to the initial solution, although the equity indexes obtained are low. In order to obtain higher equity indexes, the penalty coefficients need to be properly fine tuned.
There is some work left for the future study. First, more runs can be carried out to test the efficiency of the proposed methodology. Current results are based on only one run. Second, sensitivity analysis can be carried out to test the impact of penalty coefficients on the objective function and equity indexes values. Third, a comparison of the solutions with other methods could be carried out in order to justify the quality of the solutions.
References
- Benmohamed, L., Meerkov, S.M., 1994. Feedback control of highway congestion by a fair on-ramp metering. In: Proceedings of the 33rd Conference on Decision and Control, pp. 2437–2442.
- Performance evaluation of adaptive ramp-metering algorithms using microscopic traffic simulation model. Journal of Transportation Engineering. 2004;130(3):330-338.
- [Google Scholar]
- The cell transmission model: a dynamic representation of highway traffic consistent with the hydrodynamic theory. Transportation Research Part B. 1994;28(4):269-287.
- [Google Scholar]
- The cell transmission model. Part II: Network traffic. Transportation Research Part B. 1995;29(2):79-93.
- [Google Scholar]
- Genetic Algorithms and Engineering Design. New York: John Wiley; 1996.
- Examining the potential of using ramp metering as a component of an ATMS. Transportation Research Record. 1995;1494:169-172.
- [Google Scholar]
- Highway Capacity Manual, 2000. Transportation Research Board. National Research Council, Washington, DC.
- Real time metering algorithm for centralized control. Transportation Research Record. 1989;1232:17-26.
- [Google Scholar]
- Kalashnikov, V.V., Kalashnykova, N.I., Vallejo, J.F.C., 2008. A penalty function approach to solve the bilevel tolls problem. In: Proceedings of the Third International Conference on Innovative Computing Information and Control.
- Nonlinear optimal control applied to coordinated ramp metering. IEEE Transactions on Control Systems Technology. 2004;12(6):920-933.
- [Google Scholar]
- Levinson, D., Zhang, L., 2004. Evaluating the effectiveness of ramp meters: evidence from the Twin Cities ramp meter shut-off. In: Gillen, D., Levinson, D. (Eds.), Assessing the Benefits and Costs of ITS. Kluwer Academic, The Netherlands.
- Ramp meters on trial: evidence from the Twin Cities metering holiday. Transportation Research Part A. 2006;40:810-828.
- [Google Scholar]
- A Pareto-optimization approach for a fair ramp metering. Transportation Research Part C. 2010;18(4):489-506.
- [Google Scholar]
- An equivalent continuously differentiable model and a locally convergent algorithm for the continuous network design problem. Transportation Research Part B. 2001;35:83-105.
- [Google Scholar]
- Munoz, L., Sun, X., Sun, D., Gomes, G., Horowitz, R., 2004. Methodological calibration of the cell transmission model. In: Proceeding of the 2004 American Control Conference, Boston, MA, June 30–July 2, 2004, pp. 798–803.
- Freeway ramp metering: an overview. IEEE Transactions on Intelligent Transportation Systems. 2002;3(4):271-281.
- [Google Scholar]
- Papageorgiou, M., Kotsialos, A., 2001. Efficiency versus fairness in network-wide ramp metering. In: Proceedings of the IEEE Intelligent Transportation Systems Conference, pp. 1189–1194.
- Modeling and real-time control of traffic flow on the southern part of Boulevard Peripherique in Paris. Part II: Coordinated on-ramp metering. Transportation Research Part A. 1990;24:361-370.
- [Google Scholar]
- ALINEA: a local feedback control law for on-ramp metering. Transportation Research Record. 1991;1320:58-64.
- [Google Scholar]
- Properties of a genetic algorithm equipped with a dynamic penalty function. Computational Materials Science. 2009;45:77-83.
- [Google Scholar]
- Richardson, Palmer, M.R., Liepins, G., Hilliard, M., 1989. Some guidelines for genetic algorithms with penalty functions. In: Proceedings of the Third International Conference on Genetic Algorithms, pp. 191–197.
- Smith, A.E., Coit, D.W., 1995. Penalty functions. In: Baeck, T., Fogel, D., Michalewicz, Z. (Eds.), Handbook of Evolutionary Computation. Oxford University Press.
- Road user charging design: dealing with multi-objectives and constraints. Transportation. 2009;36:167-186.
- [Google Scholar]
- Tessema, B., Yen, G.G., 2006. A self adaptive penalty function based algorithm for constrained optimization. In: IEEE Congress on Evolutionary Computation, Vancouver, Canada, July 16–21, pp. 246–253.
- Multi-class network toll design problem with social and spatial equity constraints. Journal of Transportation Engineering. 2002;128(5):420-428.
- [Google Scholar]
- Traffic assignment and traffic control in general freeway arterial corridor systems. Transportation Research Part B. 1994;28(6):463-486.
- [Google Scholar]
- Yin, Y., Liu, H., Benouar, H., 2004. A note on equity of ramp metering. In: Proceedings of IEEE Intelligent Transportation Systems Conference, pp. 497–502.
- Some general results on the optimal ramp control problem. Transportation Research Part C. 1996;4(2):51-69.
- [Google Scholar]
- Balancing efficiency and equity of ramp meters. Journal of Transportation Engineering. 2005;131(6):477-481.
- [Google Scholar]







