Dynamic behaviors of a fractional order nonlinear oscillator

Mobin Kavyanpoor; Saeed Shokrollahi

doi:10.1016/j.jksus.2017.03.006

View/Download PDF

Buy Reprints

PDF

Translate this page into:

31 (

); 14-20

doi:

10.1016/j.jksus.2017.03.006

Dynamic behaviors of a fractional order nonlinear oscillator

Mobin Kavyanpoor, Saeed Shokrollahi^⁎

Department of Aerospace Engineering, Malek Ashtar University of Technology, Tehran, Iran

⁎Corresponding author. s_shokrollahi@mut.ac.ir (Saeed Shokrollahi)

Received: 2017-2-5, Accepted: 2017-3-15, Published: 2017-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In the present paper, the primary resonance of a special type of nonlinear Duffing oscillator with fractional-order derivative is studied by the averaging method. First, the parametric amplitude-frequency equation is obtained, and then, the effects of the some parameters such as fractional order, nonlinear coefficients and force amplitude on the system dynamics are investigated. Moreover, experimental test were performed on the case study and a suitable model is identified. The obtained results are very useful in the nonlinear identification field.

Keywords

Fractional-order derivative

Averaging method

Amplitude-frequency curve

Nonlinear identification

Inertial and geometrical nonlinearity

Show Related Articles from PubMed

1 Introduction

Fractional-order derivative was first introduced in the late 1700 s, since then, many investigations on the theory and application of this method have been published by many authors (Samko et al., 1993; Kiryakova, 1994; Lakshmikanthama and Vatsalab, 2008; Kilbas et al., 2006; Podlubny, 1998 ). In recent years, according to the various applications in the fields of engineering and physics, growing interest is devoted to the fractional differential equations (West et al., 2003). Many significant phenomena in control engineering (Li et al., 2010; Das, 2008), signal processing (Chen et al., 2012), fluid mechanics (Chen et al., 2011), vibrations and dynamics (Padovan and Sawicki, 1998; Metzler and Klafter; 2000; Li et al., 2001; Shen et al., 2012a; Zhang et al., 2009 ) are simulated by fractional-order differential equations. The fractional derivative without singular kernel is an appropriate tool for modeling the thermal problems (Yang et al., 2016a,c,b; Atangana and Baleanu, 2016; Yang, 2016 ). Atangana and Koca (2016), Alkahtani (2016) and Gómez-Aguilar (2017) proposed a new operator with fractional-order based upon the Mittag-Leffler function, in which the derivative has no singular kernel.

The effect of the fractional-order derivative on the behavior of nonlinear dynamical system is very interesting and it is addressed in many researches. The calculation of the fractional-order derivative has been studied using different analytical and numerical techniques including averaging method (Shen et al., 2014b,a), multiple-scale approach (Xu et al., 2013), the homotopy analysis method (Ghazanfari and Veisi, 2011; Mishra et al., 2016), the differential transform method (Arikoglu and Ozkol, 2007) and some numerical methods (Atanackovic and Stankovic, 2008; Cao et al., 2010; Sheu et al., 2007 ).

In the current literature, despite the existence of many valuable researches in this field, only some important nonlinear techniques would be introduced. Shen et al. (2012b) and Shen et al. (2012c) investigated the Duffing oscillator with fractional-order derivative using the averaging method and Shen et al. (2016) used harmonic balance method for studying the Duffing oscillator. In this paper, we investigated a special type of Duffing oscillator with an additional nonlinear term, which governs the nonlinear vibration of the structures with large deflection. Accordingly, an experimental case study is tested and suitable parameters for the nonlinear model are identified. The proposed approach is useful for researchers in the field of mathematical model identification.

2 An approximate analytical solution for a special type of Duffing oscillator

The considered special type of Duffing oscillator with fractional-order derivatives is established as

(1)

m \ddot{x} (t) + c \dot{x} (t) + kx (t) + C_{2} x (t) {\dot{x}}^{2} (t) + C_{3} x^{3} (t) + K_{1} D^{p} [x (t)] = F \cos (ω t)

where m, c, k, C₂, C₃, F and ω are the system mass, linear viscous damping coefficient, linear stiffness coefficient, inertial nonlinearity coefficient, nonlinear stiffness coefficient, excitation amplitude, and excitation frequency, respectively. As can be seen, Eq. (1) is a special kind of Duffing equation due to the existence of inertial nonlinear term (

x (t) {\dot{x}}^{2} (t)

D^{p} [x (t)]

is the p-order derivative of x(t) (0 ≤ p ≤ 1), with the fractional coefficient of K₁ (K₁ > 0). Several definitions are proposed for fractional-order derivative; however, for a wide class of functions, they are equivalent under some conditions. In this paper, the Caputo’s definition is used (Shen et al. (2012b))

(2)

D^{p} [x (t)] = \frac{1}{Γ (1 - p)} \int_{0}^{t} \frac{x^{'} (u)}{{(t - u)}^{p}} du

where

Γ (x)

is Gamma function, which satisfies

Γ (x + 1) = x Γ (x)

. Using the coordinates transformation (this transformation satisfies, formally, the averaging method requirement (Nayfeh and Mook, 1995; Sanders et al., 2007; Burd, 2007 ) as follows:

ω_{0} = \sqrt{\frac{k}{m}}, 2 ε μ = \frac{c}{m}, ε c_{2} = \frac{C_{2}}{m}, ε c_{3} = \frac{C_{3}}{m}, ε k_{1} = \frac{K_{1}}{m}, ε f = \frac{F}{m}

Eq. (1) becomes:

(3)

\ddot{x} (t) + 2 ε μ \dot{x} (t) + ω_{0}^{2} x (t) + ε c_{2} x (t) {\dot{x}}^{2} (t) + ε c_{3} x^{3} (t) + ε k_{1} D^{p} [x (t)] = ε f \cos (ω t)

In order to study the primary resonance of the oscillator; the excitation frequency is considered close to the natural frequency, i.e. $ω \approx ω_{0}$ ., we have:

(4)

ω^{2} = ω_{0}^{2} + ε σ

where σ is the detuning factor. Eq. (3) can be rewritten in the following form:

(5)

\ddot{x} (t) + ω^{2} x (t) = ε \{f \cos (ω t) + σ x (t) - 2 μ \dot{x} (t) - c_{2} x (t) {\dot{x}}^{2} (t) - c_{3} x^{3} (t) - k_{1} D^{p} [x (t)]\}

Supposing Eq. (5) has the solution given by

(6a)

x (t) = a \cos φ

(6b)

\dot{x} (t) = - a ω \sin φ

where the amplitude a and the generalized phase

φ

(

φ = ω t + θ

) are slow-varying function of time. In accordance with the averaging method, one could obtain:

(6a)

\dot{a} = \frac{- 1}{ω} [P_{1} (a, θ) + P_{2} (a, θ)] \sin φ

(6b)

a \dot{θ} = \frac{- 1}{ω} [P_{1} (a, θ) + P_{2} (a, θ)] \cos φ

where

(7a)

P_{1} (a, θ) = ε [f \cos (φ - θ) + σ a \cos φ + 2 μ a ω s in φ - c_{2} a^{3} ω^{2} \cos φ \sin^{2} φ - c_{3} a^{3} \cos^{3} φ]

(7b)

P_{2} (a, θ) = - ε k_{1} D^{p} [a \cos φ]

Also, applying the standard averaging procedure to Eq. (6) in time interval [0, T] would lead to:

(8a)

\dot{a} = \frac{- 1}{T ω} \int_{0}^{T} [P_{1} (a, θ) + P_{2} (a, θ)] \sin φ d φ

(8b)

a \dot{θ} = \frac{- 1}{T ω} \int_{0}^{T} [P_{1} (a, θ) + P_{2} (a, θ)] \cos φ d φ

Based on the averaging method, one could select the time terminal T as T = 2π if $P_{i} (a, θ)$ (i = 1,2) is a periodic function, or T = ∞ if $P_{i} (a, θ)$ (i = 1, 2) is aperiodic one. Thereby, the simplified forms of the first term of Eqs. (8a) and (8b) would be as:

(9a)

{\dot{a}}_{1} = \frac{- 1}{2 π ω} \int_{0}^{2 π} P_{1} (a, θ) \sin φ d φ = - \frac{ε f}{2 ω} \sin θ - ε μ a

(9b)

a {\dot{θ}}_{1} = \frac{- 1}{2 π ω} \int_{0}^{2 π} P_{1} (a, θ) \cos φ d φ = - \frac{ε f}{2 ω} \cos θ - \frac{ε σ a}{2 ω} - \frac{ε c_{2} a^{3} ω}{4} + \frac{3 ε c_{3} a^{3}}{8 ω}

Substituting Eqs. (2) and (6b) into Eqs. (8a) and (8b), the second part of these equations can be calculated as:

(10a)

{\dot{a}}_{2} = - \lim_{T \to \infty} \frac{1}{T ω} \int_{0}^{T} P_{2} (a, θ) \sin φ d φ = \lim_{T \to \infty} \frac{- ε k_{1} a}{T Γ (1 - p)} \int_{0}^{T} \{\int_{0}^{t} \frac{\sin (ω u + θ)}{{(t - u)}^{p}} du\} \sin φ d φ

(10b)

a {\dot{θ}}_{2} = - \lim_{T \to \infty} \frac{1}{T ω} \int_{0}^{T} P_{2} (a, θ) \cos φ d φ = \lim_{T \to \infty} \frac{- ε k_{1} a}{T Γ (1 - p)} \int_{0}^{T} \{\int_{0}^{t} \frac{\sin (ω u + θ)}{{(t - u)}^{p}} du\} \cos φ d φ

Two important integrals formulae are introduced based on the residue theorem and contour integration as follows (Shen et al. (2012b)):

(11a)

B_{1} = \lim_{T \to \infty} \int_{0}^{T} \frac{sin (ω t)}{t^{p}} dt = ω^{p - 1} Γ (1 - p) cos (\frac{p π}{2})

(11b)

B_{2} = \lim_{T \to \infty} \int_{0}^{T} \frac{cos (ω t)}{t^{p}} dt = ω^{p - 1} Γ (1 - p) sin (\frac{p π}{2})

Using Eq. (11) and doing some complicated but standard computation on Eq. (10), we have:

(12a)

{\dot{a}}_{2} = \frac{- ε {ak}_{1} ω^{p - 1}}{2} sin (\frac{p π}{2})

(12b)

a {\dot{θ}}_{2} = \frac{ε {ak}_{1} ω^{p - 1}}{2} cos (\frac{p π}{2})

Combining Eq. (9) with Eq. (12), Eq. (8) can be written as:

(13a)

\dot{a} = - \frac{ε f}{2 ω} \sin θ - ε μ a - \frac{ε {ak}_{1} ω^{p - 1}}{2} sin (\frac{p π}{2})

(13b)

a \dot{θ} = - \frac{ε f}{2 ω} \cos θ - \frac{ε σ a}{2 ω} - \frac{ε c_{2} a^{3} ω}{4} + \frac{3 ε c_{3} a^{3}}{8 ω} + \frac{ε {ak}_{1} ω^{p - 1}}{2} cos (\frac{p π}{2})

Substituting the new parameters with the primary ones, Eq. (13a) and Eq. (13b) becomes

(14a)

\dot{a} = - \frac{F}{2 m ω} \sin θ - \frac{ca}{2 m} - \frac{{aK}_{1} ω^{p - 1}}{2 m} sin (\frac{p π}{2})

(14b)

a \dot{θ} = - \frac{F}{2 m ω} \cos θ - \frac{ε σ a}{2 ω} - \frac{C_{2} a^{3} ω}{4 m} + \frac{3 C_{3} a^{3}}{8 m ω} + \frac{{aK}_{1} ω^{p - 1}}{2 m} cos (\frac{p π}{2})

Now, the steady-state solution, which is an important achievement in the vibration engineering (Den-Hartog, 1956; Timoshenko et al., 1974), is investigated. Letting ??̇ = 0 and $a \dot{θ}$ = 0, and eliminating ?? from Eqs. (14a) and (14b), one could obtain the amplitude-frequency equation as

(15)

\{{(\frac{c \overline{a}}{2 m} + \frac{\overline{a} K_{1} ω^{p - 1}}{2 m} sin (\frac{p π}{2}))}^{2} + {(\frac{ε σ \overline{a}}{2 ω} + \frac{C_{2} {\overline{a}}^{3} ω}{4 m} - \frac{3 C_{3} {\overline{a}}^{3}}{8 m ω} - \frac{\overline{a} K_{1} ω^{p - 1}}{2 m} cos (\frac{p π}{2}))}^{2}\} = \frac{F^{2}}{{(2 m ω)}^{2}}

where

\overline{a}

is the steady-state amplitude.

3 Study on the amplitude-frequency equation parameters

Some illustrative example systems are studied herein as defined by the system basic parameters: m = 1, ω = 10, c = 0.1. Based on Eq. (15), the effect of some parameters on the amplitude-frequency curves could be achieved as shown in Figs. 1–5 .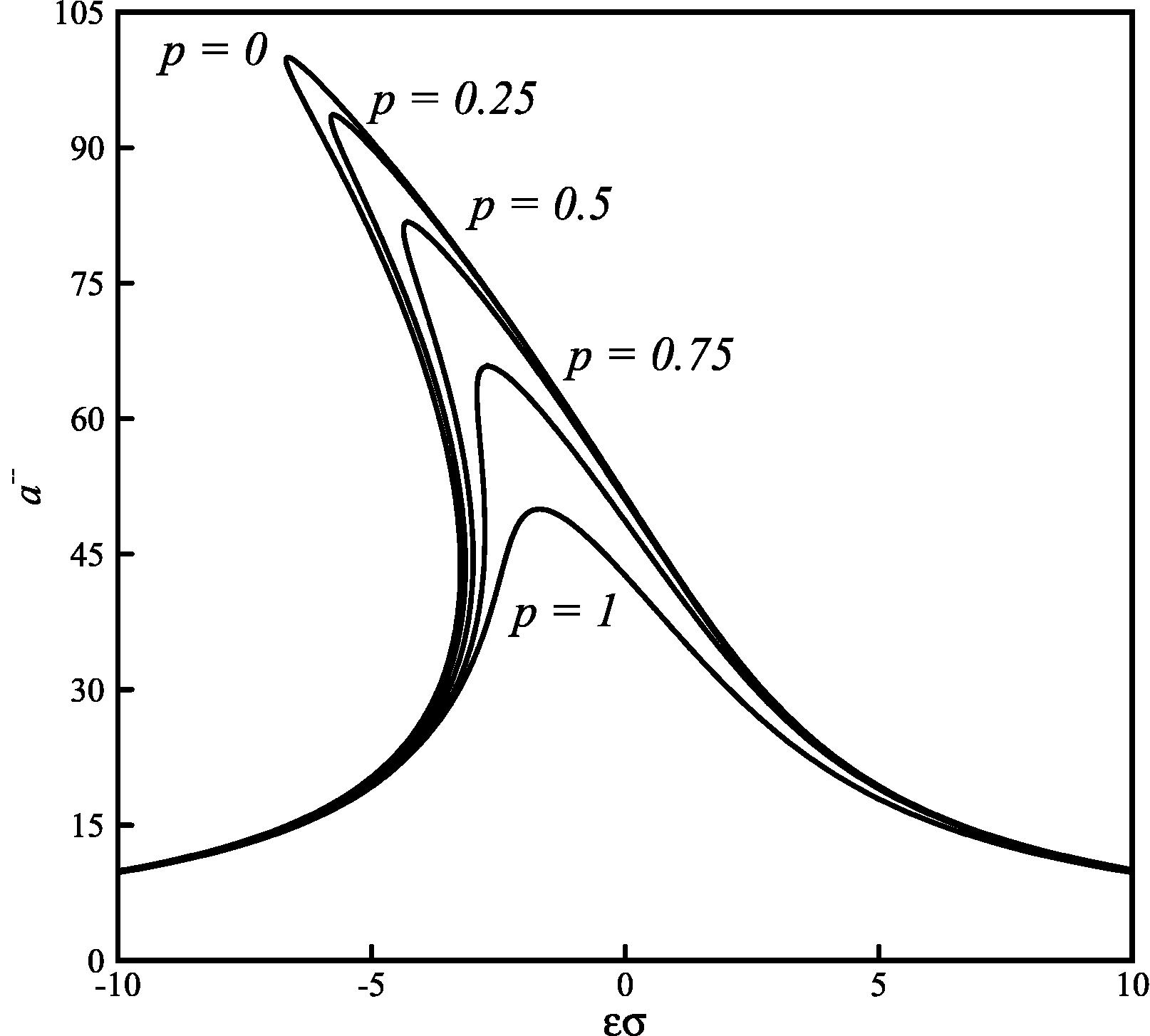

Effect of the fractional order p on the amplitude-frequency curves (C2 = 1.5 × 10−5, C3 = 1 × 10−4, K1 = 0.1 and F = 100).

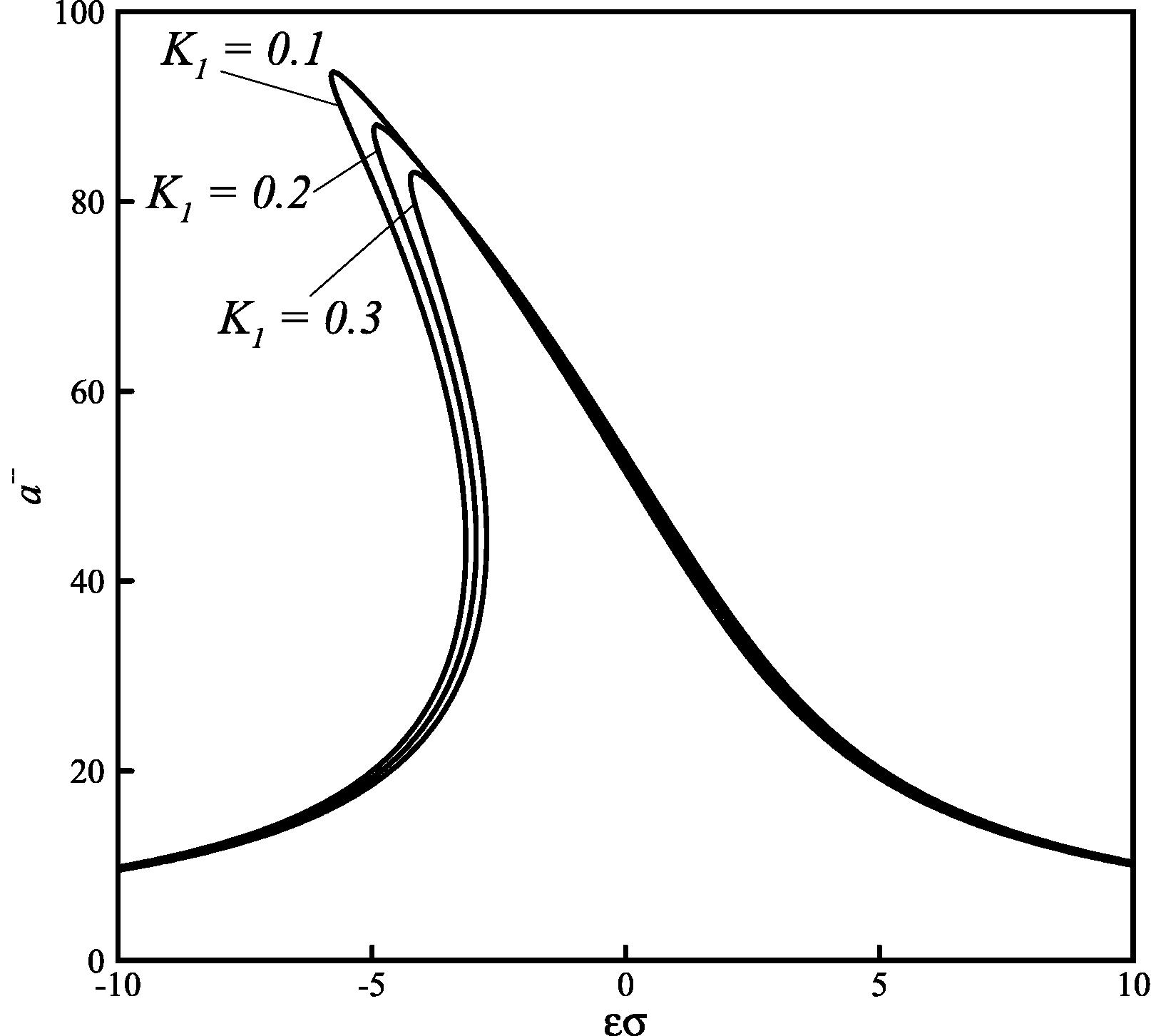
Effect of the fractional coefficient K1 on the amplitude-frequency curves (C2 = 1.5 × 10−5, C3 = 1 × 10−4, p = 0.25 and F = 100).

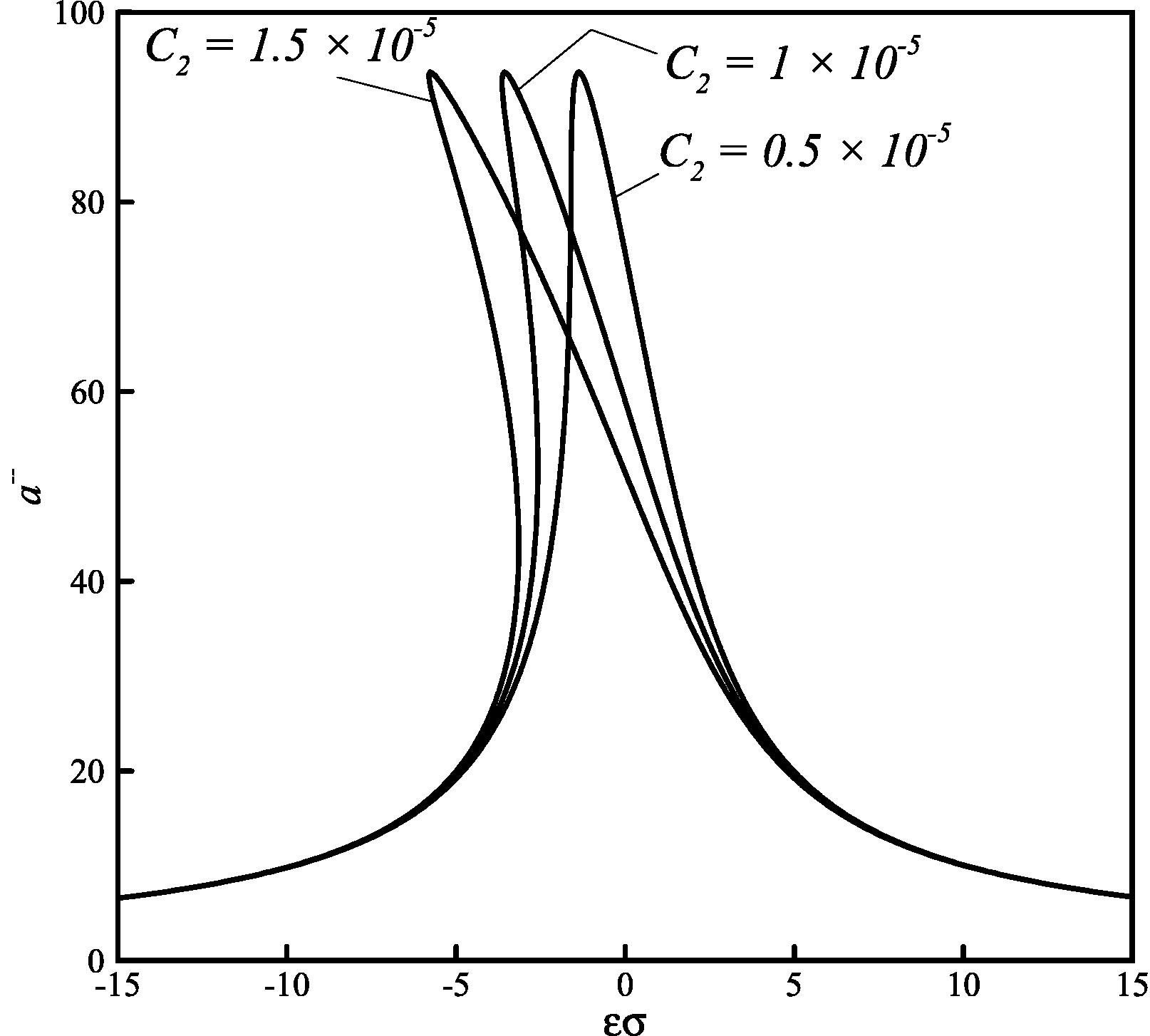
Effect of inertial nonlinearity coefficient C2 on the amplitude-frequency curves (p = 0.25, C3 = 1 × 10−4, K1 = 0.1 and F = 100).

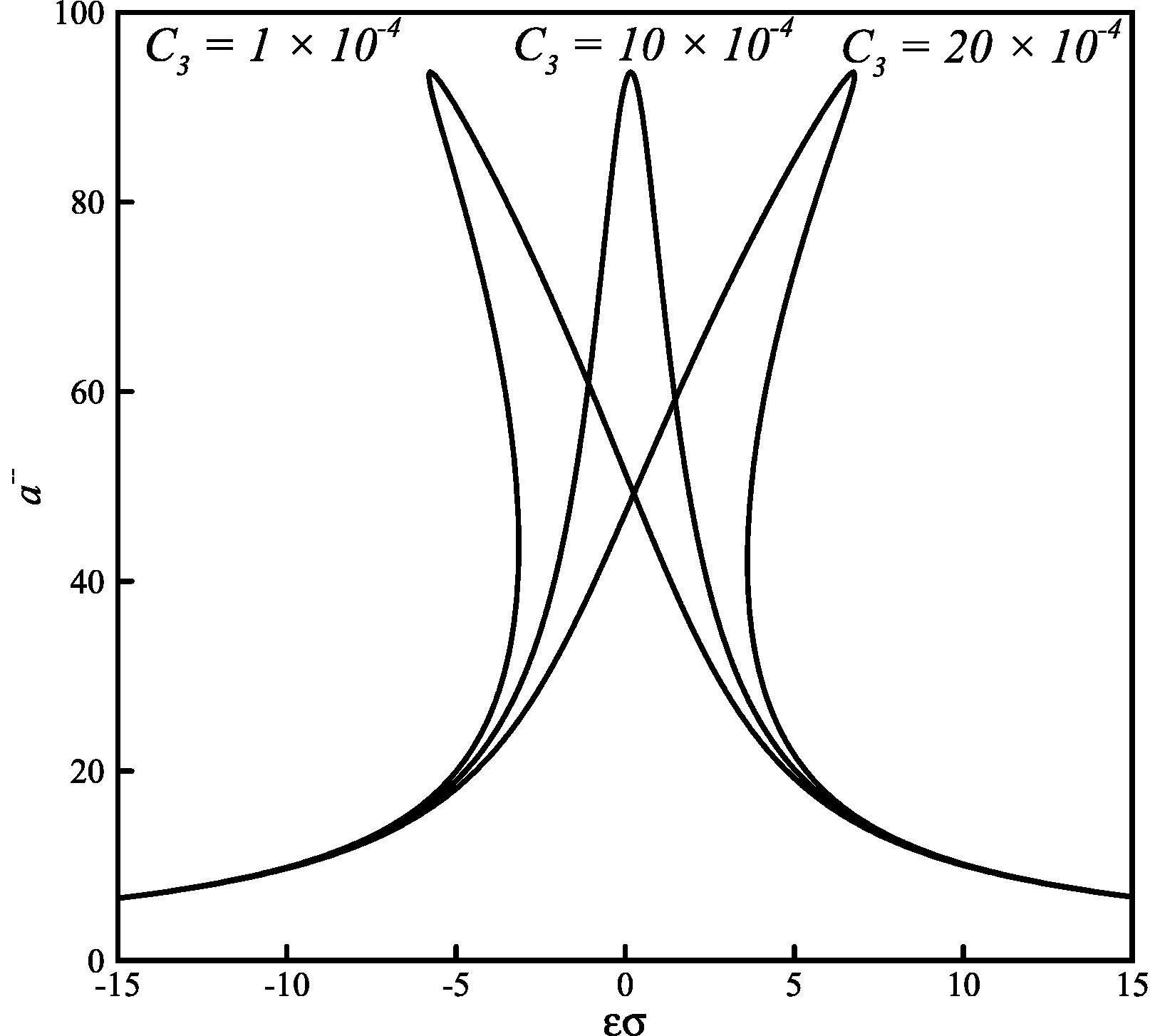
Effect of nonlinear stiffness coefficient C3 on the amplitude-frequency curves (p = 0.25, C2 = 1.5 × 10−5, K1 = 0.1 and F = 100).

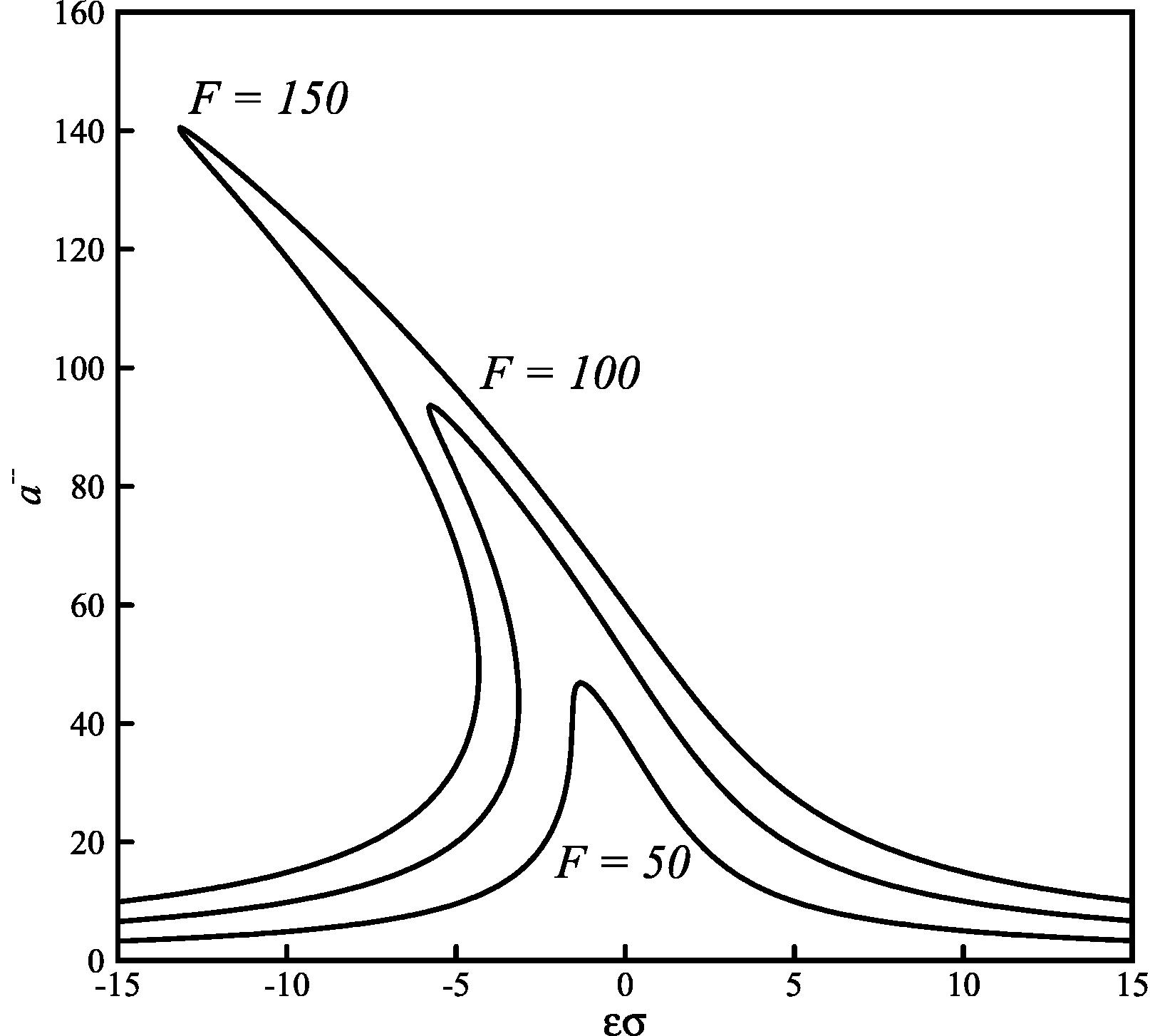
Effect of the excitation amplitude on the amplitude-frequency curves (C2 = 1.5 × 10−5, C3 = 1 × 10−4, K1 = 0.1 and p = 0.25).

The effects of the fractional-order ?? and the fractional coefficient K₁ on the amplitude–frequency curves are depicted in Figs. 1 and 2 respectively. Based on these Figs., the maximum amplitude would be smaller for the larger values of p and K₁. Accordingly, these two parameters have damping effects on the dynamic behavior of the system (Rossikhin and Shitikova, 1997). In addition, the bending amplification of the amplitude-frequency curve is more severe through the decrease in the fractional order p and the fractional coefficient K₁, because the stiffness becomes larger in this nonlinear system. Therefore, the fractional-order derivative term affects the stiffness and damping of this dynamical system, which is useful in system identification.

The effects of changing C₂, C₃ and F in Eq. (15) on the amplitude-frequency curves are shown in Figs. 3–5 , respectively. According to the figures, unlike the p and K₁ parameters, the C₂ and C₃ parameters have no effect on the maximum amplitude.

Based on Figs. 3 and 4, the peaks of amplitude-frequency curves move to the left and right by changing C₂ and C₃, which indicates that these two parameters affect the stiffness of the nonlinear oscillator. The sign of these two coefficients determine the softening nonlinearity (bends the amplitude-frequency curves to the left) or hardening nonlinearity (and vice versa). Based on Fig. 5, three values are selected for excitation amplitude. By increasing the excitation amplitude, the curves are shifted upwardly.

3.1

3.1 Experimental case study

Based on the above results, a case study is investigated experimentally. For this purpose, a slender beam element, which can be considered as a highly flexible beam is selected. Thus, the Euler-Bernoulli beam theory can be used for deriving the nonlinear equations of motion. The beam is vibrated by a harmonic excitation force applied at the base. The equation of motion according to the mentioned assumptions (in addition, the effect of axial inertia of the beam is neglected) is in the form of Eq. (1) (Nayfeh and Pai, 2004). In the present study, the excitation frequency is also selected very close to the beam second natural frequency (second primary resonance), thus, only the second mode is excited and the other modes are damped out due to the structural damping.

A cantilever Steel beam with a length of 600 mm, width of 30 mm and thickness of 1.17 mm is considered as an experimental case study. The rigid supporting base of the beam is fixed to the moving rod of an electrodynamics shaker Tira 5110 M, so the base would be excited as shown in Fig. 6. The base acceleration was recorded by a PCB B30 accelerometer attached to the beam base and the tip response of the beam was recorded by a PCB B35 miniature accelerometer. At first, a low level random excitation was applied to the base of the beam and the linear FRF was measured for tip position. In Fig. 7, the FRF associated with the base excitation is shown. The second natural frequency and associated damping coefficient of the beam are 16.25 Hz and 0.004 N.s/m respectively.

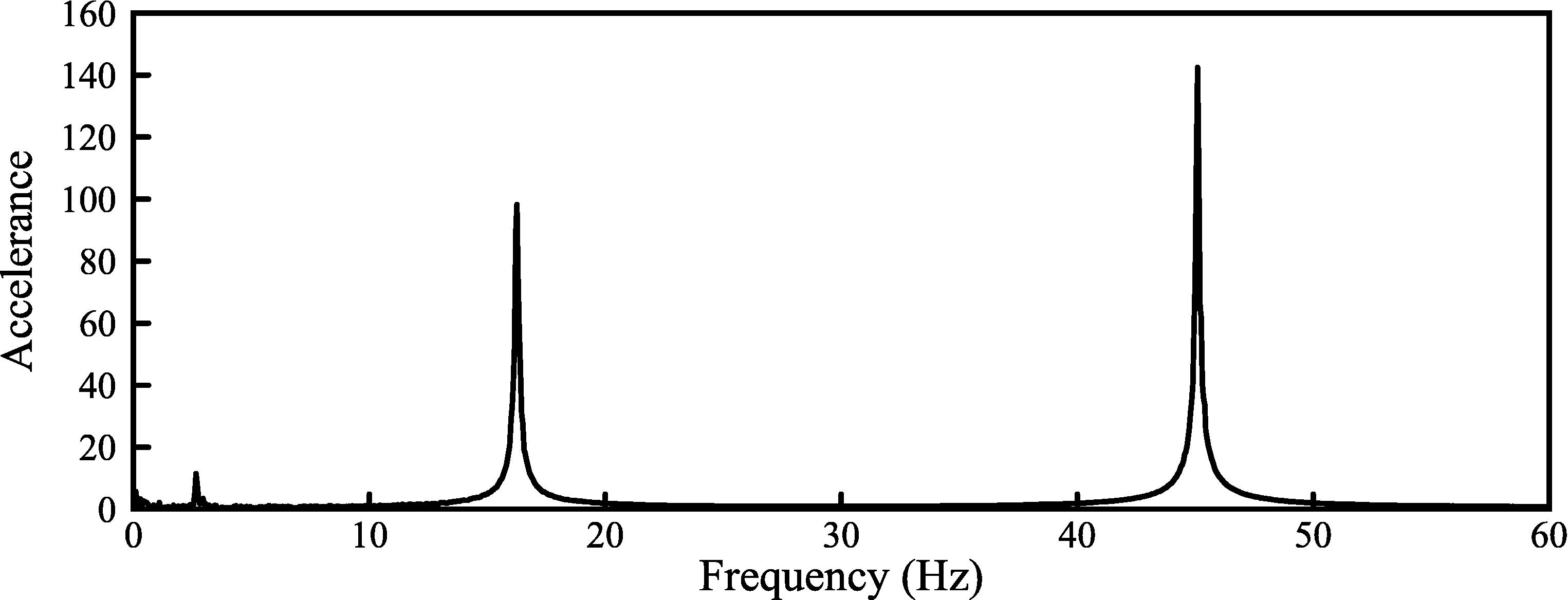
Frequency responses of beam tip at low level excitations.

For a nonlinear beam, for second or higher modes, the inertia nonlinearity is the dominant nonlinear term, whereas for the first mode, the geometrical nonlinearity is the dominant nonlinear term (Pai and Nayfeh, 1990). It has been also shown that the geometrical nonlinearity has a hardening effect, while, in contrast, the inertia nonlinearity has a softening effect (Pai and Nayfeh, 1990). These effects can be seen clearly from the experimental results. The force and response signals are recorded and then, the linearized FRF diagram was plotted using a curve fitting on the measured data close to the resonance point. In order to perform a complete identification of the nonlinear beam, a parametric approach is used based on the unknown coefficient of Eq. (1). Finding the optimum values for the unknown coefficient besides achieving the minimum error between theoretical and experimental approaches is the basis of the identification process in this research.

The identified parameters are given in Table 1. The amplitude-frequency curves obtained from the identified model and the experiments are given in Figs. 8–11 . It is concluded that by considering the fractional-order derivative nonlinear model, a good agreement between theoretical and experimental results would be achieved.

Table 1 The identified nonlinear coefficients.

Coefficients	C₂	C₃	K₁	p
Value	6.9 × 10⁻⁷	1 × 10⁻⁶	0.3	0.13

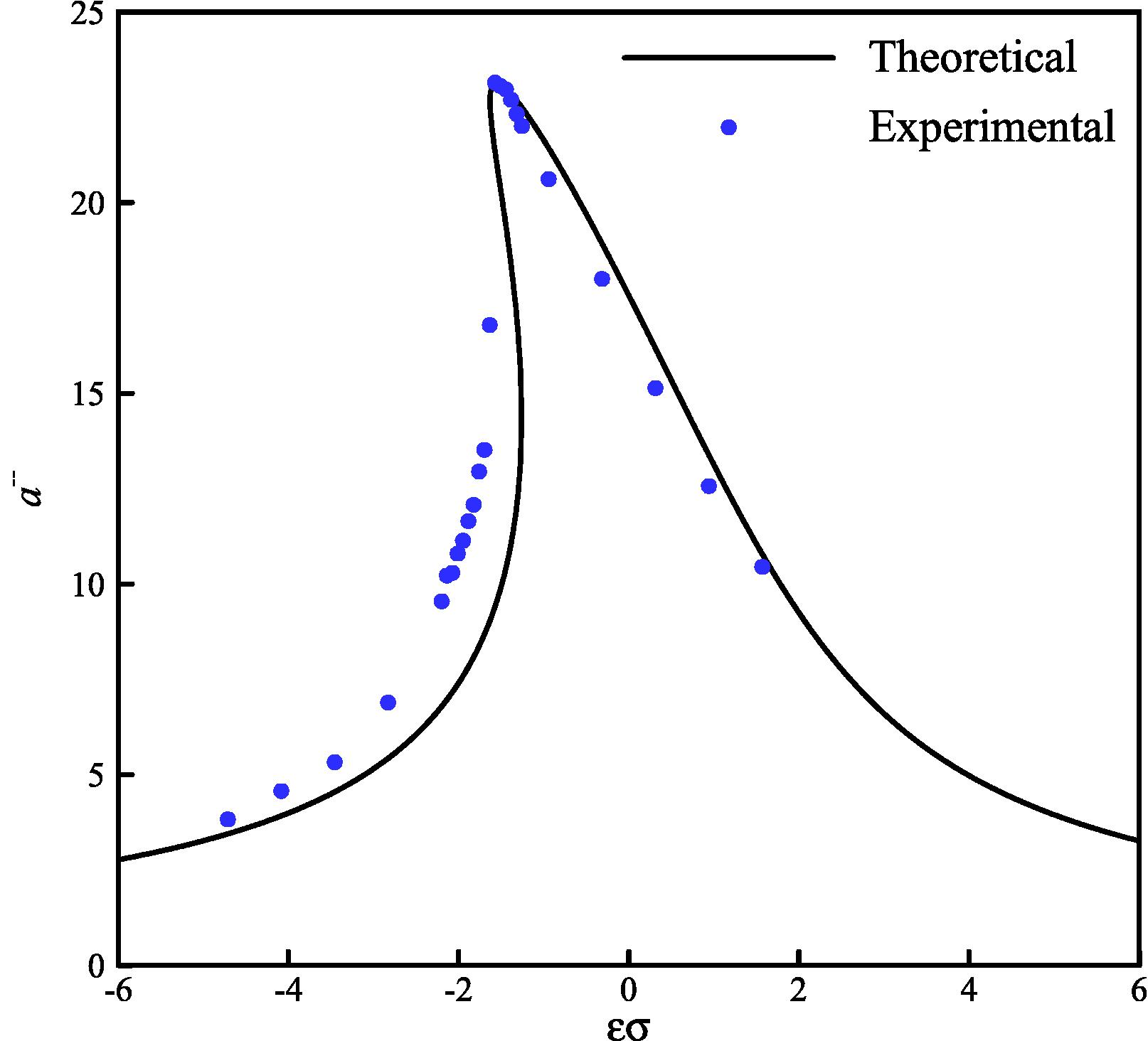
The amplitude-frequency curves of beam tip (F = 0.5 g).

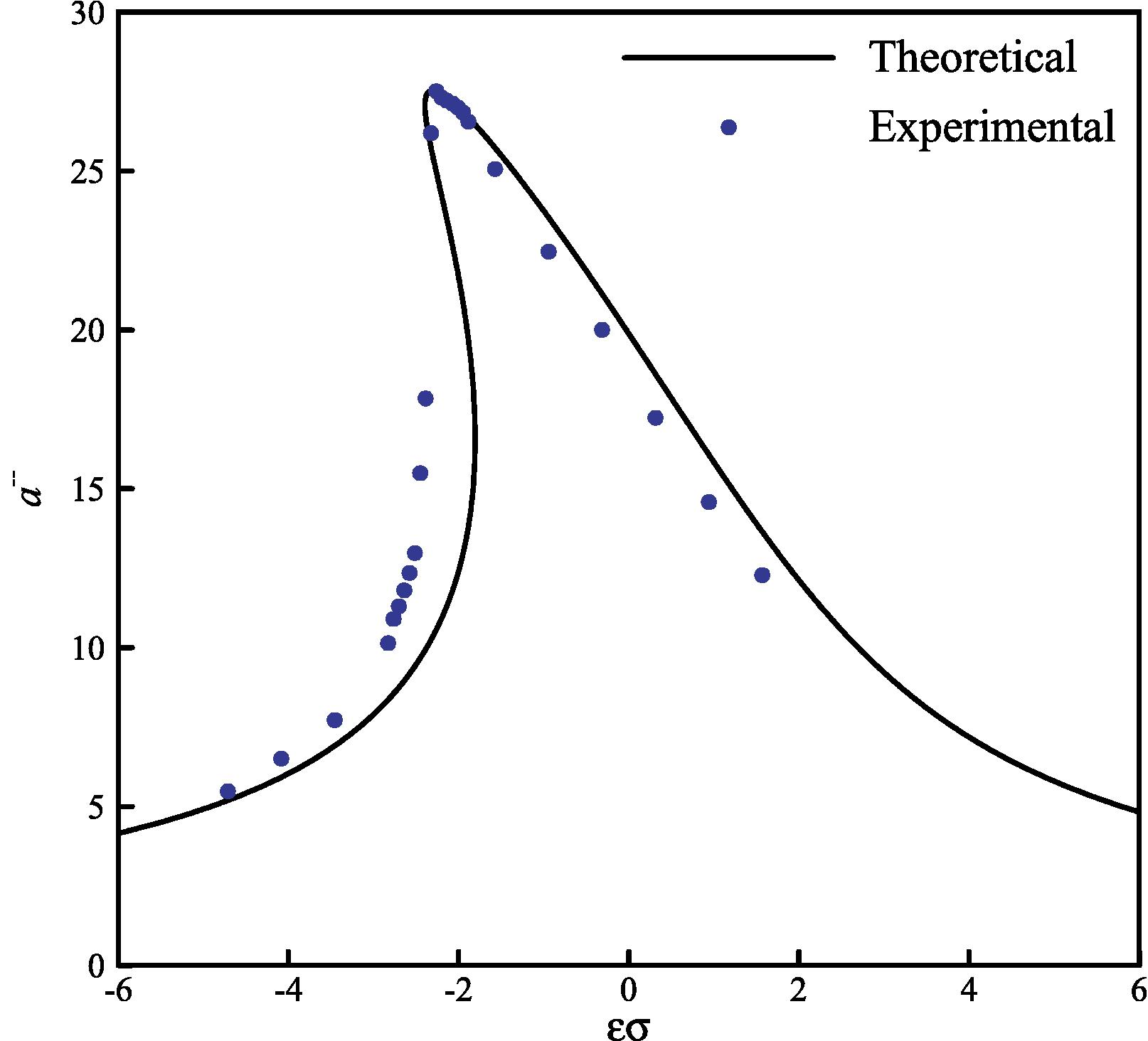
The amplitude-frequency curves of beam tip (F = 0.75 g).

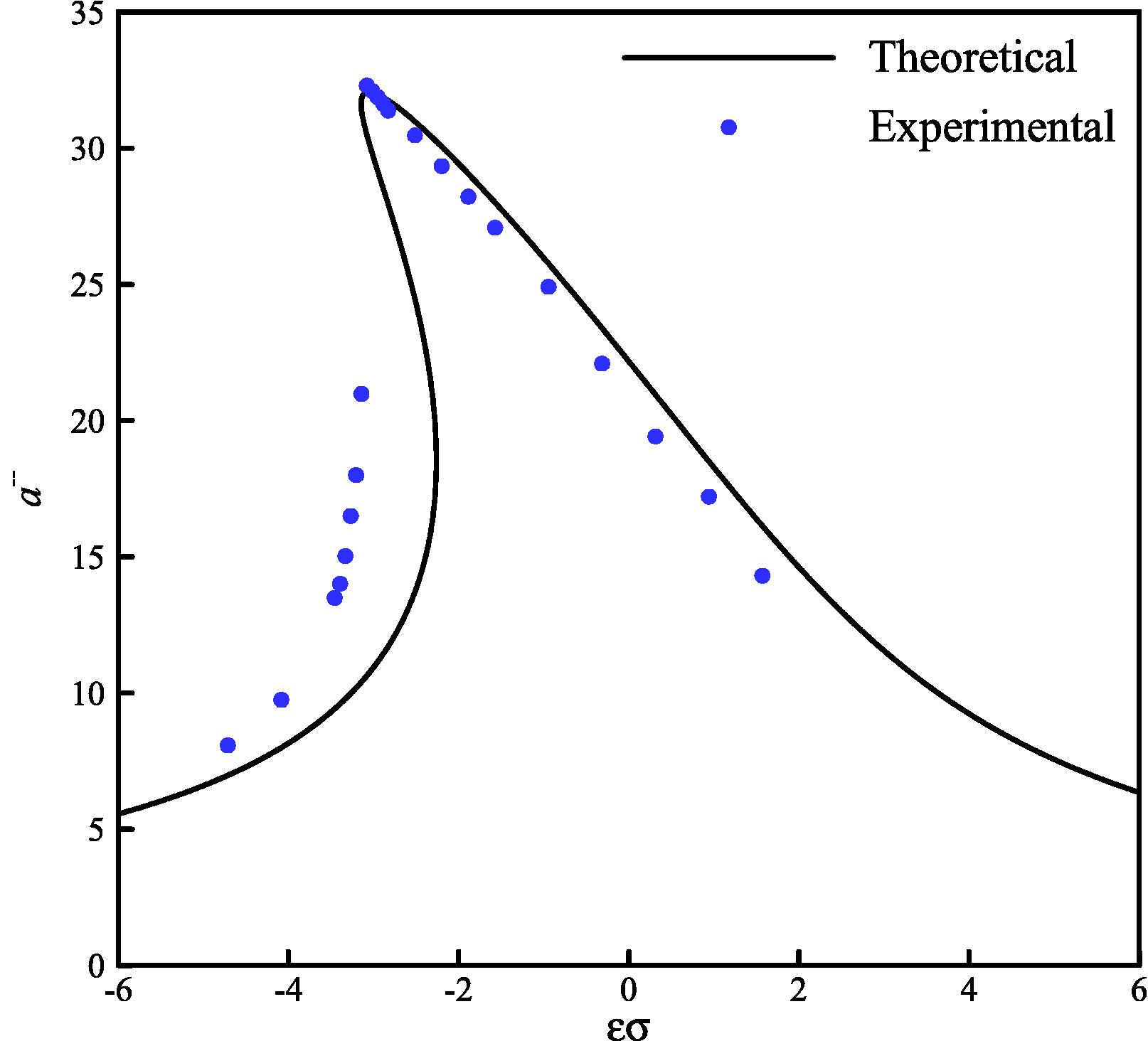
The amplitude-frequency curves of beam tip (F = 1.0 g).

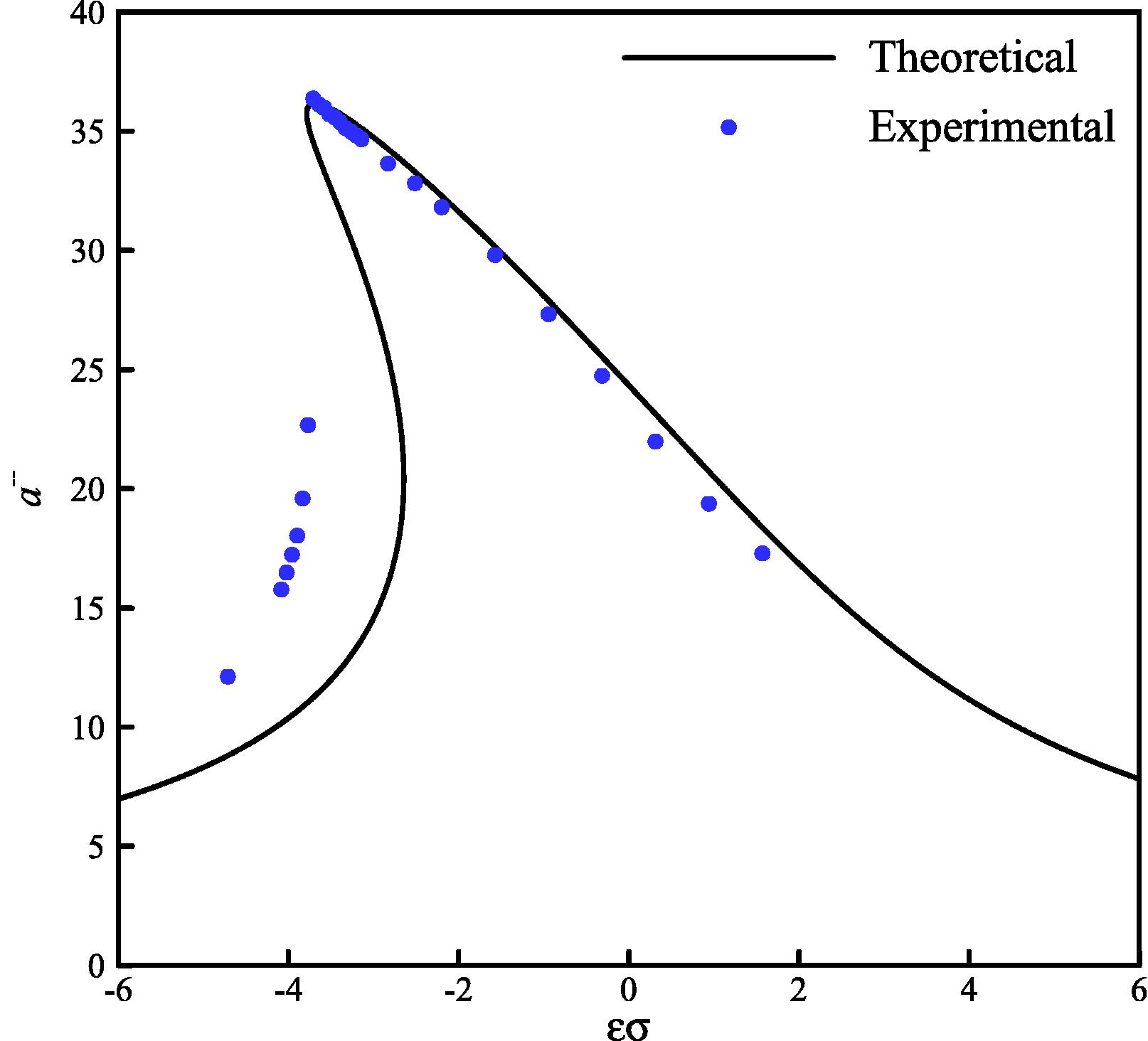
The amplitude-frequency curves of beam tip (F = 1.25 g).

The obtained results indicate the accuracy of the developed model based on Eq. (1), at the resonance point and after that (see Tables 2 and 3). Also, the jump phenomena and softening effect are predicted properly. According to the results, a deviation between the experimental data and theoretical solution is seen only in the unstable region. This deviation is reasonable, because in this region, the jump phenomena occurs in the experiments but in theoretical solution, bending of the amplitude-frequency curves leads to multi valued amplitudes mathematically (see Fig. 12).

Table 2 Comparison between theoretical and experimental results (amplitude-stable solution) near the peak of amplitude-frequency curves (F = 0.5 g & 0.75 g).

F = 0.5 g				F = 0.75 g
$ε σ$	Experimental	Theoretical	Error (%)	$ε σ$	Experimental	Theoretical	Error (%)
−1.571	23.15	23.11	0.173	−2.262	27.51	27.50	0.036
−1.508	23.06	23.09	0.130	−2.199	27.31	27.42	0.402
−1.445	22.97	22.99	0.087	−2.136	27.21	27.31	0.367
−1.382	22.7	22.85	0.660	−2.073	27.12	27.17	0.184
−1.319	22.33	22.68	1.567	−2.010	27.00	27.02	0.074
−1.257	22.01	22.50	2.226	−1.948	26.84	26.85	0.037
−0.942	20.62	21.44	3.976	−1.885	26.55	26.68	0.489

Table 3 Comparison between theoretical and experimental results (amplitude-stable solution) near the peak of amplitude-frequency curves (F = 1.0 g & 1.25 g).

F = 1.0 g				F = 1.25 g
$ε σ$	Experimental	Theoretical	Error (%)	$ε σ$	Experimental	Theoretical	Error (%)
−3.079	32.30	32.17	0.402	−3.707	36.37	36.17	0.550
−3.016	32.10	32.05	0.156	−3.644	36.12	36.15	0.083
−2.953	31.87	31.98	0.329	−3.581	35.98	36.08	0.278
−2.890	31.65	31.88	0.727	−3.518	35.72	35.98	0.728
−2.827	31.38	31.76	1.211	−3.456	35.58	35.86	0.787
−2.513	30.47	30.98	1.674	−3.393	35.37	35.73	1.018
−2.199	29.34	30.06	2.436	−3.330	35.13	35.59	1.309

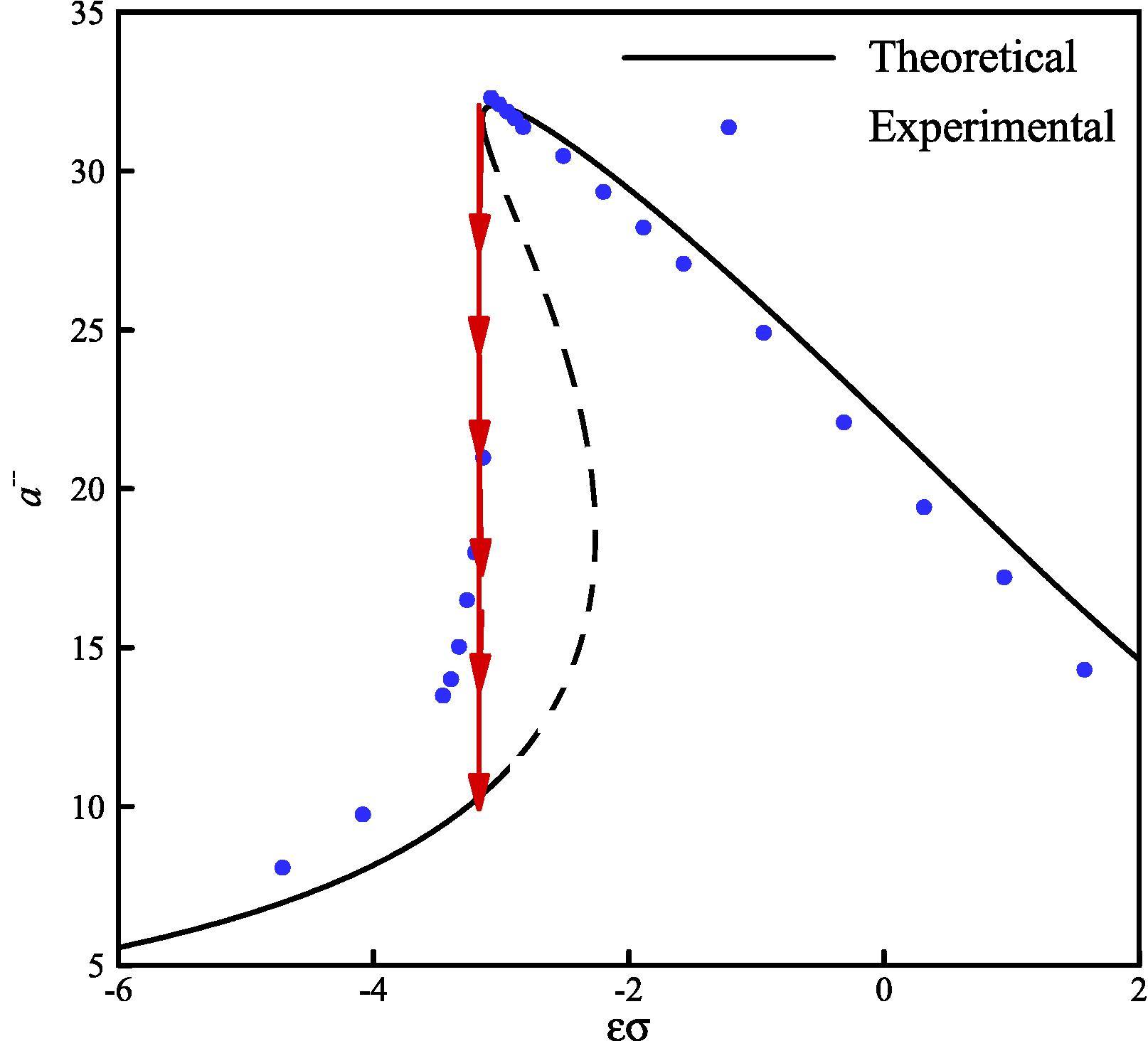
Typical amplitude-frequency curves of beam tip in F = 1.0 g, jump phenomena (the experimental point of view-the path marked with arrow) and the dashed line for unstable solution (the mathematical point of view-multivalued amplitudes).

One of the most valuable results of the current research is extracting the new nonlinear model, which can be used in any geometrically nonlinear structure. Although a single frequency excitation force was used for the identification of the current model, but there is no limitation on the loading condition; and the identified model can be used for predicting the nonlinear response in different loading condition.

4 Conclusions

The special kind of Duffing oscillator with fractional-order derivative is studied by the averaging method, and the approximately analytical solution is obtained. The effects of the fractional coefficient, the fractional-order, inertial and geometrical nonlinear coefficients and excitation amplitude on the solution are determined by the amplitude-frequency curves. Also, for an experimental case study, the model and the nonlinear coefficients are identified. The obtained results are valuable in nonlinear systems identification.

References

Alkahtani B.S.T., . Chua’s circuit model with Atangana-Baleanu derivative with fractional order. Chaos Solitons Fractals. 2016;89:547-551.
[Google Scholar]
Arikoglu A., Ozkol I., . Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals. 2007;34:1473-1481.
[Google Scholar]
Atanackovic T.M., Stankovic B., . On a numerical scheme for solving differential equations of fractional order. Mech. Res. Commun.. 2008;35:429-438.
[Google Scholar]
Atangana A., Baleanu D., . New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model. Therm. Sci.. 2016;20:763-769.
[Google Scholar]
Atangana A., Koca I., . Chaos in a simple nonlinear system with Atangana-Baleanu derivatives with fractional order. Chaos Solitons Fractals. 2016;89:447-454.
[Google Scholar]
Burd V., . Method of Averaging for Differential Equations on an Infinite interval: Theory and Applications. New York: Taylor & Francis Group; 2007.
Cao J., Ma C., Xie H., Jiang Z., . Nonlinear dynamics of Duffing system with fractional order damping. J. Comput. Nonlinear Dyn.. 2010;1:2-6.
[Google Scholar]
Chen X., Wei L., Sui J., Zhang X., Zheng L., . Solving fractional partial differential equations in fluid mechanics by generalized differential transform method. In: 2nd International Conference on Multimedia Technology (ICMT'11). 2011. p. :2573-2576.
[Google Scholar]
Chen Z., Peng Y.L., Wang S.W., Yin F.L., . From discrete to continuous-fractional signal processing theories, methods and applications. Acta Electronica Sinica. 2012;40:2282-2289.
[Google Scholar]
Das S., . Functional Fractional Calculus for System Identification and Controls. Berlin: Springer-Verlag; 2008.
Den-Hartog J.P., . Mechanical Vibrations. New York: McGraw-Hill; 1956.
Ghazanfari B., Veisi F., . Homotopy analysis method for the fractional nonlinear equations. J. King Saud Univ. Sci.. 2011;23:389-393.
[Google Scholar]
Gómez-Aguilar J.F., . Irving-Mullineux oscillator via fractional derivatives with Mittag-Leffler kernel. Chaos Solitons Fractals. 2017;95:179-186.
[Google Scholar]
Kilbas A.A., Srivastava H.M., Trujillo J.J., . Theory and applications of fractional differential equations. Amsterdam: Elsevier; 2006.
Kiryakova V., . Generalized Fractional Calculus and Applications. New York: Longman-Wiley; 1994.
Lakshmikanthama V., Vatsalab A.S., . Basic theory of fractional differential equations. Nonlinear Anal.. 2008;69:2677-2682.
[Google Scholar]
Li D.Z., Cao J., Guan S.T., Tan T.W., . Research and implementation of a fractional predictive controller. Control Theory App.. 2010;27:658-662.
[Google Scholar]
Li G., Zhu Z., Cheng C., . Dynamical stability of viscoelastic column with fractional derivative constitutive relation. Appl. Math. Mech.. 2001;22:294-303.
[Google Scholar]
Metzler R., Klafter J., . The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep.. 2000;339:1-77.
[Google Scholar]
Mishra V., Das S., Jafari H., Ong S.H., . Study of fractional order Van der Pol equation. J. King Saud Univ. Sci.. 2016;28:55-60.
[Google Scholar]
Nayfeh A.H., Mook D.T., . Nonlinear Oscillations. New York: Wiley-Interscience; 1995.
Nayfeh A.H., Pai P.F., . Linear and Nonlinear Structural Mechanics. New York: Wiley-Interscience; 2004.
Padovan J., Sawicki J.T., . Nonlinear vibrations of fractionally damped systems. Nonlinear Dyn.. 1998;16:321-336.
[Google Scholar]
Pai P.F., Nayfeh A.H., . Non-linear non-planar oscillations of a cantilever beam under lateral base excitations. Int. J. Non-Linear Mech.. 1990;25:455-474.
[Google Scholar]
Podlubny I., . Fractional Differential Equations. London: Academic; 1998.
Rossikhin Y.A., Shitikova M.V., . Application of fractional derivatives to the analysis of damped vibrations of viscoelastic single mass systems. Acta Mech.. 1997;120:109-125.
[Google Scholar]
Samko S.G., Kilbas A.A., Marichev O.I., . Fractional Integrals and Derivatives, Theory and Applications. Yverdon: Gordon and Breach; 1993.
Sanders J.A., Verhulst F., Murdock J., . Averaging Methods in Nonlinear Dynamical Systems. New York: Springer Science+Business Media; 2007.
Shen Y., Wei P., Sui C., Yang S.P., . Subharmonic resonance of van der pol oscillator with fractional-order derivative. Math. Prob. Eng. 2014:17.
[Google Scholar]
Shen Y.J., Wei P., Yang S.P., . Primary resonance of fractional-order van der Pol oscillator. Nonlinear Dyn.. 2014;77:1629-1642.
[Google Scholar]
Shen Y.J., Wen S.F., Li X.H., Yang S.P., Xing H.J., . Dynamical analysis of fractional-order nonlinear oscillator by incremental harmonic balance method. Nonlinear Dyn.. 2016;85:1457-1467.
[Google Scholar]
Shen Y.J., Yang S.P., Xing H.J., . Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative. Acta Physica Sinica. 2012;61
[Google Scholar]
Shen Y.J., Yang S.P., Xing H.J., Gao G., . Primary resonance of Duffing oscillator with fractional-order derivative. Commun. Nonlinear Sci. Numer. Simul.. 2012;17:3092-3100.
[Google Scholar]
Shen Y.J., Yang S.P., Xing H.J., Ma H.X., . Primary resonance of Duffing oscillator with two kinds of fractional-order derivatives. Int. J. Non-Linear Mech.. 2012;47:975-983.
[Google Scholar]
Sheu L.J., Chen H.K., Chen J.H., Tam L.M., . Chaotic dynamics of the fractionally damped Duffing equation. Chaos Solitons Fractals. 2007;32:1459-1468.
[Google Scholar]
Timoshenko S., Young D.H., Weaver W., . Vibration Problems in Engineering. New York: John Wiley; 1974.
West B.J., Bolognab M., Grigolini P., . Physics of Fractal Operators. New York: Springer; 2003.
Xu Y., Li Y., Liu D., Jia W., Huang H., . Responses of Duffing oscillator with fractional damping and random phase. Nonlinear Dyn.. 2013;74:745-753.
[Google Scholar]
Yang A.M., Han Y., Li J., Liu W.X., . On steady heat flow problem involving Yang-Srivastava-Machado fractional derivative without singular kernel. Therm. Sci.. 2016;20:717-721.
[Google Scholar]
Yang X.J., . Fractional derivatives of constant and variable orders applied to anomalous relaxation models in heat-transfer problems. Therm. Sci. 2016
[Google Scholar]
Yang, X.J., Srivastava, H.M., Machado, J.A.T., 2016b, A new fractional derivative without singular kernel, Application to the modelling of the steady heat flow, v. 20(0), 753–756.
Yang X.J., Zhang Z.Z., Srivastava H.M., . Some new applications for heat and fluid flows via fractional derivatives without singular kernel. Therm. Sci. 2016
[Google Scholar]
Zhang W., Liao S.K., Shimizu N., . Dynamic behaviors of nonlinear fractional-order differential oscillator. J. Mech. Sci. Technol.. 2009;23:1058-1064.
[Google Scholar]

Introduction

An approximate analytical solution for a special type of Duffing oscillator

Study on the amplitude-frequency equation parameters

Experimental case study

Conclusions

Fulltext Views
4

PDF downloads
0

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Alkahtani B.S.T., . Chua’s circuit model with Atangana-Baleanu derivative with fractional order. Chaos Solitons Fractals. 2016;89:547-551.
[Google Scholar]

[2] Arikoglu A., Ozkol I., . Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals. 2007;34:1473-1481.
[Google Scholar]

[3] Atanackovic T.M., Stankovic B., . On a numerical scheme for solving differential equations of fractional order. Mech. Res. Commun.. 2008;35:429-438.
[Google Scholar]

[4] Atangana A., Baleanu D., . New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model. Therm. Sci.. 2016;20:763-769.
[Google Scholar]

[5] Atangana A., Koca I., . Chaos in a simple nonlinear system with Atangana-Baleanu derivatives with fractional order. Chaos Solitons Fractals. 2016;89:447-454.
[Google Scholar]

[6] Burd V., . Method of Averaging for Differential Equations on an Infinite interval: Theory and Applications. New York: Taylor & Francis Group; 2007.

[7] Cao J., Ma C., Xie H., Jiang Z., . Nonlinear dynamics of Duffing system with fractional order damping. J. Comput. Nonlinear Dyn.. 2010;1:2-6.
[Google Scholar]

[8] Chen X., Wei L., Sui J., Zhang X., Zheng L., . Solving fractional partial differential equations in fluid mechanics by generalized differential transform method. In: 2nd International Conference on Multimedia Technology (ICMT'11). 2011. p. :2573-2576.
[Google Scholar]

[9] Chen Z., Peng Y.L., Wang S.W., Yin F.L., . From discrete to continuous-fractional signal processing theories, methods and applications. Acta Electronica Sinica. 2012;40:2282-2289.
[Google Scholar]

[10] Das S., . Functional Fractional Calculus for System Identification and Controls. Berlin: Springer-Verlag; 2008.

[11] Den-Hartog J.P., . Mechanical Vibrations. New York: McGraw-Hill; 1956.

[12] Ghazanfari B., Veisi F., . Homotopy analysis method for the fractional nonlinear equations. J. King Saud Univ. Sci.. 2011;23:389-393.
[Google Scholar]

[13] Gómez-Aguilar J.F., . Irving-Mullineux oscillator via fractional derivatives with Mittag-Leffler kernel. Chaos Solitons Fractals. 2017;95:179-186.
[Google Scholar]

[14] Kilbas A.A., Srivastava H.M., Trujillo J.J., . Theory and applications of fractional differential equations. Amsterdam: Elsevier; 2006.

[15] Kiryakova V., . Generalized Fractional Calculus and Applications. New York: Longman-Wiley; 1994.

[16] Lakshmikanthama V., Vatsalab A.S., . Basic theory of fractional differential equations. Nonlinear Anal.. 2008;69:2677-2682.
[Google Scholar]

[17] Li D.Z., Cao J., Guan S.T., Tan T.W., . Research and implementation of a fractional predictive controller. Control Theory App.. 2010;27:658-662.
[Google Scholar]

[18] Li G., Zhu Z., Cheng C., . Dynamical stability of viscoelastic column with fractional derivative constitutive relation. Appl. Math. Mech.. 2001;22:294-303.
[Google Scholar]

[19] Metzler R., Klafter J., . The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep.. 2000;339:1-77.
[Google Scholar]

[20] Mishra V., Das S., Jafari H., Ong S.H., . Study of fractional order Van der Pol equation. J. King Saud Univ. Sci.. 2016;28:55-60.
[Google Scholar]

[21] Nayfeh A.H., Mook D.T., . Nonlinear Oscillations. New York: Wiley-Interscience; 1995.

[22] Nayfeh A.H., Pai P.F., . Linear and Nonlinear Structural Mechanics. New York: Wiley-Interscience; 2004.

[23] Padovan J., Sawicki J.T., . Nonlinear vibrations of fractionally damped systems. Nonlinear Dyn.. 1998;16:321-336.
[Google Scholar]

[24] Pai P.F., Nayfeh A.H., . Non-linear non-planar oscillations of a cantilever beam under lateral base excitations. Int. J. Non-Linear Mech.. 1990;25:455-474.
[Google Scholar]

[25] Podlubny I., . Fractional Differential Equations. London: Academic; 1998.

[26] Rossikhin Y.A., Shitikova M.V., . Application of fractional derivatives to the analysis of damped vibrations of viscoelastic single mass systems. Acta Mech.. 1997;120:109-125.
[Google Scholar]

[27] Samko S.G., Kilbas A.A., Marichev O.I., . Fractional Integrals and Derivatives, Theory and Applications. Yverdon: Gordon and Breach; 1993.

[28] Sanders J.A., Verhulst F., Murdock J., . Averaging Methods in Nonlinear Dynamical Systems. New York: Springer Science+Business Media; 2007.

[29] Shen Y., Wei P., Sui C., Yang S.P., . Subharmonic resonance of van der pol oscillator with fractional-order derivative. Math. Prob. Eng. 2014:17.
[Google Scholar]

[30] Shen Y.J., Wei P., Yang S.P., . Primary resonance of fractional-order van der Pol oscillator. Nonlinear Dyn.. 2014;77:1629-1642.
[Google Scholar]

[31] Shen Y.J., Wen S.F., Li X.H., Yang S.P., Xing H.J., . Dynamical analysis of fractional-order nonlinear oscillator by incremental harmonic balance method. Nonlinear Dyn.. 2016;85:1457-1467.
[Google Scholar]

[32] Shen Y.J., Yang S.P., Xing H.J., . Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative. Acta Physica Sinica. 2012;61
[Google Scholar]

[33] Shen Y.J., Yang S.P., Xing H.J., Gao G., . Primary resonance of Duffing oscillator with fractional-order derivative. Commun. Nonlinear Sci. Numer. Simul.. 2012;17:3092-3100.
[Google Scholar]

[34] Shen Y.J., Yang S.P., Xing H.J., Ma H.X., . Primary resonance of Duffing oscillator with two kinds of fractional-order derivatives. Int. J. Non-Linear Mech.. 2012;47:975-983.
[Google Scholar]

[35] Sheu L.J., Chen H.K., Chen J.H., Tam L.M., . Chaotic dynamics of the fractionally damped Duffing equation. Chaos Solitons Fractals. 2007;32:1459-1468.
[Google Scholar]

[36] Timoshenko S., Young D.H., Weaver W., . Vibration Problems in Engineering. New York: John Wiley; 1974.

[37] West B.J., Bolognab M., Grigolini P., . Physics of Fractal Operators. New York: Springer; 2003.

[38] Xu Y., Li Y., Liu D., Jia W., Huang H., . Responses of Duffing oscillator with fractional damping and random phase. Nonlinear Dyn.. 2013;74:745-753.
[Google Scholar]

[39] Yang A.M., Han Y., Li J., Liu W.X., . On steady heat flow problem involving Yang-Srivastava-Machado fractional derivative without singular kernel. Therm. Sci.. 2016;20:717-721.
[Google Scholar]

[40] Yang X.J., . Fractional derivatives of constant and variable orders applied to anomalous relaxation models in heat-transfer problems. Therm. Sci. 2016
[Google Scholar]

[41] Yang, X.J., Srivastava, H.M., Machado, J.A.T., 2016b, A new fractional derivative without singular kernel, Application to the modelling of the steady heat flow, v. 20(0), 753–756.

[42] Yang X.J., Zhang Z.Z., Srivastava H.M., . Some new applications for heat and fluid flows via fractional derivatives without singular kernel. Therm. Sci. 2016
[Google Scholar]

[43] Zhang W., Liao S.K., Shimizu N., . Dynamic behaviors of nonlinear fractional-order differential oscillator. J. Mech. Sci. Technol.. 2009;23:1058-1064.
[Google Scholar]