Translate this page into:
Dispersion study of SH-wave propagation in an irregular magneto-elastic anisotropic crustal layer over an irregular heterogeneous half-space
⁎Corresponding author. alamparvez.amu@gmail.com (Parvez Alam),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
This study investigates the effect of various parameters on the propagation of seismic SH-waves in a magneto-elastic anisotropic crustal layer with corrugated boundary surfaces, lying over a heterogeneous half-space. The shear elastic modulus and mass density of half-space are the exponential functions of depth. Inclusion of the concept of corrugated irregularity with magneto-elasticity in the anisotropic (Monoclinic) medium and heterogeneity in the half-space medium brings a novelty to the existing literature related to the study of SH-wave. The expression of general dispersion relation has been established in closed form by using suitable boundary conditions. The effects of magneto-elastic coupling, heterogeneity, corrugation, undulatory and position parameters on the phase velocity of SH-wave have been computed numerically and demonstrated graphically. Moreover, different cases of free and common surface corrugations are studied which serve as a focal theme of the study.
Keywords
SH-wave
Maxwell’s
Magneto-elastic
Heterogeneity
Corrugation
Undulatory
1 Introduction
Regulation of seismic waves like propagation, reflection, transmission and refraction through an elastic layered media (coupled with different fields) is totally controlled by the properties and divergent irregular contact surfaces of the layered media. The study of seismic waves and their characteristics is often carried out to identify the structure and dynamics of the Earth’s interior as well as to detect the epicentre of earthquakes. The analysis of seismic wave propagation in some complex media is also helpful in the exploration of natural resources buried inside the Earth’s surface, e.g., oils, gases, minerals, crystals, metals and other useful hydrocarbons. It infers lot of information about the velocity of the wave, inward peculiarities of the media and forms the core tool of geophysical and earthquake sciences.
The magnetic and elastic properties of magneto-elastic materials depend on each other. The Earth’s crust is made of the great diversity of igneous, metamorphic and sedimentary rocks. These rocks are capable to generate magnetic field due to the presence of some ferromagnetic minerals like iron, nickel, cobalt, etc. Hence, these rocks can be considered as the magneto-elastic body. The investigation into the SH-wave propagation in magneto-elastic bodies is quite important for the development of fundamental work on the mechanics of a magnetic body. Moreover, it may be used in various areas of science, engineering technology such as seismology, defectoscopy, geophysics, astrophysics and geo-tectonics. Keeping in view the significance of seismic wave propagation in magneto-elastic bodies, the considerable amount of investigations is carried out by several researchers. Notable among them are Abd-Alla et al. (2016), Said (2016), Majhi et al. (2016), Calas et al. (2008), Othman and Song (2006), Chattopadhyay and Singh (2014), Song et al. (2006), Abo-Dahab et al. (2015), Singh et al. (2016a) and Mahmoud (2016). Matinfar et al. (2015) observed the interaction of electromagnetic wave with electron using the variational iteration method.
It is well-known fact that the interface between any two adjacent layers of the Earth is very complicated and irregular in nature. These irregular interfaces may be in the shape of corrugation (undulated), rectangular, parabolic or much complicated and work as a catalyst in affecting the propagation behaviour of SH-waves. Some notable references related to the study of wave phenomena in/at irregular boundary surfaces are Vishwakarma and Xu (2016a), Singh and Lakshman (2016), Kundu and his co-workers (Kundu et al., 2014, 2016a), Singh et al. (2016b), Tomar and Kaur (2007) and Chatterjee et al. (2015).
The subject of wave propagation in a heterogeneous elastic medium is of great interest since long because of continuous change in the elastic properties of the material. These studies were recorded in several treatises including Birch (1952) and Bullen (1940). Subsequently, Vishwakarma and Xu (2016b), Daros (2013), Zhou et al. (2014), Sahu et al. (2014) and Kundu et al. (2016b) discussed for seismic waves in various types of heterogeneous media.
The present study investigates the affected behaviour of horizontally polarized shear wave (i.e. SH-wave) propagation in an anisotropic crustal layer of finite thickness, lying over a heterogeneous half-space. The boundary surfaces of considered structure are corrugated irregular. The crustal anisotropic layer has been regarded as a perfect conductor. The shear elastic modulus and mass density of the half-space have been considered in terms of the exponential function of depth i.e. and , where a and b are heterogeneous parameters. The effects of magneto-elastic coupling, upper free surface corrugation, common surface corrugation, heterogeneities and some geometrical parameters (undulatory and position) on the phase velocity of SH-wave against wave number have been shown by several graphs. This investigation for the propagation of SH-waves may be of importance when such types of waves are propagated on the Earth’s surface where corrugated irregularity together with the magneto-elasticity, anisotropy and heterogeneity are present.
2 Governing equations
The Cartesian co-ordinate system has been considered in such a way that x-axis is in the direction of wave propagation and z-axis is vertically downwards. A magneto-elastic anisotropic crustal layer,
with corrugated boundary surfaces is taken in such a way that it lying over a heterogeneous half-space,
. Here, h is the thickness of magneto-elastic anisotropic crustal layer;
and
are continuous and periodic functions of x independent of y, representing the corrugated boundaries of free and common surfaces as shown in Fig. 1. The appropriate Fourier series expansion of these functions can be given as (Singh, 2011; Vishwakarma and Xu, 2016a)
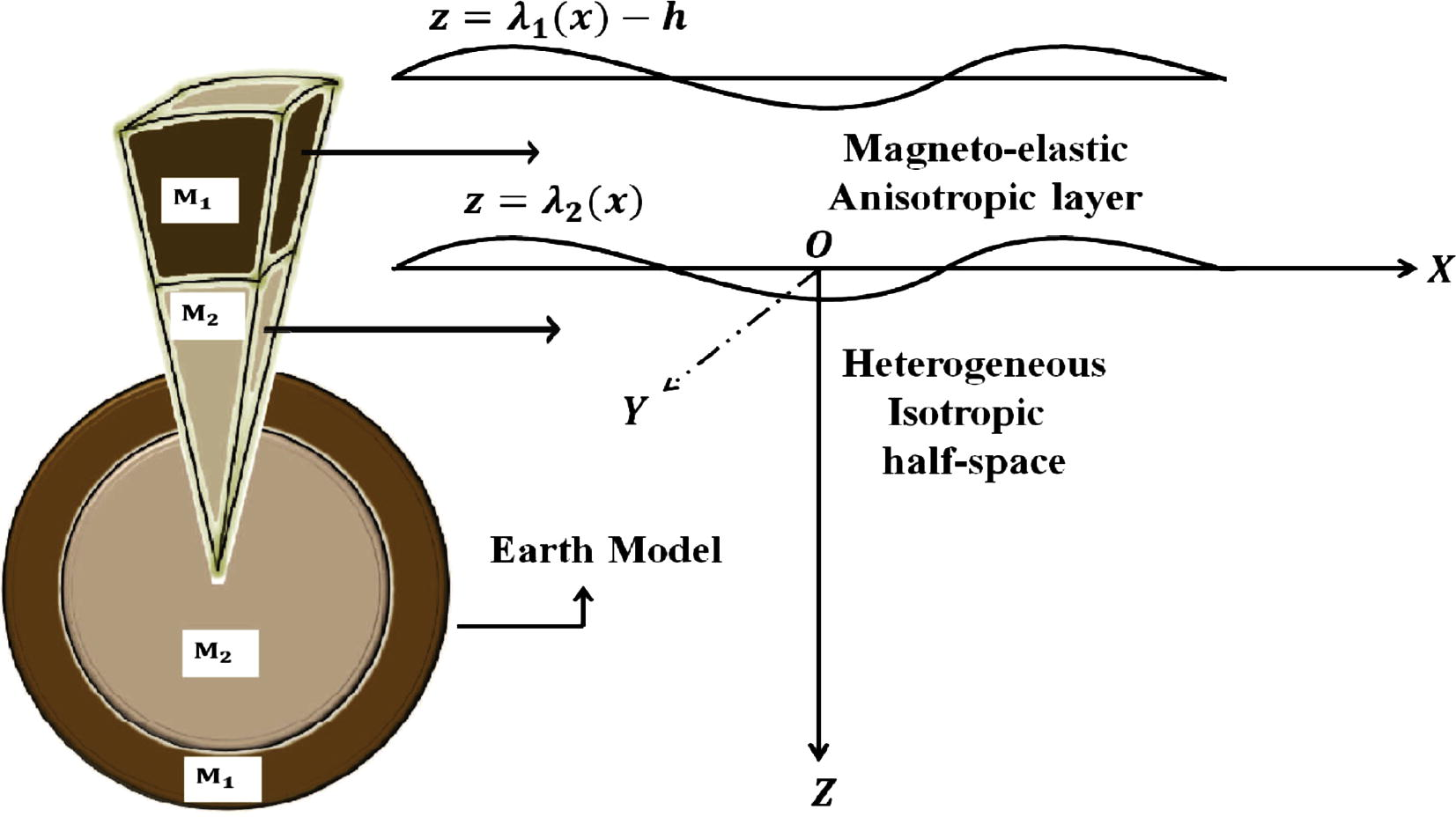
Geometry of the problem,
The corrugated upper and common boundary surfaces of the concerned problem can be expressed by only one cosine term and for the wavelength of corrugation, where and are amplitudes of the uppermost and common corrugated surfaces and is wave number of corrugation.
2.1 SH-wave in magneto-elastic anisotropic layer
Let
is the displacement vector field for anisotropic magneto-elastic layer whose components
are
and
in
and z directions respectively. Therefore, equations of motion for an anisotropic magneto-elastic layer in the presence of electromagnetic force (
) that is Lorentz force are
For the propagation of SH-wave in xz-plane
With the help of Eqs. (4) and (5), Eq. (3) becomes
The well known Maxwell’s equations governing the electromagnetic field are Chattopadhyay and Singh (2014)
Let
and
is the change in the magnetic field. Then, the linearized Maxwell’s stress tensor
due to the magnetic field is given by Chattopadhyay and Singh (2014)
In writing the above equations, we have neglected the displacement current. Now, from Eq. (7) we get
In component form, Eq. (9) can be written as
Now for a perfectly conducting medium, i.e., when
, Eq. (10) becomes
Thus, we conclude from Eq. (11) that there is no perturbation in
and
, but Eq. (12) shows there may be perturbation in
. Therefore, taking small perturbation
(say) in
, we have
We can write
, where
and
is the angle at which the wave crosses the magnetic field. Thus, we have
Using Eq. (14) in Eq. (12), we obtain
Integrating Eq. (15) with respect to t, we get
With the help of Eq. (7), we have
In view of Eqs. (6) and (17) with the values of
and
, we obtain the equation of motion for the propagation of SH-wave in anisotropic magneto-elastic medium as
Let us take a harmonic solution of Eq. (18) as
and substituting in Eq. (18), we get
The solution of Eq. (19) is obtained as
2.2 SH-wave in heterogeneous half-space
We have considered following transformations for the shear elastic modulus
and mass density
of the half-space
Let
and
are the displacement components in
and z directions respectively for the heterogeneous half-space. Then for the propagation of SH-wave, we have
The dynamical equations for the heterogeneous half-space in the absence of any body forces are given by Biot (1965)
Using Eqs. (21) and (22) in (23), the only non-vanishing equation of motion for propagation of SH-wave in heterogeneous half-space is obtained as
Let us assume a harmonic wave solution of Eq. (24) as
and substituting in Eq. (24), we get
For simplification of Eq. (25), we take the following substitution:
. Therefore Eq. (25) takes the form
Using some dimensionless quantities
and
in Eq. (26), then Eq. (26) reduces to
Eq. (27) is the well known Whittaker equation (Whittaker and Watson, 1990). The solution of Eq. (27) is given by
Now keeping in view that
, i.e.,
, the appropriate solution for the heterogeneous half-space may be taken as
Now using the asymptotic expansion of Whittaker’s function
and taking its solution up to a second term, the Eq. (29) becomes
3 Boundary conditions
The boundary conditions are as follows:
3.1 Corrugated uppermost surface of the layer is traction free
after substituting the expressions of and into the above equation, we get
3.2 Stresses are continuous at the common corrugated interface of the layer and half-pace
after substituting the expressions of and into the above equation, we obtain
3.3 Displacements are continuous at the common corrugated interface of the layer and half-space
4 Dispersion relation
Using the solutions given in (20) and (30) into the aforementioned boundary conditions, we obtain following homogeneous algebraic system of equations for
and D.
>For such a system of simultaneous equations to have a non-trivial solution, it is necessary for the determinant of the coefficients to be zero. Hence, the below Eq. (34) must satisfy for a non-trivial solution of
and D
The real part of Eq. (34) gives
5 Particular cases
5.1 Case I: in the absence of upper free surface corrugation
When layer is bounded by an upper free planar surface and lower common corrugated surface, i.e.,
and
, the dispersion relation (35) reduces to
5.2 CaseII: in the absence of common surface corrugation
When layer is bounded by an upper free corrugated surface and lower common planar surface, i.e.,
and
, then the dispersion relation (35) reduces to
5.3 Case III: for equal amplitudes of both corrugations
When the amplitude of both corrugations are equal, i.e.,
(say) which imply
, then the dispersion relation (35) changes to
5.4 Case IV: for uniform isotropic media with planar boundary surfaces
When the layer (bounded by planar surfaces) is isotropic without magnetic effect and half-space is homogeneous isotropic, i.e.,
and
, then Eq. (35) reduces to
6 Numerical calculations and discussion
In order to study the effect of various affecting parameters on the phase velocity of SH-wave based on dispersion Eq. (35), we consider
GPa,
,
,
for anisotropic magneto-elastic layer (Kumar et al., 2015) and
,
for heterogeneous half-space (Gubbins, 1990). The effect of all dimensionless parameters of considered model, namely magneto-elastic coupling parameter
, heterogeneities (
), upper free surface corrugation parameter
, lower common surface corrugation parameter
, undulatory parameter
and position parameter
has been evaluated numerically along with graphical representation in Figs. 2–11 for their different values. The curves of all figures have been plotted for the dimensionless phase velocity
against dimensionless wave number
. The vertical axis in each figure represents dimensionless phase velocity
and the horizontal axis represents dimensionless wave number
. The values of parameters are given in Table 1 and angle
has been kept fixed to
in all figures.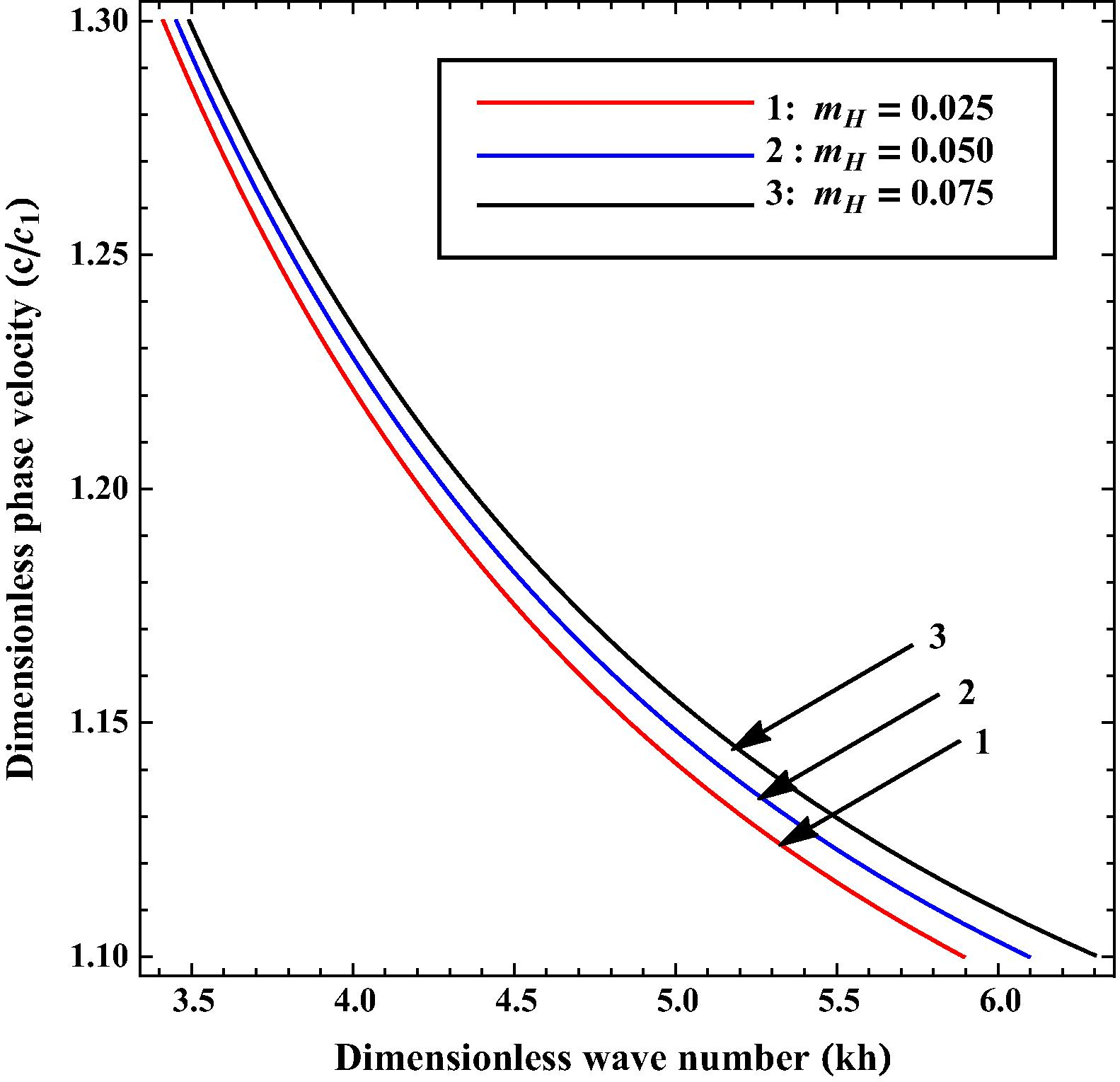
Variation of phase velocity
against wave number
for different values of
.
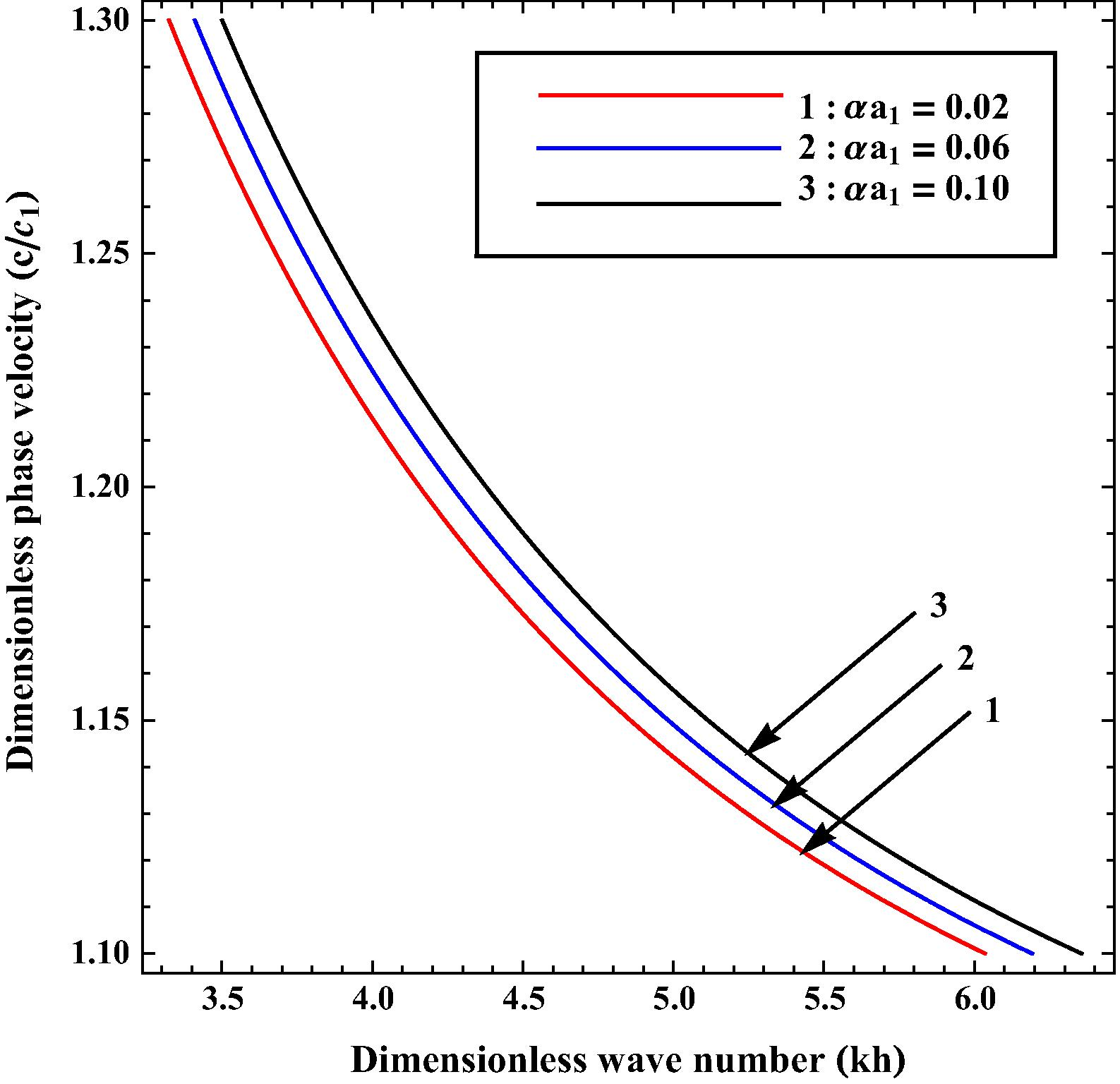
Variation of phase velocity
against wave number
for different values of
.
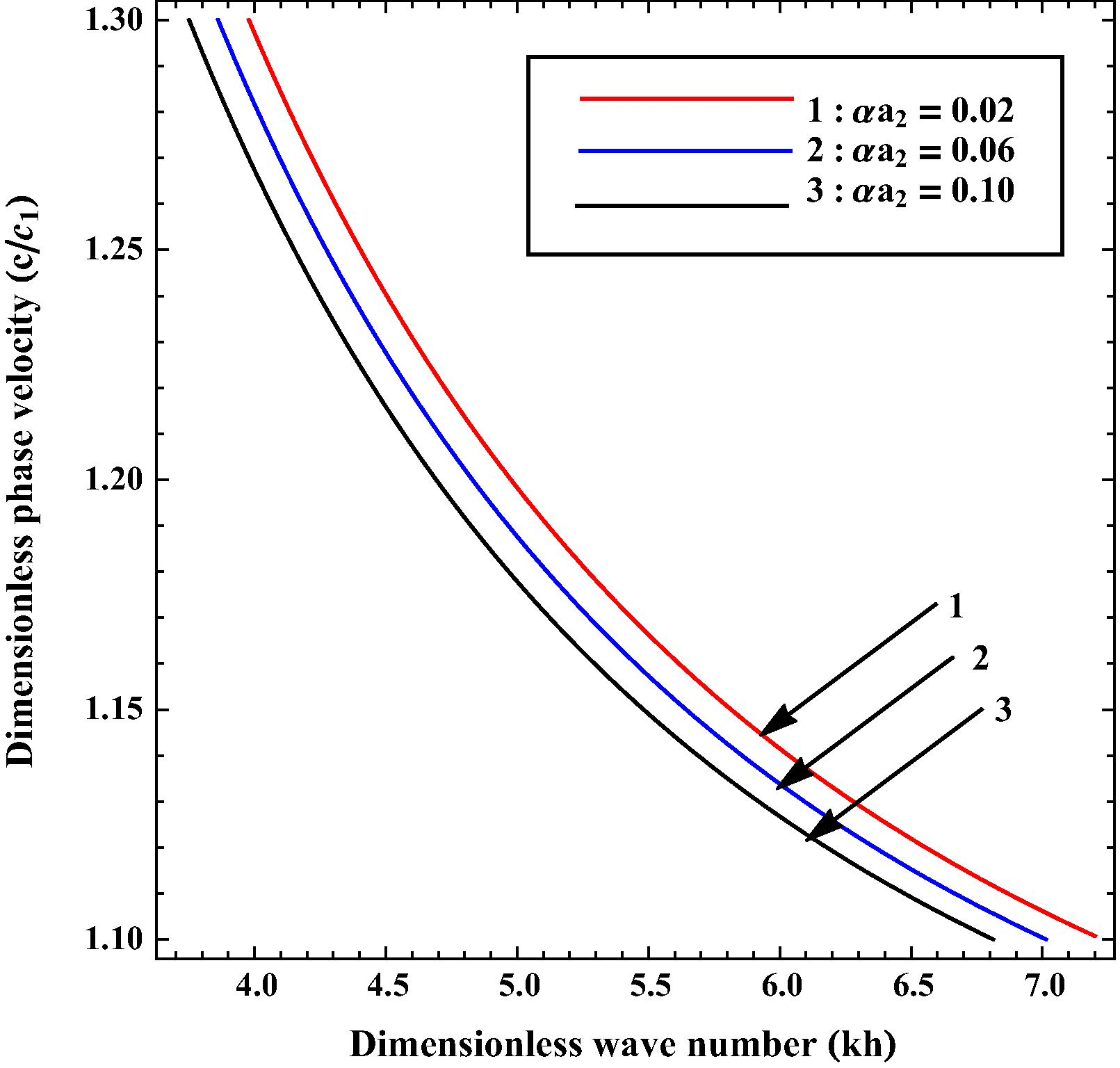
Variation of phase velocity
against wave number
for different values of
.
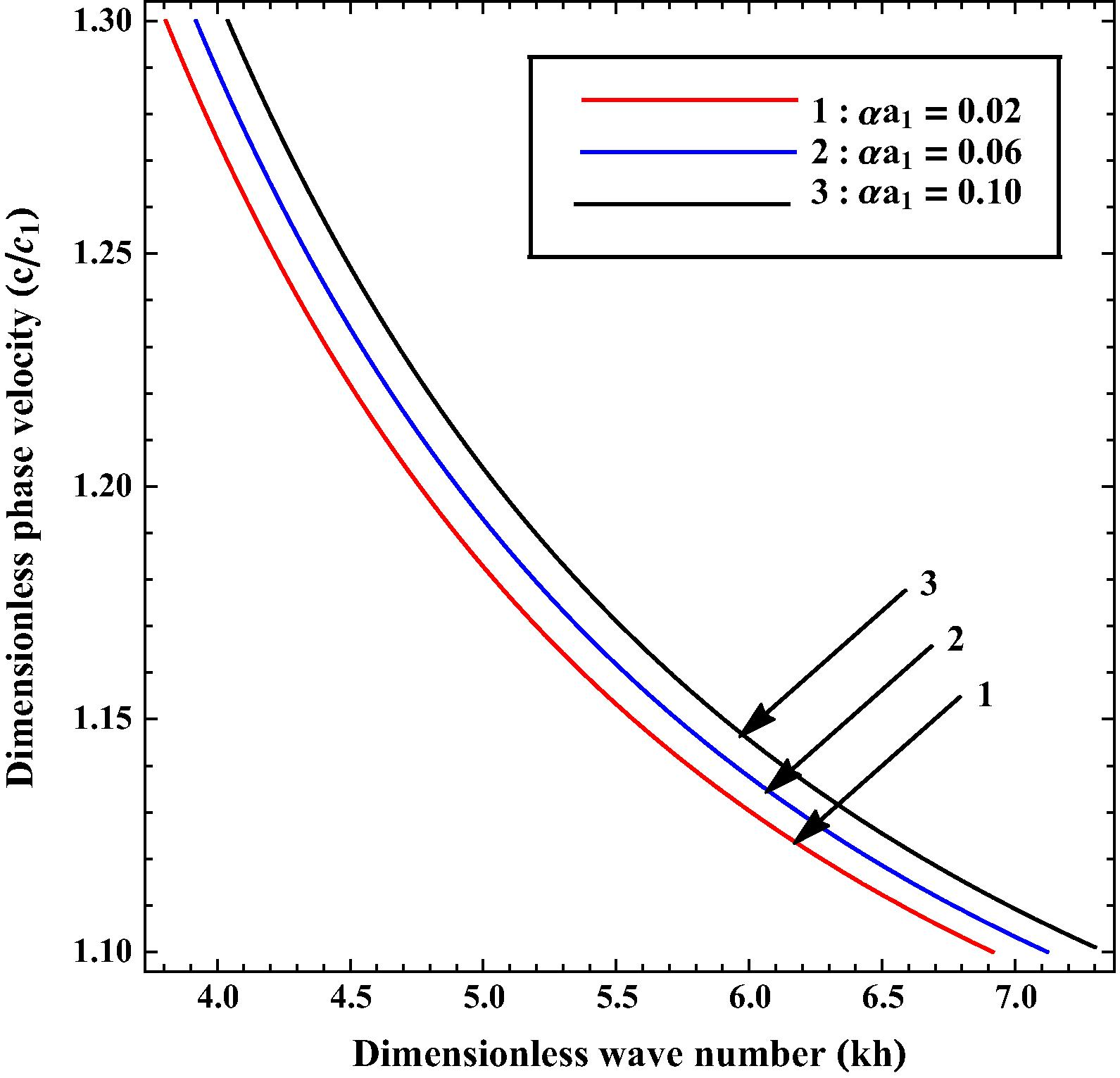
Variation of phase velocity
against wave number
for different values of
, when
.
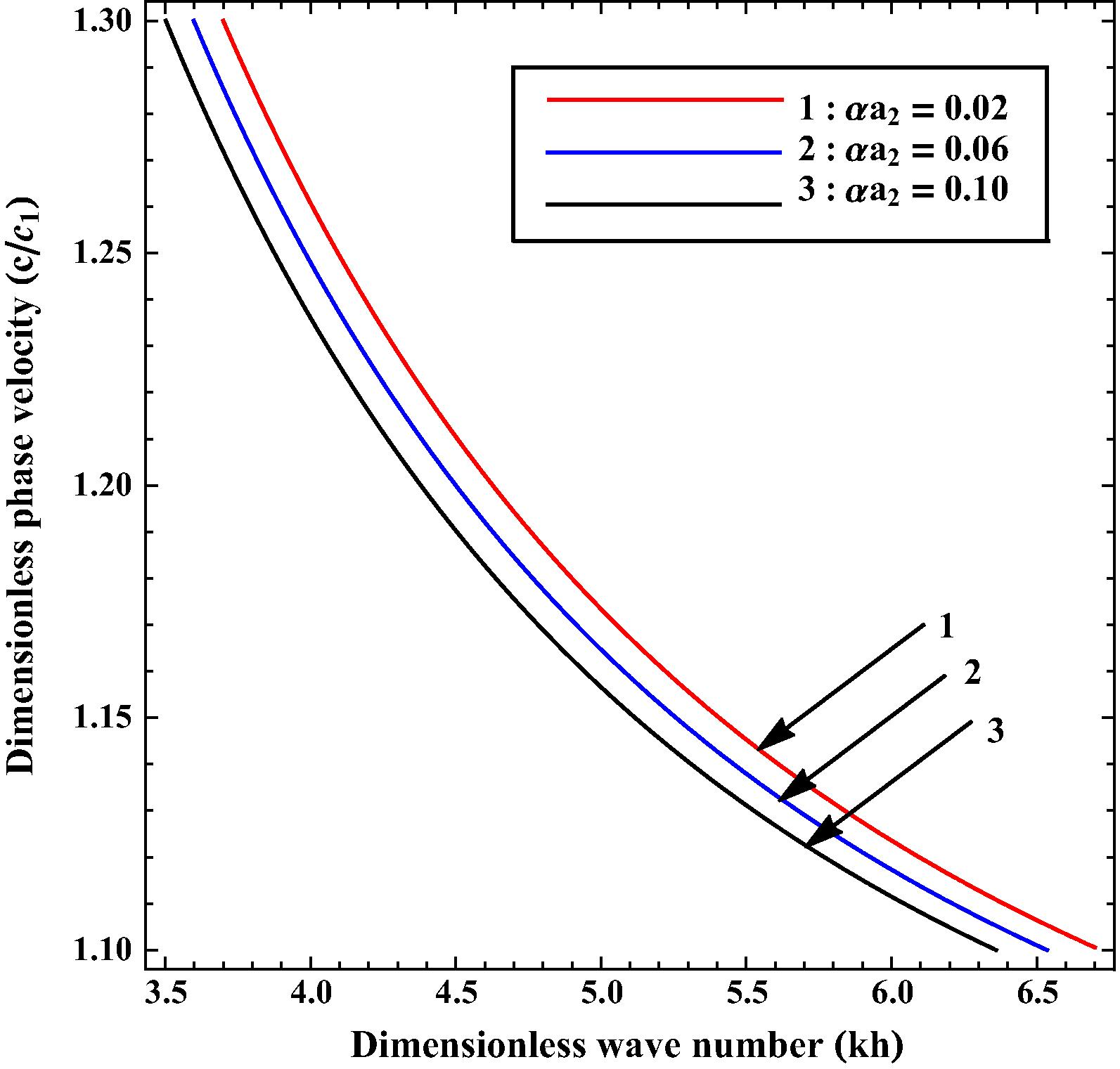
Variation of phase velocity
against wave number
for different values of
, when
.
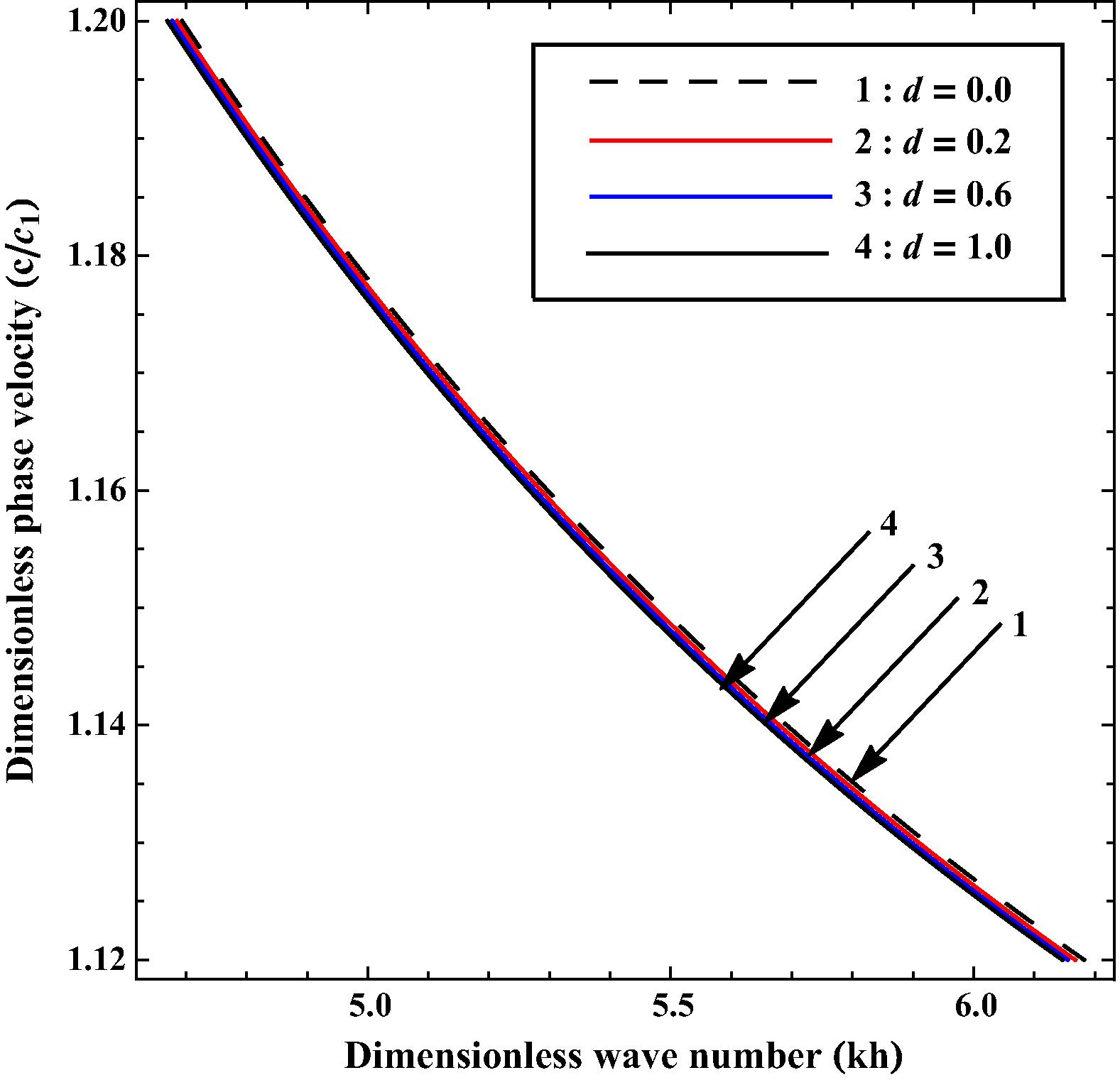
Variation of phase velocity
against wave number
for different values of
.
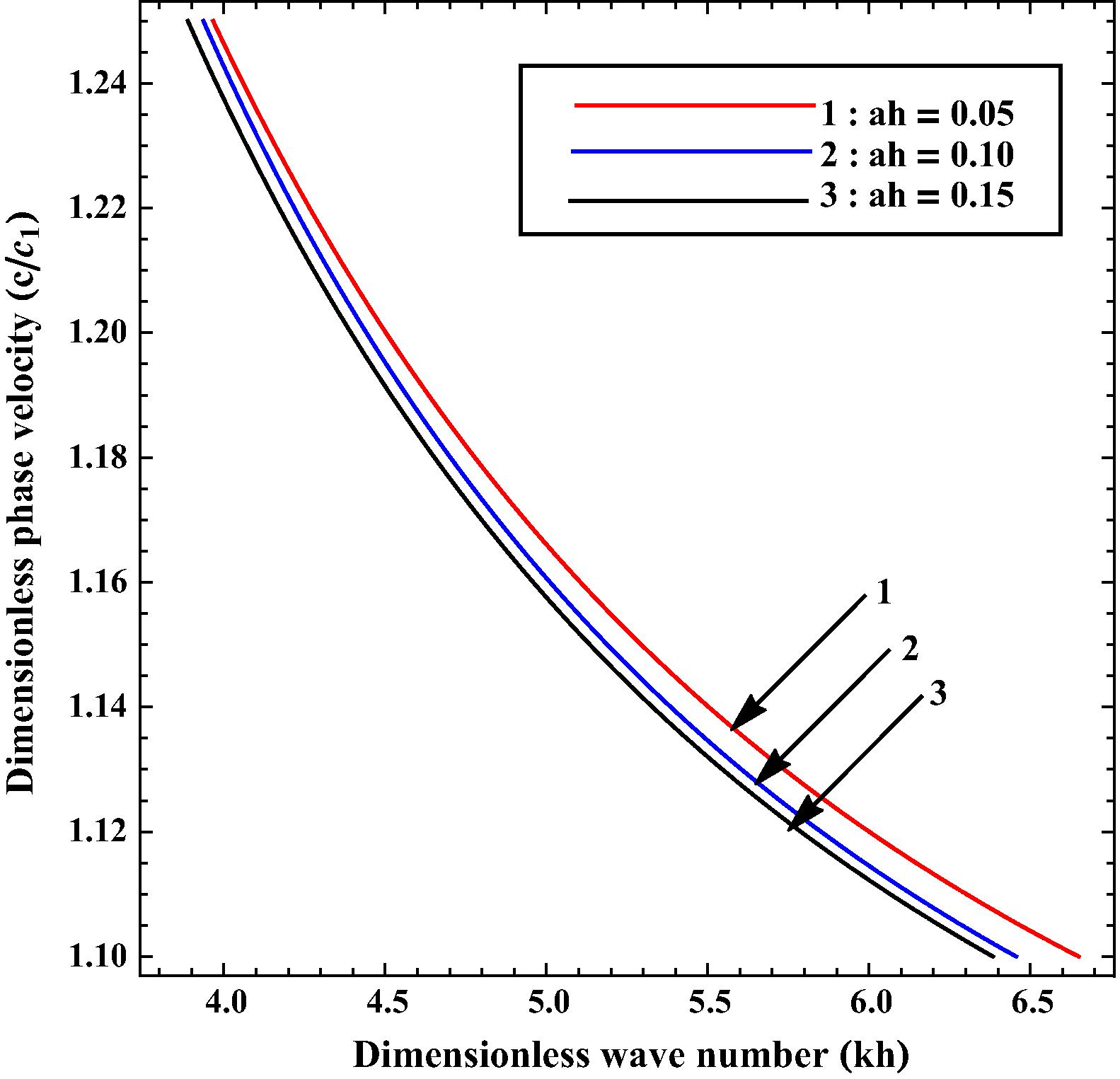
Variation of phase velocity
against wave number
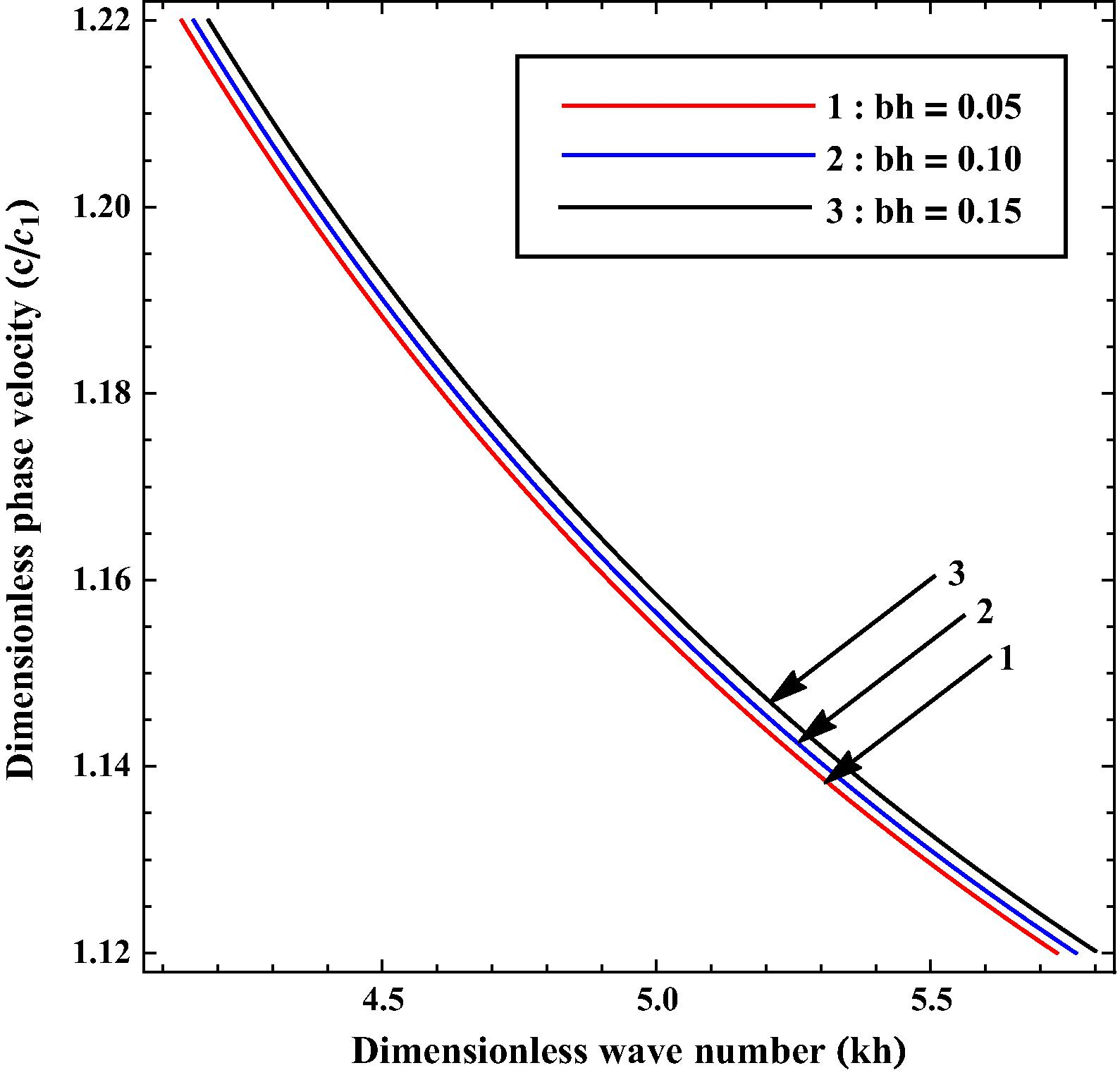
for different values of ah.
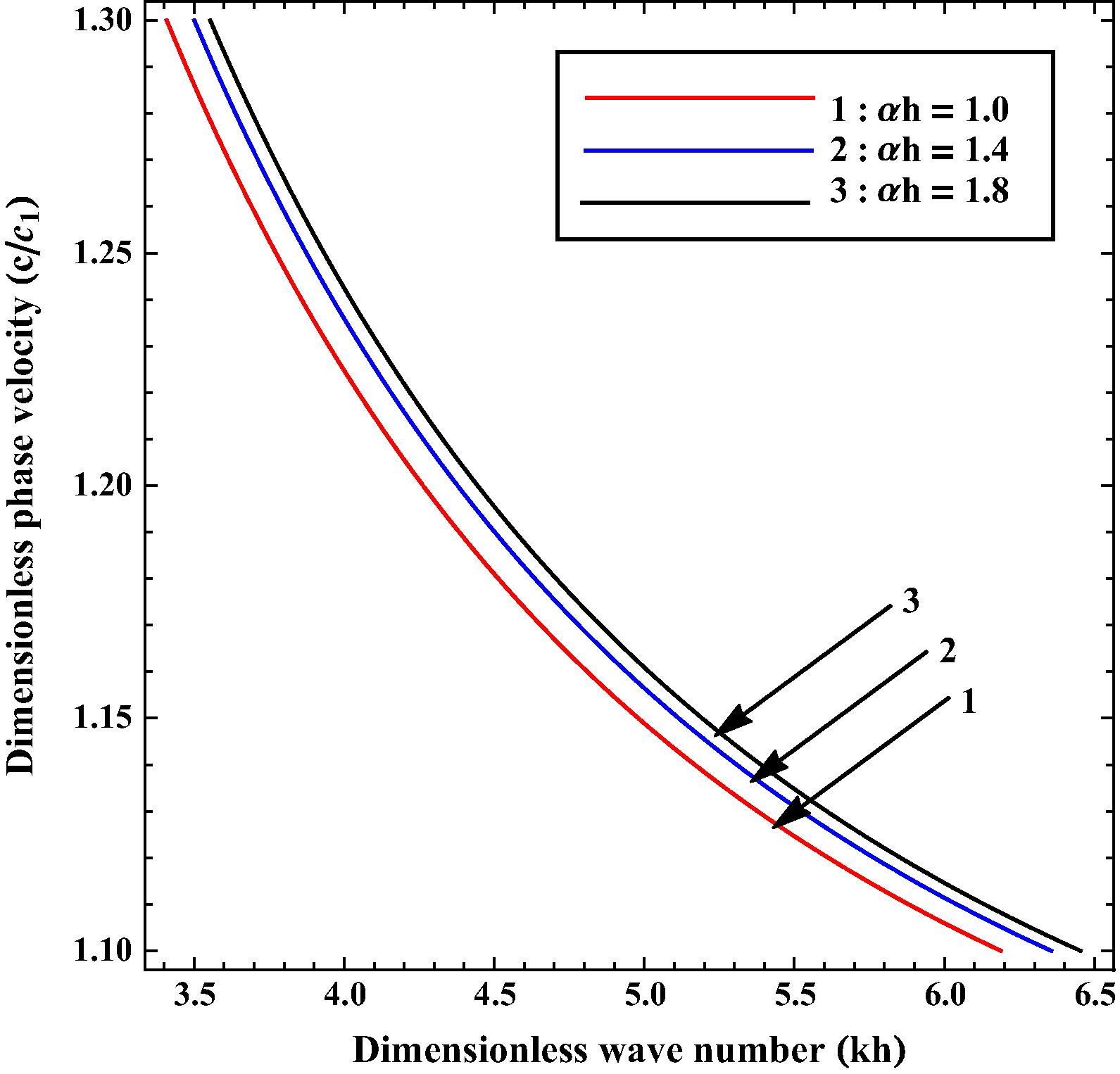
Variation of phase velocity
against wave number
for different values of bh.
Variation of phase velocity
against wave number
for different values of
.
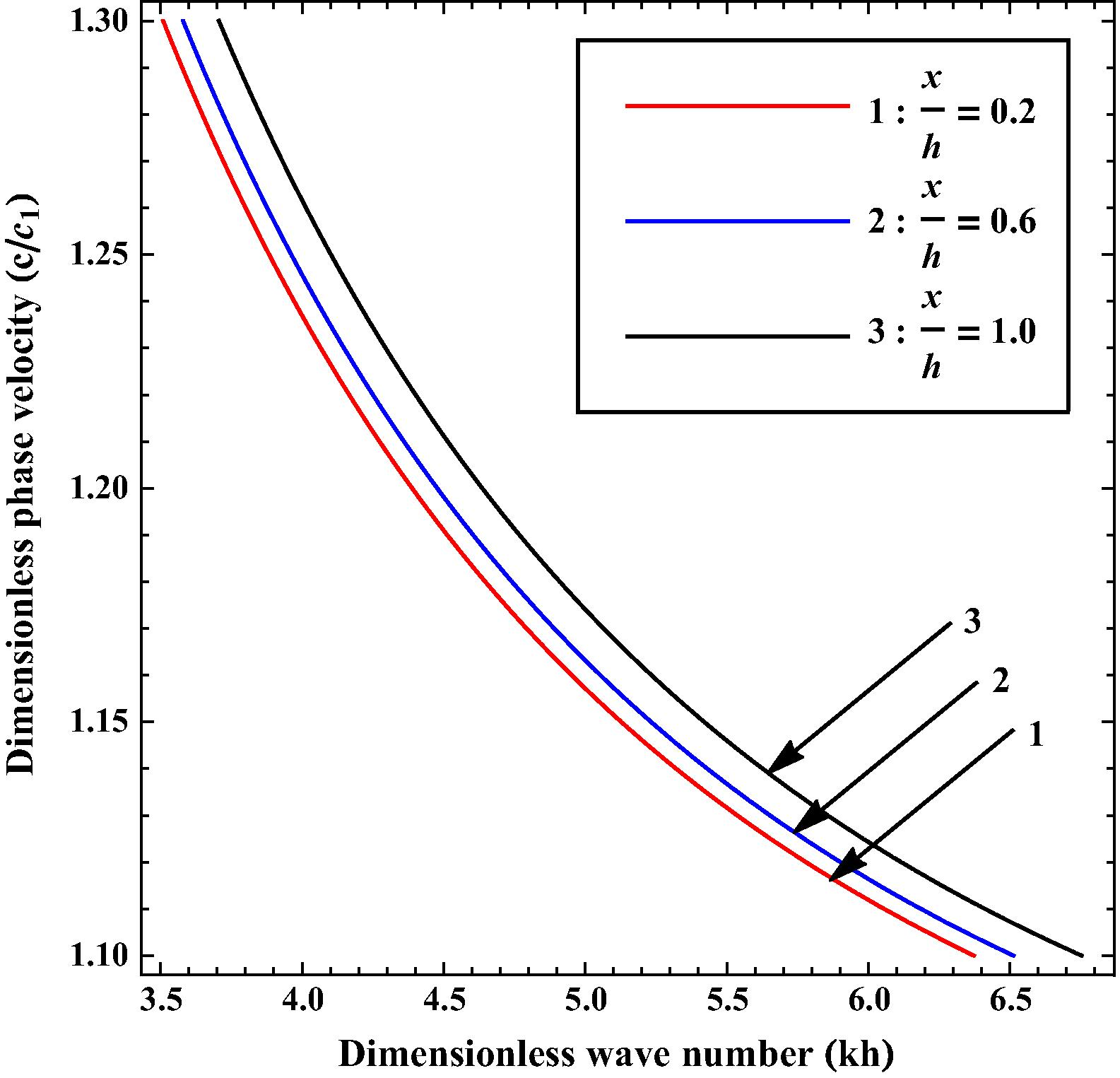
Variation of phase velocity
against wave number
for different values of
.
Figure No.
ah
bh
2
–
0.1
0.2
0.2
0.1
1.4
0.04
3
0.08
–
0.2
0.2
0.1
1.4
0.04
4
0.08
0.1
–
0.2
0.1
1.4
0.04
5
0.08
–
0
0.2
0.1
1.4
0.04
6
0.08
0
–
0.2
0.1
1.4
0.04
7
0.08
–
–
0.2
0.1
1.4
0.04
8
0.08
0.1
0.2
–
0.1
1.4
0.04
9
0.08
0.1
0.2
0.2
–
1.4
0.04
10
0.08
0.1
0.2
0.2
0.1
–
0.04
11
0.08
0.1
0.2
0.2
0.1
1.4
–
Fig. 2 shows the effect of magneto-elastic coupling parameter on the dispersion curve. Value of for curves 1–3 has been taken as 0.025, 0.050 and 0.075 respectively. It has been observed that as the value of increases the phase velocity of SH-wave also increases.
Figs. 3 and 5 describe the effect of upper corrugation parameter on the phase velocity of SH-wave. Fig. 5 is associated with case-I, in which common surface is planar i.e. . In both figures, the value of for curves 1–3 has been taken as 0.02, 0.06 and 0.10 respectively. From these figures it has been found that, the phase velocity of SH-wave increases uniformly as the value of increases.
Figs. 4 and 6 show the influence of common corrugation parameter on the phase velocity of SH-wave. The curves of Fig. 6 are associated with case-II, in which upper surface of layer is planar i.e. . Value of for curves 1–3 in both figures has been taken as 0.02, 0.06 and 0.10 respectively. It is very clear from Figs. 4 and 6 that the phase velocity of SH-wave decreases uniformly with increase in .
Curves plotted in Fig. 7 are associated with case-III and show the effect of lower and upper corrugation parameters on phase velocity, when amplitudes of both cyclic corrugations are equal i.e., (say). Also, this figure compares the effect of planar and corrugated boundary surfaces. Value of d for curves 1–4 has been taken as 0.0, 0.4, 0.8 and 1.2 respectively. The phase velocity curve 1 represents for the uniform planar boundary surfaces of the layer, i.e., . It is established through the figure that the phase velocity increases with an increase in d, but the increasing effect is negligible. On the other hand, when the uniform planar structure is compared with the corrugated structure, it has been found that the phase velocity of SH-wave is more in uniform planar boundary structure.
The influence of heterogeneous parameters ah and bh on the phase velocity of SH-wave is illustrated with the aid of Figs. 8 and 9. respectively. Values of ah and bh for curves 1–3 have been taken as 0.05, 0.10 and 0.15 respectively. Curve 2 of Fig. 8 shows for equal heterogeneity parameters i.e., . Meticulous observation of both figures concludes that phase velocity decreases with increase in ah whereas it increases with increase in bh.
Curves plotted in Fig. 10 portray the effect of undulatory parameter on the phase velocity of SH-wave. Value of for curves 1–3 has been taken as 1.0, 1.4 and 1.8 respectively. It is revealed from the figure that as increases phase velocity also increases.
Fig. 11 describes the impact of position parameter on the phase velocity of SH-wave. Value of for curves 1–3 has been taken as 0.2, 0.6 and 1.0 respectively. It has been noticed that as the value of increases the phase velocity of SH-wave also increases.
The results have been characterized by the fact that (condition of SH-wave). To follow this condition, the first mode of the dispersion curve has been obtained in the approximated frequency range 3–7 of kh. So, we have considered such interval of kh in each figure. We have ignored higher values of kh, because the velocity of surface SH-waves decays with respect to depth and finally vanishes. An overview of all the figures establishes that the phase velocity of SH-wave always decreases with increase of wave number , which is the basic characteristic of SH-wave propagation.
7 Conclusions
The propagation of SH-wave in a magneto-elastic anisotropic crustal layer (bounded by corrugated irregular surfaces) lying over a heterogeneous half-space has been studied. Maxwell’s equations have been employed to find the Lorentz force in the anisotropic layer. The non-linear differential equations are simplified by using suitable substitutions and solved using the variable separable method and Whittaker’s equation. A dispersion equation has been obtained in closed form and studied for different cases of corrugations. The dispersion equation also reduces to the classical result of Love (1920) and hence validating the solutions of the problem discussed in this manuscript. The analytical findings of this work are given below.
-
The magneto-elastic coupling parameter, position and undulatory parameters have favourable effect on phase velocity, that is phase velocity increases with an increase in these parameters.
-
The heterogeneous parameter has inverse effect on phase velocity, whereas heterogeneous parameter has favourable effect on phase velocity. But the effect of heterogeneous parameter is significant.
-
Both corrugations have remarkable but unlike effect on phase velocity. Presence of upper free surface corrugation parameter increases the phase velocity, but lower common interface corrugation parameter decreases the phase velocity.
-
The effects of both corrugations are found negligible when the amplitudes of both corrugations are equal. The phase velocity of wave is found more in the case of planar boundary surfaces of the layer.
It is very clear from the study that the presence of corrugated irregularities and magneto-elastic behaviour of layer have prominent effect on the propagation of SH-wave, especially for unequal amplitudes of corrugations. From the last two–three decades maximum earthquakes have occurred in the crust only and draw attention for seismologists to study the seismic waves in different kind of layered media. The results obtained in this paper give some essential information about the velocity of SH-wave propagation in Earth’s crustal layer which is anisotropic (Monoclinic) and corrugated irregular with magnetic behaviour. These results may play a vital role to understand well and predict the seismic wave behaviour at continental margins, mountain roots, etc.
8 Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
References
- SV-waves incidence at interface between solid-liquid media under electromagnetic field and initial stress in the context of three thermoelastic theories. J. Therm. Stresses. 2016;39(8):960-976.
- [Google Scholar]
- Magnetism and rotation effect on surface waves in fibre-reinforced anisotropic general viscoelastic media of higher order. J. Mech. Sci. Tech.. 2015;29(8):3381-3394.
- [Google Scholar]
- Mechanics of Composite Structural Elements. Berlin Heidelberg, New York: Springer-Verlag; 2004.
- Mechanics of Incremental Deformations. New York: Wiley; 1965.
- Elasticity and constitution of the earth’s interior. J. Geoph. Res.. 1952;57(2):227-286.
- [Google Scholar]
- The problem of the earth’s density variation. Bull. Seismol. Soc. Am.. 1940;30(3):235-250.
- [Google Scholar]
- Dispersion relations for SH wave in magneto-electro-elastic heterostructures. Int. J. Solids Struct.. 2008;45(20):5356-5367.
- [Google Scholar]
- Response of moving load due to irregularity in slightly compressible, finitely deformed elastic media. Mech. Res. Commun.. 2015;66:49-59.
- [Google Scholar]
- Propagation of a crack due to magnetoelastic shear waves in a self-reinforced medium. J. Vibr. Cont.. 2014;20(3):406-420.
- [Google Scholar]
- Green’s function for SH-waves in inhomogeneous anisotropic elastic solid with power-function velocity variation. Wave Motion. 2013;50(2):101-110.
- [Google Scholar]
- Seismology and Plate Tectonics. Cambridge, U.K.: Cambridge University Press; 1990.
- Reflection and transmission of plane SH-waves through an anisotropic magnetoelastic layer sandwiched between two semi-infinite inhomogeneous viscoelastic half-spaces. Pure Appl. Geophy.. 2015;172(10):2621-2634.
- [Google Scholar]
- Love wave dispersion in pre-stressed homogeneous medium over a porous half-space with irregular boundary surfaces. Intern. J. Solid Struct.. 2014;51(21):3689-3697.
- [Google Scholar]
- Effect of periodic corrugation, reinforcement, heterogeneity and initial stress on Love wave propagation. Waves Random Compl. Med. 2016
- [CrossRef] [Google Scholar]
- Impacts on the propagation of SH-waves in a heterogeneous viscoelastic layer sandwiched between an anisotropic porous layer and an initially stressed isotropic half space. J. Mech. 2016
- [CrossRef] [Google Scholar]
- Mathematical Theory of Elasticity. UK: Cambridge University Press; 1920.
- An analytical solution for the effect of initial stress, rotation, magnetic field and a periodic loading in a thermo-viscoelastic medium with a spherical cavity. Mech. Adv. Mater. Struct.. 2016;23(1):1-7.
- [Google Scholar]
- Reflection and transmission of plane SH-waves in an initially stressed inhomogeneous anisotropic magnetoelastic medium. J. Seismic. 2016
- [CrossRef] [Google Scholar]
- Solving the interaction of electromagnetic wave with electron by VIM. JKSU. 2015;27:63-70.
- [Google Scholar]
- The effect of rotation on the reflection of magneto-thermoelastic waves under thermoelasticity without energy dissipation. Acta Mech.. 2006;184(1–4):189-204.
- [Google Scholar]
- SH-Waves in viscoelastic heterogeneous layer over half-space with self-weight. Arch. Appl. Mech.. 2014;84:235-245.
- [Google Scholar]
- Influence of gravity on generalized magneto-thermoelastic medium for three-phase-lag model. J. Comput. Appl. Math.. 2016;291:142-157.
- [Google Scholar]
- Love wave at a layer medium bounded by irregular boundary surfaces. J. Vibr. Cont.. 2011;17(5):789-795.
- [Google Scholar]
- Effect of loosely bonded undulated boundary surfaces of doubly layered half-space on the propagation of torsional wave. Mech. Res. Commun.. 2016;73:91-106.
- [Google Scholar]
- Effect of smooth moving punch in an initially stressed monoclinic magnetoelastic crystalline medium due to shear wave propagation. J. Vibr. Cont.. 2016;22(11):2719-2730.
- [Google Scholar]
- Propagation of love-type wave in a corrugated fibre-reinforced layer. J. Mech. 2016
- [CrossRef] [Google Scholar]
- Magneto-thermoviscoelastic wave propagation at the interface between two micropolar viscoelastic media. Appl. Math. comput.. 2006;176(2):785-802.
- [Google Scholar]
- Shear waves at a corrugated interface between anisotropic elastic and visco-elastic solid half-spaces. J. Seismolog.. 2007;11(3):235-258.
- [Google Scholar]
- Rayleigh wave dispersion in an irregular sandy Earth’s crust over orthotropic mantle. Appl. Math. Model. 2016
- [CrossRef] [Google Scholar]
- Impact of quadratically varying rigidity and linearly varying density on the Rayleigh wave propagation: An analytic solution. Int. J. Solid Strut. 2016
- [CrossRef] [Google Scholar]
- A Course of Modern Analysis. New Delhi: Universal Book Stall; 1990.
- Elastic wave scattering and dynamic stress concentrations in exponential graded materials with two elliptic holes. Wave Motion. 2014;51(3):466-475.
- [Google Scholar]
Appendix A
Appendix B
Appendix C







