Translate this page into:
Derivation of fractional-derivative models of multiphase fluid flows in porous media
⁎Address: Energy Research Lab., College of Engineering, Effat University, Jeddah 21478, Saudi Arabia
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
This paper is devoted to deriving several fractional-order models for multiphase flows in porous media, focusing on some special cases of the two-phase flow. We derive the mass and momentum conservation laws of multiphase flow in porous media. The mass conservation-law has been developed based on the flux variation using Taylor series approximation. The fractional Taylor series's advantage is that it can represent the non-linear flux with more accuracy than the first-order linear Taylor series. The divergence term in the mass conservation equation becomes of a fractional type. The model has been developed for the general compressible flow, and the incompressible case is highlighted as a particular case. As a verification, the model can easily collapse to the traditional mass conservation equation once we select the integer-order. To complete the flow model, we present Darcy’s law (momentum conservation law in porous media) with time/space fractional memory. The modified Darcy’s law with time memory has also been considered. This version of Darcy’s law assumes that the permeability diminishes with time, which has a delay effect on the flow; therefore, the flow seems to have a time memory. The fractional Darcy’s law with space memory based on Caputo's fractional derivative is also considered to represent the nonlinear momentum flux. Then, we focus on some cases of fractional time memory of two-phase flows with countercurrent-imbibition mechanisms. Five cases are considered, namely, traditional mass equation and fractional Darcy’s law with time memory; fractional mass equation with conventional Darcy’s law; fractional mass equation and fractional Darcy’s law with space memory; fractional mass equation and fractional Darcy’s law with time memory; and traditional mass equation and fractional Darcy’s law with spatial memory.
Keywords
Fractional-derivative
Fractional Taylor series
Multiphase flow
Porous media
Mass conservation law
Momentum conservation
1 Introduction
1.1 Background
Multiphase flows and transport in porous media have many science and engineering applications, such as oil/gas reservoir simulation, enhanced oil recovery, carbon dioxide sequestration, and water soil infiltration. Multiphase flows in porous media, including highly complex physical phenomena that required very complicated nonlinear models to describe. The traditional modeling of multiphase flows and transport in porous media was built based on the continuum mechanics theory, which mainly utilizes a linear flux approximation to derive mass/momentum conservation equations (Chen et al., 2006).
The idea of using fractional derivative instead of integer one returns to three centuries ago, the era of Newton, Gauss, and Leibniz. Researches working on the fractional calculus field are familiar with the famous correspondence story between Leibniz and L’Hospital in 1695 about the possibility of having fractional derivative and the expectation that the fractional derivatives will lead to practical consequences in the future (Miller and Ross, 1993). The fractional calculus has been developed by some mathematicians such as Liouville, Riemann, Wey, Fourier, Abel, Grünwald, and Letnikov. Recently, fractional calculus has been involved in many science and engineering applications such as fluid mechanics and transport phenomena (Oldham and Spanier, 1974; Podlubny, 1999). The flow in porous media is one obvious example that can consider the fractional modeling due to their heterogeneity, such as solute transport in a groundwater aquifer, which does not follow Fickian law (Benson et al., 2000).
An application of the fractional advection–dispersion equation was presented in reference (Benson et al., 2000). Caputo (2000) has proposed a time-fractional version of Darcy’s law to describe time memory. Also, a fractional Darcy’s law with space memory has been introduced by He (1998). Wheatcraft and Meerschaert (2008) have derived a fractional mass conservation equation of a single-phase flow in porous media based on the fractional Taylor series. El-Amin et al. have presented an analytical solution of the fractional gas-flow equation in porous media using fractional power-series (El-Amin et al., 2017). Mohammadein et al. (2020) have provided an approximate similarity solution for the spatial fractional boundary-layer flow over an infinite vertical plate. Recently, El-Amin et al. (2020) investigated the fractional derivative modeling of double-diffusive free convection with von Neumann stability analysis. Further reading about fractional derivative recent developments can be found in references (Singh and Srivastava, 2020; Singh, 2020a, 2020b; Singh et al., 2019, 2020). The fractional version of the equation of reaction-advection–diffusion in porous media has been presented and solved numerically by Pandey et al. (2019). The convergence analysis of the space–time-fractional advection–diffusion equation has been investigated by Safdari et al. (2020). Recently, Kumar and Gómez-Aguilar (2020) have used an operational matrix for the Caputo-Fabrizio derivative to find numerical solutions for the reaction–diffusion, diffusion‐wave, and Cattaneo equations. Pandey et al. (2020) introduced an approximate analytical solution of the two‐dimensional space‐time fractional diffusion equation.
1.2 Research motivation
It is well-known that the mass conservation equation is usually derived using the first-order Taylor series to approximate the flux variation linearly, which means that the higher-order terms are dropped. This approximation is working very well with flows that can be represented by a linear flux variation. One may expect that as the number of terms of (higher-order) Taylor series increases, a nonlinear approximation for the flux will be obtained. This is desired for complicated flows such as multiphase flow and flow in heterogeneous media. The multiphase flows and transport in porous media are nonlinear due to the high heterogeneity in fluid flows and porous media. Fortunately, the higher-order Taylor series can be represented by a fractional Taylor series with only two terms. Thus, the fractional Taylor series will be used to describe flux in a general sense being nonlinear or linear. Therefore, it is worthy of introducing some research attempts to develop multiphase flows in porous media (certainly they have nonlinear fluxes) to be represented by fractional modeling. These types of models cover various multiphysics that can be described by different traditional derivatives. Each integer-order derivative can be replaced by a generalized fractional one. The fractional-order derivative in the new models treats the limitation of the conventional integer-order derivative. For example, the fractional mass conservation equation can represent the nonlinear flux with more accuracy than the first-order linear Taylor series. Also, including fractional Darcy’s law with time memory assumes that the permeability diminishes with time. The fluid pressure effect at the boundary delays, and the flow occurs as if the medium had a memory. Therefore, the mobilities of the wetting and the non-wetting phases inherit similar time memory. And so on, each fractional model has its own deeper physical meaning and the general sense. A fractional model is general, including the integer model as a particular case with a more in-depth physical meaning. Also, it provided several real physics that may be hidden by the traditional models. So, it worth to be considered.
1.3 Contribution
In this paper, novel models of fraction multiphase flow in porous media have been developed based on the continuum mechanics approach. All sections are mainly developed, including the general models and particular cases. The mass conservation equations are derived, and the momentum equation (Darcy’s law) is accordingly modified. Taylor series approximation has been utilized to derive the fractional mass conservation law of multiphase flow in porous media. Several versions of fractional Darcy’s law have been developed to be coupled with the fractional mass conservation equation. After the general formalization of the fractional multiphase flow model, we focus on some practical fractional two-phase models by considering the countercurrent imbibition mechanism as an example. Relative permeabilities, mobilities, and capillary pressure are also extended to their fractional versions.
1.4 Organization
The rest of the paper is arranged as follows: In Section 2, the fractional mass equation of a multiphase immiscible flow has been derived. In Section 3, we presented the fractional Darcy’s law with time memory, while the fractional Darcy’s law with space memory has been covered in Section 4. Section 5, provides five special cases listed in subsections (5.1–5.5) and discusses fractional/traditional alternatives models of mass and momentum conservation laws of two-phase flow in porous media. In Subsection 5.1, the traditional mass equation and fractional Darcy’s law with time memory are provided. Subsection 5.2 gives fractional mass equation with conventional Darcy’s law while fractional mass equation and fractional Darcy’s law with space memory are covered in Subsection 5.3. The fractional mass equation and fractional Darcy’s law with time memory are given in Subsection 5.4. Subsection 5.5 focuses on the traditional mass equation and fractional Darcy’s law with spatial memory. Finally, the conclusions are presented in Section 6.
2 Fractional mass equation of a multiphase immiscible flow
To derive the mass conservation equation of multiphase immiscible flow in porous media, we first derive the mass conservation equation of a single-phase flow. Consider mass flux across the surfaces (inflow and outflow) of the rectangular cube (control volume) with the volume
as shown in Fig. 1. The amount of mass across the inflow surface is equal with the mass outflows on another surface. From Fig. 1, it can be seen that the mass inflow across at the first face of
is,
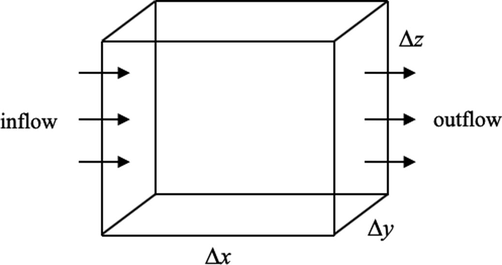
Sketch of rectangular control volume.
The equation of mass conservation for a fluid flow in a porous medium is traditionally derived using the first-order Taylor series, which represents the linear flux. Wheatcraft and Meerschaerton (He, 1998) have used the fractional Taylor series to describe the nonlinear flux. The fractional flux component in
-direction can be written using the two-term
-order fractional Taylor series expanded about
, i.e.,
Here, we assume that the medium is heterogeneous and isotropic, and
has the same value in all directions. The net mass flux through the x-direction can be obtained by subtracting (3) from (1), thus,
Similarly, the net mass flux in the y- and z-direction are given by,
Therefore, the net mass flux through the control volume is obtained by summing (5)–(7),
Based on the mass conservation concept, the net mass flux, Eq. (8), should equal the accumulation term,
. Then the mass conservation of the fluid flow in porous media can be written as,
Eq. (10) is provided for a single-phase flow which can be extended to a multiphase immiscible flow. Then the mass conservation equation is extended for each fluid phase
such that,
Now, let us work over the accumulation term (the first term of the left-hand side of Eq. (11)). We may assume that the control volume, phase density, and porosity can vary with pressure, which in turn vary with time, and the phase saturation varies with time too, thus,
Also, the bulk volume can be broken down into two terms, pore volume and rock (solid) volume,
It is clear that,
The coefficient of bulk compressibility
, solid matrix compressibility
, and pore compressibility
with respect to a unit change in the pressure p are given by,
Therefore, the bulk compressibility can be given as,
Also, porosity depends on pressure due to rock compressibility, which is often assumed to be constant (typically 10−6–10−7 psi−1) and can be defined as,
Moreover, the fluid phase compressibility
in terms of the fluid volume and density change with pressure at a constant temperature is given by,
Now, let us substituting Eqs. (16)–(20) into the accumulation term,
Therefore, by substituting Eq. (22) into Eq. (11) one gets,
Assuming q = 0, the corresponding single-phase conservation of mass equation,
On the other hand, if one assumes that the fluid is incompressible and the porous medium compressibility is negligible , the above equation reduced to,
Eq. (25) is the fractional mass conservation equation for immiscible multiphase incompressible flow. If we put
, Eq. (25) is reduced to the traditional mass conservation equation for immiscible multiphase flow (El-Amin et al., 2016, 2012; Sun et al., 2012);
3 Fractional Darcy’s law with time memory
The modified Darcy’s law with time memory has been introduced by Caputo (Benson et al., 2000). The version of Darcy’s law assumes that the permeability diminishes with time. Therefore, the effect of fluid pressure at the boundary delays and the flow occurs as if the medium had a memory. The traditional Darcy’s law may be given as,
In this equation, there is a convergence at for any value of t since it is assumed . The model (29) collapses to the traditional one (28) as does not depend on time t, and .
4 Fractional Darcy’s law with space memory:
He (Caputo, 2000) proposed a fractional Darcy’s law with space memory based on the fractional derivative of Riemann-Liouville. In this study, we are going to use the Caputo fractional derivative as stated above. In this context, we can rewrite the fractional Darcy’s law in the form,
Similarly, the fractional-order model (31) collapses to the traditional integer-order one (28) as .
5 Selected special cases of two-phase flows:
5.1 Traditional mass equation and fractional Darcy’s law with time memory
The traditional governing equations that control the process of two-phase imbibition in porous media (Fig. 2) are provided. The two-phase immiscible incompressible flow in a homogenous porous medium domain is governed by Darcy’s law and the equations of mass conservation for each phase as (El-Amin et al., 2020);
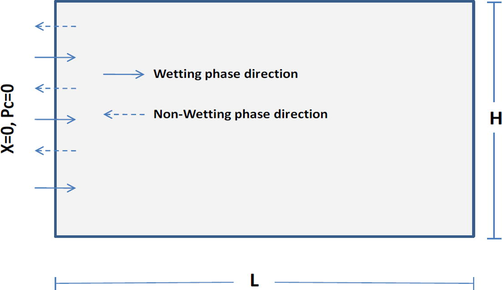
Schematic diagram of the countercurrent imbibition.
The saturations of the phases are constrained by,
Considering the memory formalism explained above, Eqs. (40) and (41) be rewritten as follows,
The fractional time derivative is defined in Eq. (32). It is clear that memory formalism implies the use of more one parameter, namely .
For the countercurrent imbibition, the sum of the velocities of the wetting and non-wetting phases vanishes. Thus,
The capillary pressure
is defined as a difference between the non-wetting and wetting phase pressures as,
Therefore, from Eq. (46) and Eq. (47) we may obtain,
One my writes Eq. (44) as,
Substituting from Eq. (49) into Eq. (42) we get,
The problem under consideration is reduced to be governed only by the above equation (50), because the capillary pressure is a function of
with the aid of the constrain (37). The capillary pressure functions are dependent upon the pore geometry, fluid physical properties and phase saturation. The two-phase capillary pressure can be expressed by Leverett dimensionless function
(Singh and Srivastava, 2020) as a function of the normalized saturation S;
Using Eqs. (52) and (53), Eq. (50) can be rewritten as,
Now let us give the definition of
and
which are also functions of
as shown above, one may get,
Therefore, Eq. (58) becomes,
To consider a certain case of study, we may use a specified empirical formula of the capillary pressure in terms of normalized saturation function. The
function typically lies between two limiting curves (drainage and imbibition) which can be obtained experimentally. The correlation of the imbibition capillary pressure data depends on the type of application. Since our current research is concerned with water–oil system (Pooladi-Darvish and Firoozabadi, 2000). The capillary pressure and the normalized wetting phase saturation are correlated as follows,
When α = 0, the above fractional-order equations will be reduced to the integer-order equations in
reference (El-Amin et al., 2013).
5.2 Fractional mass equation with traditional Darcy’s law
Recall the same model in 5.1 using the fractional mass equation derived in this work to be combined with the traditional Darcy’s law. Considering zero source/sink term, Eq. (25), maybe rewritten as,
Therefore, the 1D case becomes,
In the case of countercurrent imbibition, both the wetting phase and non-wetting phase flow through one boundary in opposite directions. So, the sum of the velocities of the wetting and non-wetting phases is zero, thus,
After some mathematical manipulation and using Eqs. (54)–(56), one can obtain the following equation,
Again, the above fractional model will be equivalent to the integer model in reference (Safdari et al., 2020) as α = 0.
5.3 Fractional mass equation and fractional Darcy’s law with space memory
Similar to the above models, one may list the following equations to represent the fractional mass conservation equation and fractional momentum conservation equation (Darcy’s law) with space memory as follows,
Therefore,
The corresponding 1D model is given as,
By analogy to Eq. (48) we may write,
Substituting (68) into (66),
Using Eqs. (51)–(53), Eq. (69) becomes,
Or in the specific case
,
which is 1D partial differential equation in x and t.
The fractional equations will collapse to the integer equations if (El-Amin et al., 2013).
5.4 Fractional mass equation and fractional Darcy’s law with time memory
In a similar fashion, the fractional mass equation and fractional Darcy’s law with time memory may be given as,
Combining the above two equations, we get,
Eq. (74) can be reduced to 1D case as follows,
Using Eq. (48) with Eq. (75),
Again, using Eqs. (51)–(53), and (55) one may write the previous equation as,
This is again a partial differential equation in x and t.
The fractional equations will collapse to the integer equations if (El-Amin et al., 2013).
5.5 Traditional mass equation and fractional Darcy’s law with space memory
In this section, we provide the fractional momentum conservation (Darcy’s law) with space memory. Starting with the traditional mass conservation and as,
Combining the above two equations, one obtains,
The 1D two equations become,
Substituting (68) into (82), we get,
Using Eqs. (51)–(53), Eq. (92) becomes,
The fractional equation collapses to the integer one as (El-Amin et al., 2013).
The fractional derivative is given in a form of partial differential equation in x and t,
6 Conclusions
In this work, we developed a fractional model to govern the multiphase flow in porous media by updating the mass conservation law and momentum conservation (Darcy’s) law. The fractional Taylor series has been used to formulate the nonlinear flux in the control volume. Therefore, the fractional version of the mass conservation law of multiphase flow in porous media has been derived. To complete the governing model, we updated Darcy’s law to be combined with the fractional mass conservation equation (saturation equation). We presented several cases for the modified Dacry’s law, namely, with time memory and with spatial memory. After that, we focused on some special two-phase cases with more details such that the two equations are treated to give one fractional saturation equation. Moreover, relative permeabilities and flow mobilities are also updated. In future work, we need to put effort into solving the developed spatial fractional system/equation, which is considered one of the difficult problems to solve. The future research directions may include computational aspects to solve the fractional models developed in the current paper. Also, providing relevant theoretical analyses for the developed fractional models could be an important research direction. Moreover, creating the fractional versions of similar problems in flow and transport in porous media could be another future research direction.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Computational Methods for Multiphase Flows in Porous Media. Philadelphia, PA, USA: SIAM Computational Science and Engineering; 2006.
- An Introduction to the Fractional Calculus and Fractional Differential Equations. New York: John Wiley and Sons. Inc.; 1993.
- The Fractional Calculus. New York: Academic Press; 1974.
- Fractional Differential Equations. San Diego: Academic Press; 1999.
- The fractional-order governing equation of Lévy motion. Water Resour. Res.. 2000;36:1413-1423.
- [Google Scholar]
- Application of a fractional advection–dispersion equation. Water Resour. Res.. 2000;36:1403-1413.
- [Google Scholar]
- Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Meth. Appl. Mech. Eng.. 1998;167:57-68.
- [Google Scholar]
- Analytical solution for fractional derivative gas-flow equation in porous media. Results Phys.. 2017;7:2432-2438.
- [Google Scholar]
- An approximate similarity solution for spatial fractional boundary-layer flow over an infinite vertical plate. Comput. Appl. Math.. 2020;39:114.
- [CrossRef] [Google Scholar]
- Fractional derivative modeling of double-diffusive free convection with von Neumann stability analysis. Int. J. Modell. Simul. 2020
- [CrossRef] [Google Scholar]
- Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials. Appl. Sci.. 2020;10:2850.
- [Google Scholar]
- Analysis for fractional dynamics of Ebola virus model. Chaos, Solitons Fractals. 2020;138:109992
- [Google Scholar]
- Numerical simulation for fractional delay differential equations. Int. J. Dynam. Control 2020
- [CrossRef] [Google Scholar]
- Solving non-linear fractional variational problems using Jacobi polynomials. Mathematics. 2019;7:224.
- [Google Scholar]
- Legendre spectral method for the fractional Bratu problem. Math. Methods Appl. Sci. 2020
- [CrossRef] [Google Scholar]
- Numerical solution of the time fractional reaction-advection-diffusion equation in porous media. J. App. Comput. Mech. 2019
- [CrossRef] [Google Scholar]
- Shifted Chebyshev collocation of the fourth kind with convergence analysis for the space–time fractional advection-diffusion equation. Eng. Comput. 2020
- [CrossRef] [Google Scholar]
- Numerical solutions for the reaction-diffusion, diffusion-wave, and Cattaneo equations using a new operational matrix for the Caputo-Fabrizio derivative. Math. Methods Appl. Sci.. 2020;43(15):8595-8607.
- [Google Scholar]
- Approximate analytical solution of two‐dimensional space‐time fractional diffusion equation. Math. Methods Appl. Sci.. 2020;43(12)
- [Google Scholar]
- Co-current and counter-current imbibition in a water-wet matrix block. SPEJ. 2000;5:3-11.
- [Google Scholar]
- An iterative implicit scheme for nanoparticles transport with two-Phase flow in porous media. Procedia Comput. Sci.. 2016;80:1344-1353.
- [CrossRef] [Google Scholar]
- Matrix-oriented implementation for the numerical solution of the partial differential equations governing flows and transport in porous media. Comput. Fluids. 2012;68:38-46.
- [Google Scholar]
- Discrete-fracture-model of multi–scale time-splitting two–phase flow including nanoparticles transport in fractured porous media. J. Comput. App. Math.. 2012;333:327-1249.
- [Google Scholar]
- Numerical and dimensional investigation of two-phase countercurrent imbibition in porous media. J. Comput. Appl. Math.. 2013;242:285-296.
- [Google Scholar]







