1 Introduction

A system with one moving part and the other static influenced by pressure gradient where lubricants are essential defined generalized Couette media (Okoya, 2007). Flow of industrial material in such a medium found its application in drilling, chemical production, medical material industry and so on. Liquids such as water, kerosene, alcohol, benzene etc. are classified as a Newtonian fluid because of their constant viscosity while slurries, mayonnaise, hydraulic grease and others are categorized as non-Newtonian fluid (Hayat et al., 2001; Nima et al., 2020). Some non-Newtonian liquids are viscoelastic while some are not in nature. Oldroyd fluids initiated by (Oldroyd, 1950) are one of the special viscoelastic non-Newtonian fluid with high industrial significance, the fluid has shear and stress characteristics which are built on the retardation and relaxation time. Of the Oldroyd fluids, Oldroyd 8-constant liquid is the generalized form of the fluid (Baris, 2001). In the absence of energy transfer and heat diffusion, the flow characteristics of Oldroyd 8-constant fluid in a channel were reported in details by the (Ellahi et al., 2008; Hayat et al., 2004; Khan et al., 2011). Meanwhile, heat transfer and dissipation considerably affect the viscosity of fluids in a configuration which leads to its low efficiency in many industries.

The exothermic heat reaction of combustible industrial materials causes a release of a substantial measure of heat that is employed in pollution control, rocket and jet propulsion, reactor atomic plant, fire extinguisher and others (Hassan et al., 2018; Makinde, 2004). Several idealized single exothermic heat diffusion have been modeled which may adequately take care of some problems by (Ajadi, 2011; Okoya, 2009; 2011;; Salawu et al., 2020a; Srivastava et al., 2020). For high flame propagation and ignition, single reaction diffusion is not enough, but a double exothermic heat reaction for complete combustion process. According to (Szabo, 1964), double combustion reaction will assist in reducing toxic pollutant of carbon-monoxide from the engines. For instance, automobile catalytic conversion is a platform for the two-step enthalpy reaction. As such, (Makinde et al., 2013) investigated thermal criticality of two-step exothermic heat reaction in a slab. A semi-analytical approach was used to provide solutions to the model in an isothermal diffusion reactant system. It was publicized that ignition rate can be guided if strong heat production terms are well controlled. (Salawu et al., 2019a, 2020b) considered two-step reaction of Newtonian diffusion fluids in a porous Poisuille medium and convective cooling walls. It was obtained that second step exothermic reaction term improved heat generation that enhances combustible heat propagation. However, increasing exothermic heat distribution of a system greatly affect its enactment due to rising energy dissipation that reduces the thermal engineering device productivity.

In several thermal systems, high rate of entropy is generated due to loss of energy to the ambient through dissipation. The irreversibility of energy lost increases entropy generation that greatly deteriorates the performance of the engineering system (Kareem et al., 2020). To analysis the amount of entropy generation and improve the reversibility of energy loss, thermodynamics second law is applied to measure system disorderliness and enhance the thermal engineering device efficiency (Fatunmbi and Salawu, 2020a). The concept of minimization of disorderliness as a result of entropy generation through thermodynamic second law was presented by (Bejan, 1982; 1995). Owing to the reduction in entropy generation, the authors (Fatunmbi and Salawu, 2020b; Salawu et al., 2019b) used second law of thermodynamic to examine different industrial hydromagnetic non-Newtonian fluids in a medium. It was stated that low heat dissipation should be encouraged in a thermal system. (Khan et al., 2018) considered minimization of an irreversibility process of nonlinear radiative nanomaterial in a moving thin needle. Revealed from the study, the system thermodynamic equilibrium can be achieved by monitoring the heat generation terms to reduce heat diffusion that can lead to disorderliness. (Hayat et al., 2018) discussed copper and silver nanomaterial with entropy generated by a rotating disk. Emphasis was given to the irreversibility analysis, thermal gradient, nanoparticles flow velocity and computational convergence process. Due to the impact of entropy generation on the efficiency of industrial machines and others, many studies have been done on the reduction of entropy generation which can be found in (Abolbashari et al., 2014; Salawu et al., 2019c, 2020c).

The present study investigated Oldroyd 8-constant liquid flow of generalized Couette media in the presence of activation energy, chemical kinetics that leads to two step exothermic reactions. The study in motivated by the industrial usefulness of the fluid and noteworthy reports on the flow characteristics and thermal criticality presented by (Hayat et al., 2004; Makinde et al., 2013; Salawu et al., 2020d). Therefore, it is important to consider the minimization of energy loss as a result of increase entropy generation and variable electric conductivity to improve hydromagnetic current carrying conductivity of a fluid by examining the current density. This is significantly valuable to the thermal science industry, biotechnology, pharmaceutical, electromechanical system and heat exchanger. Going by the literature reviewed, the study of an entropy generation and current density for a double exothermic reaction of the considered fluid have not been investigated previously despite its extensive usages. The exothermic reaction occurs in a Couette channel and the modeled problem is analytically solved with rigorous mathematical analysis of parameter sensitivity.

2 Mathematical setup

The generalized steady Couette flow of an Ohmic conducting fluid for a double combustible reaction diffusion of Oldroyd 8-constant with exothermic heat distribution is investigated. The current density of the molecular diffusive fluid is examined under the influenced of pre-exponential kinetics, and the viscoelastic fluid material is maintained by the device convective cooling. The upper wall moves with velocity U while the lower surface is statics, both walls are exposed to convectional asymmetric cooling which is defined after newton’s law of cooling. Without material consumption, the fluid momentum is not created by the species reaction, but inspired by pressure gradient and kinetics. The coolant walls are to keep the fluid material from deformation as illustrated schematically (Fig. 1).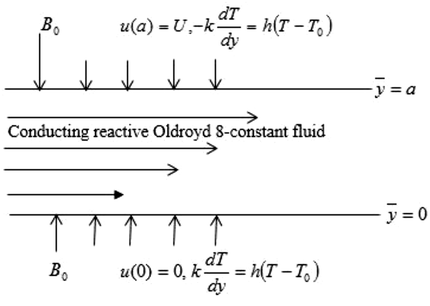

Close

Fig. 1

Flow schematic coordinate.

Export to PPT

Considering the Cartesian system of coordinates, the conservation of mass and momentum law for the rapid fluid species is given as (Okoya, 2011).

The tensors stress $T$ for Oldroyld 8-constant fluid (Ellahi et al., 2008).

The term I is tensor identity, $p$ is the pressure and the external stress $\mathit{F}\ast$ satisfies

and ${\mathit{A}}_{\mathbf{1}}={\mathit{L}}^{{\mathit{T}}_{\mathbf{1}}}+\mathit{L}$ , $\mathit{L}=grad\mathit{U}$

${\mathit{A}}_1$ depicts the first Rivlin-Ericksen tensor and $\mu ,{\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2,{\mathrm{\Gamma }}_3,{\mathrm{\Gamma }}_4,{\mathrm{\Gamma }}_5,{\mathrm{\Gamma }}_{6}and{\mathrm{\Gamma }}_7$ are the material constants. The convected contra variant $D/\mathit{Dt}$ of the flow is defined as

Oldroyld 8-constant of a non-Newtonian material for the conservation of mass, laminar and incompressible of linear momentum balance is taken (Salawu et al., 2019b, 2020b):

In which $\mathit{b}$ is the body force. The exothermic temperature equation for double steps combustible reaction is expressed as:

According to (Makinde et al., 2013; Salawu and Fatunmbi, 2020), the rate of reaction with branched chain term and activation energy of $E_{f}and{E}_s$ is written as:

Taking that the chemical reaction is not propelled by the fluid momentum, with the assumptions above, the dimensionless equations for the hydromagnetic viscoelastic Oldroyd 8–constant and double combustible heat distribution in a generalized Couette are taken as

The boundary conditions are taken as:

(Salawu and Fatunmbi, 2020; Salawu and Ogunseye, 2020) give the current density and total current produced in reactive hydromagnetic exothermic combustible system. Current density is the measure of electric current passing through per unit value of a cross sectional area $\left(A/m^2\right)$ . The current density and total current produced in the hydromagnetic exothermic flow system are given as:

The value of $M$ can only be zero $\left(i.eM=0\right)$ if the formation of short electric circuit in the loading electric field is not available.

The term ${\psi }_1$ and ${\psi }_2$ which stand for the Oldroyd fluid with the nonlinear derivatives in equations (13) and (14) are defined as:

The variables described in equation (19) alongside with equation (18) are utilized to obtain the boundary value dimensionless non-Newtonian exothermic heat dependent flow models (13)-(15). $$\overline{p}=\frac{\mu Up}{a},\overline{x}=ax,\overline{u}=uU,\overline{y}=ay,r=\frac{E_s}{E_f},\overline{T}=\frac{R{T}_o^2\theta }{E_f}+T_o,\epsilon =\frac{R{T}_o}{E_f},Br=\frac{E_f{u}^2\mu }{\mathit{KR}{T}_o^2},$$ $$M=\frac{{\sigma }_o{B}_o^2{a}^2}{\mu },G=-\frac{\mathit{dp}}{\mathit{dx}},\delta =\frac{a^2{\psi }_1}{U^2},\mathrm{\Lambda }=\frac{a^2{\psi }_2}{u^2},\beta =\frac{Q_1{C}_1{A}_f{E}_f{a}^2}{\mathit{KR}{T}_o^2}{\left(\frac{K{T}_o}{\mathit{vl}}\right)}^{n}exp\left(-\frac{1}{\epsilon }\right)$$ $$\gamma =\frac{Q_2{C}_2{A}_s}{Q_1{C}_1{A}_f}exp\left(-\frac{1}{\epsilon }\right)exp\left(\frac{1}{\epsilon }\right),\lambda =\frac{E_{\ast }}{B_{o}U}.$$

3 Thermodynamic analysis of entropy generation

Using the adapted general formulation for the volumetric rate of entropy generation provided by (Bejan, 1982; 1995;; Dalir et al., 2015), we have

From equation (20), the first term is heat conduction due to entropy generation while the second term is entropy generation caused by viscous dissipation. The dimensionless form of equation (20) is expressed as

4 Results and discussion

For the comprehensive understanding of the results, implications and applications, in graphs and tables, the results are presented. The default values are taken from the existing theoretical and experimental report as offered by (Makinde et al., 2013; Salawu et al., 2020d). As a way of establishing the accuracy and the consistence of the adopted semi-analytical method, a comparison of the method with the Runge-Kutta numerical method is considered as seen in Table 1. The validation of the computed values are taken, and found to be in a good quantitative and qualitative agreement as offered in the table. Table 2 shows the reaction kinetics (Sensitized, Arrhenius and Bimolecular) influence with different parameters on the exothermic energy distribution. As found, a variational rise in the parameters with corresponding increase in the reaction kinetics are noticed to have enhanced the exothermic energy reaction diffusion of the Oldroyd 8-constant fluid.

4.1

4.1 Oldroyd 8-constant flow velocity and temperature distributions

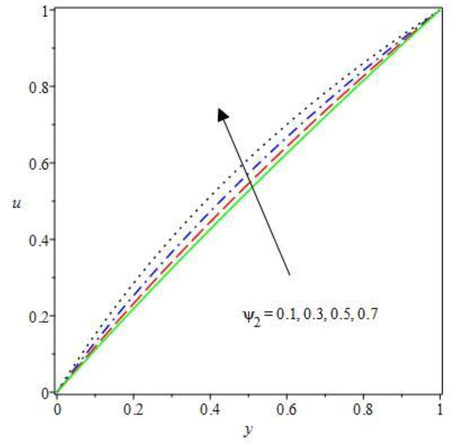
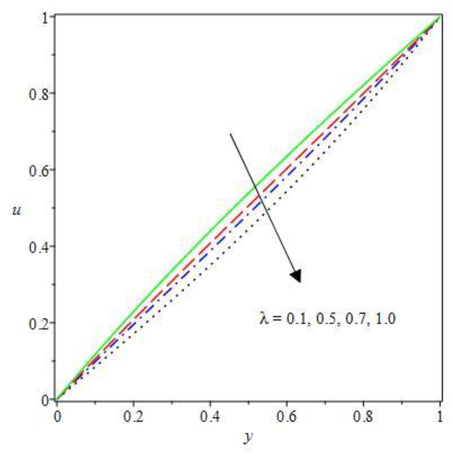
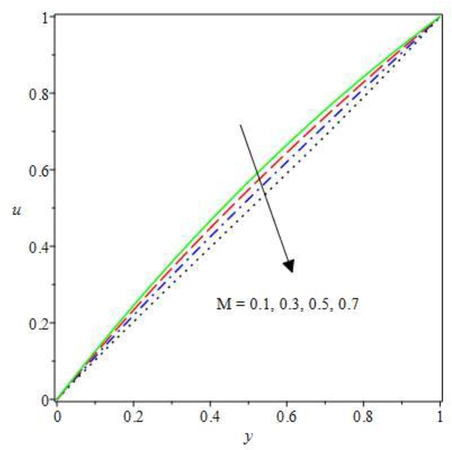
The impact of changing in some pertinent thermofluid terms on the Oldroyd fluid flow rate and heat diffusion fields are demonstrated in Figs. 2 to 10. The effect of dilatant term ${\psi }_1$ and pseudoplastic term ${\psi }_2$ on the non-Newtonian flow velocity are depicted in Figs. 2 and 3. The dilatant term (Fig. 2) which defined the shear thickness, increases the material viscosity correspondingly to the rising shear strain rate, as such, the liquid molecular bond is enhanced. As a result of the enriched shear thickness, there is reduction in the flow velocity magnitude due to complete restriction in the fluid particles motion. Meanwhile, the pseudoplastic term in Fig. 3 causes overall weakening of the fluid material shear, this thereby stimulates the bimolecular reaction kinetics that resulted in rising flow rate. As observed, the fluid viscosity reduces against the increasing shear rate by inspiring fluid particles collision. Therefore, the molecular reaction diffusion is encouraged and the velocity field is increased. In Figs. 4 and 5, the impact of increasing magnetic term $M$ and electric field loading $\lambda$ on the flow velocity magnitude is demonstrated. The magnetic term $M$ stimulates Lorentz force that resist free Oldroyd 8-constant molecular collision, and in turn decreases the flow rate as depicted in Fig. 4. While in Fig. 5, electric charge surrounds the current carrying non-Newtonian fluid particles to exert a repelling force on the other fluid charge fields which therefore causes the flow rate to decline. The electric field loading is obtained from the magnetic field with varying temperature dependent which encourages attraction of chemical molecular bonding. Therefore, as the fluid particle bonding attraction rises the velocity of the flowing Oldroyd fluid decreases under the influence of wall cooling convection.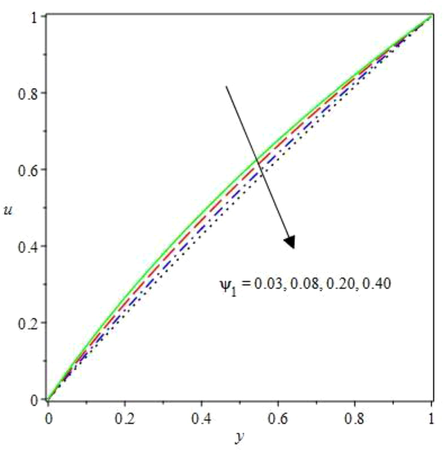

Close

Fig. 2

Velocity distribution for varying. ${\psi }_1$ .

Export to PPT

Close

Fig. 3

Flow rate profile for rising. ${\psi }_2$ .

Export to PPT

Close

Fig. 4

Variation $M$ on the fluid flow rate.

Export to PPT

Close

Fig. 5

Rising effect of $\lambda$ on the velocity field.

Export to PPT

Close

Fig. 6

Temperature field for rinsing $\lambda$ .

Export to PPT

Close

Fig. 7

Rising effect of $\varphi$ on the energy field.

Export to PPT

Close

Fig. 8

Reaction of heat field to rising $\mathit{Br}$ .

Export to PPT

Close

Fig. 9

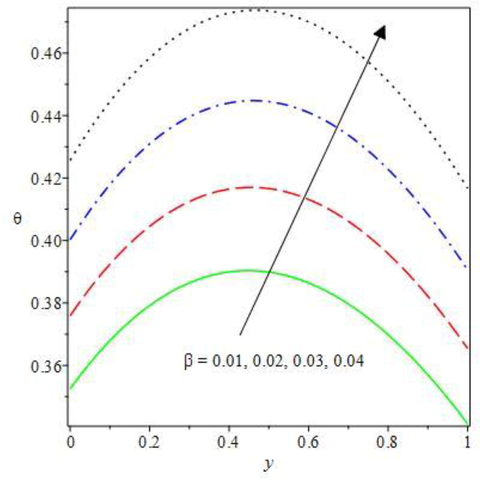
Impact of $\beta$ on the temperature field.

Export to PPT

Close

Fig. 10

Effect of ${\psi }_1$ on the entropy generation.

Export to PPT

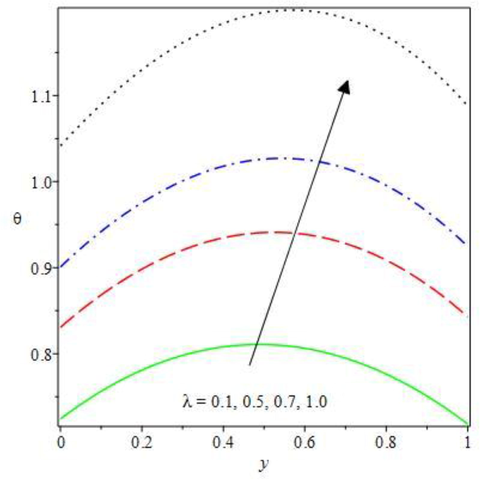
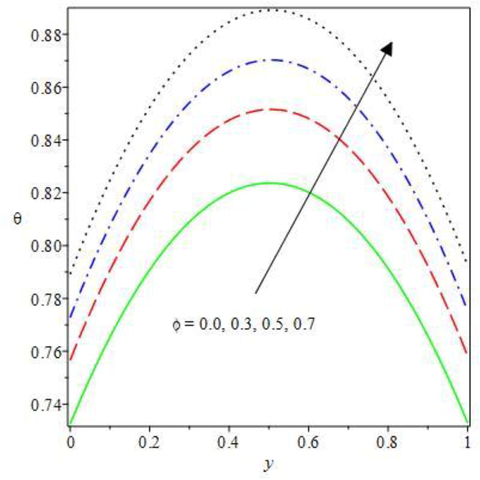
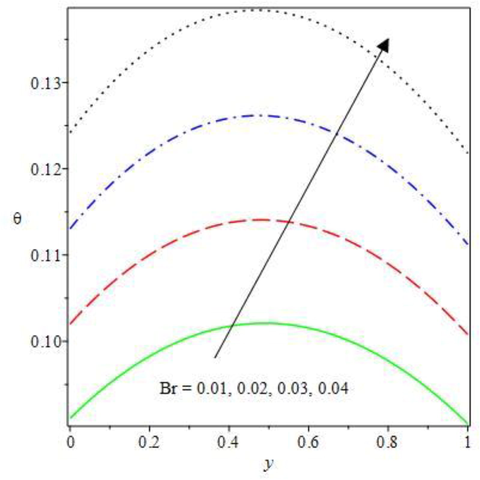
Temperature field for rising effect of different thermodynamic physical parameters are shown in Figs. 6 to 9. The plot of $\theta (y)$ against the monotonically rise in the dependent variable for increasing values of $\lambda ,\varphi ,Br$ and $\beta$ are presented. All the terms served as a strong heat generation in a double exothermic reaction regime to increase the heat transfer and diffusion of Oldroyd 8-constant reactive species. The electric field loading term $\lambda$ in Fig. 6 emboldens Lorentz force that in turn boosted the fluid friction, therefore, heat source is stimulated by the viscous friction. As detected, the temperature distribution in the convective medium is enhanced. The impact of exothermic second step term $\varphi$ is offered in Fig. 7 under the bimolecular kinetics for rising function $y.$ In the system, the combustion reaction is enthused by increasing exothermic heat distribution as the second step term values is outstretched. As such, to reduce toxic discharge that pollute the environment, double reaction diffusion in a combustive system should be encouraged. Also, as realized in Fig. 8, Brinkman term $\mathit{Br}$ increases heat generation in the reactive system by breaking the species molecular attraction force. The loss of species bonding strength causes the fluid molecules to collide dynamically which leads to rising stimulation of exothermic reaction. This thereby stir molecular dispersion and causes cumulative temperature distribution. A consequential rise in the heat transfer is observed for mounting Frank-Kamenetskii term $\beta$ in Fig. 9. The term is known as a robust heat source term in a combustion reaction that inspired viscous heating and diffusion reaction. Therefore, the Frank Kamenetskii term must be controlled and well checked to circumvent Oldroyd 8-constant reactive species solution blowup. Hence, the temperature field upsurges with corresponding rise in the computing values of the parameter $\beta .$

4.2

4.2 Entropy generation and current density profiles for different parameters

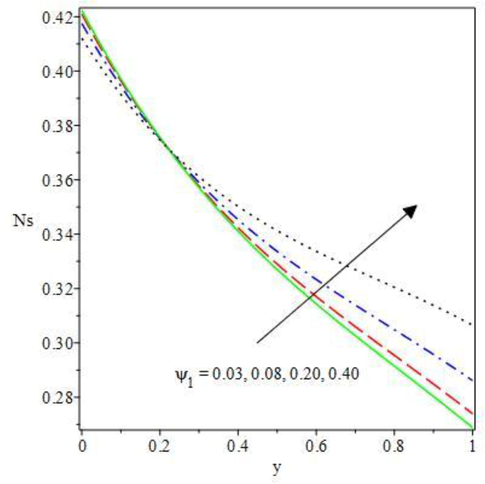
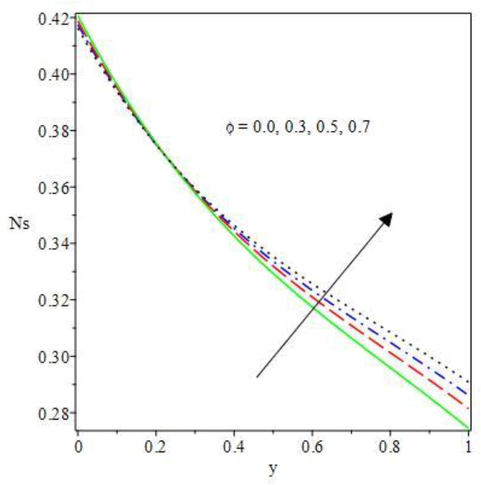
The graphical results of the entropy generation for the energy conservation and optimization, and the current density for the magneto-Oldroyd 8-constant liquid are untaken in Figs. 10 to 17. In Figs. 10 to 13, the thermodynamic second law has been used to study the irreversibility processes due to energy loss in a dynamical system that leads to entropy generation. The material parameters ${\psi }_1$ and ${\psi }_2$ in Figs. 10 and 11 encourages irreversibility process due to fluid flow friction and higher ambient heat exchange that leads to increasing entropy generation in an exothermic combustible reaction. Rising heat transfer occurs in enabling optimal flow architecture which causes high energy diffusion and dissipation to the surroundings, as such, an expanding entropy profiles are observed. Therefore, lower measureable material should be considered to improve convectional industrial output and minimized energy decay. Due to the flow being driven by pressure and finite temperature changes, the fluid molecule disorderliness as a result of heat distribution across the flow regime is augmented as the computational values of the second step reaction $\varphi$ and Frank-Kamenetskii $\beta$ rises, see Figs. 12 and 13. The viscous dissipation is amplified by the rising parameter values which meaningfully raised the entropy magnitude and irreversibility of lost energies. Close to the positive wall convective cooling, the entropy is minimized. Meanwhile, near the middle of the Couette device, entropy generation rises gradually towards the negative upper convective cooling as heat loss is inspired close to the wall. Hence, equal positive wall convective cooling needs to be encouraged to reduce entropy generation and curtail energy decay for optimal industrial productions.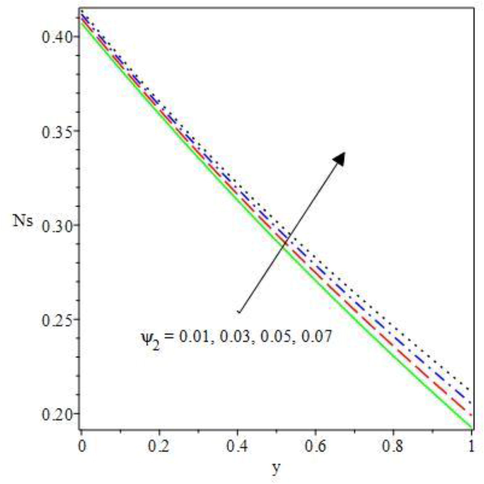

Close

Fig. 11

Irreversibility profile for rising ${\psi }_2$ .

Export to PPT

Close

Fig. 12

Impact of various $\varphi$ on the entropy field.

Export to PPT

Close

Fig. 13

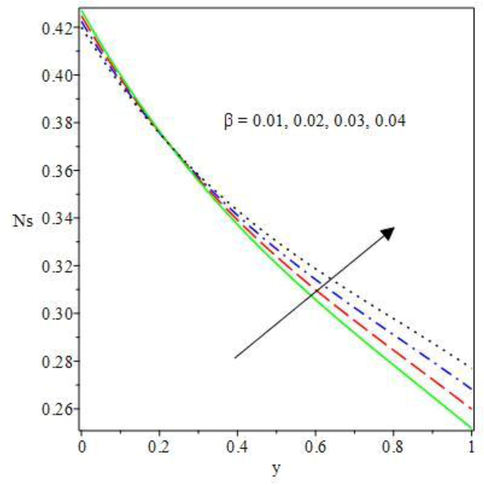
Entropy profile for different $\beta$ .

Export to PPT

Close

Fig. 14

Current density for increasing $r$ .

Export to PPT

Close

Fig. 15

Influence of $\varphi$ on the current density.

Export to PPT

Close

Fig. 16

Plot of current density for different $\mathit{Br}$ .

Export to PPT

Close

Fig. 17

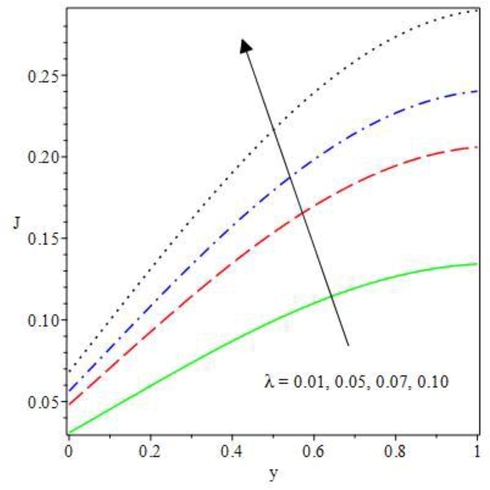
Rising $\lambda$ on the current density.

Export to PPT

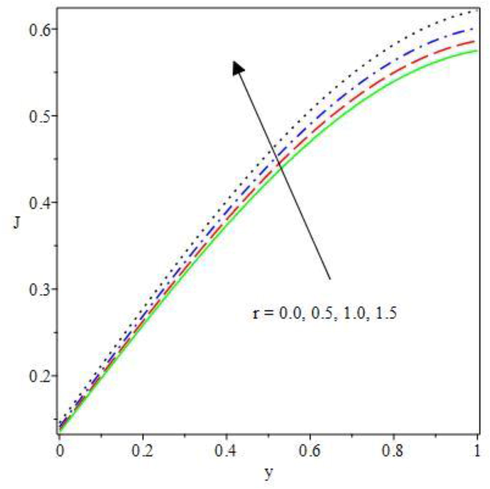
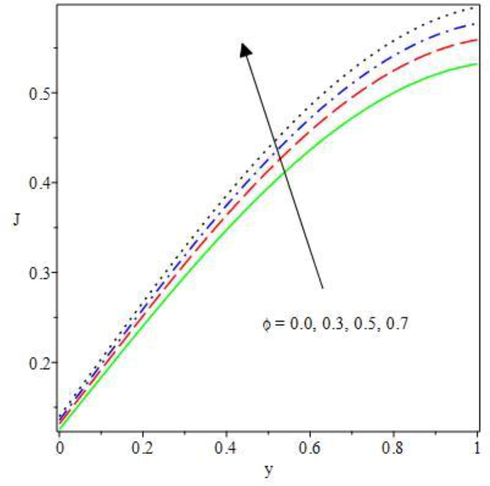
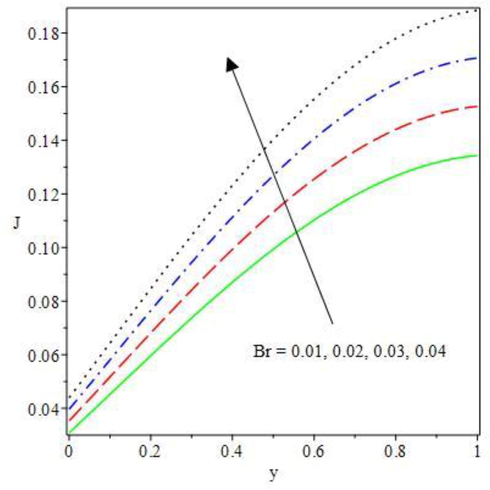
Nevertheless, the sensitivity of current density to variation in the thermodynamic parameters along the monotonically rising dependent function are revealed in Figs. 14 to 17. Flowing through a unit cross sectional region, current density is an electromagnetism that described the bulk of charge per unit time. From Fig. 14, the impact of activation energy ratio $r$ on the conducting fluid current density is shown. The fluid species reaction occur spontaneously as the ratio of the second to the first activation energy is raised, this increase the exothermic reaction that in turn outstretched the conducting fluid motion in the positive charges direction. Therefore, the conducting molecule performance of the thermodynamically non-Newtonian hydromagnetic liquid systems are enhanced as the current density level is increased. The conducting particles of the Oldroyd fluid second step combustion increases the current density field as offered in Fig. 15. As the integrated fluid particles are declined in size, in spite the lesser demand in current by small fluid molecules, high current density trend is observed to have higher fluid particles in a very small chip areas. Hence, at high collisions, the fluid conducting area becomes dominant close to the upper convective wall which raises the current density in this area. As such, the second step parameter $\varphi$ encourages current density profile. Also, a rise in the computational value of Brinkman number $\mathit{Br}$ and temperature dependent electric current loading $\lambda$ cause substantial boost in the current density distributions as depicted in Figs. 16 and 17. As noticed, the conductivity strength of the fluid particles is enriched by the increasing parameters, this thereby raises the current density. The effect is so high, as such, finite positive molecular resistance of electrical conductivity takes place which leads to high heat dissipation. Therefore, current density should be kept at appropriate quantity to prevent the fluid particles from melting by the conductors, or to have desirable fluid properties variation. Hence, the current density magnitude rises as the heat source parameters is upraised.

5 Conclusion

This study investigates the current density and entropy generation by thermodynamic second law of magneto-Oldroyd 8-constant liquid with variable conductivity and convective cooling. The exothermic two step reaction fluid is stimulated by chemical kinetics and driven by pressure gradient in a generalized Couette channel. Analytical solutions of the dimensionless model is taken by partition weighted residual analytical procedures for which the results quantitatively agreed with the numerical stimulation method. As observed, the following are the summary of the results found:

• The dilatant term ${\psi }_1$ increases the fluid viscosity by decreasing the flow rate while pseudoplastic term ${\psi }_2$ served as a monotonically increase function for the flow reaction momentum.

• The material terms raises the thermodynamic equilibrium that leads to reduce energy reversibility and in turn stirred the entropy generation.

• All the energy equation terms serves as a good heat source by strengthening the exothermic molecular heat distribution and diffusion in the channel.

• The current density is enriched by an increase in $r,\varphi ,Br$ and $\lambda$ along the Couette medium that causes rising current carrying conductivity for a bimolecular kinetics.

• The electric field loading and magnetic field increases the liquid molecular bonding force that resulted in velocity field damping.

The outcome of this study will not only assist in improving thermodynamic equilibrium for energy conservation and combustion process, but also compliment the previous studies in relation to exothermic reaction. As such, the study can be extended to other non-Newtonian liquids flow in a cylinder. Lastly, the solution procedures can serve as an operational tool in solving highly nonlinear problem in engineering and sciences.